Skip to main content
SpringerLink
Log in

Nonlinear sloshing of liquid in rigid cylindrical container with a rigid annular baffle: free vibration

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

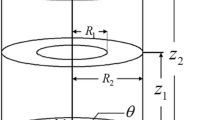
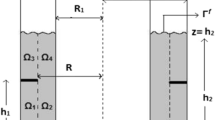
In this paper, the free nonlinear sloshing of liquid in a rigid partially liquid-filled cylindrical container with a rigid annular baffle is investigated. The liquid domain is firstly divided into four simple sub-domains so that the liquid velocity potential in each sub-domain has continuous boundary conditions of class \(\hbox {C}^{1}\). Then, based on the Bateman–Luke variational principle, the equivalent variational formulation of the free boundary problem for the liquid in a baffled container is derived. By introducing the generalized time-dependent coordinates, the surface wave height and the velocity potential are expanded in the form of generalized Fourier series. Substituting the series expression of surface wave height and velocity potential into the variational formulation enables us to obtain the infinite dimensional modal system. Finally, based on the Moiseev asymptotic relations, the infinite dimensional modal system is reduced to a finite dimensional modal system. Good agreements have been achieved by comparing the present results with those obtained from the Gavrilyuk’s solutions. The effects of baffle parameters and initial conditions on the nonlinear sloshing of liquid are discussed in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Mayer, H.C., Krechetnikov, R.: Walking with coffee: Why does it spill? Phys. Rev. E 85, 046117 (2012)

    Article  Google Scholar 

  2. Ibrahim, R.A.: Liquid Sloshing Dynamics: Theory and Applications. Cambridge University Press, Cambridge (2005)

    Book  Google Scholar 

  3. Abramson, H.N.: Slosh suppression. NASA report, SP-8031 (1969)

  4. Lloyd, N., Vaiciurgis, E., Langrish, T.A.G.: The effect of baffle design on longitudinal liquid movement in road tankers: an experimental investigation. Process Saf. Environ. Prot. 80(4), 181–185 (2002)

    Article  Google Scholar 

  5. Abramson, H.N.: The dynamic behavior of liquids in moving containers. NASA report, SP-106 (1966)

  6. Gedikli, A., Ergüven, M.E.: Seismic analysis of a liquid storage tank with a baffle. J. Sound Vib. 223, 141–155 (1999)

    Article  Google Scholar 

  7. Biswal, K.C., Bhattacharyya, S.K., Sinha, P.K.: Free vibration analysis of liquid filled tank with baffles. J. Sound Vib. 259, 177–192 (2003)

    Article  Google Scholar 

  8. Gavrilyuk, I., Lukovsky, I., Trotsenko, Y.: The fluid sloshing in a vertical circular cylindrical tank with an annular baffle Part 1: linear fundamental solutions. J. Eng. Math. 54, 71–88 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  9. Wang, J.D., Lo, S.H., Zhou, D.: Liquid sloshing in rigid cylindrical container with multiple rigid annular baffles: free vibration. J. Fluids Struct. 34, 138–156 (2012)

    Article  Google Scholar 

  10. Wang, J.D., Lo, S.H., Zhou, D.: Sloshing of liquid in rigid cylindrical container with multiple rigid annular baffles: Lateral excitations. J. Fluids Struct. 42, 421–436 (2013)

    Article  Google Scholar 

  11. Celebi, S.M., Akyildiz, H.: Nonlinear modeling of liquid sloshing in a moving rectangular tank. Ocean Eng. 29, 1527–1553 (2002)

    Article  Google Scholar 

  12. Sames, P.C., Marcouly, D., Schellin, T.: Sloshing in rectangular and cylindrical tank. J. Ship Res. 46, 186–200 (2002)

    Google Scholar 

  13. Aliabadi, S., Johnson, A., Abedi, J.: Comparison of finite element and pendulum models for simulation of sloshing. Comput. Fluids 32, 535–545 (2003)

    Article  MATH  Google Scholar 

  14. Moore, R.E., Perko, L.M.: Inviscid fluid flow in an accelerating cylindrical container. J. Fluid Mech. 22, 305–320 (1964)

    Article  Google Scholar 

  15. Perko, L.M.: Large-amplitude motions of liquid–vapour interface in an accelerating container. J. Fluid Mech. 35, 77–96 (1969)

    Article  MATH  Google Scholar 

  16. Chern, M.J., Borthwick, A.G.L., Eatock Taylor, R.: A pseudospectral \(\sigma \)-transformation model of 2-D nonlinear waves. J. Fluid Struct. 13, 607–630 (1999)

    Article  Google Scholar 

  17. La Rocca, M., Sciortino, G., Boniforti, M.A.: A fully nonlinear model for sloshing in a rotating container. Fluid Dyn. Res. 27, 23–52 (2000)

    Article  MATH  Google Scholar 

  18. Shankar, P.N., Kidambi, R.: A modal method for finite amplitude, nonlinear sloshing. Pramana-J. Phys. 59, 631–651 (2002)

    Article  Google Scholar 

  19. Narimanov, G.S.: Movement of a tank partly filled by a fluid: the taking into account of non-smallness of amplitude. J. Appl. Math. Mech. 21, 513–524 (1957)

  20. Ferrant, P., Le Touze, D.: Simulation of sloshing waves in a 3D tank based on a pseudo-spectral method. In: Proceedings of 16th International Workshop on Water Waves and Floating Bodies Hiroshima, Japan (2001)

  21. Moiseev, N.N.: To the theory of nonlinear oscillations of a limited liquid volume of a liquid. J. Appl. Math. Mech. 22, 612–621 (1958)

    Article  MathSciNet  Google Scholar 

  22. Dodge, F.T., Kana, D.D., Abramson, H.N.: Liquid surface oscillations in longitudinally excited rigid cylindrical containers. AIAA J. 3, 685–695 (1965)

    Article  MATH  Google Scholar 

  23. Gavrilyuk, I., Lukovsky, I., Trotsenko, Y., et al.: The fluid sloshing in a vertical circular cylindrical tank with an annular baffle part 2: nonlinear resonant waves. J. Eng. Math. 57, 57–78 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  24. Miles, J.W.: Internally resonant surface waves in a circular cylinder. J. Fluid Mech. 149, 1–14 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  25. Miles, J.W.: Resonantly forced surface waves in a circular cylinder. J. Fluid Mech. 149, 15–31 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  26. Lukovsky, I.A.: Variational method in the nonlinear problems of the dynamics of a limited liquid volume with free surface. In: Oscillations of Elastic Constructions with Liquid, Volna, Moscow, pp. 260–264 (1976)

  27. Miles, J.W.: Nonlinear surface waves in closed basins. J. Fluid Mech. 75, 419–448 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  28. Faltinsen, O.M., Rognebakke, O.F., Lukovsky, I.A., et al.: Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth. J. Fluid Mech. 407, 201–234 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  29. Faltinsen, O.M., Timokha, A.N.: Adaptive multimodal approach to nonlinear sloshing in a rectangular rank. J. Fluid Mech. 432, 167–200 (2001)

    MATH  Google Scholar 

  30. Faltinsen, O.M., Timokha, A.N.: Asymptotic modal approximation of nonlinear resonant sloshing in a rectangular tank with small fluid depth. J. Fluid Mech. 470, 319–357 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  31. Lukovsky, I., Ovchynnykov, D., Timokha, A.: Asymptotic nonlinear multimodal of liquid sloshing in an upright circular tank: 1. Modal equations. Nonlinear Oscil. 14, 512–525 (2012)

    Article  Google Scholar 

  32. Cheng, A.H.D., Cheng, D.T.: Heritage and early history of the boundary element method. Eng. Anal. Bound. Elem. 29(3), 268–302 (2005)

    Article  MATH  Google Scholar 

  33. Thomson, L.M.M.: Theoretical Hydrodynamics. Dover Publications, NY (1996)

    Google Scholar 

  34. Wang, J.D., Zhou, D., Liu, W.Q.: Sloshing of liquid in rigid cylindrical container with a rigid annular baffle. Part I: free vibration. Shock Vib. 19, 1185–1203 (2012)

    Article  Google Scholar 

  35. Hargneaves, R.: A pressure-integral as kinetic potential. Philos. Mag. 16, 436–444 (1908)

    Article  Google Scholar 

  36. Bateman, H.: Partial Differential Equations of Mathematical Physics. Dover Publications, NY (1944)

    MATH  Google Scholar 

  37. Luke, J.C.: A variational principle for a fluid with a free surface. J. Fluid Mech. 27(2), 395–397 (1967)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The financial support from National Natural Science Foundation of China, Grant No. 11172123 is gratefully acknowledged.

Author information

Authors and Affiliations

  1. College of Civil Engineering, Nanjing Tech University, Nanjing, 210009, People’s Republic of China

    D. Zhou, J. D. Wang & W. Q. Liu

Authors
  1. D. Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. D. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. W. Q. Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. Zhou.

Appendices

Appendix 1: Coefficients \(E_{ij}\,(i=1-5, j= 1-7)\) in Eq. (74)

$$\begin{aligned}&E_{11} =E_{21} =\pi \int _0^{r_{2}} {\left. {\varPhi _{11}^{2}} \right| _{z=z_{2}} r\hbox {d}r},\\&E_{12} =E_{22} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{01} \frac{\partial \varPhi _{11}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{13} =E_{23} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{21} \frac{\partial \varPhi _{11}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r} , \\&E_{14} =E_{24} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{3} \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{15} =E_{25} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{01}^{2} \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}}\right) } \right| _{z=z_{2}} r\hbox {d}r} , \\&E_{16} =E_{26} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{21}^{2} \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}}\right) } \right| _{z=z_{2}} r\hbox {d}r},\\&E_{17} =E_{27} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{01} \varPhi _{21} \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}}\right) } \right| _{z=z_{2}} r\hbox {d}r} , \\&E_{31} =\pi \int _0^{r_{2}} {\left. {\varPhi _{01}^{2}}\right| _{z=z_{2}} r\hbox {d}r},\\&E_{32} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{01}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{33} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{01}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{34} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{01}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r}, \\&E_{35} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \varPhi _{01} \frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{36} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \varPhi _{21} \frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}}\right) }\right| _{z=z_{2}} r\hbox {d}r} , \\&E_{37} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{3} \frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{38} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01} \varPhi _{21}^{2} \frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}}\right) }\right| _{z=z_{2}} r\hbox {d}r}, \\&E_{41} =E_{51} =\pi \int _0^{r_{2}} {\left. {\varPhi _{21}^{2}} \right| _{z=z_{2}} r\hbox {d}r},\\&E_{42} =E_{52} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{21}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r} , \\&E_{43} =E_{53} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01} \varPhi _{21} \frac{\partial \varPhi _{21}}{\partial z}}\right) }\right| _{z=z_{2}} r\hbox {d}r},\\&E_{44} =E_{54} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \varPhi _{21} \frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}}\right) } \right| _{z=z_{2}} r\hbox {d}r}, \end{aligned}$$
$$\begin{aligned}&E_{45} =E_{55} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \varPhi _{01} \frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}}\right) } \right| _{z=z_{2}} r\hbox {d}r},\\&E_{46} =E_{56} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \varPhi _{21} \frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}}\right) } \right| _{z=z_{2}} r\hbox {d}r}, \\&E_{47} =E_{57} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{3} \frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}}\right) }\right| _{z=z_{2}} r\hbox {d}r}. \end{aligned}$$

Appendix 2: Coefficients \(H_{i}\,(i=1-28)\) in Eq. (75)

$$\begin{aligned}&H_{1} =\pi \left\{ \int _0^{r_{2}} {\left. {\left[ {\varPhi _{01} \left( {\frac{\partial \varPhi _{11}}{\partial z}}\right) ^{2}}\right] } \right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad +\int _0^{r_{2}} \left. {\left( {\frac{\varPhi _{01} \varPhi _{11}^{2}}{r}}\right) }\right| _{z=z_{2}} \hbox {d}r\\&\quad \left. +\int _0^{r_{2}} {\left. {\left[ {\varPhi _{01} \left( {\frac{\partial \varPhi _{11}}{\partial r}}\right) ^{2}}\right] }\right| }_{z=z_{2}} r\hbox {d}r \right\} ,\\&H_{2} =\frac{\pi }{2}\left\{ \int _0^{r_{2}} {\left. {\left[ {\varPhi _{21} \left( {\frac{\partial \varPhi _{11}}{\partial z}}\right) ^{2}}\right] } \right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad -\int _0^{r_{2}} {\left. {\frac{\varPhi _{11}^{2} \varPhi _{21}}{r}}\right| _{z=z_{2}}} \hbox {d}r\\&\quad \left. +\int _0^{r_{2}} {\left. {\left[ {\varPhi _{21} \left( {\frac{\partial \varPhi _{11}}{\partial r}} \right) ^{2}}\right] }\right| _{z=z_{2}}} r\hbox {d}r \right\} ,\\&H_{3} =\frac{\pi }{4}\left[ 3\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad + \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{3} \frac{\partial \varPhi _{11}}{r\partial z}}\right) }\right| _{z=z_{2}}} \hbox {d}r\\&\quad \left. + 3\int _0^{r_{2}} {\left. {\left( {\frac{\partial \varPhi _{11} }{\partial r}\frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}}\right) } \right| _{z=z_{2}}} \varPhi _{11}^{2} r\hbox {d}r\right] ,\\&H_{4} =\frac{\pi }{4}\left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{11} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad + 3\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{3} \frac{\partial \varPhi _{11}}{r\partial z}} \right) }\right| _{z=z_{2}}} \hbox {d}r \end{aligned}$$
$$\begin{aligned}&\quad \left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{5} =\pi \left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{11} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad +\int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \varPhi _{11} \frac{\partial \varPhi _{11} }{r\partial z}}\right) }\right| _{z=z_{2}} \hbox {d}r} \\&\quad \left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{6} =\frac{\pi }{2}\left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{11} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad +\int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{21}^{2} \frac{\partial \varPhi _{11} }{r\partial z}}\right) }\right| _{z=z_{2}}} \hbox {d}r\\&\quad \left. +\int _0^{r_{2} } {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{7} =\pi \left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{01} \varPhi _{21} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{11} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad -\int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \varPhi _{01} \varPhi _{21} \frac{\partial \varPhi _{11} }{r\partial z}}\right) }\right| _{z=z_{2}}} \hbox {d}r\\&\quad \left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{01} \varPhi _{21} \frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{8} =\frac{\pi }{2}\left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}\frac{\partial \varPhi _{11} }{\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad -\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{3} \frac{\partial \varPhi _{11}}{r\partial z}} \right) }\right| _{z=z_{2}}} \hbox {d}r \end{aligned}$$
$$\begin{aligned}&\quad \left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}\frac{\partial \varPhi _{11}}{\partial r}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{9} =\pi \left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial \varPhi _{01}}{\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\quad \left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \frac{\partial \varPhi _{11}}{\partial r}\frac{\partial \varPhi _{01} }{\partial r}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{10} =\pi \left\{ \int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{01} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}\frac{\partial \varPhi _{01}}{\partial z}\right. \right. \right. \\&\left. \left. \left. +\frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}\right) \right] \right| _{z=h} r\hbox {d}r+\int _0^{r_{2}}\\&\left. {\left. {\left[ {\varPhi _{11} \varPhi _{01} \left( {\frac{\partial ^{2}\varPhi _{11}}{\partial z\partial r}\frac{\partial \varPhi _{01}}{\partial r}+\frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{01}}{\partial z\partial r}}\right) }\right] } \right| _{z=h}} r\hbox {d}r \right\} ,\\&H_{11} =\frac{\pi }{2}\left\{ \int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{21} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}\frac{\partial \varPhi _{01}}{\partial z}\right. \right. \right. \\&\left. \left. \left. +\frac{\partial \varPhi _{11} }{\partial z}\frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}\right) \right] \right| _{z=z_{2}} r\hbox {d}r\\&+\int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{21} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial z\partial r}\frac{\partial \varPhi _{01}}{\partial r}\right. \right. \\&\left. \left. \left. \left. +\frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{01}}{\partial z\partial r} \right) \right] \right| _{z=z_{2}} r\hbox {d}r \right\} ,\\&H_{12} =\frac{\pi }{2}\left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \frac{\partial \varPhi _{11}}{\partial z}\frac{\partial \varPhi _{21}}{\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&+\, 2\int _0^{r_{2}} {\left. {\left( {\frac{\varPhi _{11}^{2} \varPhi _{21}}{r}}\right) }\right| _{z=z_{2}}} \hbox {d}r\\&\left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{11} \frac{\partial \varPhi _{11}}{\partial r}\frac{\partial \varPhi _{21}}{\partial r}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{13} =\frac{\pi }{2}\int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{01} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}\frac{\partial \varPhi _{21}}{\partial z}\right. \right. \\&\left. \left. \left. \quad +\frac{\partial \varPhi _{11}}{\partial z}\frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}\right) \right] \right| _{z=z_{2}} r\hbox {d}r\\&\qquad \!\!+\pi \int _0^{r_{2}} \left[ \frac{\varPhi _{11} \varPhi _{01}}{r}\left( \varPhi _{21} \frac{\partial \varPhi _{11}}{\partial z}\right. \right. \end{aligned}$$
$$\begin{aligned}&\left. \left. \left. \quad +\varPhi _{1} \frac{\partial \varPhi _{21}}{\partial z}\right) \right] \right| _{z=z_{2}} \hbox {d}r\\&\qquad \!\!+\frac{\pi }{2}\int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{01} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}\frac{\partial \varPhi _{21}}{\partial r}\right. \right. \\&\left. \left. \left. \quad +\frac{\partial \varPhi _{11}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}\right) \right] \right| _{z=z_{2}} r\hbox {d}r,\\&H_{14} =\frac{\pi }{2}\left\{ \int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{21} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial z^{2}}\frac{\partial \varPhi _{21}}{\partial z}\right. \right. \right. \\&\left. \left. \left. \quad +\frac{\partial \varPhi _{11} }{\partial z}\frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}\right) \right] \right| _{z=h} r\hbox {d}r\\&\quad \,\,+\int _0^{r_{2}} \left[ \varPhi _{11} \varPhi _{21} \left( \frac{\partial ^{2}\varPhi _{11}}{\partial r\partial z}\frac{\partial \varPhi _{21}}{\partial r}\right. \right. \\&\left. \left. \left. \left. \quad +\frac{\partial \varPhi _{11} }{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}\right) \right] \right| _{z=h} r\hbox {d}r \right\} , \end{aligned}$$
$$\begin{aligned}&H_{15} =\pi \int _0^{r_{2}} \left( \varPhi _{21}^{2} \varPhi _{11} \frac{\partial \varPhi _{11}}{r\partial z}\right. \\&\left. \left. +\, \varPhi _{11}^{2} \varPhi _{21} \frac{\partial \varPhi _{21}}{r\partial z}\right) \right| _{z=z_{2}} \hbox {d}r,\\&H_{16} =2\pi \left\{ \int _0^{r_{2}} \left. \left[ \varPhi _{01} \left( {\frac{\partial \varPhi _{01}}{\partial z}}\right) ^{2}\right] \right| _{z=h_{2}} r\hbox {d}r\right. \\&\left. +\int _0^{r_{2}} {\left. {\left[ {\varPhi _{01} \left( {\frac{\partial \varPhi _{01}}{\partial r}}\right) }\right] ^{2}} \right| _{z=h_{2}}} r\hbox {d}r \right\} ,\\&H_{17} =\pi \left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{01}}{\partial z}\frac{\partial ^{2}\varPhi _{01} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{01}}{\partial r}\frac{\partial ^{2}\varPhi _{01}}{\partial r\partial z}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{18} =2\pi \left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{01}}{\partial r}\frac{\partial ^{2}\varPhi _{01} }{\partial r\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{01}}{\partial r}\frac{\partial ^{2}\varPhi _{01}}{\partial r\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{19} =\pi \left[ \int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{01}}{\partial z}\frac{\partial ^{2}\varPhi _{01} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\right. \\&\left. +\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{01}}{\partial r}\frac{\partial ^{2}\varPhi _{01}}{\partial r\partial z}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\right] ,\\&H_{20} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{21} \frac{\partial \varPhi _{01}}{\partial z}\frac{\partial \varPhi _{21}}{\partial z}}\right) } \right| _{z=z_{2}}} r\hbox {d}r\\&+\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{21} \frac{\partial \varPhi _{01}}{\partial r}\frac{\partial \varPhi _{21} }{\partial r}}\right) }\right| _{z=z_{2}}} r\hbox {d}r,\\&H_{21} =\frac{\pi }{4}\left[ \int _0^{r_{2}} \left( \varPhi _{11}^{2} \frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}\frac{\partial \varPhi _{21}}{\partial z}\right. \right. \\&\left. \left. + \varPhi _{11}^{2} \frac{\partial \varPhi _{01}}{\partial z}\frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}\right) \right| _{z=z_{2} } r\hbox {d}r\\&+ \int _0^{r_{2}} \left( \varPhi _{11}^{2} \frac{\partial ^{2}\varPhi _{01}}{\partial r\partial z}\frac{\partial \varPhi _{21}}{\partial r}\right. \\&\left. \left. \left. +\varPhi _{11}^{2} \frac{\partial \varPhi _{01}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}\right) \right| _{z=z_{2}} r\hbox {d}r\right] ,\\&H_{22} =\pi \int _0^{r_{2}} \left[ \varPhi _{01} \varPhi _{21} \left( \frac{\partial ^{2}\varPhi _{01}}{\partial z^{2}}\frac{\partial \varPhi _{21} }{\partial z}\right. \right. \end{aligned}$$
$$\begin{aligned}&\left. \left. \left. +\frac{\partial \varPhi _{01}}{\partial z}\frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}\right) \right] \right| _{z=z_{2}} r\hbox {d}r+\pi \int _0^{r_{2}}\\&{\left. {\left[ {\varPhi _{01} \varPhi _{21} \left( {\frac{\partial ^{2}\varPhi _{01}}{\partial r\partial z}\frac{\partial \varPhi _{21}}{\partial r}+\frac{\partial \varPhi _{01}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}}\right) }\right] }\right| _{z=z_{2}} } r\hbox {d}r,\\&H_{23} =\pi \int _0^{r_{2}} {\left. {\left[ {\varPhi _{01} \left( {\frac{\partial \varPhi _{21}}{\partial z}}\right) ^{2}}\right] } \right| _{z=z_{2}}} r\hbox {dr}\\&+\, 4\pi \int _0^{r_{2}} {\left. {\left( {\frac{\varPhi _{01} \varPhi _{21}^{2}}{r}}\right) }\right| _{z=z_{2}}} \hbox {dr}\\&+\, \pi \int _0^{r_{2}} {\left. {\left[ {\varPhi _{01} \left( {\frac{\partial \varPhi _{21}}{\partial r}}\right) ^{2}}\right] } \right| _{z=z_{2}}} r\hbox {dr},\\&H_{24} =\frac{\pi }{2}\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{21}}{\partial z}\frac{\partial ^{2}\varPhi _{21} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\\&+ 2\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \varPhi _{21} \frac{\partial \varPhi _{21}}{\partial z}}\right) }\right| _{z=z_{2}}} \frac{\hbox {d}r}{r}\\&+ \frac{\pi }{2}\int _0^{r_{2}} {\left. {\left( {\varPhi _{11}^{2} \frac{\partial \varPhi _{21}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r,\\&H_{25} =\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{21}}{\partial z}\frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}} \right) }\right| _{z=z_{2}}} r\hbox {d}r\\&+ 4\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \varPhi _{21} \frac{\partial \varPhi _{21}}{r\partial z}} \right) }\right| _{z=z_{2}}} \hbox {d}r\\&+ \pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{01}^{2} \frac{\partial \varPhi _{21}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r,\\&H_{26} =\frac{3\pi }{4}\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{21}}{\partial z}\frac{\partial ^{2}\varPhi _{21} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\\&+ \pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{3} \frac{\partial \varPhi _{21} }{r\partial z}}\right) }\right| _{z=z_{2}}} \hbox {d}r\\&+ \frac{3\pi }{4}\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{21}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}} \right) }\right| _{z=z_{2}}} r\hbox {d}r,\\&H_{27} =\frac{\pi }{4}\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{21}}{\partial z}\frac{\partial ^{2}\varPhi _{21} }{\partial z^{2}}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\\&+ 3\pi \int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{3} \frac{\partial \varPhi _{21} }{r\partial z}}\right) }\right| _{z=z_{2}}} \hbox {d}r\\&+ \frac{\pi }{4}\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial \varPhi _{21}}{\partial r}\frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}} \right) }\right| _{z=z_{2}}} r\hbox {d}r, \end{aligned}$$
$$\begin{aligned}&H_{28} =\frac{\pi }{2}\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial ^{2}\varPhi _{21}}{\partial z^{2}}\frac{\partial \varPhi _{21} }{\partial z}}\right) }\right| _{z=z_{2}}} r\hbox {d}r\\&- 2\pi \int _0^{r_{2}} \left. {\left( {\varPhi _{21}^{3} \frac{\partial \varPhi _{21}}{r\partial z}} \right) }\right| _{z=z_{2}} \hbox {d}r\\&+ \frac{\pi }{2}\int _0^{r_{2}} {\left. {\left( {\varPhi _{21}^{2} \frac{\partial ^{2}\varPhi _{21}}{\partial r\partial z}\frac{\partial \varPhi _{21}}{\partial r}}\right) } \right| _{z=z_{2}}} r\hbox {d}r. \end{aligned}$$

Appendix 3: Coefficients \(D_{i}\,(i=1-12)\) in Eq. (77)

$$\begin{aligned}&D_{1} =\frac{E_{11}}{H_{a}}, \quad D_{2} =\frac{E_{12} H_{a} -E_{11} H_{1}}{H_{a}^{2}}, \\&D_{3} =\frac{E_{12} H_{b} -E_{31} H_{9}}{H_{a} H_{b}}, \quad D_{4} =\frac{E_{13} H_{a} -2E_{11} H_{2}}{2H_{a}^{2}},\\&vD_{6} =\frac{4E_{11} H_{9}^{2} H_{c} -4E_{32} H_{\hbox {9}} H_{a} H_{c} \hbox {+8}E_{11} H_{\hbox {12}}^{2} H_{b} -4E_{42} H_{12} H_{a} H_{b} -8E_{11} H_{3} H_{b} H_{c} +3E_{14} H_{a} H_{b} H_{c}}{8H_{a}^{2} H_{b} H_{c}},\\&D_{5} =\frac{E_{13} H_{b} -2E_{41} H}{2H_{a} H_{c}}, \\&D_{7} =\frac{8E_{11} H_{12}^{2} -4E_{42} H_{12} H_{a} -8E_{11} H_{4} H_{c} +E_{14} H_{a} H_{c}}{8H_{a}^{2} H_{c}},\\&D_{8} =\frac{2E_{11} H_{9}^{2} -2E_{32} H_{9} H_{a} -4E_{11} H_{8} H_{b} +E_{14} H_{a} H_{b}}{4H_{a}^{2} H_{b}}, \\&D_{9} =\frac{E_{31}}{H_{b}},\\&D_{10} =\frac{E_{32} H_{a} -E_{11} H_{9}}{2H_{a} H_{b}}, \quad D_{11} =\frac{E_{41}}{H_{c}}, \\&D_{12} =\frac{E_{42} H_{a} -2E_{11} H_{12}}{2H_{a} H_{c}}. \end{aligned}$$

Appendix 4: Coefficients \(K_{i}\,(i =1-10)\) in Eq. (78)

$$\begin{aligned}&K_{1} =\frac{2H_{3} D_{1}^{2} +4E_{11} D_{6} +2E_{32} D_{10} +E_{42} D_{12} +2H_{9} D_{1} D_{9} +2H_{12} D_{1} D_{12}}{2E_{11} D_{1}},\\&K_{2} =\frac{E_{14}D_{1} +8E_{11}D_{7} +4E_{42}D_{12}}{8E_{11} D_{1}}, \\& K_{3} =\frac{E_{11}D_{3} +E_{32}D_{9}}{E_{11} D_{1}}, K_{4} =\frac{E_{13}D_{1} +2E_{11}D_{4}}{2E_{11} D_{1}},\\&K_{5} =\frac{E_{11}D_{2} +E_{12}D_{1}}{E_{11} D_{1}}, \\&K_{6} =\frac{E_{13}D_{1} +2E_{11}D_{4}}{2E_{11} D_{1}}, \quad K_{7} =-\frac{H_{2}D_{1}^{2} +2E_{41}D_{12}}{2E_{41} D_{11}},\\&K_{8} =-\frac{H_{1}D_{1}^{2} +4E_{31}D_{10}}{4E_{31} D_{9}},\\&K_{9} =-\frac{E_{13}D_{1} +2E_{41}D_{12}}{2E_{41} D_{11}}, \quad K_{10} =-\frac{E_{12}D_{1} +2E_{31}D_{10}}{2E_{31} D_{9}}. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, D., Wang, J.D. & Liu, W.Q. Nonlinear sloshing of liquid in rigid cylindrical container with a rigid annular baffle: free vibration. Nonlinear Dyn 78, 2557–2576 (2014). https://doi.org/10.1007/s11071-014-1610-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1610-z

Keywords

Search

Navigation