1 Introduction

The subject of mathematical ecology was started by the pioneering work of Lotka [1] and Volterra [2] and since then many models of ecological food-chains have been proposed [3]. The topological behaviour of food-chain models [4–7] depends upon the values of the various biological parameters involved in the model. Food-chain models with constant parameters are often found to approach a steady state in which the species coexist in equilibrium. However, if parameters are changed, sudden, discontinuous transitions to other types of dynamical behaviour may occur, i.e. the topological behaviour of the model is changed. The critical parameter values at which such transitions happen are called bifurcation points. Typical examples of bifurcations are the Hopf bifurcation which corresponds to the transition from stationary to oscillatory behaviour or the transcritical bifurcation in which two steady states meet and exchange their stability.

Almost all food-chain models have bifurcation phenomena [8–12], but it is not necessary that the systems have bifurcation phenomena with respect to all the biological parameters involved in the systems. In a bifurcation, the topological behaviour of the food-chain model changes completely. From an ecological point of view, bifurcations endanger the existence of a particular species in the food-chain. A steady state that undergoes a bifurcation will in general either lose its stability or disappear entirely. Beyond the bifurcation, the system will approach some other attractor on which the long-term dynamics will be either stationary, periodic, quasi-periodic, or chaotic. Even if the food-chain ends up in another steady state, the transition to that state will often involve the extinction of one or more levels of the food-chain. On the other hand, the entire food-chain may be encountered, which ultimately leads to local extinction of species.

In order to preserve the system under consideration in its natural state, crossing bifurcations should be avoided. Since the natural influence cannot be prevented altogether, importance must be given to determine the critical parameter values at which bifurcations occur. Knowing these, the risk induced by disturbing the system can be assessed. Bifurcations have been computed for many specific models of different complexity. In ecosystem modelling, complex models are often required to describe a given natural system realistically. However, in order to understand the general mechanisms leading to bifurcations in ecosystems, much simpler, conceptual models are needed.

In this paper, we consider a predator–prey model with Holling type-II functional response and the presence of a super predator. It is assumed that the super predator is not dynamic, but its effect is maintained at a specific constant level (this may be happening due to human consumption, etc.). The advantage of this approach is that it reduces the dimension of the system from three to two and allows the phase plane analysis for the considered system. Here we analyse the dynamics of this model in a systematic manner. We also investigate the consequences of the presence of a super predator to the predator–prey dynamics. From the study, it is possible to develop management strategies that manipulate the rate of consumption of predators for the benefit of biological control.

Let us consider the following predator–prey model given by

$$ \begin{aligned} \frac{dN}{dt}&= rN \biggl(1- \frac{N}{K} \biggr)-\frac{cNP}{a+N}, \\ \frac{dP}{dt}&= \frac{\alpha cNP}{a+N}-eP, \end{aligned} $$
(1)

where r and K respectively represent the intrinsic growth rate and carrying capacity of the prey; e is the death rate of the predator in the absence of prey; c and a are respectively the maximum rate of predation and half saturation value of the predator. System (1) is well studied and analysed from various perspectives [13]. The stability of the interior equilibrium (N,P) of system (1) depends on its position relative to the hump of the prey isocline. If the equilibrium point lies to the right (left) of this hump, then the equilibrium is asymptotically stable (unstable). Also, we know that a stable limit cycle exists about its unstable equilibrium and its amplitude increases as the equilibrium moves towards the P-axis. Now, let us consider the presence of a super predator by the term \(\frac{dP}{b+P}\). Thus we have the following coupled differential system representing predator–prey dynamics in the presence of a super predator:

$$ \begin{aligned} \frac{dN}{dt}&= rN \biggl(1- \frac{N}{K} \biggr)-\frac{cNP}{a+N}, \\ \frac{dP}{dt}&= \frac{\alpha cNP}{a+N}-\frac{dP}{b+P}-eP, \end{aligned} $$
(2)

where d is the maximum consumption rate of the super predator. Now, we shall analyse the dynamics of system (2) and study its controllability. To reduce the number of parameters, we non-dimensionalize system (2) using the transformations

$$ N=Ku,\qquad P=\frac{rK}{c}v\quad\text{and}\quad t=\frac{\tau}{r}, $$

and obtain the transformed system as follows:

$$ \begin{aligned} \frac{du}{dt}&=u(1-u)- \frac{uv}{m+u}, \\ \frac{dv}{dt}&=\frac{nuv}{m+u}-\frac{lv}{s+v}-hv, \end{aligned} $$
(3)

with

$$ u(0)\geq0,\qquad v(0)\geq0, $$
(4)

and

$$\begin{aligned} &{m=\frac{a}{K},\qquad n=\frac{c\alpha}{r},\qquad l= \frac{cd}{Kr^{2}},} \\ &{s=\frac {bc}{Kr},\qquad h=\frac{e}{r}.} \end{aligned}$$

The paper is organized as follows. General phase portrait analysis of the system is carried out in Sect. 2. In this section, we study all the possible equilibria and their stability, and possible bifurcation depending on same vital parameters of the system. In Sect. 3, we study parametric bifurcations of the model taking two parameters, n and l as the bifurcation parameters by numerical simulations. The paper ends with a brief conclusion in Sect. 4.

2 General phase portrait analysis

In this section, we analyse the model system (3) and draw some conclusions regarding the asymptotic behaviour of its trajectories. Clearly, the equilibrium points E 0(0,0) and E 1(1,0) exist for all permissible parameters. The equilibrium of the greatest interest would be an equilibrium interior to the first quadrant, so we seek conditions for such an equilibrium to exist. Let E ∗(u ∗,v ∗) be the interior equilibrium point, where v ∗ is given by

$$ v^{*}=\bigl(m+u^{*}\bigr) \bigl(1-u^{*} \bigr), $$
(5)

and u ∗ is the positive root of the following equation

$$ f(u)\equiv\theta_1 u^{3}+\theta_2 u^{2}+\theta_3 u+\theta_4=0, $$
(6)

with

$$ \begin{aligned} \theta_{1}&=n-h, \\ \theta_{2}&=h+mn-n-2hm, \\ \theta_{3}&=l+hs+2hm-ns-mn-hm^{2}, \\ \theta_{4}&=hm(m+s)+lm. \end{aligned} $$
(7)

From (5), it is clear that for v ∗ to be positive, u ∗ must be less than unity. Also we assume that n, the consumption rate of prey by the predator, must be greater than the value of h, the death rate of predator. By this assumption, we make θ 1>0 and obviously θ 4>0. The sign of θ 2 and θ 3 depends on the different values of the parameters involved in the system. By Descartes’ rule of sign, (6) has either two positive roots or no positive root. Our aim is to find the positive roots of (6) which lie between 0 and 1. So we have the following theorem.

Theorem 2.1

(i) If \(0<l<(\frac{n}{1+m}-h)s\) and f(Φ)>0, where Φ is a real number, then (6) has one root between 0 and 1. (ii) If \(l>(\frac{n}{1+m}-h)s\), then (6) has either no root or two roots lying between 0 and 1.

Proof

(i) Here we see that f(0)=θ 4>0 and f(1)=l(1+m)−s(n−h)+mhs. If f(1)<0, i.e. if \(0<l<(\frac{n}{1+m}-h)s\), then by the Bolzano theorem, we can say that (6) has either one or an odd number of roots lying between 0 and 1. Now let Φ be a real number. If f(Φ)>0, then by the Bolzano theorem (6) has one root between 1 and Φ. So in this case, the root lying between 0 and 1 is unique and the model (3) has a unique positive interior equilibrium.

(ii) Now \(l>(\frac{n}{1+m}-h)s\) means f(1)>0, f(0)>0 by the construction of the function f(u). Hence by the Bolzano theorem, (6) has either no roots or two roots lying between 0 and 1. In this case, model (3) has either no positive interior equilibrium or two positive interior equilibrium points. This completes the proof of the theorem. □

Figure 1(a) shows the existence of a unique interior equilibrium point for the parametric values m=0.4;n=2;l=0.2;s=0.3;h=0.6. In this case, the values of \(s(\frac{n}{1+m}-h)\) and f(Φ) are 0.248571 and 5.856, respectively, for Φ=2 which satisfies condition (i) of Theorem 2.1. Figure 1(b) shows the existence of two positive interior equilibrium points for the parametric values m=0.5;n=2;l=0.3;s=0.3;h=0.6. Here the values of \(s(\frac{n}{1+m}-h)\) and f(Φ) are 0.22 and 6.25, respectively, for Φ=2 which satisfies condition (ii) of Theorem 2.1.

Fig. 1
figure 1

The existence of positive interior equilibria for two different parameter sets

Full size image

From Fig. 2(a) we see that presence of the super predator increases the level of prey population when l increases. After some value of l, we see that values of u ∗ increase asymptotically below its carrying capacity. On the other hand, from Fig. 2(b), the presence of the super predator term initially increase the value of v ∗, but after some value of l∈(0.2−ϵ,0.2+ϵ), say l max, v ∗ decreases rapidly after that value (see Fig. 2(b)) and ultimately goes extinct.

Fig. 2
figure 2

Variation of prey (a) and predator (b) population at equilibrium with respect to l. The values of the parameters are m=0.4;n=2;s=0.3;h=0.6

Full size image

In order to analyse the nature of the paths of system (3), we need to evaluate the associated Jacobian at each of the above equilibrium points, which is given by

$$\begin{aligned} J(u,v)=\left ( \begin{array}{c@{\quad}c} 1-2u-\frac{mv}{(m+u)^{2}}& -\frac{u}{m+u}\\ \frac{mnv}{(m+u)^{2}}&\frac{nu}{m+u}-\frac{ls}{(s+v)^{2}}-h \end{array} \right ). \end{aligned}$$
(8)

Theorem 2.2

The equilibrium point E 0(0,0) is unstable.

Proof

At the equilibrium point E 0(0,0), the eigenvalues of the matrix (8) are λ 01=1 and \(\lambda_{02}=-\frac {l}{s}-h\). Hence the equilibrium point E 0(0,0) is a saddle point, and system (3) is unstable in the neighbourhood of E 0(0,0). □

Theorem 2.3

If \(0<l<s(\frac{n}{1+m}-h)\), then the equilibrium point E 1(1,0) of system (3) is unstable; and if \(l>s(\frac{n}{1+m}-h)\), then the equilibrium point E 1(1,0) of system (3) is asymptotically stable.

Proof

At the boundary equilibrium point E 1(1,0), the eigenvalues of the matrix (8) are λ 11=−1 and \(\lambda_{12}=\frac {n}{1+m}-\frac{l}{s}-h\). Now if \(\frac{n}{1+m}-h>0\), then two cases happen:

(i) If \(0<l<s(\frac{n}{1+m}-h)\), then the equilibrium point E 1(1,0) of (3) is a saddle point and it is unstable. In this case, system (3) has unique positive interior equilibrium.

(ii) If \(l>s(\frac{n}{1+m}-h)\), then the equilibrium point E 1(1,0) of (3) is a node and it is asymptotically stable. In this case, system (3) has either no positive equilibrium or two positive interior equilibria.

If \(\frac{n}{1+m}-h<0\), then the equilibrium point is asymptotically stable. □

At the interior equilibrium point E ∗(u ∗,v ∗), the Jacobian matrix is

$$\begin{aligned} J\bigl(u^{*},v^{*}\bigr)=\left ( \begin{array}{c@{\quad}c} -u^{*}+\frac{u^{*}v^{*}}{(m+u^{*})^{2}} & -\frac{u^{*}}{m+u^{*}} \\ \frac{mnv^{*}}{(m+u^{*})^{2}} & \frac{lv^{*}}{(s+v^{*})^{2}} \end{array} \right ). \end{aligned}$$
(9)

The characteristic equation is

$$ \lambda^{2}-A\lambda+B=0, $$
(10)

where

$$ \begin{aligned} A&=\mathrm{Trace}\bigl(J \bigl(u^{*},v^{*}\bigr)\bigr), \\ B&=\mathrm{Det}\bigl(J\bigl(u^{*},v^{*}\bigr)\bigr). \end{aligned} $$
(11)

The stability of the interior equilibrium point E ∗(u ∗,v ∗) depends on the sign of the trace and the determinant of the Jacobian matrix J(u ∗,v ∗). Here are the different cases.

Case (a):

If Trace(J)<0 and Det(J)>0, then E ∗(u ∗,v ∗) is a stable node or a stable spiral.

Case (b):

If Trace(J)>0 and Det(J)>0, then E ∗(u ∗,v ∗) is an unstable node or an unstable spiral.

Case (c):

If Det(J)<0, then E ∗(u ∗,v ∗) is a saddle point.

Case (d):

If Trace(J)=0, Det(J)>0 then there are some limit cycles around E ∗(u ∗,v ∗).

In Case (d), system (3) goes to a Hopf bifurcation. In that case, the characteristic (10) has two purely imaginary roots. Let us call them λ 1,2=±iω. Here we take the super predator consumption rate l as a bifurcation parameter. To calculate the value(s) of l, we consider the system of equations \(\dot{u}=0, \dot{v}=0\) and Trace(J)=0. Here we see that the expressions for Trace(J) and Det(J) do not explicitly depend on n and l, and it is impossible to derive some conditions depending on n and l. So alternatively we can show the sign of Trace(J) and Det(J) by taking some numerical values of the parameters and drawing the graphs of Trace(J) and Det(J) in the plane of l−n.

In Figs. 3 and 4, we see that the values of Trace(J) and Det(J) can be both positive and negative when l and n vary. Thus the cases we consider above are tenable.

Fig. 3
figure 3

Plot of Trace(J) in the l–n plane

Full size image
Fig. 4
figure 4

Plot of Det(J) in l–n plane

Full size image

3 Results based on numerical simulations

Although the numerical analysis deprives us the possibility of drawing conclusions on a general level, the analysis clearly indicates that the presence of a super predator does matter when the biological control of a predator–prey system is considered. Numerical analysis is used due to the complexity of the analytical solution, where obtainable. Using numerical analysis instead of real world data, which, of course, would be of great interest, has many advantages. It may also be noted that the simulation presented in this paper should be considered from a qualitative rather than a quantitative point of view. However, numerous scenarios covering the breadth of the biologically feasible parameter space were conducted and the results display the key features of dynamical results collected from all the scenarios tested.

Parametric bifurcation on a food chain model is nowadays carried out by several researchers [14–16]. Varying two parameters of the system parametric bifurcation curve can be drawn and one can get different types of bifurcation curve such as Hopf, fold, and transcritical bifurcation curves of equilibria as well as flip, fold [17], and transcritical bifurcation [12] curves of limit cycles. With the help of two parameter bifurcation, one can study the different stability zones in the parameter space and different routes of associated bifurcation curves along which the system shows some chaotic behaviour. This can be easily carried out by the software package MATCONT [18–21]. In a prey–predator system, when changes are made in certain parameters in their range, the whole system can be topologically unbalanced. In this section, our aim is to study the different types of bifurcation by simulations. Now we analyse model (3) numerically for some set of hypothetical data and explain the analytical results deduced in the previous sections. In the first session of the discussion, we shall discuss the stability of the different equilibrium points; and in the second session, we shall discuss the characteristics of different bifurcation points for our model. Here we want to analyse the model’s qualitative behaviour with respect to two parameters n and l. First we take a set of values of the parameters as m=2,n=4,l=0.2,s=2,h=1 and we see that for this set of data, the values of \((\frac{n}{1+m}-h)s=0.666667\), f(Φ)=57 for Φ=3, hence, by Theorem 2.1(i), we can say that system (3) has a unique positive interior equilibrium E ∗(0.733452,0.728596). The values of Trace(J(E ∗)) and det(J(E ∗)) are −0.642358 and 0.141595, respectively, hence the positive interior equilibrium E ∗ is locally asymptotically stable in the neighbourhood of E ∗.

Here we see that in absence of a super predator term, the prey population decreases and the predator population increases, which is meaningful from the ecological point of view which can be numerically verified. Later we will show that there are some values of the parameters for which system (3) is stable but in the absence of a super predator the model becomes unstable and vice-versa.

Here we see that the term lv/(s+v) is a monotone increasing function of v (see Fig. 5). That is, the number of predators consumed by the super predator increases when the number of predators increases, i.e. if the number of predators increases then the super predator catches the predator by spending less effort, also when the predator population is small then the predation rate increases rapidly, after that the increase rate becomes very slow. It is also interesting to see that when the consumption rate of a super predator increases then the predator population decreases very rapidly (see Fig. 2(b)) and at the same time when it crosses the value of m then after a long time the predator population goes extinct.

Fig. 5
figure 5

Graphical analysis of the super predator response function lv/(s+v)

Full size image

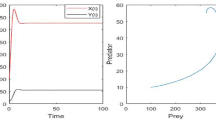
Now we discuss the stability of the various equilibrium points. System (3) has three equilibria E 0, E 10, E ∗. According to Theorem 2.2, E 0 is a saddle point (see Figs. 6(a), 6(b)) and it is unstable in the neighbourhood of E 0. So after some time, both species go extinct, which is difficult for any ecological system. (In fact, this can only occur if the prey are artificially completely eradicated, causing the predators to die of starvation. If the predators are eradicated, the prey population grows without bound in this simple model.) The conditions of Theorem 2.3 clearly indicate that the boundary equilibrium point E 1(1,0) is a saddle which is unstable (Fig. 6(a)). When the interior equilibrium is not unique, then we see that (Fig. 6(b)) the boundary equilibrium point E 1(1,0) is stable. In this case, we see that the value of n is less than l, i.e. the predator consumption rate is less than the super predator consumption rate. So when this situation occurs, the predator population goes extinct after some time, and consequently, the interior equilibrium A is an unstable spiral (see Fig. 6(b)) because at A, Trace(J) and Det(J) are both positive. If we start at some initial point in the neighbourhood of A then the system solution goes to the boundary equilibrium E 1(1,0). B is a stable node (see Fig. 6(b)) because here Trace(J)<0 and Det(J)>0. When the interior equilibrium point is unique (see Fig. 6(a)) and Trace(J)<0 and Det(J)>0, then the interior equilibrium point is a stable spiral and the solution of system (3) is stable.

Fig. 6
figure 6

Phase plane diagram (a) when the interior equilibrium is unique; (b) when there are two interior equilibria of system (3)

Full size image

Now we consider the case when Trace(J)=0 and Det(J)>0. In this case, Hopf bifurcation occurs in the system. Here we consider l, the consumption rate of the super predator, as a Hopf bifurcation parameter. Taking the set of values m=0.5,n=2,s=0.1,h=0.7, we have two values of l, 0.0232697 and 0.18. The phase portraits of the system are given in Fig. 7, and it is observed that around the positive interior equilibrium points (0.290646,0.560848) and (0.5,0.5) there are some limit cycles, and hence the system undergoes a Hopf bifurcation. The solution of the system becomes unstable in the neighbourhood of the points (0.290646,0.560848) and (0.5,0.5).

Fig. 7
figure 7

Phase portrait of the system (3) when Trace(J)=0

Full size image

Now we analyse the different bifurcation points of system (3).

From Fig. 8 it is observed that for n=2 there is a Hopf point (H) at l=0.023268 with the first Lyapunov coefficient −3.645911, which is negative and hence a stable limit cycle bifurcates from the equilibrium when it loses its stability. If l is increased further, we see that there is another Hopf point (H) with l=0.180002 and at this point the first Lyapunov coefficient is also negative (−8.426059). With further increase of l, at 0.216526 there is a limit point (LP) with one zero eigenvalue and one negative eigenvalue, and the value of the normal form coefficient is −3.970564, which is nonzero and therefore the limit point is nondegenerate. At this point, the solution of system (3) tends to a finite value as time increases. In this case, we see that system (3) has a stable manifold corresponding to the negative eigenvalue. The value l=0.216526 crosses the limit of l max (see Fig. 2(b)). So in this case, the solution of system (3) tends to the boundary equilibrium E 1(1,0). For n=2.5 the equilibrium curve has one LP at l=0.359514 with one eigenvalue zero and the other positive, meaning that the limit point is unstable, also the normal form coefficient is 4.829182, meaning it is nondegenerate. So in this case, the solution of the system approaches an infinite value as time increases. Further increase of l gives an H where the values of the eigenvalues are real and opposite, meaning their sum is zero, hence this is a neutral saddle point. At n=3, the equilibrium curve has an LP at l=0.505657, at which the system has two eigenvalues, one is zero and the other is 0.379395, and the normal form coefficient is 2.311317, this is also a nondegenerate LP, hence this limit point is unstable and the solution of system (3) becomes larger and larger as time increases. Further increasing l (at 0.341815), the system has an H point with two real opposite eigenvalues, hence it is a neutral saddle point.

Fig. 8
figure 8

Equilibrium curves when varying the parameter l for three different values of n of system (3). The values of the other parameters are m=0.5, s=0.1, h=0.7. Symbols LP and H stand for the Limit Point and Hopf Point, respectively

Full size image

Now using MATCONT package, we draw the bifurcation diagram with respect to the two parameters l and n of system (3) (see Fig. 9) in the l–n plane. Here we see that the limit point (LP) curve and the Hopf (H) point curve meet at a point in the l–n plane labelled as BT, called the Bogdanov–Takens Point, which is a codimension 2 bifurcation point. This is a point at which system (3) has two zero eigenvalues where the value of l is 0.279620. Thus in the neighbourhood of this point, the solution of system (3) becomes constant after some time. Here we see that on the limit point curve of the system there are some points at which the system becomes unstable and some points at which system (3) becomes stable. Also it is observed that when the consumption rate of the predator increases, the limit point of the system becomes unstable. Thus we can conclude that at a higher consumption rate of the predator, system (3) becomes unstable. Here we also notice that when l>0.279620 all the limit points become unstable and all the H points become neutral saddles. So on the left of this point, all the H are supercritical and all the LP points are stable limit points; and on the right of this point, all the H points are neutral saddles and all the LP are unstable. Thus we may conclude that the maximum sustainable value of l up to which system (3) will be stable is 0.279620; when l crosses this critical value, the system will be unstable (see Fig. 9). Moreover, to the left of the BT point, the branches of the curves (the H curve and the LP curve) are the stable branches of the curves, and to the right, the curves are unstable branches.

Fig. 9
figure 9

Two parametric bifurcation curves of system (3). Values of the other parameters are m=0.5, s=0.1, h=0.7. BT stands for the Bogdanov–Takens Point

Full size image

In Fig. 9, we see that the Hopf point (H) curve and the limit point (LP) curve divide the l–n plane into four regions. For all values of l and n in region I, system (3) tends to the boundary equilibrium E 1(1,0) (see Fig. 10(a)), but when l=0 we see that the system without the super predator term is stable and tends to a stable equilibrium (see Fig. 10(b)). In region II for all values of l and n, the solution of system (3) tends to the interior equilibrium (see Fig. 11). In region III, there are some values of l and n for which the interior equilibrium of (3) is unstable (see Fig. 12(a)) and there are some other values for which the solution of system (3) tends to the boundary equilibrium E 1(1,0) (see Fig. 12(b)) but in this case if we make l=0, we see that the system is always unstable (see Fig. 13(b)). In region IV for some values of l and n, the solution of system (3) tends to the boundary equilibrium E 1(1,0) (see Fig. 13(a)) and in this case also if we make l=0, the system without the super predator term becomes unstable (see Fig. 13(b)).

Fig. 10
figure 10

Solution of system (3)

Full size image
Fig. 11
figure 11

Solution of the system in region II

Full size image
Fig. 12
figure 12

Solution curves of system (3) in region III

Full size image
Fig. 13
figure 13

Solution of the system in regions III and IV

Full size image

In Fig. 14, the limit cycles are drawn by varying the parameter l and periods of the limit cycles. We see that, starting from the first H (0.023277557) point, the limit cycle continuation ends at the second H (0.17999812) point and vice-versa.

Fig. 14
figure 14

Limit cycles of different periods around H points

Full size image

4 Conclusion

We have presented a theoretical study of the potential effects of introducing a super predator in a standard predator–prey system with type-II functional response. It is assumed that the super predator is not dynamic but its effect is maintained at a specific constant level. The advantage of this approach is that it reduces the dimension of the system. Then, we analyse the dynamics of this model in a systematic manner, study the dependence of the dynamics on some vital parameters and discuss the global behaviour and controllability of the system.

We conclude that this modified version of predator–prey model with Holling type-II functional response exhibits very interesting dynamics. Theoretically, it is possible to control the dynamics of the system by manipulating the consumption rate of the super predator. It is possible to drive both the prey and predator population to a desired level within specified limits. The possibility of population oscillations is very interesting from a biological control point of view. When populations cycle, they periodically undergo peaks and troughs. This can be a double edged sword for management measures. Also, it is possible to control and eliminate any oscillations present in the system by an appropriate choice of the consumption rate of the super predator. Oscillations can also be brought into the ecosystem through provision of a super predator, if they are not present prior to the presence of the super predator. If, in the absence of a super predator, the system has stable coexistence, then the presence of a super predator may either cause monotonic decrease in the eventual value of the predator while maintaining stability, or it may bring in oscillations into the system when the consumption rate of the super predator goes beyond a specified level, leading to a stable limit cycle. Also it is observed that, if in the absence of the super predator, the system admits an interior equilibrium which is stable, it will continue to be asymptotically stable with an appropriate choice of both the consumption rate of the predator and super predator.

Finally, we may conclude that mathematical models can only be one source of guidance for biological control programmes. Other source of information will be crucial and are required for more refined parameterisations and validations of the models developed. The continual testing of models with data in different circumstances seems to be a promising strategy to approach a solution which is as good as possible. It may also be noted that the simulations presented in this paper should be considered from a qualitative, rather than a quantitative point of view. However, numerous scenarios covering the breath of the biological feasible parameter space were conducted and the results display the gamut of dynamical results collected from all the scenarios tested.