1 Introduction

Climate change is causing notable hazards and vulnerabilities to communities, socio-economy, and the natural environment. Australia is one of the most vulnerable countries to global warming having limited adaptive capacity (Mpelasoka et al. 2008). National Climate Resilience and Adaptation Strategy has therefore been developed and agreed by the Council of Australian Governments in 2007 to manage the risk of climate change and variability (Commonwealth of Australia 2015). Since 1970, one of the lowest total annual rainfalls was recorded as 351 mm in 2018–2019 (Bureau of Meteorology 2020b). During 2018–2019, reservoir storage volumes in southeastern Australia were very low. Furthermore, bushfires in eastern Australia during 2019–2020 were widespread, which destroyed more than 2000 homes with a burnt area over 5.5 million ha. A total of 25 lives were lost in New South Wales (NSW) alone (Australian Bureau of Statistics 2020) due to this bushfires and ongoing drought (King et al. 2020). Drought does not only affect a range of sectors or natural environment, but also causes adverse physiological impacts on humans. For instance, drought due to rainfall deficiency can increase suicide rate by 8% according to Nicholls et al. (2006) and this ratio in NSW was found as 8%-22% by Hanigan et al. (2012).

Shift and trend analysis are essential to understand rainfall variability and the nature of climate change. Nevertheless, long-term time series may not be consistent or homogeneous due to various non-climatic factors (e.g. station environment, location of station, instrumentation, observation practice, abrupt changes in the environment and calculation method) affecting the time series data (Peterson et al. 1998; Aguilar et al. 2003; Cao and Yan 2012; Mestre et al. 2013). The homogeneity tests of climatic time series may be classified into two groups, relative tests and absolute tests. Wijngaard et al. (2003) noted that absolute tests are more powerful than relative ones. In this study, we selected four widely used absolute homogeneity tests to detect inhomogeneities in the rainfall time series, namely the Pettitt test, the SNHT for a single break, the Buishand range test, and the Von Neumann ratio test. These absolute tests are reported to be adequate to detect the break year(s) in the data set (Wijngaard et al. 2003) and they have been adopted widely (Sahin and Cigizoglu 2010; Hosseinzadeh Talaee et al. 2014; Che Ros et al. 2016; Akinsanola and Ogunjobi 2017; Patakamuri et al. 2020) to assess the inhomogeneity in rainfall data series.

Australia is one of the countries having the highest hydro-climatic variability in the world (Drosdowsky 1993; Nicholls et al. 1997). Drought is one of the components of climatic variability in Australia (McKernan 2005). Drought is a damaging (Bryant 1991), slow-onset and recurring natural phenomenon and is defined as ‘a sustained, extended deficiency in precipitation’ by World Meteorological Organization (WMO) (1986). Hope et al. (2010) noted that much of southern Australia experienced significant rainfall decline over the last 50 years and a strong decline was observed in the southwest of eastern Australia after mid-1990s. Besides, some rainfall declines were detected by Smith (2004) and Alexander et al. (2007) in southeast and east coast of Australia. Furthermore, many studies addressed droughts in Australia both at regional and national scale (White and O'Meagher 1995; Mpelasoka et al. 2008; Barua et al. 2009; Ummenhofer et al. 2009; Gallant et al. 2013; Nazahiyah et al. 2014; McGree et al. 2016; Askarimarnani et al. 2020). Van Dijk et al. (2013), for instance, noted that since 1900, southeast Australia experienced its worst drought in the recent history, the so called millennium drought with the longest uninterrupted series of years with under median rainfall condition between 2001 and 2009.

More recently, an exceptional drought was experienced in southeastern Australia (covering 1989–2018), especially in NSW, Victoria and Queensland due to rainfall deficiency, decreased soil moisture, increased evapotranspiration and temperature (Tian et al. 2019). Gallant et al. (2013) found that the average drought lengths in parts of southeast Australia have shown a significant increase since 1911. Furthermore, southeast Australia was exposed to some of most intense drought events in terms of duration, magnitude and severity, between 2013 and 2019 (Yildirim and Rahman 2021). King et al. (2020) found that southeastern Australia, in particular Murray- Darling Basing, had been in severe drought since 2017. Stocker et al. (2013) noted (in the fifth assessment report of the IPCC) an increased temperature and decreased rainfall in southern Australia because of positive trend in the Southern Annular Mode (SAM) under the RCP4.5 or higher end scenarios. It should be noted that most of the previous studies examined trends in droughts by using only a limited number of drought indices. To fill this knowledge gap, we have used both SPI (with six different timescales) and EDI in this study to examine droughts.

Mann–Kendall (MK) trend test (Mann 1945; Kendall 1975), a rank-based nonparametric method, is the most frequently used method to examine trends in hydrometeorological, climate and environmental data (Helsel and Hirsch 1992; Lettenmaier et al. 1994; Douglas et al. 2000; Sang et al. 2014; Chebana et al. 2017; Yilmaz 2019). Although classical MK test is widely used to detect trend in time series, it may not be suitable if the serial correlation in the data is too high (Wasserstein et al. 2019). Hamed and Rao (1998) developed an empirical formulation for computing effective sample size to modify the variance of the MK statistic to eliminate the influence of the serial correlation on the MK test. They found that the modified test is superior to the original MK test. Furthermore, Yue et al. (2002) found that the original MK test may not correctly determine the probability of significance of trends. Yue and Wang (2004) investigated the influence of serial correlation on the MK test by Monte Carlo simulation. In this study, modified MK test, proposed by Yue and Wang (2004), has been adopted.

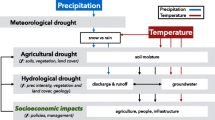
Droughts can be categorized into four groups as meteorological, hydrological, agricultural, and socioeconomic droughts (Wilhite and Glantz 1985). This study focused on assessing meteorological drought by using two drought indices: Standardized Precipitation Index (SPI) and Effective Drought Index (EDI). It should be noted that the SPI (McKee et al. 1993) was recommended by The World Meteorological Organization (WMO) to analyse meteorological droughts by national agencies (World Meteorological Organization 2012). An effective drought monitoring tool, the EDI, (Byun and Wilhite 1999) has been widely used in Australia (Deo and Şahin 2015; Deo et al. 2017) and around the world (Pandey et al. 2008; Kim et al. 2009; Yildirim 2015; Kamruzzaman et al. 2019; Malik et al. 2021).

The link between historical climate patterns, drought, and other modes of variability due to changing climate are still ambiguous. Hence, our study aims to fill this knowledge gap by identifying trends in spatiotemporal rainfall and drought data, which is one of the key research challenges as noted by Kiem et al. (2016). The specific objectives of this study are (i) to investigate the inhomogeneities in the rainfall time series data of 45 selected rainfall stations in southeast Australia, each representing a rainfall district, in order to detect reliability of climatic data set for this study; (ii) to identify changes in rainfall in terms of annual average, monthly, and seasonal rainfall by using autocorrelated MK test and Sen’s slope estimator; (iii) rigorous identification of trends in drought indices through the use of multiple timescales (3, 6, 9, 12, 24 and 36-months) SPI and EDI; and (iv) to illustrate spatial variability of trends in rainfall and drought indices via interpolation of Sen’s slope estimator (by spline interpolation technique).

2 Study area and data

This study focuses on southeast Australia, bounded by 28°S -39°S and 140° E- 154° E. This covers Victoria (VIC) and New South Wales (NSW) states in Australia that are extended over a broad range of climatic zones (arid to tropical). Southeast Australia is dominated by ‘summer’, ‘uniform’, ‘winter’, and ‘arid’ climatic conditions (Bureau of Meteorology 2016). NSW is divided into thirteen catchment regions, whereas VIC is divided into ten regions. There are many reservoirs in NSW and VIC to meet drinking water requirements of Sydney and Melbourne, the two largest cities in Australia and other regional cities and to meet agricultural needs of many farmers. The main natural climate drivers for southeast Australia affecting droughts and floods include Southern Annular Mode (SAM), Indian Ocean Dipole (IOD), Southern Oscillation (ENSO) and El Niño (CSIRO 2010).

A total of 45 rainfall stations were selected, one from each Rainfall Districts (RD) in the study area (Fig. 1). In selecting these stations, we considered that a station must have a longer period of data (more than 90 years) without maximum of 5% missing periods, and not more than one station being selected from a single RD. Also, the beginning and end of the selected data record should be the same for all the stations, which were taken as 1920 and 2019, respectively. Australia has 99 RDs, 30 and 15 of them are in NSW and VIC, respectively. The RD system was initiated in 1913, which helps to group rainfall sites in terms of relatively similar rainfall/climate. RD has no relationship with political districts, census districts, water catchments and shire boundaries. Monthly rainfall data for 45 rain gauges were obtained from Australian Bureau of Meteorology (Bureau of Meteorology 2020a) between 1920 and 2019 (Table 1). Monthly rainfall data for 100 years were used to detect change points (homogeneity), monotonic trends in rainfall (annual, seasonal, and monthly) and drought indices.

Fig. 1
figure 1

The map of Southeastern Australia illustrates the locations of spatially distributed the 45 synoptic rainfall stations. a elevation map was prepared by using the 5454 real-time rainfall stations’ elevations. b depicts the rainfall districts (RD) with locations of stations and interpolated (the spline method) average annual rainfall (AAR)

Full size image
Table 1 Studied rain gauge stations in southeastern Australia with identifier (ID), geographic co-ordinates, average annual rainfall (AAR) (mm), maximum of annual rainfall (mm) (MaxAR), minimum of annual rainfall (MinAR)
Full size table

3 Methodology

3.1 Homogeneity tests

Four homogeneity tests are selected to detect breaks (inhomogeneities) in rainfall time series data: the Pettitt test (Pettitt 1979), the SNHT for a single break (Alexandersson 1986), the Buishand range test (Buishand 1982), and the Von Neumann ratio test (Von Neumann 1941). These are regarded as absolute homogeneity tests and are capable to specify the homogeneity of a given time series data (Schönwiese and Rapp 1997; Wijngaard et al. 2003). While the Pettitt, the SNHT, and the Buishand range tests identify jump in the time series and find the break point, the Von Neumann test assumes that the time series data are not randomly distributed. This test is unable to define the year of the break. The Buishand range test and the Pettitt test are more susceptible to break points in the middle of the time series, whereas the SNHT is more sensitive to breaks near the beginning and end of the time series (Hawkins 1977; Wijngaard et al. 2003; Costa and Soares 2009). Furthermore, the SNHT and the Buishand range test assume that \(Y_{i}\) (see Eq. 4) is normally distributed. The Pettitt test, on the other hand, which is a nonparametric rank test, does not depend on this assumption.

3.1.1 Pettitt test

Pettitt test which is based on the Mann–Whitney and Wilcoxon test is a nonparametric approach to analyse the departure of homogeneity in the time series (Pettitt 1979). This nonparametric method detects the point of change in a time series (e.g. annual and monthly rainfall series).

The ranks \(r_{1} , . . . , r_{n}\) of the \(Y_{1} , . . . , Y_{n}\) are used to calculate the statistics:

$$X_{k} = 2\mathop \sum \limits_{i = 1}^{k} r_{i} - k\left( {n + 1} \right), \quad k = 1,2, . . . , n$$
(1)

If a break is found in year K, the absolute value of \(X_{k}\) approaches to maximum value.

$$X_{K} = \mathop {\max }\limits_{1 \le k \le n} \left| {X_{k} } \right|$$
(2)

Critical values associated with different significance levels for \(X_{K}\) for time series with different lengths were given by Pettitt (1979).

3.1.2 Standard normal homogeneity test

Alexandersson (1986) defined a test statistic \(T\left( k \right)\) to make comparison between the mean values of the first k years of the record and the last \(n - k\) years:

$$T\left( k \right) = k\overline{z}_{1}^{2} + \left( {n - k} \right)\overline{z}_{2}^{2} ,\quad k = 1, 2, . . . , n$$
(3)

where

$$\overline{z}_{1} = \frac{1}{k}\mathop \sum \limits_{i = 1}^{k} \frac{{\left( {Y_{i} - \overline{Y}} \right)}}{s}{\text{ and }}\overline{z}_{2} = \frac{1}{n - k}\mathop \sum \limits_{i = k + 1}^{k} \frac{{\left( {Y_{i} - \overline{Y}} \right)}}{s}$$
(4)

and

$$s = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {Y_{i} - \overline{Y}} \right)^{2}$$
(5)

When a break is found at the year \(K\), \(T\left( k \right)\) approaches at a maximum close to the year \(k = K\). The indicator, \(T_{0}\), of test statistic is explained as:

$$T_{0} = \mathop {\max }\limits_{1 \le k \le n} T\left( k \right)$$
(6)

Jarušková (1996) studied the test and defined the relationship between her \(T\left( n \right)\) and \(T_{0}\) as follow:

$$T_{0} = \frac{{n\left( {T\left( n \right)} \right)^{2} }}{{n - 2 + \left( {T\left( n \right)} \right)^{2} }}$$
(7)

If the \(T_{0}\) exceeds a certain level, then the null hypothesis is rejected, which depends on the size of the sample.

Jarušková (1996) provided critical values for the statistic \(T_{0}\) as a function of n in her study (see also Khaliq and Ouarda 2007).

3.1.3 Buishand range test

Buishand range test which is a parametric test was introduced by Buishand (1982) in order to find break points in the time series by assuming test values are independent and normally distributed. It is more sensitive to find break points in the middle of a time series (Hawkins 1977).

The adjusted partial sums of the statistics are calculated as follows:

$$S_{0}^{*} = 0\,{\text{and}}\,S_{k}^{*} = \mathop \sum \limits_{i = 1}^{k} \left( {Y_{i} - \overline{Y}} \right) \quad k = 1, 2, . . . , n$$
(8)

where \(\overline{Y}\) is the mean of time series observations and (\(Y_{1} , Y_{2 } , . ..,Y_{n}\)) and \(k\) is the number of the observation at a located break point.

The partial sum, \(S_{k}^{*}\), of the given series will fall and rise around zero when a series is homogeneous. If a break exists in year \(K\), \(S_{k}^{*}\) reaches a negative shift (maximum) or positive shift (minimum) near \(k = K\).

The significance of the shift is calculated with the ‘rescaled adjusted range’ \(R\). \(R\) is obtained as follows:

$$R = \frac{{\left( {\mathop {\max }\limits_{0 \le k \le n} S_{k}^{*} - \mathop {\min }\limits_{0 \le k \le n} S_{k}^{*} } \right)}}{s}$$
(9)

The calculated critical values for \(R/\sqrt n\) can be obtained from (Buishand 1982).

3.1.4 Von Neumann ratio test

The Von Neumann, which is a nonparametric ratio test (Von Neumann 1941), was defined as follows:

$$N = \mathop \sum \limits_{i = 1}^{n - 1} \left( {Y_{i} - Y_{i + 1} } \right)^{2} /\mathop \sum \limits_{i = 1}^{n} \left( {Y_{i} - \overline{Y}} \right)^{2}$$
(10)

If the sample is homogeneous, the expected value \(N\) is equal 2. When the sample has a break, \(N\) is generally smaller than the critical value (Buishand 1981). An increasing trend or slow oscillations in level will tend to result in small values of \(N\), vice versa, rapid variations in the mean may yield large values of \(N\) (Bingham and Nelson 1981). In contrast to the other three homogeneity tests, the Von Neumann test provides no indication of the break year. Critical values of \(N\) are given by Buishand (1981) (also see (Bingham and Nelson 1981; Buishand 1982)).

The outcomes of the homogeneity assessments of the four absolute tests for annual and monthly data set are interpreted following (Schönwiese and Rapp 1997; Wijngaard et al. 2003), i.e. an overall classification is made based on the number of test accepting the alternative hypothesis (rejecting the null hypothesis). A generally accepted method for categories is as follow: Class 1 is ‘useful’, if one or no test reject the null hypothesis at the 1%, 5% and 10% level. Class 2 is ‘doubtful’, if two tests reject the null hypothesis at the 1%, 5% and 10% level. Class 3 is ‘suspect’, if three or four tests reject the null hypothesis at the 1%, 5%, and 10% level.

Wijngaard et al. (2003) applied the same procedure for the classification of homogeneity assessment for the 1% level. We, on the other hand, extended and addressed the method for three different significance levels (1%, 5%, and 10%) to have wider perspective for homogeneity assessments of rainfall series in this study.

3.2 Drought indices

3.2.1 Standardized precipitation index

McKee et al. (1993) introduced Standardized Precipitation Index (SPI) to find drought initiation and end, magnitude, and intensity. SPI is determined by standard normal distribution.

The gamma distribution,\(g\left( x \right)\), is defined by the following:

$$g\left( x \right) = \frac{1}{{\beta^{\alpha } \Gamma \left( \alpha \right)}}x^{\alpha - 1} e^{ - x/\beta } ,{\text{ for}}\;x > 0$$
(11)

where \(\alpha { }\) represents shape parameter (\(\alpha { } > 0\)), \(\beta\) represents scale parameter (\(\beta { } > 0\)), \(x{ }\) is precipitation depth (\(x{ } > 0\)), and \(\Gamma \left( \alpha \right)\) is the gamma function. \(\alpha\) and \(\beta\) are required to be estimated from the precipitation data for each of the given timescales (3, 6, 9, 12, 24, 36-months) for each station. These scale and shape parameters were estimated by the maximum likelihood method (Thom 1958) as follow:

$$\alpha = \frac{1}{4A}\left( {1 + \sqrt{\frac{4A}{3}} } \right)\text{ and }\beta = \frac{{\overline{x}}}{\alpha }$$
(12)
$$A = \ln \left( {\overline{x}} \right) - \frac{{\mathop \sum \nolimits_{i = 1}^{n} {\text{ln}}\left( {x_{i} } \right)}}{n}$$
(13)

where \(\overline{x}\) represents the mean of data, and \(n\) is the number of data points. \(T{\text{he cumulative}} probability G\left( x \right)\) is found by

$$G\left( x \right) = \mathop \int \limits_{0}^{x} g\left( x \right)dx = \frac{1}{{\beta^{\alpha } {\Gamma }\left( \alpha \right)}}\mathop \int \limits_{0}^{x} x^{\alpha - 1} e^{ - x/\beta } dx$$
(14)

Since gamma distribution is undefined for zero values, Eq. (14) is expressed as follows:

$$H\left( x \right) = q + \left( {1 - q} \right)G\left( x \right)$$
(15)

As per Thom (1966), q is found by m/n where m is count of zeros in a given dataset of length n. The cumulative probability,\(H\left( x \right)\), can be transformed to the standard normal variate \(Z\) (the SPI value) which has a zero mean and unit variance.

3.2.2 Effective drought index

Byun and Wilhite (1999) introduced The Effective Drought Index (EDI) to define and monitor initiation-end and accumulated stress of drought. The data set to compute EDI is generally at a daily time-step (Byun and Wilhite 1996; Morid et al. 2006; Akhtari et al. 2009; Kim and Byun 2009; Kim et al. 2009). However, EDI can also be calculated from monthly rainfall time series (Smakhtin and Hughes 2007; Pandey et al. 2008; Akhtari et al. 2009). The EDI, in contrast to the SPI, is calculated only once as it does not depend on a time-step. The EDI is a function of \(PRN\) – ‘the precipitation necessary to the return to normal condition’. EP, the monthly effective precipitation can be computed as follow:

$$EP = \mathop \sum \limits_{m = 1}^{N} \left[ {\left( {\mathop \sum \limits_{i = 1}^{m} P_{i} } \right)/m} \right]$$
(16)

where \(N\) is the actual duration of preceding period and \(P_{i}\) is the precipitation. Then, the mean of each month’s \(EP\) (\(\overline{EP}\)) is calculated to find \(DEP\) which is the deviation of precipitation as:

$$DEP = EP - \overline{EP}$$
(17)
$$PRN = DEP\bigg/\mathop \sum \limits_{i = 1}^{N} \frac{1}{i}$$
(18)

Then, EDI can be found by

$$EDI = PRN/\sigma_{PRN}$$
(19)

where \(\sigma_{PRN}\) is the standard deviation of the \(PRN\) values (for relevant months).

Drought classifications of the SPI and the EDI can be found in (McKee et al. 1993; Dogan et al. 2012; Jain et al. 2015; Wable et al. 2019).

3.3 Trend analysis

3.3.1 Mann Kendall trend test

The Mann–Kendall (MK) test was developed by Mann (1945) and Kendall (1975). This is a nonparametric test to identify monotonic trend in a time series. The MK test is based on the statistic S, which can be expressed by

$$S = \mathop \sum \limits_{i = 1}^{n - 1} \mathop \sum \limits_{j = i + 1}^{n} sgn\left( {X_{j} - X_{i} } \right)$$
(20)

where \(X_{j}\) and \(X_{i}\) represent the value of sequence \(j\) and \(i\) \((j > i)\) which express the time indices associated with individual time series and n is the data length.

where

$$sgn\left( {X_{j} - X_{i} } \right) = \left\{ {\begin{array}{lll} + 1 & if & \left( {X_{j} - X_{i} } \right) > 0 \\ 0 & if & \left( {X_{j} - X_{i} } \right) = 0 \\ -1& if &\left( {X_{j} - X_{i} } \right) < 0 \\ \end{array} } \right.$$
(21)

Mann (1945) and Kendall (1975) noted that the statistic \(S\) is roughly normally distributed, under the null hypothesis, when \(n \ge 8\) (data length of 100 years in this study), with the variance and mean of statistics S as follows:

$${\text{E}}\left( {\text{S}} \right) = 0$$
(22)
$$V\left( S \right) = \frac{{n\left( {n - 1} \right)\left( {2n + 5} \right) - \mathop \sum \nolimits_{i = 1}^{m} T_{i} i\left( {i - 1} \right)\left( {2i + 5} \right)}}{18}$$
(23)

where \(T_{i}\) indicates the number of data in the ith tied group, m shows the number of tied groups. The standardized test statistic \(Z\), under the null hypothesis, is computed as follow:

$$Z = \left\{ {\begin{array}{*{20}c} {\frac{S - 1}{{\sqrt {V\left( S \right)} }}} & {{\text{if}}} & {S > 0} \\ 0 & {{\text{if}}} & {S = 0} \\ {\frac{S + 1}{{\sqrt {V\left( S \right)} }}} & {{\text{if}}} & {S < 0} \\ \end{array} } \right.$$
(24)

The standard MK statistic \(Z\) follows the standard normal distribution with zero mean and unit variance. The null hypothesis is rejected and trend is considered as significant if the absolute value of \(Z\) is higher than the critical value \(Z_{1 - \alpha }\) (increasing or decreasing trend) for two tailed test (where \(\alpha\) is the statistical significance level). Wang et al. (2020) suggests that slightly increasing of significance level, such as from 0.05 to 0.1, and longer time series will improve the power of the MK test. In this study, the statistically significant trends were tested with a significance level of \(\alpha = 0.01, \alpha = 0.05,\) and \(\alpha = 0.10\) (99%, 95%, and 90% of confidence interval).

Bayley and Hammersley (1946) investigated “effective” number of observations for autocorrelation in data by focusing a variance of the average of a length of data points n, whereas the data are autocorrelated. Yue and Wang (2004) modified the MK test to eliminate the effect of serial correlation on the MK trend. For this purpose, they documented the ability of using effective sample size (ESS) approach (Bayley and Hammersley 1946; Matalas and Langbein 1962; Lettenmaier 1976) (BHMLL-ESS) to minimize the influence of serial correlation on the MK test by Monte Carlo simulations (Yue and Wang 2004). In this study, the autocorrelation has been accounted for following the Yue and Wang method (more details about the method can be found in (Yue and Wang 2004)).

3.3.2 Sen’s slope estimator

An approach proposed by Thiel (1950) was then extended by Sen (1968) to develop the slope estimates of \(N\) pairs of data in the nonparametric procedure by using the Kendall’s tau. Hirsch et al. (1982) studied the Sen’s slope (or called Theil-Sen slope) to express the magnitude of trend as a slope. The Sen slope can be estimated by

$$X_{ij} = \left( {\frac{{Y_{j} - Y_{i} }}{{t_{j} - t_{i} }}} \right),\,(t_{j} \ne t_{i} ; t_{j} \,> \,t_{i} )\;({\text{for which}}\,\left( {i,j} \right) \in S)$$
(25)

where \(X_{ij}\) is the slope of the lines connecting each pair of points (\(t_{i}\), \(Y_{i}\)) and (\(t_{j}\),\(Y_{j}\)). \(Y_{j}\) and \(Y_{i}\) are the data values in the time \(t_{j}\) and \(t_{i}\), respectively.

The \(N\) values in Eq. 25 are arranged in ascending order of magnitude (let us denote the rth smallest value by \(X_{r}\) for \(r = 1, . . . , N\).) and the Sen’s slope (or the median of the \(N\) numbers) is computed as follows:

$$X_{{{\text{median}}}} = \left\{ {\begin{array}{*{20}c} {X_{{M + 1}} } & {{\text{if}}~\,N = 2M + 1~\left( {{\text{odd}}} \right)} \\ {~\left( {X_{M} + X_{{M + 1}} } \right)/2~~} & {~{\text{if}}\,~N = 2M~\left( {{\text{even}}} \right)} \\ \end{array} } \right.$$
(26)

\(X_{median}\) is computed by a two-sided test for three different confidence intervals (99%, 95%, and 90%) and the robust slope can be found by the nonparametric test. The negative (positive) value of \(X_{median}\) indicates a downward (upward) magnitude of a trend in the time series.

3.3.3 Spatial distribution of trends

Spatial variability of trends in rainfall and drought indices was explored through interpolation of Sen’s slope estimator by using spline interpolation method in ArcGIS environment (https://www.esri.com). The spline method was recommended and applied by several studies (Cannarozzo et al. 2006; Basistha et al. 2008; Shifteh Some'e et al. 2012; Yilmaz and Perera 2015) to interpolate Sen’s slope estimator. More details about the spline interpolation method can be found in (Talmi and Gilat 1977; Hartkamp et al. 1999).

4 Results and discussion

4.1 Homogeneity tests

Table 2 illustrates the results of the homogeneity tests on annual total rainfall (ATR) data at significance levels of 1%, 5%, and 10%. Von Neumann ratio test gives no information on the year of break, and hence, this is marked as “X” in Table 2 without referring to any year. Only station 86,090 is found to be inhomogeneous at significance level of 1% and classified as ‘suspect’ Class 3 since all the four tests reject the null hypothesis at 1% level. Table 2 clearly shows that number of inhomogeneous stations increases as confidence interval decreases in that four stations are found as ‘suspect’ at significance level of 5%. This number reaches to ten stations at significance level of 10%. Significant break years at 1% significance level is detected by the Pettitt test (Fig. 2). Figure 2a shows the change in the mean of ATR for station 86,090 occurs in 1996, which is determined by the four homogeneity tests as can be seen in Table 2. Another shift is found in 1936 at 1% significance level for station 74,087, which is detected only by the Pettitt test (Fig. 2b and Table 2). Although significant downward break points are detected at significance level of 1% for these two stations (Fig. 2), both upward and downward shifts are detected at 5% and 10% significance levels at different years for various stations (Figure S1). Besides, only the SNHT shows an abrupt change (lower mean than break point) in 2012 and 2017. Table 3 shows that 98% of the selected stations in the study area are homogenous and ‘useful’ based on significance level of 1% in terms of ATR. However, 82% and 62% of the selected stations are found to be homogeneous in terms of ATR for significance levels of 5% and 10%, respectively. Karabörk et al. (2007) suggests that a significance level of 5% is adequate in determining change points and inhomogeneities in the rainfall time series. It should be noted that at 5% level, 11 stations were found to be inhomogeneous: among these, only five show significant trends (Table 2).

Table 2 List of inhomogeneous annual total rainfall time series with break years based on four absolute homogeneity tests
Full size table
Fig. 2
figure 2

Significant change in rainfall time series with downward shift in the mean of the annual total rainfall (ATR) between 1920 and 2019. a shows station 86,090 and b shows station 74,087 (mu1 and mu2 are the mean rainfall before and after the break year, respectively)

Full size image
Table 3 Absolute homogeneity test results and classification for annual total rainfall (ATR) series. The values in parenthesis indicate the percentage of total number of stations
Full size table

The homogeneity test results of monthly total rainfall time series for the selected 45 stations in southeastern Australia indicate that 98% of stations may be assigned to Class 1 ‘useful’ for July, September, and December months, whereas for the other nine months, 100% of the stations are found to be homogeneous at significance level of 1% (Table S1; Figure S2). Non-homogenous stations for September (station ‘81,008’) and December (station ‘67,019’) are regarded as ‘doubtful’, while inhomogeneous station for July (station ‘60,036’) is rated as ‘suspect’. March, May, and August are the only months when 100% of the stations are found to be homogenous at the three significance levels. Absolute homogeneity tests based on monthly total rainfall time series show that the data set is highly homogenous at the adopted significance levels (Table S1). Homogeneity of monthly data set is crucial as drought analysis is generally undertaken based on monthly rainfall data.

4.2 Average rainfall

Spatial patterns of the average annual rainfall (AAR), standard deviation (SD), and coefficient of variation (CV) values with areal coverage are given in Fig. 3. Spline interpolation (Talmi and Gilat 1977) with natural breaks classification (Jenks 1967) is adopted to prepare Fig. 3. The results show that the AAR varies from 240 mm in the northwest to about 1483 mm in eastern and southern coasts of the study area. AAR for the entire study area is 725 mm, and more than 70% of the region have less than 725 mm annual total rainfall (ATR) in southeastern Australia (Fig. 3a). The lowest AAR (240–323 mm) is observed in northwest of the region with 30% of areal coverage, whereas the highest AAR (1295–1483 mm) is found in eastern and southern coasts, with only 2% of areal coverage.

Fig. 3
figure 3

a Average annual rainfall (AAR), b standard deviation (SD) of AAR, and c coefficient of variation (CV) in percentage of AAR with areal coverage in southeastern Australia between 1920 and 2019

Full size image

As can be seen in Fig. 3b, SD associated with the AAR varies between 97.8 mm (western part) and 492.1 mm (eastern coast). CV (the ratio of SD and AAR) varies between 15.2% and 48%. Figure 3c displays that heavy rainfall zones (eastern and southern coast) have the least variability (i.e. a smaller SD), whereas lower rainfall zones (northwest) have higher variability in rainfall, which is as expected. Our average rainfall statistics show similarities with Hajani and Rahman (2018) for NSW region, which focused on NSW alone with 200 rainfall stations covering a data period of 1945–2014.

4.3 Trend analysis

4.3.1 Rainfall trend analysis

Table 4 shows outcomes of long-term monotonic trends detected by autocorrelated Mann–Kendall (A-MK) trend test (Yue and Wang 2004). Upward trend in ATR at 25 stations (55.6%) is detected, whereas downward trend in ATR at 20 stations (44.4%) is found when significance level is ignored. It can be seen in Table 4 that as the significance level is reduced, the number of stations showing significant trends is reduced. This is since a smaller significance level is more rigorous than a higher significance level resulting in acceptance of the null hypothesis (H0: There is no trend in the data) for a greater number of stations. Our results for long-term ATR trend analysis show a decline in south of the study area (VIC) in contrast to Hennessy et al. (1999). The main reason is that the present study analyses trends for the rainfall data till 2019, whereas data availability of the previous study was limited to mid-1990s. Another reason may be abrupt changes or highly variable rainfall quantities during the last decades of the study period. Although long-term (1920–2019) ATR has been dominated by a positive trend, the last half of the data set (1970–2019) is dominated by a decreasing trend (Table 4). The medium term, 1970–2019, is dominated by a decreasing trend at 1%, 5%, and 10% significance levels. The finding of the medium-term ATR in our study is similar to Gallant et al. (2007). Positive trend, on the other hand, is dominated in the study area between 1920 and 1969.

Table 4 Number of rainfall stations showing positive and (negative) trends by A–MK trend test for annual total rainfall (ATR) for different time intervals
Full size table

Monotonic trends of monthly rainfall time series obtained by the A-MK test are shown in Table 5 where April and October rainfalls are highly dominated by negative trend in addition to decreasing/downward trends of June, July, August, and September. As an illustration, in April, negative trend is detected at 41 stations, whereas only four stations show positive trends, although it is not statistically significant. April was the only month where there was no single case with positive trend at 1%, 5%, and 10% significance levels. Statistically significant positive trend is detected in November (the month with the most increasing trends) at 31, 36, and 38 rainfall stations out of 45 at 1%, 5%, and 10% significance levels, respectively (Table 5). Furthermore, positive trends are detected in January, February, March, May, and December in contrast to Hajani and Rahman (2018). Hajani and Rahman (2018) focused changes in rainfall in NSW at 200 rainfall stations with data period of 1945 to 2014. Our findings for monthly rainfall trends for April, August, October, November, and December are similar to Hajani and Rahman (2018). One of the main reasons for different results in few cases is that VIC is included in our study area and we observe significant monthly negative trends, in particular for February, March, May, June, July, and September in south of the study area (in VIC region).

Table 5 Number of rainfall stations showing positive and (negative) trends by the A–MK trend test for monthly rainfall (between 1920 and 2019)
Full size table

The results of A-MK test of seasonal rainfall are summarized in Table 6, which depict that Summer (December-January–February) and Spring (September–October-November) seasons are dominated by significantly upward trend, while significant downward trend is observed in winter (June-July–August) at 1%, 5%, and 10% significance levels between 1920 and 2019 (Table 6) like Hajani and Rahman (2018). Autumn rainfall, on the other hand, is dominated by a positive trend at 23 stations, whereas negative trends are detected at 22 stations out of 45 (when significance level is ignored). Our results for seasonal trends show upward or downward trend; this is contradictory to Hajani and Rahman (2018), who found a decrease for each seasons in NSW over the period 1945–2014 when significance level was ignored. Besides, they did not find statistically significant decreasing trend at significance level of 1% in winter, whereas we find statistically significant downward trends at 1% level at 12 stations in winter, and 9 of these are located in NSW.

Table 6 Number of rainfall stations having positive and (negative) trends by A–MK trend test for the seasonal rainfall (between 1920 and 2019)
Full size table

4.3.2 Spatial distribution of temporal trends in rainfall

Spatial patterns of Sen’s slope and trends by the A-MK test are illustrated in Fig. 4. In southeastern Australia, summer and winter rainfalls contribute more than 50% of the ATR. Trends in summer and winter, therefore, have a direct impact on trends in ATR in the study area. Figure 4c depicts that the northeast and south-centre of the study area are experienced the lowest magnitude of trend in winter, which is similar to Taschetto and England (2009). Furthermore, the lowest trends in summer (Fig. 4a) are detected mainly in the northeast, south, southeast, and northwest of the study area. Meneghini et al. (2007) noted that the current decline of rainfall in winter might continues for longer years because of the climate driver-SAM. The highest variation in trend magnitude is monitored in spring as -1.21 and 0.82 mm/year, whereas the lowest variation is observed in summer season as -0.62 and 0.73 mm/year. Spring, on the other hand, has the most notable negative trend, -1.21 mm/year, in seasonal level (Fig. 4d). Besides, the magnitude of trend calculated by Sen’s slope of the ATR is observed to have the highest variability between -3.2 and 1.92 mm/year compared to variation in trends in seasonal level (Fig. 4e). It is found that the lowest magnitude of trends on the basis of 100 years of rainfall data is observed in the south-centre, eastern coast, and southeast of the study area in terms of four seasons and ATR similar to the study by Cai et al. (2014). Gallant et al. (2007) reported a declining trend in the eastern coast in the winter and summer, whereas spring had slightly increased trend similar to our findings. Hennessy et al. (2008) and our results in relation to the spatial patterns of ATR trend show a higher degree of similarity with only exception for southeast centre (VIC). We observe the lowest ATR trend (Fig. 4e), in contrast to Hennessy et al. (2008), for VIC region, whereas they found it for the eastern coastal region with data length between 1950 and 2007.

Fig. 4
figure 4

Spatial distribution of Sen’s slope (mm/year) and trends by A-MK test (significance level ignored) for seasonal scale and annual total rainfall (ATR) between 1920 and 2019

Full size image

Figure 5 shows the spatial distribution of temporal trends in monthly rainfall, the corresponding magnitudes (in mm/year) are computed by Sen’s slope estimator and A-MK test. The highest variation in magnitude of trend is observed for November between -0.45 and 0.54 mm/year, whereas the lowest variation is seen for September between -0.16 and 0.29 mm/year. The lowest monthly magnitude of the Sen’s slope is detected as -0.73 mm/year for October (in VIC), while the highest one is found for February with 0.64 mm/year (in NSW). Spatial patterns of Sen’s slope estimator and A-MK test outcomes clearly illustrate that April is the driest month with 91% of stations have negative trend in southeastern Australia since 1920 (Fig. 5, Table 5). March, May and April have vital importance to ‘wet up’ Victorian catchments. The magnitude of trend for April is found to be -0.5 mm/year (lowest) and 0.03 mm/year (highest). October is dominated by a significantly negative trend for 13, 17, and 19 stations at 1%, 5%, and 10% significance levels, respectively. Furthermore, October is the only month where a negative trend is observed throughout VIC (south of the study area) without any positive trend.

Fig. 5
figure 5

Spatial distribution of Sen's slope and trends for rainfall stations by A-MK (significance level ignored) test for monthly rainfall between 1920 and 2019

Full size image

4.4 Drought trend analysis

Spatial distribution maps of Sen’s slope and trends by the A-MK test for SPIs of multiple timescales and EDI are given in Fig. 6 (Sen’s slope estimator for SPIs of different timescales and EDI between 1920 and 2019 in southeastern Australia can be found in Table S2). Up and down arrows in Fig. 6 show the A-MK trends when significance level is ignored. It is found that the most of southern part of the study area (southeast of NSW and west and southern part of VIC) have a negative trends in terms of short and long-term droughts based on SPIs of different timescales and EDI for a data length of 100 years. Southwest and south-centre of the study area are the most drought prone and vulnerable area in terms of short- and long-term drought trends.

Fig. 6
figure 6

Spatial patterns of Sen's slope between 1920 and 2019 for SPIs of 3, 6, 9, 12, 24, and 36- months and EDI are given at a, b, c, d, e, f and g, respectively. Here, trends of rainfall stations are computed by A-MK test (significance level is ignored)

Full size image

Nine rainfall stations in NSW (48,168, 56,013, 57,023, 59,024, 60,036, 69,018, 70,045, 71,021, and 72,044) and seven rainfall stations in VIC (76,047, 79,008, 80,015, 82,009, 84,014, 86,090, and 90,060) are dominated by a significant negative trend in terms of short, seasonal, and long-term droughts based on the SPIs of all the timescales and EDI. EDI detects a negative trend at 20 stations (44.4%) out of 45 mainly in southern part of the region. Table 7 presents number of stations showing trends, computed by the A-MK test for SPIs of multiple timescales and EDI. Long-term drought trend analysis outcomes show that the area is dominated by a positive trend based on SPI and EDI (Table 7) when significance level is ignored. Our drought trend analysis results show similarities with those of Hennessy et al. (2004), who found both an increasing and decreasing trend in the NSW area. Rahmat et al. (2012) carried out a drought trend analysis based on a 3-month SPI and 12-month SPI at five rainfall stations covering rainfall data period 1949–2010 in VIC. They observed a downward trend at five stations for SPI of 3 and 12-month; our updated and comprehensive results support their findings, i.e. VIC is dominated by a decreasing trend in terms of short- and long-term drought.

Table 7 Number of rainfall stations presenting positive and (negative) trends by A–MK trend test for SPIs of 3, 6, 9, 12, 24, and 36–month and EDI (between 1920 and 2019)
Full size table

Furthermore, ATR trend analysis (Fig. 4e) has a high level of correlation with drought trend analysis considering SPI and EDI (Fig. 6). However, it should be noted that climatic variability of the last decades must be considered and compared with the long-term analysis to interpret the recent variabilities. Since the medium-term ATR trends, between 1970 and 2019, show a significantly negative trends in the region and we know that the severity of recent drought aggravated over the past two–three decades due to changes in rainfall and temperatures (Gallant et al. 2007; Murphy and Timbal 2008; Timbal 2009; Ummenhofer et al. 2009; Dey et al. 2019). Furthermore, Yildirim and Rahman (2021) found maximum drought quantities (the longest duration, biggest magnitude, and highest intensity) of short- and long-term droughts in various rainfall districts in southeastern Australia between 2013 and 2019. It can be concluded that the study area suffered from a prolonged drought till 2019.

5 Conclusion

This study investigates homogeneity (based on annual and monthly rainfall series), rainfall trends (annual, seasonal, and monthly) and drought trends based on SPI and EDI for southeast Australia considering rainfall data for 1920–2019. Spatial distribution of trends by spline interpolation technique is also examined. Significant change in the annual total rainfall (ATR) may not be discovered by the simple MK test, whereas A-MK test is able to eliminate the influence of serial correlation on the MK test as suggested by Hamed and Rao (1998) & Yue and Wang (2004).

Four absolute homogeneity tests (the Pettitt test, the SNHT, the Buishand, and the Von Neumann tests) are applied on a long historical ATR and monthly rainfall data from 45 selected rain gauges in southeast Australia to check data reliability. Through this process, only one station is found as inhomogeneous at a 1% significance level based on ATR and hence it is classified as ‘suspect’ station. Furthermore, four and nine stations are found to be ‘suspect’ based on ATR at significance levels of 5% and 10%, respectively. Homogeneity test results of monthly rainfall show that nine months can be regarded as 100% homogeneous and only one station as inhomogeneous for three months (July, September, and December) at 1% significance level. March, May, and August are found to be fully homogeneous at significance levels of 1%, 5%, and 10%.

Based on the A-MK trend test, a positive trend is observed at 25 stations, and a negative trend at 20 stations for ATR when significance level is ignored. South and northeastern parts of the study area are dominated by a negative trend for long-term ATR. It is found that the study area is dominated by a significantly negative trend (in relation to ATR) at significance level of 1%, 5%, and 10% in the medium term between 1970 and 2019. The rainfall decrease in the study area can be explained by a severity and increased frequency of climate driver El Niño since 1970s (Simmonds and Keay 2000; Fyfe 2003; Gallant et al. 2007) in addition to the effects of SAM and ENSO (Kiem and Verdon-Kidd 2010).

It is also found that winter is dominated by a significantly negative trend at 1%, 5% and 10% significance levels. A decreasing trend in winter is detected at 27 stations out of 45 when significance level is ignored. Summer and spring seasons are dominated by a positive trend. 33 stations in each of these seasons show an increasing trend (when significance level is ignored). On the other hand, autumn rainfall is generally dominated by a positive trend with 48.9% of the stations presenting a decreasing trend when significance level is neglected.

Results of investigation of spatial variability of trends show that mostly southern part of the study area is dominated by a negative trend in terms of seasonal scale and ATR. Besides, northeastern part of the region is highly dominated by a decreasing trend in winter season. Furthermore, April is detected (at 41 stations) as the driest month according to magnitude of Sen’s slope and A-MK trend test result. Moreover, October is seen to have the lowest magnitude of trend. June, July, August, and September are dominated by a negative trend in the study area in addition to April and October. It is also found that November and December are dominated by a statistically significant increasing trend at 1%, 5%, and 10% significance levels.

When we consider drought trend analysis, it is found that the study area is dominated by a positive trend based on short- and long-term droughts, particularly within the inner parts of the region. However, there is a good number of stations (between 36 and 44% of the total stations) that show negative trends in short- and long-term droughts based on SPI and EDI. The lowest magnitude of trend is detected mainly in the southern part of the study area based on SPI and EDI results. Negative trends of short and long-term droughts are detected in south, southeast, and northeast of the region based on SPIs of multiple timescales and EDI. Keywood et al. (2017) also reported a rainfall decline and the subsequent droughts in southern and eastern (involving NSW and VIC) Australia. The decrease in rainfall and drought due to rainfall deficiency in the study area can be explained by El Niño, which is linked to drought, which has been more frequent and severe in the past decades (Gallant et al. 2007; Freund et al. 2019).

The present study helps to understand characteristics of rainfall changes and drought trends in southeast Australia. The findings of this study will be helpful to fill important knowledge gaps in rainfall-drought trends. It is suggested that decadal climate variability of rainfall and drought should be addressed and interpreted to better understand effects of climate drivers (such as SAM, IOD, ENSO, and El Niño) on natural disaster like droughts.