Exponential Stability of Stochastic Time-Delay Neural Networks with Random Delayed Impulses

Abstract

The mean square exponential stability of stochastic time-delay neural networks (STDNNs) with random delayed impulses (RDIs) is addressed in this paper. Focusing on the variable delays in impulses, the notion of average random delay is adopted to consider these delays as a whole, and the stability criterion of STDNNs with RDIs is developed by using stochastic analysis idea and the Lyapunov method. Taking into account the impulsive effect, interference function and stabilization function of delayed impulses are explored independently. The results demonstrate that delayed impulses with random properties take a crucial role in dynamics of STDNNs, not only making stable STDNNs unstable, but also stabilizing unstable STDNNs. Our conclusions, specifically, allow for delays in both impulsive dynamics and continuous subsystems that surpass length of impulsive interval, which alleviates certain severe limitations, such as presence of upper bound for impulsive delays or requirement that impulsive delays can only exist between two impulsive events. Finally, feasibility of the theoretical results is verified through three simulation examples.

1 Introduction

Over the past decades, numerous scholars have been drawn to the dynamic behavior of impulsive neural network (INN) as a result of broad application of INN in various associated domains, such as associative memory [1], image processing [2], and so on. INN is a sort of hybrid neural network that is distinguished by continuous-time dynamical system with abrupt changes of state. The dynamical characteristics of INN have been fully studied. For example, global exponential stability [3], distributed-delay-dependent exponential stability [4], finite-time stability [5]. Additionally, stochastic interference is thought to be an inherent factor in the emergence of unstable behavior and chaos [6], such as, literature [7] investigates finite-time control strategies for stochastic nonlinear systems. Literature [8] explores the output feedback finite-time stability problem for a class of stochastic systems. Diverse qualitative theories concerning impulsive stochastic neural network (ISNN) have been put forth, see [9,10,11].

Time-delay is unavoidable due to signal transmission among neurons during the evolution process of many actual neural networks [12]. And time-delay may have a deleterious influence on dynamics of neural network, resulting in oscillations, instability, and poor performance [13, 14]. Therefore, it is crucial to analyze impulsive stochastic time-delay neural networks (STDNNs). In a variety of cases of impulsive STDNNs, Razumikhin technique [15] and Lyapunov functionals [9, 16] are typically used for analyzing stability of impulsive STDNNs. For example, in [16], stability problem of impulsive STDNNs is explored by utilizing the Lyapunov approach and average impulsive interval (AII). When Lyapunov functions that meet specific conditions can be constructed, the stability of impulsive STDNNs can be proven through Lyapunov stability conditions. Therefore, the Lyapunov functional provides stability assurance for design and control of impulsive STDNNs, which contributes to improve the reliability and security of system.

In a lot of practical networks, there might exist delays in the transmission of impulsive signals, which is referred to as impulsive delays. For instance, there is delay in fisheries industry and animal husbandry concerning impulses. Generally speaking, the impact of delayed impulsive sequences is mainly determined by the size of delays [17, 18]. In reality, impulsive delays possess a dual influence, including destabilizing or stabilizing impacts. In this respect, literature [17] completely illustrates that impulse delays have both negative and positive impacts on system dynamics, implying that delayed impulses may jeopardize stability of system and lead to unanticipated performance. On the other hand, delayed impulses may be able to stabilize unstable systems and improve performance. Recognizing the critical significance of delayed impulses, scholars have been paying close attention to dynamics of INN with delayed impulses in the past few years, see [18,19,20], with [18] on practical synchronization, [19] on exponential synchronization, [20] on synchronization of chaotic neural network. It can be seen that models of INN considered in these studies overlook random interference factors. A significant theoretical and practical significance is highlighted in [21] for investigation of stability of ISNN. In addition, there are strict limitations on impulsive delays in these literatures, where impulsive delay is often a constant or limited between two consecutive impulsive signals [22, 23]. Tragically, even when impulsive delay is permitted to be flexible between two successive impulsive events, the findings remain closed. More recently, more and more scholars have begun to focus on the unpredictability of impulses, such as stochastic impulsive density [24] and stochastic impulsive intensity [25]. However, to the best of our knowledge, dynamical behavior of stochastic time-delay neural networks with random impulsive delays (RDIs) effects have not been fully studied. Therefore, it makes sense to explore stability of STDNNs with RDIs. In practice, impulses with stochastic variable delays are more realistic. Based on this consideration, a natural question arises: Can delays in continuous systems and impulsive delays break through some limitations? That is to say, can the delays in continuous systems and the delays in impulses exceed the length of the impulsive interval? This forms the motivation of this paper. Additionally, the intercommunication between continuous behavior of STDNNs and delayed impulses will produce dynamic phenomena that differ from single continuous or discrete delayed neural networks, which will bring many hassles to stability analysis of neural networks.

On top of that, average impulsive interval (AII) [26] and mode-dependent AII (MDAII) [27] are frequently employed for describing impulsive sequences. The AII approach has the benefit of not requiring lower or upper boundaries of interval of impulses to be specified as long as AII matches specific requirement. The MDAII approach is advantageous in that it allows each impulsive function to possess its own average impulsive interval. Considering the randomness of impulsive delays, impulsive strategies still need to be developed. This is mostly owing to the fact that actual circumstance is intricate; impulsive delays are not unalterable at all times, and they will fluctuate with impulsive instant. As a result, if impulsive delays can be portrayed as a whole, we can more effectively cope with these delays. Currently, literature [28] proposes an average impulsive delay (AID) strategy, which quantifies typical delay between occurrence of an event and subsequent action. Generally speaking, analysis of impulsive sequences with random delays is more complicated. But AID strategy cannot be used to evaluate impulsive signals with uncertainty and randomness. It should be emphasized that in this paper, these constraints are overcome using average random delay (ARD), Lyapunov approach, and theoretical structure of impulses. With the help of ARD, we may reduce the influence of delay fluctuations at distinct impulsive times from an overall viewpoint, and explore the dual impacts of random delayed impulses on dynamic behavior of STDNNs, namely destabilization and stabilization.

Inspired by the above discussions, this paper concentrates on the stability of STDNNs with RDIs. Unlike typical delayed impulses, the impulsive delays in this paper have randomness, which can harm or contribute to stability. The major contributions of this paper are generalized:

• (1) In comparison to previous relevant research [19, 20, 28], the impulsive delay explored in this paper is random. Moreover, interference of stochastic factor are considered. Hence, it is more realistic to study dynamical behavior (e.g., stability) of STDNNs with random delayed impulses.

• (2) The statistical methods of uniform distribution and discrete distribution are used in this paper to handle impulsive sequences with random delays. Combining the ARD and Lyapunov method, stability criteria for STDNNs with random delayed impulses are obtained. The results show that random impulsive delay serves a crucial role on stability of STDNNs, not only disturbing the stable STDNNs, but also stabilizing the unstable STDNNs.

• (3) In comparison to prior work [18,19,20, 22, 23, 29], this paper does not require that impulsive delay be restricted to impulsive interval. Delay in continuous systems and delay in impulses are permitted to surpass the impulsive interval. As a result, the results for STDNNs with RDIs produced in this paper are more flexible.

The rest of this paper is organized as follows. In Sect. 2, we provide fundamental definitions, core lemmas, and the model of STDNNs with RDIs. In Sect. 3, sufficient conditions for mean square exponential stability of impulsive STDNNs are developed. In Sect. 4, three simulation examples are provided in order to confirm the efficacy and practicality of the generated results.

Notations Let ${\mathbb {R}}$ stand for the set of real numbers. ${\mathbb {R}}^+=(0,+\infty )$. ${\mathbb {R}}_{t_0}^+=(t_0,+\infty )$. ${\mathbb {N}}$ denotes a collection of natural integers that includes 0. ${\mathbb {N}}^+ ={\mathbb {N}}{\setminus } 0$. $(\Omega ,{\mathcal {F}},\{{\mathcal {F}} _t\}_{t\ge t_0}, P)$ represents a complete probability space with a natural filtration $\{{\mathcal {F}} _t\}_{t\ge t_0}$. Let $\omega (t)$ be a n-dimensional ${\mathcal {F}} _t$-adapted Brownian motion. $||\cdot ||$ indicates Euclidean norm. $||x||_1$ represents the 1-norm of vector x. The superscript T means the transposition of a matrix or vector. ${\mathcal {P}} {\mathcal {C}}\left( [-{\bar{\tau }},0];{\mathbb {R}}^n\right)$ is the set which contains piecewise continuous functions from $[-{\bar{\tau }},0]$ to ${\mathbb {R}}^n$ and $\phi$ is defined on $[-{\bar{\tau }},0]$ with norm $||\phi ||=\sup _{-{\bar{\tau }}\le \theta \le 0}|\phi (\theta )|$. $\iota =\tau \vee \xi$, where $\tau$, $\xi \in {\mathbb {R}}^+$. For $t\ge t_0$, ${\mathcal {P}}{\mathcal {L}}_{{\mathcal {F}}_t}^{p}$ is the family of all ${\mathcal {F}}_t$-measurable ${\mathcal {P}} {\mathcal {C}}([-{\bar{\tau }},0];{\mathbb {R}}^n)$-valued processes $\phi =\{\phi (\theta ): -{\bar{\tau }}\le \phi \le 0\}$ such that $||\phi ||_{L^p}=\sup _{-{\bar{\tau }}\le \theta \le 0}{\mathbb {E}}|\phi (\theta )|^p<+\infty$, where operator ${\mathbb {E}}$ aims to calculate the mathematical expectation. The random variable $X\sim U(a,b)$, $a,b\in {\mathbb {R}}^+$ represents that the random variable X follows a uniform distribution.

2 Model Description and Preliminaries

In this paper, we take account of a kind of stochastic time-delay neural network (STDNN) with RDIs described below:

$$\begin{aligned} \left\{ \begin{aligned} dx(t)=&[-Dx(t)+Af(x(t))+Bf(x_t)]dt\\&+g(t,x(t),x_t)d\omega (t), t\ge t_0, t\ne t_k,\\ x(t)=&I_k(t^-,x(t^-),x(t-\xi _k)^-), t=t_k, k\in {\mathbb {N}}^+,\\ x(s)=&\varphi (s), s\in [t_0-{\bar{\tau }},t_0), \end{aligned}\right. \end{aligned}$$

(1)

where $x(t)\in {\mathbb {R}}^{n}$ is state vector. $x_t=x(t-\tau )$, where $\tau \in [0,{\bar{\tau }}]$ is transmission delay. $t_k$ denotes impulsive instant. f serves as the activation function satisfying $|f(x)-f(y)|\le L|x-y|$ and $f(0)\equiv 0$, where L is $n\times n$-dimensional diagonal matrix. $D\in {\mathbb {R}}^{n\times n}$ is referred to as $n\times n$-dimensional matrix. $A\in {\mathbb {R}}^{n\times n}$ and $B\in {\mathbb {R}}^{n\times n}$ act as feedback matrix, respectively. $g(t,x(t), x_t)$ is noise disturbance from ${\mathbb {R}}_{t_0}^+\times {\mathbb {R}}^n\times {\mathbb {R}}^n$ to ${\mathbb {R}}^n$ satisfying $g(0)\equiv 0$ and $\textrm{trace}(g^T(t,x(t), x_t)g(t,x(t), x_t))\le x^T(t)K_1x(t)+x^T_t K_2x_t$, where $K_1$ and $K_2$ are $n\times n$-dimensional real matrix, respectively. $I_k: {\mathbb {R}}_{t_0}^+\times {\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\mathbb {R}}^n$ satisfying $I_k(t,0,0)\equiv 0$. Delay $\xi _k$ is a ${\mathcal {F}}_{t_k}$-measurable random variable that occurs at impulsive instant, which takes value in $[0, \xi ]$, moreover, the sequence $\{\xi _k\}$ is independent of $\omega (t)$ as well as mutually independent. Thus, $\xi _0=0$ when $t=t_0$. $\varphi \in {\mathcal {P}}{\mathcal {C}}_{{\mathcal {F}}_{t_o}}^p([t_0-\tau ,t_0])$ is initial function.

Some definitions and lemmas for consequent demands are as follows.

Definition 1

([26]) Assume that there exist positive constants $N_0$ and ${\mathcal {T}}_a$ such that

$$\begin{aligned} \frac{t-t_0}{{\mathcal {T}}_a}-N_0\le N(t,t_0)\le \frac{t-t_0}{{\mathcal {T}}_a}+N_0 \end{aligned}$$

holds for $t_0\le t\le u$, then $N_0$ and ${\mathcal {T}}_a$ are respectively called the chatter bound and AII, where $N(t,t_0)$ is referred to as the quantity of triggered impulses on $(t_0,t]$.

Definition 2

([29]) Let $N(t,t_0)$ represents the amount of impulsive occurrence on $(t_0,t]$. Assume that there exist positive number $\xi ^*$ and ${\bar{\xi }}$ such that

$$\begin{aligned} {\bar{\xi }}N(t,t_0)-\xi ^*\le \sum _{j=1}^{N(t,t_0)}{\mathbb {E}}\xi _j\le {\bar{\xi }}N(t,t_0)+\xi ^* \end{aligned}$$

holds for $t\ge t_0$, then ${\bar{\xi }}$ and $\xi ^*$ are called ARD and preset value, respectively.

Remark 1

It is clear that the notions of AII and ARD is developed to characterize impulsive moments and impulsive input delays holistically. It is worth noting that the amount of impulses serves as a link between these two ideas. Actually, Definitions 1 and 2 can yield that

$$\begin{aligned} {\bar{\xi }}\frac{t-t_0}{{\mathcal {T}}_a}-\xi ^*\le \sum _{j=1}^{N(t,t_0)}{\mathbb {E}}\xi _j\le {\bar{\xi }}\frac{t-t_0}{{\mathcal {T}}_a}+\xi ^*. \end{aligned}$$

Lemma 1

([19]) Let $x,y\in {\mathbb {R}}^n$, U is a diagonal positive definition matrix with appropriate dimension, then

$$\begin{aligned} x^Ty+y^Tx\le x^TUx+y^TU^{-1}y \end{aligned}$$

holds.

Lemma 2

([19]) If $V\in {\mathbb {R}}^{n\times n}$ is a symmetric positive definite matrix and $U\in {\mathbb {R}}^{n\times n}$ is symmetric matrix, then

$$\begin{aligned} \lambda _{min}\left( V^{-1}U\right) x^TVx\le x^TUx\le \lambda _{max}\left( V^{-1}U\right) x^TVx, x\in {\mathbb {R}}^n \end{aligned}$$

holds.

Lemma 3

([29]) Assume that V(t, x) is continuously once differentiabla in t and twice in x. There is a constant $\delta$ such that

$$\begin{aligned} {\mathbb {E}}[V(t_k-\xi _k)^-]\le {\mathbb {E}}\biggl [V((t_k-\xi _k)^-)\exp \{-\delta \xi _k\}\biggr ]\exp \{\delta {\mathbb {E}}\xi _k\} \end{aligned}$$

holds for $t_k\le t<t_{k+1}$.

Assumption 1

There exist positive definite matrices $\Gamma _{1k}$ and $\Gamma _{2k}$ satisfying for $t=t_k$,

$$\begin{aligned}&I_k^T(t^-,x(t^-),x(t-\xi _k)^-)I_k(t^-,x(t^-),x(t-\xi _k)^-)\\&\quad \le x^T(t^-)\Gamma _{1k}x(t^-)+x^T(t-\xi _k)^-\Gamma _{2k}x(t-\xi _k)^-. \end{aligned}$$

Definition 3

The trivial solution of STDNN (1) with RDIs is said to be mean square exponetially stable (MSES), if there exists a pair of positive constants $\alpha$ and $\beta$ such that for $t\ge t_0$,

$$\begin{aligned} {\mathbb {E}} |x(t)|^2\le \alpha \exp \{-\beta (t-t_0)\}\sup _{t_0-\tau \le u\le t_0}{\mathbb {E}}|\varphi (u)|^2 \end{aligned}$$

holds.

We define a differential operator ${\mathcal {L}}$ for STDNN (1),

$$\begin{aligned} {\mathcal {L}}V(t,x(t))&=V_t(t,x(t))+V_x(t,x(t))f(t,x(t-\tau (t,x(t))))\\&\quad +\frac{1}{2}trace\left[ g^T(t,x(t-\tau (t,x(t))))\right. \\&\quad \times V_{xx}(t,x(t))g(t,x(t-\tau (t,x(t))))]. \end{aligned}$$

3 Main Results

In this section, we consider positive definite function $V(t)=V(t,x)=x^T(t)Px(t)$, where P is positive definite and symmetric matrix of appropriate dimension.

3.1 STDNNs with Destabilizing Delayed Impulses

Theorem 1

Suppose that there are positive constants $\gamma >1$, $\kappa >0$, $\mu >0$, $-\theta _1>\theta _2=\lambda _{\max }\left( P^{-1}L^TU_2L\right) +\lambda _{\max }(P^{-1}K _2)>0$, and n-dimensional symmetric positive definite matrices $U_1$, $U_2$ such that

$$\begin{aligned} (\wp _1)\quad&P\le \gamma I;\\ (\wp _2)\quad&\begin{bmatrix} \Theta &{} PA &{}PB \\ *&{}-U_1 &{}0 \\ * &{} * &{}-U_2 \end{bmatrix}<0;\\ (\wp _3) \quad&N(t,t_0)(0\vee \ln \lambda )+\epsilon _0\sum _{l=0}^{N(t,t_0)} {\mathbb {E}}\xi _l-(\epsilon _0-\kappa )(t-t_0)\le \mu ; \end{aligned}$$

where I stands for identity matrix, $\Theta =-PD-D^TP+L^TU_1L+\gamma K _1-\theta _1P$, $\theta _1=\lambda _{max}\left[ -PD-D^TP+PAU_1^{-1}A^TP+L^TU_1L+PBU_2^{-1}B^TP+\gamma K_1\right]$, $\epsilon _0\in (\epsilon _1-\varepsilon _1,\epsilon _1)$, $\varepsilon _1$ is any small constant, $\epsilon _1$ is the root of the equation $\epsilon +\theta _1+\theta _2\exp \{\epsilon \tau \}=0$. Then STDNN (1) with RDIs is MSES.

Proof

For convenience, denote $\lambda _1=\gamma \lambda _{\max }\left( P^{-1}\Gamma _{1\,M}\right)$, $\lambda _2=\gamma \lambda _{\max }\left( P^{-1}\Gamma _{2\,M}\right)$, $\lambda =\lambda _1+\lambda _2$. The entire proof procedure will be fragmented into two phases.

Step 1: We first verify that, there is $t^*\in [t_{k-1},t_k)$ such that ${\mathbb {E}}x^T(t^*)Px(t^*)\exp \{\epsilon _0(t^*)-t_0\}\ne 0$ and ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}\le {\mathbb {E}}x^T(t^*)Px(t^*)\exp \{\epsilon _0 (t^*-t_0)\}$ are hold for $t_0-\tau \le t<t^*$, then one has

$$\begin{aligned} D^+{\mathbb {E}}\biggl [x^T(t)Px(t)\exp \{\epsilon _0(t-t_0)\}\biggr ]\biggr |_{t=t^*}<0. \end{aligned}$$

(2)

In accordance with the definition of ${\mathcal {L}}$, we have

$$\begin{aligned} {\mathcal {L}}[x^T(t)Px(t)]&=2x^T(t)P\biggl [-Dx(t)+Af(x(t))+Bf(x_t)\biggr ]\nonumber \\&\quad +trace \biggl [g^T(t,x(t),x_t)Pg(t,x(t),x_t)\biggr ]\nonumber \\&=-2x^T(t)PDx(t)+2x^T(t)PAf(x(t))+2x^T(t)PBf(x_t)\nonumber \\&\quad +trace \biggl [g^T(t,x(t),x_t)Pg(t,x(t),x_t)\biggr ]. \end{aligned}$$

(3)

Combining Lemma 1, Lemma 2 and condition $(\wp _1)$, we can get

$$\begin{aligned}&2x^T(t)PAf(x(t))\nonumber \\&\quad \le x^T(t)PAU_1^{-1}A^TPx(t)+f^T(x(t))U_1f(x(t))\nonumber \\&\quad \le x^T(t)PAU_1^{-1}A^TPx(t)+x^T(t)L^TU_1Lx(t), \end{aligned}$$

(4)

$$\begin{aligned}&2x^T(t)PBf(x_t)\nonumber \\&\quad \le x^T(t)PBU_2^{-1}B^TPx(t)+f^T(x_t)U_2f(x_t)\nonumber \\&\quad \le x^T(t)PBU_2^{-1}B^TPx(t)+x_t^TL^TU_2Lx_t\nonumber \\&\quad \le x^T(t)PBU_2^{-1}B^TPx(t)+\lambda _{\max }(P^{-1}L^TU_2L)x_t^TPx_t, \end{aligned}$$

(5)

$$\begin{aligned}&\qquad trace[g^T(t,x(t),x_t)Pg(t,x(t),x_t)]\nonumber \\&\quad \le \gamma trace[g^T(t,x(t),x_t)g(t,x(t),x_t)]\nonumber \\&\quad \le \gamma [x^T(t)K_1x(t)+x_t^TK_2x_t]\nonumber \\&\quad \le \gamma [x^T(t)K_1x(t)+\lambda _{\max }(P^{-1}K _2)x_t^TPx_t]. \end{aligned}$$

(6)

On the basis of condition $(\wp _2)$ and inequalities (3)–(6), we can infer that

$$\begin{aligned} {\mathcal {L}}x^T(t)Px(t)&\le x^T(t)\biggl [-PD-D^TP+PAU_1^{-1}A^TP+L^TU_1L\nonumber \\&\quad +PBU_2^{-1}B^TP+\gamma K_1\biggr ]x(t)+\biggl [\lambda _{\max }\left( P^{-1}L^TU_2L\right) \nonumber \\&\quad +\lambda _{\max }\left( P^{-1}K _2\right) \biggr ]x_t^TPx_t\nonumber \\&\le \theta _1x^T(t)Px(t)+\theta _2x_t^TPx_t. \end{aligned}$$

(7)

According to Fubini’s theorem and (7), we can calculate that

$$\begin{aligned}&D^+{\mathbb {E}}\biggl [x^T(t)Px(t)\exp \{\epsilon _0(t-t_0)\}\biggr ]\biggl |_{t=t^*}\nonumber \\&\quad =\epsilon _0{\mathbb {E}}[x^T(t^*)Px(t^*)\exp \{\epsilon _0(t^*-t_0)\}]\nonumber \\&\qquad +\exp \{\epsilon _0(t-t_0)\}{\mathbb {E}}{\mathcal {L}}[x^T(t)Px(t)]|_{t=t^*} \nonumber \\&\quad \le \epsilon _0{\mathbb {E}}[x^T(t^*)Px(t^*)\exp \{\epsilon _0(t^*-t_0)\}]\nonumber \\&\qquad +\exp \{\epsilon _0(t-t_0)\}[\theta _1{\mathbb {E}}x^T(t)Px(t)+\theta _2{\mathbb {E}}x_t^TPx_t]|_{t=t^*}\nonumber \\&\quad \le \epsilon _0{\mathbb {E}}[x^T(t^*)Px(t^*)\exp \{\epsilon _0(t^*-t_0)\}]\nonumber \\&\qquad +\theta _1{\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0(t-t_0)\}|_{t=t^*}\nonumber \\&\qquad +\theta _2{\mathbb {E}}x_t^TPx_t\exp \{\epsilon _0(t-\tau -t_0)\}\exp \{\epsilon _0\tau \}|_{t=t^*}\nonumber \\&\quad \le (\epsilon _0+\theta _1+\theta _2\exp \{\epsilon _0\tau \}){\mathbb {E}}x^T(t^*)Px(t^*)\exp \{\epsilon _0 (t^*-t_0)\}\nonumber \\&\quad \le 0. \end{aligned}$$

(8)

So (2) holds.

Step 2: Following that, we will clarify that

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t)\le \Phi _k\exp \{-\epsilon _0 (t-t_0)\} \end{aligned}$$

(9)

holds for $t_0\le t<t_k$, $k\in {\mathbb {N}}^+$, where $\Phi _k=\exp \{(k-1)(0\vee \ln \lambda )+\sum _{l=0}^{k-1}\epsilon _0 {\mathbb {E}}\xi _l\}||{\bar{\varphi }}||$, ${\bar{\varphi }}=\lambda _{\max }(P)\sup _{t_0-\tau \le u\le t_0}{\mathbb {E}}||\varphi (u) ||^2$.

Clearly, the demonstration of (9) can be turned into the confirmation of

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}\le \Phi _k, t\in [t_0,t_k), k\in {\mathbb {Z}}^+. \end{aligned}$$

(10)

To begin with, we confirm that (10) holds for $t\in [t_0-\tau ,t_1)$. It is distinctly that ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}\le {\mathbb {E}}x^T(t)Px(t)\le ||{\bar{\varphi }} ||=\Phi _1$ for $t\in [t_0-\tau ,t_0]$, which suggests that (10) is true for $t\in [t_0-\tau ,t_0]$. Now, we need to demonstrate that (10) is true for $t\in (t_0,t_1)$. Assuming the above assertion is false, then there exist some instants t such that ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}>\Phi _1$. Set $t^*=\inf \{t\in (t_0,t_1):{\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}>\Phi _1\}$. In the light of definition of $t^*$, we can obtain ${\mathbb {E}}x^T(t^*)Px(t^*)\exp \{\epsilon _0 (t^*-t_0)\}=\Phi _1$ and ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}<\Phi _1$ for $t\in [t_0-\tau ,t^*)$, and for arbitrarily small constant $\Delta t$, ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}>\Phi _1$ when $t\in (t^*,t^*+\Delta t]$. Therefore $D^+x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}|_{t=t^*}>0$, which is contradictory to (2). So, (10) holds for $t\in [t_0-\tau ,t_1)$.

Afterwards, using mathematical induction, we presuppose that (10) is valid on $k=1,2,\cdots ,M$, $M\in {\mathbb {N}}^+$, which shows

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}\le \Phi _M, t=t_M. \end{aligned}$$

(11)

The following will illustrate the validity of (10) for $k=M+1$. It is worth noting that sequence $\{\Phi _k\}$ is monotonically non-decreasing on $k\in {\mathbb {Z}}^+$. Futhermore, one can deduce that ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0(t-t_0)\}\le \Phi _M\le \Phi _{M+1}$ when $t\in [t_0-\tau ,t_M)$. Then it will be proven that ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0(t-t_0)\}\le \Phi _{M+1}$ for $t\in [t_M,t_{M+1})$.

At $t=t_M$, with the help of Assumption 1, $\lambda \le \exp \{0\vee \ln \lambda \}$, Lemma 2 and Lemma 3, we derive that

$$\begin{aligned}&{\mathbb {E}} x^T(t_M)Px(t_M)\exp \{\epsilon _0(t_M-t_0)\}\nonumber \\&\quad \le \left[ \gamma \left( {\mathbb {E}}x^T(t_M^-)\Gamma _{1M}x(t_M^-)+{\mathbb {E}}x^T(t_M-\xi _M)^-\right. \right. \nonumber \\&\qquad \left. \left. \times \Gamma _{2M}x(t_M-\xi _M)^-\right) \right] \exp \{\epsilon _0(t_M-t_0)\}\nonumber \\&\quad \le \gamma \lambda _{\max }\left( P^{-1}\Gamma _{1M}\right) {\mathbb {E}}x^T(t_M^-)Px(t_M^-)\exp \{\epsilon _0(t_M-t_0)\}\nonumber \\&\qquad +\gamma \lambda _{\max }\left( P^{-1}\Gamma _{2M}\right) {\mathbb {E}}x^T(t_M-\xi _M)^-Px(t_M-\xi _M)^-\nonumber \\&\qquad \times \exp \{\epsilon _0(t_M-\xi _M-t_0)\}\exp \{\epsilon _0{\mathbb {E}}\xi _M\}\nonumber \\&\quad \le \left[ \gamma \left( \lambda _{\max }\left( P^{-1}\Gamma _{1M}\right) +\lambda _{\max }\left( P^{-1}\Gamma _{2M}\right) \right) \right] \Phi _M\exp \{\epsilon _0{\mathbb {E}}\xi _M\}\nonumber \\&\quad =\lambda \Phi _M\exp \{\epsilon _0{\mathbb {E}}\xi _M\}\nonumber \\&\quad \le \Phi _{M+1}. \end{aligned}$$

(12)

Suppose that there is ${\tilde{t}}\in (t_M,t_{M+1})$ such that ${\mathbb {E}}x^T({\tilde{t}})Px({\tilde{t}})\exp \{\epsilon _0 ({\tilde{t}}-t_0)\}=\Phi _{M+1}$, ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}<\Phi _{M+1}$ for $t\in [t_0-\tau ,{\tilde{t}})$, and ${\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}>\Phi _{M+1}$ for $t_{M+1}>t>{\tilde{t}}$. Apparently, $D^+{\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}|_{t={\tilde{t}}}>0$, which is in contradiction with (2).

Therefore, for $t\ge t_0$, it is straightforward to gain

$$\begin{aligned}&{\mathbb {E}}x^T(t)Px(t)\exp \{\epsilon _0 (t-t_0)\}\nonumber \\&\quad \le \exp \{N(t,t_0)(0\vee \ln \lambda )+\sum _{l=0}^{N(t,t_0)}\epsilon _0 {\mathbb {E}}\xi _l\}||{\bar{\varphi }} ||. \end{aligned}$$

(13)

In addition,

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t) \le&\exp \{N(t,t_0)(0\vee \ln \lambda )\sum _{l=0}^{N(t,t_0)}\epsilon _0 {\mathbb {E}}\xi _l-\epsilon _0 (t-t_0)\}||{\bar{\varphi }} || \end{aligned}$$

(14)

holds for $t\ge t_0$. $\square$

Employing condition $(\wp _3)$, one can procure that

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t)\le \exp \{\mu -\kappa (t-t_0)\}||{\bar{\varphi }} ||, t\ge t_0. \end{aligned}$$

(15)

Then, one has

$$\begin{aligned} {\mathbb {E}}||x(t)||^2 \le&\frac{\lambda _{\max }(P)\exp \{\mu \} }{\lambda _{\min }(P)}\exp \{-\kappa (t-t_0)\}\sup _{t_0-\tau \le u\le t_0}{\mathbb {E}}||\varphi (u)||^2. \end{aligned}$$

(16)

Hence, STDNN (1) with RDIs is MSES.

Corollary 1

Provided that Assumption 1, $(\wp _1)$, and $(\wp _2)$ are all fulfilled, there exists constant $\epsilon _1$ satisfying

$$\begin{aligned} (\wp '_3)\quad {\bar{\xi }}+\frac{0\vee \ln \lambda }{\epsilon _1}<{\mathcal {T}}_a, \end{aligned}$$

where $\epsilon _1$ is unique positive solution of equation $\epsilon +\theta _1+\theta _2\exp \{\epsilon \tau \}=0$, then STDNN (1) with RDIs is MSES.

Proof

Let ${\tilde{\epsilon }}=\epsilon _1-\frac{0\vee \ln \lambda }{{\mathcal {T}}_a-{\bar{\xi }}}$ and $\varepsilon _2=\varepsilon _1\wedge {\tilde{\epsilon }}$. The condition $(\wp '_3)$ indicates that ${\tilde{\epsilon }}>0$. We can discover a constant $\epsilon _0\in (\epsilon _1-\varepsilon _2,\epsilon _1)$ satisfying

$$\begin{aligned} {\bar{\xi }}+\frac{0\vee \ln \lambda }{\epsilon _0}<{\mathcal {T}}_a. \end{aligned}$$

(17)

Combining Definitions 1 and 2, one has

$$\begin{aligned}&N(t,t_0)(0\vee \ln \lambda )+\sum _{l=0}^{N(t,t_0)}\epsilon _0 {\mathbb {E}}\xi _l-\epsilon _0 (t-t_0)\nonumber \\&\quad \le \left( \frac{t-t_0}{{\mathcal {T}}_a}+N_0\right) (0\vee \ln \lambda )+\epsilon _0[{\bar{\xi }}N(t,t_0)+\xi ^*]-\epsilon _0 (t-t_0)\nonumber \\&\quad \le \left( \frac{t-t_0}{{\mathcal {T}}_a}+N_0\right) (0\vee \ln \lambda )+\epsilon _0\left[ {\bar{\xi }}\frac{t-t_0}{{\mathcal {T}}_a}+{\bar{\xi }}N_0+\xi ^*\right] -\epsilon _0 (t-t_0)\nonumber \\&\quad \le -\left( \epsilon _0-\frac{(0\vee \ln \lambda )+\epsilon _0{\bar{\xi }}}{{\mathcal {T}}_a}\right) (t-t_0)+\epsilon _0{\bar{\xi }}N_0+\epsilon _0\xi ^*+N_0(0\vee \ln \lambda ). \end{aligned}$$

(18)

According to (17),

$$\begin{aligned} \epsilon _0-\frac{0\vee \ln \lambda +\epsilon _0{\bar{\xi }}}{{\mathcal {T}}_a}>0. \end{aligned}$$

(19)

Set that $\kappa =\epsilon _0-\frac{0\vee \ln \lambda +\epsilon _0{\bar{\xi }}}{{\mathcal {T}}_a}$ and $\mu =\epsilon _0{\bar{\xi }}N_0+\epsilon _0\xi ^*+N_0(0\vee \ln \lambda )$. Furthermore, $(\wp _3)$ is satisfied. Through Theorem 1, STDNN (1) with RDIs is MSES. $\square$

Remark 2

$\theta _2+\theta _1<0$ implies that the initial STDNN is stable in the absence of impulse action. Theorem 1 and Corollary 1 clearly demonstrate that STDNN (1) is able to remain stable when affected by unstable delayed impulses under specific conditions. $(\wp _3')$ displays a correlation between ARD and AII, indicating that when ARD grows, so does AII. Given that delayed impulses have a detrimental influence on STDNN (1), impulsive delays should not be too lengthy; otherwise, the negative impact of delayed impulses on stability will increase.

Remark 3

In Theorem 1, $(\wp _3)$ is a condition about impulsive delays, emphasizing that the impulsive delays should not be excessively long, or else $\epsilon _0$ will not exist.

In addition, compare with literature [19], there are no restrictions on $\tau$ and $\xi _l$ in this paper, which means that $\tau$ and $\xi _l$ may exceed the impulse interval when $\xi$ is large enough. Furthermore, stochastic factors are also taken account in this paper.

3.2 STDNNs with Stabilizing Delayed Impulses

Denote $t_0-\iota : = t_{-1}$, $\aleph (u)=\theta _1-u+\frac{\theta _2}{\lambda }\exp \{u(-\tau +\xi )\}$ and $\epsilon _2=\frac{1}{-\tau +\xi }\ln \frac{\lambda }{\theta _2(-\tau +\xi )}$.

Lemma 4

Take into consideration following function

$$\begin{aligned} {\mathcal {M}}(t)=\left\{ \begin{aligned}&V(t,x)\exp \{-\epsilon _0 (t-t_k)\}, t\in [t_k,t_{k+1}),\\&V(t), t\in [t_0-\tau ,t_0], \end{aligned} \right. \end{aligned}$$

(20)

where $\epsilon _0$ satisfies that

$(S_1)$ $0<\epsilon _0-{\tilde{\epsilon }}_0\ll 1$ when $\tau \ge \xi$, where ${\tilde{\epsilon }}_0=0\vee \left( \theta _1+\frac{\theta _2}{\lambda }\right)$;

$(S_2)$ $0<{\tilde{\epsilon }}_0-\epsilon _0\ll 1$ when $\tau <\xi$ and $\theta _1+\frac{\theta _2}{\lambda }<0$, where ${\tilde{\epsilon }}_0$ meets $\aleph ({\tilde{\epsilon }}_0)=0$;

$(S_3)$ $0<\epsilon _0-{\tilde{\epsilon }}_0\ll 1$ when $\tau <\xi$, $\theta _1+\frac{\theta _2}{\lambda }\ge 0$, $\lambda >\theta _2(-\tau +\xi )$ and $\theta _1(-\tau +\xi )-\ln (\lambda )+\ln (-\tau +\xi )+\ln \theta _2+1<0$, where $0<{\tilde{\epsilon }}_0<\epsilon _2$ and $\aleph ({\tilde{\epsilon }}_0)=0$. For any ${\check{t}} \in [t_k,t_{k+1})$, there is an integer $-1\le d\le k$ satisfies ${\check{t}}-\tau \in [t_d,t_{d+1})$, if ${\mathbb {E}}{\mathcal {M}}({\check{t}}-\tau )\exp \{\epsilon _0(t_k-t_d)\}\le {\mathbb {E}}{\mathcal {M}}({\check{t}})\exp \{-\ln \lambda +\epsilon _0{\mathbb {E}}\xi _{N({\check{t}},t_0)}\}$ is true, then one can infer that

$$\begin{aligned} D^+{\mathbb {E}}{\mathcal {M}}({\check{t}})<0. \end{aligned}$$

(21)

Proof

We define the auxiliary function shown below, for arbitrary $\pi >0$ and $k\in {\mathbb {N}}$,

$$\begin{aligned} {\mathcal {M}}_{\pi }(t)=\left\{ \begin{aligned} V(t,x)&\exp \{-(\epsilon _0+\pi )(t-t_k)\},\\ {}&t\in [t_k,t_{k+1}),\\ V(t), t&\in [t_0-\tau ,t_0]. \end{aligned} \right. \end{aligned}$$

(22)

According to (20), one has for ${\check{t}}\in [t_k,t_{k+1})$

$$\begin{aligned} {\mathcal {M}}({\check{t}}-\tau )=\left\{ \begin{aligned} V({\check{t}}&-\tau )\exp \{-\epsilon _0({\check{t}}-\tau -t_d)\},\\&\quad {\check{t}}-\tau \in [t_d,t_{d+1}),\\ V({\check{t}}&-\tau ),\quad {\check{t}}-\tau \in [t_0-\tau ,t_0]. \end{aligned} \right. \end{aligned}$$

(23)

Combining (7) and (23) we can generate

$$\begin{aligned}&\exp \{\pi ({\check{t}}-t_k)\}D^+{\mathbb {E}}{\mathcal {M}}_{\pi }(t)|_{t={\check{t}}}\nonumber \\&\quad =-(\epsilon _0+\pi )\exp \{-\epsilon _0({\check{t}}-t_k)\}{\mathbb {E}}V({\check{t}})+\exp \{-\epsilon _0({\check{t}}-t_k)\}D^+{\mathbb {E}}V({\check{t}})\nonumber \\&\quad \le (-\epsilon _0-\pi +\theta _1)\exp \{-\epsilon _0({\check{t}}-t_k)\}{\mathbb {E}}x^T(t)Px(t)+\theta _2\exp \{-\epsilon _0({\check{t}}-t_k)\}{\mathbb {E}}x_{{\check{t}}}^TPx_{{\check{t}}}\nonumber \\&\quad = (-\epsilon _0-\pi +\theta _1){\mathbb {E}}{\mathcal {M}}({\check{t}})+\theta _2\exp \{-\epsilon _0(\tau +t_d-t_k)\}{\mathbb {E}}{\mathcal {M}}({\check{t}}-\tau )\nonumber \\&\quad \le (-\epsilon _0-\pi +\theta _1+\theta _2\exp \{-\epsilon _0\tau \}\exp \{-\ln \lambda +\epsilon _0{\mathbb {E}}\xi _{N({\check{t}},t_0)}\}) {\mathbb {E}}{\mathcal {M}}({\check{t}})\nonumber \\&\quad \le \left( -\epsilon _0-\pi +\theta _1+\frac{\theta _2}{\lambda }\exp \{\epsilon _0(-\tau +\xi )\}\right) {\mathbb {E}}{\mathcal {M}}({\check{t}}). \end{aligned}$$

(24)

There are three situations to consider.

In terms of $(S_1)$, it leads to $\aleph ({\tilde{\epsilon }}_0)=\theta _1-{\tilde{\epsilon }}_0+\frac{\theta _2}{\lambda }\le 0$. Suppose that $0<\epsilon _0^*-{\tilde{\epsilon }}_0\ll 1$, then $\aleph (\epsilon _0^*)<0$.

In terms of $(S_2)$, it implies that $\aleph (0)<0$, $\aleph '(u)=-1+(-\tau +\xi )\frac{\theta _2}{\lambda }\exp \{u(-\tau +\xi )\}$, and $\aleph '(\epsilon _2)=0$. Apparently, if $\epsilon _2\le 0$, then $\aleph '(u)\ge 0$ on $(0,+\infty )$. If $\epsilon _2>0$, then $\aleph '(u)<0$ on $(0,\epsilon _2)$ and $\aleph '(u)>0$ on $(\epsilon _2,+\infty )$. Thus, there is unique constant ${\tilde{\epsilon }}_0$ such that $\aleph ({\tilde{\epsilon }}_0)=0$. Afterwards choose a constant $\epsilon _0^*$ that is close enough ${\tilde{\epsilon }}_0$, i.e., $0<{\tilde{\epsilon }}_0-\epsilon _0^*\ll 1$, which leads to $\aleph (\epsilon _0^*)<0$.

In terms of $(S_3)$, we can deduce that $\aleph (0)\ge 0$, $\epsilon _2>0$, $\aleph '(\epsilon _2)=0$, and $\aleph (\epsilon _2)<0$. Therefore, there is a constant ${\tilde{\epsilon }}_0\in (0,\epsilon _2)$ such that $\aleph ({\tilde{\epsilon }}_0)=0$. Select a proper constant $\epsilon _0^*$ to achieve $0<\epsilon _0^*-{\tilde{\epsilon }}_0\ll 1$, then $\aleph (\epsilon _0^*)<0$ still holds up.

In conclusion, for all the above situations, $\aleph (\epsilon _0)<0$ is the truth if $\epsilon _0=\epsilon _0^*$. As a result, (24) can be modified as $\exp \{\pi ({\check{t}}-t_k)\}D^+{\mathbb {E}}{\mathcal {M}}_{\pi }(t)|_{t={\check{t}}}\le -\pi {\mathbb {E}}{\mathcal {M}}({\check{t}})$. According to (22), one has

$$\begin{aligned}&D^+{\mathbb {E}}{\mathcal {M}}(t)|_{t={\check{t}}}\nonumber \\&\quad =\exp \{\pi ({\check{t}}-t_k)\}D^+{\mathbb {E}}{\mathcal {M}}_{\pi }({\check{t}})+\pi {\mathbb {E}}{\mathcal {M}}_{\pi }({\check{t}})\exp \{\pi ({\check{t}}-t_k)\}\nonumber \\&\quad < -\pi {\mathbb {E}}{\mathcal {M}}({\check{t}})+\pi {\mathbb {E}}{\mathcal {M}}({\check{t}})\nonumber \\&\quad =0. \end{aligned}$$

(25)

Proof of inequality (22) is completed. $\square$

Theorem 2

Under $(\wp _1)$ and $(\wp _2)$, let $\lambda _1=0$, $\lambda _2\in (0,1)$, if there are constants $\sigma$, $\kappa >0$, and $\mu \ge 0$ such that for $t\ge t_0$,

$$\begin{aligned} (\wp _4)&when~\tau >\xi , \\&\sigma N(t,t-\iota )+\epsilon _0\sum _{l=N(t-\iota ,t_0)+1}^{N(t,t_0)-1}{\mathbb {E}}\xi _l\le -\ln \lambda ;\\&when~\tau \le \xi , \\&\sigma (N(t,t-\iota )+1)+\epsilon _0\left( \sum _{l=N(t-\iota ,t_0)+1}^{N(t,t_0)-1}{\mathbb {E}}\xi _l+\sup _{l\in {\mathbb {R}}^+}{\mathbb {E}}\xi _{l}\right) \le -\ln \lambda ; \\&(\wp _5) -\sigma N(t,t_0)-\epsilon _0\sum _{l=0}^{N(t,t_0)}{\mathbb {E}}\xi _l+(\epsilon _0+\mu )(t-t_0)\le \kappa , \end{aligned}$$

where $\lambda _1$ and $\lambda _2$ are defined in Theorem 1. Then STDNN (1) with RDI is MSES.

Proof

We shell to prove the following inequality

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t)\le \Upsilon _k\exp \{\epsilon _0(t-t_0)\} \end{aligned}$$

(26)

for $t\in [t_k,t_{k+1})$, where $\Upsilon _k=||{\bar{\varphi }}||\exp \{\epsilon _0\varsigma \}\exp \{-k\sigma -\epsilon _0\sum _{i=0}^{k}{\mathbb {E}}\xi _i\}$ and $k\in {\mathbb {N}}$. Combining (26) and (20), it is equal to verify

$$\begin{aligned} {\mathbb {E}}{\mathcal {M}}(t)\le \Upsilon _k\exp \{\epsilon _0(t_k-t_0)\}, \end{aligned}$$

(27)

for $t\in [t_k,t_{k+1})$, $k\in {\mathbb {N}}$.

Notice that ${\mathbb {E}}{\mathcal {M}}(t_0)={\mathbb {E}}V(t_0)\le ||{\bar{\varphi }}||\le \Upsilon _0$. Assume that ${\mathbb {E}}{\mathcal {M}}(t)\le \Upsilon _0$ is not true for any $t_0\le t<t_1$, then there exists $t_0\le {\hat{t}}<t_1$ such that

$$\begin{aligned} {\mathbb {E}}{\mathcal {M}}({\hat{t}})&=\Upsilon _0,\nonumber \\ {\mathbb {E}}{\mathcal {M}}(t)&\le \Upsilon _0, t\in [t_0,{\hat{t}}],\nonumber \\ D^+{\mathbb {E}}{\mathcal {M}}({\hat{t}})&\ge 0. \end{aligned}$$

(28)

We analysis ${\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )$ as follow:

• (I) When $t_0\le {\hat{t}}-\tau \le {\hat{t}}$, from (28), one has ${\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )\le \Upsilon _0={\mathbb {E}}{\mathcal {M}}({\hat{t}})\le \frac{1}{\lambda }{\mathbb {E}}{\mathcal {M}}({\hat{t}})$, which is consistent with Lemma 4.

• (II) When ${\hat{t}}-\tau \in [t_0-\sigma ,t_0)$, then ${\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )={\mathbb {E}}V({\hat{t}}-\tau )\le ||{\bar{\varphi }}||\le \Upsilon _0={\mathbb {E}}{\mathcal {M}}({\hat{t}})\le \frac{1}{\lambda }{\mathbb {E}}{\mathcal {M}}({\hat{t}})$, which also satisfies Lemma 4.

Providing (27) is valid for $k\le L$, $L\in {\mathbb {N}}$. We will have

$$\begin{aligned} {\mathbb {E}}{\mathcal {M}}(t)\le \Upsilon _{L+1}\exp \{\epsilon _0(t_{L+1}-t_0)\}, \end{aligned}$$

(29)

for $t\in [t_{L+1},t_{L+2})$.

Set $R_m=[t_{L+1}-t_{m+1},t_{N+1}-t_m)$, where $m\in [-1,L]$. Hence, $t_m\le (t_{L+1}-\xi _{L+1})^-<t_{m+1}$ when $\xi _{L+1}\in R_m$. According to total probability formula and (26), one has

$$\begin{aligned}&{\mathbb {E}} \left( x^T(t_{L+1}-\xi _{L+1})^-Px(t_{L+1}-\xi _{L+1})^-\right) \nonumber \\&\quad =\sum _{m=-1}^{L}{\mathbb {E}}\left[ x^T(t_{L+1}-\xi _{L+1})^-Px(t_{L+1}-\xi _{L+1})^-\right. \nonumber \\&\qquad \left. \times |\xi _{L+1}\in R_m \right] P(\xi _{L+1}\in R_m)\nonumber \\&\quad \le \max _{-1\le m\le L}\{\Upsilon _m{\mathbb {E}}[\exp \{\epsilon _0((t_{L+1}-\xi _{L+1})^{-}-t_0)\}\nonumber \\&\qquad \times |\xi _{L+1}\in R_m]\} \sum _{m=-1}^{L}P(\xi _{N+1}\in R_m)\nonumber \\&\quad =\max _{-1\le m\le L}\{\Upsilon _m{\mathbb {E}}[\exp \{\epsilon _0((t_{L+1}-\xi _{L+1})^{-}-t_0)\} |\xi _{L+1}\in R_m]\}. \end{aligned}$$

(30)

There exists an integer $s\in [-1,L]$ such that

$$\begin{aligned}&\Upsilon _s{\mathbb {E}}[\exp \{\epsilon _0((t_{L+1}-\xi _{L+1})^{-}-t_0)\}|\xi _{L+1}\in R_s]\nonumber \\&\quad =\max _{-1\le m\le L}\{\Upsilon _m{\mathbb {E}}[\exp \{\epsilon _0((t_{L+1}-\xi _{L+1})^{-}-t_0)\}|\xi _{L+1}\in R_m]\}. \end{aligned}$$

(31)

At $t=t_{L+1}$, from (7), (20), (30) and (31), one gets

$$\begin{aligned}&{\mathbb {E}}{\mathcal {M}}(t_{L+1})={\mathbb {E}}x^T(t_{L+1})Px(t_{L+1})\nonumber \\&\quad \le \lambda \Upsilon _s{\mathbb {E}}[\exp \{\epsilon _0((t_{L+1}-\xi _{L+1})^--t_0)\}|\xi _{L+1}\in R_s]\nonumber \\&\quad \le \lambda \Upsilon _s{\mathbb {E}}[\exp \{\epsilon _0(t_{L+1}-\xi _{L+1}-t_0)\}\exp \{\epsilon _0\xi _{L+1}\}\nonumber \\&\qquad \times \exp \{-\epsilon _0{\mathbb {E}}\xi _{L+1}\}|\xi _{L+1}\in R_s]\nonumber \\&\quad \le \lambda \Upsilon _s{\mathbb {E}}[\exp \{\epsilon _0(t_{L+1}-t_0)\}\exp \{-\epsilon _0{\mathbb {E}}\xi _{L+1}\}|\xi _{L+1}\in R_s]\nonumber \\&\quad =\lambda \Upsilon _s \exp \{\epsilon _0(t_{L+1}-t_0)\}\exp \{-\epsilon _0{\mathbb {E}}\xi _{L+1}\}\nonumber \\&\quad = \lambda \Upsilon _{L+1}\exp \{\epsilon _0(t_{L+1}-t_0)\}\exp \{\sigma (L+1-s)+\epsilon _0\sum _{l=s+1}^{N}{\mathbb {E}}\xi _l\}. \end{aligned}$$

(32)

Owing to $\xi _{L+1}\in R_s$, we can get that $t_s<t_{L+1}-\xi _{L+1}\le t_{s+1}$. Therefore, when $\tau >\xi$, namely, $t_{L+1}-\iota <t_{L+1}-\xi _{L+1}\le t_{s+1}$, one can infer that $L+1-s=N(t_{L+1},t_s)\le N(t_{L+1},t_{L+1}-\iota )$ and $s+1=N(t_{s+1},t_0)\ge N(t_{L+1}-\iota ,t_0)+1$, which generate that

$$\begin{aligned}&\sigma (L+1-s)+\epsilon _0\sum _{l=s+1}^{N}{\mathbb {E}}\xi _l\nonumber \\&\quad \le \sigma N(t_{L+1},t_{L+1}-\iota )+\epsilon _0\sum _{l=N(t_{L+1}-\iota ,t_0)+1}^{N(t_{L_1},t_0)-1}{\mathbb {E}}\xi _l. \end{aligned}$$

(33)

When $\tau \le \xi$, one can ascertain that $L+1-s=N(t_{L+1},t_s)\le N(t_{L+1},t_{L+1}-\iota )+1$ and $s+1=N(t_{s+1},t_0)\ge N(t_{L+1}-\iota ,t_0)$, which mean that

$$\begin{aligned}&\sigma (L+1-s)+\epsilon _0\sum _{l=s+1}^{N}{\mathbb {E}}\xi _l\nonumber \\&\quad \le \sigma (N(t_{L+1},t_{L+1}-\iota )+1)+\epsilon _0\left( \sum _{l=N(t_{L+1}-\iota ,t_0)+1}^{N(t_{L+1},t_0)-1}{\mathbb {E}}\xi _l+{\mathbb {E}}\xi _{N(t_{L+1}-\iota ,t_0)}\right) \nonumber \\&\quad \le \sigma (N(t_{L+1},t_{L+1}-\iota )+1)+\epsilon _0\left( \sum _{l=N(t_{L+1}-\iota ,t_0)+1}^{N(t_{L+1},t_0)-1}{\mathbb {E}}\xi _l+\sup _{l\in {\mathbb {R}}^+}{\mathbb {E}}\xi _{l}\right) . \end{aligned}$$

(34)

Notice that if $N(t_{L+1},t_0)-1<N(t_{L+1}-\iota ,t_0)+1$, then $\sum _{l=N(t_{L+1}-\iota ,t_0)+1}^{N(t_{L+1},t_0)-1}{\mathbb {E}}\xi _l=0$. Integrating $(\wp _4)$, (32), (33) and (34), we can deduce that ${\mathbb {E}}{\mathcal {M}}(t_{L+1})\le \Upsilon _{L+1}\exp \{\epsilon _0(t_{N+1}-t_0)\}$, i.e., (29) holds for $t=t_{N+1}$.

Assume that there exists ${\hat{t}}\in [t_{L+1},t_{L+2})$ such that

$$\begin{aligned} {\mathbb {E}}{\mathcal {M}}({\hat{t}})&=\Upsilon _{L+1}\exp \{\epsilon _0(t_{L+1})-t_0\},\nonumber \\ {\mathbb {E}}{\mathcal {M}}(t)&\le \mathbb \ E{\mathcal {M}}({\hat{t}}), t_{N+1}\le t\le {\hat{t}},\nonumber \\ D^+{\mathbb {E}}{\mathcal {M}}({\hat{t}})&\ge 0. \end{aligned}$$

(35)

Now we discuss the position of ${\hat{t}}-\tau$. It is divided into three cases to consider.

$(\ell _1)$ When $t_{N+1}\le {\hat{t}}-\tau \le {\hat{t}}$, $d=k=L+1$ is met. It yields that

$$\begin{aligned}&{\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )\exp \{\epsilon _0(t_{k}-t_d)\}\nonumber \\&\quad \le {\mathbb {E}}{\mathcal {M}}({\hat{t}})\nonumber \\&\quad \le {\mathbb {E}}{\mathcal {M}}({\hat{t}})\exp \{-\ln \lambda +\epsilon _0{\mathbb {E}}\xi _{N({\hat{t}},t_0)}\}, \end{aligned}$$

(36)

which means condition of Lemma 4 is satisfied.

$(\ell _2)$ When $t_d\le {\hat{t}}-\tau <t_{d+1}$, where d is defined in Lemma 4 and $d\in [0,L]$, one has

$$\begin{aligned}&{\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )\exp \{\epsilon _0(t_{L+1}-t_d)\}\nonumber \\&\quad \le \Upsilon _d\exp \{\epsilon _0(t_d-t_0)+\epsilon _0(t_{L+1}-t_d)\}\nonumber \\&\quad =\Upsilon _{L+1}\exp \{\epsilon _0(t_{L+1}-t_0)\}\exp \left\{ \sigma (L+1-d)+\epsilon _0\sum _{l=d+1}^{L+1}{\mathbb {E}}\xi _l\right\} . \end{aligned}$$

(37)

Through $t_d\le {\hat{t}}-\tau<t_{d+1}\le t_{L+1}\le {\hat{t}}<t_{L+2}$, it is generated that $L+1-d=N(t_{L+1},t_d)=N({\hat{t}},{\hat{t}}-\tau )\le N({\hat{t}},{\hat{t}}-\iota )$. According to $(\wp _4)$, one can obtain

$$\begin{aligned}&\sigma (L+1-d)+\epsilon _0\sum _{l=d+1}^{L+1}{\mathbb {E}}\xi _l\nonumber \\&\quad \le \sigma N({\hat{t}},{\hat{t}}-\tau )+\epsilon _0\sum _{l=N({\hat{t}}-\iota ,t_)+1}^{N({\hat{t}},t_)}{\mathbb {E}}\xi _l\nonumber \\&\quad \le -\ln \lambda +\epsilon _0{\mathbb {E}}\xi _{N({\hat{t}},t_0)}. \end{aligned}$$

(38)

Integrating (37) and (38), we have ${\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )\exp \{\epsilon _0(t_{L+1}-t_d)\}\le {\mathbb {E}}{\mathcal {M}}({\hat{t}})\exp \{-\ln \lambda +\epsilon _0{\mathbb {E}}\xi _{N({\hat{t}},t_)}\}$, which admits condition of Lemma 4.

$(\ell _3)$ When $t_d\le {\hat{t}}-\tau <t_{d+1}$, where $d=-1$,

$$\begin{aligned}&{\mathbb {E}}{\mathcal {M}}({\hat{t}}-\tau )\exp \{\epsilon _0(t_{L+1}-t_d)\}\nonumber \\&\quad ={\mathbb {E}}x^T({\hat{t}}-\tau ) Px({\hat{t}}-\tau )\exp \{\epsilon _0(t_{L+1}-t_{-1})\}\nonumber \\&\quad \le ||{\bar{\varphi }}||\exp \{\epsilon _0\iota \}\exp \{\epsilon _0(t_{L+1}-t_0)\}\nonumber \\&\quad =\Upsilon _{L+1}\exp \{\epsilon _0(t_{L+1}-t_0)\}\exp \{\sigma (L+1)+\epsilon _0\sum _{l=0}^{L+1}{\mathbb {E}}\xi _l\}\nonumber \\&\quad = {\mathbb {E}}{\mathcal {M}}({\hat{t}})\exp \{\sigma N({\hat{t}},{\hat{t}}-\tau )+\epsilon _0\sum _{l=N({\hat{t}}-\iota ,t_0)+1}^{N({\hat{t}},t_0)}{\mathbb {E}}\xi _l\}\nonumber \\&\quad \le {\mathbb {E}}{\mathcal {M}}({\hat{t}})\exp \{-\ln \lambda +\sigma {\mathbb {E}}\xi _{N({\hat{t}},t_0)}\}, \end{aligned}$$

(39)

where $N({\hat{t}}-\iota ,t_0)$ is zero.

To sum up, applying Lemma 4, we can conclude that $D^+{\mathbb {M}}({\hat{t}})<0$, which is in conflict with (35). Consequently, (29) holds for $t\in [t_{L+1},t_{L+2})$. We infer through mathematical induction that (27) holds for any $t_k\le t<t_{k+1}$, $k\in {\mathbb {N}}$. That is,

$$\begin{aligned} {\mathbb {E}}x^T(t)Px(t) \le&||{\bar{\varphi }}||\exp \{\epsilon _0\iota \}\exp \{-\sigma N(t,t_0)-\epsilon _0\sum _{l=0}^{N(t,t_0)}{\mathbb {E}}\xi _l+\epsilon _0(t-t_0)\}. \end{aligned}$$

(40)

Futhermore, utilizing $(\wp _5)$,

$$\begin{aligned} {\mathbb {E}}||x(t)||^2 \le&\frac{\lambda _{\max }(P)}{\lambda _{\min }(P)}\exp \{\epsilon _0\iota +\kappa -\eta (t-t_0)\}\sup _{u\in [t_0-\iota ,t_0]}{\mathbb {E}}||\varphi (u)||^2. \end{aligned}$$

(41)

$\square$

Corollary 2

Set $\lambda =\lambda _1+\lambda _2$ and $\lambda _1=0$, $\lambda _2\in (0,1)$, $\epsilon _0>0$ is given in Lemma 4. Provided that there exists constant $\sigma >0$ such that $(\wp _4)$ and following inequality

$$\begin{aligned} (\wp _5')~~~~ \frac{\sigma }{\epsilon _0}+{\bar{\xi }}>{\mathcal {T}}_a \end{aligned}$$

hold, then ISTDNN (1) with RDIs is MSES.

Proof

Using Definitions 1 and 2, one has

$$\begin{aligned}&-\sigma N(t,t_0)-\epsilon _0\sum _{l=0}^{N(t,t_0)}{\mathbb {E}}\xi _l+\epsilon _0(t-t_0)\nonumber \\&\quad \le -\sigma \left( \frac{t-t_0}{{\mathcal {T}}_a}-N_0\right) -\epsilon _0({\bar{\xi }}N(t,t_0)-\xi ^*)+\epsilon _0(t-t_0)\nonumber \\&\quad \le \left( \frac{-\sigma -\epsilon _0{\bar{\xi }}+\epsilon _0{\mathcal {T}}_a}{{\mathcal {T}}_a}\right) (t-t_0)+\sigma N_0+\epsilon {\bar{\xi }}N_0+\epsilon _0\xi ^*. \end{aligned}$$

(42)

It implies that $(\wp _5)$ is satisfied under condition $(\wp _5')$ with $\eta =\frac{\sigma +\epsilon _0{\bar{\xi }}-\epsilon _0{\mathcal {T}}_a}{{\mathcal {T}}_a}$ and $\kappa =\sigma N_0+\epsilon {\bar{\xi }}N_0+\epsilon _0\xi ^*$. So, we infer from Theorem 2 that STDNNs (1) with RDIs are MSES. $\square$

Remark 4

In Theorem 2, $\theta _1>0$, which means that in the absence of impulsive behavior, the original STDNNs (1) may be unstable. Theorem 2 and Corollary 2 show that, while the continuous subsystems of STDNNs (1) may be unstable, dynamics behavior of hybrid STDNNs (1) remain stable, indicating that stabilization function of delayed impulses.

Remark 5

Condition $(\wp _5')$ exhibits not just relationship between ${\bar{\xi }}$ and ${\mathcal {T}}_a$, but also that ${\mathcal {T}}_a$ has an upper bound. We can obtain $\frac{\epsilon _0(t-t_0)}{\sigma +\epsilon _0\xi }-N_0<\frac{t-t_0}{{\mathcal {T}}_a}-N_0\le N(t,t_0)$ through incorporating Definition 1 and condition $(\wp _5')$. Inequality $\frac{t-t_0}{{\mathcal {T}}_a}-N_0\le N(t,t_0)$ contributes to stability of STDNN (1). Inequality $\frac{\epsilon _0(t-t_0)}{\sigma +\epsilon _0\xi }-N_0\le N(t,t_0)$ aids in the speedier stabilization of STDNN (1).

4 Numerical Examples

Three numerical examples are offered in this part to show the efficacy and practicality of our theoretical conclusions.

Example 1

Take into account a two-dimensional STDNN with random delayed impulses

$$\begin{aligned} \left\{ \begin{aligned} dx(t)&=[-Dx(t)+Bf(x_t)]dt+g(t,x(t),x_t)d\omega (t),\\ x(t_k)&=S_kx(t_k^-)+H_kx((t_k-\xi _k)^-), \end{aligned}\right. \end{aligned}$$

(43)

where

$$\begin{aligned} D&=\begin{bmatrix} 4&{} -0.5\\ -0.4&{}5 \end{bmatrix},~ B=\begin{bmatrix} 0.4&{} 0.6\\ 1.2&{} 0.5 \end{bmatrix},\\ S_k&=\begin{bmatrix} 0.6 &{} 0.1\\ 0.3&{} 0.4 \end{bmatrix}, H_k=\begin{bmatrix} 1.3&{} 0.3\\ 0.2&{} 1.5 \end{bmatrix}, \end{aligned}$$

for simulation, take $f(x_t)=\tanh x(t-\tau )$, matrix $P=I$, i.e., P is identity matrix and $V(t,x(t))=x^T(t)x(t)$, $g(t,x(t),x_t)=\begin{bmatrix} 0.2x_1(t-\tau )&{}0\\ 0&{} 0.3x_2(t) \end{bmatrix}$.

By counting,

$$\begin{aligned} {\mathcal {L}}x^T(t)x(t)&=2x^T(t)(-Dx(t)+Bf(x_t))\\&\quad +trace(g^T(t,x(t),x_t)g(t,x(t),x_t))\\&\le (2\lambda _{\max }(-D)+1+0.09)x^T(t)x(t)\\&\quad +(\lambda _{\max }(B^TB)+0.04)x^T(t-\tau )x(t-\tau ),\\ {\mathbb {E}}x^T(t_k)x(t_k)&\le 2\lambda _{\max }(S_k^TS_k)x^T(t_k^-)x(t_k^-)\\&\quad +2\lambda _{\max }(H_k^TH_k)x^T((t_k-\xi _k)^-)x((t_k-\xi _k)^-), \end{aligned}$$

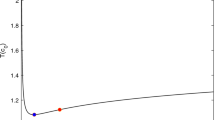
where $\lambda _{\max }(-D)=-3.8292$, $\lambda _{\max }(B^TB)=2.08$. Thus, ${\mathbb {E}}{\mathcal {L}}x^T(t)x(t)\le \theta _1{\mathbb {E}}x^T(t)x(t)+\theta _2{\mathbb {E}}x^T(t-\tau )x(t-\tau )$ with $\theta _1=-6.5684$ and $\theta _2=3.12$, which demonstrates that STDNN (43) is stable in the absence of impulses, see Fig. 1. Figure 1 shows that state trajectory of STDNN (43) without impulsive action.

Table 1 Distribution of delay in impulses

Furthermore, set $\xi _k$ complies with discrete distribution depicted in Table 1, $t_k=6k$, and $\tau =3$. The destabilizing traits of delay in impulses is clearly displayed in Fig. 2 via comparison of state trajectories of (43) with RDIs and with non-delayed impulses. Through Corollary 1, it can be determined that STDNN (43) is MSES if $\xi _k=0$, see red line in Fig. 2. The red line in Fig. 2 indicates that when (43) is only subjected to non-delayed impulses, it remains stable. However, if every delay $\xi _k$ in impulse obeys the distribution presented in Table 1, stability of STDNN (43) is jeopardized. Besides, ${\bar{\xi }}=9.72$ and ${\bar{\xi }}+\frac{\ln \lambda }{\epsilon _1}>{\mathcal {T}}_a$, $\epsilon _1=0.2360$, which fails to meet condition $(\wp _3')$, see blue line in Fig. 2. Blue line in Fig. 2 shows that when (43) is subjected to delayed impulses, its stability is disrupted. This demonstrates that impulsive delay has a detrimental influence on stability of STDNN, which can make stable STDNN unstable. This implies that, despite the fact that the impulsive strength is unvarying, delayed impulses maybe degrade dynamics behavior.

Fig. 1

Dynamic behavior of SNN (43) without impulses

Fig. 2

Dynamic behavior of SNN (43) with $\xi _k=0$ and $\xi _k$ in Table 1

Fig. 3

Dynamic behavior of SNN (43) with $\tau =3$, $t_k=6k$, and $\xi _{2k}\sim U(1,4)$, $\xi _{2k+1}\sim U(2,6)$

Fig. 4

Dynamic behavior of SNN (43) with $\tau =3$, $t_k=6k$, and $\xi _7=\xi _8=\xi _9=12$, $\xi _{k} \sim U(0,9)$, $k\ne 7,8,9$

Fig. 5

Dynamic behavior of SNN (43) with $\tau =10$, $t_k=9.9k$, and $\xi _{k} \sim U(0,1.6)$

Assume that random delay $\xi _{2k}$ obeys the uniform distribution U(1, 4), $\xi _{2k+1}$ obeys U(2, 6) and $t_k=6k$, $\tau =3$. Under Collaroy 1, $(\wp _1)$, $(\wp _2)$, and $(\wp _3')$ are valid for STDNN (43). Figure 3 further demonstrates that STDNN (43) is MSES. Compared to Fig. 1, the convergence speed of STDNN (43) may slow down, which signifies that conclusion of this paper is more comprehensive than previous research. To put it simply, with this in mind that the continuous dynamics is stable, though impulsive delays act as interference that impacts the dynamic behavior of network, STDNN (43) remains stable when faced with small input impulsive delay.

Particularly, if $\xi _7=\xi _8=\xi _9=12$, the remaining $\xi _k$, $k\ne 7,8,9$ obey uniform distribution U(0, 9), $t_k=6k$, $\tau =3$. According Corollary 1, STDNN (43) is also MSES as shown in Fig. 4.

In addition, set every $\xi _k$ obeys uniform distribution U(0, 1.6), $t_k=9.9k$ and $\tau =10$. Base on Corollary 1, STDNN (43) is MSES as shown in Fig. 5.

Figures 4 and 5 respectively indicate that stability performance of (43) remains unchanged when delay in impulses and delay in the continuous systems exceed the impulsive interval, which is not supported by literatures [18, 20, 22], etc.

Example 2

Take into account a two-dimensional STDNN with impulsive control

$$\begin{aligned} \left\{ \begin{aligned} dx(t)=&[-Ax(t)+Bf(t)+Cf(x(t-\tau ))]dt\\&+g(x(t),x(t-\tau ))d\omega (t),\\ \Delta x(t_k)&=u(t_k), \end{aligned}\right. \end{aligned}$$

(44)

where $\Delta x(t_k)=x(t_k)-x(t_k^-)$, take $u(t_k)=Hx((t_k-\xi _k)^-)-x(t_k^-)$, $V(t,x(t))=x^T(t)x(t)$, then,

$$\begin{aligned}&{\mathcal {L}}V(t,x(t),x(t-\tau ))\\&\quad \le 2x^T(t)(-Ax(t)+Bf(x(t))+Cf(x(t-\tau )))\\&\qquad +trace(g^T(x(t),x(t-\tau ))g(x(t),x(t-\tau ))). \end{aligned}$$

Table 2 Distribution of delay in impulses

Following that, two scenarios will be analyzed.

$(\ell _1)$ For emulation, we set $f(x(t))=\tanh (\frac{x(t)}{2})$

$$\begin{aligned} A&=\begin{bmatrix} 2&{} 0\\ 0&{}2 \end{bmatrix},~ B=\begin{bmatrix} 1.2&{} -0.2\\ -1.1&{} 1.2 \end{bmatrix},\\ C&=\begin{bmatrix} -0.4 &{} 1.1\\ 1.2&{} -0.4 \end{bmatrix}, H=\begin{bmatrix} 0.4&{} 0\\ 0&{} 0.4 \end{bmatrix},\\ g(x(t),x(t-\tau ))&=\begin{bmatrix} 0.2x_1(t-\tau ) &{} 0.3x_1(t)\\ 0.3x_2(t)&{} 0.2x_2(t-\tau ) \end{bmatrix}. \end{aligned}$$

By calculation,

$$\begin{aligned}&{\mathcal {L}}V(t,x(t),x(t-\tau ))\\&\quad \le \left( \lambda _{\max }\left( -A-A'+I+\frac{B'B}{4}+C'C\right) +0.09\right) x^T(t)x(t)\\&\qquad +0.29x^T(t-\tau )x(t-\tau ), \end{aligned}$$

where $I=[1,0;0,1]$, $\lambda _{\max }\left( -A-A'+I+\frac{B'B}{4}+C'C\right) =0.337$. Thus, $\theta _1=0.427$, $\theta _2=0.29$, and $\lambda =0.16$. Moreover, assume that $t_k=0.2k$, $\tau =0.4$, $\xi _k\sim U(0,0.6)$, which implies that ${\mathcal {T}}_a=0.2$, ${\bar{\xi }}=0.3$, $\iota =\xi =0.6$, $\xi ^*=N_0=0$, and $N(t,t-\iota )\le 2$. In the light of $(S_3)$, based on $\aleph ({\tilde{\epsilon }}_0)=0$, one can obtain ${\tilde{\epsilon }}_0=1.5184$. It is straightforward to calculate $\aleph (\epsilon _0)=-0.0013<0$ by taking $\epsilon _0=1.52$. Afterwards opt for $\sigma =0.0001$, $(\wp _4)$ and $(\wp _5')$ are generated. From Corollary 2, STDNN (44) is MSES, see Fig. 6.

It is worth mentioning that in $(\ell _1)$, $0<\xi _k<0.6$, $\tau =0.4$, and ${\mathcal {T}}_a=0.2$ illustrate that time-delays in impulses or continuous dynamics can be concurrently adaptable. Figure 6 shows that in this paper, the delay in continuous systems and the delay in impulses can simultaneously exceed impulsive interval.

$(\ell _2)$ Make A, B, C, and $g(x(t),x(t-\tau ))$ the same as that in $(\ell _1)$, $f(x(t))=\tanh (\frac{x(t)}{4})$, and

$$\begin{aligned} H=\begin{bmatrix} 0.6&{} 0\\ 0&{} 0.6 \end{bmatrix}. \end{aligned}$$

Then $\theta _1=0.0659$, $\theta _2=0.3529$, and $\lambda =0.36$. We suppose $\xi _k$ follows the distribution indicated in Table 2, where $Y_1\sim U(0.3,0.6)$, $Y_2\sim U(0.2,0.3)$.

In addition, $\tau =0.8$, $t_k=0.6k$, one has that $\xi =0.6$, ${\bar{\xi }}=0.32$, ${\mathcal {T}}_a=0.6$, $\iota =0.8$, and $N(t,t-\iota )\le 1$. From $(S_1)$, ${\epsilon _0}=1.0462$. Choose that $\epsilon _0=1.05$, $\sigma =1.0217$, $(\wp _4)$ and $(\wp _5')$ are hold. From Corollary 2, it can be concluded that STDNN (44) is MSES, as shown Fig. 7.

Fig. 6

Dynamic behavior for STDNNs (44) in $(\ell _1)$

Fig. 7

Dynamic behavior of $||x(t)||_1$ for STDNNs (44) in $(\ell _2)$

In Fig. 7, we can notice that the initial unstable STDNNs (44) (red line in Fig. 7) remains unstable when subjected to impulsive control without time-delay. However, as observed by blue line in Fig. 7, it becomes stable when subjected to impulsive control with random delay characteristics. This result implies that delayed impulses have a stabilizing effect on the system and contribute to its stability.

Example 3

The efficiency of stated strategy is demonstrated in this example by using the time-delay Chua’s circuit as master system

$$\begin{aligned}\left\{ \begin{aligned} {\dot{x}}_1(t)&=a(x_2(t)-m_1x_1(t)+g_1(x_1(t)))-c_1x_1(t-\tau )\\ {\dot{x}}_2(t)&=x_1(t)-x_2(t)+x_3(t)-cx_3(t)\\ {\dot{x}}_3(t)&=-bx_2(t)+c(2x_1(t-\tau )-x_3(t-\tau )) \end{aligned}\right. \end{aligned}$$

with nonlinear characteristics $g(x_1(t))=\frac{1}{2}(m_1-m_0)(|x_1(t)+1|-|x_1(t)-1|)$ and parameters $m_0=-1/7$, $m_1=2/7$, $a=9$, $b=14.28$, $c=0.1$, and time-delay $\tau =0.4$. The delayed Chua’s circuit can be rewrittrn

$$\begin{aligned} {\dot{x}}(t)=Ax(t)+A_1x(t-\tau )+Df(x), \end{aligned}$$

(45)

where

$$\begin{aligned}&A=\begin{bmatrix} -18/7&{} 9&{}0\\ 1&{}-1&{}1\\ 0&{}-14.28&{}0 \end{bmatrix},~ A_1=\begin{bmatrix} -0.1&{} 0&{}0\\ -0.1&{}0&{}0\\ 0.2&{}0&{}-0.1 \end{bmatrix},\\&D=\begin{bmatrix} 27/7 &{} 0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{bmatrix}, \end{aligned}$$

and $f(x)=(0.5|x_1(t)+1|-|x_1(t)-1|,0,0)^T$. From Fig. 8, it can be observed that dynamic behavior of (45) exhibits chaos. The corresponding response system is designed by following the same structure as the drive system but considering stochastic perturbation and delayed impulsive controllers

Fig. 8

Dynamic behavior for system (45)

Fig. 9

Dynamic behavior of system (47) under non-delayed impulses

Fig. 10

Dynamic behavior of system (47) under random delayed impulses

$$\begin{aligned} \left\{ \begin{aligned} dy(t)=&[Ay(t)+A_1y(t-\tau )+Df(y)]dt\\&+\sigma (t,y(t)-x(t),y(t-\tau )-x(t-\tau ))d\omega (t),\\ \Delta x(t_k)&=u(t_k), \end{aligned}\right. \end{aligned}$$

(46)

where $\Delta x(t_k)=x(t_k)-x(t_k^-)$, take $u(t_k)=Hx((t_k-\xi _k)^-)-x(t_k^-)$. Defining the synchronization error as $e(t)=y(t)-x(t)$, we can get the error dynamics

$$\begin{aligned} \left\{ \begin{aligned} de(t)=&[Ae(t)+A_1e(t-\tau )+D{\bar{f}}(e)]dt\\&+\sigma (t,e(t),e(t-\tau ))d\omega (t),\\ e(t_k)=&\Pi e(t_k-\xi _k), k\in {\mathbb {N}}^+, \end{aligned}\right. \end{aligned}$$

(47)

where ${\bar{f}}(e(t))=f(y(t))-f(x(t))$ and ${\bar{f}}^T(e(t)){\bar{f}}(e(t))\le e^T(t)e(t)$,

$$\begin{aligned} \Pi =\begin{bmatrix} 0.7&{} 0&{}0\\ 0&{} 0.7&{}0\\ 0&{}0&{}0.7 \end{bmatrix}. \end{aligned}$$

(48)

It should be emphasized that stochastic perturbation might arise as a result of internal errors when simulation circuits are built, such as inadequate design of coupling strength and other significant variables. Choose $V(t,e(t))=e^T(t)e(t)$, by calculation, it yields

$$\begin{aligned} {\mathcal {L}}V(t)=&\,2e^T(t)[Ae(t)+A_1e(t-\tau )+D{\bar{f}}(e)]+|\sigma (t,e(t),e(t-\tau ))|^2\nonumber \\ \le&\, 32.8081V(t)+3V(t-\tau ), t\ne t_k, \end{aligned}$$

(49)

Thus, $\theta _1=32.8081$, $\theta _2=3$, and $\lambda =0.49$. Moreover, assume that $t_k=0.5k$, $\tau =0.5$, $\xi _k=0$, $k\in {\mathbb {N}}$, i.e., no delay on impulses. From $(S_1)$, we can calculate that $\tilde{\epsilon _0}=38.9305$. Choose that $\epsilon _0=38.9$, $\sigma =12.8275$. Under non-delayed impulsive control, it is noted in Fig. 9 that the error system remains unstable. In actually, we can compute $\frac{\sigma }{\epsilon _0}\ngtr {\mathcal {T}}_a$ in this scenario. However, for $\forall k\in {\mathbb {N}}$, if random delay $\xi _k\sim U(0,0.4)$, which implies that ${\mathcal {T}}_a=0.5$, ${\bar{\xi }}=0.2$, $\iota =\xi =0.5$, $\xi ^*=N_0=0$, and $N(t,t-\iota )\le 1$, from $(S_1)$, it can be obtained that $\tilde{\epsilon _0}=38.9305$. Choose that $\epsilon _0=38.9$, $\sigma =12.8275$, $(\wp _4)$ and $(\wp _5')$ are hold. From Corollary 2, error system (47) is MSES. Furthermore, as seen in Fig. 10, error system (47) becomes stable in the presence of delayed impulses. This result implies that delayed impulses have a stabilizing function on the system and contribute to its stability. In this situation, $(\wp _5')$ corresponds to inequality (21) in literature [20] and inequality (3.18) in literature [28].

Remark 6

Despite the fact that literatures [24] and [25] have researched random impulsive systems, results on the time-delay in impulses have not yet been revealed. The unstable or stable properties of delay in impulses are described in literatures [18, 20, 22, 28], and so on, however this paper also analyzes random interference causes and random delay impulse.

5 Conclusion

In this paper, stability issue of STDNNs with RDIs is studied. Firstly, we derive a novel inequality for impulsive delay with random properties. Thereafter, integrating this inequality with ideas of AII and ARD, stability criteria for STDNNs are established by utilizing stochastic analytic techniques and linear matrix inequalities. In particular, double impact of delays on impulses is taken into account. Furthermore, we loosen stringent limitations on impulsive delays. The results obtained illustrate that impulsive delays may destabilize impulsive STDNNs, and that when subjected to tiny input impulsive delays, stability performance of STDNNs becomes sluggish. On the contrary, under delayed impulsive control, convergence rate of STDNNs improves as impulsive delays get longer. The majority of future effort will be devoted to synchronization performance of uncertain STDNNs under RDIs.