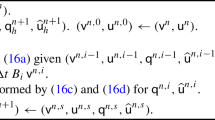Abstract
In this contribution, we apply space-time formulation on constrained rigid body dynamics. In particular, we discretize directly Hamilton’s principle using appropriate space-time approximation spaces for the variational problem. Moreover, we make use of a rotationless formulation for the rigid bodies, and thus we have to define appropriate approximation spaces for the Lagrange multipliers as well. Moreover, we make use of Livens’ principle, introducing independent quantities for the position, velocity, and momentum, where the latter can be considered as Lagrange multipliers, and we apply this concept to the space-time rigid body formulation. Finally, we demonstrate the convergence of the different approaches and the superiority in terms of computational effort, and thus total energy consumption of dynamical simulations.
Similar content being viewed by others
1 Introduction
A wide range of publications in rigid body dynamics have been available for centuries; however, nearly all of them consider a strong form of the equations in temporal direction. Accordingly, finite difference schemes are applied leading to classical time-stepping formulations. This framework has been extensively explored for rigid bodies, introducing stabilization techniques (Baumgarte [4]), numerical diffusion in time (Hilbert et al. [16]) or mechanical integrators (Betsch [5]). It is obvious that only a few titles can be cited here, as whole journals are dedicated to this issue.
Discretization techniques of the Lagrangian itself have been taken into account (so-called variational integrators, see Lew et al. [20]), as well as temporal finite elements, see, e.g., Betsch et al. [6–8] for a series on finite element formulations in time. All of them are constructed in such a way that information from the past only affects the future, as this is the natural way oneself experiences time. Hence, at the end a single or multi-step method in time is derived, avoiding the solution of the whole space-time cylinder at once and the transfer of information backwards in time. However, we will show that this is not the optimal way to consider the temporal direction of constrained mechanical systems.
Discontinuous space-time Galerkin methods have been applied in, among others, Haber [1], who applied them to the whole space-time cylinder. Continuous space-time Bubnov–Galerkin strategies on deformable bodies are presented in [15, 23, 25], see also Hughes et al. [17]. In Langer et al. [19], stabilization techniques are developed for parabolic systems using fundamental consideration of Ladyzhenskaya [18]. For inverse problems, Ströhle et al. [27] demonstrate the superiority of continuous space-time Galerkin methods.
In this contribution, we extend the concept of a continuous space-time Bubnov–Galerkin method towards rigid bodies. To be specific, we derive the formulation directly from the continuous case of nonlinear elastodynamics and constrain the body to obtain in the limit of infinitely large material parameters a set of differential algebraic equations (DAE’s) for the rigid body. To avoid unconvincing complexity, especially in the case of multiple connected rigid bodies, we circumvent the use of rotational variables to describe the orientation of the individual rigid bodies, see Betsch et al. [10] for a more detailed discussion. In this sense, we make use of a rotationless formulation by parametrization of the rotation matrix \(\boldsymbol{R}\), i.e., an element of the Lie group \(SO(n)\) with \(\boldsymbol{R}^{T}\boldsymbol{R} = \boldsymbol{I}\) and \(\operatorname{det}(\boldsymbol{R}) = 1\), denoting all matrices with orthonormal column vectors and positive determinant. This simplifies the design of a space-time formulation dramatically and allows for the design of energy-momentum schemes.
Hence, we introduce a constrained director-based kinematic, see Rubin [22] for details on the theory of Cosserat points. As usual for rigid body dynamics, the spatial integral is executed independently of the temporal integration, and thus we make use of a tensor–product structure of the shape functions in space and time. Analogous to Mortar methods in domain decomposition, a weak form of the constraints is considered, i.e., we interpolate the Lagrange multipliers and their corresponding test or trial functions in temporal direction and implement the time continuous weak form. We consider this approach as the most natural way of dealing with Hamilton’s principle. As we will show, we obtain optimal convergence and allow for an efficient, parallel solution of the space-time problem.
The manuscript is organized as follows. In Sect. 2, we introduce the basic space-time formulation, followed by the discretization in Sect. 3. Section 4 demonstrates the superiority of the chosen approach and the applicability of large systems including large rotations. Conclusions are drawn in Sect. 5.
2 Variational formulation
In this section, we develop basic concepts for a space-time formulation on constrained mechanical systems. The motion of a mechanical system is described by Hamilton’s principle, namely, we make the action integral stationary
Here, \(L := L(\boldsymbol{\varphi },\nabla _{t}\boldsymbol{\varphi })\) is the Lagrangian given as \(L = T-V\), where \(T:=T(\nabla _{t}\boldsymbol{\varphi })\) represents the specific kinetic energy, \(\nabla _{t}(\bullet )\) is the gradient in temporal direction, and \(V:=V(\boldsymbol{\varphi })\) denotes a suitable specific potential energy. Note that we do not require the existence of \(V\), only the variation of V. The Lagrangian is defined within a space-time cylinder \(\mathfrak{B}_{0}:=\Omega _{0}\times \mathcal{T}\subset \mathbb{R}^{d+1}\) with regard to its spatial \(d\)-dimensional reference configuration in the open bounded domain \(\Omega _{0}\subset \mathbb{R}^{d}\) within the time period \(\mathcal{T}:=[0,\,T^{e}]\subset \mathbb{R}\). Accordingly, we can define the mantle of the space-time cylinder \(\Sigma = \partial \Omega _{0}\times \mathcal{T}\) and the start and end configuration \(\Sigma ^{0} = \Omega _{0}\times \{0\}\) and \(\Sigma ^{T^{e}} = \Omega _{0}\times \{T^{e}\}\), respectively. As usual, the mantle can be further decomposed into non-overlapping Dirichlet boundaries \(\Sigma ^{u}\) and Neumann boundaries \(\Sigma ^{\sigma}\). Note that we make use of a space-time deformation map \(\boldsymbol{\varphi }:\mathfrak{B}_{0}\rightarrow \mathfrak{B}\), where \(\mathfrak{B}\) is the actual configuration, and \(\boldsymbol{\varphi }:=(\boldsymbol{\varphi }^{T}(\boldsymbol{X},t),t)^{T}\), where the last component is fixed in classical mechanics.
Following the theory of Cosserat points (see Rubin [22]), the deformation map is defined in terms of the mapping \(\bar{\boldsymbol{\varphi }}\) of a reference material point \(\bar{\boldsymbol{X}}\) along with a time-dependent director coordinate frame \(\{\boldsymbol{d}_{i}(t)\},\,i\in [1,\,\ldots ,\,d]\). A material point \(\boldsymbol{X}\in \Omega _{0}\) of the rigid body is given by
where we have made use of the convective coordinates \(\theta ^{i}\). Accordingly, \(\boldsymbol{\varphi }\in \mathfrak{B}\) at \(t\in \mathcal{T}\) reads
A symmetric tensor-valued kinematic constraint \(\boldsymbol{\Phi }^{rb}(t)\) must be established to prevent deformation of the director triad with coefficients
The satisfaction of the kinematic constraint (4) leads to the introduction of a symmetric tensor-valued Lagrange multiplier field \(\boldsymbol{\lambda }_{rb}(t)\). Alternatively, \(\boldsymbol{\lambda }_{rb}(t)\) can be understood as a reactive second Piola–Kirchhoff stress tensor introduced to ensure that the metric tensor defined by the director triad remains constant throughout the deformation. The specific kinetic energy is usually written in classical mechanics as follows:
where \(\rho _{0}\in \mathbb{R}\) is the reference density and \(\boldsymbol{\pi }\) is the linear momentum. Inserting the rigid body kinematic in (3) and executing spatial integration independent of the temporal integration, we obtain for the virtual work of the inertial forces
where
introduce a symmetric positive-definite mass matrix \(\mathbb{M}\in \mathbb{R}^{(d+1)d\times (d+1)d}\) and the unity matrix \(\boldsymbol{I}\in \mathbb{R}^{d\times d}\).
Remark 2.1
Using a coordinate system placed in the center of mass of \(\Omega _{0}\) yields obviously \(S^{i} = 0\). Additionally, the coordinate axes are often adjusted along the principal axis of the tensor \(\boldsymbol{E} = E^{ij}\boldsymbol{d}_{i}\otimes \boldsymbol{d}_{j}\). Moreover, the Euler tensor can be linked to the common inertia tensor via the relationship \(\boldsymbol{J} = \operatorname{tr}(\boldsymbol{E}) \boldsymbol{I}-\boldsymbol{E}\).
Assuming that the kinetic energy \(T(\nabla _{t}\boldsymbol{\varphi })\) is convex and differentiable, we can introduce the conjugate function (see Appendix A for details)
and obtain \(T^{*}(\boldsymbol{\pi }) = \frac{1}{2}\rho _{0}^{-1}\| \boldsymbol{\pi }\|^{2}\). Adapting the rigid body kinematic, we conclude that
and obtain
where we have multiplied the second equation by −1 for the ease of presentation.
The last term in the second equation refers to the incoming and outgoing linear momentum of the time interval under consideration, called by Hamilton the “law of varying action”. Often \(\delta \boldsymbol{\varphi }|_{0}^{T}\) is set to zero so that the initial and end terms vanish. It is obvious that for classical engineering tasks this is no useful assumption as we do not know the end position in advance; however, for a classical time-stepping scheme, this term does not matter at all. Applying a space-time concept, this term compares to the Neumann boundary conditions in space, either predefined or set to zero. In temporal direction, the incoming and outgoing linear momentum may neither be predefined nor zero, hence this term does not vanish, see Appendix B and also Bailey [2, 3] for further details.
Eventually, we set \(\bar{\boldsymbol{\lambda }}_{rb} = \boldsymbol{\lambda }_{rb}V\), scaled by the volume \(V\) of \(\Omega _{0}\), \(\boldsymbol{B}\) denotes a body force per unit of mass and \(\boldsymbol{T}\) is the traction vector acting on the mantle \(\Sigma ^{\sigma}\) of the space-time cylinder. Application of integration by parts in temporal direction of the first term in (10) yields
The spaces of virtual or admissible test and solution functions for (11) are
Here, \(H^{1}\) denotes the Sobolev functional space of square-integrable functions and derivatives. Note that we applied initial (essential) boundary conditions on \(\mathcal{V}^{\delta \varphi}\) and \(\mathcal{V}^{\delta \pi}\) for the initial position and initial linear momentum. However, we can also apply boundary conditions on the endpoint (e.g., the crash has happened and one wants to calculate where the car comes from) by simply applying the Dirichlet-like conditions to \(\Sigma ^{T}\) instead of \(\Sigma ^{0}\).
3 Space-time discretization
Next, we introduce the space-time discretization, following the ideas developed in Hesch et al. [13]. Although the general methodology developed in Schuss et al. [25] allows for unstructured meshes in the space-time cylinder, we make use of a tensor product structure to integrate the spatial domain independent of the temporal. The reference configuration \(\Omega _{0}\) is split into a subdivision of non-overlapping, spatial elements \(e \in \mathbb{E}\), leading to an approximate domain \(\Omega _{0}^{h}\), which satisfies
using non-overlapping elements \(e_{t}\in \mathbb{T}\) for the 1D subdivision of the temporal domain \(\mathcal{T}\). A finite-dimensional polynomial approximation of the test and trial functions for the unknown event field in the space-time domain is defined as follows:
where \(\left (M_{t}(t)N_{\varphi}(\boldsymbol{X})\right )^{A}:\mathfrak{B}_{0} \rightarrow \mathbb{R}\) are temporal and spatial shape functions associated with nodes where \(\omega = \omega _{s}\otimes \omega _{t}\), the tensor product of the set of spatial nodes \(\omega _{s}\) and the set of temporal nodes \(\omega _{t}\). Note that we require the partition of unity for the spatial and temporal shape functions. As a rigid body kinematic allows to separately solve the integral over space and time, we separate the multi-index \(A\) into \(A_{s}\) and \(A_{t}\) for the spatial and temporal shape functions, such that \(\left (M_{t}(t)N_{\varphi }(\boldsymbol{X})\right )^{A} = M_{t}^{A_{t}}(t)N_{ \varphi }^{A_{s}}(\boldsymbol{X})\). The nodal values \(\boldsymbol{q}_{A}\), \(\boldsymbol{\pi }_{A}\) and \(\delta \boldsymbol{q}_{B}\), \(\delta \boldsymbol{\pi }_{B}\) admit the following rigid body representation (refer to equation (3)):
where \(\theta ^{i}_{A_{s}}\) is the \(i\)th convective coordinate of the node \(A_{s}\) measured with respect to the reference material point \(\bar{\boldsymbol{X}}\). Insertion into the virtual work expressions (6) or (9), respectively, allows us to rewrite for the components of the discretized mass matrix \(\mathbb{M}_{h}\) given in (7) in terms of a finite element discretization of the spatial reference configuration as follows:
Eventually, the spatial discretized external contributions can be written as follows:
Note that we obtain for an external torque vector \(\boldsymbol{m}\) the relation
where \(\boldsymbol{d}^{i} = ([\boldsymbol{d}_{i}\cdot \boldsymbol{d}_{j}])^{-1} \boldsymbol{d}_{j}\) is a contravariant director. We refer to [12] for details on director-based formulations written in skew coordinates and to [24], Sect. 2.2.3 for the application on external torque. Moreover, the Lagrange multipliers to enforce the orthonormality of the director triad are approximated via
For conservation of angular momentum, see Appendix C.
Remark 3.1
Using the same shape functions for the Lagrange multipliers (and the associated trial functions) as for the solution and trial functions of the rigid body is possible, although other choices can be applied as well, see Brivadis et al. [11] for a detailed discussion on this issue in the spatial domain for NURBS. For the ease of construction, we make use of the same functions, simplifying the whole concept and the implementation of finite elements for rigid bodies in space-time. As we will show in the following section, the convergence remains optimal.
Finally, we obtain the following algebraic system of equations:
where
and \(\left (\frac{\partial \Phi ^{rb}_{kl}}{\partial \boldsymbol{d}_{i}} \right )^{h}\) follows in a straightforward manner from the last equation.
Remark 3.2
To solve the nonlinear system of equations (23), we apply a Newton–Raphson iteration. In particular, we obtain a residual vector \(\boldsymbol{R}_{A_{t}}\), derive the tangent matrix \(K_{A_{t},B_{t}}\), and solve
until a predefined stop criterion \(\sum _{A_{t}\in \omega _{t}}\|\boldsymbol{R}_{A_{t}}^{n+1}\| < \epsilon \) is obtained.
4 Results
In this section, we provide a series of numerical examples to demonstrate the accuracy and superiority of the space-time system compared to classical time-stepping schemes. Therefore, we assume that the reader is familiar with time-stepping schemes like mid- and endpoint rules (i.e., implicit Euler scheme), see [9] for details on time-stepping schemes applied to director-based rigid body formulations.
4.1 Single rigid body
We start with a prototypical 3D example to conduct suitable convergence tests. Therefore, a rectangular rigid body with dimensions \([-1,\, 1]\), \([-0.5,\, 0.5]\), and \([-0.5,\, 0.5]\) is introduced with reference density of \(\rho _{0} = 1.5\). The initial velocity of the center of mass is \([5,\,5,\,5]\); the (rotational) initial velocity of the directors is zero. Two different tests are carried out: First, a simple test with constant external momentum of \(\boldsymbol{m} = [1,\,1,\,1]\) throughout the whole time interval \(\mathcal{T}^{\operatorname{rot}} = [0,\,1]\) is applied. Note that we make use of equation (21) to apply the external momentum \(\boldsymbol{m}\) on the director formulation, i.e., \(\boldsymbol{m}\) is written in the global coordinate system, mapped to the director frame via (21). Figure 1, left displays the motion of the body, and although we call this example “simple”, the body performs a nearly \(90^{\circ}\) degree rotation within the time interval, hence large rotations are involved.
Figure 2 shows the results of a convergence test using the approach as presented in (11). For this demonstration, we made use of an overkill solution to obtain \(\boldsymbol{\varphi }^{ref}(T)\) with 1 million time steps using a mid-point rule and compared the norm of the final position and the directors minus the overkill solution
As can be seen, the implicit Euler “Timestepping endpoint”) converges linearly, whereas the midpoint rule (“Timestepping midpoint”) converges quadratically. Linear finite elements in space-time (“Space-time linear”) converge quadratic, which was expected; using quadratic Lagrange shape functions (“Space-time quad”) converges cubic as expected up to \(10^{-10}\), which was the predefined stop criterion of the Newton–Raphson iteration. Hence, the space-time formulation converges near machine precision towards the results of the overkill time-stepping approach.
A direct comparison of the runtime is difficult as modern computers scale the frequency of the CPU unpredictably depending on the temperature, peak values of the power consumption, the implementation, and many more factors. Just to give an impression: On a six-core MacBook (2.6 GHz Intel Core i7), the space-time simulation using 1000 linear finite elements and a direct solver (UMFPACK) with METIS reordering took about 12.5 seconds. The midpoint time-stepping scheme used 92.7 seconds. On our 24 core Workstation, 1000 linear finite elements took even longer as the overhead for this small number of elements is too large. However, for larger systems up to 100,000 elements, the multi-core workstations scale up as expected without any problems, resulting in a similar or even stronger advantage of one digit in the runtime. Hence, the overall energy consumption is dramatically reduced.
Remark 4.1
Interestingly, using Lagrange shape functions, only (11) worked correctly, using (10), the Newton–Raphson iteration diverges. Using B-Splines, (10) converges without any problems .Footnote 1 As we focus on the preferable formulation in (11), we do not discuss this further here. Using B-Splines or NURBS shape functions is undoubtedly possible, and we leave it to the reader to make use of the preferred framework. We refer to our preliminary work in [25] for details on the use of B-Splines in space-time.
Next, we investigate the condition number of the finite element formulation. For classical time-stepping methods using constrained dynamics (e.g., quarterions or director formulations), the condition number of the iteration matrix of the differential-algebraic equations (DAEs) can be estimated as of \(O(\Delta t^{-3})\), see Betsch [5], Appendix A. For the constrained finite element formulation at hand, we obtain the condition data shown in Fig. 3. Note that this is the condition number of the matrix for all time steps at once.
As a second example, a more complex system is introduced using the same external momentum of \(\boldsymbol{m}\), however, applied during the time interval \(\mathcal{T}^{\operatorname{rot}} = [0.5,\,1.5]\) to initiate large rotations in the temporal domain \(\mathcal{T} = [0,\,4]\). Remark that this setup can be considered as a nonsmooth system with respect to the external contributions. Figure 1, right, shows the motions throughout the time interval. It is obvious that we consider large, three-dimensional rotations of the free-flying body. Note that a rectangular load, zero for \(t = [0,\,0.5]\) and \(t = [1.5,\,4]\) and the prescribed external momentum else, is challenging for finite elements that rely on a predefined smoothness; however, this is a typical setup for rigid body problems.
Figure 4 shows the results of the rectangular load. The implicit Euler yields linear convergence, the linear space-time a quadratic convergence, and the quadratic Lagrange shape functions a cubic convergence. Note that the results cannot be as perfect as for the first example. If the time step or the element size matches exactly with the nonsmooth changes in the external load, i.e., the load initiates or terminates exactly at the element or time step boundary, the total error is better than otherwise. For the overkill solution, time-stepping schemes cannot be used any more since the condition number for the index-3 problem raises dramatically with \(O(\Delta t^{-3})\), cf. Betsch [5], and thus the stop criterion of the Newton–Raphson iteration must be lowered dramatically. Thus, we make use of a blockwise calculation of the space-time system using quadratic Lagrange shape functions with 40,000 elements within each of the 40 blocks to obtain an element size of \(2.5\times 10^{-6}\) for the overkill solution. The final position of the center of mass after 4 seconds using an initial velocity of \([5,\,5,\,5]\) is obviously \([20,\,20,\,20]\), the directors are given at \(\boldsymbol{d}_{1} = [0.392,\,-0.271,\,0.879]\), \(\boldsymbol{d}_{2} = [-0.233,\,-0.954,\,-0.190]\), and \(\boldsymbol{d}_{3} = [0.890,\,-0.131,\,-0.437]\). Note that the midpoint rule shows a quadratic convergence only below a time step size \(10^{-4}\).
Finally, we plotted the convergence of the Lagrange multipliers in Fig. 5. As shown in [11] for the case of Mortar-type boundary conditions, the convergence of a \(p/p\) pairing is restricted.
4.2 Double spherical pendulum
Here, we aim at several additional investigations following the example of a double spherical pendulum presented in Betsch [5], Sect. 4.2. First, we apply the space-time formulation on a two-body system, connected via two additional, spherical constraints using Lagrange multipliers. Second, we apply the space-time formulation block-wise, i.e., we make use of time blocks, calculated using a standard Newton–Raphson iteration for the space-time problem. Therefore, the position \(\bar{\boldsymbol{\varphi }}\) and directors \(\boldsymbol{d}_{i}\) as well as their momentum \(\bar{\boldsymbol{\pi }}\) and \(\boldsymbol{\pi }^{d}_{i}\) at the end of the time block are transferred to the next time block as initial conditions. This allows for arbitrary long temporal domains without jeopardizing the Newton–Raphson convergence as the solutions may be far away from the initial guess.
Again, we conduct two different tests. First, we apply the initial configuration as presented in Fig. 6 using two cubic geometries with length, width, and height of \([1,\,1,\, 1]\) and \([0.8,\,0.8,\, 0.8]\). The initial position of the center of mass is \(\bar{\boldsymbol{\varphi }}_{1} = 4/\sqrt{2}\times [1,\, 0,\, 1]\) for the first and \(\bar{\boldsymbol{\varphi }}_{1} = 8/\sqrt{2}\times [1,\, 0,\, 1]\) for the second body. The directors form a unity matrix for both bodies and the initial velocities are zero. A vector of gravitational acceleration is \(\boldsymbol{g}= [0,\, 0,\, -9.81]\in \mathbb{R}^{3}\), such that the corresponding energy function reads \(V(\bar{\boldsymbol{\varphi }}_{1},\bar{\boldsymbol{\varphi }}_{2}) = M_{ \varphi}^{1}\bar{\boldsymbol{\varphi }}_{1}\cdot \boldsymbol{g}+M_{ \varphi}^{2}\bar{\boldsymbol{\varphi }}_{2}\cdot \boldsymbol{g}\). The rigidity of the connecting rods gives rise to constraint functions written as
where \(L_{1}\) and \(L_{2}\) are the initial lengths. No external forces are applied so that the system is expected to behave like a two-dimensional double pendulum, equipped with two mass points. The initial velocity of both bodies is zero, the time interval is \(\mathcal{T} = [0,\,80]\), 40 blocks are used with 100 temporal elements each. Figure 7 displays the x-position of both bodies over time, whereas Fig. 8 displays the z-position. Note that for both bodies, the y-position remains below \(10^{-30}\), i.e., we obtain in fact a two-dimensional motion.
This changes dramatically if we constrain the second body not in the center of mass. Therefore, the reference point \(\bar{\varphi }_{2}\) is moved out of the center of mass at \([-0.1,\,0,\,0]\). Thus, we obtain for the mass \(M_{\bar{\varphi }_{2}} = 0.768\), which is obviously unchanged, for \(\boldsymbol{S}_{\bar{\varphi }_{2}} = [0.0768,\,0,\,0]\) and \(\boldsymbol{E}_{\bar{\varphi }_{2}} = \operatorname{diag}([0.0486,\,0.0410,\,0.0410])\). The trajectory is shown in Fig. 11; as expected the trajectory is not two-dimensional any more. For this specific example, we make use of 200 time blocks with 200 finite elements within each block. The coordinates at the end point are \(\bar{\varphi }_{1} = [0.0585,\,-0.0002,\,-3.9996]\) and \(\bar{\varphi }_{2} = [-2.3571,\,0.0002,\,-71{,}878]\).
A direct evaluation of the energy is not reasonable as this is a strong evaluation of an integral formulation. As we have shown in Hesch et al. [14], we can conduct integration by parts and compare the initial and the final values. Here, we conducted a different evaluation: For each element, we plotted the action integral in Fig. 9. As can be seen, we obtain for each block a constant function for the action integral; since the total energy is the derivative of the action integral with respect to time, the total energy is a conserved value over time. Note that we observe of an extremely small disturbance at the beginning of each block. We enforce the constraints integral in the temporal domain, i.e., they are not exactly fulfilled at a single point. Hence, if we transfer the end values of one block as initial conditions to the next block, the spherical constraints may be violated. Consequently, we do not observe this phenomenon using a single block and this instability vanishes with smaller time elements, as can be seen in Fig. 9.
In Fig. 10 all three components of the angular momentum, integrated over time for each element (see Appendix C) and added up over both bodies, are plotted. As expected, only one component is active, the other two are constants below the Newton–Raphson stop criterion over time, hence both components of the angular momentum are conserved.
For the final test, we make use of the same initial configuration of the double pendulum; however, the initial velocity is predefined for both bodies using \(\nabla _{t}\bar{\boldsymbol{\varphi }} = [0,\,1,\,0]\) and \(\nabla _{t} \boldsymbol{d}_{3} = [0,\,1,\,0]\), the initial velocity for both other directors \(\boldsymbol{d}_{1}\) and \(\boldsymbol{d}_{2}\) is set to zero. Figure 12 shows the trajectory of both centers of mass \(\bar{\boldsymbol{\varphi }}_{1}\) and \(\bar{\boldsymbol{\varphi }}_{2}\). Additionally, we obtain large, three-dimensional rotations of both rigid bodies throughout the whole time interval. As shown in Fig. 13, the action integral remains constant in each block. Except for the boundaries of the blocks, the change of the action integral element by element is below the Newton tolerance.
Finally, in Fig. 14 all three components of the angular momentum, again integrated separately for each element over time and added up over both bodies, are displayed for this three-dimensional motion. As can be seen, the \(L_{3}\) component remains constant, i.e., the third angular momentum component is zero.
5 Conclusions
In this contribution, we have shown how to apply space-time concepts to rigid multibody dynamics. In particular, constrained rigid body formulations based on a director formulation are fitted within a space-time cylinder. As the spatial components of the kinetic energy like mass matrix as well as first and second moment of inertia can be evaluated independently from the temporal components as usual in rigid body dynamics, we do not have a wave-equation like structure. Hence, we do not have to stabilize the formulation as generally necessary for mechanical space-time problems, cf. the preliminary contribution of the authors in Schuss et al. [25]. Again, we could apply an interpretation of Livens’ theorem; this allows us to simplify the application of initial and/or end conditions dramatically.
Moreover, we could show in Appendix B that the initial and end boundary conditions arise in a most natural way within the variational formulation. This resolves in our own way a decade-old discussion on the formulation of the Lagrangian itself. In the numerical examples, we could not only demonstrate the applicability of the chosen approach and its superiority against classical time-stepping formulation. Following current trends in computer hardware, we can now make use of the rising core numbers in modern architectures for rigid body simulation. Sophisticated parallelization techniques, as developed for decades, can now be applied in a straightforward manner. As we have shown, this reduces the energy consumption of multibody simulation dramatically, which is a major goal in research today.
Data Availability
The data and implementation details can be requested from the corresponding author.
Notes
Note that we make use of the same routine, only different shape functions are chosen.
References
Abedi, R., Petracovici, B., Haber, R.B.: A space-time discontinuous Galerkin method for linearized elastodynamics with element-wise momentum balance. Comput. Methods Appl. Mech. Eng. 195, 3247–3273 (2006)
Bailey, C.: Hamilton, Ritz, and elastodynamics. J. Appl. Mech. 43, 684–688 (1976)
Bailey, C.: The method of Ritz applied to the equation of Hamilton. Comput. Methods Appl. Mech. Eng. 7, 235–247 (1976)
Baumgarte, J.: Stabilization of constraints and integrals of motion in dynamical systems. Comput. Methods Appl. Mech. Eng. 1(1), 1–16 (1972)
Betsch, P.: The discrete null space method for the energy consistent integration of constrained mechanical systems Part I: Holonomic constraints. Comput. Methods Appl. Mech. Eng. 194, 5159–5190 (2005)
Betsch, P., Steinmann, P.: Inherently energy conserving time finite elements for classical mechanics. J. Comput. Phys. 160, 88–116 (2000)
Betsch, P., Steinmann, P.: Conserving properties of a time FE method - Part II: Time-stepping schemes for non-linear elastodynamics. Int. J. Numer. Methods Eng. 50, 1931–1955 (2001)
Betsch, P., Steinmann, P.: Conservation properties of a time FE method. Part III: Mechanical systems with holonomic constraints. Int. J. Numer. Methods Eng. 53, 2271–2304 (2002)
Betsch, P., Uhlar, S.: Energy-momentum conserving integration of multibody dynamics. Multibody Syst. Dyn. 17(4), 243–289 (2007)
Betsch, P., Uhlar, S., Quasem, M.: On the incorporation of servo constraints into a rotationless formulation of flexible multibody dynamics. In: Bottasso, C.L., Masarati, P., Trainelli, L. (eds.) ECCOMAS Thematic Conference, Multibody Dynamics 2007 (2007)
Brivadis, E., Buffa, A., Wohlmuth, B., Wunderlich, L.: Isogeometric mortar methods. Comput. Methods Appl. Mech. Eng. 284, 292–319 (2015)
Eugster, S.R., Hesch, C., Betsch, P., Glocker, Ch.: Director-based beam finite elements relying on the geometrically exact beam theory formulated in skew coordinates. Int. J. Numer. Methods Eng. 97, 111–129 (2014)
Hesch, C., Gil, A.J., Arranz Carreno, A., Bonet, J., Betsch, P.: A Mortar approach for fluid-structure interaction problems: immersed strategies for deformable and rigid bodies. Comput. Methods Appl. Mech. Eng. 278, 853–882 (2014)
Hesch, C., Gil, A.J., Ortigosa, R., Dittmann, M., Bilgen, C., Betsch, P., Franke, M., Janz, A., Weinberg, K.: A framework for polyconvex large strain phase-field methods to fracture. Comput. Methods Appl. Mech. Eng. 317, 649–683 (2017)
Hesch, C., Schuß, S., Dittmann, M., Eugster, S.R., Favino, M., Krause, R.: Variational space–time elements for large-scale systems. Comput. Methods Appl. Mech. Eng. 326, 541–572 (2017)
Hilbert, H.M., Hughes, T.J.R., Taylor, R.L.: Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 5, 282–292 (1977)
Hughes, T.J.R., Hulbert, G.M.: Space-time finite element methods for elastodynamics: formulations and error estimates. Comput. Methods Appl. Mech. Eng. 66, 339–363 (1988)
Ladyzhenskaya, O.A.: The Boundary Value Problems of Mathematical Physics. Springer, Berlin (1985)
Langer, U., Moore, S.E., Neumüller, M.: Space–time isogeometric analysis of parabolic evolution problems. Comput. Methods Appl. Mech. Eng. 306, 342–363 (2016)
Lew, A., Marsden, J.E., Ortiz, M., West, M.: Variational time integrators. Int. J. Numer. Methods Eng. 60, 153–212 (2004)
Pars, L.A.: A Treatise on Analytical Dynamics. Ox Bow Press (1965)
Rubin, M.B.: Cosserat Theories: Shells, Rods and Points. Kluwer Academic, Dordrecht (2000)
Saadé, C., Lejeunes, S., Eyheramendy, D., Saad, R.: Space-time isogeometric analysis for linear and non-linear elastodynamics. Comput. Struct. 254, 106594 (2021)
Sänger, N.: Elemente für die Dynamik flexibler Mehrkörpersysteme. PhD thesis, University of Siegen (2011)
Schuß, S., Glas, S., Hesch, C.: Non-linear space-time elasticity. Int. J. Numer. Methods Eng. 124, 1965–1990 (2023)
Smith, C.V., Smith, D.R.: Comment on ‘application of Hamilton’s law of varying action’. AIAA J. 15, 284–286 (1977)
Ströhle, T., Betsch, P.: A simultaneous space-time discretization approach to the inverse dynamics of geometrically exact strings. Int. J. Numer. Methods Eng. 123(11), 2573–2609 (2022)
Acknowledgements
Support for this research was provided by the Deutsche Forschungsgemeinschaft (DFG) under grant HE5943/15-1. The author, C. Hesch, gratefully acknowledges the support of the DFG.
Funding
Open Access funding enabled and organized by Projekt DEAL. See Acknowledgements.
Author information
Authors and Affiliations
Contributions
We worked together on the ideas and details of the manuscript. It doesn’t matter who did wrote which sentence.
Corresponding author
Ethics declarations
Ethical approval
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Livens’ theorem
In this section, we interpret Livens’ theorem (cf. Pars [21], Sect. 26) for rigid body systems. Therefore, we introduce first the velocity
and implement this additional condition in an augmented Lagrangian, written in terms of \(T := T(\boldsymbol{v})\), using the multiplier rule
The conditions for stationarity are given as follows:
Introducing \(\frac{\partial L^{\operatorname{aug}}}{\partial \boldsymbol{v}} = \boldsymbol{\pi }\) as already stated in (5) and noting that \(\boldsymbol{\pi } = \rho _{0}\boldsymbol{v}\), we end up with
where we have made use of the Hamiltonian \(H = T + V\). Writing the kinetic energy in the Hamiltonian in terms of \(\boldsymbol{\pi }\) via \(\boldsymbol{v} = \boldsymbol{\pi }/\rho _{0}\), the stationarity condition for arbitrary variations of \(\boldsymbol{\varphi }\) and \(\boldsymbol{\pi }\) is called “Livens’ theorem” and reproduces exactly the Legendre transformation as proposed in (8). Applying the rigid body kinematic yields
which can be inserted in the kinetic energy of the rigid body system in (6). The stationary condition in (10) follows then in a straightforward manner.
Appendix B: External contributions
We start by assuming a classical deformable body in space-time, applying the rigid body kinematic and constraints afterwards. Hence, we can write for the internal virtual work
where \(\boldsymbol{P}\) denotes the first Piola–Kirchhoff stress tensor. Applying integration by parts in temporal and spatial direction yields
using the normal vector \(\boldsymbol{N}\) in an outward direction of the reference configuration. Assuming Hamilton’s principle is valid, we have to equate \(\delta \mathfrak{L}^{\operatorname{int}}\) with suitable external contributions. Hence, we obtain
Insertion in Hamilton’s principle for rigid bodies yields (10). This result explains the results obtained by Bailey [2, 3], who called this boundary term “troublesome”, in a mathematically rigorous way.
Note that Bailey initiated a large discussion on it, see [26] for a harsh comment on Bailey’ article stating that “the variational calculus teaches how to determine the variations of functions [...], however, the variational calculus does not set the problem. The functional is established by the physics of the problem, and the physics establishes what one does with the variation of that functional”. Here, we can show that this term is a natural boundary term; ignoring this natural boundary forces the system to constrain \(\boldsymbol{\pi } = \boldsymbol{0}\) on \(t = [0,\,T]\), contradicting the physical motion. Hence, the variational calculus indeed teaches us how physics works.
Appendix C: Angular momentum
To verify conservation of angular momentum \(\boldsymbol{J}^{am}\), we substitute \(\delta \boldsymbol{q}_{A}\) in (18) with \(\boldsymbol{\mu }\times (\bar{\boldsymbol{\varphi }} + \sum _{i} \theta _{A}^{i}\boldsymbol{d}_{i})\), where \(\boldsymbol{\mu }\in \mathbb{R}^{3}\) is arbitrary and constant, and we obtain
assuming that \(S^{i} = 0\), i.e., \(\bar{\boldsymbol{\varphi }}\) represents the center of mass.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hesch, C., Glas, S. & Schuß, S. Space-time rigid multibody dynamics. Multibody Syst Dyn (2023). https://doi.org/10.1007/s11044-023-09945-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11044-023-09945-1