Skip to main content
SpringerLink
Log in

Kane’s equations for nonholonomic systems in bond-graph-compatible velocity and momentum forms

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

The authors’ previously published results on a bond-graph-compatible and nonholonomic momentum form of Kane’s equations are extended, from scleronomic to rheonomic systems. The momentum form is found to be partially Hamiltonian, and bond-graph-compatible velocity forms are also found, of which one is partially Lagrangian. The results are derived for general particle systems and then specialized to rigid-body systems. Direct dependence of kinetic energy upon time is avoided, making the results power-conserving and suitable for use with bond graphs. A new nonholonomic IC (NIC) bond-graph element is defined, and bond graphs for the partially Hamiltonian and partially Lagrangian forms are exhibited using this element.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Notes

  1. The IC field element implements only inertial (kinetic) energy storage, but does have a set of ports with effort, or C-port causality.

  2. Where feasible, we use terminology from [22], a revised and updated edition of the earlier exposition of Kane’s methodology [10]. In the earlier exposition the terminology used for the elements of \(\boldsymbol {\mathrm {f}}\) is “generalized speeds”. Cogent objections to the earlier terminology have been raised [18], and so we use the newer terminology “generalized velocities” from [22]. In the more general dynamics literature, “quasi-velocities” and “nonholonomic velocities” are also used as synonyms. Generalized velocities, as defined here, are to be distinguished from the coordinate derivatives \(\dot{\boldsymbol {\mathrm {q}}}\), unless \(\boldsymbol {\mathrm {Q}}\) is the identity matrix.

  3. The use of the adjectives “reduced” and “unreduced”, as describing the noun “Kane’s equations”, describes the process involved in proceeding from an expression equating generalized impressed and inertia forces (Sects. 3.2, 3.3), to several standard forms of ordinary differential equations, with associated matrix parameters (Sect. 3.4 et seq.). It is acknowledged that this usage does not appear in any previous published treatment the authors are aware of, and thus does not yet represent established terminology.

  4. \(\boldsymbol {\mathrm {D}}\) is intended to be a simplified version of \(\bar{\boldsymbol {\mathrm {D}}}\) in which (17) is satisfied while terms that always reduce to zero in both \(\bar{\boldsymbol {\mathrm {D}}}\boldsymbol {\mathrm {f}}\) and \(\bar{\boldsymbol {\mathrm {D}}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}\) do not appear. In Appendix B, we derive in detail the form that \(\bar{\boldsymbol {\mathrm {D}}}\) takes for rigid bodies and show that it contains such terms.

  5. The standard 6-DOF flight equations, using body-referenced velocity components as elements of \(\boldsymbol {\mathrm {f}}\), are an example of this circumstance.

  6. The utility of rheonomic constraints, expressed here at the velocity level, is sometimes obvious, e.g., for analysis of a system driven by a shaft with imposed rotational velocity. Less obviously, a rheonomic formulation is also useful for computing joint or internal reaction forces or moments by introducing fictitious degrees of freedom to the system model and then constraining the associated generalized velocities to be zero while computing the associated generalized constraint reactions.

References

  1. Amirouche, F.: Fundamentals of Multibody Dynamics: Theory and Applications. Springer, Berlin (2007)

    MATH  Google Scholar 

  2. Banerjee, A.K.: Order-n formulation of equations of motion with efficient choices of motion variables. In: Guidance, Navigation, and Control Conference. AIAA, Washington (1994). https://doi.org/10.2514/6.1994-3576

    Chapter  Google Scholar 

  3. Breedveld, P.: Multibond graph elements in physical systems theory. J. Franklin Inst. 319(1/2), 1–36 (1985)

    Article  Google Scholar 

  4. Brown, F.T.: Engineering System Dynamics, 2nd edn. CRC Press, Boca Raton (2007)

    Google Scholar 

  5. Fahrenthold, E., Wargo, J.: Vector and tensor based bond graphs for physical systems modeling. J. Franklin Inst. 328(5–6), 833–853 (1991)

    Article  MATH  Google Scholar 

  6. Firestone, F.A.: A new analogy between mechanical and electrical systems. J. Acoust. Soc. Am. 4(3), 249–267 (1933)

    Article  Google Scholar 

  7. Ingrim, M., Masada, G.: The extended bond graph notation. J. Dyn. Syst. Meas. Control 113(1), 113–117 (1991)

    Article  MATH  Google Scholar 

  8. Kane, T.R.: Dynamics of nonholonomic systems. J. Appl. Mech. 28(4), 574–578 (1961)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kane, T., Banerjee, A.: A conservation theorem for simple nonholonomic systems. J. Appl. Mech. 50(3), 647–651 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kane, T.R., Levinson, D.A.: Dynamics: Theory and Applications. McGraw-Hill, New York (1985). https://www.academia.edu/download/45461708/Dynamics-Theory_opt.pdf

    Google Scholar 

  11. Kane, T.R., Wang, C.F.: On the derivation of equations of motion. J. Soc. Ind. Appl. Math. 13(2), 487–492 (1965)

    Article  MathSciNet  MATH  Google Scholar 

  12. Karnopp, D.: An approach to derivative causality in bond graph models of mechanical systems. J. Franklin Inst. 329(1), 65–75 (1992)

    Article  MathSciNet  Google Scholar 

  13. Karnopp, D., Margolis, D., Rosenberg, R.: System Dynamics, 3rd edn. Wiley, New York (2000)

    Google Scholar 

  14. Lanczos, C.: The Variational Principles of Mechanics. University of Toronto Press, Toronto (1970)

    MATH  Google Scholar 

  15. Layton, R.A.: Principles of Analytical System Dynamics. Mechanical Engineering Series. Springer, Berlin (1998)

    Book  MATH  Google Scholar 

  16. Likins, P.W.: Analytical dynamics and nonrigid spacecraft simulation. Tech. Rep. 32-1593, NASA (1974). https://ntrs.nasa.gov/api/citations/19740023220/downloads/19740023220.pdf

  17. Mitiguy, P.C., Kane, T.R.: Motion variables leading to efficient equations of motion. Int. J. Robot. Res. 15(5), 522–532 (1996)

    Article  Google Scholar 

  18. Papastavridis, J.G.: Analytical Mechanics. World Scientific, Singapore (2014)

    Book  MATH  Google Scholar 

  19. Paynter, H.: Analysis and design of engineering systems; class notes for MIT course 2.751 (1961). https://hdl.handle.net/2027/mdp.39015064874921

  20. Phillips, J.R., Amirouche, F.: Corrigendum: A momentum form of Kane’s equations for scleronomic systems. Math. Comput. Model. Dyn. Syst. 24(4), 446–450 (2018)

    Article  MATH  Google Scholar 

  21. Phillips, J.R., Amirouche, F.: A momentum form of Kane’s equations for scleronomic systems. Math. Comput. Model. Dyn. Syst. 24(2), 143–169 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Roithmayr, C.M., Hodges, D.H.: Dynamics: Theory and Application of Kane’s Method. Cambridge University Press, Cambridge (2016)

    MATH  Google Scholar 

  23. Samin, J.C., Brüls, O., Collard, J.F., Sass, L., Fisette, P.: Multiphysics modeling and optimization of mechatronic multibody systems. Multibody Syst. Dyn. 18(3), 345–373 (2007)

    Article  MATH  Google Scholar 

  24. Sass, L., McPhee, J., Schmitke, C., Fisette, P., Grenier, D.: A comparison of different methods for modelling electromechanical multibody systems. Multibody Syst. Dyn. 12(3), 209–250 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  25. Trent, H.M.: Isomorphisms between oriented linear graphs and lumped physical systems. J. Acoust. Soc. Am. 27(3), 500–527 (1955)

    Article  MathSciNet  Google Scholar 

  26. Wang, L., Pao, Y.: Jourdain’s variational equation and Appell’s equation of motion for nonholonomic dynamical systems. Am. J. Phys. 71(1), 72–82 (2003)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Senior Applications Engineer, Applied Dynamics International, Ann Arbor, MI, USA

    James R. Phillips

  2. Department of Orthopaedic Surgery, University of Illinois at Chicago, Chicago, IL, USA

    Farid Amirouche

  3. Vice-Chairman, Department of Orthopaedic Surgery, Northshore University HealthSystem, Skokie, IL, USA

    Farid Amirouche

Authors
  1. James R. Phillips
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Farid Amirouche
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to James R. Phillips.

Ethics declarations

Competing Interests

The authors declare no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Proofs of results for rigid bodies

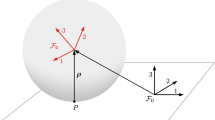
Here we provide demonstrations of the results stated above for rigid bodies, i.e., Eqs. (56)–(61). Without loss of generality, we consider only a single rigid body, with the velocity of its mass center given by \(\boldsymbol {v}_{\mathrm{c}}\) and its angular velocity given by \(\boldsymbol {\omega}\) in an inertial frame. A typical material point, with differential mass \(\mathrm{d}m\), is located at a vector radius \(\boldsymbol {\rho}\) from the mass center and has the inertial velocity

$$ \boldsymbol {v}=\boldsymbol {v}_{\mathrm{c}}+\boldsymbol {\omega}\times \boldsymbol {\rho}; $$
(64)

its partial velocity matrix is therefore

$$ \frac{\partial \boldsymbol {v}}{\partial \boldsymbol {\mathrm {f}}}= \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho}\,. $$
(65)

The second term on the right of (64) is the derivative of the radius vector, i.e.,

$$ \dot{\boldsymbol {\rho}}=\boldsymbol {\omega}\times \boldsymbol {\rho}\,. $$
(66)

By the definition of the mass and mass center, we have the following properties:

$$ \int \mathrm{d}m=m\,, $$
(67)
$$ \int \boldsymbol {\rho}\,\mathrm{d}m=\boldsymbol {0}\,. $$
(68)

The symmetric and positive-definite rotational inertia tensor \(\boldsymbol {\mathsf {I}}\) is defined as

$$ \boldsymbol {\mathsf {I}}\equiv \int \tilde{\boldsymbol {\rho}}\cdot \tilde{\boldsymbol {\rho}}^{ \mathsf{T}}\mathrm{d}m\,, $$
(69)

where \(\tilde{\boldsymbol {\rho}}\) is the antisymmetric dual tensor corresponding to the radius vector, defined as

$$ \tilde{\boldsymbol {\rho}}\equiv \boldsymbol {\mathsf {1}}\times \boldsymbol {\rho}\,, $$
(70)

and \(\boldsymbol {\mathsf {1}}\) is the identity tensor. The inertia tensor \(\boldsymbol {\mathsf {I}}\) has the property that its components are constant when expressed with respect to a set of body-fixed basis vectors; using this property, it is easy to show that the time derivative of \(\boldsymbol {\mathsf {I}}\) is given by

$$ \frac{\mathrm{d}}{\mathrm{dt}}\boldsymbol {\mathsf {I}}=\boldsymbol {\omega}\times \boldsymbol {\mathsf {I}}- \boldsymbol {\mathsf {I}}\times \boldsymbol {\omega}\,. $$
(71)

Eq. (56)

From the definition of \(\boldsymbol {\mathrm {e}}\) in (9), using (65), we have

$$\begin{aligned} \boldsymbol {\mathrm {e}} & =\int \left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right )\cdot \mathrm{d}\boldsymbol {F} \\ & =\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\cdot \int \mathrm{d}\boldsymbol {F}+\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}} \cdot \int \boldsymbol {\rho}\times \mathrm{d}\boldsymbol {F} \\ & \text{$\phantom{=}$(using properties of the scalar triple product}) \\ & =\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {F}+\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {M} \\ & \hphantom{=} (\text{by definition of}\,\boldsymbol {F}\,\text{and}\,\boldsymbol {M})\,. \end{aligned}$$

 □

Eq. (57)

From the definition of \(\boldsymbol {\mathrm {p}}\) in (20), using (64) with (65), we have

$$\begin{aligned} \boldsymbol {\mathrm {p}} & =\int \left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right )\cdot \left (\boldsymbol {v}_{\mathrm{c}}+\boldsymbol {\omega}\times \boldsymbol {\rho}\right )\mathrm{d}m \\ & =\int \left (\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\cdot \tilde{\boldsymbol {\rho}}\right )\cdot \left (\boldsymbol {v}_{\mathrm{c}}+ \boldsymbol {\omega}\cdot \tilde{\boldsymbol {\rho}}\right )\mathrm{d}m \\ & \phantom{=} (\text{by definition of}\,\tilde{\boldsymbol {\rho}}) \\ & =\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {v}_{\mathrm{c}}\int \mathrm{d}m+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\cdot \left (\int \tilde{\boldsymbol {\rho}}\cdot \tilde{\boldsymbol {\rho}}^{\mathsf{T}}\mathrm{d}m \right )\cdot \boldsymbol {\omega} \\ & \phantom{=} ( \text{using (68), and by definition of the tensor transpose operator}) \\ & =\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {v}_{\mathrm{c}}\,m+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {\mathsf {I}}\cdot \boldsymbol {\omega} \\ & \phantom{=} (\text{by definitions of}\,m\,\text{and}\,\boldsymbol {\mathsf {I}}) \\ & =\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {p}+\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\cdot \boldsymbol {h} \\ & \phantom{=} (\text{by definitions of}\,\boldsymbol {p}\,\text{and}\,\boldsymbol {h})\,. \end{aligned}$$

 □

Eq. (58)

Using (23) and (57), we have

$$\begin{aligned} \boldsymbol {\mathrm {A}} & =\frac{\partial}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\left [ \left (\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\right ) \cdot \boldsymbol {p}+\left (\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}} \right )\cdot \boldsymbol {h}\right ] \\ & =\left (\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}} \right )\cdot \frac{\partial}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\left (m \,\boldsymbol {v_{\mathrm{c}}}\right )+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \frac{\partial}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\left (\boldsymbol {\mathsf {I}}\cdot \boldsymbol {\omega}\right ) \\ & \phantom{=} ( \text{by definition of }\,\boldsymbol {p}\,\text{and}\,\boldsymbol {h}) \\ & =m\left (\frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}} \right )\cdot \left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}} \right )+\left (\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right ) \cdot \boldsymbol {\mathsf {I}}\cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )\,. \end{aligned}$$

 □

Eq. (59)

We prove this by showing first that \(\dot{\boldsymbol {\mathrm {A}}}=\boldsymbol {\mathrm {D}}+\boldsymbol {\mathrm {D}}^{\mathsf{T}}\) and second that \(\bar{\boldsymbol {\mathrm {D}}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}=\boldsymbol {\mathrm {D}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}\) when \(\boldsymbol {\mathrm {D}}\) is given by (59). N.B. it is not claimed that \(\boldsymbol {\mathrm {D}}=\bar{\boldsymbol {\mathrm {D}}}\); what is claimed is that by satisfying these properties, \(\boldsymbol {\mathrm {D}}\) may serve in place of \(\bar{\boldsymbol {\mathrm {D}}}\) in the equations of motion. Starting first then with (58) and using the definition of \(\boldsymbol {\mathrm {C}}\) in (62), by direct differentiation we have

$$\begin{aligned} \dot{\boldsymbol {\mathrm {A}}} & =\boldsymbol {\mathrm {C}}+\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \frac{\mathrm{d}}{\mathrm{d}t}\boldsymbol {\mathsf {I}}\cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \\ & =\boldsymbol {\mathrm {C}}+\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \left ( \boldsymbol {\omega}\times \frac{\partial \boldsymbol {h}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )+\left ( \boldsymbol {\omega}\times \frac{\partial \boldsymbol {h}}{\partial \boldsymbol {\mathrm {f}}}\right ) \cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \\ & \phantom{=} ( \text{using (71) and properties of the scalar triple product}) \\ & =\boldsymbol {\mathrm {D}}+\boldsymbol {\mathrm {D}}^{\mathsf{T}} \\ & \phantom{=} (\text{using (63)}) \\ & (\text{First part of proof.}) \end{aligned}$$

 □

Then for the second part of the proof, we begin with the definition of \(\bar{\boldsymbol {\mathrm {D}}}\) in (16), finding

$$\begin{aligned} \bar{\boldsymbol {\mathrm {D}}}^{\mathsf{T}}\boldsymbol {\mathrm {f}} & =\int \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \left ( \frac{\partial \boldsymbol {v}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )\boldsymbol {\mathrm {f}} \,\mathrm{d}m \\ & =\int \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \boldsymbol {v}\, \mathrm{d}m \\ & =\int \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right )\cdot \left (\boldsymbol {v}_{\mathrm{c}}+\boldsymbol {\omega}\times \boldsymbol {\rho}\right )\,\mathrm{d}m \\ & \phantom{=} (\text{using (64) and (65)}) \\ & =\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \boldsymbol {v}_{\mathrm{c}}\int \mathrm{d}m+\int \left [ \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \tilde{\boldsymbol {\rho}}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\times \left ( \boldsymbol {\omega}\cdot \tilde{\boldsymbol {\rho}}\right )\right ]\cdot \left ( \boldsymbol {\omega}\cdot \tilde{\boldsymbol {\rho}}\right )\,\mathrm{d}m \\ & \phantom{=} ( \text{using (68), (66), and (70)}) \\ & =\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \boldsymbol {v}_{\mathrm{c}}\,m+\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \left ( \int \tilde{\boldsymbol {\rho}}\cdot \tilde{\boldsymbol {\rho}}^{\mathsf{T}} \mathrm{d}m\right )\cdot \boldsymbol {\omega} \\ & \phantom{=} (\text{using the definition of }\,m\, \text{and properties of the cross product and tensor} \\ & \phantom{=}\text{transpose operator}) \\ & =\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \boldsymbol {p}+\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \boldsymbol {h} \\ & \phantom{=} (\text{using the definitions of }\,\boldsymbol {p},\,\boldsymbol {\mathsf {I}},\,\text{and}\, \boldsymbol {h})\,. \end{aligned}$$

Then using (62) and (63), we easily find that \(\boldsymbol {\mathrm {D}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}\) simplifies to the same result, so that \(\bar{\boldsymbol {\mathrm {D}}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}=\boldsymbol {\mathrm {D}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}\), as desired (second part of proof).  □

Eq. (60)

We have already found that \(\boldsymbol {\mathrm {D}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}\) simplifies to the correct result, immediately above. All that is needed is to recall that \(\boldsymbol {\mathrm {D}}^{\mathsf{T}}\boldsymbol {\mathrm {f}}=\hat{\boldsymbol {\mathrm {e}}}\) by definition from (27).  □

Eq. (61)

Let \(\boldsymbol {u}\) be an arbitrary unit vector fixed in a frame rotating with angular velocity \(\boldsymbol {\omega}\). The derivative of \(\boldsymbol {u}\), \(\dot{\boldsymbol {u}}\), is given by \(\boldsymbol {\omega}\times \boldsymbol {u}\). Using “cancellation of dots” (31) with \(\boldsymbol {u}\), we have

$$ \frac{\partial \boldsymbol {u}}{\partial q_{r}}= \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\times \boldsymbol {u}\,. $$
(72)

Differentiating this expression again with respect to \(q_{s}\), we find

$$ \frac{\partial ^{2}\boldsymbol {u}}{\partial q_{s}\partial q_{r}}= \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{s}\partial \dot{q}_{r}} \times \boldsymbol {u}+\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}} \times \frac{\partial \boldsymbol {u}}{\partial q_{s}}\,. $$

Noting that the left side of the equation is symmetric in the indices \(s\), \(r\), we may equate the right sides of the equation with reversed indices, i.e.,

$$ \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{s}\partial \dot{q}_{r}} \times \boldsymbol {u}+\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}} \times \frac{\partial \boldsymbol {u}}{\partial q_{s}}= \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{r}\partial \dot{q}_{s}} \times \boldsymbol {u}+\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{s}} \times \frac{\partial \boldsymbol {u}}{\partial q_{r}}\,, $$

from which we find

$$ \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{s}\partial \dot{q}_{r}} \times \boldsymbol {u}= \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{r}\partial \dot{q}_{s}} \times \boldsymbol {u}+\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{s}} \times \frac{\partial \boldsymbol {u}}{\partial q_{r}}- \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\times \frac{\partial \boldsymbol {u}}{\partial q_{s}}\,. $$

Using (72) again in the right side, this becomes

$$ \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{s}\partial \dot{q}_{r}} \times \boldsymbol {u}= \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{r}\partial \dot{q}_{s}} \times \boldsymbol {u}+\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{s}} \times \left (\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}} \times \boldsymbol {u}\right )- \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\times \left ( \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{s}}\times \boldsymbol {u} \right )\,. $$

Using the vector identity \(\boldsymbol {A}\times (\boldsymbol {B}\times C)-\boldsymbol {B}\times (\boldsymbol {A}\times \boldsymbol {C})=( \boldsymbol {A}\times \boldsymbol {B})\times \boldsymbol {C}\) on the right side, this becomes

$$ \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{s}\partial \dot{q}_{r}} \times \boldsymbol {u}= \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{r}\partial \dot{q}_{s}} \times \boldsymbol {u}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{s}}\times \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\right )\times \boldsymbol {u}\,. $$

Since this is true for an arbitrary unit vector \(\boldsymbol {u}\), we therefore must have

$$ \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{s}\partial \dot{q}_{r}}= \frac{\partial ^{2}\boldsymbol {\omega}}{\partial q_{r}\partial \dot{q}_{s}}+ \left (\frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{s}}\times \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\right )\,. $$

Now contracting both sides of the equation with respect to \(\dot{q}_{s}\), we find

$$\begin{aligned} &\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\right )= \frac{\partial \boldsymbol {\omega}}{\partial q_{r}}+\left (\boldsymbol {\omega} \times \frac{\partial \boldsymbol {\omega}}{\partial \dot{q}_{r}}\right )\,. \end{aligned}$$

 □

Appendix B: Derivation of \(\bar{\boldsymbol {\mathrm {D}}}\) for rigid bodies

Here we present a derivation of the exact result for \(\bar{\boldsymbol {\mathrm {D}}}\) in the case of rigid bodies, showing in detail how it differs from \(\boldsymbol {\mathrm {D}}\).

Considering first a single rigid body, by definition \(\bar{\boldsymbol {\mathrm {D}}}\) is given by Eq. (16), where \(\partial \boldsymbol {v}/\partial \boldsymbol {\mathrm {f}}\) is given by Eq. (65). The derivative of \(\partial \boldsymbol {v}/\partial \boldsymbol {\mathrm {f}}\) is therefore

$$ \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}}{\partial \boldsymbol {\mathrm {f}}}\right )= \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}\right )+ \frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\times \boldsymbol {\rho}+\left (\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}} \right )\times \left (\boldsymbol {\omega}\times \boldsymbol {\rho}\right )\,. $$
(73)

Substituting this into (16), we find

$$ \bar{\boldsymbol {\mathrm {D}}}=\int \mathrm{d}m\,\left [ \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}}+ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right ]\cdot \left [\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {v}_{\mathrm{c}}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}} \right )+\frac{\mathrm{d}}{\mathrm{d}t}\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \times \boldsymbol {\rho}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \times \left (\boldsymbol {\omega}\times \boldsymbol {\rho}\right )\right ]; $$

then using the defining properties of the center of gravity and inertia tensor, this reduces to

D ¯ = m ( ∂ v c ∂ f ) ⋅ d d t ( ∂ v c ∂ f T ) + ( ∂ ω ∂ f ) ⋅ I ⋅ d d t ( ∂ ω ∂ f T ) + ∫ d m [ ∂ ω ∂ f × ρ ] ⋅ [ ( ∂ ω ∂ f T ) × ( ω × ρ ) ] ,

or, referring to the definition of \(\boldsymbol {\mathrm {C}}\) in (62),

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\int \mathrm{d}m\,\left [ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right ]\cdot \left [\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \times \left (\boldsymbol {\omega}\times \boldsymbol {\rho}\right )\right ]\,. $$
(74)

Expanding the vector triple product in this result, we have

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\int \mathrm{d}m\,\left [ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right ]\cdot \left [\boldsymbol {\omega}\left (\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \cdot \boldsymbol {\rho}\right )-\boldsymbol {\rho}\left (\boldsymbol {\omega}\cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \right )\right ]\,, $$

which immediately reduces to

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\int \mathrm{d}m\,\left [ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \boldsymbol {\rho} \right ]\cdot \left [\boldsymbol {\omega}\left (\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \cdot \boldsymbol {\rho}\right )\right ]\,. $$
(75)

Rearranging the scalar triple product, we have

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}-\int \mathrm{d}m\,\left [ \boldsymbol {\omega}\times \boldsymbol {\rho}\right ]\cdot \left [ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\left (\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \cdot \boldsymbol {\rho}\right )\right ]\,, $$

or, using the tensor dyadic \(\boldsymbol {\rho} \boldsymbol {\rho}\),

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}-\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \left [ \boldsymbol {\omega}\times \int \mathrm{d}m\boldsymbol {\rho} \boldsymbol {\rho}\right ]\, \cdot \left [ \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ]. $$
(76)

Now it is well known, and could be derived from Eq. (69), that the inertia tensor can be expressed as

I=∫dm ( 1 | ρ | 2 − ρ ρ ) ,

so we have

−∫dmρρ=I−1∫dm | ρ | 2 ,

or

−∫dmρρ=I−m ρ 2 ‾ 1,
(77)

where \(\overline{\rho ^{2}}\) is the mass-weighted mean-square radius of the body. Substituting (77) into (76), we find

D ¯ = C T + ( ∂ ω ∂ f ) ⋅ [ ω × ( I − m ρ 2 ‾ 1 ) ] ⋅ [ ∂ ω ∂ f T ] ,

or

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \left ( \boldsymbol {\omega}\times \frac{\partial \boldsymbol {h}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )-\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot m \overline{\rho ^{2}}\left (\boldsymbol {\omega}\times \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )\,. $$
(78)

Rearranging the order of the final scalar triple product, we finally have

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {C}}^{\mathsf{T}}+\left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\right )\cdot \left ( \boldsymbol {\omega}\times \frac{\partial \boldsymbol {h}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )+m \overline{\rho ^{2}}\boldsymbol {\omega}\cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )\,. $$
(79)

This can also be written as

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {D}}+m\overline{\rho ^{2}}\boldsymbol {\omega}\cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}}\times \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )\,. $$
(80)

The final term in (79) and (80) is an obviously asymmetric matrix. Thus we have

$$\begin{aligned} \bar{\boldsymbol {\mathrm {D}}}+\bar{\boldsymbol {\mathrm {D}}}^{\mathsf{T}} = & \boldsymbol {\mathrm {C}}+\boldsymbol {\mathrm {C}}^{ \mathsf{T}}+\left (\frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}} \right )\cdot \left (\boldsymbol {\omega}\times \frac{\partial \boldsymbol {h}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right )+\left ( \boldsymbol {\omega}\times \frac{\partial \boldsymbol {h}}{\partial \boldsymbol {\mathrm {f}}}\right ) \cdot \left ( \frac{\partial \boldsymbol {\omega}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}}\right ) \\ = & \dot{\boldsymbol {\mathrm {A}}}\,, \end{aligned}$$

as expected.

Generalizing Eq. (80) to multiple rigid bodies subscripted by \(n\) and using the summation convention, we have

$$ \bar{\boldsymbol {\mathrm {D}}}=\boldsymbol {\mathrm {D}}+m_{n}\overline{\rho _{n}^{2}}\boldsymbol {\omega}_{n} \cdot \left (\frac{\partial \boldsymbol {\omega}_{n}}{\partial \boldsymbol {\mathrm {f}}} \times \frac{\partial \boldsymbol {\omega}_{n}}{\partial \boldsymbol {\mathrm {f}}^{\mathsf{T}}} \right )\,. $$
(81)

Now we see that the final term in the equation always reduces to zero when the equation is postmultiplied by \(\boldsymbol {\mathrm {f}}\) or premultiplied by \(\boldsymbol {\mathrm {f}}^{\mathsf{T}}\).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Phillips, J.R., Amirouche, F. Kane’s equations for nonholonomic systems in bond-graph-compatible velocity and momentum forms. Multibody Syst Dyn 59, 45–68 (2023). https://doi.org/10.1007/s11044-023-09919-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-023-09919-3

Keywords

Search

Navigation