1 Introduction

The time-dependent behavior of wood has been widely observed, and the following measures of time-dependent response are commonly used in experimental investigations: creep, time-dependent deformation under constant load, relaxation, the stress decay under constant deformation, stiffness variation in dynamic mechanical analysis (Ferry 1980), and rate of loading (or straining) effects (Cannell and Morgan 1987). In current wood design standards, creep is considered using a serviceability criterion: the creep deflection is defined as a multiple of the dead-load deflection. However, creep can have a significant effect on the integrity of a structure. For example, long-term creep can magnify the short-term deflections in columns, compression panels, shallow arches, and shells through the geometric coupling of axial (membrane) and bending actions (the P-A effect). This can lead to the reduction of stiffness and buckling failures (Jones and Xirouchakis 1980; Holzer et al. 1989).

In common practice, it is usually assumed that wood exhibits a linear viscoelastic response for low load levels and that the instantaneous mechanical response of wood is elastic. For high loading levels, the deviation from the linearity of the creep behavior of wood is expected. Under high sustained loads, the cracks grow and interact with viscoelasticity. Some experimental and analytical results concerning nonlinear creep can be found in the literature for concrete (see among others Bazant and L’Hermite 1988; Bazant and Gettu 1992; Mazzotti and Savoia 2003; Omar et al. 2009; Dufour et al. 2006; Omar et al. 2004; Saliba et al. 2013); for wood, there are already fewer (Schniewind 1968; Hunt 1989; Massaro and Malo 2019).

During the service-life of wooden structures, wood is loaded and delayed strains appear due to the creep phenomenon. Some theories suggest that microcracks nucleate and grow when wood is submitted to a high sustained loading, thereby contributing to the weakening of wood. Thus, it is important to understand the interaction between viscoelastic deformation and damage to design reliable civil-engineering structures. Several creep-damage theoretical models have been proposed in the literature for concrete and most of these models are based on empirical relations applied at the macroscopic scale. Coupling between creep and damage is mostly realized by adding some parameters to consider the microstructure effects (see among others Bazant and L’Hermite 1988; Bazant and Gettu 1992; Mazzotti and Savoia 2003; Omar et al. 2009; Dufour et al. 2006; Omar et al. 2004; Saliba et al. 2013). In this paper, an orthotropic viscoelastic model is combined with an orthotropic damage model because the purpose of this paper is to demonstrate the time-dependent modeling of creep and damage of wood and the application of the finite-element method to predict the long-term creep-damage behavior of wooden structures by the finite-element method.

2 Theory

The objective of this study is to propose a model that allows us to couple the damage and the memory-dependent (viscous) behavior. The goal is to accurately predict the long-term behavior of the wooden structure. In this study, three models are provided: the pure viscoelastic model, the pure damage model, and the coupled viscoelastic–damage model.

2.1 Viscoelastic orthotropic model

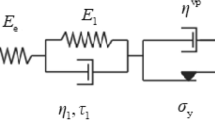
The viscoelastic model is based on a generalized orthotropic Kelvin chain according to Bažant et al. (2018). Instead of the integral-type, the rate-type implementation with an exponential algorithm is utilized in this study, which can overcome two disadvantages from the integral-type mentioned above (Yu et al. 2012; Bažant et al. 2012; Toratti 1992; Liu 1994). The viscoelastic stress–strain relation can be approximated by a rheological model (e.g., Kelvin-chain model, Maxwell-chain model) in the rate-type algorithm (Bazant and Jirásek 2002; Hanhijärvi and Mackenzie-Helnwein 2003; Fortino et al. 2009; Massaro and Malo 2019). The Kelvin-chain model (Fig. 1) is implemented in this study which consists of a series of Kelvin chain units with coupled spring and dashpot. In rate-type implementation, by transferring the incremental stress–strain relation to a quasielastic incremental stress–strain relation, the creep calculation can be simplified to a series of elasticity problems with initial strains (Bažant et al. 2018; Bazant and Jirásek 2002; Hanhijärvi and Mackenzie-Helnwein 2003; Fortino et al. 2009; Massaro and Malo 2019). Because of this simplification, the storage of previous data is no longer necessary, and the computational cost can be greatly reduced, which is important in large-scale structure analysis.

Fig. 1
figure 1

Generalized Kelvin chain

Full size image

The presented model is based on plane stress conditions, but the extension to 3D is possible in the future. Assuming plane stress, the 2D stress tensor components are written in the following vector:

$$ \boldsymbol{\sigma}^{\left ( n \right )} \equiv \boldsymbol{\sigma} \left ( t_{n} \right ) = \left ( \textstyle\begin{array}{c} \sigma _{x}\left ( t_{n} \right ) \\ \sigma _{y}\left ( t_{n} \right ) \\ \tau _{xy}\left ( t_{n} \right ) \end{array}\displaystyle \right ) \equiv \left ( \textstyle\begin{array}{c} \sigma _{L}\left ( t_{n} \right ) \\ \sigma _{R}\left ( t_{n} \right ) \\ \tau _{LR}\left ( t_{n} \right ) \end{array}\displaystyle \right ). $$
(1)

The stress at time \(t_{n}\) marked as \(\boldsymbol{\sigma}^{\left ( n \right )}\) is calculated using the known stress at time \(t_{n-1}\) marked as \(\boldsymbol{\sigma}^{\left ( n - 1 \right )}\) and the stress increment \(\Delta \boldsymbol{\sigma} \):

$$ \boldsymbol{\sigma}^{\left ( n \right )} = \boldsymbol{\sigma}^{\left ( n - 1 \right )} + \Delta \boldsymbol{\sigma}. $$
(2)

The stress increment is calculated according to Bazant and Jirásek (2002):

$$ \Delta \boldsymbol{\sigma} = \mathbf{C}^{ve}:\left ( \Delta \boldsymbol{\varepsilon} - \Delta \boldsymbol{\varepsilon}^{v} \right ), $$
(3)

where the viscoelastic stiffness matrix \(\mathbf{C}^{ve}\) is the inverse of the viscoelastic compliance matrix \(\mathbf{D}^{ve}\):

$$ \mathbf{C}^{ve} = \left ( \mathbf{D}^{ve} \right )^{ - 1} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{E_{L}^{ve}}{1 - \nu _{LR}\nu _{RL}} & \frac{\nu _{LR}E_{R}^{ve}}{1 - \nu _{LR}\nu _{RL}} & 0 \vspace*{4pt}\\ \frac{\nu _{RL}E_{L}^{ve}}{1 - \nu _{LR}\nu _{RL}} & \frac{E_{R}^{ve}}{1 - \nu _{LR}\nu _{RL}} & 0 \vspace*{4pt}\\ 0 & 0 & G_{LR}^{ve} \end{array}\displaystyle \right ], $$
(4)

where

$$ \mathbf{D}^{ve} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{E_{L}^{ve}} & \frac{ - \nu _{LR}}{E_{R}^{ve}} & 0 \vspace*{4pt}\\ \frac{ - \nu _{RL}}{E_{L}^{ve}} & \frac{1}{E_{R}^{ve}} & 0 \vspace*{4pt}\\ 0 & 0 & \frac{1}{G_{LR}^{ve}} \end{array}\displaystyle \right ]. $$
(5)

The viscoelastic compliance matrix \(\mathbf{D}^{ve}\) is assembled from the effective viscoelastic moduli, which were calculated from the following 1D relations (Bazant and Jirásek 2002):

$$ \begin{aligned}E_{L}^{ve} &= \left ( \frac{1}{D_{L0}} + \sum _{j = 1}^{M} \frac{1 - \lambda _{Lj}}{D_{Lj}} \right )^{ - 1},\qquad E_{R}^{ve} = \left ( \frac{1}{D_{R0}} + \sum _{j = 1}^{M} \frac{1 - \lambda _{Rj}}{D_{Rj}} \right )^{ - 1}, \\ G_{LR}^{ve} &= \left ( \frac{1}{D_{LR0}} + \sum _{j = 1}^{M} \frac{1 - \lambda _{LRj}}{D_{LRj}} \right )^{ - 1} \end{aligned}$$
(6)
$$ \textstyle\begin{array}{l} \tau _{Lj} = \frac{\eta _{Lj}}{E_{Lj}} \vspace*{4pt}\\ \tau _{Rj} = \frac{\eta _{Rj}}{E_{Rj}} \vspace*{4pt}\\ \tau _{LRj} = \frac{\eta _{LRj}}{G_{LRj}} \end{array}\displaystyle ,\qquad \textstyle\begin{array}{l} \beta _{Lj} = \exp \left ( \frac{ - \Delta t}{\tau _{Lj}} \right ) \vspace*{4pt}\\ \beta _{Rj} = \exp \left ( \frac{ - \Delta t}{\tau _{Rj}} \right ) \vspace*{4pt}\\ \beta _{LRj} = \exp \left ( \frac{ - \Delta t}{\tau _{LRj}} \right ) \end{array}\displaystyle ,\qquad \textstyle\begin{array}{l} \lambda _{Lj} = \frac{\tau _{Lj}}{\Delta t}\left ( 1 - \beta _{Lj} \right ) \vspace*{4pt}\\ \lambda _{Rj} = \frac{\tau _{Rj}}{\Delta t}\left ( 1 - \beta _{Rj} \right )\vspace*{4pt} \\ \lambda _{LRj} = \frac{\tau _{LRj}}{\Delta t}\left ( 1 - \beta _{LRj} \right ) \end{array}\displaystyle , $$
(7)

where \(\tau \) [s] is the retardation time and \(\eta \) [Pa s] is viscosity.

The increment of the viscous strain vector is calculated in 2D as follows:

$$ \Delta \boldsymbol{\varepsilon}^{v} = \Delta t\sum _{j = 1}^{M} \left ( \textstyle\begin{array}{c} \lambda _{Lj}\frac{d\varepsilon _{{Lj}}^{\left ( n - 1 \right )}}{dt} \vspace*{4pt}\\ \lambda _{Rj}\frac{d\varepsilon _{Rj}^{\left ( n - 1 \right )}}{dt} \vspace*{4pt}\\ \lambda _{LRj}\frac{d\gamma _{LRj}^{\left ( n - 1 \right )}}{dt} \end{array}\displaystyle \right ), $$
(8)

where the state variables calculated at the previous time \(t_{ i-1}\) are used: \(\frac{d\varepsilon _{{Lj}}^{\left ( n - 1 \right )}}{dt}\), \(\frac{d\varepsilon _{{Rj}}^{\left ( n - 1 \right )}}{dt}\), \(\frac{d\gamma _{{LRj}}^{\left ( n - 1 \right )}}{dt}\).

These state variables are needed to update and to calculate the next time step:

$$ \textstyle\begin{array}{l} \frac{d\varepsilon _{{Lj}}^{\left ( n \right )}}{dt} = \beta _{Lj}\frac{d\varepsilon _{{Lj}}^{\left ( n - 1 \right )}}{dt} + \frac{1 - \beta _{Lj}}{\Delta tD_{Lj}}\Delta \sigma _{L} \vspace*{4pt}\\ \frac{d\varepsilon _{{Rj}}^{\left ( n \right )}}{dt} = \beta _{Rj}\frac{d\varepsilon _{{Rj}}^{\left ( n - 1 \right )}}{dt} + \frac{1 - \beta _{Rj}}{\Delta tD_{Rj}}\Delta \sigma _{R} \vspace*{4pt}\\ \frac{d\gamma _{{LRj}}^{\left ( n \right )}}{dt} = \beta _{LRj}\frac{d\gamma _{{LRj}}^{\left ( n - 1 \right )}}{dt} + \frac{1 - \beta _{LRj}}{\Delta tD_{LRj}}\Delta \tau _{LR} \end{array}\displaystyle . $$
(9)

The retardation time of the \(j\)th unit of the Kelvin chain in a given material direction is the ratio of the corresponding viscosity and modulus of elasticity of the \(j\)th unit in the given material direction. These viscosities and elasticity moduli must be determined (fitted) from known measured creep curves (creep-strain dependency on time) in the given material directions of the wood. An algorithm based on the Particle-Swarm Optimization method is used in this study (Kennedy and Eberhart 1995; Shi and Eberhart 1998).

2.2 The orthotropic damage model

The damage model for orthotropic wood material has been taken from the literature (Sandhaas et al. 2020; Maimí et al. 2007, 2006; Matzenmiller et al. 1995). In these sources, a brief description of this damage model with respect to 2D plane stress is given. It is assumed that the linear elastic stiffness matrix \(C_{ijkl}^{e}\) is constant over time and the damage stiffness matrix only is reduced to \(C_{ijkl}^{dam}\left ( t_{n} \right )\).

The linear elastic stress predictor is the following:

$$ \sigma _{ij}^{e}\left ( t_{n} \right ) = C_{ijkl}\varepsilon _{kl}\left ( t_{n} \right ), $$
(10)

the resulting stress is calculated as follows:

$$ \sigma _{ij}\left ( t_{n} \right ) = C_{ijkl}^{dam}\left ( t_{n} \right )\varepsilon _{kl}\left ( t_{n} \right ) $$
(11)

and the damage criteria are defined according to Sandhaas et al. (2020), Maimí et al. (2007, 2006), Matzenmiller et al. (1995):

$$ \mathbf{F} - \boldsymbol{\kappa} = \mathbf{0}. $$
(12)

The Kuhn–Tucker and consistency conditions must hold (Sandhaas et al. 2020):

$$ \mathbf{F} - \boldsymbol{\kappa} \le \mathbf{0},\qquad \frac{d\boldsymbol{\kappa}}{dt} \ge \mathbf{0},\qquad \frac{d\boldsymbol{\kappa}}{dt}\left ( \mathbf{F} - \boldsymbol{\kappa} \right ) = 0. $$
(13)

The damage-evolution functions, state variables \(\boldsymbol{\kappa} \) are introduced, which keep track of the loading history (Sandhaas et al. 2020; Maimí et al. 2006).

If \(F_{ij}\left ( t_{n} \right ) > 1\), then

$$ \kappa _{ij}\left ( t_{n} \right ) = \max \left \{ F_{ij}\left ( t_{n} \right ),\kappa _{ij}\left ( t_{n - 1} \right ) \right \} $$

else

$$ \kappa _{ij}\left ( t_{n} \right ) = 1, $$

or, simplest

$$ \kappa _{ij}\left ( t_{n} \right ) = \max \left \{ 1,F_{ij}\left ( t_{n} \right ),\kappa _{ij}\left ( t_{n - 1} \right ) \right \}. $$
(14)

The damage parameters are calculated from these state variables according to Sandhaas et al. (2020), Maimí et al. (2006):

$$ d_{ij}\left ( t_{n} \right ) = d_{ij}\left ( \kappa _{ij}\left ( t_{n} \right ) \right ). $$
(15)

The constitutive stiffness damage matrix is then calculated as the inverse of the compliance damage matrix:

$$ C_{ijkl}^{dam} = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{\left ( 1 - d_{L} \right )E_{L}} & \frac{ - \nu _{LR}\left ( d_{L},d_{R},d_{LR} \right )}{\left ( 1 - d_{R} \right )E_{R}} & 0 \vspace*{4pt}\\ \frac{ - \nu _{RL}\left ( d_{L},d_{R},d_{LR} \right )}{\left ( 1 - d_{L} \right )E_{L}} & \frac{1}{\left ( 1 - d_{R} \right )E_{R}} & 0 \vspace*{4pt}\\ 0 & 0 & \frac{1}{\left ( 1 - d_{LR} \right )G_{LR}} \end{array}\displaystyle \right ]^{ - 1}. $$
(16)

This damage model is used for the description of both the brittle and ductile (plastic) behavior of wood using the specific state variables.

2.3 Viscoelastic–damage model

The viscoelastic–damage model is proposed, where the instantaneous behavior and memory-dependent (viscous) behavior are considered. Therefore, the total strain tensor can be decomposed into the instantaneous strain tensor and the memory-dependent strain tensor. The instantaneous strain tensor, including the elastic-strain tensor and plastic- or damage-strain tensor, will develop instantaneously after loading, while the memory-dependent strain tensor, including viscous measures like creep, will grow with time. The additive decomposition of the total strain tensor can be used while assuming small deformations:

$$ \varepsilon _{kl}\left ( t \right ) = \varepsilon _{kl}^{e}\left ( t \right ) + \varepsilon _{kl}^{p}\left ( t \right ) + \varepsilon _{kl}^{d}\left ( t \right ) + \varepsilon _{kl}^{c}\left ( t \right ), $$
(17)

where \(\varepsilon _{kl}^{e}\left ( t \right )\) is the instantaneous elastic, \(\varepsilon _{kl}^{p}\left ( t \right )\) is the instantaneous plastic, \(\varepsilon _{kl}^{d}\left ( t \right )\) is the instantaneous damage, and \(\varepsilon _{kl}^{c}\left ( t \right )\) is the memory-dependent (viscous) component – for example, creep strain.

The components of the stress tensor are calculated under the assumption that the instantaneous elastic component of the strain tensor is not only elastic but also linear and Hooke’s law is applied. In the case of wood, the yield strength is equal to the linear limit – therefore, nonlinear elasticity does not occur, and elasticity can always be considered to be linear:

$$ \sigma _{ij}\left ( t \right ) = C_{ijkl}^{e}\varepsilon _{kl}^{e}\left ( t \right ), $$
(18)

where \(C_{ijkl}^{e}\) is the constitutive stiffness matrix of the orthotropic material according to Hooke’s law. It is assumed that it does not change over time.

If the linear elastic component of the strain is expressed from the relation (17) and we substitute it into the relation (18), we obtain the following form for calculating the stress components:

$$ \sigma _{ij}\left ( t \right ) = C_{ijkl}^{e}\left ( \varepsilon _{kl}\left ( t \right ) - \varepsilon _{kl}^{p}\left ( t \right ) - \varepsilon _{kl}^{d}\left ( t \right ) - \varepsilon _{kl}^{c}\left ( t \right ) \right ). $$
(19)

It is appropriate to point out that the damage component of the deformation is usually calculated from the so-called damage parameters, which modify the original elastic constitutive stiffness matrix, and damage deformation can then be calculated from these damage parameters, and if this damage model is also used considering the plastic behavior, the plastic component of the deformation can also be calculated from it, and the following applies:

$$ \varepsilon _{kl}^{p}\left ( t \right ) + \varepsilon _{kl}^{d}\left ( t \right ) = \varepsilon _{kl}\left ( t \right ) - \varepsilon _{kl}^{c}\left ( t \right ) - \left [ C_{ijkl}^{e} \right ]^{ - 1}\sigma _{ij}\left ( t \right ), $$
(20)

where individual stress components are calculated using a damage matrix \(C_{ijkl}^{dam}\left ( t \right )\):

$$ \sigma _{ij}\left ( t \right ) = C_{ijkl}^{dam}\left ( t \right )\left ( \varepsilon _{kl}\left ( t \right ) - \varepsilon _{kl}^{c}\left ( t \right ) \right ). $$
(21)

The goal is to design, implement, and validate a numerical algorithm (numerical integration over time), that combines the two mentioned models:

a) the viscoelastic model;

b) the damage model.

At the given time \(t_{n}\), i.e., at the end of the time step \(\left \langle t_{n - 1},t_{n} \right \rangle \) of size \(\Delta t = t_{n} - t_{n - 1}\) in each iteration of the global Newton method, the procedure is as follows (in each iteration, only the increment of the total strain \(\Delta \boldsymbol{\varepsilon} \) is a variable input from the solver, otherwise the other quantities are constant and their values are taken from the previous converged time \(t_{ n-1}\)):

The creep model (generalized Kelvin chain) is applied, and the viscoelastic stress increment is calculated according to the relation:

$$ \Delta \boldsymbol{\sigma}^{ve} = \mathbf{C}^{ve}:\left ( \Delta \boldsymbol{\varepsilon} - \Delta \boldsymbol{\varepsilon}^{v} \right ) $$
(22)

and the resulting creep-strain increment is then calculated as follows:

$$ \Delta \boldsymbol{\varepsilon}^{c} = \Delta \boldsymbol{\varepsilon} - \mathbf{D}^{e}:\Delta \boldsymbol{\sigma}^{ve}, $$
(23)

where \(\mathbf{D}^{e} = \left [ \mathbf{C}^{e} \right ]^{ - 1}\) is the linear elastic compliance matrix. Due to the use of the Kelvin chain, this calculation depends only on the state variables from the previous time \(t_{ i-1}\) in the first iteration.

The damage model is used, and the resulting stresses and constitutive stiffness matrices are calculated, which already leads to the global finite-element system of equations. Within the framework of Newton’s method, another iteration can be performed to find the balance approximately gradually between the internal and external nodal forces of the entire structure under investigation.

The basic idea is that the total strain reduced by the viscous strain (creep strain) leads to the damage model, but that a certain creep component participates in the calculation of damage parameters according to this relation:

$$ \boldsymbol{\varepsilon}^{vin}\left ( t_{n} \right ) = \boldsymbol{\varepsilon}^{in}\left ( t_{n} \right ) + \alpha \boldsymbol{\varepsilon}^{c}\left ( t_{n} \right ) $$
(24)

or in incremental form:

$$ \Delta \boldsymbol{\varepsilon}^{vin} = \Delta \boldsymbol{\varepsilon}^{in} + \alpha \Delta \boldsymbol{\varepsilon}^{c}, $$
(25)

where \(\boldsymbol{\varepsilon}^{in} \left ( t_{n} \right ) = \boldsymbol{\varepsilon} \left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{c} \left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{M} \left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{T} \left ( t_{n} \right ) - \cdots\) is the instantaneous strain tensor because it corresponds to the immediate (elastic–plastic–damage) response of the material.

In this damage model, the total strain is reduced by the creep strain (like by other time-dependent initial strains, e.g., from moisture \(\boldsymbol{\varepsilon}^{M} \) or temperature changes) \(\boldsymbol{\varepsilon}^{T}\) but into the damage model enters not only instantaneous strain but also the creep strain (viscous) component according to equation (23). Let us call \(\boldsymbol{\varepsilon}^{vin}\) the viscous instantaneous component of total strain including not only instantaneous strain but also the creep-strain component. The proportion of creep strain \(\boldsymbol{\varepsilon}^{c}\) to viscous instantaneous strain \(\boldsymbol{\varepsilon}^{vin}\) is given by the alpha parameter \(\alpha \).

Let us denote the nonlinear part of the instantaneous strain as \(\boldsymbol{\varepsilon}^{d}\) (damage or plasticity) and then the instantaneous strain is equal to the linear (elastic) strain plus the strain corresponding to the nonlinearity (damage):

$$ \boldsymbol{\varepsilon}^{in} = \boldsymbol{\varepsilon}^{e} + \boldsymbol{\varepsilon}^{d}, $$
(26)

where \(\boldsymbol{\varepsilon}^{e} = \mathbf{D}^{e}:\boldsymbol{\sigma} \) and \(\boldsymbol{\varepsilon}^{d}\) is the strain mentioned above, e.g., from damage, which is still unknown, as well as the resulting stress \(\boldsymbol{\sigma} \), but both will be calculated using the damage model.

A linear elastic stress prediction can then be performed using this introduced viscous instantaneous strain \(\boldsymbol{\varepsilon}^{vin}\left ( t_{n} \right )\):

$$ \boldsymbol{\sigma}^{vin}\left ( t_{n} \right ) = \mathbf{C}:\boldsymbol{\varepsilon}^{vin}\left ( t_{n} \right ). $$
(27)

The damage parameters can be calculated using these modified (viscous instantaneous) stresses and creep strain, which means that the damage parameters are now functions of the viscous instantaneous strain, which was created by modifying the instantaneous (time-independent) strain by a component of the viscous (time-dependent) strain:

$$ \mathbf{D} = \mathbf{f}\left ( \boldsymbol{\sigma}^{vin} \right ) $$
(28)

and their calculation is carried out in a standard way, as described above (Sandhaas et al. 2020).

The resulting stress tensor is then obtained according to the common relation:

$$ \begin{aligned}\boldsymbol{\sigma} \left ( t_{n} \right ) &= \mathbf{C}^{dam}\left ( t_{n} \right ):\boldsymbol{\varepsilon}^{in}\left ( t_{n} \right ) \\ & = \left ( \mathbf{I} - \mathbf{D}\left ( \boldsymbol{\sigma}^{vin}\left ( t_{n} \right ) \right ) \right ):\mathbf{C}^{e}:\boldsymbol{\varepsilon}^{in}\left ( t_{n} \right ) \\ &= \left ( \mathbf{I} - \mathbf{D}\left ( \boldsymbol{\sigma}^{vin}\left ( t_{n} \right ) \right ) \right ):\mathbf{C}^{e}:\left ( \boldsymbol{\varepsilon} \left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{c}\left ( t_{n} \right ) \right ). \end{aligned}$$
(29)

The following options were tested for the stiffness tensor, which is used to calculate the strain increment in the next iteration within the global Newton method:

$$ \mathbf{C} = \mathbf{C}^{ve},\qquad \mathbf{C} = \mathbf{C}^{dam},\qquad \mathbf{C} = \mathbf{C}^{e} $$
(30)

and the best convergence was achieved with this first viscoelastic option \(\mathbf{C} = \mathbf{C}^{ve}\).

The strain that belongs to the damage model can be calculated using the resulting stress according to following form:

$$ \boldsymbol{\varepsilon}^{d}\left ( t_{n} \right ) = \boldsymbol{\varepsilon} \left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{c}\left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{e}\left ( t_{n} \right ) = \boldsymbol{\varepsilon} \left ( t_{n} \right ) - \boldsymbol{\varepsilon}^{c}\left ( t_{n} \right ) - \mathbf{D}^{e}:\boldsymbol{\sigma} \left ( t_{n} \right ). $$
(31)

This theory is inspired by the model for concrete (Mazzotti and Savoia 2003), where the creep strains are the components of the total strains, and they are weighted by an intensity factor \(\alpha \), which is included in the equivalent strain.

3 Methods

In this study, pure viscoelastic, pure damage, and coupled viscoelastic–damage models are implemented into Dlubal RFEM software. The model was algorithmized, programmed, implemented, and numerically validated into this finite-element method software. The implementation is based on the extension of its material library.

First, the material properties of beech wood are listed, which are divided into a) time-independent, b) time-dependent (viscous) and, as the second point, the list of the Dual benchmark tasks, which show the behavior of the given material model on different structures (various geometry, boundary conditions such as loads or supports).

3.1 Material properties of wood

The list of time-independent properties (elastic–plastic–damage properties) is given in Table 1 and Fig. 2.

Fig. 2
figure 2

Bilinear/trilinear material model with hardening a) compressive ductile (hardening) (upper left – longitudinal, lower left – transversal), b) tensional brittle (softening) behavior (upper right – longitudinal, lower right – transversal)

Full size image
Table 1 Time independent properties of wood (Ozyhar et al. 2013; Bengtsson et al. 2022)
Full size table

The stiffness properties used refer to the plane \(LR\). This approximation is suitable for most of the listed properties, except for the transversal modulus of elasticity. Indeed, several studies show that if we approximate an element, which is described by a cylindrical set of properties, with an equivalent set of Cartesian properties (\(x\), \(y\), \(z\)), then the modulus in the vertical direction (\(E_{90}\)) is lower than both \(E_{R}\) and \(E_{T}\). It does not affect the working principle of the presented model, but in order to calibrate the model with experimental results, a more accurate value should be used in later works.

For the nondiagonal elements of the wood compliance matrix several studies (Ozyhar et al. 2013) have pointed out that significant discrepancies can occur in the values of these nondiagonal elements. In these studies, for simplicity reasons, these values, based on the orthothropic symmetry of compliance are assumed as equal. In the future work, we can discuss the mechanics behind the time-dependent behavior of Poisson’s ratios based on the orthotropic symmetry and its development with time for the LR and LT planes.

The time-dependent properties (viscoelastic properties) such as creep curves and Kelvin-chain parameters are given in Fig. 3 and below.

Fig. 3
figure 3

The set of experimental creep tests were taken from Bažant and Wu (1973), Moll et al. (1991)

Full size image

The creep curves (Fig. 3) are used to fit the parameters of the orthotropic Kelvin chain, and further, to represent the viscoelastic component of the wood material model.

From a practical point of view it is therefore necessary to use the creep functions as an input of the model instead of \(M\) unknown pairs of \(E_{j}\) and \(\tau _{j} \). The implemented algorithm for the identification of the Kelvin-chain parameters is designed to work with the creep function, which is inverse to the above-mentioned compliance function. The approximation of the creep function via the Dirichlet series was modified, for the algorithm, into the following form:

$$ \varphi \left ( t \right ) =1+ \sum _{j=1}^{M} E_{j} \left ( 1- e^{- \frac{t}{\tau _{j}}} \right ). $$
(32)

The problem of identification of unknown coefficients of series from experimental data was described by Bažant and Wu (1973) who proved the use of the least-squares method (LSM) for the determination of \(E_{j}\), where the values of retardation times \(\tau _{j}\) had been chosen empirically to ensure even coverage of the time axis on a logarithmic scale. Complete identification of all parameters is possible to determine as roots of polynomials, whose coefficients are determinants of the matrices that are obtained from the values of approximated creep function and its derivatives (Moll et al. 1991). The identification can also be formulated as an optimization task. This approach is described in the work of Distéfano (1970) and Pister (1972). These authors solved the identification problem as nonlinear optimization. Concerning actual computing power, it is possible to use more demanding modern optimization algorithms based on imitation of natural processes. This idea is used within the designed algorithm where optimization is solved using the Particle-Swarm strategy (Kennedy and Eberhart 1995; Shi and Eberhart 1998).

The implemented identification algorithm is a combination of Bažant’s proposed LSM with empirically determined values of \(\tau _{j}\) and optimization where these values are refined to obtain an as accurate approximation of the user-defined creep curve as possible. The objective function is defined as an RMSE error as follows:

$$ \mathrm{RMSE} = \sqrt{\frac{\sum _{i=1}^{n} \left ( y_{i}^{*} - y_{i} \right )^{2}}{n}}, $$
(33)

where \(y_{i}^{*}\) is the creep coefficient value obtained using the Dirichlet series and \(y_{i}\) is the creep-coefficient value defined by the user and \(n\) is a number of points. Optimization constraints were defined by the following inequalities:

$$ 0.9 \tau _{j} \leq \tau _{j}^{*} \leq 1.1 \tau _{j}, $$
(34)

where \(\tau _{j}\) is the value of the empirically estimated retardation time and \(\tau _{j}^{*}\) is the value of the retardation time obtained using the Particle-Swarm optimization algorithm.

The best results were achieved for approximation with 5 Kelvin–Voight models in series. The averaged RMSE errors have reached values of 0.001266289 ± 1.27 × 10−4 for L and 0.002733644 ± 2.84 × 10−4 for \(R\). Realizations for 5 members are graphically indistinguishable from the input curves. In the case of 7 and 9 members the results were also numerically and graphically accurate enough but the average time consumption for the calculation of single identification is 1.7 times higher for 7 members and 2.6 higher for 9 members. These above-mentioned results were used to decide to use 5 members of the chain for structural analyses.

3.2 Benchmark tests methods

The benchmark tasks, which were used to test and analyze the new material model combining the viscoelastic and the damage models are the following:

A1, A2, B, and C are represented as a simple wall shell of 1 × 1 × 1 m. Geometry D is a beam represented as a shell structure under 2D plane-stress assumptions. The dimensions of the beam are 0.36 × 0.02 × 0.02 m, the supports distance is 0.3 m. The geometry E is also a beam shell structure, but with dimensions of 0.91 × 0.07 × 0.045 m, the supports distance is 0.8 m, see Fig. 4.

Fig. 4
figure 4

Overview of the benchmark tasks (Color figure online)

Full size image

The boundary conditions marked as \(u\) are displacement boundary conditions in the \(x\), \(y\), and \(z\) directions. On the other hand, the boundary conditions marked as \(\varphi \) are rotation boundary conditions around the orthotropic \(x\), \(y\), and \(z\) directions. Walls A1 and A2 have one fixed boundary and the opposite boundary loaded by 30 kN/m (A1) and 40 kN/m (A2). They represent the time-dependent response of wood to the compressive loading in longitudinal direction. The wall structure B shows the bending behavior of the shell structure with two opposite boundaries fixed and the perpendicular surface load. Task C also represents the same bending test as task B, but with four boundaries fixed. The task D shows the 2D plane stress model of the beam structure to show the example of three-point bending with short line boundary conditions representing the supports of the beam and short line load in the middle of the beam length. As for D, the task E is a beam structure, with the difference of being loaded in four-point bending. The supports and load are also applied on short lines.

4 Results

The aim is to represent the behavior of the new material model with the newly introduced alpha parameter on the resulting time response of selected benchmark tasks. For this reason, the influence of the alpha parameter on the time curves is shown on the first benchmark tasks (task A) by comparing the results with a material model without the alpha parameter and with a material model without damage, i.e., purely viscoelastic. The significant influence of the alpha parameter is demonstrated in the first tasks (Figs. 5, 6, 7, and 9), and therefore, the behavior of the material model under different loading levels is shown only with a nonzero alpha parameter in Figs. 8, 10, 11, 12, 13, and 14.

Fig. 5
figure 5

Results of benchmark tasks A1 and A2: the displacement \(u\) in the longitudinal direction of the wood in two different loading levels (30 MPa – left, 40 MPa – right)

Full size image
Fig. 6
figure 6

Results of benchmark tasks B and C: the deflection (displacement \(w\)) of the shell structure loaded by 615 kN/m2 in the transversal direction a) supported on both sides (left), b) supported on all four sides (right)

Full size image
Fig. 7
figure 7

Results of benchmark tasks D and E: the beam deflection (displacement \(v\) in the transversal \(y\) direction), a) three-point bending test, line loading of 100 kN/m (left), b) four-point bending test, two lines load of 2 × 240 kN/m (right)

Full size image
Fig. 8
figure 8

Results of benchmark tasks D and E: deflection (displacement \(v\) in the transversal \(y\) direction) for different loading levels \(f\) with the alpha parameter a) three-point bending test (left), b) four-point bending test (right)

Full size image

Figure 5 shows the time course of displacement in the longitudinal direction of the wood in two different loading levels. For both of these loading levels, the task is calculated using three cases of the material model: a) the linear viscoelastic model without the influence of the damage (generalized Kelvin chain), b) the viscoelastic model in combination with the damage model (Kelvin chain + damage model) without considering the alpha parameter, c) the viscoelastic model in combination with the damage model (Kelvin chain + damage model) with a nonzero alpha parameter set to 0.4.

It is observed that at a lower load level (30 MPa; just below the yield point of wood) the damage (plasticity) does not occur immediately after loading, but only after a certain time has passed due to creep, and only with nonzero parameter alpha = 0.4, because this is a case of uniaxial stress, where a constant external load is prescribed. Without the influence of the alpha parameter, the yield strength cannot be exceeded (Fig. 5, left). On the other hand, it can be seen that at a higher load, the yield strength will be exceeded right at the beginning after the load application, and this damage increases over time both in the case of alpha = 0.4 and also in the case of alpha = 0, because the damage response (plasticity) occurred at the very beginning and increases with creep even without the influence of the alpha parameter (Fig. 5, right). The importance and influence of the alpha parameter on the occurrence and development of damage (plasticity) over time as a result of the phenomenon of creep damage is shown here.

Figure 6 shows the application of the material model on the plates supported on both sides (left, task B) and supported on all four sides (right, task C). This plate is loaded with a continuous surface load of 615 kN/m2. The diagram shows the time courses of the deflection (displacement \(w\) in the direction perpendicular to the plane of the plate, i.e., in the \(z\) direction) depending on the setting of the material model. The material model would be set in these three variants: a) linear viscoelastic model without the influence of damage (Kelvin chain), b) viscoelastic model combined with a damage model (Kelvin chain + damage model) without consideration of the alpha parameter, c) viscoelastic model combined with a damage model (Kelvin chain + damage model) with a nonzero alpha parameter set to 0.4.

It can be seen from Fig. 6 that the new material model gives the expected results. With the linear viscoelastic model, the deflection is the lowest, in the case of the combined viscoelasticity and damage, a larger deflection even without the influence of the alpha parameter is obtained, and of course, the largest deflection in time occurs while considering the influence of the alpha parameter. If we compare the picture on the left and right sides, it is clear that in the right diagram (plate supported on all four sides), there are smaller deflections and at the beginning (immediately after the application of the load) no damage response occurs (the deflection calculated with the linear material matches the deflection calculated with nonlinear material) and during the loading period, mainly due to the nonzero alpha parameter, the deflections start to differ. On the other hand, on the left figure, slight damage occurs at the beginning (the deflections differ slightly), and this difference increases over time due to the creep. The largest deflections are again for the case of considering the influence of a nonzero alpha parameter.

Figures 7 to 14 show the application of the new material model to the beam deflection (displacement in the \(y\) direction) modeled by plane elements as a 2D plane-stress task made on two benchmark tasks: D: three-point beam bending, E: four-point beam bending.

Both benchmark tasks D and E were calculated with three different material model settings: a) the linear viscoelastic model without the influence of the damage (generalized Kelvin chain), b) the viscoelastic model combined with the damage model (Kelvin chain + damage model) without considering the alpha parameter, c) the viscoelastic model in combination with the damage model (Kelvin chain + damage model) with a nonzero alpha parameter set to 0.4.

It can be seen from Fig. 7 that in both cases the deflection of the beam depends on the setting of the material model and the combination of the damage with the creep has a major effect. The greatest influence is again in the case of a nonzero alpha parameter, and the phenomenon called creep damage is demonstrated by comparing the time courses of all the three cases: 1) viscoelastic, 2) viscoelastic + damage, 3) viscoelastic + damage with the alpha parameter.

Figure 8 shows the beam deflection time dependencies for different loading levels \(f\) (the material model set to the nonzero value of the parameter alpha = 0.4 to capture the most extreme case of possible behavior – the largest deflections). The aim was to determine for which loading levels the response of the beam is a) without damage in the middle of its length, b) with a slight development of damage in both tension and compression, c) with a largest damage development, d) with a failure of the beam. In both cases, it was shown that the beam may not fail immediately after the application of the load, but only after a certain time. Thus, time plays an important role in the failure of the structure, and to capture the real response of the structure, it is impossible to neglect these viscous phenomena, such as creep in this case. Time curves of the three-point bending test (Fig. 8, left) show that the failure occurs after 109.5 days with the line load of 110 kN/m. Time curves of the four-point bending test show that the failure occurs after 73 days with the two lines load 2 × 255 kN/m (Fig. 8, right).

Figure 9 shows damage development in the middle of the beam length at its tensile bottom side (i.e., tensile damage in the longitudinal \(x\) direction) for loading levels of a) 100 kN/m for the three-point bending (left) and b) 2 × 250 kN/m for a four-point bending (right). It is observed that in both cases the damage occurs instantaneously after the application of the load and then grows over time. The damage grows more over time for the case of the nonzero alpha.

Fig. 9
figure 9

Results of benchmark tasks D and E: beam deflection (displacement \(v\) in the transversal \(y\) direction) for a) three-point bending test, line load 100 kN/m (left), b) four-point bending test, two lines load 2 × 250 kN/m (right)

Full size image

Figure 10 shows the damage development in the middle of the beam length, at the tensile bottom side (i.e., tensile damage in the longitudinal \(x\) direction) for a fixed loading level (70 kN/m on the left for three-point bending and 2 × 180 kN/m on the right for four-point bending). In both cases, the damage does not occur instantaneously after the load application, but it occurs after a certain time, and then grows over time. The last case of the material model only is deliberately calculated, when the influence of a nonzero alpha parameter is considered and a smaller loading level is chosen, to show that the damage does not occur immediately after load application but occurs after some time as a result of creep (the so-called creep-damage phenomenon).

Fig. 10
figure 10

Results of benchmark tasks D and E: beam deflection (displacement \(v\) in the transversal \(y\) direction), use of the alpha parameter for a) three-point bending test, line load of 70 kN/m (left), b) four-point bending test, two lines load of 2 × 180 kN/m (right)

Full size image

The three- and four-point bending test benchmark tasks (Figs. 11, 12, 13, and 14) present the deflection \(v\) and the resulting damage parameter in the \(x\) direction in the time increments of 0 and 365 days, using the numerical solution of the benchmark problems. The next figures show the deflection \(v\) and the damage parameters in the \(x\) direction directly connected to the solution time.

Fig. 11
figure 11

Deflection of the beam during three-point bending test with line load 106 kN/m immediately after load application (0 days, below) and after 365 days of loading (above) (Color figure online)

Full size image
Fig. 12
figure 12

Deflection of the beam during four-point bending test with two lines load 2 × 240 kN/m immediately after load application (0 days, below) and after 365 days of loading (above) (Color figure online)

Full size image
Fig. 13
figure 13

Damage of the beam in the longitudinal \(x\) direction during three-point bending test with line load 106 kN/m at the beginning of loading (0 days, below) and after 365 days of loading (above)(Color figure online)

Full size image
Fig. 14
figure 14

Damage of the beam in the longitudinal \(x\) direction during four-point bending test with two lines load 2 × 240 kN/m at the beginning of loading (0 days, below) and after 365 days of loading (above) (Color figure online)

Full size image

Figures 11 and 12 show how the deflection (displacement in the \(y\) direction) of the wooden beam that is loaded by the three-point (Fig. 11) and the four-point (Fig. 12) bending increases over time. Shown are the instantaneous deflection after the application of the load (at time t = 0 days) and above after one year of loading. All the results are shown for alpha = 0.4. It is observed that the deflection increases significantly with increasing time. This happens for two reasons: a) because of creep itself, but also b) because of a phenomenon called creep damage (alpha = 0.4).

Figures 13 and 14 show the damage distribution inside the wooden beam, which is loaded by the three-point (Fig. 13) and the four-point (Fig. 14) bending. Only the damage component in the longitudinal \(x\)-axis direction is shown. At the bottom of the figures, the damage immediately after load application (\(t = 0\) days) is shown and at the top, the damage after one year of loading is shown in color at the bottom. All the results are shown for alpha = 0.4. In the upper part of the beam, the compression damage occurs and at the bottom, there is tensile damage. It can be seen in the figure that not only the deflection of the beam (displacement in the \(y\) direction) but also the damage increases over time due to creep.

5 Summary and conclusions

In this study, the viscoelastic–damage material model is algorithmized, implemented in the FEM solver, and tested on benchmark tasks. This material model enables the calculation of coupled creep and damage of the orthotropic wood material. The material model is based on a combination of an orthotropic viscoelastic model (generalized Kelvin chain) with the damage model. The combination of these two models is important for a more realistic time-dependent description of the behavior of wood in construction, since wood exhibits not only an instantaneous nonlinear elastic–plastic–damage response but also a time-dependent response due to the viscous nature of the material.

In this work, the phenomenon called creep damage, i.e., damage caused by wood creep, is analyzed. It is shown that: a) damage or plasticity develops over time (grows and spreads further), and that: b) wood may not be damaged or plasticized immediately after loading, but damage or plasticity may occur only after a certain time after loading, and then it develops further.

The results are calculated in three variants: 1) linear viscoelasticity, 2) viscoelasticity combined with the nonlinearity (plasticity or damage) without the influence of the creep-damage alpha parameter (the value of the alpha parameter is set to zero), 3) viscoelasticity combined with the nonlinearity (plasticity or damage) with the influence of the creep-damage alpha parameter (the value of the alpha parameter is set to 0.4). It is shown that the creep-damage parameter alpha has a significant influence on the formation and development of plasticity or damage over time and must be considered to capture the real-time-dependent behavior of wood.

The first benchmark tasks A1 and A2 show how the new material model behaves during 1D compressive stress in the elastic–plastic region in the longitudinal and transversal directions when a) plasticization develops over time (grows and spreads further), b) wood does not plasticize immediately after loading, but plasticization can occur only after a certain time after load application, and only then does it develop further.

The second set of tasks (benchmarks B, C) is supplementary, and it aims to show how the new material model behaves in a shell structure under bending load (plate model). For this purpose, a plate is continuously loaded, and it is supported only on two opposite sides, and in the second case, on all four peripheral sides. The results show again that: a) damage or plasticization develops over time (grows and spreads further), and that b) wood does not have to be damaged or plasticized immediately after loading, but the damage or plasticization can occur after a certain time from the load application, later it develops further. Because of the multiaxial stress state in the material (integration) point over the thickness of the shell element, the results are more varied in this task, and it can be observed how, under higher loads, the wood gradually plasticizes (ductilely damages) over time in the places and directions where it is stressed by compression, and in this same task, it can also be observed how it damages in a brittle manner in the points and directions where the wood is stressed by the tension or shear. The results are calculated in the three settings mentioned above.

The last two benchmark problems (D, E) are about the three-point and four-point bending of a beam modeled as a plane problem (2D plane stress) with two normal stress components and one shear stress component. These tasks showed the behavior of the new material model of wood during the bending loading of a wooden beam. The results again showed that: a) damage or plasticization develops over time (grows and spreads further), and that b) wood does not have to be damaged or plasticized immediately after loading, but damage or plasticization can occur only after a certain time from the load, and then it develops further. Because of the multiaxial stress, the results are more varied in this task, and it can be observed how, under higher loads, the wood gradually plasticizes (damaged in a ductile manner) over time in the places and directions where it is stressed by compression, and in this same task, it can also be observed how it damages the wood brittlely in places and directions where the wood is stressed by tension or shear. The results are calculated in the three variants mentioned above.

Finally, the use of the presented modular material model allows us to predict the occurrence and development of the wood damage during a time period, what means that it can be used as a tool for the evaluation of the time-dependent behavior of wooden structures and for prediction of their possible failure. The present study shows the combination of viscoelastic and damage models, but the presented modular approach allows us to include also other phenomena such as damage–plasticity combinations, the influence of moisture and thermal changes (swelling, shrinkage), the influence of cyclic moisture changes (the mechanosorptive creep) or the influence of material fatigue.