1 Introduction

In recent times, technology infrastructure, especially in imaging and computer networking, has evolved rapidly. This swift evolution, often referred to as digital transformation, presents challenges in securely storing, transmitting and sharing crucial data. In various communication platforms, from social media to highly secured military software, there’s a pressing need for infrastructures capable of meeting specific security standards, known as secure communication systems [1]. However, as new types of cyber threats emerge regularly, the notion of “security” in these systems is constantly challenged. This situation underscores the importance of having security systems that are adaptable and dynamic [2].

As technology advances globally, strengthening the defense industry has become crucial. Governments are competing to upgrade their defense infrastructures with advanced technology and to export these vehicles. In this competition, it’s essential for these vehicles to withstand physical attacks during missions and to protect the confidentiality of recorded data, like images/videos of equipment and ammunition, and thermal movements, even if captured by enemies. This necessitates the development of secure dynamic image/video encryption algorithms for recording and transmitting data. The field of image encryption is still evolving, with numerous recent studies underscoring its ongoing development and significance. [3,4,5,6]. Since most image encryption algorithms proposed in the literature are static and their performance in real-time applications is a matter of curiosity, researchers have turned to dynamic image encryption applications in recent years [7,8,9]. For this reason, chaotic systems are often preferred in dynamic encryption processes.

Chaos theory examines the behavior of dynamic nonlinear systems to be sensitive to initial values. Small changes in initial values cause larger-than-expected valence changes to be observed in chaotic systems [10, 11]. The term “chaos” was first defined by Edward Lorenz in a study [12] conducted in 1963. From past to present, many researchers have worked on chaotic systems, and the defined chaotic system models have been frequently used in important areas such as synchronization and secure communication [13]. It has revealed the idea that chaotic systems will play an important role in the production of keys used in cryptographic applications that must have unpredictability and complexity properties [14]. At the same time, the fact that the parameter values of chaotic systems are independent from each other has made the chaos-based random number generation statistically convenient [15].

Random number generators (RNGs) are divided into three basic classes: Pseudo, True, and Hybrid. Physical resources such as phase difference in oscillator circuits, noise in electronic circuits, delay time in switched circuits, and state variables of chaotic circuits are used to generate random number sequences with strong statistical properties [16,17,18] which can be given as an example of TRNG design. In these studies, researchers use the chaotic behavior called double scroll attractor observed at the output of a simple circuit model similar to the Chua circuit as an entropy source [19]. As a result of the study, random bit generation is realized with a design that is fully hardware-integrated and works in real-time. In analog circuit design based on a chaotic map as an entropy source [16], a random bit sequence is generated in a Programmable System on Chip (PSoC) reconfigurable device without the need for an external element. In 2016, a dual entropy core discrete-time chaos-based TRNG design was fabricated with 180-nm CMOS technology as a preliminary product [20]. In this design, both nonlinear functions, Bernoulli and Tent maps, provide random bit generation as a result of being sampled with a clock pulse and compared with each other. With this TRNG design, random output bits at a rate of 35 Mbps are obtained and analyzed.

In the TRNG designs, another important factor for a generated random number is that the generated key must remain secret. Based on this logic, researchers generally focus on hardware-based platforms and realize the key generation process by designing RNG in programmable hardware environments such as FPGA (Field Programmable Gate Array), which has millions of electronic/logic circuit elements despite its small size and also have a high parallel processing capacity [15, 21,22,23]. In the studies conducted for this purpose, real-time random bit generation has been realized by using both nonlinear chaotic map and circuit models together [24, 25].

In recent years, researchers have obtained new data by focusing especially on signal processing, control, and chaotic dynamics of the fractional computing approach, which has increased usability and applicability in almost every engineering field [26, 27]. Using the fractional order approach, chaotic dynamics for both existing chaotic systems in the literature and newly proposed systems are studied [28]. Many physical problems can be expressed and successfully solved with the help of fractional computing [29]. Recently, researchers have demonstrated that fractional differential equations are an effective tool for describing complex dynamics and can be used to model many physical and engineering systems more effectively [29,30,31]. In this study, a fractional order chaotic system is also used to generate true random bit series.

In many studies based on chaotic systems for generating true random numbers, the values of chaotic state variables are subjected to complex post-processing algorithms. Particularly in software platforms used for image encryption applications, a specific amount of time is required for each bit of the 8-bit key stream obtained from chaotic state variables. The bit generation in these studies follows a static structure and, typically, image encryption is performed at low frequencies [5,6,7,8]. To overcome this limitation, researchers employ more complex post-processing algorithms, increasing the computational workload. Therefore, the implementation of hardware-based true random bit generation, especially, becomes significant.

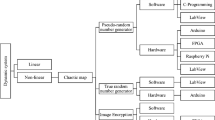
The primary motivation and novelty of this study is to generate true random bit sequences by utilizing a combination of chaotic systems on hardware as depicted in Fig. 1 below. This design aims to facilitate secure, real-time, high-speed video encryption. The implementation of this design suggests a robust, real-time video encryption method, applicable in a wide range of areas from basic cryptographic applications to military fields.

Fig. 1
figure 1

Block diagram representation for proposed high-speed true random bit generator design

Full size image

The contributions of this study to the existing literature are shown below:

  • Continuous time Lorenz and fractional order Chen-Lee chaotic systems are designed on hardware. Discrete-time Logistic and Tent chaotic maps are also designed on hardware using general-purpose operational amplifiers and special integrated circuits (IC) such as AD633 and LF398.

  • Since video data will be converted to an 8-bit grayscale format during encryption, 1 bit is extracted from each chaotic system’s state variable in parallel to obtain an 8-bit stream. This approach eliminates time loss and enables faster key generation.

  • To generate digital values at the output of chaotic systems, a quantization method is employed using a threshold value. The state variables to be converted into digital values are sampled with a 25 MHz clock pulse signal and compared with the threshold value. As a result, the bit rate of the true random number generator is 25 Mbps.

  • The 8-bit key sequence generation procedure from the state variables of chaotic systems is novel. The generated bit sequence successfully passes all statistical tests without data loss.

  • The real-time video encryption application is executed on an experimental assembly, composed of a Field Programmable Gate Array (FPGA) development kit, an OV7670 camera module, a VGA monitor, and prototype circuit boards for the chaotic systems. Consequently, encryption is performed by applying the XOR operation on FPGA to the real-time video data’s instantaneous pixel value and the generated 8-bit key value.

  • NIST SP 800 − 22 statistical tests, FIPS 140-1 standards test, chi-square test, histogram and correlation analysis, NPCR and UACI differential attack resilience tests are examined to verify the randomness of TRNG design and reliability of the encryption technique.

Herewith this introduction, equations, and analysis of four different chaotic systems are outlined in Section 2. Section 3 covers the simulations for both discrete and continuous-time chaotic systems within the Orcad-Pspice environment. Furthermore, each chaotic system’s prototype circuit is developed. In Section 4, the novel cryptographic key bit generation procedure is detailed and the encryption of the real-time video data is realized by monitoring on the FPGA-based experimental setup. The security analyses are examined such as NIST SP 800 − 22 statistical tests, FIPS 140-1, chi-square test histogram analysis, correlation analysis, NPCR, and UACI differential attacks in Section 5. At the end, the final section concludes the paper.

2 Definitions and behaviors of chaotic systems

It is possible to examine chaotic systems under two main headings continuous and discrete time. It is known in the literature that TRNG structures are designed with both types of systems [32, 33]. In these structures, which are highly sensitive to system parameters and initial conditions, it is not possible to predict the solutions of chaotic systems for long time intervals. In this section, discrete-time Logistic and Tent map, continuous time Lorenz and Chen-Lee chaotic systems are detailed with the parameters and dynamics of systems.

The Logistic map, which produces a chaotic random signal within a dynamic form, is extremely sensitive to initial conditions limited to a certain value range. Mathematically, the Logistic map is written as in Eq. 1.

$$x_\text{log}(n+1)=r\text{*}x_\text{log}\left(\text{n}\right)\text{*}\left(1-x_\text{log}\left(n\right)\right)$$
(1)

According to this equation, the map behaves stable for \(r\in \left[\text{1,3}\right]\) and unstable for \(r\in \left[\text{3,4}\right]\) when the initial value of \({x}_{\text{l}\text{o}\text{g}}\) is between \(0\) and \(1\). \(r=3.57\) is the onset of chaos, at the end of the period-doubling cascade. In Fig. 2, the Poincaré plot of the map is given for the chaos parameter \(r=3.9\) and the initial value \(x\left(0\right)=0.61\).

Fig. 2
figure 2

The Poincaré plot of the Logistic map

Full size image

Another discrete time chaotic system used in the study is the Tent map with a simple equation and only one chaos parameter. Chaotic sequences can be derived from the map equation although there are some periodic properties within a limited range of values. The larger the \(\mu\) value for the Tent map, the more periodic chaotic array occurs. The smaller the \(\mu\) value, the stronger the randomness of the chaotic sequences, but after long iterations, the state variable of the chaotic sequence is zero. The map is written as Eq. 2 below;

$$x_\text{tent}(\text{n}+1)=\left\{\begin{array}{cc}\text{a*}x_\text{tent}\left(n\right)&x_\text{tent}\left(\text{n}\right)<0.5\\\text{a*}\left(1-x_\text{tent}\left(n\right)\right)&x_\text{tent}\left(\text{n}\right)\geq0.5\end{array}\right.$$
(2)

and chaotic behavior is observed when \(\mu\) is in the range of \(\left[\text{1,2}\right]\). In Fig. 3, the Poincaré plot of the map is given for \(x\left(0\right)=0.61\) and \(\mu =1.99\).

Fig. 3
figure 3

The Poincaré plot of the Tent map

Full size image

An unconventional odd attractor is called according to the results observed in autonomous excess time systems with three or more state variables [12]. This expression is used for the extent of the system periphery but being aperiodic or divergent. The Lorenz system, known as an example of these nonlinear systems [34], is given in the set of air equations below. The chaotic behavior can be observed at \(\sigma =10, \rho =28, \beta =8/3\) parameter values and \(\left({x}_{0},{y}_{0},{z}_{0}\right)=[0.02, 0.02, 0.02]\) initial values.

$$\begin{array}{c}\dot{x}=\sigma \left(y-x\right)\\\dot{y}=x\left(\rho -z\right)-y\\\dot{z}=xy-\beta z\end{array}$$
(3)

This behavior of a chaotic system is indeed fascinating. In such systems, it’s noteworthy that the orbit never returns to its initial value and doesn’t pass through the same point. This unique characteristic is referred to “strange attractor” as shown in Fig. 4. Essentially, it means that even with specific initial conditions and parameter values, the system’s behavior remains unpredictable and non-repetitive.

Fig. 4
figure 4

3D orbital change of the Lorenz system

Full size image

Another chaotic system used in this study is the continuous time Chen-Lee system, derived from Euler’s equations for the motion of a rigid body. After this definition of the Chen-Lee system, studies are carried out to observe different dynamic behaviors of the system such as chaotic behavior, chaos control and synchronization, fractional order behavior, etc. [35]. In the differential equations of the chaotic system;

$$\begin{array}{c}\dot{x}=-yz+ax\\ \dot{y}=xz+by\\ \dot{z}=\frac{1}{3}xy+cz\end{array}$$
(4)

\(x\), \(y,\) and \(z\) are the state variables where \(a, b,\) and \(c\) are system parameters. The chaotic behavior is observed when\(\left(a, b, c\right)=(5, -10, -3.8)\). According to studies conducted in [29], the fractional order version of the Chen-Lee system is;

$$\begin{array}{c}{D}^{q1} x=-yz+ax\\ {D}^{q2} y=xz+by\\ {D}^{q3} z=\frac{1}{3}xy+cz\end{array}$$
(5)

illustrated by the equations. Here, the \({q}_{1}, {q}_{2},{q}_{3}\) values are between \(0\) and \(1\), and it has been stated that chaotic behavior is seen at the lowest order of \(2.43\) [35]. Figure 5 illustrates the trend of three-dimensional orbital change of the Chen-Lee system performed on the MATLAB platform.

Fig. 5
figure 5

3D orbital change of the Chen-Lee system

Full size image

Certainly, analyzing numerical solutions of chaotic systems for use as an entropy source in random number generation (RNG) applications is an intriguing concept. When employing a state variable as an entropy source, it’s essential to convert the state variable outputs into high-resolution digital (binary) values. This process involves sampling the state variable outputs and transforming them into a format suitable for use as a source of entropy. These high-resolution digital values can then be integrated into RNG algorithms to enhance their randomness and security.

3 Electronic circuit realizations of chaotic systems

Researchers have recently realized chaotic circuit implementations in hardware environments, reducing the number of elements to minimum levels and obtaining fast results with high operating frequencies. In addition, hardware implementations in RNG designs increase the randomness considerably, thus reducing the predictability of the generated number sequences.

Starting from the mathematical model of linear or nonlinear systems, it is possible to realize an electronic circuit equivalent to the equations of the systems [36]. In this section, simulations of electronic circuit designs in the Orcad-Pspice environment have been realized with the contribution of previous studies by making use of the mathematical models of chaotic systems. Most researchers design chaotic circuits by using active circuit elements such as operational amplifiers, analog multipliers, and multiplexers with standard passive circuit elements such as resistors, capacitors, and so on.

In the electronic circuit diagram of the Logistic map shown in Fig. 6, the components U5 and U6 are LF398 monolithic sample and hold integrated circuits with unit voltage gain. A holding capacitor is connected to the output pin of the LF398 and a sampling voltage is applied to it. The TTL-compatible square wave (clk) signal from the signal generator is used to trigger the first LF398 on the right. The bipolar common-emitter NPN 2N2222 transistor (Q1) circuit is used to generate the logic inverse of the clk signal to trigger the second LF398 on the left.

Fig. 6
figure 6

Electronic circuit diagram of Logistic map

Full size image

The mathematics of the Logistic map is executed by applying the initial value to the holding capacitor connected to the first LF398 to generate the next value of the state variable (\({x}_{\text{l}\text{o}\text{g}}(n+1)\)) in each period of the TTL signal iteratively.

The AD633 is a functionally complete analog multiplier which is named U3 in the circuit, includes high impedance, differential X and Y inputs, and a high impedance summing input Z. The transfer function of the AD633 is as follows;

$$\text{W}=\frac{\left(\text{X}1-\text{X}2\right)\text{*}\left(\text{Y}1-\text{Y}2\right)}{10}+Z$$
(6)

where \(W\) is the output of the multiplier. The translation of the Logistic map into an electronic circuit, with consideration for fundamental circuit principles and employing Eq. 1 and Eq. 6 is analyzed node by node through the following equations;

$$\text{A}=-\frac{{R}_{2}}{{R}_{1}}{x}_{log}\left(n\right)$$
(7)
$$\text{B}=-\frac{{R}_{4}}{{R}_{3}}A$$
(8)
$$\text{C}=-\frac{{R}_{6}}{{R}_{5}}A$$
(9)
$${x}_{log}(n+1)=\frac{\text{B}\left({V}_{ref}-C\right)}{10}$$
(10)
$${x}_{log}(n+1)=\frac{\frac{{R}_{4}}{{R}_{3}}\frac{{R}_{2}}{{R}_{1}}{x}_{log}\left(n\right)\left({V}_{ref}-\frac{{R}_{6}}{{R}_{5}}\frac{{R}_{2}}{{R}_{1}}{x}_{log}\left(n\right)\right)}{10}$$
(11)
$${x}_{log}(n+1)=\frac{1}{10}\frac{{R}_{4}}{{R}_{3}}\frac{{R}_{2}}{{R}_{1}}{x}_{log}\left(n\right){V}_{ref}-\frac{1}{10}\frac{{R}_{4}}{{R}_{3}}\frac{{R}_{2}^{2}}{{R}_{1}^{2}}\frac{{R}_{6}}{{R}_{5}}{x}_{log}^{2}\left(n\right)$$
(12)
$${x}_{log}(n+1)=3.9{x}_{log}\left(n\right)\left(1-{x}_{log}\left(n\right)\right)$$
(13)

where the notation \({x}_{log}(n+1)\) represents the subsequent iterative value of the Logistic map, with \({x}_{log}\left(n\right)\) denoting the current actual value. Figure 7 represents the electronic circuit board of the Logistic map. In the circuit board, there are several sockets to be able to measure and display the analog or digital outputs. There is also a sampler and comparator circuit for each chaotic system’s board which is designed with LM311 operational amplifier to obtain digital outputs. This comparator circuit structure is given at the end of this section to generalize for all chaotic systems. In Fig. 8, the chaotic time series of the Logistic map initial value \({x}_{log}\left(n\right)\) as input and next iterative value \({x}_{log}(n+1)\) as an output on an oscilloscope.

Fig. 7
figure 7

The electronic circuit board of the Logistic map

Full size image
Fig. 8
figure 8

Chaotic time series of the Logistic map initial value \({\varvec{x}}_{\varvec{l}\varvec{o}\varvec{g}}\left(\varvec{n}\right)\) and output value \({\varvec{x}}_{\varvec{l}\varvec{o}\varvec{g}}(\varvec{n}+1)\) on an oscilloscope

Full size image

In Fig. 9, a phase portrait of the Logistic map obtained from the circuit board is illustrated on an oscilloscope screen. The phase portrait indicates that the electronic circuit hardware design is compatible with the simulation result.

Fig. 9
figure 9

Phase portrait of the Logistic map obtained from the circuit board

Full size image

Another discrete time chaotic system used in this study is the Tent map. The electronic circuit diagram of the Tent map shown in Fig. 10 is quite similar to the Logistic map where the same operational amplifiers and sample and hold circuit structure are used in the diagram.

Fig. 10
figure 10

Electronic circuit diagram of Tent map

Full size image

The translation of the Tent map into an electronic circuit, with consideration for fundamental circuit principles and employing Eq. 2 is analyzed node by node through the following equations;

$$\text{A}=\left(\frac{{R}_{2}}{{R}_{1}}+1\right){x}_{tent}\left(n\right)$$
(14)
$$\text{B}=-\frac{{R}_{5}}{{R}_{4}}A-\frac{{R}_{5}}{{R}_{3}}{V}_{ref}$$
(15)
$$\text{C}=-\frac{{R}_{7}}{{R}_{6}}B$$
(16)
$$\text{D}=-\frac{{R}_{9}}{{R}_{8}}A$$
(17)
$${x}_{tent}(n+1) =-\frac{{R}_{12}}{{R}_{10}}D-\frac{{R}_{12}}{{R}_{11}}C$$
(18)
$${x}_{tent}(n+1) =\frac{{R}_{12}}{{R}_{10}}\frac{{R}_{9}}{{R}_{8}}\left(\left(\frac{{R}_{2}}{{R}_{1}}+1\right){x}_{tent}\left(n\right) \right)+\frac{{R}_{12}}{{R}_{11}}\frac{{R}_{7}}{{R}_{6}}\left(-\frac{{R}_{5}}{{R}_{4}}\left(\left(\frac{{R}_{2}}{{R}_{1}}+1\right){x}_{tent}\left(n\right) \right)-\frac{{R}_{5}}{{R}_{3}}{V}_{ref}\right)$$
(19)
$${x}_{tent}(n+1) =\frac{{R}_{12}}{{R}_{10}}\frac{{R}_{9}}{{R}_{8}}\frac{{R}_{2}}{{R}_{1}}{x}_{tent}\left(n\right) +\frac{{R}_{12}}{{R}_{10}}\frac{{R}_{9}}{{R}_{8}}{x}_{tent}\left(n\right) +\frac{{R}_{12}}{{R}_{11}}\frac{{R}_{7}}{{R}_{6}}\left(-\frac{{R}_{5}}{{R}_{4}}\frac{{R}_{2}}{{R}_{1}}{x}_{tent}\left(n\right) -\frac{{R}_{5}}{{R}_{4}}{x}_{tent}\left(n\right) -\frac{{R}_{5}}{{R}_{3}}{V}_{ref}\right)$$
(20)
$${x}_{tent}(n+1) =\frac{{R}_{12}}{{R}_{10}}\frac{{R}_{9}}{{R}_{8}}\frac{{R}_{2}}{{R}_{1}}{x}_{tent}\left(n\right) +\frac{{R}_{12}}{{R}_{10}}\frac{{R}_{9}}{{R}_{8}}{x}_{tent}\left(n\right) -\frac{{R}_{12}}{{R}_{11}}\frac{{R}_{7}}{{R}_{6}}\frac{{R}_{5}}{{R}_{4}}\frac{{R}_{2}}{{R}_{1}}{x}_{tent}\left(n\right) -\frac{{R}_{12}}{{R}_{11}}\frac{{R}_{7}}{{R}_{6}}\frac{{R}_{5}}{{R}_{4}}{x}_{tent}\left(n\right) +\frac{{R}_{12}}{{R}_{11}}\frac{{R}_{7}}{{R}_{6}}\frac{{R}_{5}}{{R}_{3}}{V}_{ref}$$
(21)
$${x}_{tent}(n+1) =\frac{{R}_{12}}{{R}_{10}}\frac{{R}_{9}}{{R}_{8}}{x}_{tent}\left(n\right) -\left\{\begin{array}{c} 0, {x}_{tent}\left(n\right) <\frac{{R}_{4}}{{2R}_{3}} \\ \frac{{R}_{12}}{{R}_{11}}\frac{{R}_{7}}{{R}_{6}}\left(\frac{{R}_{5}}{{R}_{4}}{x}_{tent}\left(n\right) -\frac{{R}_{5}}{{2R}_{3}}\right), {x}_{tent}\left(n\right) \ge \frac{{R}_{4}}{{2R}_{3}}\end{array}\right.$$
(22)

where the notation \({x}_{tent}(n+1)\) represents the subsequent iterative value of the Tent map, with \({x}_{tent}\left(n\right)\) denoting the current actual value. As all resistor values are taken into account in Eq. 22, the value of the bifurcation parameter \(a\) can be fixed at certain values by simply adjusting the \({R}_{7}\) and \({R}_{9}\) resistor connected to the feedback resistor in the operational amplifiers of \({U}_{3}\) and \({U}_{4}\). The relationship between the resistors \({R}_{7}\) and \({R}_{9}\) with the value of \(a\cong 2\) and the simplest equation for the Tent map can be obtained in Eq. 23 below.

$${x}_{tent}(n+1)=\left\{\begin{array}{ll} a{x}_{tent}\left(n\right) & {x}_{tent}\left(n\right) < \frac{1}{2} \\ a(1-{x}_{tent}(n\left)\right) & {x}_{tent}\left(n\right)\ge \frac{1}{2}\end{array}\right.$$
(23)

The electronic circuit board of the Tent map, which is the second discrete time chaotic system, is given in Fig. 11. On the circuitry, resistors \({R}_{7}\) and \({R}_{9}\) are used to adjust chaos parameter \(a\) as around \(2\).

Fig. 11
figure 11

Electronic circuit board of the Tent map

Full size image

In Fig. 12, the chaotic time series of the Tent map initial value \({x}_{tent}\left(n\right)\) as input and the next iterative value \({x}_{tent}(n+1)\) as an output on an oscilloscope. In Fig. 13, a phase portrait of the Tent map obtained from the circuit board is illustrated on the oscilloscope screen. The phase portrait indicates that the electronic circuit hardware design and compatible with the simulation result.

Fig. 12
figure 12

Chaotic time series of the Tent map initial value \({\varvec{x}}_{\varvec{t}\varvec{e}\varvec{n}\varvec{t}}\left(\varvec{n}\right)\) and output value \({\varvec{x}}_{\varvec{t}\varvec{e}\varvec{n}\varvec{t}}(\varvec{n}+1)\) on an oscilloscope

Full size image
Fig. 13
figure 13

Phase portrait of the Tent map obtained from the circuit board

Full size image

The other chaotic system used as an entropy source is the continuous time three-dimensional integer order Lorenz system. The chaotic behavior named “strange attractor” is obtained with the parameter values as \(\sigma =10, \rho =28, \beta =8/3\) and initial values as \(\left({x}_{0},{y}_{0},{z}_{0}\right)=[0.02, 0.02, 0.02]\). The electronic circuit diagram of the Lorenz system is given in Fig. 14. The equations obtained from the node analysis of the circuit are as follows:

Fig. 14
figure 14

The electronic circuit diagram of the Lorenz system

Full size image
$$A=-\left({X}_{1}\frac{{R}_{3}}{{R}_{1}}+Y\frac{{R}_{3}}{{R}_{2}}\right)$$
(24)
$$X=-\frac{1}{{R}_{4}{C}_{1}}\int A$$
(25)
$${X}_{1}=-X\frac{{R}_{6}}{{R}_{5}}$$
(26)
$$B={X}_{1}\left(1+\frac{{R}_{8}}{{R}_{7}}\right)$$
(27)
$$C=\frac{B.Z}{10}$$
(28)
$$D=-\left(X\frac{{R}_{12}}{{R}_{11}}+C\frac{{R}_{12}}{{R}_{9}}+{Y}_{1}\frac{{R}_{12}}{{R}_{10}}\right)$$
(29)
$${Y}_{1}=-Y\frac{{R}_{15}}{{R}_{14}}$$
(30)
$$Y=-\frac{1}{{R}_{13}{C}_{2}}\int D$$
(31)
$$E=\frac{B.{Y}_{1}}{10}$$
(32)
$$F=-\left(E\frac{{R}_{18}}{{R}_{16}}+{Z}_{1}\frac{{R}_{18}}{{R}_{17}}\right)$$
(33)
$${Z}_{1}=-Z\frac{{R}_{21}}{{R}_{20}}$$
(34)
$$Z=-\frac1{R_{19}C_3}\int F$$
(35)
$$\frac{dx}{dt}=Y\left(\frac{R_3}{R_4R_2C_1}\right)-X\;\left(\frac{R_3R_6}{R_1R_4R_5C_1}\right)$$
(36)
$$\frac{dy}{dt}=X\;\left(\frac{R_{12}}{R_{11}R_{13}C_2}\right)-XZ\;\left(\frac{R_6R_{12}}{10R_5R_9}-\frac{R_6R_8R_{12}}{10R_5R_7R_9}\right)-Y\;\left(\frac{R_{12}R_{15}}{R_{10}R_{14}}\right)$$
(37)
$$\frac{dz}{dt}=XY\;\left(\frac{R_6\left(R_7+R_8\right)R_{15}R_{18}}{R_5R_7R_{14}R_{16}R_{19}C_3}\right)-Z\;\left(\frac{R_{18}R_{21}}{R_{17}R_{20}}\right)$$
(38)

When the appropriate resistance and capacitance values are written into the equations, equation sets with chaotic behaviors are obtained as follows:

$$\frac{dx}{dt}=10\left(Y-X\right)$$
(39)
$$\frac{dy}{dt}=28X-Y-XZ$$
(40)
$$\frac{dz}{dt}=XY-\frac{8}{3} Z$$
(41)

The electronic circuit board of the integer order Lorenz system is given in Fig. 15. The chaotic time series of the system state variables are also illustrated in Fig. 16. Phase portraits obtained from the circuit board of the Lorenz system are respectively given in Fig. 17, X-Y plot in a Y-Z plot in b and X-Z plot in c. The phase portrait indicates that the electronic circuit hardware design is compatible with the simulation result.

Fig. 15
figure 15

Electronic circuit board of the Lorenz system

Full size image
Fig. 16
figure 16

Chaotic time series of X, Y, and Z state variables of the Lorenz system

Full size image
Fig. 17
figure 17

Lorenz system phase portraits (a) X-Y, (b) Y-Z, and (c) X-Z plots

Full size image

An electronic circuit diagram of the continuous time three-dimensional fractional order Chen-Lee chaotic system is given in Fig. 18. The chaotic behavior is obtained with the parameter values as \(a=5, b=-10, c=-3.8,\) and initial values as \(\left({x}_{0},{y}_{0},{z}_{0}\right)=[0.02, 0.02, 0.02]\). The equations obtained from the node analysis of the circuit are as follows:

$$A=\frac{Y.Z}{10}$$
(42)
$$B=-\left(A\frac{{R}_{3}}{{R}_{1}}+X\frac{{R}_{3}}{{R}_{2}}\right)$$
(43)
$$X=-\frac{1}{{R}_{4}{C}_{q1}}\int B$$
(44)
$$C=\frac{X.Z}{10}$$
(45)
$$D=-\left(C\frac{{R}_{10}}{{R}_{8}}+Y\frac{{R}_{10}}{{R}_{9}}\right)$$
(46)
$${Y}_{1}=-\frac{1}{{R}_{11}{C}_{q2}}\int D$$
(47)
$$Y=-{Y}_{1}\frac{{R}_{16}}{{R}_{15}}$$
(48)
$$E=\frac{X.{Y}_{1}}{10}$$
(49)
$$F=-\left(E\frac{{R}_{19}}{{R}_{17}}+{Z}_{1}\frac{{R}_{19}}{{R}_{18}}\right)$$
(50)
$${Z}_{1}=-Z\frac{{R}_{25}}{{R}_{24}}$$
(51)
$$Z=-\frac{1}{{R}_{20}{C}_{q3}}\int F$$
(52)
$$\frac{dx}{dt}=-YZ\left(\frac{{R}_{4}}{{10R}_{1}{R}_{4}{C}_{1}}\right)+X\left(\frac{{R}_{3}}{{R}_{2}{R}_{4}{C}_{1}}\right)$$
(53)
$$\frac{dy}{dt}=XZ\left(\frac{{R}_{10}{R}_{16}}{{10R}_{8}{R}_{11}{R}_{15}{C}_{2}}\right)-Y\left(\frac{{R}_{10}{R}_{16}}{{R}_{9}{R}_{11}{R}_{15}{C}_{2}}\right)$$
(54)
$$\frac{dz}{dt}=XY\left(\frac{{R}_{19}}{{10R}_{17}{R}_{20}{C}_{3}}\right)-Z\left(\frac{{R}_{19}{R}_{25}}{{R}_{18}{R}_{20}{R}_{24}{C}_{3}}\right)$$
(55)
Fig. 18
figure 18

Electronic circuit design of fractional order Chen-Lee chaotic system

Full size image

When the appropriate resistance and capacitance values are written into the equations, equation sets with chaotic behaviors are obtained as follows:

$$\frac{dx}{dt}=-YZ+5X$$
(56)
$$\frac{dy}{dt}=XZ-10Y$$
(57)
$$\frac{dz}{dt}=\frac{XY}{3}-\frac{83}{10} Z$$
(58)

The electronic circuit board of the 0.9 fractional order Chen-Lee system is given in Fig. 19. The chaotic time series of the system state variables are also illustrated in Fig. 20. Phase portraits obtained from the circuit board of the Chen-Lee system are respectively given in Fig. 21, X-Y plot in a Y-Z plot in b and X-Z plot in c. As a result, the phase portrait indicates that the electronic circuit hardware design is compatible with the simulation result.

Fig. 19
figure 19

The electronic circuit board of Chen-Lee chaotic system

Full size image
Fig. 20
figure 20

Chaotic time series of X, Y, and Z state variables of the Chen-Lee system

Full size image
Fig. 21
figure 21

Chen-Lee system phase portraits (a) X-Y, (b) Y-Z, and (c) X-Z plots

Full size image

Both electronic circuit diagrams and hardware board designs are compatible with each other for four different chaotic systems. The list of the electronic circuit components for each chaotic system is given in Table 1.

Table 1 List of the electronic circuit components for each chaotic circuit diagram
Full size table

Another process of the hardware designs of chaotic systems is the digitizer algorithm. Regarding the information given in Fig. 1, all state variables of the chaotic systems are digitized to generate digital values 1 or 0. The sample & hold and digitizer circuits given in Fig. 22 are connected to each state variable of the continuous-time chaotic systems while only the digitizer part is connected to state variables of the discrete-time chaotic maps. The clk signal is arranged as 25 MHz to obtain a 25 Mbps bit rate for the cryptographic key generator design.

Fig. 22
figure 22

The sample & hold and digitizer circuits

Full size image

4 Experimental setup of real-time video encryption application

This study aims to generate true random bit sequences by utilizing a combination of chaotic systems on hardware that are one-dimensional chaotic maps, and multi-dimensional fractional and integer order chaotic systems. The proposed TRBG design consists of discrete time Logistic and Tent maps, fractional order Chen-Lee and integer order Lorenz chaotic systems as an entropy source, XOR operator as a post-processor for real-time video encryption.

The proposed design aims to facilitate secure, real-time, high-speed video encryption. The proposed cryptographic key generator and the flow of the encryption process are illustrated in Fig. 23. In the application, from camera to XOR post-processor, whole operations are executed on Xilinx Zedboard FPGA. The real-time video processing modules given in Fig. 23 are used from [37, 38] where The OV7670 camera module provides 8-bit 640 × 480 data output in RBG565 format. This video frame data must be captured by the OV7670 capture module with the frequency of the pixel clock that is generated by the clock generator module. The output of the OV7670 capture module is arranged as 16-bit by simply merging two sequential pixel data. Then, the 16-bit RBG565 data is constituted as 12-bit and sent to SRAM of the FPGA. To apply XOR post-processor to an 8-bit cryptographic key and instant video frame data, 12-bit RGB pixel data must be converted to grayscale. RGB to Gray Conversion module converts the RGB pixel data to grayscale by following the equation;

$$Grayscale=0.1*R+0.6*G+0.3*B$$
(59)

where R, G, and B stand for each 4-bit pixel red, green, and blue color value, respectively. The arithmetic operations of Eq. (59) are executed in fixed point number representation format. The unsigned numbers are arranged as 17 bits where the format is considered as Qm.n. In the format, m indicates the number of bits that are arranged for the integer part of the number while n is for the fractional part. Therefore, the format is arranged as Q9.8. The resolution of the format is obtained as 2−n = 2−8 = 3.906e-3 [39]. The output of this module is arranged as an 8-bit integer grayscale after rounding the fractional part of the determined pixel value.

In the encryption stage of this study, as plain video data is in 8-bit grayscale format, the true random cryptographic key should be 8-bit length. After analyzing the state variables of four different chaotic circuits, the best option providing true random bit sequence is set as in Fig. 23 below. The digitized state variables of Logistic and Tent maps, x and y state variables of each continuous-time chaotic system are used to generate an 8-bit cryptographic key as shown in Fig. 23.

Fig. 23
figure 23

The proposed cryptographic key generator and the flow of the encryption process

Full size image

After the digitized state variables of chaotic systems are analyzed through an oscilloscope capable of a high-speed analyzer named Analog Discovery-2, the experimental setup consisting of a camera (OV7670 CMOS Camera), a Xilinx Zedboard FPGA with a high frequency (50 MHz) clock pulse generator, supply voltage sources, and a VGA monitor has been realized to implement real-time video encryption as shown in Fig. 24.

Fig. 24
figure 24

Implementation of real-time gray-level video encryption and decryption

Full size image

5 Statistical tests, analysis and results

In video encryption studies; statistical tests and differential attack analyses are extremely important to be sure the system is secure. Therefore, in the test and analysis stages, the generated cryptographic key and encrypted video data are analyzed. To obtain whole these data, an Analog Discovery-2 data analyzer is used to store as shown in Fig. 25. In Fig. 25, there is an instant screen illustrating the 8-bit secure cryptographic key data recorded from the real-time video encryption platform. This analyzer device is compatible with all kinds of analog and digital embedded devices and also is executed by an interface program on a PC.

Fig. 25
figure 25

Instant data transfer image of the 8-bit secure key used in the encryption stage

Full size image

During the testing phase, different statistical analyses are applied using the NIST SP 800 − 22 Statistical Test Suite [40], which consists of 16 tests developed by NIST. The minimum bit length to pass all of these tests successfully is 1000000 bits. A maximum of 13 test results can be successfully obtained for a bit string with a smaller number of 1000000-bit length. Within the framework of real-time application, secure cryptographic key data (true random bit sequence), original video data, and encrypted video data for 68395 Gy level pixels, with a total length of 547160-bit, are prepared for tests in MATLAB obtained with the help of Analog Discovery-2 data analyzer. Table 2 shows the NIST test results applied for the secure cryptographic key data. As all 13 tests are passed successfully, it means that the true random bit sequence is generated randomly.

Table 2 NIST test results for real-time recorded key data
Full size table

Another test module used for generating cryptographic key data is the FIPS 140-1 test standards, which specifies the requirements for evaluating cryptographic modules. The test requirements outlined in FIPS 140-1 ensure that the modules exhibit adequate levels of randomness and unpredictability. The first test of the FIPS 140-1 test module is the Monobit Test, which counts the number of 1’s in a 20,000-bit block. For the successful Monobit Test result, the count of 1’s must fall within the range of 9,654 to 10,346. The second test of the FIPS 140-1 test module is the Runs Test, which checks for consecutive sequences or runs of 1’s or 0’s. The Runs Test passes if the lengths of the runs meet specific criteria defined in the standard. Additionally, the Long Run Test, the third test of the FIPS 140-1 test module, examines the occurrence of long runs exceeding 34 consecutive identical bits. If the number of such long runs surpasses the specified threshold, the test is considered failed. The fourth and the last test of the FIPS 140-1 test module is the Poker Test which is a statistical test used to assess the randomness of a sequence of binary bits. It divides a 20,000-bit block into 5,000 4-bit chunks and counts the frequency of each chunk. The test calculates a statistic called X, which measures the deviation of observed frequencies from expected values. Regarding the FIPS 140-1 test module, the Poker Test is passed if X falls within the range of 1.03 to 57.4. This test ensures the cryptographic module exhibits satisfactory randomness and distribution in the generated bit sequence [41, 42].

These four distinct examinations, in conjunction with additional prerequisites, ascertain the compliance of cryptographic modules with the security criteria delineated in FIPS 140-1 tests. In Table 3, the conditions and results of all the tests associated with this test module can be observed. The proposed design has successfully passed all the tests present in the FIPS 140-1 module.

Table 3 FIPS 140-1 test result
Full size table

Another cryptographic validation test is the chi-square test which is a statistical method employed to assess the significance of the association between two categorical variables. It involves comparing observed and expected frequencies and calculating a chi-square statistic, which quantifies the deviation from randomness. By comparing this statistic to critical values in a table, a p-value is derived. If the p-value is lower than a predetermined significance level (e.g., α = 0.05), the null hypothesis is rejected, indicating a meaningful relationship. Conversely, if the p-value exceeds the significance level, the null hypothesis is accepted, implying no significant relationship exists [43].

The chi-square test is conducted on the complete generated bit sequence, which is constituted of 547,160 bits. The objective is to assess whether the sequence displayed characteristics of randomness. The resulting p-value is determined to be 0.44901302742262117, indicating that there is no substantial deviation from randomness. Furthermore, the computed chi-square statistic is 0.5731420916329928. Based on these outcomes, the null hypothesis cannot be rejected due to insufficient evidence, which suggests that the bit sequence can be considered random.

Plain video frame data obtained from the real-time gray-level video processing application on camera-FPGA construction is given in Fig. 26. It is observed in the figure that the raw data obtained by photographing the VGA monitor screen mostly consists of values close to white. Encryption is performed by post-processing with cryptographic random key data. At this stage, the XOR operator is used as the post-processor on the FPGA platform. The encrypted video frame image is also shown in Fig. 27 where the information of plain data is very different from the original phase. This result shows that the cryptographic key data is secure to apply encryption of real-time imaging systems.

Fig. 26
figure 26

Instant image of original and decrypted video data

Full size image
Fig. 27
figure 27

Instant image of encrypted video data

Full size image

Histogram analysis is also conducted to assess the reliability of encryption. Histogram analysis involves examining the distribution of pixel values within an image. In the context of image encryption applications, there are two critical criteria that the histogram analysis algorithm must adhere to. First, the histograms of the original and encrypted images should exhibit significant differences from each other. Second, the histogram graph of the encrypted image should display a uniform distribution [44]. Figure 28 illustrates the original video data along with its histogram, as well as the encrypted video data and its corresponding histogram. When examining the histogram graphs of the original and encrypted video data, it becomes evident that there are substantial disparities. This indicates that the histogram distribution of the encrypted video data is notably uniform. Consequently, extracting any meaningful information from the histogram of the encrypted image poses a considerable challenge for potential adversaries.

Fig. 28
figure 28

Original and encrypted images; histogram graphs of (a) original and (b) encrypted instant images of real-time video data

Full size image

In addition to histogram analysis, there are two more statistical tests to ensure the effectiveness of the encryption algorithm in image encryption applications. These measurements are the Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) tests, with an expected value of 0.99 for the NPCR test and 0.33 for the UACI test [45]. The calculated NPCR and UACI values for this study are 0.995466666666667 and 0.334722698785851, respectively. It is seen that the calculated test results are very close to the success criteria.

Another analysis method is the correlation analysis of plain and encrypted data. Correlation analysis shows the correlation of adjacent pixels in an image along diagonal (D), horizontal (H), and vertical (V) directions. This analysis tool is also used to validate inferences regarding the correlation distributions of the original and scrambled images [32, 46]. Figure 29 shows the correlation distribution of the original test image and the encrypted image with TRB in three directions. When the correlation distributions are examined, it is seen that the pixel distribution of the encrypted data is smooth along the horizontal, vertical, and diagonal directions. When this distribution is interpreted, it can be said that the encryption is successful.

Fig. 29
figure 29

Correlation distribution of (a) the original test image and (b) the encrypted image with TRB; along diagonal, horizontal, and vertical directions where each one of them is indicated as a column, respectively

Full size image

All the results of the statistical tests and analyses reveal that the true random bit generated from four different chaotic systems can be used in secure image/video encryption applications. Moreover, the proposed video encryption application passes all the tests of both statistical and differential attacks.

In Table 4, some of the image/video encryption designs in the literature are given. Many studies have been performed to encrypt images/video by using chaotic systems on embedded platforms. The main differences and advantages of this study are that the proposed design has analog hardware circuits as an entropy source, a simple post-processor function (XOR process), and a real-time application of video encryption. In this study, video encryption is performed in an FPGA environment using true random numbers obtained from analog circuits designed with multiple chaotic systems. The randomness of the generated bits is validated through multiple tests, while histogram, correlation, NCPR, and UACI analyses are conducted on the true random bits and encrypted video data. The results of tests and attacks prove that the design procedure of truly random bits from a multi-chaotic system and whole experimental system can be applied to a real-time video encryption system to have a secure transmission of data.

Table 4 Video and image encryption designs in the literature
Full size table

6 Conclusions

The originality of this paper lies in the designing of a dynamic true random number generator that utilizes hardware-based chaotic entropy sources. It incorporates fractional order calculations to enhance security and adhere to provable security principles. What truly distinguishes this study from other random number generator designs is the implementation of electronic circuits for both fractional and integer order chaotic systems, which serve as the sources of entropy.

True random bit sequences are generated from the state variables of the chaotic systems on hardware and the cryptographic key bits are applied to the encryption process with the bits of the real-time video frame. As a post-processor, the XOR function is used and all the digital processes are executed on Xilinx Zedboard FPGA. The generated true random bit series are tested by using the NIST 800.22 statistical test suite, FIPS 140-1, and chi-square tests. The cryptographic key bits have passed all 13 NIST statistical tests, FIPS 140-1 standard, and chi-square tests successfully.

Cryptanalysis processes such as histogram, NPCR-UACI, and correlation analysis are demonstrated successfully. The histogram graph of the encrypted video frame data is notably uniform. The NPCR and UACI metrics were determined very close to the success criteria 0.995466666666667 and 0.334722698785851, respectively.

Consequently, the proposed TRBG design consists of four distinct chaotic systems. Continuous time integer order Lorenz and fractional order Chen-Lee chaotic systems; discrete-time Logistic and Tent chaotic maps are designed on hardware to generate true random cryptographic key bits for robust video encryption applications. To generate digital values at the output of chaotic systems, a quantization method is employed using a threshold value. The state variables to be converted into digital values are sampled with a 25 MHz clock pulse signal and compared with the threshold value. As a result, the bit rate of the true random number generator is 25 Mbps. Therefore, the real-time and hardware-based operation of the system ensures its applicability in all areas related to secure video encryption and data transmission. In future studies, it is planned to achieve a higher output bit rate in the GHz range by using an FPGA-compatible camera that can capture video data at higher frequencies. Furthermore, the dimensions of prototype circuit boards and the area of the overall footprint of the design are aimed to be reduced.