1 Introduction

With the development of wireless multimedia sensors networks and 5G mobile communication systems, a large number of video, image and audio sources need to be transmitted, stored and processed. In order to reduce the transmission and storage burden in a communication system, data compression approach is usually employed [17]. Conventional compressions methods, such as JPEG and JPEG2000, have been used. These schemes have high complexity in encoder and low complexity in decoder. Compared with these conventional compression approaches, compressive sensing (CS) technique can provide lower computational complexity, lower power consumption and higher compressive efficiency in encoder. CS technique can simultaneously perform sampling and compression [7] on the encoder side, and the original signal can be exactly reconstructed on the decoder side by using very few samples that obtained on the encoder side. The cost is that the CS-based decoder has high computational complexity.

However, compared with the conventional compression schemes, the CS-based image coding scheme still has a significant gap in terms of the reconstruction performance [5, 10]. For the CS, the research work mainly focuses on three issues: transform sparsity, measurement matrix design, and signal reconstruction algorithm. Although the three issues are related to each other, the measurement matrix plays a key role in improving the CS performance [15]. In this work, our goal is to design the measurement matrix to achieve excellent reconstruction performance of image-based CS.

1.1 Motivation and contribution

Improving the reconstruction quality of images is the main issue in CS. This performance mainly depends on the choosing of measurement matrix. In the exiting literatures, the conventional measurement matrices usually fall into three types or groups: Random measurement matrices, such as Gaussian matrices and Bernoulli matrices, chaos-based measurement matrix [45], and structurally random matrices (SRM) [13]. In image-based CS filed, random matrices are widely used as the measurement matrix due to its universality. However, in practical implementation, random matrix requires huge storage space and high computational complexity [51]. Chaos-based measurement matrix, which is generated from chaotic systems, can achieve compression and encryption in one single step for image-based CS. Different from the above two types of measurement matrices, SRM are usually generated from orthogonal matrix such as discrete cosine transform (DCT) [43], discrete Hartley transform (DHT) [44], Hadamard matrix [52], and other types of orthogonal matrices. Among the above three measurement matrices, the performance of SRM outperforms that of the other types of measurement matrices [43, 44].

On the other hand, in the previous literatures, most of the image-based CS schemes use real-valued measurement matrix, the complex-valued measurement matrices have hardly ever been considered. In ref. [39], a complex-valued measurement matrix is used to reconstruct one-dimensional signal. Inspired by the idea in [39], we employ a complex-valued DFT matrix to generate the measurement matrix for image-based CS. Our experiment results show that the complex-valued DFT measurement matrix can greatly improve the quality of image reconstruction in image-based CS. Therefore, in order to improve the quality of image reconstruction in image-based CS, the research and design of complex-valued measurement matrix is a valuable topic. In this work, we mainly focus on parallel BCS scheme using complex-valued measurement matrix which can provide both high reconstruction quality and low computational complexity. The main contributions of our work are as follows.

First, an image parallel BCS using DFT measurement matrix is proposed. The whole image is divided into small blocks with the same size. Each column of every image block is sampled by the same DFT measurement matrix. The theoretical analysis and simulation results both show that the performance of the proposed measurement matrix based on DFT matrix is better than those of the other conventional structurally random matrices, such as partial DCT, partial DHT, and partial Hadamard matrix.

Second, a quantization scheme corresponding to the complex-valued CS is given, in which the real part and imaginary part of the compressed image data are quantized independently. The effect of quantization on the performance of parallel BCS is also analyzed. The simulation results show that the influence of quantization on the quality of the recovered image can almost be ignored when the block size of image is 32 × 32.

Third, reconstructed performance and computational complexity of the parallel BCS with different block sizes are studied. The experiment results show that the 32 × 32 block size is preferrable considering the balance between computational complexity and recovered image quality. In this case, the loss of quality performance of the recovered image is very small.

1.2 Related work

With the development of internet, a large number of image signals need to be processed or transmitted on the internet network every day, where security and efficiency are two confronted issues. When image data is transmitted over networks, the risk of privacy information leakage increases. In order to protect the privacy of images, many image encryption schemes have been proposed. Meanwhile, image steganography schemes are also proposed [23, 29, 31] in recent years. The idea of steganography is to embed useful information into an image and does not attract the attention of an attacker. On the other hand, due to the strong correlation of images, compression technique is usually employed for images to improve the transmission efficiency. Image-based CS is one of the main compression approaches. In order to obtain high quality of reconstructed performance in the image-based CS framework, the selection of measurement matrix is a key issue [30, 33]. Many advanced image-based CS have been proposed [36, 47]. To achieve compression and encryption at the same time, many joint compression-encryption schemes have been reported [8, 41, 53].

Compared with the conventional compression approach, the complexity of CS-based image decoding is very high [5]. Reducing the complexity of image-based CS is still an important issue. Block compressive sensing (BCS) and parallel compressive sensing (PCS) are commonly used methods. For the whole image CS, the complexity of the reconstruction algorithm is very high due to the use of high-dimensional measurement matrix. In order to solve this issue, BCS is proposed [14, 46]. The idea of BCS is that every sblock image is compressively sampled by the same low-dimensional measurement matrix. In [4], the authors proposed an efficient scrambled BCS scheme, in which a partial Hadamard matrix is chosen to serve as the measurement matrix. Meanwhile, to decrease the computational complexity of the whole image CS, PCS scheme is also proposed. In the conventional image-based CS scheme, a whole image is rearranged into a one-dimensional vector, which is then sampled by a measurement matrix. The idea of PCS is that the whole image is compressively sampled column by column using the same measurement matrix. Therefore, the size of measurement matrix in PCS is much smaller than that of the conventional whole image-based CS, and the complexity of PCS is correspondingly lower than that of whole image-based CS scheme. In [12], a PCS with permutation was proposed, which has low storage space and computational complexity for low dimensional size of measurement matrix. To further improve the computational efficiency of CS, many parallel BCS schemes were proposed in [1, 3]. The idea of image parallel BCS is that each column of every block image is sampled using the same measurement matrix. In recent years, joint PCS with encryption schemes have been reported [20, 22, 24, 37, 42]. In this work, we mainly focus on the image parallel BCS schemes. Our goal is to optimize the measurement matrix in terms of reconstructed quality and computational complexity for parallel BCS framework.

Besides, in [21], the authors proposed a simultaneous image PCS and encryption scheme for CS frameworks. By introducing a counter operation in the construction of chaotic measurement matrix, the resistance to chosen plaintext attack (CPA) is realized. Thus, the security of the scheme in [21] is improved when compared with the other compression-encryption schemes.

However, the above-mentioned image-based CS schemes didn’t address how to obtain high quality reconstruction performance of the compressed image. The current limitation of the reconstruction performance in image-based CS is the design of measurement matrix, and almost all image-based CS schemes choose real-valued measurement matrix.

In recent years, the design of measurement matrix based on complex-valued DFT matrix has attracted attention. In [2, 6, 19, 25, 49], the measurement matrix construction based on DFT matrix is proposed, which is based on the minimizing mutual coherence of the sensing matrix. Nevertheless, the application of the partial DFT matrix in image-based CS is seldom researched. The image-based CS performance comparison of different measurement matrices, such as DFT measurement matrix, DHT measurement matrix, and Hadamard measurement matrix, has also seldom been studied.

Designing and optimizing the measurement matrix is one of the main issues in image-based CS filed. There are many reported references on how to design an optimum measurement matrix. A simple method to characterize the reconstruction ability of a measurement matrix is to measure the mutual coherence between sparse basis matrix and measurement matrix. The smaller the maximum (or average) mutual coherence is, the better the reconstruction performance of measurement matrix [11, 28] will be. In order to obtain low value of the mutual coherence for a measurement matrix, abundant efforts have been made [27, 35, 38, 47]. However, the recently researched results show that optimized design of the measurement matrix based on minimizing the mutual coherence is not robust when the sparse representation error (SRE) is considered [18, 28]. In [9, 48, 50], an optimized design method of measurement matrix is proposed according to the theory of minimum Frobenius norm.

On the other hand, the effect of quantization on image-based CS performance has not been paid much attention. In [16], a joint compression and encryption CS scheme using chaos system is proposed, in which the compressed data is transformed into bit stream by quantizing. Then for the resulting bit-level data, bitwise XOR operation is employed to improve the security level of the proposed scheme. However, the influence of the quantization on the performance of imaged-based CS was not analyzed in [16]. In this work, we will study the effect of quantization on CS performance.

The remainder of this paper is organized as follows. In Section 2, the principle of the proposed image parallel BCS is given. The construction of the measurement matrix based on DFT matrix and the quantization method are introduced in detail. In Section 3, an optimized method for the measurement matrix is analyzed and discussed. The theoretical analysis shows the advantage of the proposed parallel BCS scheme. In Section 4, simulations and discussions are presented. The simulation results demonstrate the effectiveness of the measurement matrix based DFT matrix. In Section 5, conclusions are drawn.

2 System and principle

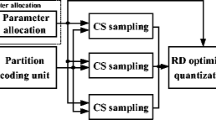
In this section, we first briefly introduce the background of compressive sensing (CS). After that, we elaborate the proposed image parallel BCS system principle, including partial DFT measurement matrix and quantization method. The diagram of the proposed parallel BCS system is given in Fig. 1.

Fig. 1
figure 1

The quantized block image compressed sensing scheme

Full size image

2.1 Background

According to the CS theory [7], if a signal x with size of N is K–sparse under some orthogonal sparse matrix Ψ ∈ N × N, the signal x can be denoted as x = Ψs, where s is the sparse signal. The signal x can be compressively sampled using a measurement matrix Ψ, and the sampled signal can be expressed as

$$\mathbf{y}=\boldsymbol{\Phi} \boldsymbol{\Psi} \mathbf{s}=\boldsymbol{\Theta} \mathbf{s}$$
(1)

where Φ denotes the measurement matrix, and Θ = ΦΨ is usually called a sensing matrix. At the receiver side, the sparse signal s can be recovered by reconstructed algorithms from the sampled signal y with size of M = Ο(KlogN) [7]. The estimation of s can be obtained by solving the following ℓ1 optimization problem,

$$\hat{s}=\mathrm{argmin}{\left\Vert s\right\Vert}_1\ \mathrm{for}\kern0.5em y=\boldsymbol{\Phi} \boldsymbol{\Psi} \mathbf{s}$$
(2)

In this optimization problem, both Φ and Ψ are assumed to be known. Many reconstruction algorithms such as matching pursuit (MP) [32], orthogonal matching pursuit (OMP) [40], and smooth l0 norm (SL0) [34] are employed to solve the optimization problem.

2.2 Proposed image parallel block compressive sensing

In order to reduce the computational complexity of CS, block CS is usually employed. A diagram of the proposed parallel BCS is given in Fig. 1. With BCS, an image is first divided into many non-overlapping blocks with size of NB × NB, and then each block is independently compressively sampled column by column using the same DFT measurement matrix. The DFT measurement matrix is composed of some randomly selected rows from a standard DFT matrix, which is defined as

$$F=\left[{f}_{i,j}={\exp}^{-j\frac{2\pi ij}{N}}\right]$$
(3)

where i ∈ {0, ⋯, N − 1}and j ∈ {0, ⋯, N − 1} denote the row number and column number of the matrix, respectively. Based on the DFT matrix F, the DFT measurement matrix can be obtained according to the following expression:

$$\boldsymbol{\Phi} =\mathbf{DRF}$$
(4)

where R ∈ ℝN × N is a row permutation matrix, which is generated from a chaotic Logistic map. D ∈ ℝN × N is a selecting matrix, which chooses the former M rows from a matrix with size of N × N.

Let Xj with size of NB × NB denote the j-th block original image, then each column of Xj is transformed into a sparse signal by sparse DCT basis matrix Ψ, which can be expressed as

$${\mathbf{X}}_i^j={\boldsymbol{\Psi} \mathbf{S}}_i^j,i=1,\cdots, N$$
(5)

where \({\mathbf{X}}_i^j\) and \({\mathbf{S}}_i^j\) denote the i-th column of the j-th block original image and i-th column of the j-th block transformed sparse image data, respectively. After that, the j-th block image is compressed sampled column by column, and the i-th column measured signal of j-th block image can be written as.

$${\mathbf{Y}}_i^j={\boldsymbol{\Phi} \mathbf{X}}_i^j={\boldsymbol{\Phi} \boldsymbol{\Psi} \mathbf{S}}_i^j={\boldsymbol{\Theta} \mathbf{S}}_i^j,i=1,\cdots, N$$
(6)

where Θ = ΦΨ denotes a sensing matrix. In this way, the whole measured j-th block image data is expressed as \({\mathbf{Y}}^j=\left[{\mathbf{Y}}_1^j,{\mathbf{Y}}_2^j,\cdots {\mathbf{Y}}_N^j\right]\). According to CS theory, each column of j-th block transformed data Sij can be recovered in parallel through solving the l1 optimization problem,

$${\mathbf{\hat{S}}}_i^j=\mathit{\arg}\min {\left\Vert {\mathbf{S}}_i^j\right\Vert}_1\kern0.5em s.t.\kern0.5em {\mathbf{Y}}_i^j={\mathbf\varTheta} {\mathbf{S}}_i^j$$
(7)

According to Eq. (7), the estimation of i-th column of j-th block original image can be found as

$${\mathbf{X}}_i^j=\boldsymbol{\Psi} {\left({\boldsymbol{\Theta}}^T\boldsymbol{\Theta} \right)}^{-1}{\boldsymbol{\Theta}}^T{\mathbf{Y}}_i^j$$
(8)

where (ΘTΘ)−1 denotes the pseudo-inverse matrix of product of matrices. The resulting column-by-column reconstructed signals combine a reconstructed j-th block image. The whole j-th block image can be reconstructed and expressed as \({\mathbf{X}}^j=\left[{\mathbf{X}}_1^j,{\mathbf{X}}_2^j,\cdots {\mathbf{X}}_N^j\right]\). Then all reconstructed image blocks are combined to form the original whole image. In this work, the conventional orthogonal matching pursuit (OMP) algorithm [40] is employed to evaluate our proposed image parallel BCS.

2.3 Design of partial DFT measurement matrix

In reference [37], the plain image is transformed to a sparse signal using discrete wavelet transform (DWT) sparse basis matrix. Then the resulting sparse signal is scrambled by an index sequence generated from a Logistic map. Similar to the idea in [37], we use a Logistic map to scramble a standard DFT matrix and achieve a DFT measurement matrix in CS framework. A Logistic map can be expressed as follows [26],

$${x}_{n+1}=\mu {x}_n\left(1-{x}_n\right),{x}_n\in \left(0,1\right)$$
(9)

where μ ∈ (3.75, 4], it is a control parameter, x0 denotes the initial value of the chaotic system. Based on Eq. (9), a chaotic real-valued sequence x = [x1x2⋯xN] can be obtained. Then, an integer sequence can be obtained according to the following method.

Assume v with size of N denote the generated chaos integer sequence, then the n-th element of vector v can be expressed as:

$$v(n)=\operatorname{mod}\left( floor\left(\left({x}_n+100\right)\times {10}^{10}\right),N\right)+1$$
(10)

Assume F with size of N × N be the conventional DFT matrix, which is expressed as follows:

$$\mathbf{F}={\left[\mathbf{F}(1)\mathbf{F}(2)\cdots \mathbf{F}(N)\right]}^T$$
(11)

where F(n) denotes the n-th row of F, and (⋅)T denotes the transpose operation. The rows of the matrix F are scrambled by the integer chaos sequencev.The resulting chaotic DFT is given by:

$${F}_{chaos}={\left[F\left(v(1)\right)\kern0.5em F\left(v(2)\right)\kern0.5em \cdots \kern0.5em F\left(v(N)\right)\right]}^T$$
(12)

where F(v(n)) denotes the v(n)-th row of the generated DFT matrix. Finally, the former Mrows of Fchaos forms a partial DFT measurement matrix Φ with size of M × N, which is expressed as:

$$\boldsymbol{\Phi} ={\left[\boldsymbol{\Phi} (1)\boldsymbol{\Phi} (2)\cdots \boldsymbol{\Phi} (M)\right]}^T$$
(13)

The obtained DFT measurement matrix will be used in the proposed image parallel BCS scheme.

2.4 Quantization

In the modern communication systems, various sources need to be transformed into bit streams. In this work, the measurement matrix in parallel BCS is generated from the conventional DFT matrix, whose elements are complex-valued. Hence, the data measured by DFT measurement matrix is complex and cannot be directly quantized. In order to solve this issue, we divide the measured complex data into two parts, the real part and imaginary part. The quantized scheme corresponding to the BCS using complex DFT measurement matrix is shown in Fig. 1, where the resulting real part and imaginary part are quantized into real-based bit stream and imaginary-based bit stream, respectively.

The real part of the measured complex data is quantized as follows [16]:

$${\hat{Y}}_{p,q}^{real}= round\left(255\times \left({Y}_{p,q}^{real}-\mathrm{R}\_\min \right)/\left(\mathrm{R}\_\max -\mathrm{R}\_\min \right)\right)$$
(14)

where round (x) denotes the nearest integer value to x. \({Y}_{p,q}^{real}\) is the p-row and q-column element of the real part of the measured data Yj, R _ min R _ maxare the minimum value and maximum value of the real part of Yj, and \({\hat{Y}}_{p,q}^{real}\) is the quantized value. Finally, the quantized \({\hat{Y}}_{p,q}^{real}\) is transformed into bit stream. The same quantization process is employed to the imaginary part of Yj. Finally, the real-based bit stream is placed side by side with the imaginary-based bit stream, and sent to wireless channel. In the received side, inverse quantization operation is used to recover the measured data.

3 Optimizing the measurement matrix

Generally, image signals are real-valued numbers, so real measurement matrix, such as partial Hadamard matrix, partial DCT matrix, are usually used. In fact, complex measurement matrix can also be used in real image CS. At the transmitted side, the real part and imaginary part of the resulting measured complex data are quantized into bit streams separately, which are then placed side by side to form one bit stream. At the received side, this bit stream is redivided into two bit streams, and each bit stream is operated by inverse quantization processing to form two real data streams, which are then combined into a complex data stream. The obtained complex data is served as the input signal of the reconstructed algorithm of CS framework. According to the theoretical analysis in [50], the optimum sensing matrix can be obtained by solving the following equation,

$$\hat{\boldsymbol{\Phi}}=\underset{\varPhi }{\mathrm{argmin}}{\left\Vert {\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-I\right\Vert}_F^2$$
(15)

where ‖⋅‖Fdenotes Frobenius norm, Iis an identity matrix with size of N × N, and (⋅)H denotes conjugate transpose operation. According to the relationship between the Frobenius norm and the trace, \({\left\Vert \mathbf{Q}\right\Vert}_F^2= tr\left({\mathbf{QQ}}^H\right)\), \({\left\Vert {\boldsymbol{\Psi}}^H{\boldsymbol{\Phi}}^H\boldsymbol{\Phi} \boldsymbol{\Psi} -{\mathbf{I}}_N\right\Vert}_F^2\) can be further expressed as follows [50],

$$ {\displaystyle \begin{array}{c}{\left\Vert {\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-{\textbf{I}}_N\right\Vert}_F^2\\ {}= tr\left({\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right){\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-2{\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)+{\textbf{I}}_N\right)\\ {}= tr\left(\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right){\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right){\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H-2\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right){\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H+{\textbf{I}}_M\right)+\left(N-M\right)\\ {}={\left\Vert \left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right){\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H-{\textbf{I}}_M\right\Vert}_F^2+\left(N-M\right)\end{array}} $$
(16)

In Eq. (16), the first term is always positive, so the lower bound of Eq. (16) is N − M. Based on Eq. (16), the reconstructed performance of measurement matrices can be evaluated. The smaller the value of \({\left\Vert {\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-{\mathbf{I}}_M\right\Vert}_F^2\), the better the reconstructed performance of CS. Figure 2 shows the relationship between the Frobenius norms \( {\left\Vert {\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-{\textbf{I}}_M\right\Vert}_F^2 \) and the compressive ratio according to Eq. (16) for different measurement matrices. In the simulation, a conventional DCT matrix is used to serve as the sparse basis. The size of the sparse basis DCT matrix Ψ is fixed at N × N = 256 × 256, and the size of the measurement matrix is fixed at M × N = M × 256(M < 256). From the experiment results in Fig. 2, we can see that the Frobenius performance of the DFT measurement matrix is almost the same as that of the Hadamard measurement matrix. The Frobenius performances of the DFT matrix and the Hadamard matrix are better than those of the DCT matrix and the DHT matrix.

Fig. 2
figure 2

Frobenius norm versus compressive ratio for different measurement matrices. The sparse matrix is a DCT with block size of 256 × 256

Full size image

Figure 3 shows the relationship between Frobenius norms \( {\left\Vert {\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-{\textbf{I}}_M\right\Vert}_F^2 \) and compressive ratio according to Eq. (16) for different measurement matrix with the same DCT sparse basis. Different from Fig. 2, the size of the sparse DCT basis matrixΨ is fixed at N × N = 32 × 32, and the size of the measurement matrix is fixed at M × N = M × 32(M < 32). From Fig. 3, it can be seen that the Frobenius norms \( {\left\Vert {\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)}^H\left(\boldsymbol{\Phi} \boldsymbol{\Psi} \right)-{\textbf{I}}_M\right\Vert}_F^2 \) of the partial DFT matrix is the smallest. When the compressive ratio M/N is bigger than 0.8, the Frobenius norm of the DFT measurement matrix is almost the same as that of the Hadamard measurement matrix. Therefore, based on the theoretical analysis, the DFT measurement matrix has the best reconstructed performance of CS under the same DCT sparse basis. This will be confirmed by the simulation results in Section 4.

Fig. 3
figure 3

Frobenius norm versus compressive ratio for different measurement matrices. The sparse matrix is a DCT with block size of 32 × 32

Full size image

4 Simulation results and analysis

In this section, simulation experiments are conducted to evaluate the performance of the image parallel BCS scheme. All the experiments were operated in the environment of MATLAB 2014b on a portable computer with a 2.20 GHz Intel Core i5 CPU and 4GB memory, running on the windows 7 operating system.

For the generality of our simulation experiment, six standard grey-level images with size of 256 × 256 are used as our test images, namely Lena, Cameraman, Barbara, Boats, Foreman and Parrots. In addition, four RGB color images with size of 256 × 256, namely House, Couple, Girl and Lena are also used. The test images are shown in Fig. 4. In order to show the advantage of our proposed DFT measurement matrix, the CS performance using DFT measurement matrix is compared with that using other conventional Fourier measurement matrices, such as DCT measurement matrix, Hadamard measurement matrix, DHT measurement matrix and chaos-based measurement matrix [45]. The experiment results show the superiority performance of the partial DFT measurement matrix in our proposed parallel BCS framework. In the simulation experiments, the same OMP algorithm is used to recover the original images.

Fig. 4
figure 4

Ten test images. Lena, Cameraman, Barbara, Boats, Foreman, Parrots, House (color), Couple (color), Girl (color)，and Lena (color) (from top to bottom and from left to right)

Full size image

In the simulation experiments, the initial value of Logistic map and control parameter are chosen asx0 = 0.33, and μ = 4. Additionally, the compressive ratio (CR) is defined as

$$CR=M/N$$
(17)

where M and N represent the number of rows and columns of a measurement matrix, respectively.

4.1 Comparison of reconstruction performance

The quality of the reconstructed image is usually evaluated by using PSNR, which is defined as

$$PSNR=10{\log}_{10}\frac{256\times 256}{\frac{1}{N^2}\sum \limits_{i=1}^N\sum \limits_{j=1}^N{\left(I\left(i,j\right)-{I}^{\prime}\left(i,j\right)\right)}^2}$$
(18)

where I(i, j) and I′(i, j) denote the pixel value of the original image and the reconstructed image, respectively. The test image size is N × N. The higher the PSNR, the better the reconstructed image quality.

On the other hand, the index of structural similarity index (SSIM) is used for evaluating the similarity of two images. The SSIM is defined as [8].

$$\mathrm{SSIM}=\left[\left(2{\mu}_x{\mu}_y+{C}_1\right)\left(2{\sigma}_{xy}+{C}_2\right)\right]/\left[\left({\mu}_x^2+{\mu}_y^2+{C}_1\right)\left({\sigma}_x^2+{\sigma}_y^2+{C}_2\right)\right]$$
(19)

In Eq. (19), μ and σ are the local mean and standard deviation of the two signals/images (input and output), C1 andC2 are constants used to stabilize the equation in the presence of weak denominators, and σxy is the sample cross correlation (zero mean). Conventionally, C1 = (k1L)2 and C2 = (k2L)2, where k1 = 0.01, k2 = 0.03, and L is the dynamic range of the pixel values.

In this sub section, we will evaluate and compare the performance of different matrices for the whole image CS case. Table 1 shows the PSNR and SSIM values using different measurement matrices for six test images with size of 256 × 256. The CR is fixed at 0.2, 0.4, 0.6, and 0.8, respectively. To study the influence of different measurement matrices on image-based CS, the same reconstruction algorithm OMP is used in the CS decoder. It can be seen that the PSNR of the reconstructed image with DFT measurement matrix is higher than that with the other measurement matrices, such as DCT matrix, Hadamard matrix, DHT matrix and chaos-based measurement matrix. Take Lena image with CR of 0.6 as an example, the PSNR of DFT measurement matrix is 2.1 dB, 2.2 dB, 2.1 dB and 3.4 dB better than that of the Hadamard matrix, DCT matrix, DHT matrix, and chaos-based measurement matrix, respectively. In addition, there is little difference in PSNR performance between Hadamard measurement matrix, DCT measurement matrix, and DHT measurement matrix, while the PSNR performance with chaos-based measurement matrix is much worse. This conclusion is in agreement with the theoretical analysis in Section 3. In addition, the proposed scheme also has advantage over the other exiting measurement matrices in terms of SSIM metric. From Table 1, we can see that the SSIM values of the proposed DFT measurement matrix are the highest compared with those of the other measurement matrices. Therefore, the performance of the proposed image-based CS using DFT measurement matrix significantly outperforms the other exiting measurement matrices in terms of the PSNR and SSIM.

Table 1 PSNR (dB) and SSIM results with different measurement matrices for different CRs
Full size table

4.2 Optimization of image block size

In this sub section, the effect of block size of image on PSNR and SSIM performance of the proposed image-based CS is evaluated for different measurement matrices under CR of 0.6. Table 2 shows the PSNR and SSIM results of different measurement matrices under different block sizes. It can be seen that the PSNR of the reconstructed image with DFT measurement matrix is higher than that of the other measurement matrices, such as DCT matrix, Hadamard matrix, DHT matrix and chaos-based measurement matrix, for different block sizes. For the SSIM metric, the performance of the proposed DFT measurement is also the best.

Table 2 PSNR (dB) and SSIM results with different measurement matrices for different block sizes
Full size table

Similar to the results of Table 1, measurement matrices based on DCT, Hadamard, DHT have similar CS performance in terms of PSNR and SSIM metrics for different block sizes. Besides, the CS performance difference is very small between blocks sizes of 32 × 32,64 × 64 and128 × 128 for different measurement matrices. Moreover, we find an interesting phenomenon from Table 2, that is, the CS performance for block size of 16 × 16 is the worst for most cases, while the CS performance for the whole image is not always the best.

In addition to the reconstruction quality, computational complexity is another key issue that needs to be considered for parallel BCS scheme. Hence, the run time of the proposed parallel BCS scheme for DFT measurement matrix under different block sizes are evaluated. Figure 5 shows the run time of different block sizes for Cameraman image. It can be seen that with the decrease of block size, the run time of the parallel BCS is greatly reduced. On the other hand, the quality of the reconstructed images for different block size was also evaluated. Figure 6 shows the PSNR performance of different block size for Cameraman image. From Fig. 6, it can be seen that with the increase of block size, the PSNR of the reconstructed image becomes better. However, the advantage of PSNR performance for block size of 256 × 256 and 128 × 128 is not obvious, and the difference of PSNR performance between block size of 64 × 64 and 32 × 32 is very small. Hence, considering both the computational complexity and reconstructed quality, the block size of 32 × 32 is preferrable. In the following simulation experiments, we mainly focus on the parallel BCS performance with block size of 32 × 32.

Fig. 5
figure 5

Run time versus compressive ratio of the parallel BCS under different block sizes for Cameraman image

Full size image
Fig. 6
figure 6

PSNR versus compressive ratio under different block sizes for Cameraman image

Full size image

Figure 7 presents the reconstructed images using different measurement matrices with CR of 0.5 for Cameraman image. The size of the original Cameraman image is 256 × 256, and the size of block is 256 × 256. Figure 7a–d shows the reconstructed images for partial DFT measurement matrix, partial DCT measurement matrix, partial DHT measurement matrix and partial Hadamard measurement matrix, respectively. The PSNR values of the reconstructed images in Fig. 7a–d are 24.6244 dB, 21.9315 dB, 21.9296 dB, and 21.9681 dB, respectively. It can be seen that the reconstructed quality using DFT measurement matrix is better than those of the other SRM measurement matrices.

Fig. 7
figure 7

Reconstructed Cameraman image using different measurement matrices with block size of 256 × 256. a DFT measurement matrix; b DCT measurement matrix; c DHT measurement matrix; d Hadamard measurement matrix

Full size image

In addition, we also gave the reconstructed images using different measurement matrices for block size of 32 × 32 case. Figure 8 presents the reconstructed Cameraman image for different measurement matrices with CR of 0.5. The original Cameraman image size is also 256 × 256, and the size of image block is 32 × 32. Figure 8a–d are the reconstructed images for DFT measurement matrix, DCT measurement matrix, DHT measurement matrix and Hadamard measurement matrix, respectively. Conclusions similar to Fig. 7 can be obtained. The corresponding PSNR values of the reconstructed images in Fig. 8a–d are 24.6353 dB, 21.9901 dB, 21.5305 dB and 22.2062 dB, respectively. It can be seen that the reconstructed quality using measurement matrix based DFT is better than those of the other SRM measurement matrices.

Fig. 8
figure 8

Reconstructed Cameraman image using different measurement matrices with block size of 32 × 32. a DFT measurement matrix; b DCT measurement matrix; c DHT measurement matrix; d Hadamard measurement matrix

Full size image

4.3 Effect of quantization

In the research related to CS, the impact of quantization on the performance of CS has rarely been concerned. In fact, the measured data of CS has to be transformed into quantized data by quantizing operation in communication network systems. Therefore, the effect of quantization on the performance of CS should be considered when we study the performance of the partial DFT measurement matrix. In this sub section, we evaluated the PSNR performance using the DFT measurement matrix with- and without quantization. In general, the quantization will cause a little loss of PSNR performance.

Figure 9 shows the PSNR performance of image CS using DFT measurement matrix with- and without quantization. Uniform quantization is used in our simulation experiments. Two images, namely Lean and Cameraman, are served as the test images. The sizes of the two images are both 256 × 256and block sizes are also 256 × 256. It can be seen that the loss of PSNR performance becomes larger with the increase of CR. At CR of 0.7, the PSNR performance of the reconstructed image with quantization is about 0.3 dB lower than that of the reconstructed image without quantization.

Fig. 9
figure 9

PSNR versus compressive ratio for Cameraman image and Lena image with block size of 256 × 256 with- and without quantization

Full size image

Figure 10 shows the PSNR performance using DFT measurement matrix with- and without quantization. The block size is fixed at 32 × 32. It can be seen that the effect of quantization on the PSNR of the reconstructed image is almost negligible. Similar to the results in Fig. 9, the PSNR performance of the reconstructed Lean image is better than that of the reconstructed Cameraman image.

Fig. 10
figure 10

PSNR versus compressive ratio for Cameraman image and Lena image with block size of 32 × 32 with- and without quantization

Full size image

4.4 Reconstructed performance of color images

The proposed parallel BCS scheme using DFT measurement matrix is also valid for color images. Four RGB color images with size of 256 × 256, namely House, Girl, Couple and Lena, are used to study the reconstructed performance of our proposed CS scheme. The quality of the reconstructed images is also evaluated in terms of PSNR and SSIM values. Similar to the gray image experiments, we first calculated the PSNR and SSIM using four different measurement matrices for the whole image CS case at different CRs, and the results are shown in Table 3. From Table 3, it can be seen that with the increase of CR value, the reconstruction performance is improved in terms of PSNR and SSIM metrics. Among the four measurement matrices, the proposed DFT measurement matrix has the best performance. For instance, for color Girl test image under CR of 0.6, the PSNR value using DFT measurement matrix is 2.1 dB, 2 dB, 2.2 dB, and 3.3 dB higher than that using Hadamard matrix, DHT matrix, and DCT matrix and chaos-based measurement matrix, respectively. On the other hand, the performance of chaos-based measurement matrix is the worst. These conclusions are similar to those of the previous gray image-based CS case.

Table 3 PSNR (dB) and SSIM results for different measurement matrices
Full size table

Additionally, the influence of block size on reconstructed performance of our proposed CS scheme is also evaluated for color test images. Table 4 shows the PSNR and SSIM performance under different block sizes for four color test images. The rightmost two columns in Table 4 are the PSNR and SSIM performance using the proposed DFT measurement matrix under different block sizes. It can be seen that the PSNR and SSIM performance for bock size of 16 × 16 is the worst. The difference of PSNR and SSIM performance for the other block sizes is very small. Therefore, considering both the reconstruction performance and computation complexity, block size of 32 × 32 is preferrable. Moreover, from Table 4, our proposed DFT measurement matrix has the best reconstruction performance for all block sizes and images. These results are similar to those of the previous gray image experiment. Therefore, the proposed scheme is also efficient for color image-based CS.

Table 4 PSNR (dB) and SSIM results for different block sizes
Full size table

4.5 Computational complexity analysis

DFT matrix is a complex matrix, hence, the complexity of image-based CS using DFT measurement matrix will be higher than that using real measurement matrices, such as DCT matrix, DHT and Hadamard matrices. The complexity comparison of different measurement matrices can be done according to the CS model \({Y}_i^j=\Phi {\mathrm{X}}_i^j\), where \({Y}_i^j\) has a size of M × 1, Φ has a size ofM × N, and \({\mathrm{X}}_i^j\) has a size ofN × 1. The complexity for different measurement matrices is shown in Table 5. Here, the evaluation of complexity didn’t consider the possible fast algorithm. The number of complex additions and complex multiplications for partial chaos DFT matrix are given in the second row of Table 5. The corresponding results for the other three measurement matrices are shown in the bottom three rows of Table 5. These computational operations are called out in real numbers. Therefore, the computational complexity of DFT measurement matrix is much higher than that of the other real-valued measurement matrices. However, at the expense of increased complexity, the reconstructed performance of CS can be greatly improved.

Table 5 Complexity comparison for different measurement matrices
Full size table

Figure 11 shows the run time comparison for different measurement matrices. The size of the test image Cameraman is 256 × 256, the block size is also 256 × 256. We can see that the run time of the measurement matrix based on DFT is the longest. The other three real transform matrices have less complexity and require less memory for storages compared with that of the complex DFT measurement matrix. However, the previous analysis and experiment results both show that the reconstructed performance of the measurement matrix based on DFT is the best. The only disadvantage of the DFT measurement matrix is that its complexity is increased.

Fig. 11
figure 11

Run time versus compressive ratio for different measurement matrices with Cameraman image with block size of 256 × 256

Full size image

Figure 12 shows the run time comparison for different measurement matrices. The size of the test image Cameraman is also 256 × 256, while the block size is 32 × 32 for the parallel BCS. We can see that the increased run time using measurement matrix based DFT is small. Therefore, although the complexity is increased using DFT measurement matrix, the corresponding performance is greatly improved.

Fig. 12
figure 12

Run time versus compressive ratio for different measurement matrices with Cameraman image with block size of 32 × 32

Full size image

5 Conclusion

An image parallel BCS scheme using a complex-valued DFT measurement matrix was proposed to improve the reconstruction quality of image CS encoder. Theoretical analysis based on minimum Frobenius norm method was given to characterize the performance of different measurement matrix. And then, simulation experiments of reconstructed performance were done for ten test images. The theoretical analysis and simulation results both show that the reconstructed performance in terms of PSNR and SSIM of the proposed DFT measurement matrix is better than that using other measurement matrices, such as partial DCT matrix, partial Hadamard matrix, and DHT matrix and chaos-based measurement matrix. Although the computational complexity is increased for DFT measurement matrix, the improvement in reconstructed performance of CS is obvious. In this work, we mainly focus on the improvement of the reconstructed quality of image by using complex-valued DFT measurement matrix. In the near future, we will continuously study how to design complex-valued CS framework with low complexity and high the reconstructed quality. Moreover, the chaotic complex-valued measurement matrix can be served as the key of an encrypted image, hence, how to achieve simultaneous compressed sampling and encryption of an image is also our near future work.