1 Introduction

Haumea, one of the largest bodies in the Kuiper Belt, is also one of the most intriguing objects in this distant population. Its rapid rotation rate, multiple satellites, and dynamically-related family members all suggest an early giant impact (Brown et al. 2007). Its surface spectrum reveals a nearly pure water ice surface (Barkume et al. 2006; Trujillo et al. 2007; Merlin et al. 2007; Dumas et al. 2011), with constraints on other organic compounds with upper bounds \(<\)8 % (Pinilla-Alonso et al. 2009). Lacerda and Jewitt (2008) also find evidence for a dark spot on one side of the rotating body, make the surface albedo non-uniform. Even more interesting is that shape modeling has suggested a density higher than nearly anything else known in the Kuiper belt and consistent with a body almost thoroughly dominated by rock (Rabinowitz et al. 2006; Lacerda and Jewitt 2008; Lellouch et al. 2010). Lacerda and Jewitt (2007) concluded a density of 2.551 g cm\(^{-3}\) and follow up work found consistent values between 2.55 and 2.59 g cm\(^{-3}\), depending on the model used. Such a rocky body with an icy exterior could be a product of initial differentiation before giant impact and subsequent removal of a significant amount of the icy mantle. Leinhardt et al. (2010) demonstrate that such an impact is possible in a graze and merge collision between equal size bodies, and are able to reproduce the properties of the Haumea family system.

Much of our attempt at understanding the history of Haumea relies on the estimate of the high density of the body. Haumea’s large-amplitude light curve and rapid rotation have been used to infer an elongated shape for the body. Assuming that the rotation axis lies in the same plane as the plane of the satellites, the amplitude of the light curve then gives a ratio of the surface areas along the major and minor axes of the bodies. If the further assumption is made that Haumea is large enough to be in hydrostatic equilibrium, the full shape can be uniquely inferred to be a Jacobi ellipsoid with fixed ratios of the three axes. From this shape and from the known rotation velocity, the density is precisely determined. Finally, with the mass of Haumea known from the dynamics of the two satellites (Ragozzine and Brown 2009), the full size and shape of Haumea is known (Rabinowitz et al. 2006; Lacerda and Jewitt 2008; Lellouch et al. 2010).

The major assumption in this chain of reasoning is that Haumea is a figure of equilibrium. While it is true that a strengthless body can instantaneously have shapes very different from figures of equilibrium (Holsapple 2007), long-term deformation at the pressures obtained in a body this size should lead to essentially fluid behavior, at least at depth. Indeed, any non-spinning body large enough to become round due to self-gravity has attained the appropriate figure of equilibrium. While the size at which this rounding occurs in the outer solar system is not well known, the asteroid Ceres, with a diameter of 900 km is essentially round (Millis et al. 1987; Thomas et al. 2005), while among the icy satellites, everything the size of Mimas and larger (\(\sim\)400 km) is essentially round. It thus seems reasonable to assume that a non-spinning Haumea, with a diameter of \(\sim\)1,240 km (Lellouch et al. 2013; Fornasier et al. 2013) would be round, thus a rapidly-spinning Haumea should likewise have a shape close to that of the Jacobi ellipsoid defined by Haumea’s density and spin rate.

Nonetheless, given the importance of understanding the interior structure of Haumea and the unusually high density inferred from these assumptions, we find it important to attempt independent size and density measurements of this object. Here we use unpublished photometric data from the Hubble space telescope (HST) to determine a best-fit Jacobi ellipsoid model. We then compare the predicted thermal flux from this best-fit Jacobi ellipsoid to thermal flux measured from the Spitzer Space Telescope (first presented in Stansberry et al. 2008) and consider these constraints on the size and shape of the body.

2 Observations

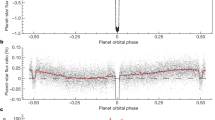
Haumea was imaged on 2009 February 4 using the PC chip on the Wide Field/Planetary Camera 2 on HST. We obtained 68 100s exposures using the F606W filter, summarized in Table 1. The observations were obtained over 5 consecutive HST orbits, which provides a full sample of Haumea’s 3.9154 h rotational lightcurve (Rabinowitz et al. 2006). With a pixel scale of \(\sim\)5,500 km at the distance of Haumea and semi-major axes of \(\sim\)50,000 and \(\sim\)25,000 km for Hi’iaka and Namaka, respectively (Ragozzine and Brown 2009), this is the first published dataset where the object is resolved from its satellites, providing a pure lightcurve of the primary. During the observation both satellites are sufficiently spatially separated from the primary that we are able to perform circular aperture photometry. Basic photometric calibrations are performed on the data including flat fielding, biasing, removing charge transfer efficiency effects, and identifying and removing hot pixels and cosmic rays.Footnote 1 In five of our images the primary is contaminated by cosmic rays so we do not include these data. A 0.5\(^{\prime \prime }\) aperture is used to measure the object, and we apply an infinite aperture correction of 0.1 magnitudes (Holtzman et al. 1995). We present and model the data in the STMAG magnitude system, but a convolution of the F606W filter with the Johnson V filter shows a difference of approximately 0.1 magnitudes. This difference, along with the satellite flux contributions of \(\sim\)10 % (Ragozzine and Brown 2009) included in previous photometry of the dwarf planet, indicate that the magnitude and amplitude of the lightcurve presented here (\(\varDelta \hbox {m} = 0.32\)) is consistent with the findings of Rabinowitz et al. (2006) (\(\varDelta \hbox {m} = 0.28\)) and Lacerda and Jewitt (2008) (\(\varDelta \hbox {m} = 0.29\)). The rotational period of Haumea is known sufficiently precisely that all of the observations are easily phased. We combine our data with that of Rabinowitz et al. (2006) and Lacerda and Jewitt (2008) to get a 4-year baseline of observations and find a period of \(3.91531 \pm 0.00005\) h using phase dispersion minimization (Stellingwerf 1978). This period is consistent with that of Lellouch et al. (2010) (\(\hbox {P} = 3.915341 \pm 0.000005\) h derived from a longer baseline), whose more precise solution we use to phase all observations, visible and infrared. With this period, there is a 60 s uncertainty in the phasing over the 1.5 years between observations. We define a phase of 0 to be the point of absolute minimum brightness of Haumea and define a longitude system in which \(\lambda = [(JD-2454867.042]\) modulo \(360^{\circ }\). This result is given in JD at Haumea, which is consistent with the phased data of Lacerda and Jewitt (2008), and Lellouch et al. (2010) who instead quote their phasing in JD at the Earth. The photometric results are shown in Fig. 1.

Table 1 HST F606W flux of Haumea
Full size table
Fig. 1
figure 1

The visible lightcurve, geometric albedo, and thermal lightcurve plotted over one rotation. The error bars in the top two panels are smaller than the size of the plotted point. The visible photometry are fit with a Jacobi ellipsoid of dimensions \(1920\times 1540 \times 990\,\hbox {km}\) with the modest longitudinal variation in reflectance shown. This ellipsoid model provides a quite good fit to the \(70\,\upmu \hbox {m}\) thermal data from Spitzer

Full size image

The thermal radiometry of Haumea was obtained 2007 July 13–19 using the \(70\,\upmu\hbox{m}\) band of the MIPS instrument (Rieke et al. 2004) aboard the Spitzer space telescope (SST). Haumea’s lightcurve was unknown at the time, and the objective of the observations was simply to detect the thermal emission at a reasonably high signal to noise ratio (SNR). The data were collected as three 176 min long observations, each of which is nearly as long as the (now known) lightcurve period. Stansberry et al. (2008) published the flux obtained by combining all three observations, as well as models indicating a diameter of about \(1150 \pm 175\,\hbox {km}\). Contemporaneously, Haumea’s lightcurve was published Lacerda and Jewitt (2008), a result that led us to consider re-analysing the Spitzer data to try and detect a thermal lightcurve. To that end, we split the original 176 min exposures (each made up of many much shorter exposures) into 4 sub-observations, each 44 min long. The resulting data was processed using the MIPS Instrument Team pipeline Gordon et al. (2005), resulting in flux calibrated mosaics for each of the 12 sub-observations. These individual observations are presented in Table 2. One of the points was obviously discrepant and was removed from the analysis. The data were also re-processed using improved (relative to the 2007 processing published in Stansberry et al. 2008) knowledge of Haumea’s ephemeris. The reprocessing was undertaken as part of a project to reprocess all Spitzer/MIPS observations of TNOs (described in Mommert et al. 2012) and is key to obtaining the highest SNR from the data. Had Haumea’s lightcurve been known at the time the Spitzer observations were planned, the observations probably would have been taken, for example, as a series of about 10 approximately 60 min exposures spaced about 4.1 rotations apart. The non-optimal observation plan may in part explain why the the uncertainties on the flux measurements appear to be somewhat optimistic, as discussed in more detail below.

The motion of Haumea was significant over the 6-day observing interval, so we were able to make a clean image of the background sources (i.e. one without contamination from Haumea), and then subtract that sky image from our mosaics. The procedure used has been described previously, e.g. by Stansberry et al. (2008). We performed photometry on the sky-subtracted images, obtaining significantly smaller uncertainties than was possible using the original mosaics. The raw photometry was corrected for the size of the photometric aperture (\(15^{\prime \prime }\) radius). The signal-to-noise ratio of the resulting detections was about 7 in each of the 12 epochs. An additional calibration uncertainty of 6 % should be systematically applied to the entire dataset. The thermal results are shown in Fig. 1 . Where multiple observations are made at the same phase, these observations are averaged, and the uncertainty is taken from the standard deviation of the mean (or the full range if only two points go into the mean).

Though the uncertainties are large, the thermal light curve appears in-phase with the measured visible light curve. To robustly ascertain the detection of a thermal lightcurve, we look for a correlation between the thermal and visible datasets. We compare the mean visible flux during the phase of each 44 min long thermal observation with the measured thermal flux during that observation (Fig. 2). A linear fit to the data suggests that a positive correlation between the optical and thermal brightness. As noted above, the deviation of the measurements from the model are larger than expected, so we assess the significance of the correlation between the optical and thermal data using the non-parametric Spearman rank correlation test (Spearman 1904). With this test, we find that the two data sets are correlated at the 97 % confidence level, and that the correlation is positive, that is: the observed optical and thermal flux increase and decrease in phase and there is only a 3 % chance that this phase correlation is random. This positive correlation between the thermal and visible data sets indicates that we are viewing an elongated body and that the visible light curve must be caused—at least in part—by the geometric effects of this elongated body.

3 Photometric Model

We begin with the assumption that Haumea is indeed a Jacobi ellipsoid whose shape is defined by its density and spin period. To find the Jacobi ellipsoid which best fits the photometric data, we model the expected surface reflection from an ellipsoid by creating a mesh of 4,000 triangular facets covering the triaxial ellipsoid and then determining the the total visible light from the sum of the light reflected back toward the observer from each facet. Facets are approximately equal-sized equilateral triangles with length equal to 5\(^{\circ }\) of longitude along the largest circumference of the body. Mesh sizes a factor of 2 larger or smaller give identical results. For each facet we use a Hapke photometric model (Hapke 1993) to determine the reflectance as a function of emission angle. This model accounts for the effects of low phase angle observations, such as coherent backscattering and shadow hiding, and has been used to model the reflectance of many icy surfaces. For concreteness, we adopt parameters determined by Karkoschka (2001) for Ariel, a large satellite which exhibits deep water ice absorption and a high geometric albedo. We utilize the published values for the mean surface roughness (\(\bar{\theta } = 23^\circ\)), single-scattering albedo (\(\varpi = 0.64\)), asymmetry parameter (\(g = -.28\)), and magnitude(\(S(0)\)) and width (\(h\)) of the coherent backscattering and shadowing functions, \(S(0)_{CB} = 4.0, h_{CB} = 0.001, S(0)_{SH} = 1.0\), and \(h_{SH} =0.025\) (Karkoschka 2001). While we have chosen Ariel because it is perhaps a good photometric analog to Haumea, we do note that within the range of Hapke parameters of icy objects throughout the solar system (\(\varpi \sim 0.4-0.9\), \(g = -.43\) to \(-.17\), \(\bar{\theta } = 10-36^\circ\)), including the icy Galilean satellites and Triton (Buratti 1995; Hillier et al. 1990), the precise parameters chosen will affect only the geometric albedo and the beaming parameter, as discussed below.

The visible flux reflected from the body then becomes:

$$\begin{aligned} F_{vis} = p_{vis} \frac{F_{\odot , 606}}{{R_{AU}}^2} A \frac{H \cos e}{\pi \varDelta ^2} \end{aligned}$$
(1)

where \(p_{vis}\) is the visual albedo, \(F_{\odot ,606}\) is the solar luminosity over the bandwidth of the F606W filter, \(A\) is the projected surface area, \(H\) is the Hapke reflectance function, \(e\) is the angle of incidence, \(\varDelta\) is the geocentric distance to the body, and \(R\) is the heliocentric distance.

Our modeled body is rotated about the pole perpendicular to our line of sight—consistent with the hypothesis that the rotation pole is similar to the orbital pole of the satellites—and the photometric light curve is predicted. For such a model, the peak and trough of the visible lightcurve correspond to the largest and smallest cross-sectional areas of the body, and the ratio of the length of the largest non-rotational axis (\(a\)) to the smallest non-rotation axis (\(b\)) controls the magnitude of the photometric variation. With a uniform albedo across the surface of Haumea, however, no triaxial ellipsoid can fit the asymmetric observed lightcurve. We confirm the assertion of Lellouch et al. (2010) that the photometric variations of Haumea are caused primarily by shape and that surface albedo variations add a only minor modulation. In this approximation, the brightest peak and brightest trough of the data are assumed to be from essentially uniform albedo surfaces and are modeled to determine the ratio of the axes of the body. For plausible values of the dimension of the rotational axis (\(c\)), the measured peak-to-trough amplitude in the lightcurve of \(\varDelta m = 0.32 \pm 0.006\) is best modeled with an axis ratio of \(b/a =0.80 \pm 0.01\). Using the brightest trough and darkest peak instead, the axial ratio would be \(b/a=0.83\), but the surface heterogeneity necessary for this assertion is less likely than the single darker spot proposed here and observed by others (Lacerda and Jewitt 2008).

Our measured value of 0.80 differs from previous measurements of \(b/a\) of .78 (Rabinowitz et al. 2006) and .87 (Lacerda and Jewitt 2008) for a number of reasons. Our visible dataset resolves Haumea from its satellites which results in a slightly deeper lightcurve. More to the point, including a realistic surface reflectance model changes that estimated shape significantly. Rabinowitz et al. (2006) do not actually model the shape of the body, while Lacerda and Jewitt (2008) assume the surface to be uniformly smooth, giving a value for \(b/a\) that is too high. More recently, Lellouch et al. (2010) confirm a more elongated body (\(b/a = .80\)), after having tested two different models, including that of Lacerda and Jewitt (2008).

With the ratio of the axes fixed, we now find the simplest surface normal albedo model consistent with the data. We divide the surface longitudinally into 8 slices and allow the albedo to vary independently between sections to account for the possible hemispherical variation apparent in our data and explored by others (Lacerda and Jewitt 2008; Lacerda 2009). Dividing the surface further does not significantly improve the fit. The middle panel of Fig. 1 shows how the geometric albedo varies across the surface of the body.

Assuming that Haumea is indeed a Jacobi ellipsoid, the ratio \(b/a=0.80\) combined with the rotation period uniquely defines \(c/a=0.517\) and a density of 2.6 g cm\(^{-3}\). Combining these parameters with the known mass of Haumea from Ragozzine and Brown (2009) implies \(a= 960\) km, \(b= 770\) km, and \(c=495\) km. These radii agree with the ones obtained by Lellouch et al. (2010) using a Lommel-Seelinger reflectance function.

4 Thermal Model

To calculate the thermal emission from our shape and albedo model we first determine the temperature of each facet of the body. Due to Haumea’s rapid rotation, the temperature of any given face of the surface does not have time to equilibrate with the instantaneous incoming insolation. Instead we calculate the average amount of sunlight received by a facet during a full rotation, which is only dependent on the angle between rotational pole and the facet normal. Although we implement a standard thermal model, the rapidly spinning object gives rise to surface temperatures indicative of an isothermal latitude model (Stansberry et al. 2008), which we precisely calculate for the non-spherical geometry of the object. Indeed the agreement between the visible and infrared datasets as seen in Fig. 2 supports the hypothesis of a body with negligible thermal conductivity.

Fig. 2
figure 2

The correlation of the relative optical and thermal flux. The dashed line shows a one-to-one correlation while the solid line shows the best fit. A rank correlation test shows that the two distributions are correlated at the 97 % confidence level. The in-phase thermal light curve of Haumea demonstrates that it is an elongated body

Full size image

We model the average amount of sunlight absorbed for each facet by multiplying the geometric albedo of each facet by an effective phase integral \(q\) and averaging over a full rotation. The average facet phase integral is a mild function of the shape of the body, but for simplicity we simply adopt a value of \(q=0.8\), as used by Stansberry et al. (2008) for large, bright KBOs. In fact, the precise value used has little impact on our final results.

If we assume the surface is in thermal equilibrium, the temperature of each facet, is determined by balancing this absorbed sunlight with the emitted thermal radiation. We choose a typical thermal emissivity of 0.9 and invoke a beaming parameter, \(\eta\), which is a simple correction to the total amount of energy radiated in the sunward direction, usually assumed to be caused by surface roughness, but which can be taken as a generic correction factor to the assumed temperature distribution. For asteroids of known sizes, Lebofsky et al. (1986) found \(\eta\) to be approximately 0.756, a correction which agrees well with measurements of icy satellites in the outer solar system (Brown et al. 1982a, b). The beaming parameter value range for Trans-Neptunian objects is fully described in Lellouch et al. (2010), who found \(\eta\) of 1.15–1.35 for Haumea, with hemispherical variations consistent with a much lower value (\(\eta \sim\).4–.5). The MIPS and PACS fluxes values presented in Lellouch et al. (2010) were updated and presented in Fornasier et al. (2013), who, also using the SPIRE data, found a beaming factor of \(0.95^{0.33}_{-0.26}\) with a NEATM model. We leave this as a free parameter in our modeling but consider an inclusive range.

For each rotational angle of our model, we predict the total thermal flux by calculating the blackbody spectrum from each visible facet and integrating this flux in the full 70 \(\upmu\)m band pass of MIPS, according to

$$\begin{aligned} F_{IR} = \frac{A \cos e}{\pi ^2 \varDelta ^2}\epsilon \int {B_{\lambda } (T(\theta , \phi )) \sin \theta d\theta d\phi } \end{aligned}$$
(2)

where \(A\) is the cross-sectional surface area, \(\epsilon = 0.9\) is the emissivity, \(B\) is the Planck function and \(T\) is the temperature at each piece of the surface. Assuming a solar flux at 70 \(\upmu\)m of \(S\) at the distance of Haumea, \(R\), then \(T\) is calculated for an edge-on rotating body and

$$\begin{aligned} T = \left[ \frac{S*(1-qp_{vis})}{\epsilon \sigma \eta R^2}\right] ^{1/4} \end{aligned}$$
(3)

Figure 1 shows the measured Spitzer flux along with the flux predicted from a model for the theoretical Jacobi ellipsoid with \(a=960\) km and \(a\):\(b\):\(c = 1.00\):\(0.80\):\(0.52\) and a thermal beaming parameter of \(\eta =0.76\). The best fit is obtained by assuming \(\eta =0.89\), but values of \(\eta\) between 0.82 and 0.97 are within the 1-\(\sigma\) error limits. The larger values measured by Lellouch et al. (2010) and quoted for the majority of Kuiper Belt objects (\(\sim\)1.2 by Stansberry et al. 2008 and \(\sim\)1–2.5 by Lellouch et al. 2013) are consistent with our result if we consider the difference of thermal models employed. Stansberry et al. (2008) explain that the surface temperature difference between an isothermal latitude model (that is used in this work) and a standard thermal model (used by Lacerda 2009 and Lellouch et al. 2010 is simply a factor of \(\pi ^{-\frac{1}{4}}\)). If this value is incorporated into the beaming factor, the inconsistency between the models and resulting beaming parameters is resolved. Remarkably, the shape and albedo model constructed from only photometric observations and the assumption of fluid equilibrium provides an acceptable prediction of the total thermal flux at 70 \(\upmu\)m and its rotational variation.

5 Discussion

The thermal and photometric light curves of Haumea are consistent with the assumption that Haumea is a fluidly relaxed, rapidly rotating Jacobi ellipsoid with a density of 2.6 g cm\(^{-3}\) and minor albedo variation across its surface. Although we allow the albedo to change longitudinally, we have demonstrated that the reason for the double-peaked lightcurve of Haumea is in fact a shape effect. This work presents new data and an informed Hapke model that agree with the findings of previous authors (Lellouch et al. 2010; Lacerda and Jewitt 2008; Rabinowitz et al. 2006).

The lightcurve in several colors (Lacerda and Jewitt 2008; Lacerda 2009) indicates that the albedo variation is concentrated in a large spot on one side of the body, an argument supported by our allowed albedo variation. The precise geometric albedo presented here is less than that of Fornasier et al. (2013), but with a small variation in either the single-scattering albedo or the asymmetry parameter, we easily find agreement between the two values. We do not focus on the absolute value of the albedo here, as it is closely tied to the unknown Hapke parameters for the surface. The only affect this has on the thermal fit is to change the best fit beaming parameter, which does not differ by more than 1-\(\sigma\) from the reported value. The important point here, however, is that our precise visible data set agrees with the dark spot proposed by Lacerda and Jewitt (2008).

There are still a number of questions remaining regarding this KBO. The temperature of the dark spot is still uncertain and our data are not precise enough to constrain it, although the lower albedo we use to match the visible data agree well with a warmer region. Another assumption used here that could be disputed is the rotation axis of the body as perpendicular to our line of sight. However, assuming that the majority of the depth of the light curve is from the major axes of the body, the pole position will only affect the size of the third dimension of the body and the thermal beaming factor, which become somewhat degenerate when fitting the thermal data anyway. If the body were not mostly edge-on, it would be difficult to explain the particular surface patterning needed to recreate the visible lightcurve.

While it is encouraging that a dense Jacobi ellipsoid fits both data sets, it is important to point out that we can only obtain a unique solution under the assumption that the object has a prescribed shape. If Haumea is modeled as an arbitrary triaxial ellipsoid rather than a Jacobi ellipsoid, large families of solutions are possible. To first order, the photometric data constrain the ratio \(b/a\), while the thermal flux is roughly proportional to the emitting surface area which is proportional to \(ac\) and \(bc\). As long as the ratio of \(b/a\) is kept constant, however, equally good fits can be obtained from very elongated ellipsoids with a very short rotation axis, or from only moderately elongated ellipsoids with a large rotation axis, as long as the value \(ac\) is approximately constant. For this unconstrained problem, densities anywhere between 1 g cm\(^{-3}\) (for very elongated objects) and 3 g cm\(^{-3}\) for compact objects are compatible with both data sets. While such large deviations from an equilibrium shape appear implausible, the thermal data alone cannot rule them out.

Table 2 Thermal flux of Haumea
Full size table