Closed-form solutions for two-layer Timoshenko beams with interlayer slip, uplift and rotation compliance

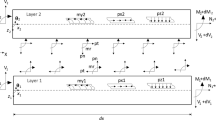
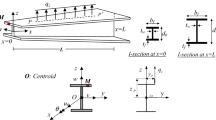
Abstract

An analytical model for a two-layer Timoshenko beam allowing for interlayer slip, uplift, and relative rotations of the layers’ cross-sections (distortion) is presented and solved in closed form. Each kinematic field at the interface is related to a corresponding traction by means of a linear-elastic law. The proposed model introduces the rotational stiffness at the interface, completely separate from the tangential and normal stiffness, that may restrict the amount of interlayer distortion at the interface. The derived closed-form solutions provide an exact stiffness matrix for any case of boundary and continuity conditions. All solutions are also valid if the effect of the rotational stiffness is excluded. Based on the presented parametric studies it can be concluded that in addition to the known effects of the tangential and normal stiffness of the interface, its rotational stiffness may strongly affect the behaviour of a composite beam. It has been also noticed that for certain combinations of parameters of the interface, a layer that is not directly loaded can bend opposite from the direction of the load. This peculiar effect has been discussed in detail, showing that it is not an artefact of the present model, but a possible physical behaviour that may have practical implications.

Appendices

Appendix A: Closed-form solutions for the case of equal layers

By assuming that $EA=EA_2\equiv EA_1$, $GA=GA_{s.2}\equiv GA_{s.1}$, $EI=EI_2\equiv EI_1$ and $h=h_2\equiv h_1$, Eqs. (4), and (22)–(27) give the following system of 7 equations

$$\begin{aligned}&p_t-K_t\left[ u_1-u_2-\frac{h}{2}\left( \theta _2+\theta _1\right) \right] =0,{} & {} \end{aligned}$$

(A.1)

$$\begin{aligned}&EA\,u_1^{\prime \prime }-p_t+p_{x.1}=0,{} & {} \end{aligned}$$

(A.2)

$$\begin{aligned}&EA\,u_2^{\prime \prime }+p_t+p_{x.2}=0,{} & {} \end{aligned}$$

(A.3)

$$\begin{aligned}&GA\,\left( w_1^{\prime \prime }+\theta _1^{\prime }\right) -K_n\,\Delta w+p_{z.1}=0,{} & {} \end{aligned}$$

(A.4)

$$\begin{aligned}&GA\,\left( w_2^{\prime \prime }+\theta _2^{\prime }\right) +K_n\,\Delta w+p_{z.2}=0,{} & {} \end{aligned}$$

(A.5)

$$\begin{aligned}&EI\,\theta _1^{\prime \prime }-GA\,\left( w_2^{\prime }+\theta _1\right) +\frac{h}{2}\,p_t-K_r\,\Delta \theta +m_{y.1}=0,{} & {} \end{aligned}$$

(A.6)

$$\begin{aligned}&EI\,\theta _2^{\prime \prime }-GA\,\left( w_1^{\prime }+\theta _2\right) +\frac{h}{2}\,p_t+K_r\,\Delta \theta +m_{y.2}=0,{} & {} \end{aligned}$$

(A.7)

that, if (2) and (3) are taken into account, has 7 unknowns ($u_i$, $w_i$, $\theta _i$ and $p_t$, where $i=1,2$). By introducing

$$\begin{aligned} w_s\,&=w_1+w_2,{} & {} \end{aligned}$$

(A.8)

$$\begin{aligned} \theta _s\,&=\theta _1+\theta _2,{} & {} \end{aligned}$$

(A.9)

and summing and subtracting Eqs. (A.5) with (A.4), and (A.7) with (A.6), the following equations are obtained

$$\begin{aligned}&GA\,w_s^{\prime \prime }+GA\,\theta _s^{\prime }+p_{z.0}=0,{} & {} \end{aligned}$$

(A.10)

$$\begin{aligned}&-GA\,\Delta w^{\prime \prime }-GA\,\Delta \theta ^{\prime }+2\,K_n\,\Delta w+p_{z.2}-p_{z.1}=0,{} & {} \end{aligned}$$

(A.11)

$$\begin{aligned}&EI\,\theta _s^{\prime \prime }-GA\,w_s^{\prime }-GA\,\theta _s+h\,p_t+m_{y.0}=0,{} & {} \end{aligned}$$

(A.12)

$$\begin{aligned}&-EI\,\Delta \theta ^{\prime \prime }+GA\,\Delta w^{\prime }+\left( GA+2\,K_r\right) \,\Delta \theta \nonumber \\&\quad +m_{y.2}-m_{y.1}=0.{} & {} \end{aligned}$$

(A.13)

By expressing $\Delta \theta ^{\prime \prime }$ from the first derivative of Eq. (A.11), $\Delta \theta$ can be expressed from Eq. (A.13) as

$$\begin{aligned}&\Delta \theta {=}-\frac{EI}{GA+2\,K_r}\,\Delta w^{\prime \prime \prime }+\frac{2\,EI\,K_n-GA^2}{GA\,\left( GA+2\,K_r\right) }\,\Delta w^{\prime }\nonumber \\&\quad +\frac{m_{y.0}}{GA+2\,K_r}.{} & {} \end{aligned}$$

(A.14)

By substituting $\Delta \theta ^{\prime }$ in Eq. (A.11) with the first derivative of Eq. (A.14), a fourth-order differential equation in $\Delta w$ is obtained as

$$\begin{aligned} \Delta w^{\textrm{IV}}-\tilde{\chi }_1\,\Delta w^{\prime \prime }+\tilde{\chi }_2\,\Delta w+\tilde{\chi }_3=0,{} & {} \end{aligned}$$

(A.15)

where

$$\begin{aligned}&\tilde{\chi }_1=2\left( \frac{K_n}{GA}+\frac{K_r}{EI}\right) , \quad \tilde{\chi }_2=2\,K_n\,\tilde{\chi} _0,\quad \nonumber \\&\tilde{\chi }_3=\tilde{\chi} _0\left( p_{z.2}-p_{z.1}\right){} & {} \end{aligned}$$

(A.16)

and

$$\begin{aligned} \tilde{\chi }_0=\frac{2K_r+GA}{GA\,EI}.{} & {} \end{aligned}$$

(A.17)

Note that depending on the values of geometrical and material properties of the layers, as well values of the parameters of the interface, characteristic equation of (A.15) can have four real roots, two real roots with double multiplicity or four complex roots. These three cases along with the corresponding closed-form solutions are omitted here for the sake of brevity, but can be found in [66].

By substituting $u_1^{\prime \prime }$ and $u_2^{\prime \prime }$ in the second derivative of Eq. (A.1) using (A.2) and (A.3), the following equation is obtained

$$\begin{aligned} \frac{p_t^{\prime \prime }}{K_t}-\frac{2\,p_t}{EA}+\frac{h}{2}\theta _s^{\prime \prime }-\frac{p_{x.2}-p_{x.1}}{EA}=0.{} & {} \end{aligned}$$

(A.18)

By using (A.10), Equations (A.18) and the first derivative of (A.12) give the following system

$$\begin{aligned}&\frac{p_t^{\prime \prime }}{K_t}-\frac{2\,p_t}{EA}+\frac{h}{2}w_s^{\prime \prime \prime }-\frac{p_{x.2}-p_{x.1}}{EA}=0,{} & {} \nonumber \\&h\,p_t^{\prime }-EI\,w_s^{\textrm{IV}}+p_{z.0}=0,{} & {} \end{aligned}$$

(A.19)

which can be solved in $w_s$ to finally give

$$\begin{aligned} w_s^{\textrm{VI}}-\tilde{\chi }_4\,w_s^{\textrm{IV}}+\tilde{\chi }_5=0,{} & {} \end{aligned}$$

(A.20)

where

$$\begin{aligned} \tilde{\chi }_4=K_t\left( \frac{2}{EA}+\frac{h^2}{2\,EI}\right) ,\quad \tilde{\chi }_5=K_t\frac{2\,p_{z.0}}{EA\,EI}.{} & {} \end{aligned}$$

(A.21)

Equation (A.20) can be easily reduced to a second-order differential equation so that the final solution reads

$$\begin{aligned}&w_s{=}\frac{1}{\tilde{\chi }_4^2}\left( e^{\sqrt{\tilde{\chi }_4}\,x}\,C_5+e^{-\sqrt{\tilde{\chi }_4}\,x}\,C_6\right) \nonumber \\&\quad +\frac{\tilde{\chi }_5}{\tilde{\chi }_4}\frac{x^4}{24}+C_7\,x^3+C_8\,x^2+C_9\,x+C_{10},{} & {} \end{aligned}$$

(A.22)

where $\sqrt{\tilde{\chi }_4}$ is a real number because $\tilde{\chi }_4>0$ for $K_t>0$. Using the solutions for $\Delta w$ and $w_s$, $w_1$ and $w_2$ can be easily obtained. $\theta _1$ and $\theta _2$ can be obtained in a similar fashion if $\Delta \theta$ and $\theta _s$ are known. $\Delta \theta$ can be obtained from (A.14), while $\theta _s$ can be obtained from (A.12) using the first derivative of (A.10) to substitute $\theta _s^{\prime \prime }$. $p_t$ is obtained by solving system (A.19). In order to obtain $u_2$, Eq. (A.3) must be integrated twice, which produces two new unknown constants ($C_{11}$ and $C_{12}$). Finally, $u_1$ is obtained from Eq. (A.1). Stress resultants follow from Eqs. (19)–(21).

Appendix B: Closed-form solutions for $\Delta w$ in the general case

Summing up Eqs. (24) and (25) and substituting $w_1$ obtained from Eq. (2), $\theta _1^{\prime }$ extracted from Eq. (24), and the first derivative of $\theta _2$ from Eq. (26), gives

$$\begin{aligned} \alpha _1\,w_2^{\textrm{IV}}+\alpha _2\,\Delta w^{\prime \prime }-\alpha _3\,p_t^{\prime }-\alpha _4\,\Delta w+\alpha _5=0,{} & {} \end{aligned}$$

(B.1)

where

$$\begin{aligned} &\alpha _1=\frac{EI_2\,GA_{s.1}}{K_r}, \quad \alpha _2=GA_{s.1}\,\left( 1+\frac{EI_2\,K_n}{GA_{s.2}\,K_r}\right) , \quad \nonumber \\ &\alpha _3=\frac{GA_{s.1}\,h_2}{2\,K_r},{} \nonumber \\ &\alpha _4=K_n\,\left( 1+GA_{s.1}\,\left( \frac{1}{GA_{s.2}}+\frac{1}{K_r}\right) \right) , \quad \nonumber \\&\alpha _5=p_{z.1}-\left( \frac{\alpha _4}{K_n}-1\right) \,p_{z.2}.{} \end{aligned}$$

(B.2)

If $p_t^{\prime }$ from Eq. (B.1) is substituted in the first derivative of Eq. (22), it follows that

$$\begin{aligned} \alpha _6\,w_2^{\textrm{IV}}+\alpha _7\Delta w^{\prime \prime }-\alpha _8\,\Delta w-\frac{EA_1}{2}\,u_1^{\prime \prime \prime }+\alpha _9=0,{} & {} \end{aligned}$$

(B.3)

where

$$\begin{aligned} \alpha _6&=\frac{EI_2}{h_2}, \quad \alpha _7=\frac{\alpha _6\,K_n}{GA_{s.2}}+\frac{K_r}{h_2}, \quad \nonumber \\\alpha _8&=K_n\,\frac{GA_{s.p}+GA_{s.0}\,K_r}{GA_{s.p}\,h_2},{} \nonumber \\ \alpha _9&=\frac{K_r}{h_2}\left( \frac{p_{z.1}}{GA_{s.1}}-\frac{p_{z.2}}{GA_{s.2}}\right) -\frac{p_{z.2}}{h_2},{} & {} \end{aligned}$$

(B.4)

and $GA_{s.0}=GA_{s.1}+GA_{s.2}$ and $GA_{s.p}=GA_{s.1}\,GA_{s.2}$. If Eq. (23) is re-expressed using the second derivative of $u_2$ from Eq. (4), $p_t$ from Eq. (22), $\theta _1^{\prime \prime }$ from the second derivative of Eq. (27), $\theta _2^{\prime \prime }$ from the first derivative of Eq. (25), and $w_1$ from Eq. (2), it becomes

$$\begin{aligned} u_1^{\textrm{IV}}-\alpha _{10}\,\Delta w^{\prime \prime \prime }-\alpha _{11}\,w_2^{\prime \prime \prime }-\alpha _{12}\,u_1^{\prime \prime }-\alpha _{13}\,\Delta w^{\prime }-\alpha _{14}=0,{} & {} \end{aligned}$$

(B.5)

where

$$\begin{aligned} \alpha _{10}&=\frac{EA_2\,h_1}{2\,EA_p}\,K_t, \quad \alpha _{11}=\frac{2\,\alpha _{10}\,h_0}{h_1}, \quad \quad \alpha _{12}=\frac{EA_0\,K_t}{EA_p},&\nonumber \\ \alpha _{13}&=\frac{\alpha _{10}}{h_1}\,\left( \frac{h_2}{GA_{s.2}}-\frac{h_1}{GA_{s.1}}\right) \,K_n, \quad \alpha _{14}=\frac{K_t\,p_{x.0}}{EA_p},{} & {} \end{aligned}$$

(B.6)

and $EA_0=EA_1+EA_2$ and $EA_p=EA_1\,EA_2$. The derivatives of $u_1$ in Eqs. (B.5) and (B.3) can be eliminated by taking the first derivative of Eq. (B.3), extracting $u_1^{\textrm{IV}}$ and replacing it in Eq. (B.5). By collecting $u_1^{\prime \prime }$ from the latter and substituting it back in Eq. (B.3), $u_1^{\prime \prime \prime }$ is eliminated and we obtain

$$\begin{aligned}&w_2^{\textrm{VI}}-\alpha _{15}\,w_2^{\textrm{IV}}+\alpha _{16}\,\Delta w^{\textrm{IV}}-\alpha _{17}\,\Delta w^{\prime \prime }\nonumber \\&\quad +\alpha _{18}\,\Delta w+\alpha _{19}=0,{} & {} \end{aligned}$$

(B.7)

where

$$\begin{aligned} \alpha _{15}&=\alpha _{12}+\frac{K_t\,H}{4\,\alpha _6}, \quad \alpha _{16}=\frac{K_n}{GA_{s.2}}+\frac{K_r}{EI_2}-\frac{K_t\,h_1}{4\,\alpha _6},{} & {} \nonumber \\ \alpha _{17}&=\alpha _{12}\,\left( \frac{K_n}{GA_{s.2}}+\frac{K_r}{EI_2}\,\right) +\frac{K_n}{EI_2}\,\nonumber \\&\left( 1+\frac{GA_{s.0}\,K_r}{GA_{s.p}}+\frac{K_t}{4}\,\left( \frac{h_2^2}{GA_{s.2}}-\frac{h_2\,h_1}{GA_{s.1}}\right) \right) ,{} & {} \nonumber \\ \alpha _{18}&=\alpha _{12}\,\frac{\alpha _8}{\alpha _6}, \quad \alpha _{19}=-\alpha _{12}\,\frac{\alpha _9}{\alpha _6},{} & {} \end{aligned}$$

(B.8)

and $H=h_1+h_2$. Summing up Eqs. (26) and (27) and substituting in the first derivative of the resulting equation $w_1$ from Eq. (2), $\theta _1^{\prime }$ from Eq. (24), the first derivative of $\theta _2$ from Eq. (26), and $p_t^{\prime }$ from Eq. (B.1), we obtain

$$\begin{aligned} \Gamma _1\,\Delta w^{\textrm{IV}}-\Gamma _2\,\Delta w^{\prime \prime }+\Gamma _3\,\Delta w+\Gamma _4\,w_2^{\textrm{IV}}+\Gamma _5=0,{} & {} \end{aligned}$$

(B.9)

where

$$\begin{aligned} \Gamma _1&=EI_1\,h_2, \quad \Gamma _2=H\,K_r+K_n\,\left( \frac{EI_1\,h_2}{GA_{s.1}}+\frac{EI_2\,h_1}{GA_{s.2}}\right) ,{} & {} \nonumber \\ \Gamma _3&=\alpha _8\,H\,h_2, \quad \Gamma _4=h_2\,EI_1-h_1\,EI_2,\nonumber \\ \Gamma _5&=p_{z.2}\,h_1-p_{z.1}\,h_2+K_r\,H\,\left( \frac{p_{z.2}}{GA_{s.2}}-\frac{p_{z.1}}{GA_{s.1}}\right) .{} & {} \end{aligned}$$

(B.10)

For $\Gamma _4=0$, Eq. (B.9) provides a fourth-order differential equation in a single unknown ($\Delta w$), while for $\Gamma _4\ne 0$ a sixth-order differential equation in the same single unknown may be obtained by substituting $w_2^{\textrm{IV}}$ from (B.9) in (B.7). However, unless the layers are equal ($h_2\,EI_1=h_1\,EI_2$), it is very unlikely that $\Gamma _4=0$ will be obtained. Therefore, the closed-form solutions for the case with equal layers are given separately in Appendix A, with $\Gamma _4=0$ can be found in [66]. Here, only the general case with $\Gamma _4\ne 0$ will be analysed.

After substituting $w_2^{\textrm{IV}}$ from Eq. (B.9) and $w_2^{\textrm{VI}}$ from the second derivative of the same equation in (B.7), the following differential equation in $\Delta w$ is obtained

$$\begin{aligned} \Delta w^{\textrm{VI}}-\xi _1\,\Delta w^{\textrm{IV}}+\xi _2\,\Delta w^{\prime \prime }-\xi _3\,\Delta w-\xi _4{=}0,{} & {} \end{aligned}$$

(B.11)

where

$$\begin{aligned} \xi _1&=K_n\frac{GA_{s.0}}{GA_{s.p}}+\xi _{1.0},\quad \xi _2=K_r\,\xi _{2.0}\nonumber \\&+K_n\left( \frac{EI_0}{EI_p}+\xi _{1.0}\frac{GA_{s.0}}{GA_{s.p}}\right) ,\nonumber \\ \xi _3&=K_n\,\xi _{2.0}\left( K_r\frac{GA_{s.0}}{GA_{s.p}}+1\right) ,\nonumber \\ \xi _4&=\xi _{2.0}\,K_r\,\left( \frac{p_{z.2}}{GA_{s.2}}-\frac{p_{z.1}}{GA_{s.1}}\right) \nonumber \\&+K_t\left[ \frac{EA_0}{EA_p}\left( \frac{p_{z.2}}{EI_2}-\frac{p_{z.1}}{EI_1}\right) +h_0\,\frac{h_1\,p_{z.2}-h_2\,p_{z.1}}{2\,EI_p}\right] ,{} & {} \end{aligned}$$

(B.12)

and

$$\begin{aligned} \xi _{1.0}&=K_t\left( \frac{EA_0}{EA_p}+\frac{EI_1\,h_2^2+EI_2\,h_1^2}{4\,EI_p}\right) +K_r\frac{EI_0}{EI_p},\nonumber \\ \xi _{2.0}&=\frac{K_t}{EI_p}\left( \frac{EA_0\,EI_0}{EA_p}+h_0^2\right) ,{} & {} \end{aligned}$$

(B.13)

with $EI_0=EI_1+EI_2$ and $EI_p=EI_1\,EI_2$. Note that coefficients $\xi _i$ ($i=1, \ldots , 4$) in Eq. (B.12) have non-zero values even for $K_r=0$, assuming that $K_t\ne 0$ and $K_n\ne 0$. This implies that the character of the solution of (B.11) does not change if the rotational stiffness of the interface is not taken into account, i.e. $K_r=0$. On the other hand, setting $K_t=0$ gives $\xi _4=0$, which eliminates the particular solution of (B.11), while $K_n=0$ gives $\xi _3=0$ and in turn changes the characteristic equation of (B.11). Obviously, setting $K_t=0$ and/or $K_n=0$ leads to different forms of closed-form solutions with respect to the general case with $K_t\ne 0$, $K_n\ne 0$ and $K_r\ne 0$. However, these cases are not investigated in the present work, which is aimed at simulating a compliant interface capable of transferring both the shear and the normal interlayer tractions.

Equation (B.11) is a non-homogeneous sixth-order differential equation with constant coefficients where the particular solution reads

$$\begin{aligned} \Delta w_p {=}-\frac{\xi _4}{\xi _3}.{} & {} \end{aligned}$$

(B.14)

The homogeneous part of Eq. (B.11) results in a characteristic polynomial equation of degree six

$$\begin{aligned} \psi ^6-\xi _1\,\psi ^4+\xi _2\,\psi ^2-\xi _3{=}0,{} & {} \end{aligned}$$

(B.15)

with $\psi _i$ ($i=1, \ldots , 6$) as the roots. Substituting $n=\psi ^2$ into (B.15), it gives the following cubic equation

$$\begin{aligned} g(n)=n^3-\xi _1\,n^2+\xi _2\,n-\xi _3=0.{} & {} \end{aligned}$$

(B.16)

Equation (B.16) has always one positive real root, while the remaining two can be either positive real or complex conjugate. However, considering that for $K_n>0$ and $K_t>0$ coefficients $\xi _1$, $\xi _2$ and $\xi _3$ are all positive (see Eq. (B.12)), it is obvious that only positive real values of n can give $g(n)=0$ in Eq. (B.16). All the roots of Eq. (B.16), according to Cardano’s solution [67] satisfy

$$\begin{aligned} n {=}\frac{\xi _1}{3}+\root 3 \of {t_1}+\root 3 \of {t_2},{} & {} \end{aligned}$$

(B.17)

where

$$\begin{aligned} t_1\,&=-\frac{q_2}{2}+\sqrt{\Phi },\quad t_2 {=}-\frac{q_2}{2}-\sqrt{\Phi },{} & {} \end{aligned}$$

(B.18)

and

$$\begin{aligned} & q_1=\xi _2-\frac{\xi _1^2}{3},\quad q_2 {=}\frac{\xi _1\,\xi _2}{3}-\frac{2\,\xi _1^3}{27}-\xi _3, \quad \nonumber \\ &\Phi =\frac{q_2^2}{4}+\frac{q_1^3}{27},{} & {} \end{aligned}$$

(B.19)

It is very important to note that $\Phi$ in general can be positive, negative or equal to zero. Therefore, the solutions of Eq. (B.16) depend on the sign of $\Phi$. Complete closed-form solutions in terms of $\Delta w$ are given below for all possible values of $\Phi$. Although $\Phi =0$ is very unlikely to occur, this case is given in Appendix B.3 just for the sake of completeness. In our numerical examples, solutions with both $\Phi >0$ and $\Phi <0$ were encountered (see details in Sect. 6).

1.1 Appendix B.1: Case of $\Phi >0$

In case when $\Phi \ge 0$, $\sqrt{\Phi }\in \mathbb {R}$ and all the roots of the cubic Eq. (B.16) can be written as

$$\begin{aligned} n_1\,&=\root 3 \of {t_1}+\root 3 \of {t_2}+\frac{\xi _1}{3}, \end{aligned}$$

(B.20)

$$\begin{aligned} n_2\,&=\frac{-1+i\,\sqrt{3}}{2}\root 3 \of {t_1}+\frac{-1-i\,\sqrt{3}}{2}\root 3 \of {t_2}+\frac{\xi _1}{3}, \end{aligned}$$

(B.21)

$$\begin{aligned} n_3\,&=\frac{-1-i\,\sqrt{3}}{2}\root 3 \of {t_1}+\frac{-1+i\,\sqrt{3}}{2}\root 3 \of {t_2}+\frac{\xi _1}{3}.{} & {} \end{aligned}$$

(B.22)

However, depending of whether $\Phi >0$, $\Phi =0$ and $q_2\ne 0$, or $\Phi =0$ and $q_2=0$, these roots may be simple or multiple. Below only the solution for $\Phi >0$ is given, while the solutions for the other two cases can be found in Appendix B.3. If $\Phi >0$, Eq. (B.16) has one real and two conjugate-complex roots, i.e. Eq. (B.15) has two real and two pair of conjugate-complex roots given by De Moivre’s formula [67], all of them with single multiplicity, given as

$$\begin{aligned} \psi _{1}\,&=\sqrt{n_1},\quad \psi _{2}{=}-\sqrt{n_1},\nonumber \\ \psi _{3}\,&{=}D_1+i\,B_1, \quad \psi _{4}{=}D_1-i\ B_1,{} \nonumber \\ \psi _{5}\,&=D_2+i\ B_2,\quad \psi _{6}{=}D_2-i\ B_2,{} \end{aligned}$$

(B.23)

where,

$$\begin{aligned} D_1\,&=\sqrt{r}\,\cos \left( \frac{v_1}{2}\right) ,\quad D_2 {=}-\sqrt{r}\,\cos \left( \frac{v_2}{2}\right) ,{} & {} \nonumber \\ B_1\,&=\sqrt{r}\,\sin \left( \frac{v_1}{2}\right) ,\quad B_2 {=}-\sqrt{r}\,\sin \left( \frac{v_2}{2}\right) ,{} & {} \end{aligned}$$

(B.24)

and r is the modulus of complex numbers $n_2$ and $n_3$, while $v_1$ and $v_2$ are their arguments. Note that, because $n_1$ must be real and positive, $\psi _{1}$ and $\psi _{2}$ are also real roots. Therefore, the solution of differential Eq. (B.11) is

$$\begin{aligned}&\Delta w{=}C_1\,e^{\psi _{1}\,x}+C_2\,e^{\psi _{2}\,x}+e^{D_1\,x}\left( C_3\,\cos \left( B_1\,x\right) \right. \nonumber \\&\quad \left. +C_4\,\sin \left( B_1\,x\right) \right) +\nonumber \\&\quad +e^{D_2\,x}\left( C_5\,\cos \left( B_2\,x\right) +C_6\,\sin \left( B_2\,x\right) \right) -\frac{\xi _4}{\xi _3}. \end{aligned}$$

(B.25)

1.2 Appendix B.2: Case of $\Phi <0$

In this case $\sqrt{\Phi }$ is imaginary and $t_1$ and $t_2$ from (B.19) can be written as

$$\begin{aligned} t_1\,&=-\frac{q_2}{2}+i\,\sqrt{-\Phi },\quad t_2 {=}-\frac{q_2}{2}-i\,\sqrt{-\Phi }.{} & {} \end{aligned}$$

(B.26)

De Moivre’s formula [67] is used to calculate the cubic root of $t_1$ and $t_2$ as

$$\begin{aligned} \root 3 \of {t_1}\,&=\root 3 \of {r}\,\left( \cos \frac{v_1+2\,\pi \,k}{3}+i\,\sin \frac{v_1+2\,\pi \,k}{3}\right) , \end{aligned}$$

(B.27)

$$\begin{aligned} \root 3 \of {t_2}\,&=\root 3 \of {r}\,\left( \cos \frac{-v_1+2\,\pi \,k}{3}+i\,\sin \frac{-v_1+2\,\pi \,k}{3}\right) ,{} & {} \end{aligned}$$

(B.28)

for $k=0,1,2$ and (B.17) gives the following three real roots

$$\begin{aligned} n_1\,&=2\sqrt{-\frac{q_1}{3}}\,\cos \frac{v_1}{3}+\frac{\xi _1}{3}, \end{aligned}$$

(B.29)

$$\begin{aligned} n_2\,&=2\sqrt{-\frac{q_1}{3}}\,\cos \frac{v_1+2\,\pi }{3}+\frac{\xi _1}{3}, \end{aligned}$$

(B.30)

$$\begin{aligned} n_3\,&=2\sqrt{-\frac{q_1}{3}}\,\cos \frac{v_1+4\,\pi }{3}+\frac{\xi _1}{3},{} & {} \end{aligned}$$

(B.31)

where $r {=}\sqrt{-q_1^3/27}$ is the modulus of $t_1$ and $t_2$, while $v_1$ and $v_2=-v_1$ are the corresponding arguments. Equation (B.15) thus has six different real roots

$$\begin{aligned} \psi _{1}\,&=\sqrt{n_1},\quad \psi _{2}{=}-\sqrt{n_1},\quad \psi _{3}{=}\sqrt{n_2},{} & {} \nonumber \\ \psi _{4}\,&=-\sqrt{n_2},\quad \psi _{5}{=}\sqrt{n_3},\quad \psi _{6}{=}-\sqrt{n_3},{} & {} \end{aligned}$$

(B.32)

and the solution of differential Eq. (B.11) is now

$$\begin{aligned}&\Delta w{=}C_1\,e^{\psi _{1}\,x}+C_2\,e^{\psi _{2}\,x}+C_3\,e^{\psi _{3}\,x}+C_4\,e^{\psi _{4}\,x}\nonumber \\&\quad +C_5\,e^{\psi _{5}\,x}+C_6\,e^{\psi _{6}\,x}-\frac{\xi _4}{\xi _3},{} & {} \end{aligned}$$

(B.33)

which may be also expressed in terms of hyperbolic functions $\cosh$ and $\sinh$ to obtain a form of the solution analogous to (B.25).

1.3 Appendix B.3: Case of $\Phi =0$

When $\Phi =0$, two different cases should be considered:

${\textbf {a)}}$:

If $\Phi =0$, but $q_2\ne 0$ (thus also implying $q_1<0$), Eq. (B.16) has one simple and one double root, i.e. Eq. (B.15) has only real roots, two of them with single multiplicity and the remaining two with double multiplicity, as given below

$$\begin{aligned} \psi _{1}\,&=\sqrt{-2\root 3 \of {\frac{q_2}{2}}+\frac{\xi _1}{3}},\quad \psi _{2}{=}-\sqrt{-2\root 3 \of {\frac{q_2}{2}}+\frac{\xi _1}{3}},{} & {} \nonumber \\ \psi _{3}\,&=\sqrt{\root 3 \of {\frac{q_2}{2}}+\frac{\xi _1}{3}},\quad \psi _{4}{=}-\sqrt{\root 3 \of {\frac{q_2}{2}}+\frac{\xi _1}{3}}.{} & {} \end{aligned}$$

(B.34)

Thus, the solution of differential Eq. (B.11) is

$$\begin{aligned}&\Delta w{=}C_1\,e^{\psi _{1}\,x}+C_2\,e^{\psi _{2}\,x}+e^{\psi _{3}\,x}\left( C_3\,+x\,C_4\right) \nonumber \\&\quad +e^{\psi _{4}\,x}\left( C_5+x\,C_6\right) -\frac{\xi _4}{\xi _3}.{} & {} \end{aligned}$$

(B.35)

${\textbf {b)}}$:

If $\Phi =q_2=0$, which implies $q_1=0$ and is equivalent to $\xi _2=\frac{\xi _1^2}{3}$ and $\xi _3=\frac{\xi _1^3}{27}$, Eq. (B.16) has one triple real root, i.e. Eq. (B.15) has two real roots with triple multiplicity

$$\begin{aligned} \psi _{1}\,&=\sqrt{\frac{\xi _1}{3}},\quad \psi _{2}{=}-\sqrt{\frac{\xi _1}{3}},{} & {} \end{aligned}$$

(B.36)

which gives solution of the differential Eq. (B.11)

$$\begin{aligned}&\Delta w{=}e^{\psi _{1}\,x}\left( C_1+x\,C_2+x^2\,C_3\right) \nonumber \\&\quad +e^{\psi _{2}\,x}\left( C_4\,+x\,C_5+x^2\,C_6\right) -\frac{\xi _4}{\xi _3}.{} & {} \end{aligned}$$

(B.37)

Appendix C: Obtaining the remaining kinematic fields and stress resultants for the case of $\Gamma _4\ne 0$

As shown in Appendix B, regardless of the value of $\Phi$, the solution for $\Delta w$ has six unknown constants $C_i$ ($i=1, \ldots ,6$). The result for $w_2^{\textrm{IV}}$ can be now easily expressed and from Eq. (B.9) integrated four times to obtain $w_2$. Thus, four additional unknown constants (e.g. $C_7$, $C_8$, $C_9$ and $C_{10}$) exist in the solution for $w_2$. This is in accordance with the derivation presented in Appendix A for the case of equal layers (and $\Gamma _4=0$). Therefore, it can be concluded that regardless of the value of $\Gamma _4$ and $\Phi$, the closed-form solutions for $\Delta w$ and $w_2$ require ten unknown constants $C_i$ ($i=1, \ldots , 10$) in total.

When $\Gamma _4\ne 0$, the most obvious way to obtain $u_1$ would be to integrate Eq. (B.3) thrice, since $\Delta w$ and $w_2$ have been previously determined. However, such procedure would generate three additional integration constants, which is a number that can be reduced if a different path is chosen. Indeed, by extracting $u_1^{\prime \prime \prime }$ from Eq. (B.3), differentiating one time and substituting it in Eq. (B.5), we obtain

$$\begin{aligned} u_1^{\prime \prime }{=}\eta _{1}\,w_2^{\textrm{V}}+\eta _{2}\,\Delta w^{\prime \prime \prime }-\eta _{3}\,w_2^{\prime \prime \prime }+\eta _{4}\,\Delta w^{\prime }-\eta _{5},{} & {} \end{aligned}$$

(C.1)

where

$$\begin{aligned}&\eta _{1}=\frac{2\,EA_2\,EI_2}{EA_0\,h_2\,K_t},\quad \nonumber \\& \eta _{2}=\frac{EA_2}{EA_0}\left( \frac{2}{h_2\,K_t}\left( K_r+\frac{EI_2\,K_n}{GA_{s.2}}\right) -\frac{h_1}{2}\right) ,{} & {} \nonumber \\&\eta _{3}=\frac{EA_2\,h_0}{EA_0},\quad \eta _{5}=\frac{p_{x.0}}{EA_0},{} & {} \nonumber \\&\eta _{4}=\frac{K_n\,EA_2}{EA_0}\left( \frac{1}{2}\left( \frac{h_1}{GA_{s.1}}-\frac{h_2}{GA_{s.2}}\right) \right. \nonumber \\&\quad \left. -\frac{2}{h_2\,K_t}\left( 1+\frac{GA_{s.0}}{GA_{s.p}}K_r\right) \right) .{} & {} \end{aligned}$$

(C.2)

Therefore, $u_1$ is obtained after integrating twice Eq. (C.1), which gives only two additional integration constants ($C_{11}$ and $C_{12}$). Note that at this stage there are already 12 integration constants, which coincides with the number of the unknown functions that need to be determined. Therefore, it is essential to obtain the remaining unknown functions without introducing any additional integration constants.

The unknown functions $w_1$ and $p_t$ can be easily obtained in closed form from Eqs. (2) and (22) respectively without introducing new constants. Although, $\theta _1$ and $\theta _2$ can be obtained from Eqs. (24) and (25), respectively, by integrating them once, this path is not chosen because it would generate new integration constants. Instead, Eq. (26) is added to Eq. (27), which gives the solution for $\theta _2$ as a function of $p_t$ (previously obtained), the first derivatives of $w_2$ and $w_1$ (previously obtained) and the second derivatives of $\theta _1$ and $\theta _2$. The latter can be substituted using the first derivative of $\theta _2$ obtained from Eq. (25) and $\theta _1$ extracted from Eq. (27) that involve only the previously obtained functions for $w_2$ and $w_1$, giving

$$\begin{aligned}&\theta _2{=}\beta _{1}\,w_2^{\textrm{V}}+\beta _{2}\,\Delta w^{\prime \prime \prime }-\beta _{3}\,w_2^{\prime \prime \prime }-\beta _{4}\,p_t^{\prime \prime }-\beta _{5}\,\Delta w^{\prime }\nonumber \\&\quad -w_2^{\prime }+\beta _{6}\,p_t+\beta _{7},{} & {} \end{aligned}$$

(C.3)

where

$$\begin{aligned} \beta _{1}&=\frac{EI_p}{GA_{s.p}+GA_{s.0}\,K_r},\quad \beta _{2}=\beta _{1}\,\frac{K_n}{GA_{s.2}},\quad \nonumber \\ \beta _{3}&=\frac{\beta _{1}}{EI_p}\,\left( EI_2\,GA_{s.1}+EI_0\,K_r\right) ,{} & {} \nonumber \\ \beta _{4}&=\beta _{1}\,\frac{h_2}{2EI_2}, \nonumber \\ \beta _{5}&=\frac{\beta _{1}}{EI_p}\,\left( EI_1\,K_n+GA_{s.1}\,K_r\right)+\beta _{3}\,\frac{K_n}{GA_{s.2}},{} & {} \nonumber \\ \beta _{6}&=\frac{\beta _{1}}{EI_p}\left( GA_{s.1}\,\frac{h_2}{2}+h_0\,K_r\right) ,\quad \nonumber \\&\beta _{7}=\frac{\beta _{1}}{EI_p}\left( GA_{s.1}\,m_{y.2}+K_r\,m_{y.0}\right) .{} & {} \end{aligned}$$

(C.4)

Analogously, the same can be done for $\theta _1$. In fact, if $\theta _1^{\prime }$ is expressed from Eq. (24), deriving it one time and replacing $\theta _1^{\prime \prime }$ in Eq. (26), $\theta _1$ can be expressed as

$$\begin{aligned} \theta _1\,&=\frac{1}{GA_{s.1}+K_r}\left[ -EI_1\left( \Delta w^{\prime \prime \prime }+w_2^{\prime \prime \prime }\right) \right. \nonumber \\&+\left( \frac{EI_1\,K_n}{GA_{s.1}}-GA_{s.1}\right) \Delta w^{\prime }-\nonumber \\&\left. -GA_{s.1}\,w_2^{\prime }+K_r\,\theta _2+\frac{h_1}{2}p_t+m_{y.1}\right] .{} & {} \end{aligned}$$

(C.5)

Finally, $u_2$ is directly obtained from (22) and (4). Therefore, all kinematic quantities ($u_i$, $w_i$ and $\theta _i$, $i=1,2$) as well as the tangential tractions at the interface ($p_t$) can be expressed in closed form with a total number of 12 unknown constants. After that, stress resultants ($N_i$, $T_i$ and $M_i$, $i=1,2$) can be expressed form (19)–(21) without introducing new constants.

Appendix D: Contribution of the interface to the residual vector and stiffness matrix for the geometrically exact multi-layer beam model

According to [56], the residual vector of a multi-layer beam with n layers and $n-1$ interfaces is composed by taking into account internal forces in the layers and external loads applied on them, as well as internal forces in the interfaces. In order to account for the rotational stiffness at the interface, the third row with relative rotations between the layers is added to the vector of relative displacements, which for a horizontal two-layer beam with a zero-thickness interface, according to [56], reads

$$\begin{aligned} \varvec{z}=\left\{ \begin{matrix} u_2-u_1+\frac{h_2}{2}\sin \theta _2+\frac{h_1}{2}\sin \theta _1\\ w_2-w_1+\frac{h_2}{2}(1-\cos \theta _2)+\frac{h_1}{2}(1-\cos \theta _1)\\ \theta _2-\theta _1\end{matrix} \right\} . \end{aligned}$$

(D.1)

It can be noticed that after linearisation ($\sin \theta _i\rightarrow \theta _i$ and $\cos \theta _i\rightarrow 1$, where $i=1,2$) $\varvec{z}=-\lbrace \Delta u\quad \Delta w\quad \Delta \theta \rbrace ^{\textsf{T}}$, where $\Delta u$, $\Delta w$ and $\Delta \theta$ are defined in Eqs. (1)–(3). The minus sign appears because the co-ordinate system used in [56] is different than that used in the present work. In particular, according to [56], transversal displacements $w_i$ are positive upwards.

In geometrically non-linear analysis, especially when the displacements and rotations are not small, it becomes difficult to uniquely define what interlayer slip and uplift are, because, in contrast to the geometrically linear analysis, they cannot be defined with respect to the initial (undeformed) configuration. Thus, it is necessary to define the directions of interlayer slip and uplift in the deformed configuration. Following the idea proposed in [56], here we assume that the direction of the interlayer uplift is defined by the mean value of the cross-sectional rotations of both layers, i.e. by the angle $\theta ^m=(\theta _1+\theta _2)/2$ with respect to the $z-$axis. The direction of the interlayer slip is perpendicular to the direction of the interlayer uplift, i.e. it is defined by the angle $\theta ^m$ with respect to the $x-$axis. Interlayer distortion is defined in the same manner as in the geometrically linear analysis, i.e. according to Eq. (3), but with opposite sign.

Nodal degrees of freedom for a two-layer beam are collected in vector $\varvec{p}_G=\lbrace \begin{matrix} u_1&w_1&\theta _1&u_2&w_2&\theta _2\end{matrix}\rbrace ^{\textsf{T}}$, which means that the nodal vector of residual forces and nodal stiffness matrix have dimensions $6\times 1$ and $6\times 6$, respectively. After discretising the domain $\left[ 0,L\right]$ in N nodes, the contribution of the interface to the vector of internal forces for node j can be defined as[56]

$$\begin{aligned} \varvec{q}^{int}_{j}=b_{int}\int \limits _0^L\left( \varvec{Y}\varvec{R}_{j}\right) ^{\textsf{T}}\varvec{\omega }\textrm{d}x, \end{aligned}$$

(D.2)

where $b_{int}$ is the width of the interface, while

$$\begin{aligned} \varvec{Y}=\hat{\varvec{t}}_3\varvec{\Lambda }^m\varvec{z}\varvec{\varphi }^{\textsf{T}}+\varvec{\Lambda }^m\varvec{B}, \end{aligned}$$

(D.3)

with

$$\begin{aligned}{} & {} \hat{\varvec{t}}_3=\begin{bmatrix} 0 &{} -1 &{}0\\ 1 &{} 0 &{} 0\\ 0 &{} 0 &{}0 \end{bmatrix}\text {,} \quad \varvec{\Lambda }^m=\begin{bmatrix} \cos \theta ^m &{} -\sin \theta ^m &{} 0\\ \sin \theta ^m &{} \cos \theta ^m &{} 0\\ 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

(D.4)

$$\begin{aligned}{} & {} \varvec{\varphi }^{\textsf{T}}=\frac{1}{2}\lbrace \begin{matrix} 0&0&1&0&0&1\end{matrix}\rbrace , \end{aligned}$$

(D.5)

$$\begin{aligned}{} & {} \varvec{B}=\begin{bmatrix} -1 &{} 0 &{} \cos \theta _1\frac{h_1}{2} &{} 1 &{} 0 &{} \cos \theta _2\frac{h_2}{2}\\ 0 &{} -1 &{} \sin \theta _1\frac{h_1}{2} &{} 0 &{} 1 &{} \sin \theta _2\frac{h_2}{2}\\ 0 &{} 0 &{} -1&{} 0 &{} 0 &{} 1 \end{bmatrix}, \end{aligned}$$

(D.6)

and

$$\begin{aligned} \varvec{R}=\psi _j(x)\varvec{I}_{6\times 6}, \end{aligned}$$

(D.7)

where $\psi _j(x)$ is the interpolation function for node j and $\varvec{I}_{6\times 6}$ is 6$\times$ 6 unity matrix. Note that dimensions of matrices matrices $\hat{\varvec{t}}_3$, $\varvec{\Lambda }^m$ and $\varvec{B}$ are increased with respect to those presented in [56] in order to account for the rotational degree of freedom at the interface. As a result, matrix $\varvec{Y}$ now has dimensions $3\times 6$. Tractions at the interface are given as

$$\begin{aligned} \varvec{\omega }=\varvec{S}\varvec{\Lambda }^m\varvec{z}, \end{aligned}$$

(D.8)

where

$$\begin{aligned} \varvec{S}=\frac{1}{b_{int}}\begin{bmatrix} K_t&{} 0 &{} 0\\ 0 &{} K_n&{} 0\\ 0 &{} 0 &{} K_r\end{bmatrix}. \end{aligned}$$

(D.9)

Note that in the third row of $\varvec{\omega }$, rotational tractions at the interface are given. Moreover, first two rows of product $\varvec{\Lambda }^m\varvec{z}$ give relative displacements at the interface that correspond to interlayer slip and uplift, while the interlayer distortion is given in the third row. Finally, contribution of the interface to the nodal stiffness matrix can be obtained by linearising the nodal vector of residual forces (D.2) as

$$\begin{aligned} \varvec{K}_{j.k}=\int \limits _0^L\varvec{R}_j^{\textsf{T}}\varvec{Y}^{\textsf{T}}\varvec{S}\varvec{Y}\varvec{R}_k\textrm{d}x. \end{aligned}$$

(D.10)

For the integration of Eqs. (D.2) and (D.10) 3-point Simpson’s rule is recommended [68]. The contributions of the layers to the vector of residual forces and stiffness matrix are not reported here for the sake of brevity, but a detailed derivation is given in [56]. Global vector of residual and stiffness matrix are assembled using the standard finite-element procedure. For the analyses presented in Sect. 6.3, load-control solution procedure has been employed.