Skip to main content
SpringerLink
Log in

Periodic regimes of motion of capsule system on rough plane

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

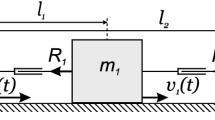
The motion of a capsule system along a line on a rough horizontal plane is considered. The capsule consists of a hull and an internal mass moving periodically inside the hull parallel to the line of the motion of the system. The velocity of the internal mass relative to the hull is supposed to be a continuous function of time. Periodic regimes of motion of the system are considered. A periodic regime of motion is the motion of the system in which the periodic change in the position of the internal mass relative to the hull provides the periodicity of the velocity of the hull. In such a motion, the system travels the same distance over each time period. We prove, that the periodic regime of motion of the capsule system exists, is unique, and is stable with respect to the initial conditions. The velocity of the hull for any initial condition converges to the periodic velocity of the hull exponentially or in finite time. The criterion is found that defines whether the convergence is exponential or in finite time. Examples illustrating both types of the convergence are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

The manuscript has no associated data.

References

  1. Ivanov AP (2020) Analysis of an impact-driven capsule robot. Int J Nonlinear Mech 119:103257. https://doi.org/10.1016/j.ijnonlinmec.2019.103257

    Article  Google Scholar 

  2. Fang HB, Xu J (2011) Dynamic analysis and optimization of a three-phase control mode of a mobile system with an internal mass. J Vib Control 17(1):19–26. https://doi.org/10.1177/1077546309345631

    Article  MathSciNet  MATH  Google Scholar 

  3. Fang H, Wang KW (2017) Piezoelectric vibration-driven locomotion systems - exploiting resonance and bistable dynamics. J Sound Vib 391:153–169. https://doi.org/10.1016/j.jsv.2016.12.009

    Article  Google Scholar 

  4. Fang HB, Xu J (2011) Dynamics of a mobile system with an internal acceleration-controlled mass in a resistive medium. J Sound Vib 330(16):4002–4018. https://doi.org/10.1016/j.jsv.2011.03.010

    Article  Google Scholar 

  5. Liu Y, Pavlovskaia E, Wiercigroch M, Peng ZK (2015) Forward and backward motion control of a vibro-impact capsule system. Int J Nonlinear Mech 70:30–46. https://doi.org/10.1016/j.ijnonlinmec.2014.10.009

    Article  Google Scholar 

  6. Yan Y, Liu Y, Manfredi L, Prasad S (2019) Modelling of a vibro-impact self-propelled capsule in the small intestine. Nonlinear Dyn 96:123–144. https://doi.org/10.1007/s11071-019-04779-z

    Article  Google Scholar 

  7. Guo B, Ley E, Tian J, Zhang J, Liu Y, Prasad S (2020) Experimental and numerical studies of intestinal frictions for propulsive force optimisation of a vibro-impact capsule system. Nonlinear Dyn 101:65–83. https://doi.org/10.1007/s11071-020-05767-4

    Article  Google Scholar 

  8. Golitsyna MV (2018) Periodic regime of motion of a vibratory robot under a control constraint. Mech Solids 53:49–59. https://doi.org/10.3103/S002565441803007X

    Article  MATH  Google Scholar 

  9. Bardin B, Panev A (2016) On dynamics of a rigid body moving on a horizontal plane by means of motion of an internal particle. Vibroeng PROCEDIA 8:135–141

    Google Scholar 

  10. Bardin BS, Panev AS (2018) On the motion of a body with a moving internal mass on a rough horizontal plane. Rus J Nonlin Dyn 14(4):519–542. https://doi.org/10.20537/nd180407

    Article  MathSciNet  MATH  Google Scholar 

  11. Liu Y, Islam S, Pavlovskaya E, Wiercigroch M (2016) Optimization of the vibro-impact capsule system. J Mech Eng 62:430–439. https://doi.org/10.5545/sv-jme.2016.3754

    Article  Google Scholar 

  12. Nunuparov A, Becker F, Bolotnik N, Zeidis I, Zimmermann K (2019) Dynamics and motion control of a capsule robot with an opposing spring. Arch Appl Mech 89:2193–2208. https://doi.org/10.1007/s00419-019-01571-8

    Article  Google Scholar 

  13. Tahmasian S, Jafaryzad A, Bulzoni NL, Staples AE (2020) Dynamic analysis and design optimization of a drag-based vibratory swimmer. Fluids 5:38. https://doi.org/10.3390/fluids5010038

    Article  Google Scholar 

  14. Guo B, Liu Y, Prasad S (2019) Modelling of capsule-intestine contact for a self-propelled capsule robot via experimental and numerical investigation. Nonlinear Dyn 98:3155–3167. https://doi.org/10.1007/s11071-019-05061-y

    Article  Google Scholar 

  15. Sobolev NA, Sorokin KS (2007) Experimental investigation of a model of a vibration-driven robot with rotating masses. J Comput Syst Sci Int 46:826–835. https://doi.org/10.1134/S1064230707050140

    Article  MATH  Google Scholar 

  16. Chernousko FL (2008) On the optimal motion of a body with an internal mass in a resistive medium. J Vib Control 14(1–2):197–208. https://doi.org/10.1177/1077546307079398

    Article  MathSciNet  MATH  Google Scholar 

  17. Bolotnik NN, Figurina TY, Chernous’ko FL (2012) Optimal control of the rectilinear motion of a two-body system in a resistive medium. J Appl Math Mech 76(1):1–14. https://doi.org/10.1016/j.jappmathmech.2012.03.001

    Article  MathSciNet  MATH  Google Scholar 

  18. Tahmasian S (2021) Dynamic analysis and optimal control of drag-based vibratory systems using averaging. Nonlinear Dyn 104:2201–2217. https://doi.org/10.1007/s11071-021-06440-0

    Article  Google Scholar 

  19. Yan Y, Liu Y, Liao M (2017) A comparative study of the vibro-impact capsule systems with one-sided and two-sided constraints. Nonlinear Dyn 89:1063–1087. https://doi.org/10.1007/s11071-017-3500-7

    Article  Google Scholar 

  20. Egorov AG, Zakharova OS (2015) The energy-optimal motion of a vibration-driven robot in a medium with a inherited law of resistance. J Comput Syst Sci Int 54:495–503. https://doi.org/10.1134/S1064230715030065

    Article  MathSciNet  MATH  Google Scholar 

  21. Yegorov AG, Zakharova OS (2010) The energy-optimal motion of a vibration-driven robot in a resistive medium. J Appl Math Mech 74(4):443–451. https://doi.org/10.1016/j.jappmathmech.2010.09.010

    Article  MathSciNet  MATH  Google Scholar 

  22. Chernous’ko FL (2005) On the motion of a body containing a movable internal mass. Dokl Phys 50:593–597. https://doi.org/10.1134/1.2137795

    Article  Google Scholar 

  23. Figurina TY (2007) Optimal motion control for a system of two bodies on a straight line. J Comput Syst Sci Int 46(2):227–233. https://doi.org/10.1134/S1064230707020086

    Article  MathSciNet  MATH  Google Scholar 

  24. Knyaz’kov DY, Figurina TY (2020) On the existence, uniqueness, and stability of periodic modes of motion of a locomotion system with a mobile internal mass. J Comput Syst Sci Int 59:129–137. https://doi.org/10.1134/S1064230719060108

    Article  MathSciNet  MATH  Google Scholar 

  25. Knyazkov D, Figurina T (2019) Periodic regimes of motion of a body with a moving internal mass. In: proceedings of 2019 24th international conference on methods and models in automation and robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2019, pp. 331–336 . https://doi.org/10.1109/mmar.2019.8864630

  26. Figurina T, Knyazkov D (2022) Periodic gaits of a locomotion system of interacting bodies. Meccanica 57:1463–1476. https://doi.org/10.1007/s11012-022-01473-0

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

We appreciate Prof. Bolotnik N.N. for reading the manuscript and useful comments.

Funding

This study was supported by Russian Science Foundation, Project No. 18-11-00307, https://rscf.ru/en/project/18-11-00307/.

Author information

Author notes

  1. Tatiana Figurina and Dmitri Knyazkov contributed equally to this work.

Authors and Affiliations

  1. Ishlinsky Institute for Problems in Mechanics RAS, Prospekt Vernadskogo 101-1, Moscow, 119526, Russia

    Tatiana Figurina & Dmitri Knyazkov

Authors
  1. Tatiana Figurina
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dmitri Knyazkov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dmitri Knyazkov.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Figurina, T., Knyazkov, D. Periodic regimes of motion of capsule system on rough plane. Meccanica 58, 493–507 (2023). https://doi.org/10.1007/s11012-022-01572-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-022-01572-y

Keywords

Search

Navigation