A finite difference method for the static limit analysis of masonry domes under seismic loads

Abstract

The static limit analysis of axially symmetric masonry domes subject to pseudo-static seismic forces is addressed. The stress state in the dome is represented by the shell stress resultants (normal-force tensor, bending-moment tensor, and shear-force vector) on the dome mid-surface. The classical differential equilibrium equations of shells are resorted to for imposing the equilibrium of the dome. Heyman’s assumptions of infinite compressive and vanishing tensile strength, alongside with cohesive-frictional shear response, are adopted for imposing the admissibility of the stress state. A finite difference method is proposed for the numerical discretization of the problem, based on the use of two staggered rectangular grids in the parameter space generating the dome mid-surface. The resulting discrete static limit analysis problem results to be a second-order cone programming problem, to be effectively solved by available convex optimization softwares. In addition to a convergence analysis, numerical simulations are presented, dealing with the parametric analysis of the collapse capacity under seismic forces of spherical and ogival domes with parameterized geometry. In particular, the influence that the shear response of masonry material and the distribution of horizontal forces along the height of the dome have on the collapse capacity is explored. The obtained results, that are new in the literature, show the computational merit of the proposed method, and quantitatively shed light on the seismic resistance of masonry domes.

1 Introduction

Masonry domes, especially used as coverings for historical monumental buildings, represent invaluable pieces of cultural heritage, whose conservation and restoration often requires a seismic structural assessment. Limit analysis appears as an effective structural analysis strategy to that aim, because allowing a direct estimate of the structural capacity under prescribed loading conditions. Nevertheless, the limit analysis of masonry domes under horizontal forces is at present still an open problem [17].

The application of limit analysis theory to masonry structures traces back to the work by Heyman, and his observation that the assumptions of infinite compressive strength, vanishing tensile strength, and no-sliding condition are applicable to masonry material for the computation of the structural bearing capacity [29]. In the last decades, prompted by the development and availability of personal computers, the classical limit analysis theorems have been progressively translated into a variety of computational methods.

In the context of static limit analysis approaches, computational methods addressing, or applicable to, the analysis of masonry domes can be broadly classified into three groups, referred to as lunar-slices, thrust surface analysis and thrust network methods.

Lunar-slices methods are based on the centuries-old idea that a masonry dome subjected to its self-weight can be studied as a collection of independent meridian slices (or lunes) [55]. In fact, because the typical meridian slice is an arch of variable width, the structural assessment of the dome is reduced to the thrust line analysis of an arch (to be addressed by classical graphic static tools or more advanced computational methods, e.g. [44, 58]). An improvement of that original idea requires to take into account the beneficial effect of statically indeterminate hoop stresses, by which the meridian slices of the dome may interact with each other. In fact, the development of compressive hoop stresses in the upper part of the dome (or dome cap) proves in some cases essential for a reliable, but not over-conservative, prediction on the stability of the dome [30]. The introduction of hoop stresses in lunar-slices methods has been extensively explored, especially resorting to constructive techniques (e.g., see [1, 34, 52, 61]). The possibility to conceive a fully automatic procedure for taking into account hoop stresses has also been recently proven, based on their discretization and numerical optimization through the solution of a simple linear programming problem [46, 47].

Such as lunar-slices methods relate the statics of a masonry dome under its self-weight to the statics of an arch, thrust surface analysis and thrust network methods emphasize the membrane behavior of general masonry vaults. In fact, they postulate that a purely membrane stress state, acting on a thrust membrane to be determined within the thickness of the vault, ensures the load transfer to its supporting structures.

In thrust surface analysis methods, a continuous modeling of both the stress state and of the thrust membrane is embraced (e.g., see [2, 3, 6, 22]). When gravitational loads are applied to the vault, the formulation takes advantage of an Airy stress potential to characterize the membrane stresses identically satisfying the horizontal equilibrium equations. Then, basing on the parameterization of the thrust membrane as the graph of an unknown function, the vertical equilibrium equation is formulated as a nonlinear differential equation, involving the product of the stress potential and of the thrust membrane elevation. The admissibility conditions on the stress state are finally imposed, prescribing the stress potential to be concave and the thrust membrane elevation to be contained within the dome thickness.

In contrast, thrust network methods represent an intrinsically discrete approach, inspired by the funicular analysis of vaulted structures in [51] and later on developed in [10]. Indeed, the existence of a 3D network within the vault, comprising nodes connected by branches (or edges), is conceived to describe the vault equilibrium state. In detail, the external loads acting on the vault are transformed into equivalent nodal loads, and compressive forces (or thrusts) within the branches are designated to guarantee nodal equilibrium (e.g., see [8, 9, 11, 23, 24, 40]). Also in this case, the nodal equilibrium equations result to be nonlinear in the unknown nodal elevations and thrust values. When only vertical loads are considered, that nonlinearity is circumvented by addressing horizontal and vertical nodal equilibrium equations the ones after the others. Accordingly, the horizontal projection of the thrusts in the branches of the network are first characterized. The elevation of the network is subsequently determined, to be bounded within the thickness of the dome for its admissibility to be ensured.

The extension of the above static limit analysis approaches to include horizontal actions (such as pseudo-static seismic forces) has received increasing attention in the last decade. Despite lunar-slices methods are mostly suited to the axially symmetric framework, a simple formulation has been proposed in [60], where experimental results have also been obtained by testing small-scale models of block masonry domes on a tilting table. In [16], horizontal forces proportional to the dome’s self-weight have been included in the thrust surface analysis method, by analyzing a suitably rotated configuration of the dome, in which the external loads are a system of vertical forces. Applications of the thrust network method to masonry arches and domes subject to horizontal forces can be respectively found in [40, 41], based on an iterative solution strategy for alleviating the nonlinearity of the equilibrium equations.

Concerning kinematic approaches to the limit analysis of masonry domes, a description of potential collapse mechanisms requires to identify a series of cracks, whose opening implies a mechanism of rigid bodies. Dual formulations to the aforementioned lunar-slices methods, to be applied for the assessment of domes under gravitational loads, have been e.g. discussed in [20, 54]. They exploit the classical argument that masonry domes usually exhibit meridional cracks, which are generally produced by slight outward radial settlements of their supporting structures [15, 30]. Accordingly, the kinematic theorem of limit analysis is applied to the typical lunar slice of the dome.

Conversely, an adaptive approach for determining the potential collapse mechanisms, and hence the collapse capacity, of masonry domes under horizontal forces has been proposed in [27]. Basic idea is that, after generating a mesh on the dome, its elements and edges respectively constitute a system of rigid bodies and cracks, potentially implying a mechanism. Accordingly, the actual collapse mechanism can be determined by adaptively changing that mesh. As a peculiarity of the method, the problem unknowns practically coincide with the position and the geometry of floating cracks on the dome, parameterized as NURBS curves (for the concept of free discontinuities in masonry structures, see also [21]). As a consequence, a nonlinear optimization problem is formulated for computing the actual collapse mechanism of the dome. Provided such a mechanism only involves few rigid bodies, the size of that optimization problem is limited. Meta-heuristic algorithms are adopted for its numerical solution [28].

As opposed to adaptive limit analysis approaches [27, 28], which trade the increased nonlinearity of the governing optimization problem for its reduced size, it is worth to mention block-based methods. In fact, the latter regard masonry structures as being constituted by rigid and infinite strength blocks, which interact with each other through their shared interfaces. Because cracks can only open at the interfaces between the blocks, the limit analysis problem can be formulated as a linear programming problem. On the other hand, whether the blocks are considered as physical units or as the result of a numerical discretization, a large number of blocks is expected, resulting in a large-size optimization problem. Following the initial idea proposed in [35, 36], block-based methods have been broadly used for the limit analysis of both 2D and 3D masonry structures in the last twenty years (e.g., see [32, 39, 56, 57]), also assuming non-associative friction flow law (e.g., see [5, 12, 19, 25, 49, 53]). An extension to masonry domes under horizontal forces has been discussed in [4, 13], taking advantage of a point contact model which simplifies the imposition of the failure conditions at block interfaces and results in a cone programming problem.

In a recent work [48], the authors have proposed an innovative formulation for the static limit analysis of masonry domes, which overcomes several of the difficulties mentioned above. Key point is to resort to the classical statics of shells for characterizing the stress state and formulating the equilibrium equations of the dome. The latter are linear in the unknown shell stress resultants (normal-force and bending-moment tensors, and shear-force vector) defined on the dome mid-surface. In addition to the implicit merit of a static formulation to provide results on the safe side, such a novel, theoretically sound shell-based paradigm is preparatory to conceive effective computational strategies, that naturally and effectively address the limit analysis of masonry domes, also subject to horizontal forces. In particular, a finite-volume discretization approach has been proposed in [48], exploiting an integral formulation of the shell equilibrium equations.

From a modeling viewpoint, the shell-based static limit analysis approach allows to characterize the admissible stress states in the dome through the introduction of a strength domain in the space of the shell stress resultants. Classical Heyman’s assumptions solely imply the imposition of unilateral conditions (e.g., see [37]). However, the no-sliding hypothesis, which is commonly acceptable for masonry domes with usual material properties subject to self-weight (e.g., see [59]), might require further considerations in presence of horizontal forces. Accordingly, for a safe estimation of the structural collapse capacity, suitable shear admissibility conditions might be taken into account (e.g., see [7, 18, 38, 59]).

Set in the framework of such a shell-based formulation, the present work investigates a finite difference computational strategy for the static limit analysis of masonry domes under pseudo-static seismic loads. It is based on a differential formulation of the shell equilibrium equations. Their finite difference discretization is accomplished by the introduction of two staggered rectangular grids, defined in the parameter space generating the dome mid-surface. The unknown shell stress resultants are located at the nodes of one grid (main grid). The equilibrium equations are then imposed, in the finite difference sense, at the nodes of the other grid (auxiliary grid). The formulation is complemented by the admissibility conditions on the shell stress resultants, to be enforced at the nodes of the main grid. As a particular choice of the strength domain in the space of shell stress resultants, Heyman’s assumptions of infinite compressive and vanishing tensile strengths are here adopted, alongside with a cohesive-frictional shear response. Accordingly, a cohesion term and friction coefficient are the only constitutive parameters needed in the formulation. Though more general strength domains might be considered, e.g. accounting for non-vanishing tensile strength due to combined effect of friction and masonry texture [7, 14], such a choice conservatively covers the pseudo-static seismic assessment of both dry-masonry structures and masonry structures with mortar. As a consequence, a discrete static limit analysis problem is derived, in the form of a second-order conic programming problem, which is addressed by available high-performance convex optimization softwares. Simplicity of implementation and computational efficiency are among the advantages of the proposed methodology, alongside with the capability to equally address gravitational forces and horizontal loads with arbitrary distribution.

For those advantages to be highlighted, numerical results are presented. After investigating the convergence performances of the formulation, parametric analyses dealing with the collapse capacity of spherical and ogival domes, with parameterized geometry and subject to horizontal forces, are addressed. In view of seismic applications, the influence exerted by the shear response of masonry material and by the distribution of horizontal forces along the height of the dome is explored. In the former respect, results pertaining to different shear models, namely Heyman’s no-sliding behavior, cohesionless frictional behavior, and cohesive-frictional behavior, are presented. In the latter respect, uniform and linear distributions of horizontal forces are considered. Besides proving the computational merit of the method, the obtained numerical results, that seem to be novel in the literature, have an intrinsic engineering significance, enabling a pseudo-static seismic assessment of masonry domes.

The remaining part of the present paper is organized as follows. In Sect. 2 the problem formulation is discussed. That is preparatory for the finite difference solution scheme proposed in Sect. 3. Numerical simulations are presented in Sect. 4, and conclusions are outlined in Sect. 5. Finally, some closed-form formulas for the implementation of the proposed finite-difference scheme are discussed in Appendix A.

2 Problem formulation

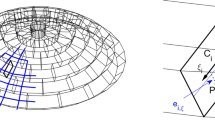
A masonry dome of revolution is considered. Its mid-surface, shown in Fig. 1a, is parameterized in terms of an arbitrary meridional parameter $t$ and of a longitude angle $\vartheta$ by the position vector:

$$\begin{aligned} \varvec{x}= r\varvec{e}_r+ z\varvec{k}, \quad \varvec{e}_r= \cos \vartheta \, \varvec{i}+ \sin \vartheta \, \varvec{j}. \end{aligned}$$

(1)

Here, for $\varvec{i}$, $\varvec{j}$ and $\varvec{k}$ unit vectors lying along the axes of a Cartesian reference frame, $r(t)$ and $z({t})$ denote the distance from the revolution axis (in the radial direction $\varvec{e}_r$) and the elevation of point $\varvec{x}$, respectively. Parallel and meridian curves on the dome mid-surface respectively correspond to coordinate curves with constant $t$ and $\vartheta$. In particular, meridian curves are characterized by a tangential angle $\varphi$ and by a radius of curvature $\rho$ given by:

$$\begin{aligned} \tan {\varphi } = -\frac{{z\!}_{/t}}{{r\!}_{/t}}, \quad \rho = -\frac{({{r\!}_{/t}^{\,2}+{z\!}_{/t}^{\,2}})^{3/2}}{{z\!}_{/tt}{r\!}_{/t} - {z\!}_{/t}{r\!}_{/tt}}, \end{aligned}$$

(2)

the slash symbol standing for differentiation with respect to the indicated variable. As customary in the statics of shells, by using relationship (2)$_{\text {1}}$, the tangential angle $\varphi$ is henceforth used as meridional parameter in place of $t$. The following physical basis vectors are introduced on the dome mid-surface:

$$\begin{aligned} \varvec{e}_{\varphi }&= \cos \varphi \, \varvec{e}_r- \sin \varphi \, \varvec{k}, \\ \varvec{e}_{\vartheta }&= -\sin \vartheta \, \varvec{i}+ \cos \vartheta \, \varvec{j}, \\\varvec{n}&= \sin \varphi \, \varvec{e}_r+ \cos \varphi \,\varvec{k}, \end{aligned} $$

(3)

such that $\varvec{e}_{\varphi }$ and $\varvec{e}_{\vartheta }$ are unit vectors respectively tangent to meridian and parallel curves, whereas $\varvec{n}$ is the exterior normal unit vector to the mid-surface. The dome thickness, measured along the normal direction $\varvec{n}$, is denoted as $h$.

Fig. 1

Formulation: a three-dimensional view of the mid-surface of an axially symmetric masonry dome, and b shell stress resultants acting on the mid-surface of the dome

External loads acting on the dome are reduced to statically equivalent surface distributions of external forces $\varvec{q}$ and couples $\varvec{m}$ applied to its mid-surface [45, 48]. For mimicking pseudo-static seismic loads, those distributions are assumed of the form:

$$\begin{aligned} \varvec{q}= \varvec{q}_{\text {d}}+ \lambda \varvec{q}_{\text {l}}, \quad \varvec{m}= \varvec{m}_{\text {d}}+ \lambda \varvec{m}_{\text {l}}, \end{aligned}$$

(4)

i.e. as the sum of dead and live contributions, with $\lambda$ as a scalar multiplier of basic live loads. Postponing further details on the treatment of dead and live loads to Sect. 4, it is here explicitly noticed that surface couples $\varvec{m}$ do not involve drilling couples.

Resorting to the classical statics of shells (e.g., see [26, 33]), also the stress state in the dome is described on its mid-surface, by the introduction of a normal-force tensor $\varvec{N}$, a shear-force vector $\varvec{Q}$, and a bending-moment tensor $\varvec{M}$. They are tangent fields on the dome mid-surface, which admit the following matrix representation in the basis $\left( \varvec{e}_{\varphi }, \, \varvec{e}_{\vartheta } \right)$:

$$\begin{aligned} \varvec{N}= \left[ \begin{matrix} N_{\varphi } &{} N_{\varphi \vartheta } \\ N_{\vartheta \varphi } &{} N_{\vartheta } \end{matrix} \right] , \quad \varvec{Q}= \left( \begin{matrix} Q_{\varphi } \\ Q_{\vartheta }\end{matrix} \right) , \quad \varvec{M}= \left[ \begin{matrix} M_{\varphi } &{} M_{\varphi \vartheta } \\ M_{\vartheta \varphi } &{} M_{\vartheta } \end{matrix} \right] . \end{aligned}$$

(5)

A mechanical interpretation of their components is offered in Fig. 1b, where they are recognized as the stress resultants per unit length emerging on the boundary of a mid-surface area element having its edges parallel to the coordinate curves.

Exploiting Eqs. (4)–(5), the equilibrium conditions of the dome, formulated in differential form referring to its mid-surface, read (e.g., see [26, 33], with a slight change of notation due to switching the indices of the off-diagonal components of the stress tensors):

$$\begin{aligned} 0&= {\left( rN_\varphi \right) \!}_{/\varphi } + \rho N_{\varphi \vartheta / \vartheta } - \rho \cos \varphi N_{\vartheta } + rQ_{\varphi } + r\!\rho q_{\varphi }, \\ 0&= {\left( rN_{\vartheta \varphi } \right) \!}_{/\varphi } + \rho N_{\vartheta / \vartheta } + \rho \cos \varphi N_{\varphi \vartheta } + \rho \sin \varphi \, Q_{\vartheta }+ r\!\rho q_{\vartheta }, \\ 0&= {\left( rQ_{\varphi } \right) \!}_{/\varphi } + \rho Q_{\vartheta / \vartheta } -rN_{\varphi } \, - \rho \sin \varphi N_{\vartheta } + r\!\rho q_{n}, \\ 0&= {\left( rM_\varphi \right) \!}_{/\varphi } + \rho M_{\varphi \vartheta / \vartheta } - \rho \cos \varphi M_{\vartheta } - r\!\rho Q_{\varphi } + r\!\rho m_{\varphi }, \\ 0&= {\left( rM_{\vartheta \varphi } \right) \!}_{/\varphi } + \rho M_{\vartheta / \vartheta } + \rho \cos \varphi M_{\varphi \vartheta } - r\!\rho Q_{\vartheta }+ r\!\rho m_{\vartheta }, \\ 0&= r\!\rho \left( N_{\vartheta \varphi } - N_{\varphi \vartheta } \right) + rM_{\vartheta \varphi } -\rho \sin \varphi M_{\varphi \vartheta }. \end{aligned} $$

(6)

In detail, the first [resp., last] three equations imply translational [resp., rotational] equilibrium along the physical basis vectors $\left( \varvec{e}_{\varphi }, \varvec{e}_{\vartheta }, \varvec{n} \right)$. Accordingly, the components in the physical basis of the surface forces $\varvec{q}$ and of the surface couples $\varvec{m}$ are involved. The differential equilibrium equations (6) are possibly complemented by the imposition of boundary conditions on the free edges of the dome mid-surface. For the sake of simplicity, it is here assumed that the supporting structures of the dome are sufficiently resistant to withstand the transmitted actions. Hence, no boundary conditions is enforced on the supported edges.

In the classical statics of shells, non-symmetric normal-force and bending-moment tensors are commonly employed, as introduced in equations (5)$_{\text {1,3}}$. However, a consistent derivation of the shell stress resultants from a 3D stress state, i.e. via a thickness integration involving the Cauchy stress tensor, shows that the bending-moment tensor can be assumed symmetric:

$$\begin{aligned} M_{\vartheta \varphi } = M_{\varphi \vartheta }. \end{aligned}$$

(7)

Such a conclusion is e.g. arrived at in [43] in the context of Cosserat surfaces. A simple and self-contained proof is presented in [48].

For the characterization of the admissible stress states in the dome, the classical Heyman’s assumptions of infinite compressive and vanishing tensile strengths are adopted [31]. Hence, the shell stress resultants are required to obey the following unilateral conditions (e.g., see [37, 48]):

$$\begin{aligned}&{{\,\mathrm{sym}\,}}\varvec{N}\preceq \varvec{0}, \\& {{\,\mathrm{sym}\,}}\left( \varvec{M}- \varvec{N}h/2 \right) \succeq \varvec{0}, \nonumber \\&{{\,\mathrm{sym}\,}}\left( \varvec{M}+ \varvec{N}h/2 \right) \preceq \varvec{0}, \end{aligned}$$

(8)

where ${{\,\mathrm{sym}\,}}$ denotes the symmetric part operator and the notation $\varvec{S}\succeq \varvec{0}$ [resp., $\varvec{S}\preceq \varvec{0}$] is adopted for the symmetric tensor $\varvec{S}$ to be positive [resp., negative] semidefinite. Such conditions imply the normal forces to be compressive and the center of pressure to lie inside the thickness of the dome, consistently with the assumed infinite compressive strength and vanishing tensile strength of the material. In passing, it is noticed that the first of those conditions is linearly dependent on the remaining two, whence it is dropped off.

Concerning the shear strength, a cohesive-frictional behavior is assumed. Denoting by $c$ and $\mu$ respectively a cohesion term and the friction coefficient, the following shear condition is enforced on the shell stress resultants (e.g., see [7, 18, 38, 59]):

$$\begin{aligned} \sqrt{\left( \varvec{N}\varvec{\nu }\cdot \varvec{\tau } \right) ^2 + \left( \varvec{Q}\cdot \varvec{\nu } \right) ^2} \le c- \mu \, \varvec{N}\varvec{\nu }\cdot \varvec{\nu }, \end{aligned}$$

(9)

to hold for any pair $\left( \varvec{\nu }, \varvec{\tau } \right)$ of orthonormal vectors tangent to the dome mid-surface. Accordingly, the resultant of in-plane and out-of-plane shear stress resultants is contained within the Coulomb friction cone. In passing, it is observed that the introduction of such cohesive-frictional model within the present lower-bound limit analysis approach carries an underlying assumption of associative friction flow law.

Conditions (8) and (9) describe the adopted masonry strength domain in the space of shell stress resultants. More general strength domains might be considered within the present approach, e.g. accounting for non-vanishing tensile strength due to friction and masonry texture (e.g., see [7, 14]). However, the reliability of such strength contributions might be questionable in presence of seismic loadings.

Finally, the static theorem of limit analysis (e.g., see [15, 31]), characterizes the collapse value of the load multiplier $\lambda$ of the basic live loads as the solution of the following optimization problem:

$$\begin{aligned}&\underset{\left\{ \lambda ,\, \varvec{N}, \, \varvec{Q}, \, \varvec{M} \right\} }{\text {max}} \lambda , \\&\quad \,\, \text {s.t.} \quad \text {conditions~}(6), (7), (8)_{\text {2,3}}, \text {and~}(9) \text { hold.} \end{aligned} $$

(10)

In the next section, a finite difference discretization method will be proposed for achieving an efficient computational solution strategy.

3 Finite difference discretization method

In this section, a finite difference method is proposed for a discretization and a computational solution strategy of the static limit analysis problem (10), which involves the shell stress resultants as unknown functions, in addition to the collapse multiplier of the basic live loads.

Fig. 2

Finite difference discretization method: main and auxiliary staggered rectangular grids in the parameter space $\left( \varphi , \vartheta \right)$. The nodes of the auxiliary grids (blue squares) are the centers of the finite difference cells of the main grid, i.e. of the cells having the nodes of the main grid (red bullets) as their vertices

To do so, two rectangular grids are introduced in the parameter space $\left( \varphi , \vartheta \right)$, with grid spacing $\varDelta \varphi$ and $\varDelta \vartheta$ along the two directions, respectively, as shown in Fig. 2. One grid, referred to as the main one, has nodes labeled by indices $\left( i, \, j \right)$, with $i$ and $j$ running along $\varphi$- and $\vartheta$-direction, respectively. The other grid, referred to as the auxiliary one, is staggered by half the grid spacing, in both directions, with respect to the main grid. Accordingly, its nodes, labeled by indices $\left( i+1/2, \, j+1/2 \right)$, are the centers of the finite difference cells of the main grid, i.e. of the rectangles having the nodes of the main grid as their vertices.

The shell stress resultants are located at the nodes of the main grid. For convenience, the relevant nodal values are collected in the following $10 \times 1$ vector:

$$\begin{aligned}&{\varvec{X}}^{\left( i, \, j \right) } = \left( {N_{\varphi }}^{\left( i, \, j \right) }; {N_{\vartheta \varphi }}^{\left( i, \, j \right) }; {N_{\varphi \vartheta }}^{\left( i, \, j \right) }; {N_{\vartheta }}^{\left( i, \, j \right) }; \,\, {Q_{\varphi }}^{\left( i, \, j \right) }; {Q_{\vartheta }}^{\left( i, \, j \right) }; \right. \nonumber \\&\left. \quad\quad\quad{M_{\varphi }}^{\left( i, \, j \right) }; {M_{\vartheta \varphi }}^{\left( i, \, j \right) }; {M_{\varphi \vartheta }}^{\left( i, \, j \right) }; {M_{\vartheta }}^{\left( i, \, j \right) } \right) . \end{aligned}$$

(11)

A finite difference approximation of the typical stress component T, and of its partial derivatives ${T\!}_{/\varphi }$ and ${T\!}_{/\vartheta }$, is also derived at the nodes of the auxiliary grid:

$$\begin{aligned} {T}^{\left( i+1/2, \, j+1/2 \right) }&= \frac{1}{4}\left[ {T}^{\left( i, \, j \right) } + {T}^{\left( i+1, \, j \right) } \right.\\& \qquad \quad\left. +\, {T}^{\left( i+1, \, j+1 \right) } + {T}^{\left( i, \, j+1 \right) } \right] , \\[1ex] {T}^{\left( i+1/2, \, j+1/2 \right) }_{/\varphi }&= \frac{1}{2\varDelta \varphi }\left[ -{T}^{\left( i, \, j \right) } + {T}^{\left( i+1, \, j \right) } \right. \\& \qquad \quad \left.+\, {T}^{\left( i+1, \, j+1 \right) } - {T}^{\left( i, \, j+1 \right) } \right] , \\[1ex] {T}^{\left( i+1/2, \, j+1/2 \right) }_{/\vartheta }&= \frac{1}{2\varDelta \vartheta }\left[ -{T}^{\left( i, \, j \right) } - {T}^{\left( i+1, \, j \right) } \right.\\& \qquad \quad \left. +\, {T}^{\left( i+1, \, j+1 \right) } + {T}^{\left( i, \, j+1 \right) } \right] . \end{aligned} $$

(12)

In light of such approximation, the differential equilibrium equations (6), the boundary conditions on the free edges, the symmetry requirement on the bending-moment tensor (7), the unilateral conditions (8)$_{\text {2,3}}$, and the frictional conditions (9), whose imposition is required by the static limit analysis problem (10), are addressed under a computational standpoint.

The differential equilibrium equations (6) are enforced in the finite difference sense at the nodes of the auxiliary grid. After simple algebra, they can be put in the form:

$$\begin{aligned}\varvec{0}&= \sum _{k,l = 0, 1}{\varvec{E}}^{\left( i+k, \, j+l \right) }{\varvec{X}}^{\left( i+k, \, j+l \right) }\nonumber \\&+\varvec{f}_{\text {d}}^{\left( i+k, \, j+l \right) } + \lambda \varvec{f}_{\text {l}}^{\left( i+k, \, j+l \right) }, \end{aligned}$$

(13)

where ${\varvec{E}}^{\left( i+k, \, j+l \right) }$ is a $6\times 10$ equilibrium matrix, and $\varvec{f}_{\bullet }^{\left( i+k, \, j+l \right) }$, with $\bullet = \left\{ \text {d},\, \text {l} \right\}$, are $6\times 1$ vectors of nodal forces, whose expressions are given in Appendix A. It is remarked that equations (13) enjoy the mechanical interpretation of equilibrium equations of the portion of the dome mid-surface which is the image, through the parameterization (1), of the typical finite difference cell.

Due to their algebraic nature, the boundary conditions on the free edges and the symmetry requirement on the bending-moment tensor (7) are straightforwardly enforced at the nodes of the main grid.

The admissibility requirements on the shell stress resultants are also enforced at the nodes of the main grid. In detail, the unilateral conditions (8)$_{\text {2,3}}$ are recast in the following second-order conic constraint:

$$\begin{aligned} \varvec{U}_{\pm } {\varvec{X}}^{\left( i, \, j \right) } \in {\mathcal {K}}_{\text {r}}, \end{aligned}$$

(14)

where ${\mathcal {K}}_{\text {r}} \subset \mathbb {R}^3$ is the rotated quadratic cone in $\mathbb {R}^3$ [42], and $\varvec{U}_{\pm }$ are two $3 \times 10$ admissibility matrices, whose expressions are given in Appendix A. On the other hand, by checking the frictional condition (9) for a discrete set of $S$ pairs $\left( \varvec{\nu }_{s}, \varvec{\tau }_{s} \right)$ of orthonormal vectors tangent to the dome mid-surface, a set of $S$ second-order conic constraints is obtained:

$$\begin{aligned} \varvec{F}_{s}{\varvec{X}}^{\left( i, \, j \right) } + \varvec{c}\in {\mathcal {K}}, \quad s= 1, \dots , S, \end{aligned}$$

(15)

in which ${\mathcal {K}}$ is the standard quadratic cone in $\mathbb {R}^3$ [42], $\varvec{F}_{s}$ are $3 \times 10$ friction admissibility matrices, and $\varvec{c}$ is a $3 \times 1$ cohesion vector. They are detailed in Appendix A.

Finally, the discretized version of the static limit analysis problem (10) is obtained through an assembling procedure which is similar to that customarily implemented in finite element computer programs. It reads:

$$\begin{aligned} &\underset{\lambda ,\, \varvec{X}}{\text {max}} \quad \lambda , \\&\text {s.t.} \quad \varvec{E}\varvec{X}+ \varvec{f}_{\text {d}}+ \lambda \varvec{f}_{\text {l}}= \varvec{0}, \quad \varvec{B}\varvec{X}= \varvec{0}, \\&\quad \quad \varvec{\Omega }\varvec{X}= \varvec{0}, \\&\quad \quad \varvec{{\mathcal {U}}}_{\pm }^{\left( i,j \right) } \varvec{X}\in {\mathcal {K}}_{\text {r}}, \quad \text { for all } \left( i,\, j \right) , \\&\quad \quad \varvec{{\mathcal {F}}}_{s}^{\left( i,j \right) } \varvec{X}+ \varvec{c}\in {\mathcal {K}}, \quad s= 1, \dots {}, S, \quad \text { for all } \left( i,\, j \right) , \end{aligned} $$

(16)

in which $\varvec{X}$ is a vector collecting all the nodal unknowns of the main grid; $\varvec{E}$ and $\varvec{f}_{\bullet }$ respectively are the structural equilibrium matrix and the vectors of nodal forces; $\varvec{B}$ and $\varvec{\Omega }$ are suitable matrices respectively enforcing the boundary conditions on the free edges and the symmetry requirement on the bending-moment tensor; $\varvec{{\mathcal {U}}}_{\pm }^{\left( i,j \right) }$ and $\varvec{{\mathcal {F}}}_{s}^{\left( i,j \right) }$ respectively are the structural unilateral and frictional admissibility operators relevant to node $\left( i,\,j \right)$ of the main grid. That in equation (16) is a convex optimization problem, known in mathematical programming as a second-order cone programming problem. For its solution standard and effective optimization softwares are available.

Remark 1

Problem (16) admits the following dual version, to be interpreted as the discrete upper-bound formulation of the limit analysis problem:

$$\begin{aligned} &\underset{\{\varvec{\eta },\, \varvec{\eta }_{\text {b}}, \,\varvec{\omega }, \, \varvec{z}^{\left( i,j \right) }_{\pm }, \, \varvec{w}^{\left( i,j \right) }_{s}\}}{\text {min}} &&-\varvec{\eta }^T\varvec{f}_{\text {d}}+ \sum _{i, j}\sum _{s} \left( \varvec{w}^{\left( i,j \right) }_{s} \right) ^T\!\varvec{c}, \\& \quad \quad \, \text {s.t.} && \varvec{E}^T\varvec{\eta }+ \varvec{B}^T\varvec{\eta }_{\text {b}} + \varvec{\Omega }^T\varvec{\omega }\\[1ex]& && + \sum _{i, j}\left( \varvec{{\mathcal {U}}}^{\left( i,j \right) }_{\pm } \right) ^{\!T}\!\varvec{z}^{\left( i,j \right) }_{\pm }\\& &&+ \sum _{i, j}\sum _{s}\left( \varvec{{\mathcal {F}}}^{\left( i,j \right) }_{s} \right) ^{\!T}\!\varvec{w}^{\left( i,j \right) }_{s}= \varvec{0}, \\& && 1-\varvec{\eta }^T\varvec{f}_{\text {l}}= 0, \\[1ex]& && \varvec{z}^{\left( i,j \right) }_{\pm } \in {\mathcal {K}}_{\text {r}}^{*}, \, \text { for all } \left( i,\, j \right) , \\[1ex]& && \varvec{w}^{\left( i,j \right) }_{s}\in {\mathcal {K}}^{*}, \, s= 1, \dots {}, S, \, \text { for all } \left( i,\, j \right) . \end{aligned}$$

(17)

Here $\varvec{\eta }$ is the vector of displacements/rotations dual to the element equilibrium equations (13), $\varvec{\eta }_{\text {b}}$ is the vector of displacements/rotations dual to the boundary conditions on the free edges, and $\varvec{\omega }$ is the vector of drilling distortions dual to the symmetry condition (7) on the bending-moment tensor. In addition, $\varvec{z}^{\left( i,j \right) }_{\pm }$ [resp., $\varvec{w}^{\left( i,j \right) }_{s}$] are the vectors collecting the flow multipliers dual to the nodal unilateral [resp., friction] admissibility conditions (14) [resp., (15)]. Those parameters describe a mechanism of the dome, possibly involving detachments or opening of hinges [resp., slidings] at the nodes of the main grid where the unilateral [resp., friction] admissibility conditions are activated. A compatibility equation and dual admissibility conditions on the flow multipliers ensure the mechanism to be kinematically admissible. In fact, ${\mathcal {K}}_{\text {r}}^{*}$ [resp., ${\mathcal {K}}^{*}$] is the dual cone of ${\mathcal {K}}_{\text {r}}$ [resp., ${\mathcal {K}}$]. Hence, problem (17) searches for the mechanism that minimizes the sum of the resisting work of dead loads, $-\varvec{\eta }^T\varvec{f}_{\text {d}}$, and of the cohesive dissipation, $\sum _{i, j}\sum _{s}\left( \varvec{w}^{\left( i,j \right) }_{s} \right) ^T\!\varvec{c}$, in the class of kinematically admissible mechanisms, which also obey the normalization condition $1-\varvec{\eta }^T\varvec{f}_{\text {l}}= 0$.

It is pointed out that, when solving problem (16) by a standard convex optimization tool, in addition to the static unknowns $\varvec{X}$, and at no further computational cost, the displacements/rotations $\varvec{\eta }$ and $\varvec{\eta }_{\text {b}}$, the drilling distortions $\varvec{\omega }$, and the unilateral and friction flow multipliers, $\varvec{z}^{\left( i,j \right) }_{\pm }$ and $\varvec{w}^{\left( i,j \right) }_{s}$ respectively, are supplied as well. Accordingly, the resulting collapse mechanism can be computed as a by-product of the static limit analysis, as shown in the numerical simulations. $\square$

4 Numerical results

This section is devoted to numerical simulations, which are aimed to assess the merit of the proposed finite difference method for the static limit analysis of masonry domes subjected to pseudo-static seismic loads. In detail, the seismic capacity of spherical and ogival domes with parameterized geometry (Fig. 3) is investigated in Sects. 4.1 and 4.2, respectively.

Fig. 3

Numerical simulations: a spherical, and b ogival domes. Three-dimensional view of the mid-surface (top row) and meridian section with highlighted geometric parameters (bottom row)

Attention is especially focused on the influence that the shear response of masonry material and the distribution of seismic loads along the height of the dome exert on the structural collapse capacity.

In the former respect, the sets of shear models investigated in the numerical simulations are listed in Table 1. Classical Heyman’s no-sliding assumption (H) is adopted as first model, consisting in not enforcing the shear admissibility conditions (9). A second model is represented by a cohesionless frictional behavior (F), which might be indicated for dry masonry. In such a case, the influence of the friction coefficient $\mu$, representing the only constitutive parameter, is evaluated by comparing numerical results for $\mu = \left\{ 0.7, 1, 1.5 \right\}$ (respectively labeled as (F1), (F2) and (F3)). It is remarked that a cohesionless frictional material (with finite friction coefficient) is unable to withstand uniaxial compression. In particular, such a model is unable to predict the well-known experimental evidence that domes under self-weight present meridional cracks developing from their base up to a certain meridian angle (e.g., see [15, 31]). Accordingly, though its experimental determination might generally be difficult and/or uncertain, one might infer that some cohesion term $c$ is available in a masonry that is not perfectly dry, at least under gravitational loads. For drawing the consequences of this observation, a cohesive-frictional behavior (CF) is considered as third shear model, which might be appropriate for a masonry with mortar. In particular, a friction coefficient $\mu = 0.7$ is considered. Moreover, aiming to conservative results, a special value of the cohesion term, denoted as $c_{\text {min}}$, is here adopted as constitutive parameter. That is computed as the minimum cohesion term that guarantees the uniaxial compression at the base of a cracked dome under its self-weight to be sustained. It is a simple matter to check that:

$$\begin{aligned} c_{\text {min}} = \frac{1-\sin {\phi }}{2\cos {\phi }} \, \left. \left( -N_{\varphi } - \frac{Q_{\varphi }^2}{N_{\varphi }} \right) \right| _{\text {base}}, \end{aligned}$$

(18)

where $\phi =\arctan \mu$ denotes the friction angle, and the stress resultants $N_{\varphi }$ and $Q_{\varphi }$ are computed at the base of the dome subject to its self-weight and in minimum thrust configuration. Despite $c_{\text {min}}$ depends on the geometry, the unit weight and the size of the dome, its value is in practice attained for a very small material cohesion, i.e. in the order of $0.05\,\text {MPa}$. Nevertheless, whether such a cohesion can be relied on under seismic loading conditions should be evaluated by the analyst on the basis of the particular masonry material under investigation.

Table 1 Sets of models and pertaining constitutive parameters adopted for enforcing the shear admissibility conditions (9)

Concerning the seismic loads distribution, following [27], horizontal accelerations that are uniformly or linearly distributed along the height of the dome are considered, in accordance to the Italian norms for constructions NTC 2018 [50]. To do so, the dome self-weight is first reduced to statically equivalent surface distributions of dead forces $\varvec{q}_{\text {d}}$ and couples $\varvec{m}_{\text {d}}$ applied to its mid-surface (for a detailed derivation of the relevant reduction formulas, see [45, 48]):

$$\begin{aligned} \varvec{q}_{\text {d}}&= - q\varvec{k},\quad q= \left( 1 + \frac{h^2}{12\rho } \,\, \frac{\sin \varphi }{r} \right) \gamma h, \\ \varvec{m}_{\text {d}}&= m\sin \varphi \, \varvec{e}_{\varphi },\quad m= \left( \frac{1}{\rho } + \frac{\sin \varphi }{r} \right) \frac{\gamma h^3}{12}, \end{aligned} $$

(19)

where $\gamma$ denotes the specific weight of masonry material. Then, on considering seismic accelerations along direction $\varvec{\imath }$, with distribution $\ell$ along the height of the dome, the basic live forces $\varvec{q}_{\text {l}}$ and couples $\varvec{m}_{\text {l}}$ applied to the dome mid-surface are derived:

$$\begin{aligned} \varvec{q}_{\text {l}}= \frac{W}{S} \, \ell q\varvec{\imath }, \quad \varvec{m}_{\text {l}}= \frac{W}{S} \, \ell m\,\, {}^{s}\varvec{\imath }. \end{aligned}$$

(20)

in which $W$, i.e. the weight of the dome, and $S$ are respectively computed as the integral of $q$ and of $\ell q$ over the dome mid-surface, whereas ${}\!^{s}\varvec{\imath }$ denotes the projection of the unit vector $\varvec{\imath }$ on the tangent plane to the dome mid-surface. Uniform or linear seismic acceleration distributions correspond to the choices $\ell = 1$ or $\ell = z$, respectively.

Taking advantage of the axially symmetric geometry of the dome, in all simulations it is assumed, without loss of generality, that the direction $\varvec{\imath }$ of the seismic loads coincides with the direction $\varvec{i}$. Accordingly, the problem under investigation results to be symmetric with respect to the xz-plane, whence only half of the dome is modeled, with suitable boundary conditions imposed on the symmetry edges.

All numerical analyses have been performed by means of an in-house MATLAB$^\circledR$ code, and the computations have been done on a single machine with dual Intel$^\circledR$ Xeon$^\circledR$ CPU Gold 6226R @ 2.89 GHz and 256 GB RAM. The optimization problem (16) has been solved by Mosek$^\circledR$ optimization software (version 9.2) [42].

4.1 Spherical domes

Spherical domes are considered, as shown in Fig. 3a. Their geometry is described by the mid-surface radius $R$, the normalized thickness $h/R$, and the embrace angle $\beta$.

Table 2 Spherical domes: convergence analysis of the collapse load multiplier $\lambda$ of a hemispherical dome with normalized thickness $h/R= 0.1$, with respect to the mesh size and to the number $S$ of nodal discrete friction admissibility conditions on the shear stress resultants. Shear models (H) or (F1), as defined in Table 1, and uniformly distributed pseudo-static seismic loads along the height of the dome, are considered. For a single normalized thickness, computation times range from $0.32 \,\text {s}$ to $120 \,\text {s}$ for the meshes ranging from $4 \times 8$ to $32 \times 64$

Initially, the convergence performances of the proposed finite difference discretization method are addressed with respect to (i) the mesh size and (ii) the number $S$ of discrete friction admissibility conditions enforced at the nodes of the main grid. To that aim, a hemispherical dome with normalized thickness $h/R= 0.1$ is considered subject to uniformly distributed pseudo-static seismic loads along the height of the dome. Concerning (i), a sequence of progressively finer finite difference meshes is analyzed. The typical one involves two staggered rectangular grids, subdividing $\varphi$- and $\vartheta$-domains respectively into m and 2m intervals, and is hence labeled as $m \times 2m$. Seven discretizations are investigated, corresponding to $m = \left\{ 4, 6, 8, 12, 16, 24, 32 \right\}$. Concerning (ii), the friction admissibility conditions (15) are checked at any node of the main grid for a set of $S= \left\{ 2, 4, 8, 16, 32, 64 \right\}$ pairs of orthonormal vectors tangent to the dome mid-surface.

In Table 2, the obtained collapse multiplier $\lambda$ are reported under the assumption of shear models (H) or (F1), as defined in Table 1. In the former case, friction admissibility conditions are not enforced and only convergence with respect to the finite difference mesh is of interest. It is reasonably achieved for the $24 \times 48$ discretization. Conversely, in the latter case, the double convergence has to be explored. For fixed mesh size, the collapse multiplier is practically converged with respect to the number of nodal friction admissibility conditions for $S=32$. It is observed that such a convergence is decreasing monotonic and uniform with respect to the mesh size. On the other hand, for prescribed number of nodal friction admissibility conditions, it is confirmed that the convergence with respect to the finite difference mesh is reached in engineering terms adopting the $24 \times 48$ discretization. Such a convergence is not increasing monotonic because, despite the classes of equilibrated and statically admissible stress states become larger and larger under mesh refinement, they do not in general constitute an increasing sequence. It is remarked that the present formulation also enjoys computational efficiency. In fact, computation times for a single normalized thickness analysis range from $0.32 \,\text {s}$ to $120 \,\text {s}$ for the discretizations ranging from $4 \times 8$ to $32 \times 64$. Numerical results relevant to the $24 \times 48$ finite difference mesh are henceforth discussed.

Fig. 4

Spherical domes: incipient collapse mechanism under uniformly or linearly distributed pseudo-static seismic loads along the height of the dome, considering shear models (H) or (F1) in Table 1. Hemispherical dome with normalized thickness $h/R=0.1$ is considered. A $24 \times 48$ finite difference mesh has been adopted in the computations

The case of a hemispherical dome with normalized thickness $h/R= 0.1$ is further investigated to explore how its collapse capacity depends on the adopted shear model and on the distribution of pseudo-static seismic loads along its height. It recalled that under Heyman’s no-sliding assumption, i.e. shear model (H) in Table 1, the normalized minimum thickness of a hemispherical dome is 0.04284 [46], whence the geometric safety factor [31] for $h/R= 0.1$ is 2.334. The corresponding collapse load multiplier is estimated to be $\lambda = 0.411$ [resp., $\lambda = 0.325$] for uniformly [resp., linearly] distributed pseudo-static seismic loads. The relevant incipient collapse mechanisms are shown in Fig. 4(top row). From a qualitative point of view, both mechanisms are produced by the formation, in the half of the dome in the positive direction of the seismic loads, of three curved flexural hinges along likewise parallel curves. Two of them, developing at the extrados of the dome, are located at its base and in the vicinity of its apex. The remaining one develops at the intrados of the dome in the haunch region. In addition, diffused detachments take place in the hoop direction for kinematic compatibility. Despite the qualitative similarities of the two mechanisms, the distribution of seismic loads affects the position of the two uppermost curved hinges, which shift upward when linearly distributed seismic loads are concerned. In fact, that is responsible for a slight reduction in the collapse multiplier, compared to the case of uniformly distributed seismic loads.

Fig. 5

Spherical domes: principal directions (with length proportional to relevant eigenvalue), and minimum and maximum eigenvalues of the symmetric part of the normal-force tensor $\varvec{N}$, under uniformly distributed pseudo-static seismic loads along the height of the dome (acting from left to right), considering (a) shear model (H) or (b) shear model (F1), Table 1. Hemispherical dome with normalized thickness $h/R=0.1$ is considered. A $24 \times 48$ finite difference mesh has been adopted in the computations

By contrast, if cohesionless frictional behavior is assumed, the collapse load multiplier of the dome significantly reduces. In fact, for shear model (F1) in Table 1, it is estimated to be $\lambda = 0.172$ [resp., $\lambda = 0.133$] on considering uniformly [resp., linearly] distributed pseudo-static seismic loads. Analogously, numerical predictions for shear model (F2) are $\lambda = 0.268$ [resp., $\lambda = 0.207$], whereas for shear model (F3) they result to be $\lambda = 0.342$ [resp., $\lambda = 0.266$], consistently with the increased value of the friction coefficient. The corresponding incipient collapse mechanisms are similar to each other. In Fig. 4(bottom row), the one pertaining to shear model (F1) is shown. Though the formation of three curved flexural hinges is still clearly recognizable, in-plane [resp., out-of-plane] sliding failures occur in the lateral [resp., back and front] portions of the dome. Also in this case, switching from a uniform to a linear distribution of pseudo-static seismic loads tends to raise the position of the two uppermost curved hinges, and induces a slight reduction in the collapse multiplier.

The previous evidences are complemented by the observation that, assuming the cohesive-frictional shear model (CF) in Table 1, the collapse load multiplier is predicted to be $\lambda = 0.407$ [resp., $\lambda = 0.322$] for uniformly [resp., linearly] distributed pseudo-static seismic loads. Remarkably, despite the value adopted for the cohesion term is very small (equation (18)), such results are practically coincident with those obtained under no-sliding assumption (H). That finding is justified because a cohesive-frictional material, contrarily to a cohesionless frictional one, is able to withstand uniaxial compression. As a proof of such a statement, the principal directions and the contour plots of the minimum and maximum eigenvalues of the symmetric part of the normal-force tensor $\varvec{N}$ are shown in Fig. 5. Specifically, in panels (a) and (b), shear models (H) and (F1) are respectively assumed. Concerning the former, it is observed that uniaxial compression is predominant, with the maximum eigenvalue that is vanishing in large regions of the dome. Instead, in the case of cohesionless frictional material, a small transverse compression is forced to arise in those same regions to withstand the main compression, accompanied by a reduction of the latter. As a result, a significant drop of the structural collapse capacity is observed. Though not reported here, collapse mechanisms and principal directions for shear model (CF) are qualitatively similar to those pertaining to shear model (H).

Fig. 6

Spherical domes: collapse load multiplier $\lambda$ versus normalized thickness $h/R$, for selected values of the embrace angle $\beta$. Shear models listed in Table 1, and seismic loads that are (a) uniformly or (b) linearly distributed along the height of the dome, are considered. A $24 \times 48$ finite difference mesh has been adopted in the computations. In (a), the star-shaped marker refers to the experimental results obtained for small-scale dry-masonry dome models with $\beta =90^\circ$ and $\mu =0.7$ in [60]

The influence on the collapse capacity of spherical domes exerted by shear response of masonry material and seismic loads distribution is systematically explored in a parametric analysis of the collapse multiplier with respect to the dome geometry. Results are shown in Fig. 6, with panels (a) and (b) respectively referring to uniformly and linearly distributed seismic loads along the height of the dome. Specifically, curves of the collapse multiplier $\lambda$ versus the normalized thickness $h/R$ are plotted, for embrace angles $\beta = \left\{ 70^{\circ }, 80^{\circ }, 90^{\circ } \right\}$ and assuming the shear models listed in Table 1. Results in panel (a) are in good agreement with benchmark ones, as presented in [48]. In particular, they prove the collapse capacity of spherical domes to increase with $h/R$ and to decrease with $\beta$. The same trends are confirmed in panel (b) for linearly distributed seismic loads, up to a slight reduction of the collapse multiplier. Irrespective of the seismic load distribution, the collapse multiplier $\lambda$ is revealed to be pronouncedly dependent on the shear response of masonry material. In detail, the adoption of Heyman’s no-sliding assumption, shear model (H), provides the most optimistic estimate of the structural capacity. Significantly reduced collapse multipliers are obtained if a cohesionless frictional behavior is assumed, shear models (F), in which case $\lambda$ increases with the friction coefficient $\mu$. However, it suffices to pass to a cohesive-frictional behavior with a minimal cohesion term, shear model (CF), to practically recover predictions pertaining to no-sliding assumption.

As an experimental validation, a star-shaped marker is reported in Fig. 6a, corresponding to the experimental results obtained in [60]. Therein, small-scale dome models, made of about a hundred dry blocks, were tested on a tilting table in order to reproduce a uniform distribution of pseudo-static seismic loads. The friction coefficient was experimentally measured as $\mu =0.7$. In particular, domes with $h/R=0.1$ and $\beta =90^\circ$ were tested, resulting in an experimentally estimated collapse multiplier of 0.18 [60]. From a modeling perspective, because of the dry joints between the blocks, a cohesionless frictional behavior seems appropriate to describe the shear response of the experimentally investigated masonry material. Accordingly, within the present notation, experimental tests match the shear model (F1) in Table 1. The numerically predicted collapse multiplier is then recalled to be $\lambda = 0.172$ (see also Figs. 4 and 5). Additional experimental results considering domes with $h/R=0.2$ and $\beta =90^\circ$ are available in [60]. Though the relevant normalized thickness falls outside the range investigated in the parametric analysis, the experimentally and numerically predicted collapse multipliers respectively are 0.46 and 0.40.

As a concluding remark, the present results highlight the computational merit of the proposed finite difference method in the static limit analysis of masonry domes. From an applicative viewpoint, the importance of accurately modeling the shear response of masonry material is pointed out. In particular, that requires to ponder whether cohesion, even small, can be relied on, and, if it is not the case, to confidently estimate the friction coefficient. When reasonable material shear resistance is exhibited, masonry domes are shown to be capable to withstand moderate seismic loads, also in relationship to the loads distribution.

4.2 Ogival domes

In this section, the collapse capacity of ogival domes under pseudo-static seismic loads is addressed. A typical ogival dome is depicted in Fig. 3b, where $R$ is the mid-surface radius, $h/R$ is the normalized thickness, $\delta$ is the ogival angle, $\beta$ is the embrace angle.

Fig. 7

Ogival domes: incipient collapse mechanism under uniformly or linearly distributed pseudo-static seismic loads along the height of the dome, considering shear models (H) or (F1) in Table 1. Ogival dome with embrace angle $\beta =90^\circ$, ogival angle $\delta =2\arctan (3/2)-\beta = 22.6^\circ$ (corresponding to rise-to-half-span ratio 3/2), and normalized thickness $h/R=0.07$ is considered. A $24 \times 48$ finite difference mesh has been adopted in the computations

Fig. 8

Ogival domes: collapse load multiplier $\lambda$ versus normalized thickness $h/R$, for selected values of the ogival and embrace angles, $\delta$ and $\beta$ respectively. Shear models listed in Table 1, and seismic loads that are a, c uniformly or b, d linearly distributed along the height of the dome, are considered. A $24 \times 48$ finite difference mesh has been adopted in the computations

To begin with, an ogival dome characterized by $h/R=0.07$, $\beta =90^\circ$ and $\delta =2\arctan (3/2)-\beta = 22.6^\circ$ (corresponding to rise-to-half-span ratio 3/2) is considered.

In view of the results, not presented here, of a convergence analysis similar to that carried out for spherical shells, it is checked that a $24 \times 48$ finite difference mesh with $S=32$ nodal friction admissibility conditions provides converged results, which are henceforth discussed.

Basing on the normalized minimum thickness estimation of 0.02228 [47] holding under Heyman’s no-sliding assumption, i.e. adopting shear model (H) in Table 1, the geometric safety factor of the dome [31] is 3.142. The corresponding collapse load multiplier for uniformly distributed seismic loads along the height of the dome results to be $\lambda = 0.394$, which reduces to $\lambda = 0.294$ for linearly distributed seismic loads. The incipient collapse mechanisms relevant to both seismic load distributions are shown in Fig. 7(top row). As for spherical domes, both mechanisms are qualitatively caused by the opening of three parallel hinges, two at the extrados and one at the intrados, in the half of the dome in the positive direction of the horizontal forces. However, due to the increased complexity in the dome geometry, those hinges are not as much clearly identified, and expected relative rotations concentrated in a single parallel curve appear to be diffused between several consecutive parallel curves. On the other hand, it is confirmed that the collapse capacity reduction observed for linearly, instead of uniformly, distributed seismic loads, reflects the higher position of the two uppermost parallel hinges.

Significantly smaller collapse load multipliers are predicted when considering cohesionless frictional behavior. For shear model (F1) in Table 1, the estimate 0.130 [resp., 0.097] for uniformly [resp., linearly] distributed seismic loads along the height of the dome is obtained, which becomes 0.233 [resp., 0.173] for shear model (F2), and 0.313 [resp., 0.232] for shear model (F3). As the corresponding incipient collapse mechanisms are qualitatively quite similar, only the one pertaining to shear model (F1) is examined, as shown in Fig. 7(bottom row). Analogously to the case of spherical domes, though the formation of parallel hinges is still observed, the notable drop in the collapse capacity of the dome is caused by in-plane [resp., out of plane] slidings in its lateral [resp., back and front] regions. Those effects are even more pronounced for ogival domes, because of their more slender shape.

However, as already highlighted for spherical domes, it suffices to introduce a small cohesion term in the material shear response, as comprised in shear model (CF) in Table 1, to recover the collapse capacity prediction obtained under no-sliding assumption. In fact, the collapse multiplier is estimated to be 0.391 [resp., 0.293], and the incipient collapse mechanism becomes practically indistinguishable from that in Fig. 7(top row). It is also confirmed that such an increase in the structural capacity is explained by the retrieved capability of masonry material to withstand uniaxial compression stress states, thus enabling the attainment of more effective equilibrated and admissible static regimes within the dome.

A parametric analysis on the collapse load multiplier is then performed for ogival domes with parameterized geometry. Results are shown in Fig. 8, where the collapse load multiplier $\lambda$ is plotted as a function of the normalized thickness $h/R$ for the values $\beta = \left\{ 70^\circ , 80^\circ , 90^\circ \right\}$ of the embrace angle $\beta$. In panels (a, b) and (c, d) the ogival angle is respectively set as $\delta = \left\{ 10^\circ , 30^\circ \right\}$, whereas in panels (a, c) and (b, d) uniform and linear seismic loads along the height of the dome are respectively considered. For comparison, results relevant to shear models listed in Table 1 are reported.

Concerning uniform seismic loads, panels (a, c), the collapse capacity of ogival domes increases with $h/R$ and decreases with $\beta$. Under no-sliding assumption or cohesive-frictional behavior, shear models (H) and (CF), very similar estimates of the collapse multiplier are obtained. Significantly smaller values follow from cohesionless frictional behavior, shear models (F), though remarkably increasing with the friction coefficient $\mu$. Similar trends are also partially found in the case of linear seismic loads, panels (b, d), though with a slightly reduced structural resistance. As a difference, it can be here recognized that, for sufficiently large normalized thicknesses $h/R$ compared to the minimum one, the beneficial effect of increasing the ogival angle $\delta$ progressively reduces, and even becomes detrimental (e.g., for $\beta =90^\circ$, the curves corresponding to $\delta =30^\circ$ lay below those corresponding to $\delta =10^\circ$ for $h/R$ approximately larger than 0.09).

In closing, the obtained results on the seismic capacity of masonry ogival domes are, to the best of the authors’ knowledge, novel to the literature. In addition to their intrinsic interest, which primarily recalls the role played by the shear response of masonry material and secondarily quantifies the influence of the seismic loads distribution, they confirm the capabilities of the proposed finite difference method for the static limit analysis of masonry domes.

4.3 Dome on mausoleum of Faraj Ibn Barquq

As an application to a real structure, the dome on mausoleum of sultan Faraj Ibn Barquq in Cairo, Egypt, is considered (Fig. 9a). Figure 9b reproduces the meridian section of the dome and of the supporting drum, as reported in [34]. An ogival dome idealization is therein proposed, assuming mid-surface radius $R=8.23 \,\text {m}$ ($27 \,\text {ft}$), normalized thickness $h/R=0.045$, ogival angle $\delta =10.4^\circ$, and embrace angle $\beta =83.1^\circ$ [34]. Such an idealization, highlighted in Fig. 9b, is here adopted in the analysis.

Fig. 9

Dome on mausoleum of Faraj Ibn Barquq: a picture of the dome and of the supporting drum, and b meridian section with highlighted ogival dome idealization [34]

Table 3 Dome on mausoleum of Faraj Ibn Barquq: collapse load multiplier $\lambda$ for uniformly or linearly distributed pseudo-static seismic loads along the height of the dome, considering shear models listed in Table 1. A $24 \times 48$ finite difference mesh has been adopted in the computations

A pseudo-static seismic assessment of the dome is carried out by the present finite difference static limit analysis method. A stability assessment of the dome subject to its self-weight, performed under Heyman’s no-sliding assumption by the method in [46, 47], predicts a normalized minimum thickness for the dome of 0.01355, corresponding to a geometric safety factor [31] of 3.321. In Table 3, the collapse multiplier $\lambda$ of uniformly or linearly distributed seismic loads along the height of the dome is reported for the shear models in Table 1. Those results are exemplary of the considerations developed in the previous section, descending from the parametric analysis of ogival domes. In particular, the dome exhibits a seismic resistance, which is markedly affected by the shear response of masonry material and slightly reduces passing from uniform to linear distribution of seismic loads.

5 Conclusions

A computational method has been presented for the seismic assessment of masonry domes, exploiting an application of the static theorem of limit analysis. The shell stress resultants defined on the dome mid-surface, namely normal-force tensor, bending-moment tensor and shear-force vector, have been introduced as representative of the stress state in the dome. Accordingly, the classical differential equilibrium equations of shells have been used for the equilibrium formulation. The admissible stress states in the dome have been characterized by adopting Heyman’s assumptions of infinite compressive and vanishing tensile strengths, and by considering a cohesive-frictional shear behavior. An original finite difference method has been proposed for numerically solving the limit analysis problem, taking advantage from the introduction of two staggered finite difference grids in the parameter space generating the dome mid-surface. The shell stress resultants have been located at the nodes of the main grid, where the admissibility conditions have been also naturally enforced. Conversely, the differential equilibrium equations have been imposed, in the finite difference sense, at the nodes of the auxiliary grid. A discrete limit analysis problem has been thus obtained, consisting in a second-order cone programming problem. From a computational standpoint, the proposed method enjoys simplicity of implementation, with equilibrium and admissibility operators provided in closed form, and effectiveness of solution, as ensured by standard optimization tools. From a modeling point of view, axially symmetric domes with arbitrary meridian section can be analyzed, under both gravitational forces and horizontal actions with user-defined distribution. Those merits have been especially demonstrated by numerical simulations. As an engineering conclusion, the collapse capacity of masonry domes under pseudo-static seismic forces has been highlighted, and the influence of dome geometry, shear response and horizontal forces distribution has been quantitatively evidenced.

Implementation details

Some implementation details are here discussed on the finite difference method proposed in Sect. 3. In particular, the derivation of the discrete equilibrium Eqs (13) and Heyman’s admissibility conditions (14) is addressed, as a preparatory step for arriving at the discrete static limit analysis problem (16).

Referring to Sect. 3 for the notation, it is recalled that the shell stress resultants are located at the nodes $\left( i, \, j \right)$ of the main grid, equation (11). Then, the discrete equilibrium equations descend from imposing the differential equilibrium equations (6) in the finite difference sense at the nodes $\left( i+1/2, \, j+1/2 \right)$ of the auxiliary grid. In fact, taking advantage of the finite difference approximation formulas (12), and provided the following positions are introduced, with $k,l=\left\{ 0,1 \right\}$:

$$\begin{aligned}&d_{\varphi }^{\left( i+k, j+l \right) } = \frac{\left( -1 \right) ^{k+1}}{2\varDelta \varphi } \, {r}^{\left( i+k, \, j+l \right) }, \\&d_{\vartheta }^{\left( i+k, j+l \right) } = \frac{\left( -1 \right) ^{l+1}}{2\varDelta \vartheta } \, {\rho }^{\left( i+k, \, j+l \right) }, \\&a^{\left( i+k, j+l \right) } = \frac{1}{4} \, {\left( r\rho \right) }^{\left( i+k, \, j+l \right) }, \\&b^{\left( i+k, j+l \right) } = \frac{1}{4} \, {r}^{\left( i+k, \, j+l \right) }, \\&c^{\left( i+k, j+l \right) } = \frac{1}{4} \, {\left( \rho \cos \varphi \right) }^{\left( i+k, \, j+l \right) }, \\&s^{\left( i+k, j+l \right) } = \frac{1}{4} \, {\left( \rho \sin \varphi \right) }^{\left( i+k, \, j+l \right) }, \end{aligned} $$

(A.1)

it is a simple matter to check that the equilibrium matrices ${\varvec{E}}^{\left( i+k, \, j+l \right) }$ and the vector of nodal forces $\varvec{f}_{\bullet }^{\left( i+k,\, j+l \right) }$, with $\bullet = \left\{ \text {d},\, \text {l} \right\}$, in equation (13) result to be:

$$\begin{aligned} &{\varvec{E}}^{\left( i+k, \, j+l \right) } = \left[ \begin{array}{llllllllll} d_{\varphi }&{} \cdot &{} d_{\vartheta }&{} - c&{}b&{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ \cdot &{} d_{\varphi }&{} c&{} d_{\vartheta }&{} \cdot &{} s&{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ - b&{} \cdot &{} \cdot &{} -s&{} d_{\varphi }&{} d_{\vartheta }&{} \cdot &{} \cdot &{} \cdot &{} \cdot \\ \cdot &{} \cdot &{} \cdot &{} \cdot &{} a&{} \cdot &{} d_{\varphi }&{} \cdot &{} d_{\vartheta }&{} -c\\ \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} -a&{} \cdot &{} d_{\varphi }&{} c&{} d_{\vartheta }\\ \cdot &{} a&{} -a&{} \cdot &{} \cdot &{} \cdot &{} \cdot &{}b&{} -s&{} \cdot \end{array} \right] ,\\&\varvec{f}_{\bullet }^{\left( i+k,\, j+l \right) } = a\left( \begin{array}{l} \varvec{q}_{\bullet } \\ \varvec{m}_{\bullet } \end{array} \right) . \end{aligned}$$

(A.2)

Here, for improving readability, superscripts $\left( i+k, j+l \right)$ have been omitted in the right hand-side of the equations.

On the other hand, the discrete unilateral admissibility conditions are obtained by checking the counterpart semidefinite matrix constraints (8)$_{\text {2,3}}$ at the nodes $\left( i,\, j \right)$ of the main grid. In particular, those semidefinite matrix constraints can be expressed as the second-order cone constraints (14), provided ${\mathcal {K}}_{\text {r}}$ is the rotated quadratic cone in $\mathbb {R}^3$ [42]:

$$\begin{aligned} {\mathcal {K}}_{\text {r}} = \left\{ \left( \xi _1; \xi _2, \xi _3 \right) \in \mathbb {R}^3 \, :\, 2 \xi _1 \xi _2 \ge \xi _3^2, \,\, \xi _1 \ge 0, \,\, \xi _2 \ge 0 \right\} , \end{aligned}$$

(A.3)

and the admissibility matrices $\varvec{U}_{\pm }$ are given by:

$$\begin{aligned} \varvec{U}_{\pm } = \left[ \begin{matrix} -\frac{h}{2} &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \pm 1 &{} \cdot &{} \cdot &{} \cdot \\ \cdot &{} \cdot &{} \cdot &{} -\frac{h}{2} &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \pm 1 \\ \cdot &{} -\frac{\sqrt{2}}{4}h &{} -\frac{\sqrt{2}}{4}h &{} \cdot &{} \cdot &{} \cdot &{} \cdot &{} \pm \frac{\sqrt{2}}{2} &{} \pm \frac{\sqrt{2}}{2} &{} \cdot \end{matrix} \right] . \end{aligned}$$

(A.4)

Analogously, the discrete frictional admissibility conditions follow from enforcing requirement (9) at the nodes $\left( i,\, j \right)$ of the main grid. At each node, the fulfillment of that condition is checked for a set of $S$ pairs $\left( \varvec{\nu }_{s}, \varvec{\tau }_{s} \right)$ of orthonormal vectors tangent to the dome mid-surface, selected as:

$$\begin{aligned}&\varvec{\nu }_{s}= \cos \alpha _{s}\, \varvec{e}_{\varphi }+ \sin \alpha _{s}\, \varvec{e}_{\vartheta }, \nonumber \\&\varvec{\tau }_{s}= -\sin \alpha _{s}\, \varvec{e}_{\varphi }+ \cos \alpha _{s}\, \varvec{e}_{\vartheta }, \end{aligned}$$

(A.5)

where $\left\{ \alpha _{1}, \dots {}, \alpha _{S} \right\}$ are uniformly-spaced angles within the interval $\left[ 0, \pi \right]$. Each of the resulting conditions can be then recast as in equation (15), provided ${\mathcal {K}}$ is the standard quadratic cone in $\mathbb {R}^3$ [42]:

$$\begin{aligned} {\mathcal {K}}= \left\{ \left( \xi _1; \xi _2, \xi _3 \right) \in \mathbb {R}^3 \, :\,\xi _1 \ge \sqrt{\xi _2^2 + \xi _3^2}\, \right\} , \end{aligned}$$

(A.6)

the following definition holds for the $3 \times 10$ friction admissibility matrices $\varvec{F}_{s}$:

$$\begin{aligned} \varvec{F}_{s}= \left[ \begin{matrix} -\mu \cos ^2\!\alpha _{s}&{} -\mu \sin \alpha _{s}\cos \alpha _{s}&{} -\mu \sin \alpha _{s}\cos \alpha _{s}&{} -\mu \sin ^2\!\alpha _{s}&{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ -\sin \alpha _{s}\cos \alpha _{s}&{} \cos ^2\!\alpha _{s}&{} -\sin ^2\!\alpha _{s}&{} \sin \alpha _{s}\cos \alpha _{s}&{} 0 &{} 0 &{} 0 &{} 0 &{}0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \cos \alpha _{s}&{} \sin \alpha _{s}&{} 0 &{} 0 &{} 0 &{} 0 \end{matrix} \right] , \end{aligned}$$

(A.7)

and the $3 \times 1$ cohesion vector is taken as $\varvec{c}= \left( c; \,0; \,0 \right)$. In particular, it is noticed that $\varvec{F}_{s}$ is independent of the node of the main grid.