Skip to main content
SpringerLink
Log in

Wave-based approach for dynamical analysis of a coupled rectangular cavity: fundamental properties of eigenpairs

  • Published:
Meccanica Aims and scope Submit manuscript

Abstract

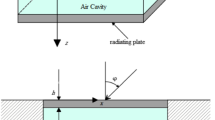
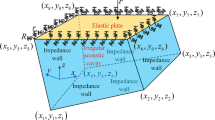
This study is concerned with an eigenvalue problem of a vibro-acoustic coupled system. In the conventional modal coupling method, the particle velocity normal to the surface of a panel is always calculated as zero, and the wave motion in the cavity cannot be directly treated. To overcome the problem, this study presents a novel formulation for a coupled system that expresses the correct boundary condition at the coupling plane and the wave motion in the cavity. First, a transfer matrix is introduced which can describe the characteristics of the sound field based on the wave dynamics. It is then clarified that if the panel vibration is regarded as the input to the cavity, the boundary condition of the sound field at the coupling plane should be a rigid wall. This is followed by the formulation of the eigenvalue problem of a vibro-acoustic coupled system. Finally, some numerical simulations are conducted, thereby clarifying the principles of the shift of natural frequencies and mode shapes, the accuracy of boundary condition at a coupling plane, and the orthogonality of coupled modes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

Code availability

Not applicable.

References

  1. Dowell ED, Voss HM (1963) The effect of a cavity on panel vibration. AIAA J 1:476–477. https://doi.org/10.2514/3.1568

    Article  Google Scholar 

  2. Pretlove AJ (1965) Free vibrations of a rectangular panel backed by a closed rectangular cavity by a closed rectangular cavity. J Sound Vib 2:197–209. https://doi.org/10.1016/0022-460X(65)90108-2

    Article  Google Scholar 

  3. Pretlove AJ (1966) Forced vibrations of a rectangular panel backed by a closed rectangular cavity. J Sound Vib 3:252–261. https://doi.org/10.1016/0022-460X(66)90094-0

    Article  Google Scholar 

  4. Dowell EH, Gorman GF III, Smith DA (1977) Acoustoelasticity: general theory, acoustic natural modes and forced response to sinusoidal excitation, including comparisons with experiment. J Sound Vib 52:519–542. https://doi.org/10.1016/0022-460X(77)90368-6

    Article  MATH  Google Scholar 

  5. Hong KL, Kim J (1995) Analysis of free vibration of structural-acoustic coupled systems, Part I: development and verification of the procedure. J Sound Vib 188:561–575. https://doi.org/10.1006/jsvi.1995.0611

    Article  Google Scholar 

  6. Hong KL, Kim J (1995) Analysis of free vibration of structural-acoustic coupled systems, Part II: Two- and three-dimensional examples. J Sound Vib 188:577–600. https://doi.org/10.1006/jsvi.1995.0612

    Article  Google Scholar 

  7. Pan J, Bies DA (1990) The effect of fluid-structural coupling on sound waves in an enclosure—theoretical part. J Acoust Soc Am 87:691–707. https://doi.org/10.1121/1.398939

    Article  Google Scholar 

  8. Pan J, Bies DA (1990) The effect of fluid-structural coupling on sound waves in an enclosure—experimental part. J Acoust Soc Am 87:708–717. https://doi.org/10.1121/1.398940

    Article  Google Scholar 

  9. Kim SM, Brennan MJ (1999) A compact matrix formulation using the impedance and mobility approach for the analysis of structural-acoustic systems. J Sound Vib 223:97–113. https://doi.org/10.1006/jsvi.1998.2096

    Article  Google Scholar 

  10. Jain NL, Sonti VR (2017) Structural acoustics of a rectangular panel backed by a cavity: an analytical matrix approach. ASME J Vib Acoust 139:031004. https://doi.org/10.1115/1.4035378

    Article  Google Scholar 

  11. Craggs A (1971) The transient response of a coupled plate-Acoustic system using plate and acoustic finite elements. J Sound Vib 15:509–528. https://doi.org/10.1016/0022-460X(71)90408-1

    Article  Google Scholar 

  12. MacNeal RH, Citerley R, Chargin R (1980) A symmetric modal formulation of fluid-structure interaction. ASME Paper 180-C2/PVP-117.

  13. Sandberg G (1995) A new strategy for solving fluid-structure problems. Int J Numer Methods Eng 38:357–370. https://doi.org/10.1002/nme.1620380302

    Article  MathSciNet  MATH  Google Scholar 

  14. Everstine GC (1981) A symmetric potential formulation for fluid-structure interaction. J Sound Vib 79:157–160. https://doi.org/10.1016/0022-460X(81)90335-7

    Article  Google Scholar 

  15. Olson LG, Bathe KJ (1985) Analysis of fluid-structure interactions. A direct symmetric coupled formulation based on the fluid velocity potential. Comput Struct 21:21–32. https://doi.org/10.1016/0045-7949(85)90226-3

    Article  MATH  Google Scholar 

  16. Sandberg G, Goransson P (1988) A symmetric finite element formulation for acoustic fluid-structure interaction analysis. J Sound Vib 123:507–515. https://doi.org/10.1016/S0022-460X(88)80166-4

    Article  Google Scholar 

  17. Olson LG, Bathe KJ (1983) A study of displacement-based fluid finite elements for calculating frequencies of fluid and fluid-structure systems. Nucl Eng Des 76:137–151. https://doi.org/10.1016/0029-5493(83)90130-9

    Article  Google Scholar 

  18. Bermudezs A, Hervella-Nieto L (1999) Finite element computation of three-dimensional elastoacoustic vibrations. J Sound Vib 219:279–306. https://doi.org/10.1006/jsvi.1998.1873

    Article  MATH  Google Scholar 

  19. Ishikawa S, Matsuo A, Akayama Y, Kijimoto S (2017) Coupled analysis of two dimensional acoustic and membrane vibration by concentrated mass model. Adv Mech Eng 9:1–13

    Article  Google Scholar 

  20. Pan J, Hansen CH, Bies DA (1990) Active control of noise transmission through a panel into a cavity: I. Analytical study J Acoust Soc Am 87:2098–2108. https://doi.org/10.1121/1.399555

    Article  Google Scholar 

  21. Kim SM, Brennan MJ (2000) Active control of harmonic sound transmission into an acoustic enclosure using both structural and acoustic actuators. J Acoust Soc Am 107:2523–2534. https://doi.org/10.1121/1.428640

    Article  Google Scholar 

  22. Tanaka N, Kobayashi K (2006) Cluster control of acoustic potential energy in a structural/acoustic cavity. J Acoust Soc Am 119:2758–2771. https://doi.org/10.1121/1.2188815

    Article  Google Scholar 

  23. Kaizuka T, Nakano K (2018) Active control of sound transmission into an enclosure using structural modal filters. J Sound Vib 431:328–345. https://doi.org/10.1016/j.jsv.2018.06.012

    Article  Google Scholar 

  24. Tanaka N, Takara Y, Iwamoto H (2012) Eigenpairs of a coupled rectangular cavity and its fundamental properties. J Acoust Soc Am 131:1910–1921. https://doi.org/10.1121/1.3682046

    Article  Google Scholar 

  25. Sadri M, Younesian D (2016) Vibroacoustic analysis of a sandwich panel coupled with an enclosure cavity. Compos Struct 146:159–175. https://doi.org/10.1016/j.compstruct.2016.03.024

    Article  Google Scholar 

  26. Iwamoto H, Tanaka N, Sanada A (2011) Noise reduction in a rectangular enclosure using active wave control. J Environ Eng 6:107–117. https://doi.org/10.1299/jee.6.107

    Article  Google Scholar 

  27. Iwamoto H, Tanaka N, Sanada A (2018) Wave-filter-based approach for generation of a quiet space in a rectangular cavity. Mech Syst Signal Pr 100:570–587. https://doi.org/10.1016/j.ymssp.2017.07.050

    Article  Google Scholar 

  28. Iwamoto H, Tanaka N (2014) Transfer-matrix-based approach for an eigenvalue problem of a coupled rectangular cavity. Proceedings of the 43rd International Congress on Noise Control Engineering (inter.noise 2014), Melbourne, Australia, 2014–11–16/19

  29. Kondo K (1993) Vibration Theory (in Japanese). Baifukan, Tokyo

    Google Scholar 

  30. Zhu F (1994) Rayleigh quotients for coupled free vibrations. J Sound Vib 171:641–649. https://doi.org/10.1006/jsvi.1994.1146

    Article  MATH  Google Scholar 

Download references

Acknowledgement

The authors gratefully acknowledge the financial support from the Japan Society for the Promotion of Science (Project No. 23760208 and 25420192) and grant-in-aid for scientific research of Seikei University for this study.

Funding

This study was financially supported by the following organizations. Japan Society for the Promotion of Science (Project No. 23760208 and 25420192). Seikei University for this study (grant-in-aid for scientific research).

Author information

Authors and Affiliations

  1. Department of Systems Design, Seikei University, 3-3-1 Kichijoji-kitamachi, Musashino-shi, Tokyo, 180-8633, Japan

    Hiroyuki Iwamoto & Shotaro Hisano

  2. Department of Aerospace Engineering, Tokyo Metropolitan University, 6-6 Asahigaoka, Hino-shi, Tokyo, 191-0065, Japan

    Nobuo Tanaka

Authors
  1. Hiroyuki Iwamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shotaro Hisano
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Nobuo Tanaka
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hiroyuki Iwamoto.

Ethics declarations

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Availability of data and material

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Iwamoto, H., Hisano, S. & Tanaka, N. Wave-based approach for dynamical analysis of a coupled rectangular cavity: fundamental properties of eigenpairs. Meccanica 56, 1655–1674 (2021). https://doi.org/10.1007/s11012-021-01331-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-021-01331-5

Keywords

Search

Navigation