1 Introduction

The realistic description of the wheel-rail interaction is crucial in railway systems because the contact forces deeply influence the vehicle dynamics, the wear of the contact surfaces and the vehicle safety.

Since the numerical performances (computation times and memory consumption) are very important in the multibody applications, the contact phenomena cannot be usually modelled, in practise, by considering the wheel and the rail as generic elastic continuous bodies. To overcome these limitations, the multibody contact models are generally characterised by three main logical parts: the contact point detection, the normal problem solution and the tangential problem solution, that comprises the adhesion model.

The detection of the contact point permits to calculate the contact point position on the wheel and rail surfaces. The main approaches employ either constraint equations [42, 43] or exact analytical methods aimed at the reduction of the algebraic problem dimension [9, 10, 15, 22, 23, 34]. Generally, the normal problem solution is based on the Lagrange multipliers [42, 43] and on improvements of Hertz theory [6, 11, 29]. Finally, concerning the solution of the tangential problem, different strategies have been considered in the last decades [14, 45]. The most significant approaches include the linear Kalker theory (saturated through the Johnson-Vermeulen formula) [19, 21, 28–30], the non-linear Kalker theory implemented in the FASTSIM algorithm [25–27, 29, 30, 32, 53, 54] and the Polach theory [38–41] that allows the description of the adhesion coefficient decrease with increasing creepage (excluding the spin creepage) and to well fit the experimental data. All the three steps of the contact model have to assure a good accuracy and, at the same time, a high numerical efficiency. High numerical performances are fundamental to implement the contact model directly online inside more general multibody vehicle models (developed in dedicated environments like Matlab-Simulink and Simpack), without employing discretized look-up table (LUT) [1, 2].

The main strategies employed to solve the tangential problem (comprising the adhesion model) usually do not take into account the important topic of the degraded adhesion between wheel and rail, that still remains an open problem. The substantial lack of literature characterising these issues is mainly caused by the difficulty to get a realistic adhesion law because of the presence of external unknown contaminants (the third body) and the complex and non-linear behaviour of the adhesion coefficient. The problem becomes even more complicated when degraded adhesion yields a high energy dissipation and, consequently, an adhesion recovery.

Many important analyses have been carried out over the years to investigate the role of so-called third body between the contact surfaces. More particularly the analyses have been performed both on laboratory test rigs and through on-track railway tests by considering natural and artificial external contaminants and friction modifiers [7, 8, 16, 18, 20, 24, 36, 50].

Contemporaneously, to better study the degraded adhesion non-linear behaviour, also the high energy dissipation at the contact interface and the consequent adhesion recovery have begun to be more accurately investigated [4, 5, 12, 13, 17, 33, 35, 49, 51, 52].

In this work the authors describe an innovative adhesion model aimed at increasing the accuracy in reproducing degraded adhesion conditions in multibody vehicle dynamics and railway systems. The new model, according to the recent trends of the state of the art (see the previous bibliographic references), focuses on the main phenomena behind the degraded adhesion, with particular attention to the energy dissipation at the contact interface, the consequent cleaning effect and the resulting adhesion recovery due to the removal of external unknown contaminants. Moreover, the followed approach minimises the number of hardly measurable physical quantities required by the model; this is a very important feature because most of the physical characteristics of the contaminants are totally unknown in practise.

The new model will have to assure a good accuracy to well reproduce the non-linear phenomena characterising the degraded adhesion; at the same time, it will have to guarantee high computational performances so that the whole contact model (including the adhesion model) could be implemented directly online within more general multibody models of railway vehicles.

The new adhesion model has been validated through experimental data provided by Trenitalia S. p. A. and coming from on-track tests carried out in Velim (Czech Republic) on a straight railway track characterised by degraded adhesion conditions. The tests have been performed with the railway vehicle UIC-Z1 equipped with a fully-working Wheel Slide Protection (WSP) system.

The structure of the paper is the following: the general architecture of the model will be illustrated in Sect. 2 while in Sect. 3 the multibody model, comprising the railway vehicle model and the wheel-rail contact model, will be described in detail. In Sect. 4 the experimental data will be introduced and in Sects. 5, 6 and 7 the validation of the new model will be discussed. Finally conclusions and further developments will be proposed in Sect. 8.

2 General architecture of the model

The architecture of the multibody model is briefly reported in Fig. 1.

Fig. 1
figure 1

Architecture of the multibody model

Full size image

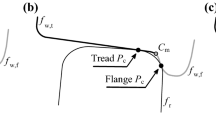
From a logical point of view, the multibody model consists of two different parts that mutually interact, directly online, during the dynamical simulation (at each integration time step): the three-dimensional (3D) model of the railway vehicle (the geometrical and physical characteristics of which are known) and the 3D wheel-rail contact model. At each time step the multibody vehicle model calculates the kinematic variables of each wheel (position \(\underline{G} _{w}\), orientation \(\underline{\varPhi}_{w}\), velocity \(\underline{v} _{w}\) and angular velocity \(\underline{\omega}_{w}\)) while the contact model, starting from the knowledge of these quantities, of the track geometry and of the wheel and rail profiles, evaluates the normal and tangential contact forces \(\underline{N} _{c}\), \(\underline{T} _{c}\) (applied to the wheel in the contact point \(\underline{P} _{c}\)) and the adhesion coefficient f, needed to carry on the dynamical simulation. Both the vehicle model and the contact model have been implemented in the Matlab-Simulink environment.

The wheel-rail contact model comprises three different steps (see Fig. 2). The detection of the contact points \(\underline{P} _{c}\) is based on some innovative procedures recently developed by the authors in previous works [10, 22, 34]. The normal contact problem is then solved through the global Hertz theory [6, 11, 29] to evaluate the normal contact forces \(\underline{N} _{c}\). Finally the solution of the tangential contact problem is performed by means of the global Kalker-Polach theory [38–41] to compute the tangential contact forces \(\underline{T} _{c}\) and the adhesion coefficient f.

Fig. 2
figure 2

Architecture of the wheel-rail contact model

Full size image

The strategy to solve the tangential contact problem includes the innovative degraded adhesion model developed by the authors in this work (see Fig. 3). The main inputs of the degraded adhesion model are the wheel velocity \(\underline{v}_{w}\), the wheel angular velocity \(\underline{\omega}_{w}\), the normal force at the contact interface \(\underline{N}_{c}\) and the position of the contact points \(\underline{P}_{c}\). The model also requires the knowledge of some wheel-rail and contact parameters that will be introduced along the paper. The outputs of the degraded adhesion model are the desired values of the adhesion coefficient f and of the tangential contact force \(\underline{T}_{c}\).

Fig. 3
figure 3

Inputs and outputs of the degraded adhesion model

Full size image

3 The multibody model

In this chapter the multibody model is described in detail. Firstly the 3D railway vehicle model will be analysed; secondly the attention will focus on the 3D wheel-rail contact model (comprising the contact point detection, the normal problem and the tangential problem) and, in particular, on the new degraded adhesion model.

3.1 The vehicle model

The considered railway vehicle is the UIC-Z1 wagon (illustrated in Figs. 4 and 5); its geometrical and physical characteristics are provided by Trenitalia S. p. A. [46]. The considered vehicle is equipped with a Wheel Slide Protection (WSP) system [5, 46, 48].

Fig. 4
figure 4

The UIC-Z1 wagon

Full size image
Fig. 5
figure 5

Multibody vehicle model

Full size image

The wagon is composed of one carbody, two bogie frames, eight axlebox links, eight axleboxes and four wheelsets. The primary suspension, including springs and vertical dampers, connects the bogie frame to the four axleboxes while the secondary suspension, including springs, longitudinal, lateral and vertical dampers, lateral bump-stops, anti-roll bar and traction rod (the last three elements are not visible in the schematics reported in the paper), connects the carbody to the bogie frames (see Fig. 6). In Table 1 the main properties of the railway vehicle are given.

Fig. 6
figure 6

Vehicle bogie

Full size image
Table 1 Main characteristics of the railway vehicle
Full size table

The multibody vehicle model takes into account all the degrees of freedom (DOFs) of the system bodies (one carbody, two bogie frames, eight axlebox links eight axleboxes, and four wheelsets). Considering the kinematic constraints that link to each other bogie frames, axlebox links, axleboxes and wheelsets (all cylindrical 1DOF joints) and without including the wheel-rail contacts, the whole system has 40 DOFs. The main inertial properties of the bodies are summarised in Table 2 [46].

Table 2 Inertial properties of the rigid bodies
Full size table

Both the primary suspension (springs and vertical dampers) and the secondary suspension (springs, longitudinal, lateral and vertical dampers, lateral bump-stops, anti-roll bar and traction rod) have been modelled through 3D visco-elastic force elements able to describe all the main non-linearities of the system (see Figs. 6, 7 and 8).

Fig. 7
figure 7

Primary suspensions

Full size image
Fig. 8
figure 8

Secondary suspensions

Full size image

In Table 3 the characteristics of the main linear elastic force elements (springs, anti-roll bar) of both the suspension stages are reported [46]. The non-linear elastic force elements (dampers, lateral bump-stops, traction rod) have been modelled through non-linear functions that correlate the displacements and the relative velocities of the force elements connection points to the elastic and damping forces exchanged by the bodies. By way of example the non-linear characteristic of a vertical damper of the primary suspension is illustrated in Fig. 9.

Fig. 9
figure 9

Example of non-linear characteristic: vertical damper of the primary suspension

Full size image
Table 3 Main linear elastic characteristics of the two stage suspensions
Full size table

The characteristics of the non-linear force elements (dampers, lateral bump-stops, traction rod) have been directly provided by Trenitalia S. p. A. More specifically, these mechanical nonlinear force elements are developed to satisfy the technical specifications required by the considered vehicle project and then experimentally tested to properly verify the desired performance [46]. Finally, also the Wheel Slide Protection (WSP) system of the railway wagon UIC-Z1 has been modelled to better investigate the vehicle behaviour during the braking phase under degraded adhesion conditions [5, 48]. The whole vehicle model has been implemented in the Matlab-Simulink environment [1].

3.2 The wheel-rail contact model

In this section the three logical parts of the wheel-rail contact model (contact point detection, normal problem and tangential problem) will be analysed with particular regard to the new degraded adhesion model. The model inputs are the kinematic variables of each wheel (position \(\underline{G} _{w}\), orientation \(\underline{\varPhi}_{w}\), velocity \(\underline{v} _{w}\) and angular velocity \(\underline{\omega}_{w}\)) together with the track geometry and the wheel and rail profiles while the outputs the normal and tangential contact forces \(\underline{N} _{c}\), \(\underline{T} _{c}\) (applied to the wheel in the contact point \(\underline{P} _{c}\)) and the adhesion coefficient f.

3.2.1 The contact point detection

Referring to Fig. 2 the contact point detection algorithm allows the calculation of the contact points \(\underline{P} _{c}\) starting from the wheel position \(\underline{G} _{w}\) and orientation \(\underline{\varPhi}_{w}\), the track geometry and the wheel and rail profiles. The detection procedure has been developed by the authors in previous works [10, 22, 34] and is based on the reduction of the algebraic problem dimension through exact analytical techniques; this reduction represents the main feature of the new algorithm. The main characteristics of the innovative procedure can be summarised as follows:

  • it is a fully 3D algorithm that takes into account all the six relative DOFs between wheel and rail;

  • it is able to support generic railway tracks and generic wheel and rail profiles;

  • it assures a general and accurate treatment of the multiple contact without introducing simplifying assumptions on the problem geometry and kinematics and limits on the number of contact points detected;

  • it assures high numerical efficiency making possible the online implementation within the commercial multibody software (like Simpack Rail and Adams Rail) without discrete LUT [1, 2].

The contact point position can be evaluated imposing the following parallelism conditions [15]:

$$ \begin{aligned} &\underline{n}_r^r\bigl( \underline{P}_r^r\bigr) \times\underline {n}_w^r\bigl(\underline{P}_w^r \bigr) = \underline{n}_r^r\bigl(\underline{P}_r^r \bigr) \times{R_w^r}\underline{n}_w^w \bigl(\underline{P}_w^w\bigr) = \underline{0} \\ &\underline{n}_r^r\bigl(\underline{P}_r^r \bigr) \times{\underline{d}^r} = \underline{0} \end{aligned} $$
(1)

where

$$ \begin{aligned} &\underline{P}_w^w({x_w},{y_w}) = \bigl( { \begin{array}{ccc} {{x_w}} & {{y_w}} & { - \sqrt{w{{({y_w})}^2} - x_w^2} } \end{array} } \bigr)^T \\ &\underline{P}_r^r({x_r},{y_r}) = \bigl( { \begin{array}{ccc} {{x_r}} & {{y_r}} & {{r({y_r})}} \end{array} } \bigr)^T \end{aligned} $$
(2)

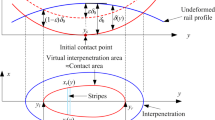
are the positions of the generic points on the wheel surface and on the rail surface (expressed in the reference systems G w x w y w z w and O r x r y r z r ), w(y w ) and r(y r ) are the wheel and rail profiles (supposed to be known), \(\underline{n}_{w}^{w}\) and \(\underline {n}_{r}^{r}\) are the outgoing normal unit vectors to the wheel and rail surfaces (in the reference systems G w x w y w z w and O r x r y r z r ), \(R_{w}^{r}\) is the rotation matrix that links the reference system G w x w y w z w to the reference system O r x r y r z r and \(\underline{d}^{r}\) is the distance vector between two generic points on the wheel surface and on the rail surface (both referred to the reference system O r x r y r z r ): \({\underline {d}^{r}}({x_{w}},{y_{w}},{x_{r}},{y_{r}}) = \underline{P}_{w}^{r}({x_{w}},{y_{w}}) - \underline{P}_{r}^{r}({x_{r}},{y_{r}})\) in which \(\underline{P}_{w}^{r}= \underline {O}_{w}^{r} + {R_{w}^{r}}\underline{P}_{w}^{w}({x_{w}},{y_{w}})\) is the position of the generic point of the wheel surface expressed in the reference system O r x r y r z r (see Fig. 10).

Fig. 10
figure 10

Wheel-rail contact point detection

Full size image

The first condition of the system (1) imposes the parallelism between the normal unit vectors, while the second one requires the parallelism between the normal unit vector to the rail surface and the distance vector. The system (1) consists of six non-linear equations in the unknowns (x w ,y w ,x r ,y r ) (only four equations are independent and therefore the problem is 4D). However it is possible to exactly express three of the four variables (in this case (x w ,x r ,y r )) as a function of y w , reducing the original 4D problem to a single 1D scalar equation in the variable y w [10, 22, 34]:

$$ F(y_w)=0. $$
(3)

At this point the simple scalar Eq. (3) can be easily solved through appropriate numerical algorithms. Finally, once obtained the generic solution y wc of Eq. (3), the complete solution (x wc , y wc , x rc , y rc ) of the system (1) and consequently the contact points \(\underline{P}_{wc}^{r}=\underline {P}_{w}^{r}(x_{wc},y_{wc})\) and \(\underline{P}_{rc}^{r}=\underline {P}_{r}^{r}(x_{rc},y_{rc})\) can be found by substitution.

3.2.2 The normal contact problem

Starting from the kinematic variables of the wheel and the contact point position \(\underline{P} _{c}\), the normal forces \(\underline{N} _{c}\) are calculated through the global Hertz theory for each contact point (see the Figs. 2, 10, 11 and 12) [6, 10, 11, 29]:

$$ {\underline{N} _c = N_c \underline{n}_w }, \qquad {N_c = \Vert{\underline{N} _c } \Vert} . $$
(4)

The main physical hypotheses behind the Hertz global theory are the following [6, 10, 11, 29]:

  • linear elasticity;

  • contact patch dimensions small if compared to the curvature radii of the contact bodies surfaces;

  • not-conformal contact;

  • elliptic contact area.

The scalar value N c of \(\underline{N} _{c}\) can be evaluated as follows:

$$\begin{aligned} {N_c} =& \biggl[ { - {k_h} {{\vert {{p}_n} \vert}^\gamma} + {k_v}\vert {{v_n}} \vert\frac{{\operatorname{sign} ( {{v_n}} ) - 1}}{2}} \biggr] \\ &{}\times\frac{{\operatorname{sign} ( {{p}_n} ) - 1}}{2} \end{aligned}$$
(5)

where \(p_{n}=\max( \underline{d}^{r} \cdot\underline{n} _{w} ^{r} ,0) \) is the normal penetration, γ is the Hertz’s exponent equal to 3/2, k v is the contact damping constant, \(v_{n}=\underline{V}_{c} \cdot \underline{n}_{r}^{r}\) is the normal penetration velocity (\(\underline{V} = \underline{v} _{w} + \underline{\omega}_{w} \times(\underline{P} _{c} - \underline{G} _{w} )\) is the velocity of the contact point rigidly connected to the wheel). The quantity k h is the Hertzian constant, function both of the material properties (the Young modulus E, the shear modulus G and the Poisson coefficient σ) and of the contact bodies geometry through the curvatures of the contact surfaces (easily computable if the contact point position \(\underline{P} _{c}\) is known).

Fig. 11
figure 11

Contact forces

Full size image
Fig. 12
figure 12

Contact surfaces

Full size image

Finally it is worth noting that the Hertz theory allows also the calculation of the semi-axes a and b of the elliptical contact patch, depending on the material properties, the curvatures of the contact surfaces and the normal contact force N c (or, equivalently, the normal penetration p n ) [6, 10, 11, 29].

3.2.3 The tangential contact problem and the degraded adhesion model

In this section the tangential contact forces \(\underline{T} _{c}\) and the adhesion coefficient f will be calculated solving the tangential contact problem [38–41]. Particularly the attention will focus on the new adhesion model especially developed for degraded adhesion conditions. The inputs of the model are kinematic variables of the wheel (position \(\underline{G} _{w}\), orientation \(\underline{\varPhi}_{w}\), velocity \(\underline{v} _{w}\) and angular velocity \(\underline{\omega}_{w}\)), the contact point position \(\underline{P} _{c}\) and the normal contact forces \(\underline{N} _{c}\) (see the Figs. 2, 3, 10, 11 and 12).

In this case the main hypotheses behind the Kalker-Polach global theory, on which the new adhesion model is based, can be summarised as follows [38–41]:

  • linear proportionality between tangential displacements and tangential stresses;

  • subdivision of the contact patch into adhesion area and slip area;

  • constant friction coefficient inside the contact patch.

The global Hertz and Kalker-Polach theories are usually employed in the railway field because they permit to study most of the interesting physical cases and represent a very good compromise between accuracy and numerical efficiency in this research area.

With regard to Figs. 11 and 12, for each contact point \(\underline{P} _{c}\), it is possible to determine the sliding \(\underline{s} \) (with its longitudinal and lateral components s x , s y ):

$$ \begin{aligned} &\underline{s} = \underline{v} _w + \underline{\omega}_w \times (\underline{P} _c - \underline{G} _w ) \\ &s = \Vert{\underline{s} } \Vert , \qquad s_x = \underline{s} \cdot\underline{t} _{1w} , \qquad s_y = \underline{s} \cdot\underline{t} _{2w} \end{aligned} $$
(6)

where \(\underline{n}_{w}\), \(\underline{t} _{1w}\) and \(\underline{t} _{1w}\) are respectively the normal unit vector and the tangential unit vectors (in longitudinal and lateral direction) corresponding to the generic contact point \(\underline{P} _{c}\) (see Fig. 12). Subsequently the creepage \(\underline{e}\) can be introduced

$$ \begin{aligned} &\underline{e} = \frac{{\underline{s} }}{{v_w }}, \qquad v_w = \Vert {\underline{v} _w } \Vert \\ &e_x = \underline{e} \cdot\underline{t} _{1w} , \qquad e_y = \underline{e} \cdot\underline{t} _{2w} \end{aligned} $$
(7)

together with the adhesion coefficient f and the specific dissipated energy W sp at the contact area:

$$ \begin{aligned} &e = \Vert{\underline{e} } \Vert, \qquad T_c = \Vert{\underline{T} _c } \Vert \\ &T_x = \underline{T} _c \cdot\underline{t} _{1w} = T_c \frac{{e_x }}{e}, \qquad T_y = \underline{T} _c \cdot\underline{t} _{2w} = T_c \frac{{e_y }}{e} \\ &f = \frac{{T_c }}{{N_c }}, \qquad W_{sp} = \underline{T} _c \cdot \underline{e} = T_c e = fN_c e \end{aligned} $$
(8)

in this way the specific dissipated energy W sp can also be interpreted as the energy dissipated at the contact for unit of distance travelled by the railway vehicle (see Eqs. (7) and (8)).

The main phenomena characterising the degraded adhesion are the large sliding occurring at the contact interface and, consequently, the high energy dissipation. Such a dissipation causes a cleaning effect on the contact surfaces and finally an adhesion recovery due to the removal of external contaminants. When the specific dissipated energy W sp is low the cleaning effect is almost absent, the contaminant level h does not change and the adhesion coefficient f is equal to its original value in degraded adhesion conditions f d . As the energy W sp increases, the cleaning effect increases too, the contaminant level h becomes thinner and the adhesion coefficient f raises. In the end, for large values of W sp , all the contaminant is removed (h is null) and the adhesion coefficient f reaches its maximum value f r ; the adhesion recovery due to the removal of external contaminants is now completed. At the same time if the energy dissipation begins to decrease, due for example to a lower sliding, the reverse process occurs (see Figs. 13 and 14).

Fig. 13
figure 13

Standard behaviour of the adhesion coefficient f

Full size image
Fig. 14
figure 14

The adhesion coefficient f and the specific dissipated energy W sp under degraded adhesion conditions

Full size image

Since the contaminant level h and its characteristics are usually totally unknown, it is useful trying to experimentally correlate the adhesion coefficient f directly with the specific dissipated energy W sp (see Eq. (8)). To reproduce the qualitative trend previously described and to allow the adhesion coefficient to vary between the extreme values f d and f r , the following expression for f is proposed:

$$ f = \bigl[1 - \lambda(W_{sp} ) \bigr]f_d + \lambda (W_{sp} )f_r $$
(9)

where λ(W sp ) is an unknown transition function between degraded adhesion and adhesion recovery. The function λ(W sp ) has to be positive and monotonous increasing; moreover the following boundary conditions are supposed to be verified: λ(0)=0 and λ(+∞)=1.

This way the authors suppose that the transition between degraded adhesion and adhesion recovery only depends on W sp . This hypothesis is obviously only an approximation but, as it will be clearer in the next chapters, it well describes the adhesion behaviour. Initially, to catch the physical essence of the problem without introducing a large number of unmanageable and unmeasurable parameters, the authors have chosen the following simple expression for λ(W sp ):

$$ \lambda(W_{sp} ) = 1 - e^{ - \tau W_{sp} } $$
(10)

where τ is now the only unknown parameter to be tuned on the base of the experimental data.

At this step of the research activity, the analytical transition function λ(W sp ) has been thought to describe in the best possible way the asymptotic transition from degraded adhesion (low dissipated energy) to full adhesion recovery (high dissipated energy). In particular, the choice of function and boundary conditions has been inspired by the asymptotic behaviour of the experimental transition function \(\lambda^{sp} (W_{sp}^{sp} )\) (clearly visible in the Figs. 18, 19, 20 of Sect. 5.1 and Figs. 24, 25, 26 of Sect. 5.2).

Concerning the choice of the specific transition function, there are different possible functions (obviously satisfying the previous boundary conditions) to correctly approximate the experimental data. In this circumstance, an exponential function seems to reproduce in a very natural way the qualitative behaviour of the experimental transition function \(\lambda^{sp} (W_{sp}^{sp} )\). Moreover the chosen function is very simple: it is characterised by only one unknown parameter and, consequently, it is very easy to be tuned. This is a fundamental feature because a larger number of unknown parameters would make the model more difficult to be tuned and validated and more depending on the specific considered scenario.

In this research activity the two main adhesion coefficients f d and f r (degraded adhesion and adhesion recovery) have been calculated according to Polach [29, 38, 39]:

$$ \begin{aligned} &{f_d = \frac{{2\mu_d }}{\pi} \biggl[ { \frac{{k_{ad} \varepsilon_d }}{{1 + (k_{ad} \varepsilon_d )^2 }} + \operatorname{arctg}(k_{sd} \varepsilon_d )} \biggr]} \\ &{f_r = \frac{{2\mu_r }}{\pi} \biggl[ {\frac{{k_{ar} \varepsilon_r }}{{1 + (k_{ar} \varepsilon_r )^2 }} + \operatorname{arctg}(k_{sr} \varepsilon_r )} \biggr]} \end{aligned} $$
(11)

where

$$ {\varepsilon_d = \frac{2}{3} \frac{{C\pi a^2 b }}{{\mu_d N_c }}e}, \qquad {\varepsilon_r = \frac{2}{3} \frac{{C\pi a^2 b }}{{\mu _r N_c }}e} . $$
(12)

The quantities k ad , k sd and k ar , k sr are the Polach reduction factors (for degraded adhesion and adhesion recovery respectively) and μ d , μ r are the friction coefficient defined as follows

$$ \begin{aligned} &{\mu_d = \biggl( {\frac{{\mu_{cd} }}{{A_d }} - \mu_{cd} } \biggr)e^{ - \gamma_d s} + \mu_{cd} } \\ &{\mu_r = \biggl( {\frac{{\mu_{cr} }}{{A_r }} - \mu_{cr} } \biggr)e^{ - \gamma_r s} + \mu_{cr} } \end{aligned} $$
(13)

in which μ cd , μ cr are the kinetic friction coefficients, A d , A r are the ratios between the kinetic friction coefficients and the static ones and γ d , γ d are the friction decrease rates. The Polach approach (see Eq. (11)) has been followed since it permits to describe the decrease of the adhesion coefficient with increasing creepage and to better fit the experimental data (see Figs. 13 and 14).

Finally it has to be noticed that the semi-axes a and b of the contact patch (see Eq. (12)) depend only on the material properties, the contact point position P c on wheel and rail (through the curvatures of the contact surfaces in the contact point) and the normal force N c , while the contact shear stiffness C (N/m3) is a function only of material properties, the contact patch semi-axes a and b and the creepages. More particularly, the following relation holds [29]:

$$ C = \frac{{3G}}{{8a}}\sqrt{ \biggl( {c_{11} \frac{{e_x }}{e}} \biggr)^2 + \biggl( {c_{22} \frac{{e_y }}{e}} \biggr)^2 } $$
(14)

where c 11=c 11(σ,a/b) and c 22=c 22(σ,a/b) are the Kalker coefficients.

In the end, the desired values of the adhesion coefficient f and of the tangential contact force T c =fN c can be evaluated by solving the algebraic Eq. (9) in which the explicit expression of W sp has been inserted (see Eq. (8)):

$$ f = \Im(f ,t ) $$
(15)

where ℑ indicates the generic functional dependence. Due to the simplicity of the transition function λ(W sp ), the solution can be easily obtained through standard non-linear solvers [31]. From a computational point of view, the adhesion coefficient f i can be computed at each integration time t i as follows

$$ f_i = \Im(f_i ,t_i ). $$
(16)

Eventually, the vector tangential contact force \(\underline{T} _{c}\) has to be calculated. To this aim the creepage \(\underline{e}\) can be employed:

$$ \begin{aligned} &{T_x = T_c \frac{{e_x }}{e}}, \qquad {T_y = T_c \frac{{e_y }}{e}} \\ &{\underline{T} _c = T_x \underline{t} _{w1} + T_y \underline{t} _{w2} }. \end{aligned} $$
(17)

In this phase of the research activity concerning the degraded adhesion, the contact spin at the wheel-rail interface has not been considered. The components of the spin moment \(\underline{M} _{sp}=M _{sp} \underline{n}_{w}\) produced by the spin creepage \(e_{sp} = \underline{\omega}_{w} \cdot\underline{n}_{w} / v_{w}\) and by the lateral creepage e y can be neglected because they are quite small. On the other hand the effect of the spin creepage e sp on the lateral contact force T y may be not negligible. This limitation can be partially overcome thanks to the Polach theory [38, 39] that takes into account, in an approximated way, the effect of the spin creepage on the lateral contact force T sp :

$$ \begin{aligned} &{T_x = T_c^{\prime} \frac{{e_x }}{{e_m }}} \\ &{T_y = T_c^{\prime} \frac{{e_y }}{{e_m }} + T_{sp} \frac{{e_{sp} }}{{e_m }}} \end{aligned} $$
(18)

where e m is the modulus of the modified translational creepage \(\underline{e}_{m}\), T sp is the lateral contact force caused by the spin creepage e sp and \(T_{c}^{\prime}\) is the modulus of the old tangential contact force calculated before. The quantities T sp and \(\underline{e}_{m}\) are evaluated in [38] starting from the geometrical and physical characteristics of the system; however T sp , differently from \(T_{c}^{\prime}\), does not consider the decrease of the adhesion coefficient with increasing creepage and the adhesion recovery under degraded adhesion conditions introduced by the authors.

More in general, the role of the contact spin under degraded adhesion conditions, especially in presence of adhesion recovery, is still an open problem.

4 The experimental data

The degraded adhesion model has been validated by means of experimental data [47], provided by Trenitalia S. p. A., coming from on-track tests performed in Velim (Czech Republic) with the coach UIC-Z1 (see Figs. 4 and 5). The considered vehicle is equipped with a fully-working Wheel Slide Protection (WSP) system [46, 48].

The experimental tests have been carried out on a straight railway track. The wheel profile is the ORE S1002 (with a wheelset width d w equal to 1.5 m and a wheel radius r equal to 0.445 m) while the rail profile is the UIC60 (with a gauge d r equal to 1.435 m and a laying angle equal to 1/20 rad). In Table 4 the main wheel, rail and contact parameters are reported [3, 38, 39].

Table 4 Main wheel, rail and contact parameters
Full size table

The value of the kinetic friction coefficient under degraded adhesion conditions μ cd depends on the test performed on the track; the degraded adhesion conditions are usually reproduced using a watery solution containing surface-active agents, e.g. a solution sprinkled by a specially provided nozzle directly on the wheel-rail interface on the first wheelset in the running direction. The surface-active agent concentration in the solution varies according to the type of test and the desired friction level. The value of the kinetic friction coefficient under full adhesion recovery μ cs corresponds to the classical kinetic friction coefficient under dry conditions.

During the experimental campaign six different braking tests have been performed. The six tests have been split into two groups (A and B): the first group has been used to tune the degraded adhesion model (in particular the unknown parameter τ, see Sect. 3.2.3, Eq. (10)) while the second one to properly validate the tuned model. The initial vehicle velocities corresponding to the considered tests are reported in Table 5.

Table 5 Test initial velocities
Full size table

For each test the following physical quantities have been experimentally measured (with a sample time Δt s equal to 0.01 s):

  • the longitudinal vehicle velocity \(v_{v}^{sp}\). For the sake of simplicity all the longitudinal wheel velocities \(v_{wj}^{sp}\) (j represents the j-th wheel) are considered equal to \(v_{v}^{sp}\). The acceleration of the vehicle \(a_{v}^{sp}\) and of the wheels \(a_{wj}^{sp}\) can be obtained by derivation and by properly filtering the numerical noise.

  • the rotation velocities of all the wheels \(\omega_{wj}^{sp}\).

  • the vertical loads \(N_{wj}^{sp}\) on the wheels. The vertical contact forces \(N_{cj}^{sp}\) can be approximately evaluated starting from \(N_{wj}^{sp}\) by taking into account the weight of the wheels. Also in this case the angular accelerations \(\dot{\omega}_{wj}^{sp}\) can be calculated by derivation and by properly filtering.

  • the traction or braking torques \(C_{wj}^{sp}\) applied to the wheels.

By way of example in Fig. 15 the wheel translational and rotational velocities \(v_{w1}^{sp}\) and \(r \omega _{w1}^{sp}\) are reported for the I test of the group A; both the WSP intervention and the adhesion recovery in the second part of the braking manoeuvre are clearly visible.

Fig. 15
figure 15

Wheel translational and rotational velocities \(v_{w1}^{sp}\) and \(r \omega_{w1}^{sp}\) for the I test of the group A

Full size image

On the base of the measured data, the experimental outputs of the degraded adhesion model, e.g. the adhesion coefficient \(f^{sp}_{j}\), the tangential contact force \(T^{sp}_{cj}\) and the transition function \(\lambda^{sp}_{j}\) have now to be computed for all the tests. These experimental quantities are fundamental for the validation both of the degraded adhesion model (Sect. 5) and of the whole multibody model (Sect. 6). To reach this goal and to effectively exploit the measured data, in this phase the wheelset is supposed to be placed in its centred position; in this way the position of the single contact point P c can be supposed to be known and nearly constant and the surface curvatures in the contact points, the semi-axes of the contact patch a, b and the contact shear stiffness C can be easily calculated [29]. Moreover the following simplified expressions for the sliding \(s^{sp}_{j}\), for the creepage \(e^{sp}_{j}\) and for C hold:

$$ \begin{aligned} &{s_j^{sp} = v_{wj}^{sp} - r \omega_{wj}^{sp} }, \qquad {e_j^{sp} = \frac{{s_j^{sp} }}{{v_{wj}^{sp} }}} \\ &{C = \frac{{3Gc_{11} }}{{8a}}} . \end{aligned} $$
(19)

Starting from \(s^{sp}_{j}\) and \(e^{sp}_{j}\), \(T^{sp}_{cj}\) can be estimated through the rotational equilibrium of the wheel with respect to the origin G w :

$$ J_w \dot{\omega}_{wj}^{sp} = C_{wj}^{sp} - r T_{cj}^{sp} $$
(20)

in which J w =160 kg m2 is the wheel inertia. Subsequently Eq. (8) permits to calculate \(f^{sp}_{j}\) and the specific dissipation energy \(W^{sp}_{spj}\) while \(f^{sp}_{dj}\), \(f^{sp}_{rj}\) can be computed directly through Eq. (11). Finally, from the knowledge of \(W^{sp}_{spj}\) and \(f^{sp}_{j}\), \(f^{sp}_{dj}\), \(f^{sp}_{rj}\), the trend of the experimental transition function \(\lambda^{sp}_{j} (W^{sp}_{spj})\) can be determined by means of Eq. (9). For instance in Fig. 16 the adhesion coefficient \(f^{sp}_{1}\) and its limit values \(f^{sp}_{d1}\), \(f^{sp}_{r1}\) under degraded adhesion and adhesion recovery are illustrated always for the I test of the group A (the adhesion recovery in the second part of the braking manoeuvre is clear). Figure 17 shows the experimental trend of the transition function \(\lambda^{sp}_{1}\).

Fig. 16
figure 16

Adhesion coefficient \(f^{sp}_{1}\) and its limit values \(f^{sp}_{d1}\), \(f^{sp}_{r1}\) for the I test of the group A

Full size image
Fig. 17
figure 17

Experimental transition function \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the I test of the group A

Full size image

5 Tuning and validation of the degraded adhesion model

In this chapter the tuning and the validation of the degraded adhesion model will be described. Both the tuning and the validation will be performed without considering the complete vehicle dynamics that, on the contrary, will be taken into account in the Sect. 6.

5.1 Model tuning

During this phase of the research activity, the degraded adhesion model has been tuned on the base of the three experimental braking tests of the group A. In particular the attention focused on the transition function λ(W sp ) and on the τ parameter. Starting from the experimental transition functions \(\lambda^{sp}_{j} (W^{sp}_{spj})\) corresponding to the three tests of the group A, the parameter τ within λ(W sp ) has been tuned through a Non-linear Least Square Optimisation (NLSO) by minimising the following error function [1, 31, 37]:

$$ \begin{aligned}[b] g(\tau) = \sum_{k = 1}^3 {\sum_{i = 1}^{N_t } {\sum _{j = 1}^{N_w } { \bigl[ {\lambda_{jk}^{sp} \bigl(W_{jk}^{sp} (t_i ) \bigr) - \lambda \bigl(W_{jk}^{sp} (t_i ) \bigr)} \bigr]^2 } } } \end{aligned} $$
(21)

where N w is the wheel number and N t is the measured sample number; this time the index k indicates the k-th test of the group A. In this case the optimisation process provided the optimum value τ=1.9×10−4 m/J. For instance the comparisons between the optimised analytical transition function λ(W sp ) and the experimental transition function \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) are shown for the three tests of the group A in Figs. 18, 19 and 20.

Fig. 18
figure 18

Comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the I test of the group A

Full size image
Fig. 19
figure 19

Comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the II test of the group A

Full size image
Fig. 20
figure 20

Comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the III test of the group A

Full size image

Subsequently, always for the tests of the group A, the adhesion coefficient f j has been calculated according to Sect. 3.2.3 by means of Eq. (16) starting from the knowledge of the experimental inputs \(v_{wj}^{sp}\), \(\omega_{wj}^{sp}\) and \(N_{cj}^{sp}\); as in Sect. 4, the simplified relations of Eq. (19) have been employed. In this circumstance the optimised analytical transition function λ(W sp ) has been used. The behaviour of the calculated adhesion coefficient f j has been compared with the experimental one \(f^{sp}_{j}\) (see Sect. 4). By way of example, in Figs. 21, 22, 23 the time histories of f 1 and \(f^{sp}_{1}\) are reported for all the tests of the group A.

Fig. 21
figure 21

Comparison between f 1 and \(f^{sp}_{1}\) for the I test of the group A

Full size image
Fig. 22
figure 22

Comparison between f 1 and \(f^{sp}_{1}\) for the II test of the group A

Full size image
Fig. 23
figure 23

Comparison between f 1 and \(f^{sp}_{1}\) for the III test of the group A

Full size image

The results of the tuning process highlight the good capability of the simple analytical transition function, λ(W sp ) in reproducing the experimental trend of \(\lambda^{sp}_{j} (W^{sp}_{spj})\) for all the tests of the group A. The good behaviour of the analytical transition function despite its simplicity (only one unknown parameter is involved), allows also a good matching of the experimental data in terms of the adhesion coefficient (see the trend of f j and \(f^{sp}_{j}\) and the adhesion recovery in the second part of the braking manoeuvre).

5.2 Model validation

The real validation of the degraded adhesion model has been carried out by means of the three experimental braking tests of the group B. Also in this case the attention focused, first of all, on the analytical transition function λ(W sp ) (the same tuned in Sect. 5.1 with τ=1.9×10−4 m/J) and on its capability in matching the behaviour of the experimental transition functions \(\lambda^{sp}_{j} (W^{sp}_{spj})\). The comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) is illustrated in Figs. 24, 25, 26 for the tests of the group B.

Fig. 24
figure 24

Comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the I test of the group B

Full size image
Fig. 25
figure 25

Comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the II test of the group B

Full size image
Fig. 26
figure 26

Comparison between λ(W sp ) and \(\lambda^{sp}_{1} (W^{sp}_{sp1})\) for the III test of the group B

Full size image

Similarly to Sect. 5.1 the adhesion coefficient f j has been calculated for the tests of the group B (see Sect. 3.2.3 and Eq. (16)) starting from the knowledge of the experimental inputs \(v_{wj}^{sp}\), \(\omega_{wj}^{sp}\) and \(N_{cj}^{sp}\) (the simplified relations of Eq. (19) in Sect. 4 have been used). Obviously, the same analytical transition function λ(W sp ) optimised in Sect. 5.1 has been employed. The behaviour of the calculated adhesion coefficient f j and the experimental one \(f^{sp}_{j}\) (see Sect. 4) have been compared again. For instance in Figs. 27, 28, 29 the time histories of f 1 and \(f^{sp}_{1}\) are reported for all the tests of the group B.

Fig. 27
figure 27

Comparison between f 1 and \(f^{sp}_{1}\) for the I test of the group B

Full size image
Fig. 28
figure 28

Comparison between f 1 and \(f^{sp}_{1}\) for the II test of the group B

Full size image
Fig. 29
figure 29

Comparison between f 1 and \(f^{sp}_{1}\) for the III test of the group B

Full size image

The results of the model validation are encouraging and highlight the good matching between the analytical transition function λ(W sp ) (tuned in Sect. 5.1 on the base of the tests of the group A) and the new experimental data \(\lambda^{sp}_{j} (W^{sp}_{spj})\) corresponding to the tests of the group B. At the same time, also for the group B, there is a good correspondence between the time histories of the calculated adhesion coefficient f j and those of the experimental one \(f^{sp}_{j}\) (see the adhesion recovery in the second part of the braking manoeuvre). The satisfying results obtained for the validation group B confirm the capability of the simple analytical transition function λ(W sp ) in approximating the complex and highly non-linear behaviour of the degraded adhesion.

Moreover the new degraded adhesion model present two important advantages. Firstly, it only introduces one additional parameter (e.g. the τ rate), very easy to be experimentally tuned, without requiring the knowledge of further unknown physical properties of the contaminant. Secondly, the model guarantees a very low computational load, making possible the online implementation of the procedure within more general multibody models built in dedicated environments [1, 2].

On the other hand, at this phase of the research activity, the adhesion model is characterised by two main limitations:

  • the limitedness of the experimental campaign (needed for the model tuning and validation), especially in terms of analysed scenarios (in this case braking on straight track under degraded adhesion conditions). Anyway the two different sets of experimental tests employed in this work for the model tuning and validation are completely independent. This confirms the accuracy of the model in reproducing the complex system behaviour despite the criticality of the considered scenario and the nonlinearity and the chaoticity of the phenomenon;

  • the considered transition function λ(W sp ) (that is the relation between the adhesion coefficient f and the specific dissipated energy W sp ) is based on the fitting of experimental data and not on more elementary physical phenomena.

The next steps of the research will be fundamental to overcome the previous limitations and to better investigate the degraded adhesion from a physical viewpoint (see Sect. 8).

6 The validation of the whole multibody model

In this chapter the behaviour of the complete multibody model described in Sect. 3 will be analysed. The vehicle dynamic analysis is focused on the translation and rotational wheel velocities v wj , rω wj corresponding to the tests of the tuning group A and the validation group B; more precisely, in this case v wj is the longitudinal component of \(\underline{v}_{wj}\), ω wj is the component of \(\underline{\omega}_{wj}\) along the wheel rotation axis and, for the sake of simplicity, r is always the nominal wheel radius. These variables have been chosen because they are the most important physical quantities in a braking manoeuvre under degraded adhesion conditions. The variables coming from the 3D multibody model have been compared with the correspondent experimental quantities \(v_{wj}^{sp}\), \(r \omega_{wj}^{sp}\) (see Sect. 4).

Firstly, to better highlight the role played by the adhesion recovery in the 3D analysis of the complete vehicle dynamics, the authors report the comparison between the new degraded adhesion model and a classic adhesion model equal to the previous one but not taking into account the adhesion recovery due to the cleaning effect of the friction forces (Fig. 30).

Fig. 30
figure 30

Experimental velocity \(v_{w1}^{sp}\), the velocity provided by the new model \(v_{w1}^{new}\) and the velocity provided by the classic model \(v_{w1}^{cl}\) for the I test of group A

Full size image

The comparison (performed for the I test of group A) focuses on the translational velocities of vehicle wheels: the experimental velocity \(v_{w1}^{sp}\), the velocity provided by the new model \(v_{w1}^{new}\) and the velocity \(v_{w1}^{cl}\) provided by the classic model. This simple example well underlines the importance of the adhesion recovery (caused by the energy dissipation at the contact interface) during the braking of railway vehicles under degraded adhesion conditions. More particularly such example effectively highlights the absence of adhesion recovery in the second phase of the braking manoeuvre, in disagreement with the experimental data.

Secondly, by way of example the time histories of the translational velocities v w1, \(v_{w1}^{sp}\) and the rotational velocities rω w1, \(r \omega_{w1}^{sp}\) are reported in Figs. 31, 32, 33 and Figs. 34, 35, 36 for all the three tests of the groups A and B.

Fig. 31
figure 31

Translational velocities v w1, \(v_{w1}^{sp}\) and rotational velocities rω w1, \(r \omega_{w1}^{sp}\) of the I test of the group A

Full size image
Fig. 32
figure 32

Translational velocities v w1, \(v_{w1}^{sp}\) and rotational velocities rω w1, \(r \omega_{w1}^{sp}\) of the II test of the group A

Full size image
Fig. 33
figure 33

Translational velocities v w1, \(v_{w1}^{sp}\) and rotational velocities rω w1, \(r \omega_{w1}^{sp}\) of the III test of the group A

Full size image
Fig. 34
figure 34

Translational velocities v w1, \(v_{w1}^{sp}\) and rotational velocities rω w1, \(r \omega_{w1}^{sp}\) of the I test of the group B

Full size image
Fig. 35
figure 35

Translational velocities v w1, \(v_{w1}^{sp}\) and rotational velocities rω w1, \(r \omega_{w1}^{sp}\) of the II test of the group B

Full size image
Fig. 36
figure 36

Translational velocities v w1, \(v_{w1}^{sp}\) and rotational velocities rω w1, \(r \omega_{w1}^{sp}\) of the III test of the group B

Full size image

Additionally the maximum velocity errors E j for all the performed tests are considered as well (see the Table 6 for E 1):

$$ E_{j} = \mathop{\max}\limits _{t \in[T_I ,T_F ]} \bigl\vert {v_{wj}^{sp} - v_{wj} } \bigr\vert . $$
(22)
Table 6 Maximum velocity errors E 1, sliding means \(\bar{s}_{1}\), \(\bar{s}_{1}^{sp}\) and sliding standard deviations Δ1, \(\Delta_{1}^{sp}\)
Full size table

The results of the analysis show a good agreement in terms of translational velocities v wj , \(v_{wj}^{sp}\), especially in the second part of the braking manoeuvre where the adhesion recovery occurs. Concerning the rotational velocities rω wj , \(r \omega _{wj}^{sp}\) (and thus the angular velocities) the matching is satisfying. However these physical quantities cannot be locally compared to each other because of the complexity and the chaoticity of the system due, for instance, to the presence of discontinuous and non-linear threshold elements like the WSP. To better evaluate the behaviour of rω wj and \(r \omega_{wj}^{sp}\) from a global point of view, it is useful to introduce the statistical means \(\bar{s}_{j}\), \(\bar{s}_{j}^{sp}\) and standard deviations Δ j , \(\Delta _{j}^{sp}\) of the calculated slidings s j and of the experimental ones \(s_{j}^{sp}\):

$$ \begin{aligned} &{s_j = v_{wj} - r \omega_{wj} } \\ &{s_j^{sp} = v_{wj}^{sp} - r \omega_{wj}^{sp} ;} \end{aligned} $$
(23)

the statistical indices are then evaluated as follows:

$$ \begin{aligned} &{\bar{s}_j = \frac{1}{{T_F - T_I }}\int _{T_I }^{T_F } {s_j dt} } \\ &{\bar{s}_j^{sp} = \frac{1}{{T_F - T_I }}\int _{T_I }^{T_F } {s_j^{sp} dt} } \\ &{\Delta_j = \sqrt{\frac{1}{{T_F - T_I }}\int _{T_I }^{T_F } {(s_j - \bar{s}_j )^2 dt} } } \\ &{\Delta_j^{sp} = \sqrt{\frac{1}{{T_F - T_I }}\int _{T_I }^{T_F } {\bigl(s_j^{sp} - \bar{s}_j^{sp} \bigr)^2 dt} } } \end{aligned} $$
(24)

where T I and T F are initial and final times of the simulation respectively. For instance the means \(\bar{s}_{1}\), \(\bar{s}_{1}^{sp}\) and the standard deviations Δ1, \(\Delta_{1}^{sp}\) of the slidings s 1, \(s_{j}^{sp}\) are summarised in Table 6 for all the three tests of the groups A and B; they confirm the good matching also in terms of slidings and rotational velocities.

In conclusion, the numerical simulations of the vehicle dynamics during the braking manoeuvre highlight again the capability of the developed model in approximating the complex and highly non-linear behaviour of the degraded adhesion. The result is encouraging especially considering the simplicity of the whole model (only one unknown parameter is involved) and the computational times are very low.

7 Computational times

As previously said inside the paper, the wheel-rail contact model comprising the new degraded adhesion model is suitable for multibody applications, very important in the study of the railway vehicle dynamics. In particular high computational performances are required so that the contact model could be directly implemented online within more general multibody models developed in dedicated environments (in this case Matlab-Simulink) [1, 2].

The data corresponding to the CPU employed in the numerical simulations (see Sect. 6) and the main integration parameters of the ordinary differential equations (ODE) solver are reported in Table 7 [1, 44].

Table 7 CPU data and integration parameters
Full size table

To verify the computational efficiency of the new degraded adhesion model, the simulation times concerning the whole railway vehicle model (3D multibody model of the vehicle and 3D wheel rail contact model) have been measured. The computation times reported in Table 8 are referred to the I test of the group A and are divided into the computation times related to the 3D multibody vehicle model and the ones related to the 3D wheel-rail contact model. More particularly, four different contact models (always implemented directly online within the multibody model of the vehicle) have been considered. All the contact models share the same contact point detection algorithm [10, 22, 34] and the solution of the normal problem [6, 11, 29] while, as regards the tangential contact problem, the following options have been taken into account: the global Kalker theory saturated through the Johnson-Vermeulen formula [28, 29], the Kalker FASTSIM algorithm [29, 30], the Polach model [38, 39] and the new degraded adhesion model.

Table 8 Computation times of the different wheel-rail contact models
Full size table

As the results summarised in Table 8 show, the numerical efficiency of the new degraded adhesion model is substantially the same of the other wheel-rail contact models that do not consider degraded adhesion conditions. The achievement of this goal has been possible thanks to the simplicity of the new procedure and allows an easy and efficient online implementability of the adhesion model within more generic multibody models.

8 Conclusions and further developments

In this paper the authors described a model aimed to obtain a better accuracy in reproducing degraded adhesion conditions in vehicle dynamics and railway systems. The followed approach turns out to be quite suitable for the multibody modelling (for instance in Matlab-Simulink and Simpack environments), a very important tool in the considered research areas; furthermore it assures high computational performances that permit to implement the degraded adhesion model direct online within more general multibody models of railway vehicles.

The innovative model focuses on the main phenomena characterising the degraded adhesion: the energy dissipation at the contact interface, the consequent cleaning effect and the resulting adhesion recovery due to the removal of external unknown contaminants. Moreover, the simplicity of the followed approach allows the minimisation of the number of hardly measurable physical quantities required by the model. This interesting feature is fundamental because most of the physical characteristics of the contaminants are totally unknown in practise.

The new adhesion model has been validated through experimental data provided by Trenitalia S. p. A. and coming from on-track tests carried out in Velim (Czech Republic) on a straight railway track characterised by degraded adhesion conditions. The tests have been performed with the railway vehicle UIC-Z1 equipped with a fully-working Wheel Slide Protection (WSP) system.

Concerning the future developments, firstly further and more exhaustive experimental campaigns are currently being carried out by Trenitalia and Rete Ferroviaria Italiana to test the new degraded adhesion model on a large number of different scenarios and, in particular, on generic curvilinear tracks (negotiating them at different travelling speeds and with different kinds and levels of contaminants). The new experimental data will allow a better tuning of the model geometrical and physical parameters and a better validation of the model itself. The model will be also compared to other contact models which do not consider the adhesion recovery to better investigate the role of this phenomenon.

Secondly many model improvements will be taken into account. More particularly, new theoretical and experimental relations among the adhesion coefficient f, the specific dissipated energy W sp and the limit adhesion levels f d , f r (degraded adhesion and adhesion recovery) will be introduced and analysed. This way the physical origin and meaning of the transition function λ(W sp ) will be better investigated, trying to connect it to more elementary physical and tribological phenomena (for example phenomena related to wear of the wheel and rail profiles on which the authors have recently worked; see for instance the references [9, 25, 53, 54]).

Finally the new degraded adhesion model will be implemented within 3D multibody models of different railway vehicles (developed in dedicated environments like Matlab-Simulink, Simpack, etc.) operating on generic railway tracks. This way the degraded adhesion effect on the railway vehicle dynamics, the wheel-rail contact and the wear affecting the wheel and rail surfaces will be better investigated.