Stochastic Differential Games on Optimal Investment and Reinsurance Strategy with Delay Under the CEV Model

Abstract

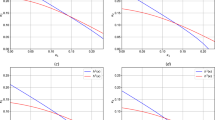
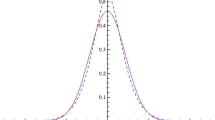
In this paper, supposing that the price process of the risky asset is described by a CEV stochastic volatility model, we investigate a stochastic differential investment and proportional reinsurance game problem with delay between two competing insurers. Each insurer’s risk process is described by the diffusion approximated process of the classical Cramér-Lundberg model. Each insurer can purchase the proportional reinsurance to mitigate their claim risks; and can invest in one risk-free asset and one risky asset whose price dynamics follows the CEV model. The main objective of each insurer is to maximize the utility of his terminal surplus relative to that of his competitor. For the representative cases of the mean-variance utility and exponential utility, we derive the explicit equilibrium reinsurance and investment strategies by applying the techniques of differential game theory and stochastic control theory. Finally, we perform some numerical examples to illustrate the influence of model parameters on the equilibrium reinsurance and investment strategies. Numerical simulation results indicate that: whether delay information and the elasticity parameter is considered or not will greatly affect the final equilibrium reinsurance strategy and optimal investment strategy. The more value of wealth at an earlier time is considered, the insurer will be more cautious and rational in their investment; however, the investment strategy of the insurer with the relative performance concern is riskier than that without the concern; meanwhile, the elasticity parameter will significantly affect the investment strategy of the insurer, and its influence trend varies with the price of risky assets.

Appendices

Appendix A

Proof of Theorem 2.  To solve (19)–(22), we try to conjecture the solutions in the following forms

$$\begin{aligned} \left\{ \begin{array}{l} W_i(t,s,\hat{x}_i,y_i,y_j) = A^i(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + \frac{B^i(t) + C^i(t,s)}{\gamma _i}, \\ g_i(t,s,\hat{x}_i,y_i,y_j) = F^i(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + \frac{G^i(t) + H^i(t,s)}{\gamma _i} \end{array}\right. \end{aligned}$$

(48)

with the boundary conditions $A^i(T) = F^i(T) = 1$, $B^i(T) = G^i(T) = 0$, and $C^i(t,s) = H^i(t,s) = 0$. Substituting (48) with its partial derivatives into (19) and (21), we get

$$\begin{aligned} \begin{aligned} \sup \limits _{\pi _i \in \Pi _i}&\left\{ A_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + \frac{1}{\gamma _i}B_{it}(t) + \frac{1}{\gamma _i}C_{it}(t,s) + \frac{1}{\gamma _i}\mu sC_{is}(t,s)\right. \\&+ \bigg [\beta _ix_i - \kappa _i\beta _jx_j + \tilde{\tau }_iy_i - \kappa _i\tilde{\tau }_jy_j + \varphi _iz_i - \kappa _i\varphi _jz_j + a_i\varsigma _i - \kappa _ia_j\varsigma _j\bigg . \\&\left. + a_i\theta _iq_i(t) - \kappa _ia_j\theta _jq_j^*(t) + (\mu - r)\left( u_i(t) - \kappa _iu_j^*(t)\right) \right] A_i(t) \\&- \frac{\gamma _i}{2}\left[ \sigma ^2s^{2k}u_i^2(t) - 2\sigma ^2s^{2k}\kappa _iu_i(t)u_j^*(t) + \sigma ^2s^{2k}\kappa _i^2u_j^{*2}(t)\right. \\&\left. + b_i^2q_i^2(t) - 2\rho \kappa _ib_ib_jq_i(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t)\right] F_i^2(t)\\&- \sigma ^2s^{2k + 1}\left[ u_i(t) - \kappa _iu_j^*(t)\right] F_i(t) \cdot H_{is}(t,s) + \frac{1}{2\gamma _i}\sigma ^2s^{2k + 2}\left[ C_{iss}(t,s) - H_{is}^2(t,s)\right] \\&\left. + \omega _i\left( x_i - \delta _iy_i - \mathrm{{e}}^{-\delta _ih_i}z_i \right) A_i(t) - \kappa _i\omega _j\left( x_j - \delta _jy_j - \mathrm{{e}}^{-\delta _jh_j}z_j\right) A_i(t)\right\} = 0 \end{aligned} \end{aligned}$$

(49)

and

$$\begin{aligned} \begin{aligned}&F_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + \frac{1}{\gamma _i}G_{it}(t) + \frac{1}{\gamma _i}H_{it}(t,s) + \frac{1}{\gamma _i}\mu sH_{is}(t,s) \\&+ \bigg [\beta _ix_i - \kappa _i\beta _jx_j + \tilde{\tau }_iy_i - \kappa _i\tilde{\tau }_jy_j + \varphi _iz_i - \kappa _i\varphi _jz_j + a_i\varsigma _i - \kappa _ia_j\varsigma _j \bigg . \\&\left. + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t) + (\mu - r)\left( u_i^*(t) - \kappa _iu_j^*(t)\right) \right] F_i(t) \\&+ \frac{1}{2\gamma _i}\sigma ^2s^{2k + 2}H_{iss}(t,s) + \omega _i\left( x_i - \delta _iy_i - \mathrm{{e}}^{-\delta _ih_i}z_i\right) F_i(t) - \kappa _i\omega _j\left( x_j - \delta _jy_j - \mathrm{{e}}^{-\delta _jh_j}z_j\right) F_i(t) = 0. \end{aligned} \end{aligned}$$

(50)

By differentiating (49) with respect to $q_i$ and $u_i$, we obtain

$$\begin{aligned} \left\{ {\begin{array}{l} q_i^*(t) = \frac{\rho \kappa _ib_j}{b_i}q_j^*(t) + \frac{a_i\theta _iA_i(t)}{b_i^2\gamma _iF_i^2(t)}, \\ u_i^*(t) = \kappa _iu_j^*(t) + \frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{\sigma ^2s^{2k}\gamma _iF_i^2(t)}. \\ \end{array}}\right. \end{aligned}$$

(51)

Substituting (51) back into (49) and (50), and conditionally on $\varphi _i =\omega _i\mathrm {e}^{-\delta _ih_i}$, the following equations hold:

$$\begin{aligned} \begin{aligned}&A_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + \frac{1}{\gamma _i}B_{it}(t) + \frac{1}{\gamma _i}C_{it}(t,s) + \frac{1}{\gamma _i}\mu sC_{is}(t,s) \\&+ \bigg [\beta _ix_i - \kappa _i\beta _jx_j + \tilde{\tau }_iy_i - \kappa _i\tilde{\tau }_jy_j + a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t) \bigg . \\&\left. + (\mu - r)\frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{\sigma ^2s^{2k}\gamma _iF_i^2(t)}\right] A_i(t) - \frac{\gamma _i}{2}\left[ \sigma ^2s^{2k}\left( \frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{\sigma ^2s^{2k}\gamma _iF_i^2(t)}\right) ^2 \right. \\&\left. + b_i^2q_i^{*2}(t) - 2\rho \kappa _ib_ib_jq_i^*(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t)\right] F_i^2(t) - \frac{1}{\gamma _i}\cdot s\frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{F_i(t)}H_{is}(t,s) \\&+ \frac{1}{2\gamma _i}\sigma ^2s^{2k + 2}\left[ C_{iss}(t,s) - H_{is}^2(t,s)\right] + \omega _i(x_i - \delta _iy_i)A_i(t) - \kappa _i\omega _j(x_j - \delta _jy_j)A_i(t) = 0, \end{aligned} \end{aligned}$$

(52)

and

$$\begin{aligned} \begin{aligned}&F_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + \frac{1}{\gamma _i}G_{it}(t) + \frac{1}{\gamma _i}H_{it}(t,s) + \frac{1}{\gamma _i}\mu sH_{is}(t,s) \\&+ \bigg [\beta _ix_i - \kappa _i\beta _jx_j + \tilde{\tau }_iy_i - \kappa _i\tilde{\tau }_jy_j + a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t) \bigg . \\&\left. + (\mu - r)\frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{\sigma ^2s^{2k}\gamma _iF_i^2(t)}\right] F_i(t) + \frac{1}{2\gamma _i}\sigma ^2s^{2k + 2}H_{iss}(t,s) \\&+ \omega _(x_i - \delta _iy_i)F_i(t) - \kappa _i\omega _j(x_j - \delta _jy_j)F_i(t) = 0. \end{aligned} \end{aligned}$$

(53)

With the condition of $\beta _1 + \omega _1 = \beta _2 + \omega _2$ in Theorem 2, and separating the variables with $\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right)$, we obtain

$$\begin{aligned} A_{it}(t) + A_i(t)(\beta _i + \omega _i) = 0, \quad F_{it}(t) + F_i(t)(\beta _i + \omega _i) = 0, \end{aligned}$$

(54)

$$\begin{aligned} \begin{aligned} B_{it}(t)&+ \gamma _i\left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t)\right] A_i(t) \\&- \frac{\gamma _i^2}{2}\left[ b_i^2q_i^{*2}(t) - 2\rho \kappa _ib_ib_jq_i^*(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t)\right] F_i^2(t) = 0, \end{aligned} \end{aligned}$$

(55)

$$\begin{aligned} G_{it}(t) + \gamma _i\left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t)\right] F_i(t) = 0, \end{aligned}$$

(56)

$$\begin{aligned} \begin{aligned} C_{it}&(t,s) + \mu sC_{is}(t,s) + (\mu - r)\frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{\sigma ^2s^{2k}F_i^2(t)}\cdot A_i(t) \\&- \frac{\left[ (\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)\right] ^2}{2\sigma ^2s^{2k}F_i^2(t)} - s\frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{F_i(t)}H_{is}(t,s) \\&+ \frac{1}{2}\sigma ^2s^{2k + 2}\left[ C_{iss}(t,s) - H_{is}^2(t,s)\right] = 0, \end{aligned} \end{aligned}$$

(57)

$$\begin{aligned} H_{it}(t,s) + \mu sH_{is}(t,s) + (\mu - r)\frac{(\mu - r)A_i(t) - \sigma ^2s^{2k + 1}F_i(t) \cdot H_{is}(t,s)}{\sigma ^2s^{2k}F_i(t)} + \frac{1}{2}\sigma ^2s^{2k + 2}H_{iss}(t,s) = 0. \end{aligned}$$

(58)

Considering the boundary conditions, we have

$$\begin{aligned} A_i(t) = F_i(t) = \mathrm {e}^{(\beta _i + \omega _i)(T - t)}, \end{aligned}$$

(59)

$$\begin{aligned} \begin{aligned} B_i(t) =&\gamma _i\int _{t}^{T}\left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(s) - \kappa _ia_j\theta _jq_j^*(s)\right] \mathrm {e}^{(\beta _i + \omega _i)(T - s)}\mathrm {d}s \\&- \frac{\gamma _i^2}{2}\int _{t}^{T}\left[ b_i^2q_i^{*2}(s) - 2\rho \kappa _ib_ib_jq_i^*(s)q_j^*(s) + \kappa _i^2b_j^2q_j^{*2}(s)\right] \mathrm {e}^{2(\beta _i + \omega _i)(T - 2)}\mathrm {d}s, \end{aligned} \end{aligned}$$

(60)

$$\begin{aligned} G_i(t) = \gamma _i\int _{t}^{T}\left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(s) - \kappa _ia_j\theta _jq_j^*(s)\right] \mathrm {e}^{(\beta _i + \omega _i)(T - s)}\mathrm {d}s, \end{aligned}$$

(61)

To solve (58), we assume that $H_i(t,s)$ admits the following affine form:

$$\begin{aligned} H_i(t,s) = M(t) + N(t)s^{-2k} \end{aligned}$$

(62)

when substituting M(t) and N(t) into (58), we have

$$\begin{aligned} M_t + N_ts^{-2k} - 2k\mu s^{-2k}N(t) + \frac{(\mu - r)^2}{\sigma ^2s^{2k}} + 2k(\mu - r)s^{-2k}N(t) + k(2k + 1)\sigma ^2N(t) = 0. \end{aligned}$$

(63)

Matching coefficients yields

$$\begin{aligned} \left\{ \begin{array}{l} M_t + k(2k + 1)\sigma ^2N(t) = 0, \\ M(T) = 0. \end{array}\right. \end{aligned}$$

(64)

and

$$\begin{aligned} \left\{ \begin{array}{l} N_t - 2r\mu N(t) + \frac{(\mu - r)^2}{\sigma ^2} = 0, \\ N(T) = 0. \end{array}\right. \end{aligned}$$

(65)

Recalling the boundary conditions, we can obtain

$$\begin{aligned} \left\{ \begin{array}{l} M(t) = \frac{(2k + 1)(\mu - r)^2}{4kr^2}\left[ \mathrm {e}^{2kr(t - T)} - 1\right] - \frac{(2k + 1)(\mu - r)^2}{2r}(t - T), \\ N(t) = - \frac{(\mu - r)^2}{2kr\sigma ^2}\left[ \mathrm {e}^{2kr(t - T)} - 1\right] . \end{array}\right. \end{aligned}$$

(66)

Similiarly, we can get that $C_i(t, s)$ is a solution of the linear ordinary differential equations, which admits the form in (29).

Moreover, the time-consistent Nash equilibrium reinsurance-investment strategy of insurer i should satisfy

$$\begin{aligned} \left\{ {\begin{array}{l} q_i^*(t) = \frac{\rho \kappa _ib_j}{b_i}q_j^*(t) + \frac{a_i\theta _i}{b_i^2\gamma _i\mathrm {e}^{(\beta _i + \omega _i)(T - t)}}, \\ u_i^*(t) = \kappa _iu_j^*(t) + \frac{(\mu - r) + 2k\sigma ^2N(t)}{\sigma ^2s^{2k}\gamma _i\mathrm {e}^{(\beta _i + \omega _i)(T - t)}}. \\ \end{array}}\right. \end{aligned}$$

(67)

From (67), we can get explicit expressions for the equilibrium reinsurance and investment strategy of each insurer as displayed in (25) and (26).

The proof of Theorem 2 is completed.

Appendix B

Proof of Theorem 3.

To solve HJB Eq. (37), consider the following Ansatz:

$$\begin{aligned} W_i(t,s,\hat{x}_i,y_i,y_j) = -\frac{1}{\nu _i}\exp \left\{ \nu _i\left[ R_i(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) - O_i(t) + \tilde{C}_i(t,s)\right] \right\} , \end{aligned}$$

(68)

with $R_i(T) = 1$, $O_i(T) = 0$ and $\tilde{C}_i(T, s) = 0$, for all $s \in \mathbb {R}$. By some simple calculation, we obtain the partial derivatives of $W_i$, which are shown as follows

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial {W_i}}{\partial t} = -\nu _i\left[ R_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) - O_{it}(t) + \tilde{C}_{it}(t,s)\right] W_i, \quad \frac{\partial {W_i}}{\partial \hat{x}_i} = - \nu _i{R_i}(t)W_i, \\ \frac{\partial ^2{W_i}}{\partial \hat{x}_i^2} = \nu _i^2R_i^2(t)W_i, \quad \frac{\partial {W_i}}{\partial s} = -\nu _i\tilde{C}_{is}(t,s)W_i, \quad \frac{\partial ^2{W_i}}{\partial s^2} = \left[ \nu _i^2\tilde{C}_{is}^2(t,s) - \nu _i\tilde{C}_{iss}(t,s)\right] W_i, \\ \frac{\partial ^2{W_i}}{\partial {\hat{x}_i}\partial s} = \nu _i^2R_i(t)\tilde{C}_{is}(t,s)W_i,\quad \frac{\partial {W_i}}{\partial {y_i}} = -\nu _iR_i(t)\omega _iW_i, \quad \frac{\partial {W_i}}{\partial {y_j}} = \nu _i\kappa _i\omega _jR_i(t)W_i. \end{array}\right. \end{aligned}$$

(69)

Inserting (68) and (69) into (37) yields

$$\begin{aligned} \begin{aligned}&\sup \limits _{\pi _i \in \Pi _i}\left\{ -\nu _i\left[ R_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) - O_{it}(t) + \tilde{C}_{it}(t,s)\right] - \mu s\nu _i\tilde{C}_{is}(t,s) - \left[ \beta _ix_i - \kappa _i\beta _jx_j + \tilde{\tau }_iy_i \right. \right. \\&\left. - \kappa _i\tilde{\tau }_jy_j + \varphi _iz_i - \kappa _i\varphi _jz_j + a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i(t) - \kappa _ia_j\theta _jq_j^*(t) + (\mu - r)\left( u_i(t) - \kappa _iu_j(t)^*\right) \right] \nu _iR_i(t)\\&+ \frac{1}{2}\left[ b_i^2q_i^2(t) - 2\rho \kappa _ib_ib_jq_i(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t) + \sigma ^2s^{2k}u_i^2(t) - 2\sigma ^2s^{2k}\kappa _iu_i(t)u_j^*(t) + \sigma ^2s^{2k}\kappa _i^2u_j^{*2}\right] \nu _i^2R_i^2(t)\\&+ \sigma ^2s^{2k+1}\left[ u_i(t) - \kappa _iu_j^*(t)\right] \nu _i^2R_i(t)\tilde{C}_{is}(t,s) + \frac{1}{2}\sigma ^2s^{2k+2}\left[ \nu _i^2\tilde{C}_{is}^2(t,s) - \nu _i\tilde{C}_{iss}(t,s)\right] \\&\left. - \left( x_i - \delta _iy_i - \mathrm{{e}}^{-\delta _ih_i}z_i\right) \nu _iR_i(t)\omega _i + \left( x_j - \delta _jy_j - \mathrm{{e}}^{-\delta _jh_j}z_j\right) \nu _i\kappa _i\omega _jR_i(t)\right\} = 0. \end{aligned} \end{aligned}$$

(70)

By differentiating (70) with respect to $q_i$ and $u_i$, we obtain

$$\begin{aligned} \left\{ {\begin{array}{l} q_i^*(t) = \frac{\rho \kappa _ib_j}{b_i}q_j^*(t) + \frac{a_i\theta _i}{b_i^2\nu _iR_i(t)}, \\ u_i^*(t) = \kappa _iu_j^*(t) + \frac{(\mu - r) - \sigma ^2s^{2k + 1}\nu _i\tilde{C}_{is}(t,s)}{\sigma ^2s^{2k}\nu _iR_i(t)}. \\ \end{array}}\right. \end{aligned}$$

(71)

Substituting (71) back into (70), we obtain

$$\begin{aligned} \begin{array}{l} -\left[ R_{it}(t)\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) - O_{it}(t) + \tilde{C}_{it}(t,s)\right] - \mu s\tilde{C}_{is}(t,s) - \left[ \beta _ix_i - \kappa _i\beta _jx_j + \tilde{\tau }_iy_i \right. \\ \left. - \kappa _i\tilde{\tau }_jy_j + \varphi _iz_i - \kappa _i\varphi _jz_j + a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t) + (\mu - r)\left( u_i^*(t) - \kappa _iu_j(t)^*\right) \right] R_i(t)\\ + \frac{1}{2}\left[ b_i^2q_i^{*2}(t) - 2\rho \kappa _ib_ib_jq_i^*(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t) + \sigma ^2s^{2k}u_i^{*2}(t) - 2\sigma ^2s^{2k}\kappa _iu_i^*(t)u_j^*(t) + \sigma ^2s^{2k}\kappa _i^2u_j^{*2}\right] \nu _iR_i^2(t)\\ + \sigma ^2s^{2k+1}\left[ u_i^*(t) - \kappa _iu_j^*(t)\right] \nu _iR_i(t)\tilde{C}_{is}(t,s) + \frac{1}{2}\sigma ^2s^{2k+2}\left[ \nu _i\tilde{C}_{is}^2(t,s) - \tilde{C}_{iss}(t,s)\right] \\ - \left( x_i - \delta _iy_i - \mathrm{{e}}^{-\delta _ih_i}z_i\right) R_i(t)\omega _i + \left( x_j - \delta _jy_j - \mathrm{{e}}^{-\delta _jh_j}z_j\right) \kappa _i\omega _jR_i(t) = 0. \end{array} \end{aligned}$$

(72)

With the condition of $\beta _1 + \omega _1 = \beta _2 + \omega _2$ in Theorem 3, we can further get

$$\begin{aligned} \begin{aligned}&-\left[ R_{it}(t) + R_i(t)\left( \beta _i + \omega _i\right) \left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right) + O_{it}(t) - \tilde{C}_{it}(t,s)\right] - \mu s\tilde{C}_{is}(t,s) \\&- \left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t) + (\mu - r)\left( u_i^*(t) - \kappa _iu_j(t)^*\right) \right] R_i(t)\\&+ \frac{1}{2}\left[ b_i^2q_i^{*2}(t) - 2\rho \kappa _ib_ib_jq_i^*(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t) + \sigma ^2s^{2k}u_i^{*2}(t) - 2\sigma ^2s^{2k}\kappa _iu_i^*(t)u_j^*(t) \right. \\&\left. + \sigma ^2s^{2k}\kappa _i^2u_j^{*2}\right] \nu _iR_i^2(t) + \sigma ^2s^{2k+1}\left[ u_i^*(t) - \kappa _iu_j^*(t)\right] \nu _iR_i(t)\tilde{C}_{is}(t,s) \\&+ \frac{1}{2}\sigma ^2s^{2k+2}\left[ \nu _i\tilde{C}_{is}^2(t,s) - \tilde{C}_{iss}(t,s)\right] = 0. \end{aligned} \end{aligned}$$

(73)

By separating the variables with and without $\left( \hat{x}_i + \omega _iy_i - \kappa _i\omega _jy_j\right)$, we can derive the following equations:

$$\begin{aligned} R_{it}(t) + R_i(t)\left( \beta _i + \omega _i\right) = 0, \end{aligned}$$

(74)

$$\begin{aligned} \begin{aligned}&O_{it}(t) - \left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(t) - \kappa _ia_j\theta _jq_j^*(t)\right] R_i(t)\\&+ \frac{1}{2}\left[ b_i^2q_i^{*2}(t) - 2\rho \kappa _ib_ib_jq_i^*(t)q_j^*(t) + \kappa _i^2b_j^2q_j^{*2}(t)\right] \nu _iR_i^2(t) = 0, \end{aligned} \end{aligned}$$

(75)

$$\begin{aligned} \begin{aligned}&-\tilde{C}_{it}(t,s) - \mu s\tilde{C}_{is}(t,s) - (\mu - r)\left( u_i^*(t) - \kappa _iu_j(t)^*\right) R_i(t)\\&+ \frac{1}{2}\sigma ^2s^{2k}\left[ u_i^*(t) - \kappa _iu_j^*(t)\right] ^2\nu _iR_i^2(t) + \sigma ^2s^{2k+1}\left[ u_i^*(t) - \kappa _iu_j^*(t)\right] \nu _iR_i(t)\tilde{C}_{is}(t,s) \\&+ \frac{1}{2}\sigma ^2s^{2k+2}\left[ \nu _i\tilde{C}_{is}^2(t,s) - \tilde{C}_{iss}(t,s)\right] = 0. \end{aligned} \end{aligned}$$

(76)

Considering the boundary conditions, we have

$$\begin{aligned} R_i(t) = \mathrm {e}^{(\beta _i + \omega _i)(T - t)}, \end{aligned}$$

(77)

$$\begin{aligned} \begin{aligned} O_i(t) =&\int _{t}^{T}\left[ a_i\varsigma _i - \kappa _ia_j\varsigma _j + a_i\theta _iq_i^*(s) - \kappa _ia_j\theta _jq_j^*(s)\right] \mathrm {e}^{(\beta _i + \omega _i)(T - s)}\\&+ \frac{1}{2}\left[ b_i^2q_i^{*2}(s) - 2\rho \kappa _ib_ib_jq_i^*(s)q_j^*(s) + \kappa _i^2b_j^2q_j^{*2}(s)\right] \nu _i\mathrm {e}^{2(\beta _i + \omega _i)(T - s)}. \end{aligned} \end{aligned}$$

(78)

Substituting $u_i^*(t)$ in (71) into the Eq. (76), we have

$$\begin{aligned} \begin{aligned}&-\tilde{C}_{it}(t,s) - \mu s\tilde{C}_{is}(t,s) - (\mu - r)\frac{(\mu - r) - \sigma ^2s^{2k + 1}\nu _i\tilde{C}_{is}(t,s)}{\sigma ^2s^{2k}\nu _i}\\&+ \frac{\left[ (\mu - r) - \sigma ^2s^{2k + 1}\nu _i\tilde{C}_{is}(t,s)\right] ^2}{2\sigma ^2s^{2k}\nu _i}&+ s\left[ (\mu - r) - \sigma ^2s^{2k + 1}\nu _i\tilde{C}_{is}(t,s)\right] \tilde{C}_{is}(t,s) \\&+ \frac{1}{2}\sigma ^2s^{2k+2}\left[ \nu _i\tilde{C}_{is}^2(t,s) - \tilde{C}_{iss}(t,s)\right] = 0. \end{aligned} \end{aligned}$$

(79)

To solve (79), we assume that $\tilde{C}_i(t,s)$ admits the following affine form:

$$\begin{aligned} \tilde{C}_i(t,s) = \tilde{M}(t) + \tilde{N}(t)s^{-2k} \end{aligned}$$

(80)

when substituting $\tilde{M}(t)$ and $\tilde{N}(t)$ into (79), we have

$$\begin{aligned} -(\tilde{M}_t + \tilde{N}_ts^{-2k}) +2krs^{-2k}\tilde{N}(t) - \frac{(\mu - r)^2}{2\sigma ^2s^{2k}\nu _i} - k(2k + 1)\sigma ^2\tilde{N}(t) = 0. \end{aligned}$$

(81)

Matching coefficients yields

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{M}_t + k(2k + 1)\sigma ^2\tilde{N}(t) = 0, \\ \tilde{M}(T) = 0. \end{array}\right. \end{aligned}$$

(82)

and

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{N}_t - 2kr\tilde{N} + \frac{(\mu - r)^2}{2\sigma ^2\nu _i} = 0, \\ \tilde{N}(T) = 0. \end{array}\right. \end{aligned}$$

(83)

Recalling the boundary conditions, we can obtain

$$\begin{aligned} \left\{ \begin{array}{l} \tilde{M}(t) = \frac{(2k + 1)(\mu - r)^2}{8kr^2\nu _i}\left[ \mathrm {e}^{2rk(t - T)} - 1\right] - \frac{(2k + 1)(\mu - r)^2}{4r\nu _i}(t - T), \\ \tilde{N}(t) = - \frac{(\mu - r)^2}{4kr\sigma ^2\nu _i}\left[ \mathrm {e}^{2kr(t - T)} - 1\right] . \end{array}\right. \end{aligned}$$

(84)

Plugging $R_i(t)$ and $C_i(t,s)$ into (71) implies

$$\begin{aligned} \left\{ {\begin{array}{l} q_i^*(t) = \frac{\rho \kappa _ib_j}{b_i}q_j^*(t) + \frac{a_i\theta _i}{b_i^2\nu _i\mathrm {e}^{(\beta _i + \omega _i)(T - t)}}, \\ u_i^*(t) = \kappa _iu_j^*(t) + \frac{(\mu - r) + 2k\sigma ^2\nu _i\tilde{N}(t)}{\sigma ^2s^{2k}\nu _i\mathrm {e}^{(\beta _i + \omega _i)(T - t)}}. \\ \end{array}}\right. \end{aligned}$$

(85)

From (85), the desired expressions of the Nash equilibrium strategies are given by (41) and (42).

This completes the proof of Theorem 3.