Abstract
It is well-known that the deformation problem of a compact coisotropic submanifold C in a symplectic manifold is obstructed in general. We show that it becomes unobstructed if one only allows coisotropic deformations whose characteristic foliation is diffeomorphic to that of C. This extends an unobstructedness result in the setting of integral coisotropic submanifolds due to Ruan.
Similar content being viewed by others
1 Introduction
Lagrangian submanifolds are fundamental objects in symplectic geometry with a simple deformation theory. Given a Lagrangian submanifold \(L\subset (M,\omega )\), Weinstein’s Lagrangian neighborhood theorem [26] states that one can identify \((M,\omega )\) with the cotangent bundle \((T^{*}L,\omega _{can})\) around L. This implies that deformations of L correspond with small closed one-forms on L. Hence, the Lagrangian deformation problem is linear and unobstructed.
Coisotropic submanifolds encompass the Lagrangian ones, and these submanifolds show up naturally in various contexts (e.g., zero level sets of moment maps, first class constraints in mechanics). A coisotropic submanifold \(C\subset (M,\omega )\) carries a characteristic foliation \(\mathcal {F}\), which plays a key role in the deformation problem of C. Gotay’s theorem [13] provides an extension of Weinstein’s Lagrangian neighborhood theorem, showing that one can identify \((M,\omega )\) with \((U,\Omega _G)\) around C. Here, U is a neighborhood of the zero section of \(T^{*}\mathcal {F}\), and \(\Omega _G\) is a symplectic form constructed out of a complement G to \(T\mathcal {F}\). In contrast to the Lagrangian case, the coisotropic sections of \((U,\Omega _G)\) are cut out by a highly nonlinear equation, which is actually the Maurer–Cartan equation of a suitable \(L_{\infty }\)-algebra [18, 21]. Moreover, the coisotropic deformation problem is obstructed in general, meaning that there may exist first-order deformations which are not tangent to any path of deformations [27].
In this note, we revisit the obstructedness problem for compact coisotropic submanifolds. It appears that obstructedness of the coisotropic deformation problem of C is intimately related with instability of its characteristic foliation. This is suggested by the following two results, going in opposite directions:
-
Zambon constructed an obstructed example in [27], featuring a compact coisotropic submanifold C with arbitrarily \(\mathcal {C}^{1}\)-small deformations whose characteristic foliation is not diffeomorphic to that of C.
-
A compact coisotropic submanifold is called integral if its characteristic foliation \(\mathcal {F}\) is given by the fibers of a fiber bundle \(C\rightarrow C/\mathcal {F}\). Ruan showed that the deformation problem of an integral coisotropic submanifold—within the class of such submanifolds—is unobstructed [20].
These results are our motivation to look at a restricted version of the coisotropic deformation problem of C, which only allows deformations whose characteristic foliation is diffeomorphic to that of C. In other words, we deform C within the class
Our main result states that this deformation problem is unobstructed (see Theorem 3.5).
Main Theorem. Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold with characteristic foliation \(\mathcal {F}\). The deformation problem of C within \(\text {Def}_{\mathcal {F}}(C)\) is unobstructed.
We would like to interpret this unobstructedness result as follows. Zambon’s example [27] shows that the space of compact coisotropic submanifolds of a symplectic manifold \((M,\omega )\) is not smooth in general. More precisely, it may fail to be a Fréchet submanifold of the Fréchet manifold consisting of all compact submanifolds of M. However, if we define an equivalence relation on the space of compact coisotropic submanifolds of \((M,\omega )\), declaring \((C,\mathcal {F})\) and \((C',\mathcal {F}')\) to be equivalent if there exists a foliated diffeomorphism between them, then our Main Theorem states that the resulting equivalence classes are smooth, in a loose way. It would be interesting to know if this can be made sense of in a more precise way.
Overview of the paper.
Section 1 collects some background information about coisotropic submanifolds and the Gotay normal form. We recall that as a consequence of this normal form, first-order deformations of a coisotropic submanifold C are leafwise closed one-forms on its characteristic foliation \(\mathcal {F}\). With the aim of this note in mind, we also review the well-known fact that first-order deformations of the foliation \(\mathcal {F}\), modulo those induced by isotopies, are given by the first foliated cohomology group with values in the normal bundle \(H^{1}(\mathcal {F};N\mathcal {F})\).
In Sect. 2, we argue what are the appropriate first-order deformations when deforming a coisotropic submanifold C inside \(\text {Def}_{\mathcal {F}}(C)\). By the above, these are closed foliated one-forms which in a way should give rise to a trivial class in \(H^{1}(\mathcal {F};N\mathcal {F})\). This assignment is achieved by a tool which is central in this paper, namely a canonical transverse differentiation map
We should note here that since \(\mathcal {F}\) is transversely symplectic, there is a canonical isomorphism \(H^{1}(\mathcal {F};N\mathcal {F})\cong H^{1}(\mathcal {F};N^{*}\mathcal {F})\). Hence, the map \(d_{\nu }\) does indeed give a way to relate first-order deformations of C—as a coisotropic submanifold—with first-order deformations of its foliation \(\mathcal {F}\). We obtain the following description for the first-order deformations of C within the class \(\text {Def}_{\mathcal {F}}(C)\) (see Lemma 2.6 and Proposition 2.10).
Proposition
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold. When deforming C inside \(\text {Def}_{\mathcal {F}}(C)\), a first-order deformation is a closed foliated one-form \(\beta \in \Omega ^{1}(\mathcal {F})\) whose cohomology class lies in the kernel of \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F}).\)
First-order deformations have the following geometric interpretation (see Lemma 2.12): they are exactly the foliated one-forms \(\beta \in \Omega ^{1}(\mathcal {F})\) admitting an extension \(\widetilde{\beta }\in \Omega ^{1}(C)\) that satisfies \(d\widetilde{\beta }\in \Omega ^{2}_{bas}(C)\). Here \(\Omega _{bas}(C)\) are the differential forms on C that are basic with respect to \(\mathcal {F}\); morally, they are the differential forms on the leaf space \(C/\mathcal {F}\).
In case the coisotropic submanifold C is integral, then our notion of first-order deformation reduces to closed foliated one-forms \(\beta \in \Omega ^{1}(\mathcal {F})\) defining flat sections of the vector bundle \((\mathcal {H}^{1},\nabla )\) made up by the first cohomology groups of the fibers of \(C\rightarrow C/\mathcal {F}\) (see Example 2.13). These are exactly the first-order deformations considered by Ruan in the deformation problem of integral coisotropic submanifolds [20].
Section 3 is the core of this note, as it contains the proof of the Main Theorem. We show that every first-order deformation \(\beta \in \Omega ^{1}(\mathcal {F})\) of C—as defined in the above Proposition—is tangent to a path of coisotropic sections \(\alpha _t\) of the Gotay local model \((U,\Omega _G)\), whose characteristic foliation is diffeomorphic to \(\mathcal {F}\). The proof is purely geometric, its main ingredient being a Moser argument (see Lemma 3.4). In case the coisotropic submanifold \((C,\mathcal {F})\) is integral, our notion of first-order deformation recovers that of Ruan (see above), and the path \(\alpha _t\) obtained via the Main Theorem again consists of integral coisotropic submanifolds. So our Main Theorem extends Ruan’s result [20] stating that the deformation problem of an integral coisotropic submanifold—within the class of such submanifolds—is unobstructed.
At last, Sect. 4 discusses two implications that our Main Theorem has for the classical coisotropic deformation problem, which allows all coisotropic deformations of C.
First, the Main Theorem yields a partial unobstructedness result in this context. It shows that first-order deformations of C—i.e., closed foliated one-forms on \(\mathcal {F}\)—are unobstructed, if their cohomology class lies in \(\ker (d_{\nu })\). We like to interpret this result in the following way.
It is clear geometrically that first-order deformations \(\beta \in \Omega ^{1}(\mathcal {F})\) admitting a closed extension are unobstructed, since the latter yields a symplectic vector field on \((U,\Omega _G)\) whose flow generates a path of coisotropic sections prolonging \(\beta \). In practice, however, this procedure does not yield many unobstructed first-order deformations: it only concerns those closed \(\beta \in \Omega ^{1}(\mathcal {F})\) whose cohomology class lies in the image of the restriction map \(H^{1}(C)\rightarrow H^{1}(\mathcal {F})\), which is a finite dimensional subspace. Since the existence of a closed extension implies that \([\beta ]\) lies in the kernel of \(d_{\nu }\), the partial unobstructedness statement resulting from our Main Theorem extends the geometric fact just mentioned. By contrast, the kernel of \(d_{\nu }\) is infinite dimensional in general (see Example 4.4), hence our partial unobstructedness result has the potential to generate much more unobstructed first-order deformations.
Second, we already remarked that there is an \(L_{\infty }\)-algebra [16] governing the coisotropic deformation problem of C [18, 21]. It is given by \(\big (\Gamma (\wedge T^{*}\mathcal {F}),\{\lambda _k\}\big )\), and it has the property that its Maurer–Cartan elements correspond with coisotropic sections of the Gotay local model \((U,\Omega _G)\). The multibrackets \(\lambda _k\) are constructed out of \(\Omega _G\), in particular they depend on the choice of complement G to \(T\mathcal {F}\). The \(L_{\infty }\)-algebra gives a way to detect obstructed first-order deformations of C. Namely, for a first-order deformation to be unobstructed, it needs to define a class in the kernel of the Kuranishi map
The partial unobstructedness result following from the Main Theorem implies that \(\ker (d_{\nu })\) is contained in \(\ker (Kr)\). We double-check that this is indeed the case (see Corollary 4.15). Actually, we prove a more interesting result. We show that although the multibrackets \(\lambda _k\) depend on the choice of complement G, the Kuranishi map has a canonical description in terms of the map \(d_{\nu }\) and the induced presymplectic form on C. This highlights once more the role played by the transverse differentiation map \(d_{\nu }\) in the coisotropic deformation problem, and it implies in particular that \(\ker (d_{\nu })\) is contained in \(\ker (Kr)\).
2 Background and setup
In this section, we first collect some background material about coisotropic submanifolds in symplectic geometry. We then introduce in detail the deformation problem that we will consider in this note. Namely, we want to study small deformations of a given coisotropic submanifold \(C\subset (M,\omega )\), whose characteristic foliation is diffeomorphic with that of C. At last, we recall the necessary preliminaries about infinitesimal deformations of coisotropic submanifolds and foliations.
2.1 Coisotropic submanifolds and the Gotay normal form
We recall what it means for a submanifold C of a symplectic manifold \((M,\omega )\) to be coisotropic. The definition involves the symplectic orthogonal \(TC^{\omega }\), which is defined by
We also recall Gotay’s theorem [13], which provides a normal form for \((M,\omega )\) around a coisotropic submanifold C. Such a normal form is useful to study small deformations of C.
Definition 1.1
A submanifold C of \((M,\omega )\) is called coisotropic if \(TC^{\omega }\subset TC\).
We list some alternative characterisations of coisotropic submanifolds \(C\subset (M,\omega )\). They involve the pullback \(\omega _C\in \Omega ^{2}(C)\) of \(\omega \) to C and are proved by straightforward linear algebra.
Lemma 1.2
For any submanifold \(C^{k}\subset (M^{2n},\omega )\), the following are equivalent:
-
(i)
\(C^{k}\subset (M^{2n},\omega )\) is coisotropic.
-
(ii)
\(\omega _{C}\) has constant rank equal to \(2(k-n)\).
-
(iii)
\(\omega _{C}^{k-n+1}=0\).
The pullback \(\omega _{C}\) is a closed two-form of constant rank, so it defines a presymplectic structure on C. Consequently, a coisotropic submanifold C has an induced foliation \(\mathcal {F}\), defined by \(T\mathcal {F}=\ker (\omega _{C})\). We refer to \(\mathcal {F}\) as the characteristic foliation of \(C\subset (M,\omega )\).
Gotay’s theorem [13] provides a normal form for a symplectic manifold \((M,\omega )\) around a coisotropic submanifold C. The local model lives on a neighborhood of the zero section of the vector bundle \(p:T^{*}\mathcal {F}\rightarrow C\), and it is defined as follows. Choose a complement G to \(T\mathcal {F}\) inside TC, and let \(j:T^{*}\mathcal {F}\hookrightarrow T^{*}C\) be the induced inclusion. Denoting by \(\omega _{can}\) the canonical symplectic form on \(T^{*}C\), the closed two-form
is non-degenerate along C, hence it is a symplectic form on a neighborhood U of \(C\subset T^{*}\mathcal {F}\).
Theorem 1.3
(Gotay [13]) If \(C\subset (M,\omega )\) is a coisotropic submanifold, then a neighborhood of C in M is symplectomorphic with the local model \((U,\Omega _G)\). This symplectomorphism can be chosen such that it restricts to the identity map on C.
The notation just introduced will be used throughout the paper:

By Gotay’s theorem, studying \(\mathcal {C}^{1}\)-small deformations of \(C\subset (M,\omega )\) amounts to studying small sections of the local model \((U,\Omega _G)\) whose graph is coisotropic. The following result gives a convenient description for the coisotropic sections of \((U,\Omega _G)\). The statement and its proof use the following pieces of notation. A section \(\alpha \in \Gamma (U)\) defines a diffeomorphism onto its image, which we denote by \(\tau _\alpha :C\rightarrow \text {Graph}(\alpha )\). We set \(i_{\alpha }:\text {Graph}(\alpha )\hookrightarrow U\) to be the inclusion map, so we have \(\alpha =i_{\alpha }\circ \tau _\alpha \) as maps \(C\rightarrow U\).
Proposition 1.4
Let \(C^k\subset (M^{2n},\omega )\) be coisotropic with Gotay local model \((U,\Omega _{G})\). For any section \(\alpha \in \Gamma (U)\), we have
Consequently, the following are equivalent:
- (i):
-
\(\text {Graph}(\alpha )\subset (U,\Omega _{G})\) is coisotropic.
- (ii):
-
\(\big (\alpha ^{*}\Omega _G\big )^{k-n+1}=0\).
- (iii):
-
\(\omega _{C}-d(j(\alpha ))\in \Omega ^{2}(C)\) has constant rank, equal to the rank of \(\omega _{C}\).
Proof
We first check that the equality (1) holds. Denoting by \(\theta _{can}\) the tautological one-form on \(T^{*}C\), we have
Here, the second equality uses that \(p\circ \alpha =\text {Id}_{C}\), and the third equality holds by the defining property of the tautological one-form (see [5, Prop. 3.4]), which states that the section \(j\circ \alpha \in \Gamma (T^{*}C)\) pulls back the tautological one-form \(\theta _{can}\in \Omega ^{1}(T^{*}C)\) to \(j(\alpha )\in \Omega ^{1}(C)\).
We now show that (i), (ii) and (iii) are equivalent. By Lemma 1.2, \(\text {Graph}(\alpha )\subset (U,\Omega _G)\) is coisotropic exactly when the pullback \(i_{\alpha }^{*}\Omega _G\in \Omega ^{2}(\text {Graph}(\alpha ))\) has constant rank equal to \(2(k-n)\), or equivalently, when \((i_{\alpha }^{*}\Omega _G)^{k-n+1}=0\). Since the map \(\tau _\alpha :C\rightarrow \text {Graph}(\alpha )\) is a diffeomorphism, the former statement is equivalent with \(\tau _\alpha ^{*}(i_{\alpha }^{*}\Omega _G)=\alpha ^{*}\Omega _{G}\) having constant rank \(2(k-n)\), and the latter with \((\alpha ^{*}\Omega _{G})^{k-n+1}=\tau _\alpha ^{*}((i_{\alpha }^{*}\Omega _G)^{k-n+1})=0\). Along with the equality (1), this proves that (i), (ii) and (iii) are indeed equivalent. \(\square \)
Proposition 1.4 shows that a coisotropic deformation of C defines an exact deformation of the presymplectic structure \(\omega _{C}\), i.e., we have an assignment
Instead of working with coisotropic sections of \((U,\Omega _G)\), it is more convenient to work with the associated presymplectic forms, because these are all defined on the same manifold C.
2.2 Deformations with fixed characteristic foliation
Given a coisotropic submanifold \(C\subset (M,\omega )\) with characteristic foliation \(\mathcal {F}\), our aim is to study deformations of C whose characteristic foliation is diffeomorphic to \(\mathcal {F}\). We will now introduce this deformation space, and a local model for it which conveniently describes small deformations.
Definition 1.5
We define \(\text {Def}_{\mathcal {F}}(C)\) to be the space of coisotropic submanifolds \(C'\) of \((M,\omega )\) for which there exists a foliated diffeomorphism \((C',\mathcal {F}')\overset{\sim }{\rightarrow }\ (C,\mathcal {F})\).
We are interested in elements of \(\text {Def}_{\mathcal {F}}(C)\) \(\mathcal {C}^{1}\)-close to C. That is, passing to the Gotay local model \((U,\Omega _{G})\) of C, we look at coisotropic sections \(\alpha \in \Gamma (U)\) for which \((\text {Graph}(\alpha ),\ker (i_{\alpha }^{*}\Omega _{G}))\) and \((C,\ker \omega _{C})\) are diffeomorphic as foliated manifolds. In this respect, note the following.
Lemma 1.6
For any coisotropic section \(\alpha \) of \((U,\Omega _G)\), the following are equivalent:
-
(i)
There exists a foliated diffeomorphism \(\psi :(C,\ker \omega _{C})\rightarrow (\text {Graph}(\alpha ),\ker (i_{\alpha }^{*}\Omega _{G}))\).
-
(ii)
There exists a foliated diffeomorphism \(\phi :(C,\ker \omega _{C})\rightarrow \big (C,\ker (\omega _{C}-d(j(\alpha )))\big )\).
Proof
Recall from Proposition 1.4 that the section \(\alpha \) defines a diffeomorphism \(\tau _\alpha :C\rightarrow \text {Graph}(\alpha )\) with inverse \(p|_{\text {Graph}(\alpha )}:\text {Graph}(\alpha )\rightarrow C\), satisfying \(\tau _\alpha ^{*}(i_{\alpha }^{*}\Omega _{G})=\omega _{C}-d(j(\alpha ))\). Consequently, given \(\psi \), we define \(\phi :=p|_{\text {Graph}(\alpha )}\circ \psi \). Conversely, given \(\phi \), we set \(\psi :=\tau _\alpha \circ \phi \). \(\square \)
The lemma above motivates the following definition, which introduces the local model \(\text {Def}^{U}_{\mathcal {F}}(C)\) for the space \(\text {Def}_{\mathcal {F}}(C)\). This is the key object of study in this note.
Definition 1.7
Let \(C\subset (M,\omega )\) be a coisotropic submanifold with characteristic foliation \(\mathcal {F}\) and Gotay local model \((U,\Omega _G)\). We set \(\text {Def}^{U}_{\mathcal {F}}(C)\) to be the space of \(\alpha \in \Gamma (U)\) such that
Remark 1.8
The existence of a foliated diffeomorphism \((C,\ker \omega _{C})\overset{\sim }{\rightarrow }\big (C,\ker (\omega _{C}-d(j(\alpha )))\big )\) actually implies that \(\text {Graph}(\alpha )\) is coisotropic in \((U,\Omega _G)\), because of Proposition 1.4. Nevertheless, we prefer to include the first requirement in Definition 1.7 for the sake of clarity.
In conclusion, the map (2), combined with the map which takes a constant rank two-form to its kernel, yields a two-step process
which assigns to a coisotropic deformation \(\alpha \in \Gamma (U)\) of C a deformation of its characteristic foliation \(\mathcal {F}\). We restrict attention to those elements \(\alpha \in \text {Def}_{U}(C)\) for which the image under this map is equivalent with \(\mathcal {F}\) by means of a diffeomorphism.
Example 1.9
We present a class of coisotropic submanifolds that have an abundance of deformations with diffeomorphic characteristic foliation. If \(C\subset (M^{2n},\omega )\) is coisotropic of codimension q, then C is called of q-contact type [3] if there exist \(\alpha _1,\ldots ,\alpha _q\in \Omega ^{1}(C)\) such that:
-
(1)
\(d\alpha _i=\omega _{C}\) for \(i=1,\ldots ,q\).
-
(2)
\(\alpha _1\wedge \ldots \wedge \alpha _q\wedge \omega _{C}^{n-q}\) is nowhere zero on C.
We give some concrete examples. First, a Lagrangian torus \(C\subset (M^{2n},\omega )\) is of n-contact type with \(\alpha _i=d\theta _i\), where \((\theta _1,\ldots ,\theta _n)\) are the angular coordinates on the torus C. Second, the unit sphere \(S^{3}\subset (\mathbb {R}^{4},\omega _{can})\) is of 1-contact type with \(\alpha \) equal to the usual connection one-form on \(S^{3}\) for the Hopf fibration, i.e.,
There is a normal form around coisotropic submanifolds of q-contact type [3, Lemma 1] which refines Gotay’s theorem, stating that a neighborhood of C in \((M,\omega )\) is symplectomorphic with the model
Here, \(B_{\epsilon }^{q}\) is the \(\epsilon \)-ball in \(\mathbb {R}^{q}\) centered at the origin, \((y_1,\ldots ,y_q)\) are the coordinates on \(B_{\epsilon }^{q}\) and \(p:C\times B_{\epsilon }^{q}\rightarrow C\) is the projection. As a consequence of this normal form, all slices \(C\times \{h\}\) for small enough \(h\in B_{\epsilon }^{q}\) are coisotropic deformations of C whose characteristic foliation is diffeomorphic with that of C. Indeed, pulling back the symplectic form (3) to \(C\times \{h\}\), we obtain
This shows that as long as \(\Vert h\Vert \) is small enough so that \(1+\sum _{i=1}^{q}h_i\) is nonzero, then \(C\times \{h\}\) is coisotropic, and the projection \(p|_{C\times \{h\}}:C\times \{h\}\rightarrow C\) is a diffeomorphism which matches the characteristic foliations of \(C\times \{h\}\) and C.
2.3 First-order deformations of coisotropic submanifolds and foliations
There are two classes of geometric objects whose deformation theory is important in this note, namely coisotropic submanifolds and foliations. At the infinitesimal level, the deformations of these objects are governed by certain cochain complexes and their associated cohomology groups, which we now recall.
2.3.1 Coisotropic submanifolds
Let \(C\subset (M,\omega )\) be a coisotropic submanifold with characteristic foliation \(\mathcal {F}\). It is well-known that the complex governing infinitesimal deformations of C is the leafwise de Rham complex \(\big (\Omega ^{\bullet }(\mathcal {F}),d_{\mathcal {F}}\big )\), see [18, 22]. Here \(\Omega ^{k}(\mathcal {F}):=\Gamma (\wedge ^{k}T^{*}\mathcal {F})\), and the differential \(d_{\mathcal {F}}\) is defined by the usual Koszul formula
We spell this out in the following lemma, which was already obtained in [22, Cor. 2.5] using Poisson geometry. We give a simple alternative argument, which only relies on Proposition 1.4.
Lemma 1.10
Let \(C^{k}\subset (M^{2n},\omega )\) be coisotropic with Gotay local model \((U,\Omega _G)\). If \(\alpha _t\) is a smooth one-parameter family of coisotropic sections of U starting at the zero section \(\alpha _0=0\), then  is closed with respect to \(d_{\mathcal {F}}\).
is closed with respect to \(d_{\mathcal {F}}\).
Proof
By Proposition 1.4, we have

also using that the pullback of \(\Omega _G\) to the zero section is \(\omega _C\). Since C is coisotropic, we know that \(k\ge n\), hence (4) implies that  . So for all \(V,W\in \Gamma (T\mathcal {F})\), we have
. So for all \(V,W\in \Gamma (T\mathcal {F})\), we have

By Lemma 1.2 (ii), the rank of \(\omega _{C}\) is \(2(k-n)\), so that \(\omega _{C}^{k-n}\) is nowhere zero. So we necessarily have that  vanishes, which shows that
vanishes, which shows that  . \(\square \)
. \(\square \)
This result motivates the following definition.
Definition 1.11
Assume that \(C\subset (M,\omega )\) is a coisotropic submanifold with characteristic foliation \(\mathcal {F}\) and Gotay local model \((U,\Omega _G)\).
-
(i)
A first-order deformation of C is a foliated one-form \(\beta \in \Omega ^{1}(\mathcal {F})\) which is \(d_{\mathcal {F}}\)-closed.
-
(ii)
A first-order deformation \(\beta \) is said to be unobstructed if there exists a smooth path \(\alpha _t\) of coisotropic sections of U starting at the zero section \(\alpha _0=0\), satisfying
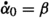 . Otherwise, we say that \(\beta \) is obstructed.
. Otherwise, we say that \(\beta \) is obstructed.
It is well-known that a coisotropic submanifold C has obstructed first-order deformations in general, reflecting the fact that the space of coisotropic submanifolds may fail to be smooth around C. See [27] for an example where this occurs.
2.3.2 Foliations
Let \(\mathcal {F}\) be a foliation on a manifold C. The normal bundle \(N\mathcal {F}:=TC/T\mathcal {F}\) carries a flat \(T\mathcal {F}\)-connection, called the Bott connection, which is defined by
We obtain a complex \(\big (\Omega ^{\bullet }(\mathcal {F};N\mathcal {F}),d_{\nabla }\big )\), where \(\Omega ^{k}(\mathcal {F};N\mathcal {F}):=\Gamma (\wedge ^{k}T^{*}\mathcal {F}\otimes N\mathcal {F})\) are foliated forms with values in \(N\mathcal {F}\), and the differential \(d_{\nabla }\) is defined by
The work [14] of Heitsch shows that infinitesimal deformations of the foliation \(\mathcal {F}\) are one-cocycles in \(\big (\Omega ^{\bullet }(\mathcal {F};N\mathcal {F}),d_{\nabla }\big )\). Moreover, if a smooth deformation of \(\mathcal {F}\) is obtained applying an isotopy to \(\mathcal {F}\), then the corresponding infinitesimal deformation is a one-coboundary in \(\big (\Omega ^{\bullet }(\mathcal {F};N\mathcal {F}),d_{\nabla }\big )\). We now spell this out in a bit more detail.
Assume we are given a smooth path of foliations \(\mathcal {F}_{t}\) with \(\mathcal {F}_{0}=\mathcal {F}\). We fix a complement G to \(T\mathcal {F}\) and identify \(G\cong N\mathcal {F}\). The induced Bott connection on G is given by
where \(\text {pr}_{G}:TC\rightarrow G\) is the projection. Say that C is compact, then there exists \(\epsilon >0\) such that \(T\mathcal {F}_t\) is still transverse to G for \(0\le t\le \epsilon \). We can therefore assume that
for some \(\eta _t\in \Gamma (T^{*}\mathcal {F}\otimes G)\). The next result is essentially [14, Cor. 2.11] and [14, Prop. 2.12].
Lemma 1.12
In the setup described above, we have:
-
(1)
The infinitesimal deformation
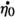 is closed with respect to \(d_{\nabla }\).
is closed with respect to \(d_{\nabla }\). -
(2)
If the path \(\mathcal {F}_t\) is generated by an isotopy \((\phi _t)\), i.e., \(T\mathcal {F}_t=(\phi _t)_{*}T\mathcal {F}\), then the corresponding infinitesimal deformation is exact. Indeed,
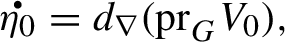
where \((V_t)\) is the time-dependent vector field corresponding with the isotopy \((\phi _t)\).
Remark 1.13
Actually, [14, Prop. 2.12] only concerns infinitesimal deformations arising from a path of foliations generated by the flow of a (time-independent) vector field. However, it is clear that the proof still works when the vector field is time-dependent, and the resulting statement is part (2) of Lemma 1.12.
Lemma 1.12 justifies the following definition.
Definition 1.14
Let \(\mathcal {F}\) be a foliation on a manifold C.
-
(i)
A first-order deformation of \(\mathcal {F}\) is an element \(\eta \in \Omega ^{1}(\mathcal {F};N\mathcal {F})\) which is \(d_{\nabla }\)-closed.
-
(ii)
We call \(\mathcal {F}\) infinitesimally rigid if the cohomology group \(H^{1}(\mathcal {F};N\mathcal {F})\) vanishes.
Let us also mention here that the Bott connection \(\nabla \) on \(N\mathcal {F}\) induces a flat \(T\mathcal {F}\)-connection \(\nabla ^{*}\) on \(N^{*}\mathcal {F}\cong T\mathcal {F}^{0}\). The two are related by the Leibniz rule
Of particular interest to us is the case in which the foliation \(\mathcal {F}\) is transversely symplectic, i.e., \(T\mathcal {F}=\ker \omega _C\) for a closed two-form \(\omega _C\in \Omega ^{2}(C)\). Then, we have a vector bundle isomorphism \(\omega _C^{\flat }:N\mathcal {F}\rightarrow N^{*}\mathcal {F}\), and it was noticed in [23, Lemma 5.2] that this isomorphism is compatible with the flat connections \(\nabla \) and \(\nabla ^{*}\), i.e.,
It follows that \(\omega _C^{\flat }\) induces an isomorphism of complexes
hence also an isomorphism in cohomology \( H^{\bullet }(\mathcal {F};N\mathcal {F})\overset{\sim }{\rightarrow } H^{\bullet }(\mathcal {F};N^{*}\mathcal {F})\).
3 First-order deformations and the transverse differentiation map
In this section, we investigate what happens at the infinitesimal level when deforming a coisotropic submanifold C inside the class \(\text {Def}_{\mathcal {F}}(C)\). We argue that first-order deformations of C are leafwise closed one-forms \(\alpha \in \Omega ^{1}(\mathcal {F})\) whose cohomology class \([\alpha ]\) lies in the kernel of a certain transverse differentiation map \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\).
3.1 Smooth paths in \(\mathbf {\text {Def}^{U}_{\mathcal {F}}(C)}\)
In order to linearize the conditions in Definition 1.7, we first need to specify what are smooth paths in the local deformation space \(\mathbf {\text {Def}^{U}_{\mathcal {F}}(C)}\). We will start by defining a notion of smooth path in \(\text {Def}_{\mathcal {F}}(C)\), which we use to induce a notion of smooth path in \(\mathbf {\text {Def}^{U}_{\mathcal {F}}(C)}\).
Definition 2.1
A path \(C_t\) in \(\text {Def}_{\mathcal {F}}(C)\) is smooth if there is a smooth path of embeddings \(\Phi _t:C\hookrightarrow M\) such that \(C_{t}=\Phi _t(C)\) and \(\Phi _t:(C,\mathcal {F})\rightarrow (C_t,\mathcal {F}_{t})\) is a foliated diffeomorphism.
In what follows, it is crucial that a smooth path in \(\text {Def}_{\mathcal {F}}(C)\) comes with a smooth family of foliated diffeomorphisms. We comment some more on Definition 2.1 in the following remark.
Remark 2.2
Note that there is a 1 : 1 correspondence between the spaces
and
There is an obvious notion of smooth path in \(\text {Emb}_{\mathcal {F}}(C)\), while \(\text {Pairs}_{\mathcal {F}}(C)\) clearly surjects onto \(\text {Def}_{\mathcal {F}}(C)\). We obtain our notion of smooth path in \(\text {Def}_{\mathcal {F}}(C)\), by declaring a path \((C_t)\) in \(\text {Def}_{\mathcal {F}}(C)\) to be smooth if it lifts to a smooth path in \(\text {Pairs}_{\mathcal {F}}(C)\cong \text {Emb}_{\mathcal {F}}(C)\).
We now make a choice of tubular neighborhood of C via Gotay’s theorem, and we restrict to \(\mathcal {C}^{1}\)-small deformations of C that stay inside this neighborhood \((U,\Omega _{G})\).
Definition 2.3
A path \(\alpha _t\) in \(\text {Def}^{U}_{\mathcal {F}}(C)\) is smooth if there is a smooth path of embeddings \(\Phi _t:C\hookrightarrow U\) such that \(\text {Graph}(\alpha _t)=\Phi _t(C)\) and \(p\circ \Phi _t:(C,\ker \omega _{C})\rightarrow \big (C,\ker (\omega _{C}-d(j(\alpha _t)))\big )\) is a foliated diffeomorphism.
Remark 2.4
As in Rem. 2.2, there is a 1 : 1 correspondence between the spaces
and
Explicitly, the correspondence is given by
with inverse
Again, there is an obvious notion of smooth path in \(\text {Emb}_{\mathcal {F}}^{U}\), while \(\text {Pairs}_{\mathcal {F}}^{U}(C)\) clearly surjects onto \(\text {Def}_{\mathcal {F}}^{U}(C)\). We then obtain our notion of smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\), by declaring a path \((\alpha _t)\) in \(\text {Def}_{\mathcal {F}}^{U}(C)\) to be smooth if it lifts to a smooth path in \(\text {Pairs}_{\mathcal {F}}^{U}(C)\cong \text {Emb}_{\mathcal {F}}^{U}(C)\).
3.2 First-order deformations
Given a smooth path \(\alpha _t\) in \(\text {Def}^{U}_{\mathcal {F}}(C)\) deforming C, we will now figure out what properties are satisfied by the corresponding infinitesimal deformation  . We first give a non-canonical description of infinitesimal deformations in terms of a certain chain map. We then rephrase this description in a canonical way by passing to cohomology.
. We first give a non-canonical description of infinitesimal deformations in terms of a certain chain map. We then rephrase this description in a canonical way by passing to cohomology.
3.2.1 A provisional definition
One would expect that in some way, the infinitesimal deformation  gives rise to a trivial infinitesimal deformation of the foliation \(\mathcal {F}\), namely a 1-coboundary in the Bott complex \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\). We claim that this happens by means of the following map, which we denote provisionally by \(\Phi \).
gives rise to a trivial infinitesimal deformation of the foliation \(\mathcal {F}\), namely a 1-coboundary in the Bott complex \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\). We claim that this happens by means of the following map, which we denote provisionally by \(\Phi \).
Definition 2.5
Let \(\Phi :\Gamma (\wedge ^{k}T^{*}\mathcal {F})\rightarrow \Gamma (\wedge ^{k}T^{*}\mathcal {F}\otimes G)\) denote the map defined by
for \(\alpha \in \Gamma (\wedge ^{k}T^{*}\mathcal {F}), \beta \in \Gamma (G^{*})\) and \(V_{1},\ldots ,V_{k}\in \Gamma (T\mathcal {F})\).
In other words, the map \(\Phi \) is defined as follows. For \(\alpha \in \Gamma (\wedge ^{k}T^{*}\mathcal {F})\), we have that
The map \(\Phi \) picks the component in \(\Gamma (\wedge ^{k}T^{*}\mathcal {F}\otimes G^{*})\), and then applies the isomorphism
Lemma 2.6
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold with local model \((U,\Omega _G)\). Assume that \(\alpha _t\) is a smooth curve in \(\text {Def}_{\mathcal {F}}^{U}(C)\) passing through C at time \(t=0\). Then, the infinitesimal deformation  satisfies the following:
satisfies the following:
-
(1)
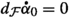 ,
, -
(2)
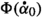 is exact in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\).
is exact in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\).
Proof
We already know that item (i) holds by Lemma 1.10, so we only have to prove (ii). Compactness of C implies that there exists \(\epsilon >0\) such that \(\ker \big (\omega _{C}-d(j(\alpha _t))\big )\subset T\mathcal {F}\oplus G\) is still transverse to G for all \(0\le t\le \epsilon \). This means that there exist \(\eta _t\in \Gamma (T^{*}\mathcal {F}\otimes G)\) such that \(\ker \big (\omega _{C}-d(j(\alpha _t))\big )=\text {Graph}(\eta _{t})\) for all \(t\in [0,\epsilon ]\). So for all \(v\in T\mathcal {F}\), we have that \(v+\eta _t(v)\in \ker \big (\omega _{C}-d(j(\alpha _t))\big )\), it follows that
Differentiating at \(t=0\), we get

Consequently, for any \(\beta \in G^{*}\), we have

showing that  . It remains to argue that
. It remains to argue that  is a coboundary in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\). Since \(\alpha _t\) is a smooth path in \(\text {Def}^{U}_{\mathcal {F}}(C)\), Definition 2.3 guarantees that there exists a smooth family \((\phi _t)\in \text {Diff}(C)\) such that
is a coboundary in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\). Since \(\alpha _t\) is a smooth path in \(\text {Def}^{U}_{\mathcal {F}}(C)\), Definition 2.3 guarantees that there exists a smooth family \((\phi _t)\in \text {Diff}(C)\) such that
Precomposing \(\phi _t\) with \(\phi _{0}^{-1}\), we can assume that \(\phi _0=\text {Id}_{C}\), so that the family of foliations \(\text {Graph}(\eta _t)\) for \(t\in [0,\epsilon ]\) is generated by applying an isotopy to \(T\mathcal {F}\). Part (2) of Lemma 1.12 now implies that  is indeed exact in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\). This finishes the proof. \(\square \)
is indeed exact in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\). This finishes the proof. \(\square \)
The above lemma motivates the following provisional definition.
Definition 2.7
(Provisional) When deforming C inside \(\text {Def}_{\mathcal {F}}(C)\), a first-order deformation is a foliated one-form \(\beta \in \Omega ^{1}(\mathcal {F})\) such that \(d_{\mathcal {F}}\beta =0\) and \(\Phi (\beta )\) is exact in \(\big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big )\).
3.2.2 A canonical definition
Definition 2.7 is not entirely satisfactory, since it makes reference to the chosen complement G. In what follows, we derive an equivalent definition which is completely canonical. This is done by showing that \(\Phi \) is a chain map (up to sign), and that the induced map in cohomology is canonical (i.e., independent of the complement G). The proofs of these statements use ingredients from the spectral sequence of the foliation \(\mathcal {F}\). We defer the proofs to Sect. 5.1 in Appendix, to avoid disrupting the flow of the paper.
The description of the map in cohomology induced by \(\Phi \) involves the following well-known operation in foliation theory. Recall that any foliation \(\mathcal {F}\) comes with a transverse differentiation map, denoted by
This map is constructed as follows [19]. If \(r:\Omega ^{\bullet }(C)\rightarrow \Omega ^{\bullet }(\mathcal {F})\) denotes the restriction to the leaves of \(\mathcal {F}\), then there is a short exact sequence of complexes
It induces a long exact sequence in cohomology
The connecting homomorphism \(\mathfrak {d}\) is defined as
where \(\widetilde{\alpha }\in \Omega ^{k}(C)\) is any extension of \(\alpha \in \Omega ^{k}(\mathcal {F})\). Next, let \(p:\Omega ^{k+1}_{\mathcal {F}}(C)\rightarrow \Omega ^{k}(\mathcal {F},N^{*}\mathcal {F})\) denote the map characterized by
for \(V_1,\ldots ,V_k\in \Gamma (T\mathcal {F})\) and \(\overline{N}\in \Gamma (N\mathcal {F})\). This map is well-defined because forms in \(\Omega ^{\bullet }_{\mathcal {F}}(C)\) vanish when evaluated on elements of \(\Gamma (T\mathcal {F})\). Since p commutes with the differentials d and \(d_{\nabla ^{*}}\), there is an induced map in cohomology
The transverse differentiation map (6) is obtained by composing the maps (7) and (8).
Definition 2.8
The transverse differentiation map \(d_{\nu }\) is defined by
where \(\widetilde{\alpha }\in \Omega ^{k}(C)\) is any extension of \(\alpha \in \Omega ^{k}(\mathcal {F})\).
Remark 2.9
The map \(d_{\nu }\) appears for instance in the study of symplectic foliations \((\mathcal {F},\omega )\). There \(d_{\nu }[\omega ]\in H^{2}(\mathcal {F};N^{*}\mathcal {F})\) measures the transverse variation of the leafwise symplectic form \(\omega \in \Omega ^{2}(\mathcal {F})\), which plays a role in the integrability problem for the associated regular Poisson structure [8, §5].
The following result allows us to describe first-order deformations of C inside \(\text {Def}_{\mathcal {F}}(C)\) in a canonical way. For the proof, we refer to Sect. 5.1 in Appendix.
Proposition 2.10
-
(i)
The map
$$\begin{aligned} \Phi :\big (\Omega ^{\bullet }(\mathcal {F}),d_{\mathcal {F}}\big )\rightarrow \big (\Omega ^{\bullet }(\mathcal {F};G),d_{\nabla }\big ) \end{aligned}$$is a chain map, up to sign. That is, \(\Phi \circ d_{\mathcal {F}}=-d_{\nabla }\circ \Phi \).
-
(ii)
The map \([\Phi ]\) induced in cohomology is canonical, since it agrees with
$$\begin{aligned} \big [-\text {Id}\otimes (\omega _{C}^{\flat })^{-1}\big ]\circ d_{\nu }:H^{\bullet }(\mathcal {F})\rightarrow H^{\bullet }(\mathcal {F};N\mathcal {F}). \end{aligned}$$
Because the map \(\big [-\text {Id}\otimes (\omega _{C}^{\flat })^{-1}\big ]:H^{\bullet }(\mathcal {F};N^{*}\mathcal {F})\rightarrow H^{\bullet }(\mathcal {F};N\mathcal {F})\) appearing in Proposition 2.10 is an isomorphism, we can now rephrase Definition 2.7 as follows.
Definition 2.11
When deforming C inside \(\text {Def}_{\mathcal {F}}(C)\), a first-order deformation is a foliated one-form \(\beta \in \Omega ^{1}(\mathcal {F})\) such that \(d_{\mathcal {F}}\beta =0\) and the cohomology class \([\beta ]\in H^{1}(\mathcal {F})\) lies in the kernel of the transverse differentiation map \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\).
We finish this section by giving a geometric description of first-order deformations. For the proof, see again Sect. 5.1 in Appendix.
Lemma 2.12
Let C be a manifold with a foliation \(\mathcal {F}\). For any \(\beta \in \Omega ^{1}(\mathcal {F})\), the following are equivalent:
-
(1)
\(d_{\mathcal {F}}\beta =0\) and \(d_{\nu }[\beta ]=0\),
-
(2)
There exists an extension \(\widetilde{\beta }\in \Omega ^{1}(C)\) of \(\beta \) such that \(\iota _{V}d\widetilde{\beta }=0\) for all \(V\in \Gamma (T\mathcal {F})\).
Recall that a differential form \(\eta \) on a foliated manifold \((C,\mathcal {F})\) is called basic if \(\iota _{V}\eta =0\) and \(\pounds _{V}\eta =0\) for all \(V\in \Gamma (T\mathcal {F})\). If the foliation \(\mathcal {F}\) is simple, this means that \(\eta \) descends to the leaf space \(C/\mathcal {F}\). The basic differential forms constitute a subcomplex \((\Omega ^{\bullet }_{bas}(C),d)\) of the de Rham complex. Statement (2) in Lemma 2.12 says that \(d\tilde{\beta }\in \Omega ^{2}_{bas}(C)\).
Example 2.13
(The integral case) Let C be a compact coisotropic submanifold whose characteristic foliation \(\mathcal {F}\) is given by the fibers of a smooth fiber bundle \(pr:C\rightarrow C/\mathcal {F}\). Such coisotropic submanifolds are called integral, and they are studied in [20]. To facilitate the computation of first-order deformations of such C, it is useful to note that the cohomology groups \(H^{1}(\mathcal {F})\) and \(H^{1}(\mathcal {F};N^{*}\mathcal {F})\) have the following convenient descriptions [15, Thm. I.5.2].
-
The first cohomology groups of the fibers of pr constitute a vector bundle \(\mathcal {H}^{1}\) over \(C/\mathcal {F}\), i.e.,
$$\begin{aligned} \mathcal {H}^{1}_{q}=H^{1}(pr^{-1}(q))\hspace{0.5cm}\forall q\in C/\mathcal {F}, \end{aligned}$$(9)and \(H^{1}(\mathcal {F})\) can be identified canonically with the space of sections \(\Gamma (\mathcal {H}^{1})\). Namely, the class \([\beta ]\in H^{1}(\mathcal {F})\) corresponds with the section \(\tau _{\beta }\in \Gamma (\mathcal {H}^{1})\) given by
$$\begin{aligned} \tau _{\beta }:q\mapsto \left[ \beta |_{pr^{-1}(q)}\right] . \end{aligned}$$Moreover, the vector bundle \(\mathcal {H}^{1}\) carries a natural flat connection \(\nabla \), called the Gauss–Manin connection, which is defined as follows. Denoting by \(\mathfrak {X}(C)^{\mathcal {F}}\) the Lie subalgebra of \((\mathfrak {X}(C),[\cdot ,\cdot ])\) consisting of projectable vector fields,
$$\begin{aligned} \mathfrak {X}(C)^{\mathcal {F}}:=\left\{ Y\in \mathfrak {X}(C):[Y,\Gamma (T\mathcal {F})]\subset \Gamma (T\mathcal {F})\right\} , \end{aligned}$$we have a short exact sequence
$$\begin{aligned} 0\rightarrow \Gamma (T\mathcal {F})\hookrightarrow \mathfrak {X}(C)^{\mathcal {F}}\rightarrow \mathfrak {X}(C/\mathcal {F})\rightarrow 0. \end{aligned}$$(10)The Gauss–Manin connection is then defined as follows, for \(V\in \mathfrak {X}(C/\mathcal {F})\):
$$\begin{aligned} \nabla _{V}\tau _{\beta }:=\tau _{\pounds _{\widetilde{V}}\beta }, \end{aligned}$$where \(\widetilde{V}\in \mathfrak {X}(C)^{\mathcal {F}}\) is any lift of V in (10). The connection is well-defined because of Cartan’s magic formula, and it is flat because \([\widetilde{V},\widetilde{W}]\) is a lift of [V, W] whenever \(\widetilde{V},\widetilde{W}\in \mathfrak {X}(C)^{\mathcal {F}}\) are lifts of \(V,W\in \mathfrak {X}(C/\mathcal {F})\).
-
The cohomology group \(H^{1}(\mathcal {F},N^{*}\mathcal {F})\) can be identified with the space of one-forms on \(C/\mathcal {F}\) with values in the vector bundle \(\mathcal {H}^{1}\):
$$\begin{aligned} H^{1}(\mathcal {F};N^{*}\mathcal {F})\cong \Gamma (T^{*}(C/\mathcal {F})\otimes \mathcal {H}^{1}). \end{aligned}$$(11)
We now compute the kernel of \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F},N^{*}\mathcal {F})\). Fix a class \([\beta ]\in H^{1}(\mathcal {F})\), and let \(\widetilde{\beta }\in \Omega ^{1}(C)\) be any extension of \(\beta \). Denoting by \(r:\Omega ^{1}(C)\rightarrow \Omega ^{1}(\mathcal {F})\) the restriction map and using the isomorphism (11), we have
Hence, according to Definition 2.11, first-order deformations of an integral coisotropic submanifold are closed foliated one-forms that define flat sections of the vector bundle \(\big (\mathcal {H}^1,\nabla \big )\).
In [20], Ruan studies the deformation problem of an integral coisotropic submanifold C, within the class of integral coisotropic submanifolds. He shows that first-order deformations in this case are indeed closed foliated one-forms on C which define flat sections of \(\big (\mathcal {H}^1,\nabla \big )\), see [20, Lemma 2]. Hence, our Definition 2.11 is consistent with Ruan’s work.
4 Unobstructedness of first-order deformations
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold. It is known that the coisotropic deformation problem of C is obstructed in general, i.e., there may exist first-order deformations of C that are not tangent to any path of deformations [27]. However, Ruan proved that the deformation problem becomes unobstructed when restricting to integral coisotropic submanifolds [20], i.e., those for which the characteristic foliation is given by a fibration.
This section contains our main result, which states that the deformation problem of a compact coisotropic submanifold C inside the class \(\text {Def}_{\mathcal {F}}(C)\) (see Definition 1.5) is unobstructed. This is an extension of Ruan’s unobstructedness result, since the first-order deformations from Definition 2.11 reduce to those considered by Ruan in case \((C,\mathcal {F})\) is integral (see Example 2.13).
Definition 3.1
Given a compact coisotropic submanifold \(C\subset (M,\omega )\), a first-order deformation \(\beta \) of C (see Definition 2.11) is unobstructed if there exists a smooth path \(\alpha _{t}\) in \(\text {Def}_{\mathcal {F}}^{U}(C)\) (see Definition 2.3) such that \(\alpha _0=0\) and  . The deformation problem of C inside \(\text {Def}_{\mathcal {F}}(C)\) is unobstructed if all first-order deformations are unobstructed.
. The deformation problem of C inside \(\text {Def}_{\mathcal {F}}(C)\) is unobstructed if all first-order deformations are unobstructed.
As a first step, we consider the distinguished class of first-order deformations consisting of foliated one-forms \(\beta \in \Omega ^{1}(\mathcal {F})\) that admit a closed extension \(\widetilde{\beta }\in \Omega ^{1}(C)\). Such \(\beta \) indeed satisfy the requirements of Definition 2.11. These first-order deformations are easily proved to be unobstructed. The following lemma is just an enhancement of [22, Rem. 4.6].
Lemma 3.2
Let \(C\subset (M,\omega )\) be compact coisotropic submanifold with characteristic foliation \(\mathcal {F}\). If \(\beta \in \Omega ^{1}(\mathcal {F})\) admits a closed extension \(\widetilde{\beta }\in \Omega ^{1}(C)\), then \(\beta \) is an unobstructed first-order deformation of C.
Proof
Let \((U,\Omega _{G})\) be the Gotay local model for some choice of splitting \(TC=T\mathcal {F}\oplus G\), and denote by \(p:U\rightarrow C\) the projection. By assumption, we have a closed one-form \(p^{*}\tilde{\beta }\) on U, which gives rise to a symplectic vector field
Let \((\phi _t)\) denote the flow of X, and note that compactness of C implies that there exists \(\epsilon >0\) such that flow lines of X starting at points of C exist up to time \(\epsilon \). Shrinking \(\epsilon \) if necessary, we can assume that the submanifolds \(\phi _t(C)\) for \(0\le t<\epsilon \) are graphs of sections \(\alpha _t\in \Gamma (U)\). We now check that \(\alpha _t\) is a smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\), as defined in Definition 2.3.
It is clear that \(\text {Graph}(\alpha _t)\) is coisotropic, since C is coisotropic and the \(\phi _t\) are symplectomorphisms. It remains to check that
is a foliated diffeomorphism. To do so, note that
Since \(\phi _t^{*}\Omega _G=\Omega _G\), we have
and therefore
Also invoking Proposition 1.4, this confirms that (12) is a foliated diffeomorphism.
Finally, we check that \(\beta \) is tangent to the path \(\alpha _{t}\). By [22, Lemma 3.13], we have that  is the section of \(T^{*}\mathcal {F}\) defined by the vertical fiberwise constant vector field P(X) on U. Here, P denotes the restriction to C composed with the vertical projection in the splitting \(TU|_{C}=TC\oplus T^{*}\mathcal {F}\). Using Lemma 5.6 in Appendix, we conclude that
is the section of \(T^{*}\mathcal {F}\) defined by the vertical fiberwise constant vector field P(X) on U. Here, P denotes the restriction to C composed with the vertical projection in the splitting \(TU|_{C}=TC\oplus T^{*}\mathcal {F}\). Using Lemma 5.6 in Appendix, we conclude that

Here, the second equality uses the fact that \(\Omega _G(TC,T\mathcal {F})=0\). This finishes the proof. \(\square \)
One can use Lemma 3.2 to show that the deformation problem of C inside \(\text {Def}_{\mathcal {F}}(C)\) is unobstructed whenever \(C\rightarrow C/\mathcal {F}\) is a fiber bundle admitting a global section. That is to say, a special case of Ruan’s unobstructedness result for integral coisotropic submanifolds follows from Lemma 3.2. We provide the details in the following example.
Example 3.3
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold for which \(pr:C\rightarrow C/\mathcal {F}\) is a fiber bundle admitting a global section \(\sigma \). If \(\beta \in \Omega ^{1}(\mathcal {F})\) is a first-order deformation of C inside \(\text {Def}_{\mathcal {F}}(C)\), then according to Lemma 2.12, \(\beta \) has an extension \(\widetilde{\beta }\in \Omega ^{1}(C)\) satisfying
for some \(\gamma \in \Omega ^{2}(C/\mathcal {F})\). Moreover, since \(pr\circ \sigma =\text {Id}\), we have
This implies that \(\widetilde{\beta }-pr^{*}(\sigma ^{*}\widetilde{\beta })\) is a closed extension of \(\beta \). By Lemma 3.2, \(\beta \) is unobstructed.
A concrete example of this type is the coisotropic submanifold considered in [27]. There C is the torus \(\mathbb {T}^{4}\) with presymplectic form \(\omega _{C}=d\theta _1\wedge d\theta _2\). The characteristic foliation \(\mathcal {F}\) is given by the fibers of the trivial \(\mathbb {T}^{2}\)-bundle
Choosing \(G:=\text {Span}\{\partial _{\theta _1},\partial _{\theta _2}\}\) as a complement, C is coisotropic in the Gotay local model
where \((\xi _1,\xi _2)\) are the fiber coordinates corresponding with the frame \(\{d\theta _3,d\theta _4\}\) of \(T^{*}\mathcal {F}\). It was shown in [27] that the deformation problem of C—as a coisotropic submanifold—is obstructed. That is, there exist closed foliated one-forms \(\beta \in \Omega ^{1}(\mathcal {F})\) that are not tangent to a path of coisotropic deformations. By contrast, the restricted deformation problem of C inside \(\text {Def}_{\mathcal {F}}(C)\) is unobstructed. That is, any closed foliated one-form \(\beta \in \Omega ^{1}(\mathcal {F})\) that gives rise to a class in the kernel of \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\) is tangent to a path of coisotropic deformations, whose characteristic foliation is moreover diffeomorphic with \(\mathcal {F}\).
We now proceed to the proof of our main theorem. The argument relies on the following lemma, which is based on a result in the forthcoming work [24].
Lemma 3.4
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold with Gotay local model \((U,\Omega _G)\). Assume that \(\{\eta _t\}_{0\le t\le \epsilon }\) is a smooth family of presymplectic structures on C with

Shrinking \(\epsilon \) if necessary, there exist a smooth path \(\{\sigma _t\}_{0\le t\le \epsilon }\subset \text {Def}_{\mathcal {F}}^{U}(C)\) with \(\sigma _0=0\), and a smooth family of diffeomorphisms \(\{\psi _t\}_{0\le t\le \epsilon }\subset \text {Diff}_{0}(C)\) such that \(\psi _{0}=\text {Id}\) and
The lemma gives sufficient conditions for presymplectic structures close to \(\omega _C\) to be obtained from coisotropic sections of the local model \((U,\Omega _G)\), up to isotopy. In other words, it gives presymplectic structures that lie in the image of the map (2), when we quotient the codomain by the equivalence relation given by isotopies.
Proof of Lemma 3.4
For each value of \(t\in [0,\epsilon ]\), we can use G as a complement to \(\ker \eta _t\). Constructing the associated Gotay local models, we get a family of symplectic structures
defined on a neighborhood \(U_t\) of \(C\subset T^{*}\mathcal {F}\). The tube lemma implies that the intersection \(\cap _{t\in [0,\epsilon ]}U_t\) is an open neighborhood of C; hence shrinking U if necessary, we can assume that all \(\omega _t\) are symplectic on U for \(t\in [0,\epsilon ]\).
Since the inclusion \(i:C\hookrightarrow U\) induces an isomorphism in cohomology and the class \([\eta _t]\in H^{2}(C)\) is constant, the same holds for the class \([\omega _t]\in H^{2}(U)\):
Choosing primitives \(\frac{d}{dt}\omega _t=d\beta _t\), we now apply Moser’s argument. We make the ansatz
where \((\phi _t)\) is an isotopy with corresponding time-dependent vector field \((X_t)\). We can solve the equation \(\iota _{X_t}\omega _t=-\beta _t\) for \(X_t\in \mathfrak {X}(U)\). Since C is compact, we can shrink \(\epsilon >0\) such that \(\phi _{t}^{-1}(C)\) is the graph of a section \(\sigma _t\in \Gamma (U)\) for each \(0\le t\le \epsilon \). For such t, the map
is a diffeomorphism and we have
We claim that the pair \((\sigma _t,\psi _t:=f_t^{-1})\) meets the requirements of the lemma. To show that \(\sigma _t\) is a smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\) (see Definition 2.3), we first check that \(\text {Graph}(\sigma _t)\subset (U,\Omega _G)\) is coisotropic. By the first equality in (15), we have
and this implies that
This shows that the rank of \(\sigma _{t}^{*}\Omega _G\) is equal to the rank of \(\eta _t\), which by assumption equals the rank of \(\omega _{C}\). Hence, \(\text {Graph}(\sigma _t)\subset (U,\Omega _G)\) is coisotropic, by Proposition 1.4. We also showed at the same time that the equality (14) is satisfied. It only remains to check that the map
is a foliated diffeomorphism. With Proposition 1.4 in mind, the equality (16) shows that
hence \(f_t\) takes the foliation \(\ker \eta _t=\ker \omega _C\) to the foliation \(\ker (\omega _{C}-d(j(\sigma _t)))\). \(\square \)
At last, we can prove our main result.
Theorem 3.5
If \(C\subset (M,\omega )\) is a compact coisotropic submanifold, then the deformation problem of C inside \(\text {Def}_{\mathcal {F}}(C)\) is unobstructed.
Proof
Let \(\beta \) be a first-order deformation of C, as defined in Definition 2.11. We will construct a smooth path \(\alpha _t\) in \(\text {Def}_{\mathcal {F}}^{U}(C)\) such that \(\alpha _0=0\) and  .
.
By Lemma 2.12, \(\beta \) has an extension \(\tilde{\beta }\in \Omega ^{1}(C)\) satisfying \(\iota _{V}d\tilde{\beta }=0\) for all \(V\in \Gamma (T\mathcal {F})\). Consider the family of two-forms \(\{\omega _C-td\tilde{\beta }\}_{t\ge 0}\) on C. By compactness, there exists \(\epsilon >0\) such that \(rk(\omega _C-td\tilde{\beta })_{p}\ge rk(\omega _C)_{p}\) for all \(0\le t\le \epsilon \) and \(p\in C\). But we also know that \(\ker \omega _C\subset \ker (\omega _C-td\tilde{\beta })\), so \(rk(\omega _C-td\tilde{\beta })_{p}\le rk(\omega _C)_{p}\) for all \(p\in C\) and \(t\ge 0\). In conclusion, for all \(0\le t\le \epsilon \), the two-form \(\omega _C-td\tilde{\beta }\) is presymplectic with the same kernel as \(\omega _C\).
We now apply Lemma 3.4. Shrinking \(\epsilon \) if necessary, there exist a smooth path \(\{\sigma _t\}_{0\le t\le \epsilon }\) in \(\text {Def}_{\mathcal {F}}^{U}(C)\) with \(\sigma _0=0\) and a smooth family of diffeomorphisms \(\{\psi _t\}_{0\le t\le \epsilon }\subset \text {Diff}_{0}(C)\) such that \(\psi _0=\text {Id}\) and
Let \((X_t)\) be the time-dependent vector field of \((\psi _t)\). Differentiating the equality (17) gives

Evaluating at \(t=0\), we get

and therefore

Let us denote the closed one-form between brackets by \(\theta \in \Omega ^{1}(C)\). It gives rise to a symplectic vector field \(Z:=(\Omega _{G}^{\flat })^{-1}(p^{*}\theta )\) on \((U,\Omega _G)\), with flow \((\phi _t)\). Shrinking \(\epsilon \) if necessary, we can make sure that the submanifolds \(\phi _t(\text {Graph}(\sigma _t))\) are graphs of sections \(\alpha _t\in \Gamma (U)\).
We claim that \(\alpha _t\) is a smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\). It is clear that \(\text {Graph}(\alpha _t)\subset (U,\Omega _G)\) is coisotropic, since \(\text {Graph}(\sigma _t)\) is coisotropic and \(\phi _t\) is a symplectomorphism. Because \(\sigma _t\) is a smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\), there exists a smooth path of embeddings \(\Phi _t:C\hookrightarrow U\) such that \(\text {Graph}(\sigma _t)=\Phi _t(C)\) and
is a foliated diffeomorphism. To conclude that \(\alpha _t\) is a smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\), it suffices to check that the embeddings \(\phi _t\circ \Phi _t:C\hookrightarrow U\) are such that
is a foliated diffeomorphism. To do so, we argue as in the proof of Lemma 3.2. Let us first define diffeomorphisms
so that
Because \(\phi _{t}^{*}\Omega _G=\Omega _G\), we have
hence by Proposition 1.4 this shows that
is a foliated diffeomorphism. Composing with (18), we get a foliated diffeomorphism
Since by (20), we have
this confirms that (19) is a foliated diffeomorphism. Hence, \(\alpha _t\) is a smooth path in \(\text {Def}_{\mathcal {F}}^{U}(C)\).
At last, we check that \(\beta \) is tangent to the path \(\alpha _t\). We denote by P the vertical projection induced by the splitting \(T(T^{*}\mathcal {F})|_{C}=TC\oplus T^{*}\mathcal {F}\). Using the expression (21) and the chain rule, we get for \(q\in C\) that

Here, we used that the last summand in the third line above is tangent to C. By Lemma 5.6 in the Appendix, we have that \(P(Z)\in \Gamma (T^{*}\mathcal {F})\) is the restriction to \(T\mathcal {F}\) of the one-form \(-\theta \in \Omega ^{1}(C)\), see the computation (13). That is,

and inserting this equality into (22), we obtain that  , as desired. \(\square \)
, as desired. \(\square \)
Remark 3.6
The coisotropic sections \(\sigma _t\) obtained in Lemma 3.4 are not uniquely determined since they depend on a choice of primitive, as the proof of Lemma 3.4 shows. Nevertheless, the proof of Theorem 3.5 shows that any path \(\sigma _t\) thus obtained can be used to prolong a first-order deformation \(\beta \), up to modifying the \(\sigma _t\) suitably by a symplectic isotopy.
Alternatively, instead of using the conclusion of Lemma 3.4, one can prove Theorem 3.5 by running the proof of Lemma 3.4 explicitly using a well-chosen primitive. Then, the coisotropic sections \(\sigma _t\) obtained this way do not need to be corrected anymore by a symplectic isotopy. This approach yields a simple algorithm which produces out of a first-order deformation \(\beta \) a path \(\{\sigma _t\}\) in \(\text {Def}_{\mathcal {F}}^{U}(C)\) with \(\sigma _0=0\) and  . It consists of the following steps:
. It consists of the following steps:
-
(1)
Fix an extension \(\widetilde{\beta }\in \Omega ^{1}(C)\) of \(\beta \) as in Lemma 2.12.
-
(2)
For small enough t, the two-forms
$$\begin{aligned} \omega _t:=p^{*}(\omega _C-td\tilde{\beta })+j^{*}\omega _{can}=\Omega _G-tp^{*}d\tilde{\beta } \end{aligned}$$are symplectic on a neighborhood of \(C\subset T^{*}\mathcal {F}\). There, one can solve the equation
$$\begin{aligned} \iota _{X_t}\omega _t=p^{*}\tilde{\beta }. \end{aligned}$$(23) -
(3)
Let \((\phi _t)\) be the flow of \(X_t\). For small enough t, we have \(\phi _t^{-1}(C)=\text {Graph}(\sigma _t)\) for a smooth path \(\sigma _t\) in \(\text {Def}_{\mathcal {F}}^{U}(C)\). Now
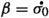 .
.
We have to justify that  . Since the time-dependent vector field of the isotopy \((\phi _t^{-1})\) is \(Z_t:=-(\phi _t^{-1})_{*}X_t\), it follows from [22, Lemma 3.13] that
. Since the time-dependent vector field of the isotopy \((\phi _t^{-1})\) is \(Z_t:=-(\phi _t^{-1})_{*}X_t\), it follows from [22, Lemma 3.13] that  is the foliated one-form defined by \(P(Z_0)=-P(X_0)\), where P is the vertical projection along the zero section \(C\subset T^{*}\mathcal {F}\). By Lemma 5.6, the latter is given by
is the foliated one-form defined by \(P(Z_0)=-P(X_0)\), where P is the vertical projection along the zero section \(C\subset T^{*}\mathcal {F}\). By Lemma 5.6, the latter is given by
The equality (23) says that
hence \(\Omega _G^{\flat }(X_0)=p^{*}\tilde{\beta }\). Inserting this in the expression (24), we obtain

5 Implications for the coisotropic deformation problem
We discuss what Theorem 3.5 tells us about the classical coisotropic deformation problem, which allows all coisotropic deformations of C instead of just those whose characteristic foliation is diffeomorphic with \(\mathcal {F}\). First, Theorem 3.5 gives a partial unobstructedness result in this context, for which we provide some examples. Second, Theorem 3.5 implies that the Kuranishi map of the \(L_{\infty }\)-algebra governing coisotropic deformations of C should vanish on elements of \(\ker (d_{\nu })\). We confirm that this is the case, by establishing a canonical description for the Kuranishi map in terms of the transverse differentiation map \(d_{\nu }\).
5.1 A partial unobstructedness result
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold with characteristic foliation \(\mathcal {F}\). As recalled in Sect. 1.3.1, first-order deformations of C—as a coisotropic submanifold—are closed foliated one-forms on \(\mathcal {F}\), and these are generally obstructed. It is however clear geometrically that a first-order deformation is unobstructed if it admits a closed extension, see [22, Rem. 4.6] or the proof of Lemma 3.2. Let us state this result for future reference.
Lemma 4.1
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold. Any first-order deformation \(\beta \in \Omega ^{1}(\mathcal {F})\) of C admitting a closed extension \(\widetilde{\beta }\in \Omega ^{1}(C)\) is unobstructed.
By Theorem 3.5 and Definition 2.11, we obtain the following partial unobstructedness result, which extends Lemma 4.1.
Corollary 4.2
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold. Any first-order deformation \(\beta \in \Omega ^{1}(\mathcal {F})\) of C whose cohomology class \([\beta ]\in H^{1}(\mathcal {F})\) lies in the kernel of the transverse differentiation map \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\) is unobstructed.
The following example illustrates how we can use Corollary 4.2 to find unobstructed first-order deformations which cannot be detected with Lemma 4.1.
Example 4.3
Let \(C^{2n-q}\subset (M^{2n},\omega )\) be a compact coisotropic submanifold of q-contact type, as introduced in Example 1.9. So there exist \(\alpha _1,\ldots ,\alpha _q\in \Omega ^{1}(C)\) such that:
-
(1)
\(d\alpha _i=\omega _C\) for \(i=1,\ldots ,q\).
-
(2)
\(\alpha _1\wedge \ldots \wedge \alpha _q\wedge \omega _C^{n-q}\) is nowhere zero on C.
Assume moreover that \(q<n\), to exclude the possibility that C is Lagrangian. As before, we denote \(r:\Omega ^{1}(C)\rightarrow \Omega ^{1}(\mathcal {F})\) the restriction map. We claim that the foliated one-forms \(r(\alpha _1),\ldots ,r(\alpha _q)\) are unobstructed first-order deformations of C by virtue of Corollary 4.2. We also claim that none of them admits a closed extension, showing that this unobstructedness result cannot be obtained via Lemma 4.1.
First note that item (1) implies that \(r(\alpha _i)\) is leafwise closed, so it indeed defines a first-order deformation of C. Moreover, the extension \(\alpha _i\in \Omega ^{1}(C)\) of \(r(\alpha _i)\in \Omega ^{1}(\mathcal {F})\) is such that \(d\alpha _i=\omega _C\in \Omega ^{2}_{bas}(C)\). Hence, it follows from Lemma 2.12 that \([r(\alpha _i)]\in H^{1}(\mathcal {F})\) lies in the kernel of \(d_{\nu }\). By Corollary 4.2, the first-order deformations \(r(\alpha _i)\) of C are unobstructed.
We now argue that the \(r(\alpha _i)\) do not admit closed extensions. The crucial observation is that the characteristic foliation \(\mathcal {F}\) of C is taut, i.e., there exists a Riemannian metric on C such that all the leaves of \(\mathcal {F}\) become minimal submanifolds.
Claim: The characteristic foliation \(\mathcal {F}\) is taut.
To prove the claim, recall that by Rummler’s criterion [4, Thm. 10.5.9], a q-dimensional foliation \(\mathcal {F}\) on C is taut exactly when there exists \(\gamma \in \Omega ^{q}(C)\) such that:
-
(i)
\(\gamma \) restricts to a volume form on each leaf of \(\mathcal {F}\),
-
(ii)
\(\gamma \) is \(\mathcal {F}\)-closed, i.e., \(d\gamma (V_1,\ldots ,V_{q+1})=0\) whenever at least q of the arguments \(V_1,\ldots ,V_{q+1}\) are tangent to \(\mathcal {F}\).
In the q-contact case, we can take \(\gamma :=\alpha _1\wedge \ldots \wedge \alpha _q\in \Omega ^{q}(C)\). Requirement (2) states that \(\alpha _1\wedge \ldots \wedge \alpha _q\) is nowhere zero when restricted to \(\ker \omega _C=T\mathcal {F}\). This means that \(\alpha _1\wedge \ldots \wedge \alpha _q\) restricts to a volume form on each leaf of \(\mathcal {F}\). Moreover, evaluating
on vector fields \(V_1,\ldots ,V_{q+1}\), at least q of which are tangent to \(\mathcal {F}\), gives zero. Indeed, the factor \(\omega _C\) gets paired with two vector fields, at least one of which belongs to \(T\mathcal {F}=\ker \omega _C\).
The above claim ensures that the class \([\omega _C]\in H^{2}_{bas}(C)\) is non-trivial. Indeed, if \(\mathcal {F}\) is a taut codimension 2m foliation on a compact oriented manifold C, such that \(\mathcal {F}\) is defined by a closed two-form \(\omega _C\in \Omega ^{2}(C)\), then the cohomology classes \([\omega _{C}^{k}]\in H^{2k}_{bas}(C)\) for \(k=1,\ldots ,m\) are non-trivial [25, Thm. 4.33]. In the q-contact setting, the manifold C is indeed oriented because \(\alpha _1\wedge \ldots \wedge \alpha _q\wedge \omega _C^{n-q}\) is a volume form on C.
We can now show that \(r(\alpha _i)\) does not admit a closed extension. Assume by contradiction that \(\beta _i\) is a closed extension of \(r(\alpha _i)\). Then, \(\alpha _i-\beta _i\in \Omega ^{1}_{bas}(C)\), because for \(V\in \Gamma (T\mathcal {F})\) we have \(\iota _{V}(\alpha _i-\beta _i)=0\) and
It follows that the basic form \(d(\alpha _i-\beta _i)=\omega _C\) has a basic primitive \(\alpha _i-\beta _i\), i.e., the class \([\omega _C]\in H^{2}_{bas}(C)\) is trivial. This is a contradiction, so \(r(\alpha _i)\) has no closed extension.
Clearly, Lemma 4.1 does not yield many unobstructed first-order deformations in practice. It only concerns closed \(\beta \in \Omega ^{1}(\mathcal {F})\) whose cohomology class lies in the image of the restriction map \([r]:H^{1}(C)\rightarrow H^{1}(\mathcal {F})\), and the latter is a finite dimensional subspace of \(H^{1}(\mathcal {F})\).
By contrast, the kernel of \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\) is infinite dimensional in general.Footnote 1 Hence, Corollary 4.2 has the potential to generate considerably more unobstructed first-order deformations. The following is an example in which \(\ker (d_{\nu })\) is infinite dimensional.
Example 4.4
Consider \(\mathbb {T}^{3}\) endowed with the presymplectic form \(d\theta _2\wedge (d\theta _3-\cos (\theta _2)d\theta _1)\). The associated foliation is given by
Hence, for every fixed value of \(\theta _2\), we get either an \(S^{1}\)-fibration or a Kronecker foliation on \((\mathbb {T}^{2},\theta _1,\theta _3)\), depending on whether \(\cos (\theta _2)\) is rational or irrational. The conormal bundle is \(N^{*}\mathcal {F}=\text {Span}\{d\theta _2,d\theta _3-\cos (\theta _2)d\theta _1\}\), so we can use \(\{\overline{d\theta _1}\}\) as a frame for \(T^{*}\mathcal {F}=T^{*}\mathbb {T}^{3}/N^{*}\mathcal {F}\). Embedding this presymplectic manifold in its Gotay local model, it becomes a coisotropic submanifold. We claim that \(\ker (d_{\nu })\) is infinite dimensional in this example.
The map \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\) is given by
To see which elements are trivial in \(H^{1}(\mathcal {F};N^{*}\mathcal {F})\), note that for \(k,l\in C^{\infty }(\mathbb {T}^{3})\) we have
and
We will now focus on foliated one-forms of the type \(g(\theta _2)\overline{d\theta _1}\).
If such a class \([g(\theta _2)\overline{d\theta _1}]\) lies in the kernel of \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\), then (25), (26) and (27) give
for some \(k,l\in C^{\infty }(\mathbb {T}^{3})\). For a fixed value \(\theta _2=\theta _2^{0}\), the second equation in (28) says that \(l(\theta _1,\theta _2^{0},\theta _3)\) is a basic function for the foliated manifold \(\big (\mathbb {T}^{2},\text {Span}\{\partial _{\theta _1}+\cos (\theta _2^{0})\partial _{\theta _3}\}\big )\). This implies that \(l(\theta _1,\theta _2^{0},\theta _3)\) is constant when \(\cos (\theta _2^{0})\) is irrational. Since the set of \(\theta _2^{0}\in S^{1}\) for which \(\cos (\theta _2^{0})\) is irrational is dense in \(S^{1}\), it follows that the system of equalities
holds on a dense subset of \(\mathbb {T}^{3}\), hence on all of \(\mathbb {T}^{3}\). It follows that \(l=l(\theta _2)\). The first equation in (28) then implies that
so integrating around tori \(S^{1}\times \{\theta _2\}\times S^1\) we see that both sides must be zero. In conclusion,
Let us now consider the subspace
We claim that it is infinite dimensional. If not, then there would exist \(m\in \mathbb {N}\) such that
are linearly dependent. So there exist \(c_0,\ldots ,c_m\in \mathbb {R}\), not all zero, such that
for some \(h\in C^{\infty }(\mathbb {T}^{3})\). Integrating over the tori \(S^{1}\times \{\theta _2\}\times S^1\), this implies that
But the polynomial \(\sum _{i=0}^{m}c_ix^{i}\) has at most m roots, whereas \(\cos (\theta _2)\) takes on infinitely many values as \(\theta _2\) ranges over \(S^{1}\). Hence, we reach a contradiction, and therefore the subspace (29) is infinite dimensional. The same then holds for \(\ker (d_{\nu })\).
We finish this subsection by highlighting a particular case of Corollary 4.2, which is important in the spirit of this note. Given a compact coisotropic submanifold \(C\subset (M,\omega )\), we noted in Sect. 1.3.2 that the presymplectic form \(\omega _C\) induces an isomorphism \(H^{1}(\mathcal {F};N^{*}\mathcal {F})\cong H^{1}(\mathcal {F};N\mathcal {F})\). Therefore, Corollary 4.2 implies that the coisotropic deformation problem of C is unobstructed when \(H^{1}(\mathcal {F};N\mathcal {F})\) vanishes. The latter condition is the infinitesimal requirement for rigidity of the foliation \(\mathcal {F}\), see Definition 1.14.
Corollary 4.5
Let \(C\subset (M,\omega )\) be a compact coisotropic submanifold with characteristic foliation \(\mathcal {F}\). If \(H^{1}(\mathcal {F};N\mathcal {F})\) vanishes, then the deformation problem of C is unobstructed.
We now display a non-trivial example of this type.
Example 4.6
We revisit certain suspension foliations on mapping tori which were shown to be rigid in [11]. We find conditions under which such a foliation \(\mathcal {F}\) is given by the kernel of a presymplectic form. Gotay’s theorem then guarantees that the mapping torus in question arises as a coisotropic submanifold with characteristic foliation \(\mathcal {F}\).
Pick a matrix \(A\in SL(n,\mathbb {Z})\), where \(n\ge 2\), which is diagonalizable over \(\mathbb {R}\) with positive eigenvalues. Denote the eigenvalues by
where \(p+q=n\). We view A as a diffeomorphism of the torus \(\mathbb {T}^{n}\). Pick independent linear vector fields \(X_1,\ldots ,X_p,Y_1,\ldots ,Y_q\in \mathfrak {X}(\mathbb {T}^{n})\) such thatFootnote 2
The foliation \(\text {Span}\{X_1,\ldots ,X_p\}\) on \(\mathbb {T}^{n}\) is invariant under A, hence the product foliation \(\text {Span}\{X_1,\ldots ,X_p,\partial _t\}\) on \(\mathbb {T}^{n}\times \mathbb {R}\) descends to a foliation \(\mathcal {F}\) on the mapping torus
Assume moreover that the matrix A satisfies the following two conditions:
-
(1)
The eigenvalues \(\lambda _k\) and the quotients \(\lambda _k/\mu _j\) are different from 1.
-
(2)
There is a basis of \(\mathbb {R}^{n}\) given by eigenvectors \(v_1,\ldots ,v_p,w_1,\ldots ,w_q\) of A (corresponding respectively to the eigenvalues \(\mu _1,\ldots ,\mu _p,\lambda _1,\ldots ,\lambda _q\)) with the property that for any \(i=1,\ldots ,p\), the coordinates \(v_i^{1},\ldots ,v_i^{n}\) of \(v_i\) are linearly independent over \(\mathbb {Q}\).
Under these assumptions, also the eigenvalues \(\mu _1,\ldots ,\mu _p\) are different from 1, and therefore A is an Anosov diffeomorphism of \(\mathbb {T}^{n}\). If the eigenvalues of A are all different, then condition (2) is satisfied exactly when the characteristic polynomial of A is irreducible over \(\mathbb {Q}\).
The main result of [11] is that, under conditions (1) and (2), the foliation \(\mathcal {F}\) is rigid. The proof proceeds by showing that the Bott complex \(\big (\Omega ^{\bullet }(\mathcal {F};N\mathcal {F}),d_{\nabla }\big )\) admits “tame” homotopy operators; this implies in particular that \(H^{1}(\mathcal {F};N\mathcal {F})\) vanishes. To realize \((\mathbb {T}_{A},\mathcal {F})\) as an instance of Corollary 4.5, we have to find out when \(\mathcal {F}\) is defined by a presymplectic form.
Claim: The foliation \(\mathcal {F}\) is defined by a presymplectic form on \(\mathbb {T}_{A}\) exactly when the multiset \(\{\lambda _1,\ldots ,\lambda _q\}\) has the following property: if \(\xi \) occurs with multiplicity m, then also \(1/\xi \) occurs with multiplicity m.
Recall that all eigenvalues are assumed to be positive and different from 1. Hence, the property mentioned in the claim implies in particular that q is even, as it should be. To prove the claim, we denote by \(\{\alpha _1,\ldots ,\alpha _p,\beta _1,\ldots ,\beta _q\}\) the frame of \(T^{*}\mathbb {T}^{n}\) dual to the frame \(\{X_1,\ldots ,X_p,Y_1,\ldots ,Y_q\}\) of \(T\mathbb {T}^{n}\). This way, we obtain a frame
for \(T^{*}\mathbb {T}_{A}\). These are indeed 1-forms on \(\mathbb {T}^{n}\times \mathbb {R}\) invariant under the identification in (30).
-
(i)
For the forward implication, assume that \(\omega \) is a presymplectic form on \(\mathbb {T}_{A}\) with kernel \(T\mathcal {F}\). Expressing \(\omega \) in the frame (31) gives an equation of the form
$$\begin{aligned} \omega =\sum _{i<j}f_{ij}(\theta ,t)\lambda _i^{-t}\lambda _j^{-t}\beta _i\wedge \beta _j, \end{aligned}$$where \(f_{ij}\) satisfies
$$\begin{aligned} f_{ij}\big (A(\theta ),t+1\big )=f_{ij}(\theta ,t). \end{aligned}$$(32)We now assert that, if \(f_{ij}\) is not identically zero, then \(\lambda _i\lambda _j=1\). To prove this, note that since \(\pounds _{\partial _t}\omega \) vanishes, we have
$$\begin{aligned} f_{ij}\big (A(\theta ),t\big )\lambda _i^{-t}\lambda _j^{-t}=f_{ij}\big (A(\theta ),t+1\big )\lambda _i^{-t-1}\lambda _j^{-t-1}=f_{ij}(\theta ,t)\lambda _i^{-t-1}\lambda _j^{-t-1}, \end{aligned}$$where we also used (32). This implies that
$$\begin{aligned} \lambda _i\lambda _jf_{ij}\big (A(\theta ),t)=f_{ij}(\theta ,t). \end{aligned}$$(33)Now take a rational point \((\theta _1,\ldots ,\theta _n)\in \mathbb {Q}^{n}/\mathbb {Z}^{n}\). Such a point is periodic for A. Indeed, it can be written as \((p_1/q,\ldots ,p_n/q)\) for some \(0\le p_j<q\), and applying iterates of A to it yields values in the finite set
$$\begin{aligned} \big \{(q_1/q,\ldots ,q_n/q):\ 0\le q_j<q\big \}. \end{aligned}$$Hence, the equality (33) implies that for any point \((\theta _1,\ldots ,\theta _n,t)\in \mathbb {Q}^{n}/\mathbb {Z}^{n}\times \mathbb {R}\), there exists an integer \(k\ge 1\) such that
$$\begin{aligned} (\lambda _i\lambda _j)^{k}f_{ij}(\theta ,t)=f_{ij}(\theta ,t). \end{aligned}$$(34)If \(f_{ij}\) is not identically zero, then there exists a point \((\theta _1,\ldots ,\theta _n,t)\in \mathbb {Q}^{n}/\mathbb {Z}^{n}\times \mathbb {R}\) where \(f_{ij}\) does not vanish. Hence, the equality (34), along with the fact that the eigenvalues are positive, yields that \(\lambda _i\lambda _j=1\). The assertion is proved. This shows that, if \(\xi \) occurs in the list \(\{\lambda _1,\ldots ,\lambda _q\}\), then also \(1/\xi \) occurs in that list. For otherwise, there would exist \(j\in \{1,\ldots ,q\}\) so that the vector field \(\xi ^{t} Y_j\in \mathfrak {X}(\mathbb {T}_{A})\) lies in the kernel of \(\omega \), while also being transverse to \(\mathcal {F}\). To show that the multiplicities of \(\xi \) and \(1/\xi \) agree, we can assume that they are given by k and l respectively, and that
$$\begin{aligned} \lambda _1=\cdots =\lambda _k=\xi \hspace{1cm}\text {and}\hspace{1cm}\lambda _{k+1}=\cdots =\lambda _{k+l}=1/\xi . \end{aligned}$$We know that the presymplectic form \(\omega \) defines an isomorphism
$$\begin{aligned} \omega ^{\flat }:\text {Span}\big \{\lambda _1^{t}Y_1,\ldots ,\lambda _q^{t}Y_q\big \}\overset{\sim }{\longrightarrow }\text {Span}\big \{\lambda _1^{-t}\beta _1,\ldots ,\lambda _q^{-t}\beta _q\big \}, \end{aligned}$$and that at every point, it takes the subspace spanned by \(\xi ^{t}Y_1,\ldots ,\xi ^{t}Y_k\) into the subspace spanned by \((1/\xi )^{-t}\beta _{k+1},\ldots ,(1/\xi )^{-t}\beta _{k+l}\). Hence, \(l\ge k\). Because the argument is symmetric in \(\xi \) and \(1/\xi \), it follows that \(l=k\). This proves the forward implication.
-
(ii)
For the backward implication, we have by assumption that \(q=2k\). Moreover, after renumbering the elements of the list \(\lambda _1,\ldots ,\lambda _q\), we can assume that it is given by
$$\begin{aligned} \lambda _1,\ldots ,\lambda _k,\lambda _{k+1}=\lambda _1^{-1},\ldots ,\lambda _{q}=\lambda _k^{-1}. \end{aligned}$$We can then write down a well-defined two-form \(\omega \in \Omega ^{2}(\mathbb {T}_{A})\), given by
$$\begin{aligned} \omega =\sum _{i=1}^{k}\beta _i\wedge \beta _{k+i}. \end{aligned}$$Note that the \(\beta _i\in \Omega ^{1}(\mathbb {T}^{n})\) are closed, since they are part of the frame dual to the commuting frame \(\{X_1,\ldots ,X_p,Y_1,\ldots ,Y_q\}\) of \(T\mathbb {T}^{n}\). This implies that \(\omega \) is also closed. Clearly, the kernel of \(\omega \) is given by \(T\mathcal {F}\). This proves the backward implication.
Let us now give a concrete example of the type we just described. To find a matrix \(A\in SL(n,\mathbb {Z})\) which satisfies the property mentioned in the claim above, it is useful to consider symplectic matrices. These always have determinant equal to 1 [17, Lemma 1.1.15], and their characteristic polynomial has the property that, if \(\xi \) is a root of multiplicity m, then also \(1/\xi \) is a root of the same multiplicity [17, Lemma 2.2.2]. Take for instance.Footnote 3
The eigenvalues are
in particular they are all distinct. The characteristic polynomial is
Its image in \((\mathbb {Z}/2\mathbb {Z})[X]\) is the irreducible polynomial \(X^{4}+X^{3}+X^{2}+X+1\), hence the characteristic polynomial is irreducible over \(\mathbb {Z}\) and therefore over \(\mathbb {Q}\). It follows that the assumptions (1) and (2) from [11] are satisfied. Hence, taking for instance linear vector fields \(X_1,X_2\) on \(\mathbb {T}^{4}\) satisfying
the associated suspension foliation \(\mathcal {F}\) on the mapping torus \(\mathbb {T}_{A}\) is rigid. Now pick a presymplectic form \(\omega \) on \(\mathbb {T}_{A}\) with kernel \(T\mathcal {F}\) and embed \((\mathbb {T}_{A},\omega )\) coisotropically into its Gotay local model. The result is a coisotropic submanifold whose deformation problem is unobstructed.
Remark 4.7
The fact that the deformation problem of the coisotropic submanifolds from Example 4.6 is unobstructed also follows from Lemma 4.1, because the restriction
is surjective. To see why, we recall that leafwise cohomology of suspension foliations can be computed explicitly using a Mayer–Vietoris argument, see [2, §1.3.3]. Denoting by \(\mathcal {F}_{0}\) the foliation on \(\mathbb {T}^{n}\) given by
one gets
The assumptions (1) and (2) from [11] (recalled in Example 4.6) ensure that \(\mathcal {F}_{0}\) is a so-called Diophantine linear foliation on \(\mathbb {T}^{n}\), and leafwise cohomology of such foliations was computed in [1] (see also [2, Thm. 1.3.7]). Continuing in the notation of Example 4.6, one has
where \(r:\Omega ^{1}(\mathbb {T}^{n})\rightarrow \Omega ^{1}(\mathcal {F}_{0})\) is the restriction map. Because \(A^{*}\alpha _j=\mu _j\alpha _j\) and \(\mu _1,\ldots ,\mu _q\) are different from 1, it follows that the map \(\text {Id}-[A^{*}]:H^{1}(\mathcal {F}_{0})\rightarrow H^{1}(\mathcal {F}_{0})\) is injective, hence the first summand in (36) vanishes. Because the leaves of \(\mathcal {F}_{0}\) are dense, \(H^{0}(\mathcal {F}_{0})\) consists of just the constant functions on \(\mathbb {T}^{n}\). Hence, the expression (36) shows that \(H^{1}(\mathcal {F})\cong \mathbb {R}\).
A representative is given by the restriction of dt to the leaves of \(\mathcal {F}\). To see that this is a non-exact foliated one-form, let L be the leaf of \(\mathcal {F}\) through a rational point \(\overline{(\theta ,t)}\in \mathbb {T}_{A}\), i.e., \(\theta \in \mathbb {Q}^{n}/\mathbb {Z}^{n}\). The flow line of \(\partial _t\) through \(\overline{(\theta ,t)}\) stays inside L and is closed, because \(\theta \) is a periodic point for A (see Example 4.6(i)). By Stokes’ theorem, the restriction of dt to the leaf L cannot be exact. Since \(H^{1}(\mathcal {F})\) is spanned by the class of dt, it is now clear that the restriction map (35) is indeed surjective.
5.2 The Kuranishi criterion
In this subsection, we recall that the deformation problem of a coisotropic submanifold \(C\subset (M,\omega )\) is governed by a suitable \(L_{\infty }[1]\)-algebra. The latter comes with a tool that allows one to detect obstructed first-order deformations, called the Kuranishi criterion. We check that the partial unobstructedness result from Corollary 4.2 is consistent with this criterion.
Definition 4.8
-
(i)
An \(\mathbf {L_{\infty }[1]}\)-algebra is a \(\mathbb {Z}\)-graded vector space W, equipped with a collection of graded symmetric multibrackets \((\lambda _k:W^{\otimes k}\rightarrow W)_{k\ge 1}\) of degree 1 which satisfy a collection of relations [16] called higher Jacobi identities.
-
(ii)
The Maurer–Cartan series of an element \(w\in W\) of degree 0 is the infinite sum
$$\begin{aligned} MC(w):=\sum _{k=1}^{\infty }\frac{1}{k!}\lambda _k(w^{\otimes k}). \end{aligned}$$A Maurer–Cartan element is a degree zero element \(w\in W\) for which the Maurer–Cartan series converges to zero.
-
(iii)
We say that an \(L_{\infty }[1]\)-algebra \(\big (W,\{\lambda _k\}\big )\) governs a certain deformation problem if small deformations correspond with Maurer–Cartan elements of \(\big (W,\{\lambda _k\}\big )\).
Remark 4.9
The higher Jacobi identities mentioned above imply in particular that \(\lambda _1\) is a differential, which gives rise to cohomology groups H(W). Moreover, the binary bracket \(\lambda _2\) descends to the cohomology H(W), and this fact which will be essential in the sequel.
Oh and Park showed in [18] that every coisotropic submanifold \(C\subset (M,\omega )\) has an attached \(L_{\infty }[1]\)-algebra structure. We recall an elegant description of it in terms of derived brackets, which is due to Cattaneo and Felder [7]. The \(L_{\infty }[1]\)-algebra associated with \(C\subset (M,\omega )\) is obtained using the Gotay local model \((U,\Omega _G)\), for a choice of complement G to the characteristic foliation \(T\mathcal {F}\) on C. Its multibrackets \(\{\lambda _k\}_{k\ge 1}\) are defined on the graded vector space \(\Gamma (\wedge T^{*}\mathcal {F})[1]\), by the formulaFootnote 4
Here \(\Pi _G:=-\Omega _G^{-1}\) denotes the Poisson structure corresponding with \(\Omega _G\), and we consider the sections \(\xi _i\in \Gamma (\wedge T^{*}\mathcal {F})\) as vertical fiberwise constant multivector fields on \(T^{*}\mathcal {F}\) via the correspondence in Rem. 5.7. The bracket \([-,-]\) appearing in (37) is the Schouten-Nijenhuis bracket of multivector fields, and the map P acts on multivector fields by first restricting them to C and then taking the vertical projection \(\Gamma (\wedge ^{\bullet }T(T^{*}\mathcal {F})|_{C})\rightarrow \Gamma (\wedge ^{\bullet }T^{*}\mathcal {F})\) coming from the splitting \(T(T^{*}\mathcal {F})|_{C}=TC\oplus T^{*}\mathcal {F}\). While the work of Oh-Park addresses formal deformations of C, it was shown by Schätz-Zambon in [21] that the \(L_{\infty }[1]\)-algebra \(\big (\Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\big )\) actually governs the smooth coisotropic deformation problem of C.
Proposition 4.10
([21]) Let \(C\subset (M,\omega )\) be a coisotropic submanifold with Gotay local model \((U,\Omega _G)\). For any \(\alpha \in \Gamma (T^{*}\mathcal {F})\) whose graph is contained in U, the Maurer–Cartan series \(MC(-\alpha )\) is pointwise convergent. For such \(\alpha \), the following are equivalent:
-
(1)
\(\text {Graph}(\alpha )\) is coisotropic in \((U,\Omega _G)\),
-
(i)
The Maurer–Cartan series \(MC(-\alpha )\) converges to zero.
The differential \(\lambda _1\) is just the leafwise de Rham differential \(d_{\mathcal {F}}\) up to sign, see [21, Proof of Prop. 3.5]. Hence, the linearization of the Maurer–Cartan equation is just the closedness condition with respect to \(d_{\mathcal {F}}\). This is another way to see that first-order deformations of C are closed foliated one-forms \(\beta \in \Omega ^{1}(\mathcal {F})\), a result which we already proved in Lemma 1.10.
If \(\beta \in \Omega ^{1}(\mathcal {F})\) is an unobstructed first-order deformation of C, then there exists a smooth path \(\alpha _t\) of coisotropic sections of \((U,\Omega _G)\) starting at \(\alpha _0=0\), satisfying  . By Proposition 4.10, \(-\alpha _t\) is a Maurer–Cartan element of \(\big (\Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\big )\) for all t. Differentiating twice the equality
. By Proposition 4.10, \(-\alpha _t\) is a Maurer–Cartan element of \(\big (\Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\big )\) for all t. Differentiating twice the equality
and evaluating at time \(t=0\), it follows that \(\lambda _2(\beta ,\beta )\) is exact in \(\big (\Omega (\mathcal {F}),d_{\mathcal {F}}\big )\). This is the Kuranishi criterion for unobstructedness of a first-order deformation [18, Thm. 11.4].
Proposition 4.11
The Kuranishi map of the \(L_{\infty }[1]\)-algebra \(\big (\Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\big )\) is
If \(\beta \in \Omega ^{1}(\mathcal {F})\) is an unobstructed first-order deformation of C, then \(Kr([\beta ])\) vanishes.
We know from Corollary 4.2 that first-order deformations \(\beta \) whose cohomology class lies in the kernel of \(d_{\nu }:H^{1}(\mathcal {F})\rightarrow H^{1}(\mathcal {F};N^{*}\mathcal {F})\) are unobstructed. Hence, we should have that \(\ker (d_{\nu })\subset \ker (Kr)\). In the following, we double-check that this inclusion holds.
We will actually prove a more interesting result. It is clear from the expression (37) that the multibrackets \(\lambda _k\) of the \(L_{\infty }[1]\)-algebra \(\big (\Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\big )\) depend on the choice of complement G to \(T\mathcal {F}\). By contrast, we will show that the Kuranishi map admits a canonical description in terms of the presymplectic form \(\omega _C\) and the map \(d_{\nu }\). This result highlights once more the role played by the transverse differentiation map \(d_{\nu }\) in the coisotropic deformation problem, and it will imply in particular that \(\ker (d_{\nu })\subset \ker (Kr)\).
Proposition 4.12
Let \(C\subset (M,\omega )\) be a coisotropic submanifold. Choose a complement G to the characteristic distribution \(T\mathcal {F}\), and let \(\left( \Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\right) \) denote the \(L_{\infty }[1]\)-algebra associated with the corresponding Gotay local model. Its binary bracket satisfies
In the statement of the proposition, we denoted by \(\langle \!\langle \bullet ,\bullet \rangle \!\rangle \) the duality pairing
By writing \(\tau \circ d_{1,0}\), we used the bi-degree language introduced in Sect. 5.1 of Appendix.
Remark 4.13
The original paper [18] by Oh-Park contains a formula for \(\lambda _2\) which looks somewhat similar to (38). However, the Oh-Park formula depends not only on the choice of complement G, but also on a choice of coordinates, since it involves a non-canonical connection defined in a suitable chart. By contrast, the expression (38) is global, due to the fact that it uses the operator \(d_{1,0}\) instead of the aforementioned local connection. It is easy to check that, when expressed in coordinates, our equation (38) reduces to the formula given by Oh-Park, hence it provides an invariant description for the latter.
Proof of Proposition 4.12
Using the definition (37) of \(\lambda _2\) and the identification in Lemma 5.6 between sections of \(T^{*}\mathcal {F}\) and vertical fiberwise constant vector fields on U, we have
By Rem. 5.7, the associated foliated two-form is
In the first equality, we used that \(\Omega _G(TC,T\mathcal {F})=0\), and the second equality uses that \(\wedge \Pi _G^{\sharp }\) intertwines \([\Pi _G,\bullet ]\) and \(-d\) (see [10, Lemma 2.1.3]). To simplify the expression (40), note that for \(\gamma _1,\gamma _2,\gamma _3\in \Omega ^{1}(U)\), we have
where \([\bullet ,\bullet ]_{\Pi _G}\) denotes the Koszul bracket associated with \(\Pi _G\) (see [23, §4.1]). The identity (41) is proved using the derivation rules for the Schouten bracket and the Koszul bracket, along with the fact that \(\Pi _G^{\sharp }\) intertwines these brackets when applied to vector fields and one-forms, respectively. Consequently, the expression (40) becomes
To simplify this further, we will first study the Poisson structure \(\Pi _G\) along the zero section.
Claim 1: The bivector field \(Z:=\wedge ^{2}p_{*}(\Pi _{G}|_{C})\in \Gamma (\wedge ^{2}TC)\) actually lies in \(\Gamma (\wedge ^{2}G)\). It is characterized by the requirement that \(Z^{\sharp }:G^{*}\rightarrow G\) equals \(-(\omega _{C}^{\flat })^{-1}\).
We prove the claim, starting from the decomposition \(T^{*}\mathcal {F}|_{C}=TC\oplus T^{*}\mathcal {F}=(T\mathcal {F}\oplus G)\oplus T^{*}\mathcal {F}\). As shown in the proof of [12, Prop. 2.14], the symplectic form \(\Omega _G\) decomposes as follows at points \(x\in C\):

for invertible matrices A, B. Note that \(B^{T}\) represents the isomorphism \(\omega _C^{\flat }:G\rightarrow G^{*}\). Consequently, the Poisson structure \(\Pi _G\) decomposes as follows at points \(x\in C\):

Since the bivector \(Z_{x}\) is represented by the \((2\times 2)\) top-left block matrix in (42), this shows that \(Z\in \Gamma (\wedge ^{2}G)\) and \(Z^{\sharp }=(-B^{-1})^{T}=-(\omega _{C}^{\flat })^{-1}\) as maps \(G^{*}\rightarrow G\). The proves the claim.
Claim 2: For any \(\gamma _1,\gamma _2\in \Omega ^{1}(C)\), we have
To prove Claim 2, we compute using Claim 1:
We now finish the proof of the proposition, by showing that
Note that both sides are linear in \(d(j(\alpha ))\). This is clear for the left hand side, and for the right hand side this follows from the fact that \(d_{1,0}\alpha \) is just the component of \(d(j(\alpha ))\) lying in \(\Gamma (G^{*}\otimes T^{*}\mathcal {F})\). Hence, to prove the equality (43), we may assume that
Using Claim 1 and Claim 2, the left-hand side in (43) is given by
On the other hand, from (44) it immediately follows that
hence the right-hand side in (43) is given by
This shows that the equality (43) holds, and this in turn proves the proposition. \(\square \)
Remark 4.14
If the complement G is involutive, then the proof of Proposition 4.12 becomes more geometric. In that case, we have a symplectic foliation \((G,\omega _C)\) defining a Poisson structure \(\Pi _{base}\) on C, and the projection \(p:(U,\Pi _G)\rightarrow (C,\Pi _{base})\) is a Poisson map. This immediately implies Claim 1 in the proof above. It also implies Claim 2, because of the following. Recall that the since p is a Poisson map, the pullback bundle \(p^{*}T^{*}C\) carries a natural Lie algebroid structure \((\rho ,[\bullet ,\bullet ]_{p^{*}})\) determined by
When \(p^{*}T^{*}C\) is endowed with this Lie algebroid structure and \(T^{*}U\) carries its usual cotangent Lie algebroid structure \((\Pi _G^{\sharp },[\bullet ,\bullet ]_{\Pi _G})\), the natural map \(p^{*}T^{*}C\rightarrow T^{*}U\) is a Lie algebroid morphism [6, Prop. 1.10]. But since \(p:U\rightarrow C\) is a submersion, the map \(p^{*}T^{*}C\rightarrow T^{*}U\) is injective, hence \((p^{*}T^{*}C,\rho ,[\bullet ,\bullet ]_{p^{*}})\) becomes a Lie subalgebroid of \((T^{*}U,\Pi _G^{\sharp },[\bullet ,\bullet ]_{\Pi _G})\). Compatibility of their Lie brackets implies Claim 2 in the proof above.
At last, we pass to cohomology. The pairing (39) descends to
the map \((-1)^{\bullet }(\tau \circ d_{1,0})\) descends to \(d_{\nu }\) by Corollary 5.4, and we have an isomorphism
see Sect. 1.3.2. Hence, Proposition 4.12 immediately implies the following.
Corollary 4.15
The Kuranishi map of \(\big (\Gamma (\wedge T^{*}\mathcal {F})[1],\{\lambda _k\}\big )\) is given canonically by
In particular, \(\ker (d_{\nu })\) is contained in \(\ker (Kr)\).
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Notes
Note however that in the integral coisotropic setting considered by Ruan [20], this space is always finite dimensional. Indeed, if \((C,\mathcal {F})\) is integral then \(\ker (d_{\nu })\) reduces to the space of flat sections of \((\mathcal {H}^{1},\nabla )\), see Example 2.13. The latter is a finite dimensional vector space.
Put differently, \(X_j\) (resp. \(Y_k\)) is a vector field whose coefficients are constant, given by the components of an eigenvector of A for the eigenvalue \(\mu _j\) (resp. \(\lambda _k\)).
A useful way to construct symplectic matrices is the following [9, Example 17] Let X and Y be two symmetric \(n\times n\) matrices, with X invertible. Then,
$$\begin{aligned} S:=\begin{pmatrix} X+YX^{-1}Y &{} YX^{-1}\\ X^{-1}Y &{} X^{-1} \end{pmatrix} \end{aligned}$$is a symplectic matrix. The matrix A above is obtained by taking
$$\begin{aligned} X=\begin{pmatrix} 1 &{} 0\\ 0 &{} 1 \end{pmatrix},\ Y=\begin{pmatrix} 1 &{} 1\\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$The graded vector space \(\Gamma (\wedge T^{*}\mathcal {F})[1]\) is just \(\Gamma (\wedge T^{*}\mathcal {F})\) up to degree shift. Namely, a degree k element of \(\Gamma (\wedge T^{*}\mathcal {F})[1]\) lives in \(\Gamma (\wedge ^{k+1} T^{*}\mathcal {F})\).
References
Arraut, J.L., dos Santos, N.M.: Linear foliations of \(\mathbb{T} ^n\). Bol. Soc. Bras. Mat. 21(2), 189–204 (1991)
Asaoka, M., El Kacimi-Alaoui, A., Hurder, S., Richardson, K.: Foliations: Dynamics, Geometry and Topology. Advanced Courses in Mathematics CRM Barcelona, Birkhäuser, Basel (2014)
Bolle, P.: A contact condition for \(p\)-codimensional submanifolds of a symplectic manifold \((2\le p\le n)\). Math. Z. 227(2), 211–230 (1998)
Candel, A., Conlon, L.: Foliations I, Graduate Studies in Mathematics, vol. 23. American Mathematical Society, Providence (2000)
Cannas da Silva, A.: Lectures on Symplectic Geometry. Lecture Notes in Mathematics, vol. 1764. Springer, Berlin (2001)
Caseiro, R., Fernandes, R.L.: The modular class of a Poisson map. Ann. Inst. Fourier 63(4), 1285–1329 (2013)
Cattaneo, A., Felder, G.: Relative formality theorem and quantisation of coisotropic submanifolds. Adv. Math. 208(2), 521–548 (2007)
Crainic, M., Fernandes, R.L.: Integrability of Poisson brackets. J. Differ. Geom. 66(1), 71–137 (2004)
de Grosson, M.: Introduction to Symplectic Mechanics: Lectures I-II-III (2006). https://www.ime.usp.br/~piccione/Downloads/LecturesIME.pdf
Dufour, J.P., Zung, N.T.: Poisson Structures and Their Normal Forms. Progress in Mathematics, vol. 242. Birkhäuser Verlag, Basel (2005)
El Kacimi-Alaoui, A., Nicolau, M.: A class of \(C^{\infty }\)-stable foliations. Ergod. Theory Dyn. Syst. 13(4), 697–704 (2008)
Geudens, S., Zambon, M.: Coisotropic submanifolds in b-symplectic geometry. Can. J. Math. 73(3), 737–768 (2021)
Gotay, M.J.: On coisotropic imbeddings of presymplectic manifolds. Proc. Am. Math. Soc. 84(1), 111–114 (1982)
Heitsch, J.L.: A cohomology for foliated manifolds. Comment. Math. Helv. 50(1), 197–218 (1975)
Hoster, M.: Derived Secondary Classes for Flags of Foliations. Ph.D. thesis, Ludwig-Maximilians-Universität München (2001)
Lada, T., Stasheff, J.: Introduction to SH Lie algebras for physicists. Int. J. Theor. Phys. 32(7), 1087–1103 (1993)
McDuff, D., Salamon, D.: Introduction to Symplectic Topology. Oxford Graduate Texts in Mathematics, vol. 27. Oxford University Press, Oxford (2017)
Oh, Y.-G., Park, Y.-S.: Deformations of coisotropic submanifolds and strong homotopy Lie algebroids. Invent. Math. 161(2), 287–360 (2005)
Osorno-Torres, B.: Codimension-one Symplectic Foliations: Constructions and Examples. Ph.D. thesis, Utrecht University (2015)
Ruan, W.-D.: Deformation of integral coisotropic submanifolds in symplectic manifolds. J. Symplectic Geom. 3(2), 161–169 (2005)
Schätz, F., Zambon, M.: Deformations of coisotropic submanifolds for fibrewise entire Poisson structures. Lett. Math. Phys. 103(7), 777–791 (2013)
Schätz, F., Zambon, M.: Equivalences of coisotropic submanifolds. J. Symplectic Geom. 15(1), 107–149 (2017)
Schätz, F., Zambon, M.: Deformations of pre-symplectic structures and the Koszul \(L_\infty \)-algebra. Int. Math. Res. Not. 2020(14), 4191–4237 (2020)
Schätz, F., Zambon, M.: From coisotropic to presymplectic structures: relating the deformation theories (preparation)
Tondeur, P.: Geometry of Foliations. Monographs in Mathematics, vol. 90. Springer, Basel (1997)
Weinstein, A.: Symplectic manifolds and their Lagrangian submanifolds. Adv. Math. 6(3), 329–346 (1971)
Zambon, M.: An example of coisotropic submanifolds \(C^{1}\)-close to a given coisotropic submanifold. Differ. Geom. Appl. 26(6), 635–637 (2008)
Acknowledgements
Part of this work was done while visiting the Max Planck Institute for Mathematics. I would like to thank the institute for its hospitality and the financial support. I also acknowledge support from the UCL Institute for Mathematics & Statistical Science (IMSS). I would like to thank Marco Zambon and Ioan Mărcuţ for useful conversations. I am particularly grateful to Marco Zambon for sharing his forthcoming work [24].
Funding
During the preparation of this article, the author was funded by the Max Planck Institute for Mathematics in Bonn and the UCL Institute for Mathematics and Statistical Science (IMSS).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The author has no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proofs for results in Sect. 2.2.2
This subsection is devoted to the proofs of Proposition 2.10 and Lemma 2.12. Both proofs will use some ingredients of the spectral sequence of the foliation \(\mathcal {F}\), which we introduce now.
Recall that we fixed a complement G to the characteristic distribution \(T\mathcal {F}\) on C.
The decomposition \(TC=T\mathcal {F}\oplus G\) induces a bi-grading on \(\Omega (C)\), namely
where
With respect to this bi-grading, the de Rham differential splits into a sum of bihomogeneous components
where the subscript (i, j) indicates the bi-degree of the component \(d_{i,j}\). Note that \(d_{2,-1}\) vanishes exactly when the complement G is involutive. We will use the following explicit formulae for \(d_{0,1}\) and \(d_{1,0}\), which can be found in [25, Chapter 4]. If \(\omega \in \Omega ^{u,v}(C)\), then
and
1.1.1 The proof of Proposition 2.10
To prove Proposition 2.10, we rewrite the map \(\Phi \) from Definition 2.5 in terms of the bihomogeneous component \( d_{1,0}:\Gamma (\wedge ^{\bullet }T^{*}\mathcal {F})\rightarrow \Gamma (G^{*}\otimes \wedge ^{\bullet }T^{*}\mathcal {F}). \) More precisely, we have that
for \(\alpha \in \Gamma (\wedge ^{k}T^{*}\mathcal {F}),\beta \in \Gamma (G^{*})\) and \(V_1,\ldots ,V_k\in \Gamma (T\mathcal {F})\). If we use the obvious identification
determined by
then we obtain the following description of the map \(\Phi \).
Lemma 5.1
The map \(\Phi :\Gamma (\wedge ^{k}T^{*}\mathcal {F})\rightarrow \Gamma (\wedge ^{k}T^{*}\mathcal {F}\otimes G)\) is given by
It follows that in order to study \(\Phi \), one only has to understand the map
We now show that this map intertwines the differentials \(d_{\mathcal {F}}\) and \(d_{\nabla ^{*}}\).
Lemma 5.2
We have a chain map
Proof
We start by expressing the complexes \(\big (\Omega ^{\bullet }(\mathcal {F}),d_{\mathcal {F}}\big )\) and \(\big (\Omega ^{\bullet }(\mathcal {F};G^{*}),d_{\nabla ^{*}}\big )\) in the bi-degree language introduced above. We claim that the following hold.
Since (i) is clear, we only justify (ii). Pick \(\beta \in \Omega ^{1,k}(C)\), and let \(V_1,\ldots ,V_{k+1}\in \Gamma (T\mathcal {F})\) and \(Y\in \Gamma (G)\). On one hand, we have
On the other hand,
Here,
and
Upon comparison, we see that \(\tau (d_{0,1}\beta )=-d_{\nabla ^{*}}(\tau (\beta ))\), hence the claim is proved.
Next, we relate the bihomogeneous components of the de Rham differential d with each other. By the decomposition (45), we have that \(d^{2}\) maps \(\Omega ^{u,v}(C)\) into
Because each component of \(d^{2}\) must be zero, we obtain
At last, we prove the statement of the lemma. Using the second relation in (47) and (ii) of the claim above, we have for \(\alpha \in \Gamma (\wedge ^{\bullet }T^{*}\mathcal {F})\) that
Since by (i) of the claim above, the restriction of \(d_{0,1}\) to \(\Gamma (\wedge ^{\bullet }T^{*}\mathcal {F})\) coincides with the foliated de Rham differential \(d_{\mathcal {F}}\), this finishes the proof.
\(\square \)
Item (i) of Proposition 2.10 is now immediate.
Corollary 5.3
The map
is a chain map, up to sign.
Proof
From the expression (46), we get that for \(\alpha \in \Omega ^{k}(\mathcal {F})\),
Here, we also used that \(\text {Id}\otimes (\omega _C^{\flat })^{-1}\) intertwines \(d_{\nabla ^{*}}\) and \(d_{\nabla }\), see Sect. 1.3.2. \(\square \)
Also item (ii) of Proposition 2.10 is a consequence of Lemma 5.2.
Corollary 5.4
-
(1)
The following is a chain map, up to sign:
$$\begin{aligned} (-1)^{\bullet }(\tau \circ d_{1,0}):\big (\Omega ^{\bullet }(\mathcal {F}),d_{\mathcal {F}}\big )\rightarrow \big (\Omega ^{\bullet }(\mathcal {F};G^{*}),d_{\nabla ^{*}}\big ). \end{aligned}$$ -
(2)
The map induced by \((-1)^{\bullet }(\tau \circ d_{1,0})\) in cohomology is canonical, since it coincides with the transverse differentiation map \( d_{\nu }:H^{\bullet }(\mathcal {F})\rightarrow H^{\bullet }(\mathcal {F};N^{*}\mathcal {F}). \)
-
(3)
The map \(\Phi \) induces a canonical map in cohomology, namely
$$\begin{aligned} \big [-\text {Id}\otimes (\omega _{C}^{\flat })^{-1}\big ]\circ d_{\nu }:H^{\bullet }(\mathcal {F})\rightarrow H^{\bullet }(\mathcal {F};N\mathcal {F}). \end{aligned}$$
Proof
For \(\alpha \in \Omega ^{k}(\mathcal {F})\), we have
which proves (1). To prove item (2), we will identify \(N^{*}\mathcal {F}\cong G^{*}\). For a closed foliated form \(\alpha \in \Gamma (\wedge ^{k}T^{*}\mathcal {F})\), note that one can compute \(d_{\nu }[\alpha ]\) as follows. First extend \(\alpha \) by zero on the complement G, so that we can view \(\alpha \) as an element of \(\Omega ^{k}(C)\). Then, pick the component of
lying in \(\Gamma (\wedge ^{k}T^{*}\mathcal {F}\otimes G^{*})\). This immediately implies item (2). Item (3) is now a consequence of item (2) and the expression (46). \(\square \)
We now showed that the canonical map \(d_{\nu }\) in cohomology is induced by a cochain map, which can be defined at the expense of choosing a complement G to \(T\mathcal {F}\). The cochain map in question is essentially the component \(d_{1,0}\). This implies that the space \(\ker (d_{\nu })\) is a term on the page \(E_2\) of the spectral sequence of the foliation \(\mathcal {F}\). This gives more insight into the space of first-order deformations, see Definition 2.11. We give the details in the following remark.
Remark 5.5
Given an arbitrary foliation \(\mathcal {F}\), recall that its spectral sequence \(\{E_k,d_k\}\) arises from a descending filtration of the de Rham complex, given by the spaces
Picking a complement G to \(T\mathcal {F}\), we see that \(\Omega ^{r}_{k}\) is the ideal in \(\Omega ^{r}(C)\) generated by \(\Gamma (\wedge ^{k}G^{*})\). The page \(E_0\) has terms given by
and it is equipped with the differential \(d_{0,1}\) defined in (45). More concisely, \(E_0=\big (\Omega (C),d_{0,1}\big )\). The page \(E_1\) is the cohomology of \(E_0\), endowed with the differential induced by \(d_{1,0}\), i.e.,
Using implicitly the identifications from the claim in Lemma 5.2, we see that the first two columns of the page \(E_1\) look as follows:

The page \(E_2\) consists of the cohomology groups of the complex \(E_1\), i.e.,
Also using Corollary 5.4, we see in particular that
This point of view explains in a more conceptual way why the first-order deformations in Definition 2.11 reduce in the integral case to those considered by Ruan [20]. We checked this fact by direct computation in Example 2.13. A simpler way is remarking that in case \(\mathcal {F}\) is given by the fibers of a fiber bundle, then the spectral sequence of \(\mathcal {F}\) reduces to the Leray spectral sequence of \(C\rightarrow C/\mathcal {F}\). Indeed, if C is compact and \(\mathcal {F}\) is given by a fiber bundle, then the Leray–Serre theorem [15, Cor. I.5.3] states that
where \(\mathcal {H}^{1}\) is the flat vector bundle defined in (9). Therefore, \(E^{0,1}_{2}\) can be identified with the space of flat sections of \((\mathcal {H}^{1},\nabla )\), showing that Definition 2.11 is consistent with Ruan’s work.
1.1.2 The proof of Lemma 2.12
At last, we give the proof of Lemma 2.12. It relies on the results proved in Sect. 5.1.1, namely on the proof of Lemma 5.2 and on Corollary 5.4.
Proof of Lemma 2.12
Fix a complement G to \(T\mathcal {F}\). By the claim in the proof of Lemma 5.2 and Corollary 5.4 (2), we have to show that the following two statements are equivalent:
-
(1)
\(d_{0,1}\beta =0\) and \(d_{1,0}\beta \) is exact in \(\big (\Omega ^{1,\bullet }(C),d_{0,1}\big )\).
-
(2)
There exists an extension \(\widetilde{\beta }\in \Omega ^{1}(C)\) of \(\beta \) such that \(\iota _{V}d\widetilde{\beta }=0\) for all \(V\in \Gamma (T\mathcal {F})\).
For one implication, assume that \(d_{0,1}\beta =0\) and that \(d_{1,0}\beta =d_{0,1}\gamma \) for some \(\gamma \in \Gamma (G^{*})\). Then \(\widetilde{\beta }:=\beta -\gamma \in \Gamma (T^{*}\mathcal {F}\oplus G^{*})\) is an extension of \(\beta \) satisfying
The latter belongs to \(\Gamma (\wedge ^{2}G^{*})\), and therefore \(\iota _{V}d\widetilde{\beta }=0\) for all \(V\in \Gamma (T\mathcal {F})\).
For the converse, we can write the given extension as \(\widetilde{\beta }=\beta +\gamma \) for some \(\gamma \in \Gamma (G^{*})\). Decomposing \(d\widetilde{\beta }\) in the direct sum
we have
Since by assumption, the components in \(\Gamma (\wedge ^{2}T^{*}\mathcal {F})\) and \(\Gamma (G^{*}\otimes T^{*}\mathcal {F})\) vanish, we get
\(\square \)
1.2 A computation in the Gotay local model
Given a coisotropic submanifold \(C\subset (M,\omega )\) with characteristic foliation \(\mathcal {F}\), consider the Gotay local model \((U,\Omega _G)\) associated with a choice of splitting \(TC=T\mathcal {F}\oplus G\). Throughout this paper, we frequently identified vertical fiberwise constant vector fields on U with sections of \(T^{*}\mathcal {F}\). In Lemma 5.6, we give the explicit formulae underlying this correspondence. This result is essentially [22, Lemma 4.4], up to an additional minus sign. To justify this difference, we include a detailed proof in coordinates.
As before, \(p:U\rightarrow C\) denotes the projection and \(j:T^{*}\mathcal {F}\hookrightarrow T^{*}C\) the inclusion induced by G. Also, \(\Pi _G=-\Omega _G^{-1}\) is the Poisson structure corresponding with \(\Omega _G\), \(i:C\hookrightarrow U\) is the inclusion map and \(r:T^{*}C\rightarrow T^{*}\mathcal {F}\) is the restriction to the leaves of \(\mathcal {F}\).
Lemma 5.6
There is a natural correspondence
with inverse
Proof
Choose coordinates \((q_1,\ldots ,q_k,q_{k+1},\ldots ,q_n)\) on C such that \(T\mathcal {F}=\text {Span}\{\partial _{q_1},\ldots ,\partial _{q_k}\}\). Let \((y_1,\ldots ,y_n)\) denote the conjugate coordinates on \(T^{*}C\). We have to show that the correspondence described above reads as follows in these coordinates:
We start by expressing the symplectic form \(\Omega _G\) in coordinates. Since G is transverse to the first summand in the decomposition
there exists a fiberwise linear map \(\Psi \) such that
Let us write for \(l=k+1,\ldots ,n\):
We then obtain for \(i=1,\ldots ,k\) that
This shows that
and therefore
Hence, expressing the map \(j:T^{*}\mathcal {F}\hookrightarrow T^{*}C\) in coordinates gives
It follows that
hence the symplectic form \(\Omega _G\) looks like
It is now clear that the correspondence described in the statement of the lemma acts as required in (49), since we have
\(\square \)
Remark 5.7
The correspondence from Lemma 5.6 extends to foliated differential forms and vertical fiberwise constant multivector fields. Explicitly, it is given by
with inverse
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geudens, S. On deformations of coisotropic submanifolds with fixed characteristic foliation. Lett Math Phys 114, 5 (2024). https://doi.org/10.1007/s11005-023-01750-3
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-023-01750-3




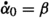 . Otherwise, we say that
. Otherwise, we say that 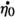 is closed with respect to
is closed with respect to 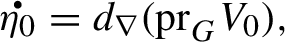
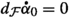 ,
,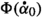 is exact in
is exact in 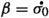 .
.