1 Introduction

Elastic mechanical metamaterials (Hussein et al. 2014) exhibit interesting frequency-dependent unusual physical properties like negative mass and negative Young’s modulus in a specific regime of the excitation frequency. These idiosyncratic physical properties are caused by the out-of-phase motion of multiple resonating units simultaneously, making effective mass or effective stiffness of the designed metamaterial negative in a certain frequency range. Generally, in other materials, the unusual existence of band structure (Huang and Sun 2010a, b) is not common; that is why metamaterials need to be investigated for better vibration attenuation and energy harvesting applications. The spatial periodicity of mechanical unit cells (coupled spring-mass system) yields mechanical metamaterials (Srivastava 2016; Nemat-Nasser et al. 2015). Numerous physical systems derived from various research areas like phononics (Lu and Srivastava 2018; Yong et al. 200; Mokhtari et al. 2019), condensed matter physics (Meinzer et al. 2014; Volz et al. 2016), optics (Liu et al. 2011; Christensen and de Abajo 2012), composites (Sun et al. 1968a, b; Nemat-Nasser 1972), engineering mechanics (Yang et al. 2008; Banerjee et al. 2017; Mei et al. 2012), aerospace structures (Mead 1973; Banerjee et al. 2019) can be comprehended as a one-dimensional periodic arrangement of the coupled spring-mass system. The single representative unit of a mass-in-mass metamaterial can be represented as a special case of the tuned mass damper (Malik 1990). Traditionally tuned mass dampers are operational for narrow bandwidth excitation frequency; however, in mechanical metamaterials, attenuation bandwidth can be increased by tuning the physical system parameters (Tan et al. 2012). Inspired by the characteristic of elastic mechanical metamaterials that exhibit pass and stop bands like the periodic medium for wave propagation, simultaneous energy harvesting, and vibration control can be proposed by embedding piezoelectric material in the resonators. Elastic mechanical metamaterial has local resonators, which help in bandgap formation due to the local resonance phenomenon, hence distributes the energy to each of the local resonators. These bandgaps can be tailored as it depends on critical parameters like the natural frequency and mass ratio of the local resonators. Hence, vibration can be damped in a wide frequency range. In the proposed system, the piezoelectric material is attached to the local resonators. This electro-mechanical resonator can easily harvest the energy as it is prone to oscillate with high amplitude. Hence by distributing the energy to each of the local resonators, the vibration can be damped for a wide specific frequency range, and that energy can also be harvested. Based on interesting physical properties of the metamaterials, it can be characterized as negative mass (Srivastava 2015; Pope and Laalej 2014; Yao et al. 2008; Huang et al. 2009; Pope et al. 2012), negative stiffness (Huang et al. 2016; Huang and Sun 2011; Goldsberry and Haberman 2018; Huang and Sun 2012; Tan et al. 2019; Dwivedi et al. 2020), negative Poisson’s ratio (Meena et al. 2019; Chen et al. 2018; Alipour and Shariyat 2017; Chen et al. 2017; Friis et al. 1988; Dirrenberger et al. 2013).

Fig. 1
figure 1

Piezo-embedded negative mass metamaterial. A mass-in-mass system, inside the primary mass \(m_{1}\) a resonating mass \(m_{2}\), is present. A piezoelectric material having an electromechanical coupling coefficient \(\theta \) is embedded in the resonating unit

Full size image

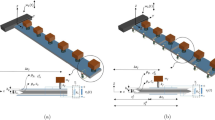
Figure 1 portrays a conceptual illustration of the piezo-embedded negative mass metamaterial. For a unit, inside the main mass (\(m_{1}\)), a resonating mass (\(m_{2}\)) is present (mass-in-mass). These masses are coupled with an electromechanical resonator having stiffness \(k_{2}\) and an electromechanical coupling coefficient \(\theta \). This unit is periodic and connected with stiffness \(k_{1}\) to another unit. Physically negative mass metamaterials can be comprehended as silicone-coated steel balls in the epoxy matrix (Banerjee 2011). These silicone coated steel balls act as an internal resonating unit in a mass-in-mass metamaterial, in which steel ball contributes to mass and silicone coating for stiffness. In mass-in-mass resonating metamaterial, the internal mass response is much larger than that of the external mass near the resonating frequency of the internal mass. In a specific frequency band higher than the resonating frequency of the internal system, the response of internal mass is out of phase with the excitation given. Therefore, the net momentum of a unit becomes out of phase with the external excitation. This phenomenon can be emulated by assigning negative mass to the equivalent single degree of freedom system. Hence, this type of resonating mass-in-mass metamaterial is called negative mass metamaterial. In the mechanical metamaterials, simultaneous out-of-the-phase motion of multiple resonating units makes the effective physical properties (mass or stiffness) of the system frequency contingent due to local resonance phenomenon occurring; hence effective dynamic mass and stiffness of the system alter with the frequency. Virtually changing natural frequency (mass and stiffness) of the local resonators in the metamaterial, edging frequencies of the bandgap can be changed. For wavelengths much higher than the lattice length of a unit (long-wavelength approximation), locally resonant units in the designed metamaterial can enable bandgap formation. Therefore, dynamic physical properties modulate wave propagation inside the designed metamaterials. Every unit of the metamaterial induces frequency contingent impedance to the medium and restricts the energy dispersion from the transmitted wave to the resonating frequency domain. Therefore, in the attenuation band, energy cannot propagate along with the units in the designed metamaterial; however, this energy flows through all the resonating units. It causes a high amplitude of vibration in the resonating units. Embedding the piezoelectric material in the resonating units enables such systems to harness the vibrational energy to electrical energy efficiently. That is why the application of mechanical metamaterials can be extended to vibration-based energy harvesting with vibration attenuation in recent years (Carrara et al. 2013; Mikoshiba et al. 2013; Hu et al. 2017; Shivashankar and Gopalakrishnan 2020).

Vibration-based energy harvesting has fascinated the researchers for numerous applications such as low-power sensors and devices for structural health monitoring, micro-electromechanical systems, wireless and portable electronic devices. For the long wave approximation, the electromechanical resonators in metamaterials enable bandgap formation, which helps in energy harvesting and vibration control. Based on this, Sugino and Erturk (2018) have proposed a multifunctional piezoelectric metastructure for low-frequency vibration attenuation and energy harvesting. They have concluded that energy can be actively harvested from locally resonant bandgaps without affecting vibration attenuation significantly. Based on a similar objective, Hu et al. (2017) proposed a piezo-embedded metastructure for vibration suppression and energy harvesting. They also carried out a dimensionless parametric study to tune the system for optimum energy harvesting and vibration attenuation. In our recent work on piezo-embedded negative stiffness metamaterial (Dwivedi et al. 2020), we have also presented simultaneous energy harvesting and vibration attenuation for a finite chain of the metamaterial units. We derived closed-form expression for the effective stiffness of the system along with critical physical parameters, which affect the vibration attenuation and energy harvested. Earlier, Sugino et al. (2017) have also suggested a general theory for bandgap estimation in locally resonant metamaterials. Through this study, they concluded that more number of resonators are required to identify the bandgap in higher vibration modes. Subsequently, they have also investigated critical parameters for tuning the bandgap in the desired frequency range (Sugino et al. 2016, 2017). Natural frequency and the total mass ratio of the resonator are parameters that contribute considerably to higher attenuation bandwidth. Based on the bandgap formation approach, Chen et al. Chen et al. (2014) designed an active elastic metamaterial having negative capacitance piezoelectric shunting. They varied bandgap by changing the stiffness and selecting the proper negative capacitance. They concluded that by tuning the negative capacitance of shunted piezoelectric material, the metamaterial band structure could be varied. By mechanical and electromechanical resonators in metamaterials, locally resonant bandgaps can be formed. Inspired by this, Sugino et al. (2018) investigated the interaction of mechanical and electromechanical bandgaps in hybrid metamaterial cantilever under bending vibration for the continuous system. However, in mechanical metamaterials finding the physical system parameters which govern the formation of mechanical and electromechanical bandgaps is still open in the literature. The optimization of these system parameters for the maximum width of the first attenuation band has also not been reported in the literature. For this, we present a mass-in-mass type discrete system with an electromechanical resonator to understand the formation of various bandgaps in mechanical metamaterials. Through the extensive mathematical study of the system, we derive physical parameters that govern the formation of mechanical and electromechanical bandgaps.

In this article, we present the mathematical model for piezo-embedded negative mass metamaterials. Periodic structure problems can be solved using the Bloch theorem. Hence, for a finite number of metamaterial units coupled equation of motion of the system is deduced using the generalized Bloch theorem. The relationship between frequency and wavenumber can be derived through this theory. The band structure of piezo-embedded negative mass metamaterial is plotted and analyzed for different system parameters using this dispersion relationship. Embedding the piezoelectric material in the resonating units endorses good tunability of the system due to an enlarged attenuation band. Consecutively, the power produced is estimated using the backward substitution method for purely resistive and shunted inductor energy harvesting circuits by considering a finite number of metamaterial units. There can be infinite circuit designs, which can be essential to enhance the energy harvesting capabilities. As far as the circuits taken in this research are concerned, these two circuits, namely purely resistive and shunted inductor, are the fundamental circuits widely used in the literature (Sugino et al. 2017; Adhikari et al. 2009). The proposed system is also explored mathematically in the non-dimensional domain to identify the critical system parameters for the formation of mechanical and electromechanical bandgaps. This investigation produces an in-depth idea about mechanical and electromechanical bandgaps forming through the derived physical parameters. Using the dispersion relationship obtained through the non-dimensional study of the system, we find the optimized numerical values of the system parameters for maximum first attenuation bandwidth. It gives a benchmark about the range of the system parameters for designing the piezo-embedded mechanical metamaterials having wideband vibration control potential. The following section elucidates the dynamics of Pietro-embedded negative mass metamaterial.

2 Mathematical formulation

Figure 1 elucidates piezo-embedded negative mass metamaterial. In each unit \(m_{1}\) is outer mass and corresponding stiffness and displacement are \(k_{1}\) and \(x_{m}\), respectively whereas, \(m_{2}\) is inner resonating mass and corresponding stiffness and displacement are \(k_{2}\) and \(x_{r}\), respectively. The resonating unit is coupled with a piezoelectric material having an electromechanical coupling coefficient of \(\theta \) for energy harvesting. The voltage produced by piezoelectric material is denoted by v. Each unit of piezo-embedded negative mass metamaterial vibrates with harmonic excitation given to the system. The equation of motion of the above system can be written by taking the equilibrium of forces along the X direction for the ith unit of the piezo-embedded negative mass metamaterial. This gives the following equation

$$\begin{aligned}&m_{1} {\ddot{x}}_{m(i)} +k_1(2x_{m(i)}-x_{m(i-1)}-x_{m(i+1)})\nonumber \\&\quad +\,k_2(x_{m(i)}-x_{r(i)})-\theta v_i = 0 \end{aligned}$$
(1)

Also, the equation of motion of ith resonating mass can be written as

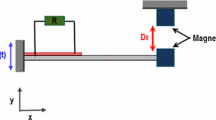
$$\begin{aligned} m_{2} {\ddot{x}}_{r(i)}+k_2(x_{r(i)}-x_{m(i)})+\theta v_i = 0 \end{aligned}$$
(2)

In Fig. 2, two types of energy harvesting circuits are considered, namely (a) purely resistive circuit and (b) circuit with the parallel configuration of inductor and resistor.

Fig. 2
figure 2

Energy harvesting circuits. a Purely resistive energy harvesting circuit. b Energy harvesting circuit with the shunted inductor

Full size image

For a purely resistive energy harvesting circuit, governing equation of ith piezo-embedded resonating unit due to electromechanical coupling (Adhikari et al. 2009) can be written as

$$\begin{aligned} {\frac{v_i}{R} }+C^p{\dot{v}}_{i}-\theta (\dot{x}_{r(i)}-\dot{x}_{m(i)})=0 \end{aligned}$$
(3)

where \(C^p\) is the capacitance of piezoelectric material, R is load resistance, and v is the voltage across load resistance.

Since voltage and displacement parameters of each unit are varying with time; hence for solving these coupled equations, the generalized solution can be presumed as \(a_{i}=A_i e^{\lambda t}\), where \(\lambda \) is complex for sinusoidally varying motion and real for exponentially decaying vibration. Hence the Laplace transform of Eqs. 2 and 3 yields

$$\begin{aligned} (\lambda ^2m_{2}+k_{2}) X_{r(i)}-k_2X_{m(i)}+\theta V_i = 0 \end{aligned}$$
(4)

and

$$\begin{aligned} -\theta \lambda X_{r(i)}+\theta \lambda X_{m(i)}+(\frac{1}{R}+\lambda C^p) V_i = 0 \end{aligned}$$
(5)

Equations 4 and 5 could be written in the form of a matrix as

$$\begin{aligned} \begin{bmatrix} \lambda ^2m_{2}+k_{2} &\quad {\theta } \\ -\theta \lambda &\quad \frac{1}{R}+\lambda C^p \end{bmatrix} \begin{Bmatrix} X_{r(i)} \\ V_i \end{Bmatrix} = \begin{Bmatrix} k_2 \\ -\theta \lambda \end{Bmatrix}X_{m(i)} \end{aligned}$$
(6)

Hence the linear solution for \( X_{r(i)}\) and \(V_i\) yields

$$\begin{aligned} X_{r(i)}=B_{1}(\lambda )X_{m(i)} \quad \text {and} \quad V_i =B_{2}(\lambda )X_{m(i)} \end{aligned}$$
(7)

where \(B_{1}\) and \(B_{2}\) are function of \(\lambda \).

Correspondingly, for energy harvesting circuit with the shunted inductor, governing equation of ith piezo-embedded resonating unit due to electromechanical coupling (Renno et al. 2009) can be written as

$$\begin{aligned} {\frac{\dot{v}_i}{R} }+{\frac{v_i}{L} }+C^p{\ddot{v}}_{i}-\theta (\ddot{x}_{r(i)}-\ddot{x}_{m(i)})=0 \end{aligned}$$
(8)

where L is inductance of the circuit.

Hence like Eq. 6, coupled equation of motion of the system can also be written as

$$\begin{aligned} \begin{bmatrix} \lambda ^2m_{2}+k_{2} &\quad {\theta } \\ -\theta \lambda ^2 &\quad \frac{\lambda }{R}+\frac{1}{L}+\lambda ^2 C^p \end{bmatrix} \begin{Bmatrix} X_{r(i)} \\ V_i \end{Bmatrix} = \begin{Bmatrix} k_2 \\ -\theta \lambda ^2 \end{Bmatrix}X_{m(i)} \end{aligned}$$
(9)

Therefore the inclusion of the inductor in the energy harvesting circuit modifies \(B_{1}\) and \(B_{2}\) in Eq. 7, hence the value of \(B_{1}\) and \(B_{2}\) will alter for energy harvesting circuit with the shunted inductor.

As the system shown in Fig. 1 is spatially periodic; hence the generalized Bloch’s theorem (Hussein and Frazier 2013, 2010; Hussein 2009b, a; Bacquet et al. 2018) is adopted here to transform Eq. 1 in the frequency domain, which states the solution of the wave equation can be obtained by using the following displacement relations

$$\begin{aligned} x_{j}= & x e^{(ik\alpha +\psi t)}= {\bar{x}} e^{\psi t} \nonumber \\ x_{j+n}= & x e^{(ik(\alpha +nl)+\psi t)}= x_{j} e^{inkl} \end{aligned}$$
(10)

where x is the amplitude of the wave, k is the wavenumber, \(\alpha \) is the position vector of the particle, l is the wavelength, n is the particle number of a wave, displacement of which to be found, and \(\psi \) is the frequency function. Following the long-wavelength approximation, the geometry of each unit of the metamaterial is assumed to be less than one-tenth of the wavelength of the transmitted wave. So that size of the unit neither interferes nor scatters the wave.

Therefore by taking the Laplace transform of Eq. 1 and using Bloch formulation from Eq. 10, we can transform Eq. 1 as

$$\begin{aligned}&\lambda ^2 m_{1} {X}_{m(i)} +k_1(2X_{m(i)}-X_{m(i-1)}e^{-ikl}-X_{m(i+1)}e^{ikl})\nonumber \\&\quad +\,k_2(X_{m(i)}-X_{r(i)})-\theta V_i = 0 \end{aligned}$$
(11)

Afterwards substituting values of \(X_{r(i)}\) and \(V_i\) from Eq. 7 and on simplification, following relation can be deduced

$$\begin{aligned}[\lambda ^2 m_{1}+(1-B_{1})k_{2}-\theta B_{2}] {X}_{m(i)} +2k_1[(1-\cos (\mu ))]{X}_{m(i)}=0 \end{aligned}$$
(12)

where \(\mu =kl\) and it is called the non-dimensional wave number.

Equation 12 represents the dispersion relationship for the piezo-embedded negative mass metamaterial. It can be plotted to obtain the band structure of the system, which is explained in detail in Sect. 4. The next section describes the formulation for voltage and displacement calculations from each unit of the piezo-embedded negative mass metamaterial.

3 Vibrational amplitude and voltage estimation

The vibrational amplitude of a metamaterial unit provides an intuitive idea of amplifying and decaying the nature of waves in transmission and attenuation bands, respectively. Here, the vibrational amplitude of each unit of the piezo-embedded negative mass metamaterial is derived using the backward substitution technique (Dwivedi et al. 2019; Banerjee et al. 2016) by the following explained method.

Equation of motion for the last unit in the piezo-embedded negative mass metamaterial can be rewritten as

$$\begin{aligned} m_{1} {\ddot{x}}_{m(i)} +k_1(x_{m(i)}-x_{m(i-1)}) +k_2(x_{m(i)}-x_{r(i)})-\theta v_i = 0 \end{aligned}$$
(13)

The forced-free boundary condition is assumed for finite number of units of the metamaterial chain in which one end is forced to move with the form \(a=A e^{{\bar{\omega }} t}\), where \( {\bar{\omega }} \) is the excitation frequency function. On taking the Laplace transform of Eq. 13 and substituting values of \(x_r\) and \(v_i\) from Eq. 7, we can obtain following relation for displacements

$$\begin{aligned} X_{m(i-1)}={\frac{(-{{\bar{\omega }}}^2 {m_1}+k_2(1-B_{1}(\lambda ))-\theta B_{2}(\lambda ))}{k_1} }X_{m(i)} \end{aligned}$$
(14)

Equation 14 can be used to find the vibrational amplitude of the last unit of the piezo-embedded negative mass metamaterial. For intermediate units above relation of displacements will not be valid. The following procedure can obtain it.

Substituting values of \(x_r\) and \(v_i\) from Eq. 7 in Eq. 1 and applying the Laplace transform, yields the following relation for displacements

$$\begin{aligned} X_{m(i-1)}={\frac{(-{{\bar{\omega }}}^2 {m_1}+2k_1+k_2(1-B_{1}(\lambda ))-\theta B_{2}(\lambda ))}{k_1} }X_{m(i)} -X_{m(i+1)} \end{aligned}$$
(15)

Hence Eq. 15 can be used to find vibrational amplitude for intermediate units of the piezo-embedded negative mass metamaterial.

For voltage estimation, Eq. 2 can be solved simultaneously with Eqs. 3 and 8 for both the energy harvesting circuits considered. For a purely resistive energy harvesting circuit, taking the Laplace transform of Eqs. 2 and 3, after that solving these equations simultaneously for \(V_i\), will yield the following relation

$$\begin{aligned} V_i={\frac{{m_2}{{\bar{\omega }}}^2{\theta }{X_{m(i)}}}{(k_2 C^p-{m_2}{{\bar{\omega }}}^2C^p+{\theta }^2)+(\frac{{m_2}{{\bar{\omega }}}}{R}-\frac{k_2}{R{{\bar{\omega }}}})j} } \end{aligned}$$
(16)

Similarly, for energy harvesting circuit with the shunted inductor, from Eqs. 2 and 8, \(V_i\) can be found by the following relation

$$\begin{aligned} V_i={\frac{{m_2}{{\bar{\omega }}}^4{L}{\theta }{X_{m(i)}}}{(-{m_2}{{\bar{\omega }}}^4{C^p}{L}+{{m_2}{{{\bar{\omega }}}^3}}+{{{{\bar{\omega }}}^2}{C^p}{L}{k_2} }+{{{\bar{\omega }}}^2}{\theta }^2{L}-{k_2}) +({{m_2}{{\bar{\omega }}}^3}-{k_2}{{{\bar{\omega }}}})j} } \end{aligned}$$
(17)

Therefore by following the above methodology, we can obtain vibrational amplitude (\(X_{m(i)}\)) of each unit of the piezo-embedded negative mass metamaterial through Eqs. 14 and 15. Successively using Eqs. 16 and 17, we can calculate voltage produced for the corresponding energy harvesting circuits, by each unit of the piezo-embedded negative mass metamaterial.

4 Results and discussions

4.1 Band structure and power output for piezo-embedded negative mass metamaterial

All the numerical simulations in this section are performed for \(m_{2}=0.5\) kg, \(k_{1}=1.0\) N/m and, \(k_{2}=0.5\) N/m. The dimension of a unit of the piezo-embedded negative mass metamaterial is 0.1 m. The electrical parameters considered in both the energy harvesting circuits are having numerical values: \( C^{p}=5\ \upmu \)F, \(R=1\ \hbox {M}\Omega \), \(L=1\ \upmu \)H and, \(\theta =6.32\times 10^{-4}\) N/V. In the following subsections, band structure and power output for piezo-embedded negative mass metamaterial for both the energy harvesting circuits considered in Sect. 2 are investigated in detail.

4.1.1 Purely resistive energy harvesting circuit

Fig. 3
figure 3

Band structure and power output for piezo-embedded negative mass metamaterial for a purely resistive energy harvesting circuit. a Comparison of the band structure of the piezo-embedded negative mass metamaterial with simple negative mass metamaterial. b The power produced by the piezo- embedded negative mass metamaterial. c The plot of the effective mass of negative mass metamaterial

Full size image

Figure 3a demonstrates the band structure of the piezo-embedded negative mass metamaterial for a purely resistive energy harvesting circuit. On x and y axes, normalized excitation frequency \({\omega }\) and non-dimensional wave number \( \mu \) are shown respectively. For \(m_{1}=2.0\) kg, both the transmission bands are highlighted, which shows the existence of attenuation bands after each transmission band. The edging frequencies corresponding to the lower and upper limit of the first attenuation band are \( f_{1}\) and \(f_{2}\), respectively, and \(f_{3}\) is the edging frequency corresponding to the upper limit of the second transmission band. The lower part of the first attenuation band will be designated as LA1, and the higher part by HA1. The first attenuation band is divided into two sub-bands (LA1 and HA1) about unity on the frequency axis. The lower part of the first attenuation band (LA1) is associated with the low-frequency attenuation region, whereas the higher part (HA1) belongs to the high-frequency attenuation region. The lower part of the first attenuation band (LA1) can be calculated by subtracting edging frequency \( f_{1} \) from unity, whereas the higher part (HA1) is obtained by subtracting edging frequency \( f_{2} \) and unity. The first attenuation band alone cannot provide information about low or high frequency attenuation regions. The lower (LA1) and higher (HA1) parts of the first attenuation band can quantify the first attenuation bandwidth increase in lower and higher frequency regions, respectively. It can be advantageous as per different practical applications for tuning of the attenuation band. Therefore, LA1 and HA1 are critical for maximizing the first attenuation bandwidth in low and high-frequency regions, respectively, as it provides quantitative information on the frequency scale. That is why the first attenuation band is divided into two sub-bands. The summation of LA1 and HA1 will give the width of the first attenuation band (A1). The second attenuation bandwidth is theoretically infinite, but the practical limit goes until the long-wavelength approximation is valid. The second transmission band will be designated as T2. Width of T2 could be found by subtracting \( f_{3} \) and \( f_{2} \). The higher part (HA1) of the first attenuation band also contributes to T2; its width increases for minimum HA1.

The band structure of a simple negative mass metamaterial and piezo-embedded negative mass metamaterial is obtained considering the outer mass, \(m_{1}=2.0\) kg. We found for piezo-embedded negative mass metamaterial, the width of first and second transmission bands increases along with the first attenuation bandwidth, whereas that of the second attenuation band decreases. There is a substantial increase in the first attenuation bandwidth due to the inclusion of piezoelectric material in the resonating units of the negative mass metamaterial. Likewise, for the increased value of the outer mass, \(m_{1}\), in a piezo-embedded negative mass metamaterial, the width of first and second transmission bands increases along with the first attenuation band; in contrast, the width of the second attenuation band decreases. Figure 3a can easily perceive it. The first transmission bandwidth increase is due to a decreased lower part (LA1) of the first attenuation band. The lower part (LA1) of the first attenuation band decreases because of the increase of edging frequency \(f_{1}\). The width of the second transmission band (T2) increases due to the effectively high rate of increase of \( f_{3} \) to \( f_{2} \). On the other hand, HA1 increases because of an increase in the edging frequency \(f_{2}\). Hence it results in wider width of the first attenuation band as the rate of inflation of HA1 recompenses the decrease of LA1. A wider attenuation band is beneficial for vibration attenuation and energy harvesting as well.

During attenuation, the energy cannot propagate to the outer masses; hence, it goes to inner resonating units. It causes the high amplitude of vibration in the inner resonating mass embedded with a piezoelectric material. Thus the maximum production of electrical energy occurs in the proximity of the resonating frequency region. Figure 3b elucidates the power produced by piezo-embedded negative mass metamaterial for the finite number of units. On x and y axes, normalized excitation frequency \({\omega }\) and number of units are shown respectively. The power produced is presented for \(m_{1}=1.0\) kg in both the transmission and attenuation bands. The power produced is significantly more in both the attenuation bands than the produced power in both the transmission bands. When excitation frequency \({\omega }\) is in the first attenuation band, near resonating frequency close to \({\omega }=1\), the power produced is maximum. Therefore, at frequencies in the proximity of bandgap associated with local resonance, where the system is exhibiting negative mass, as shown in Fig. 3c, produced power is significant. In the second attenuation band, the power production is also maximum at higher frequencies associated with the Bragg’s scattering region.

Hence, from this analysis, it is evident that a substantial amount of power is produced in both the attenuation bands compared to the transmission bands by units of the piezo-embedded negative mass metamaterial.

4.1.2 Energy harvesting circuit with shunted inductor

Fig. 4
figure 4

Band structure and power output for piezo-embedded negative mass metamaterial for the energy harvesting circuit with the shunted inductor. a The band structure of the piezo-embedded negative mass metamaterial. b The power produced by piezo-embedded negative mass metamaterial

Full size image

Figure 4a describes the band structure of the piezo-embedded negative mass metamaterial for the energy harvesting circuit with the shunted inductor. For \(m_{1}=2.0\) kg, both the transmission bands are highlighted. For the increased value of \(m_{1}\) in a piezo-embedded negative mass metamaterial, the width of first and second transmission bands along with the first attenuation band increase, whereas the width of the second attenuation band decreases. From Figs. 3a and 4a, it is evident that locally resonant bandgaps are extensively unaffected by switching to another energy harvesting circuit, but it shifts slightly to a lower frequency region. Figure 4b demonstrates the power produced by piezo-embedded negative mass metamaterial for a finite number of units. The power produced is showing a similar trend as in Fig. 3b. The power produced is shown for \(m_{1}=1.0\) kg in both the transmission and attenuation bands.

Fig. 5
figure 5

Wave pattern investigation in the piezo-embedded negative mass metamaterial in the frequency domain. a purely resistive energy harvesting circuit. b energy harvesting circuit with the shunted inductor

Full size image

When excitation frequency \({\omega }\) is in the first attenuation band, in the proximity of resonating frequency close to \({\omega }=1\), the power produced is maximum by initial units. However, it decreases in the farthermost units as the effect of excitation starts weakening. In both the attenuation bands, the initial units produce a significant amount of power compared to the farthermost units. Although the power output is relatively low compared to the purely resistive harvesting circuit for the same assumed parameters as power, it depends primarily on the electromechanical coupling coefficient.

4.2 Wave pattern exploration through units of the piezo-embedded negative mass metamaterial

Figure 5a, b elucidate the wave propagation pattern for the assumed energy harvesting circuits in various frequency domains of the band structure of the piezo-embedded negative mass metamaterial along with a finite number of units. The normalized excitation frequency (\( \omega \)), the logarithmic displacement ratio of main mass (\( m_1 \)), and the number of units of the metamaterial on the logarithmic scale are shown over x, y and z axes, respectively. These plots deliver a glimpse of the amplifying and decaying nature of waves along the metamaterial units in both transmission and attenuation bands. In the first transmission band, waves propagate along with all the metamaterial units with different amplitudes in the low-frequency domain. In contrast, in the first attenuation band, waves are decaying exponentially, which can be easily perceptible from Fig. 5a, b. Likewise, in the high-frequency domain in the second transmission band, all waves are propagating with different amplitudes along with all units of the metamaterial. Finally, in the second attenuation band, all waves show an exponentially decaying nature, which can be easily perceived from the plot of the wave pattern shown above.

Fig. 6
figure 6

Visualization of attenuation and transmission bands in the piezo-embedded negative mass metamaterial through 2D plots. a Purely resistive energy harvesting circuit. b Energy harvesting circuit with the shunted inductor. The logarithmic of transmissibility is shown on the color axis

Full size image

Two dimensional plots corresponding to Fig. 5a, b are also represented in Fig. 6a, b, respectively for the ease of understanding the nature of wave propagation in transmission and attenuation bands. The logarithmic displacement ratio is shown on the color axis. In both the attenuation bands decaying nature of waves along the metamaterial units can be seen with the gray color scale. Hence, from these displacement transmissibility plots, both the attenuation bands can be easily comprehended. The first attenuation band lies between 1 and 1.5 whereas, the second attenuation band exists after 2.25 on the frequency scale, as observed from these plots. The displacement transmissibility in the attenuation bands is negative, but it is finite. It implies, the small amplitude of vibration persists in the last unit of the metamaterial. As the number of units keeps on increasing, displacement transmissibility in the attenuation band is decreasing rapidly.

5 Analysis of the system in non-dimensional domain

For identifying the parametric space in more efficient way and to understand the reliance of the response on the system parameters, non-dimenonalization of Eqs. 4, 5, 9 and, 12 is carried out by assuming \(x(t)=D{\bar{X}}(\tau )\) and \(v(t)=B_v{\bar{V}}(\tau )\), where D is the diameter of outer mass and \( B_v \) is arbitrary dimensional parameter corresponding to voltage. D and \( B_v \) relate dimensional displacement and voltage to non-dimensional displacement and voltage respectively.

Non-dimensionlized form of Eqs. 4 and 5 yield the following equation in the matrix form

$$\begin{aligned} \begin{bmatrix} \eta _2^2+1 &\quad 1 \\ 1 &\quad -(\frac{1}{h_1}+\frac{1}{h_2 \eta _2}) \end{bmatrix} \begin{Bmatrix} {{\bar{X}}}_{r(i)} \\ {{\bar{V}}}_i \end{Bmatrix} = \begin{Bmatrix} 1 \\ 1 \end{Bmatrix}{{\bar{X}}}_{m(i)} \end{aligned}$$
(18)

where \( \eta _2 \) is non-dimensional excitation frequency, which is ratio of \( \lambda \) and \( \omega _2 \). \( \lambda \) is the frequency function and \( \omega _2 \) is the natural frequency of the inner resonating mass (\( m_2 \)). \( h_1 \) and \( h_2 \) are non-dimensional capacitive and resistive parameters, respectively.

Similarly the non-dimensionalized coupled equation of Eq. 9 for energy harvesting circuit with the shunted inductor can be written as

$$\begin{aligned} \begin{bmatrix} \eta _2^2+1 &\quad 1 \\ 1 &\quad -(\frac{1}{h_1}+\frac{1}{h_2 \eta _2}+\frac{1}{h_2 h_3 \eta _2^2}) \end{bmatrix} \begin{Bmatrix} {{\bar{X}}}_{r(i)} \\ {{\bar{V}}}_i \end{Bmatrix} = \begin{Bmatrix} 1 \\ 1 \end{Bmatrix}{{\bar{X}}}_{m(i)} \end{aligned}$$
(19)

where \( h_3 \) is the non-dimensional inductive parameter.

Likewise the non-dimensional form of Eq. 12 yields

$$\begin{aligned} \eta _2^2 \eta _s^2-(B_1+ B_2 -1)\rho \eta _s^2 +2(1-\cos (\mu ))=0 \end{aligned}$$
(20)

where \( \eta _s \) is the structural frequency ratio, and \( \rho \) is the mass ratio.

Therefore all the non-dimensional parameters derived in the above formulation can be briefed as

$$\begin{aligned} \eta _s=\frac{\omega _2}{\omega _1},\rho =\frac{m_2}{m_1}, h_1=\frac{\theta ^2}{k_2 C^p},h_2=\frac{R \omega _2 \theta ^2}{k_2},h_3={\omega _2^2}{L C^p} \end{aligned}$$
(21)

Using Eqs. 18 and 7, the following equation can be obtained

$$\begin{aligned} \begin{bmatrix} \eta _2^2+1 &\quad 1 \\ 1 &\quad -(\frac{1}{h_1}+\frac{1}{h_2 \eta _2}) \end{bmatrix} \begin{Bmatrix} B_1 \\ B_2 \end{Bmatrix} = \begin{Bmatrix} 1 \\ 1 \end{Bmatrix} \end{aligned}$$
(22)

For a purely resistive energy harvesting circuit, the linear solution of Eq. 22 yields, \( B_1 \) and \( B_2 \) as

$$\begin{aligned} B_1= & \frac{h_1 h_2 \eta _2+h_2 \eta _2+h_1}{h_2 \eta _2^3+h_1 \eta _2^2+h_2(h_1+1) \eta _2+h_1} \nonumber \\ B_2= & \frac{-h_1 h_2 \eta _2^3}{h_2 \eta _2^3+h_1 \eta _2^2+h_2(h_1+1) \eta _2+h_1} \end{aligned}$$
(23)

Similarly using Eqs. 19 and 7, for energy harvesting circuit with the shunted inductor, \( B_1 \) and \( B_2 \) can be found as

$$\begin{aligned} B_1= & \frac{h_1 h_2 h_3 \eta _2^2+h_2 h_3 \eta _2^2+h_1 h_3 \eta _2+ h_2}{h_2 h_3 \eta _2^4+h_1 h_3 \eta _2^3+h_2(h_1 h_3 +h_3 +1) \eta _2^2+h_1 h_3 \eta _2+h_2} \nonumber \\ B_2= & \frac{-h_1 h_3 h_2 \eta _2^4}{h_2 h_3 \eta _2^4+h_1 h_3 \eta _2^3+h_2(h_1 h_3 +h_3 +1) \eta _2^2+h_1 h_3 \eta _2+h_2} \end{aligned}$$
(24)

From Eq. 23, substitution of values of \( B_1 \) and \( B_2 \) in Eq. 20 gives the following equation

$$\begin{aligned}&\eta _2^2 \eta _s^2-\left( \frac{h_1 h_2 \eta _2+h_2 \eta _2+h_1}{h_2 \eta _2^3+h_1 \eta _2^2+h_2(h_1+1) \eta _2+h_1} \right. \nonumber \\&\quad -\,\left. \frac{h_1 h_2\eta _2^3}{h_2 \eta _2^3+h_1 \eta _2^2+h_2(h_1+1)\eta _2+h_1}-1\right) \eta _s^2 \rho \nonumber \\&\quad +\,2(1-\cos (\mu ))=0 \end{aligned}$$
(25)

Expansion of Eq. 25 yields fifth order equation in \(\eta _2\) .

$$\begin{aligned}&(\eta _s^2 h_2)\eta _2^5+(\eta _s^2h_1)\eta _2^4 +h_2(\eta _s^2 h_1 \rho +\eta _s^2 h_1+\eta _s^2 \rho +\eta _s^2 \nonumber \\&\quad + \,2 -2\cos (\mu ))\eta _2^3 +h_1(\eta _s^2 \rho +\eta _s^2+2-2\cos (\mu ) )\eta _2^2\nonumber \\&\quad +\,2h_2 (h_1+1) {(1-\cos (\mu ) )}\eta _2 +2h_1 (1-\cos (\mu ))=0 \end{aligned}$$
(26)

It is quintic polynomial in \(\eta _2\), and by solving this, one real and two complex conjugate solutions can be found.

Similarly from Eqs. 20 and 24, sixth-order equation in \(\eta _2\) for inductive energy harvesting circuit could also be written as

$$\begin{aligned}&(\eta _s^2 h_2 h_3)\eta _2^6+(\eta _s^2 h_1 h_3 )\eta _2^5+ h_2(\eta _s^2 h_1 h_3 \rho +\eta _s^2 h_1 h_3+\eta _s^2 h_3 \rho \nonumber \\&\quad +\,\eta _s^2 h_3 +\eta _s^2+2h_3- 2 h_3 \cos (\mu ) )\eta _2^4 \nonumber \\&\quad +\,h_1 h_3 (\eta _s^2 \rho +\eta _s^2-2\cos (\mu )+2)\eta _2^3 +h_2(\eta _s^2 \rho +\eta _s^2 + 2 h_1 h_3\nonumber \\&\quad +\,2 h_3 +2 -2(h_1 h_3+h_3+1) \cos (\mu ) )\eta _2^2 +2h_1 h_3 {(1-\cos (\mu ))}\eta _2+2h_2 (1-\cos (\mu ))=0 \end{aligned}$$
(27)

It is hexic polynomial in \(\eta _2\), and on solving this, the complex conjugate solutions can be found.

6 Results and discussions on the non-dimensional study

The non-dimensional study of the system is essential to discern critical parameters of the system. The lower (LA1) and higher (HA1) parts of the first attenuation band (A1) are essential parameters of the band structure for conducive energy harvesting and vibration control. Therefore in this section, exhaustive research is done to explain how non-dimensional parameters stated in Eq. 21 affect the bandwidth parameters like LA1, HA1, and hence, the width of the first attenuation band (A1).

Fig. 7
figure 7

Contour plots for LA1 in non-dimensional frequency domain \( \eta _2 \). Rows (1) to (2) represent values 0.16 and 1 respectively of non-dimensional capacitive parameter \( h_1 \) and Columns (a) to (b) represent same for resistive parameter \( h_2 \)

Full size image

Figures 7, 8, and 9 elucidate contour plots for LA1, HA1, and A1 on the coordinate axes \( (\rho -\eta _s) \) in each subplot. Rows (1) to (2) represent values 0.16 and 1 of non-dimensional capacitive parameter \( h_1 \) and columns (a) to (b) represent the same for resistive parameter \( h_2 \). The value of LA1 and HA1 depend on edging frequencies \( f_1 \) and \( f_2 \), respectively. In the case of LA1, when it is positive and close to 1, the width of the first transmission is small, which results in the elongated first attenuation band. A negative value of LA1 indicates a wider first transmission band and contracted first attenuation band, whereas a high value of HA1 indicates a wider first attenuation band. Hence, overall, when LA1 and HA1 have high values, the first attenuation (A1) width is wider.

Fig. 8
figure 8

Contour plots for HA1 in non-dimensional frequency domain \( \eta _2 \). Rows (1) to (2) represent values 0.16 and 1 respectively of non-dimensional capacitive parameter \( h_1 \) and Columns (a) to (b) represent same for resistive parameter \( h_2 \)

Full size image
Fig. 9
figure 9

Contour plots for A1 in non-dimensional frequency domain \( \eta _2 \). Rows (1) to (2) represent values 0.16 and 1 respectively of non-dimensional capacitive parameter \( h_1 \) and Columns (a) to (b) represent same for resistive parameter \( h_2 \)

Full size image

In Fig. 7 at higher values of the mass ratio \(\rho \) and structural frequency ratio \(\eta _s\), LA1 has a maximum value 0.8 in all the subplots. In contrast, at a lower value of the structural frequency ratio \(\eta _s\), LA1 has a minimum value of −0.5. It implies a wider first attenuation band is possible for higher values of \(\rho \) and \(\eta _s\). At a low value of \(\eta _s\), the first attenuation (A1) width is contracted. In Fig. 8, contour plots of HA1 show that at a fixed value of the mass ratio \(\rho \), HA1 is independent of the structural frequency ratio \(\eta _s\). Here, we observe that for a range of values of \(\rho \), HA1 is constant and independent of \(\eta _s\). In each subplot at a higher value of \(\rho \) and \(\eta _s\), HA1 is having a maximum value of 3.0. Hence at higher values of \(\rho \) and \(\eta _s\), the width of the first attenuation band (A1) is elongated. The summation of LA1 and HA1 gives the width of the first attenuation band (A1); hence contour plots of A1 in Fig. 9 are exhibiting wider width of the first attenuation band at higher values of the mass ratio \(\rho \) and structural frequency ratio \(\eta _s\).

7 Maximizing the width of the mechanical and electromechanical bandgap formation in mechanical metamaterials

In this section, we optimize the derived system parameters stated in Eq. 21 for the maximum width of the attenuation bands of the piezo-embedded negative mass metamaterials. For the purely resistive energy harvesting circuit, the dispersion relation derived in Eq. 26 is solved numerically, and optimized values of the system parameters are found for the maximum width of the attenuation band. Likewise, for the inductive energy harvesting circuit, the dispersion relation stated in Eq. 27 is also solved numerically for the maximum width of the attenuation band. It gives criteria for the system parameters range while designing piezo-embedded mechanical metamaterials for wideband vibration control and energy harvesting.

Fig. 10
figure 10

The flow chart for the maximization of the attenuation bandwidth

Full size image

Quintic and Hexic polynomials stated in Eqs. 26 and 27 are solved numerically for \(\eta _2\) through optimization technique. In an explicit solution (\(\eta _2\)) of these equations, optimized parameters are desired, which directs to minimize Eqs. 26 and 27. For solving non-linear optimization problems, solver and problem-based approaches can be used. In this problem, the solver based non-linear optimization approach is implemented. To characterize the optimization problem for a solution in the solver based approach, selecting the suitable solver and defining the optimization function with constraints is essential. For input parameters and method shown through the flowchart of the optimization process in Fig. 10, these polynomials will give complex solutions for \(\eta _2\). Through a solver based approach, minimal functional value for the solution of this non-linear multivariable function is found. To obtain the maximum width of the attenuation band, the difference between imaginary parts of the \(\eta _2\) should be maximum. For varying values of \(\mu \), these polynomials are solved numerically and obtained values of \(\eta _2\), \(\eta _s\), \( h_1 \), \( h_2 \) and \( h_3 \) are stored in columns of a matrix P. From matrix P another matrix Q is calculated in which columns contain the difference of imaginary parts of \(\eta _2\). Now from matrix Q, the element having maximum absolute value is identified and corresponding to this element, values of \(\eta _s\), \( h_1 \), \( h_2 \) and \( h_3 \) are retracted from the matrix P.

These numerical calculations are subjected to constraints \(0.5<\eta _s<3.0 \), \(0.16<h_1<1.0 \) and \(0.16<h_2<1.0\), \(0.16<h_3<1.0\). While doing these numerical calculations the mass ratio \( \rho =0.8 \) is taken. For the optimized system parameters, the band structure of the system can be plotted, as shown in Fig. 11 for the purely resistive energy harvesting circuit and in Fig. 12 for the inductive energy harvesting circuit.

Fig. 11
figure 11

The band structure of the piezo-embedded negative mass metamaterial for the optimized system parameters by considering a purely resistive energy harvesting circuit. The band structure of the system is also plotted for varying b capacitive parameter \( h_1 \), c resistive parameter \( h_2 \), and d structural frequency ratio \( \eta _s \)

Full size image
Fig. 12
figure 12

The band structure of the piezo-embedded negative mass metamaterial for the optimized system parameters by considering energy harvesting circuit with the shunted inductor. The band structure of the system is also plotted for varying b capacitive parameter \( h_1 \), c resistive parameter \( h_2 \), d inductive parameter \( h_3 \), and e structural frequency ratio \( \eta _s \)

Full size image

It gives exhaustive physics happening inside the locally resonant bandgaps. We examine thoroughly, the bandgap formation for both the energy harvesting circuits considered. This framework will help designing mechanical metamaterials for wider band vibration attenuation and energy harvesting.

In Fig. 11, plots are drawn by considering a purely resistive energy harvesting circuit. Non-dimensional excitation frequency \( \eta _2 \) and wave number \( \mu \) are shown on x and y axes, respectively. Plot (a) exhibits the maximum width of the first attenuation for the optimized system parameters \( h_1 \), \( h_2 \) and \( \eta _s \). The highlighted section is the optimized first attenuation band (A1) of the piezo-embedded negative mass metamaterial. On the other hand, plots (b) to (d) characterize the variation of the band structure of piezo-embedded negative mass metamaterial with varying values of the capacitive parameter \( h_1 \), resistive parameter \( h_2 \), and structural frequency ratio \( \eta _s \). From plots (b) and (c), we can conclude that the width of the first attenuation band is maximum for optimum values of the capacitive parameter (\( h_1=1.0 \)) and resistive parameter (\(h_2=1.0\)). By analyzing plot (d), the effect of the structural frequency ratio \(\eta _s\) on LA1, HA1, and hence on the width of the first attenuation band (A1) can be easily perceived. The lower part (LA1) of the first attenuation increases with an increase in \( \eta _s \) (0.5 to 3.0). It is due to a decrease in lower edging frequency \(f_1 \), which results in the first transmission band contraction and elongation of the first attenuation band. At \( \eta _s=3.0 \), LA1 has maximum value and at \( \eta _s=0.5 \), it has minimum value. It can be easily perceived by the plot (d) shown. When we talk about HA1, it remains constant, with an increase of \( \eta _s \) (0.5 to 3.0). It only depends on the non-dimensional capacitive parameter \( h_1 \) and resistive parameter \( h_2 \) and the mass ratio \( \rho \) as already shown in Fig. 8. For a specific value of \( h_1 \), \( h_2 \), and \( \rho \), HA1 is going to be constant. Hence the width of the first attenuation band predominantly depends on LA1. On the other side, T2 decreases with an increase of \( \eta _s \) (0.5 to 3.0). Hence, the second transmission bandwidth will decrease at higher values of structural frequency ratio \( \eta _s \). As already shown in Fig. 8, for a specific value of \( h_1 \) and \( h_2 \), at increasing value of \(\rho \), HA1 shifts to right. As there is minimal change in LA1, the width of the first attenuation band (A1) is going to be increased effectively. Also, in the case of T2, there is a nominal increase in width. When the value of \( h_1 \) and \( h_2 \) is increased, as done in plots (b) and (c), similar behavior is shown by LA1, HA1, A1, and T2. In plot (a), we observe a substantial increase in HA1; hence, the first attenuation band (A1) increases. Shifting of HA1 to the left infers attenuation in the lower frequency region and contraction of the first attenuation band, whereas shifting HA1 to the right promotes attenuation in the higher frequency region and elongation of the first attenuation band. Similarly, in the case of LA1, when it shifts to the right, it contracts the first attenuation band. It promotes attenuation in the higher frequency region, but when LA1 shifts to the left, it elongates the first attenuation band and encourages attenuation in the lower frequency region.

In Fig. 12, plots (a) to (e) exhibits the band structure of the piezo-embedded negative mass metamaterial for energy harvesting circuit with the shunted inductor. Plot (a) is drawn for optimized system parameters \( h_1 \), \( h_2 \), \( h_3 \) and \( \eta _s \) to get the maximum width of the first attenuation band. Here, we observe an additional bandgap due to a shunted inductor in the energy harvesting circuit. If we compare this with the plot (a) discussed in Fig. 11, then it can be easily comprehended that the non-dimensional capacitive parameter \( h_1 \) and resistive parameter \( h_2 \) contribute to mechanical bandgap (MBG) and inductive parameter \(h_3\) contributes to electromechanical bandgap (EMBG). This is also obvious from the mathematical relations of \( h_1 \), \( h_2 \) and \( h_3 \) derived in Eq. 21. The lower frequency region in any system is stiffness controlled, and the electromechanical bandgap (EMBG) is present in a lower frequency region, so the width of the EMBG will be dependent on the stiffness of the system along with the inductive parameter \( h_3 \). On another side, the mechanical bandgap (MBG) is present in a higher frequency region, and this region is mainly mass controlled, so the width of the MBG will depend on the mass of the system along with the capacitive parameter \( h_1 \) and resistive parameter \( h_2 \). Two bandgaps are observed in the proximity of resonating frequency. The electromechanical bandgap (EMBG) exists before the resonating frequency, and the mechanical bandgap (MBG) exits after the resonating frequency. If these parameters are tuned properly, we can get wider bandgaps by combining mechanical and electromechanical bandgaps. A cumulative mechanical and electromechanical bandgap can be perceived when the frequency domain in both bandgaps is adjacent. If the two frequency domains are divergent, then it leads to the two detached bandgaps. There can be a possibility of merging these two bandgaps, which the designer should avoid due to no bandgap. It is also essential to consider the level of attenuation in the bandgaps because, with the bandwidth increase, the level of attenuation reduces. So, it is like a trade-off between level of attenuation and bandwidth.

Therefore, the piezo-embedded negative mass metamaterial can be engineered for wideband attenuation by tuning the non-dimensional system parameters as explicated above. These physical system parameters govern the formation of mechanical and electromechanical parameters. This in-depth study of the band structure helps in designing mechanical metamaterials as per various applications in lower and higher frequency domains. It also enhances performance in terms of vibration attenuation and energy harvesting. Here, we have not included any damping in the system as we are primarily focusing on the bandgap formation mechanism and optimal bandgap in piezo-embedded mechanical metamaterials. The analysis of the system will become more complicated because of the consideration of any mathematical model of the assumed damping. As far as the effect on the results is concerned, any damping in mechanical metamaterials will increase the bandgap.

For achieving these optimal system parameters realistically in experiments, it is needed to think of the equivalent continuous system corresponding to the discrete elements in the proposed piezo-embedded mechanical metamaterials. The equivalent system can have a primary beam with attached resonators. Bandgap estimation can be done by getting the transmissibility plots (Sugino et al. 2017). The piezoelectric material can be embedded with the energy harvesting circuit (purely resistive or inductor and resistor combination) in the attached resonators.

8 Summary and conclusions

A wider attenuation band is always anticipated for the various application while designing mechanical metamaterials. We presented mathematical modeling of piezo-embedded negative mass metamaterial using the generalized Bloch theorem for efficient dual functionality of the system. The band structure of the piezo-embedded negative mass metamaterial is investigated in detail with different system parameters. Successively using the backward substitution method, the power harvested by inner resonating units is estimated by considering purely resistive and shunted inductor energy harvesting circuits for a finite number of piezo-embedded negative mass metamaterial units. The power produced is maximum in both the attenuation bands, but it decreases in the furthermost units of the metamaterial. Through the extensive exploration of the system in the non-dimensional domain, we find the optimal combination of the quintessential parameters useful while designing piezo-embedded negative mass metamaterials as per various applications. We also identified the governing system parameters for the formation of the mechanical and electromechanical bandgaps. Electromechanical and mechanical bandgaps are observed before and after the resonant frequency of the electromechanical resonator, respectively, for the energy harvesting circuit with the shunted inductor. The electromechanical bandgap is contingent on the stiffness and inductance of the system, and the mechanical bandgap on the mass of the system. The width of the first attenuation band can be increased extensively by tuning these parameters. We find optimum values of the derived system parameters for the maximum width of the first attenuation band for purely resistive and shunted inductor energy harvesting circuits. It gives design versatility to enhance the engineered mechanical metamaterial performance in wider vibration attenuation and energy harvesting applications.