Approximate structure learning for large Bayesian networks

Abstract

We present approximate structure learning algorithms for Bayesian networks. We discuss the two main phases of the task: the preparation of the cache of the scores and structure optimization, both with bounded and unbounded treewidth. We improve on state-of-the-art methods that rely on an ordering-based search by sampling more effectively the space of the orders. This allows for a remarkable improvement in learning Bayesian networks from thousands of variables. We also present a thorough study of the accuracy and the running time of inference, comparing bounded-treewidth and unbounded-treewidth models.

1 Introduction

Score-based structure learning of Bayesian networks is the task of finding the highest-scoring directed acyclic graph (DAG), where the score function measures the appropriateness of the DAG for the data. This task is NP-hard (Chickering et al. 2014), and is the subject of intense, cutting-edge research. Even using the most recent theoretical advances (Cussens et al. 2017) exact learning can be impractical, even if one restricts themselves to cases where the best DAG has at most two parents per node. Hence, approximate methods are necessary to tackle structure learning, especially in order to scale to domains with a large number of variables.

The task is usually accomplished in two phases: identification of a list of candidate parent sets for each node (which we call parent set identification) and optimal assignment of the parent set of each node (which we call structure optimization). Most research so far has focused on structure optimization. For instance, there are exact approaches based on dynamic programming (Koivisto and Sood 2004; Silander and Myllymaki 2006), branch and bound (de Campos et al. 2009; de Campos and Ji 2011), linear and integer programming (Jaakkola et al. 2010), shortest-path heuristics (Yuan and Malone 2012, 2013), to name a few. A state-of-the-art approach is implemented by the software Gobnilp (Bartlett and Cussens 2017; Cussens 2011), which adopts a branch-and-cut idea using linear integer programming. This is an anytime algorithm; thus it provides an approximate solution at any step of the computation (as long as a first valid graph has been found) until it eventually reaches the exact solution. Yet, exact solvers do not scale to domains with a large number of variables. Experiments so far arrive up to few hundreds of variables at their best, and only in particular instances. One of the most scalable approaches with good empirical results to score-based structure learning is the Acyclic Selection Ordering-Based Search (Scanagatta et al. 2015); this is an approximate algorithm that scales up to thousands of variables.

Once the Bayesian network has been learned, one can gain insights into how variables relate to each other; for instance, this is an important goal when studying gene regulatory networks. Yet, in other applications, efficient inference is required in order to make predictions using the model. The time complexity of (exact) inference grows exponentially with a property of the DAG called treewidth (Bodlaender et al. 2001). The solvers discussed so far learn expressive models that are suitable to understanding the domain and analyzing the relationship among variables, but they perform structure learning without bounding the treewidth of the learned model. Learning Bayesian networks with bounded treewidth is indeed very challenging, since it generalizes the unbounded problem (and even determining the treewidth of a DAG is NP-hard). Because of that, the machine learning community has put effort in developing alternative modeling techniques in order to obtain tractable inference, such as arithmetic circuits (Darwiche 2009, Chap.12) and their learning from data (Lowd and Domingos 2008), sum-product networks (Poon and Domingos 2011; Rooshenas and Lowd 2014), among others.

Recent advances have made possible to achieve some results for structure learning of Bayesian networks with bounded treewidth. Some exact methods (Berg et al. 2014; Korhonen and Parviainen 2013; Parviainen et al. 2014) have been proposed, but they do not scale to more than hundreds of variables. Later, some approximate approaches have been devised (Nie et al. 2015), which scale to a few hundreds of variables. A recent breakthrough in the number of variables is the k-G algorithm (Scanagatta et al. 2016), which is able to learn bounded-treewidth models of reasonable accuracy from thousands of variables.

In this paper we present a series of approximate techniques for score-based structure learning of Bayesian networks; they include methods for parent set identification and structure optimization, both with bounded and unbounded treewidth. The algorithms scale up to several thousands of variables, even in the more challenging case of bounded treewidth. We build a unified presentation based on findings from Scanagatta et al. (2015, 2016). The algorithms for structure optimization that we present are ordering-based search methods; as a novel contribution we propose an approach for effectively sampling the orders, which remarkably improves the performance of both algorithms. Such an approach is general and might be helpful for any ordering-based algorithm.

2 Bayesian networks

Consider the task of learning the structure of a Bayesian Network from a data set of N instances $\mathcal {D} = \{D_1, \ldots , D_N\}$. The set of n random variables is $\mathcal {X}=\{X_1, \ldots , X_n\}$. We assume the variables to be categorical (with a finite number of states) and the data set to be complete. The goal is to find the highest-scoring DAG $\mathcal {G}$ over nodes $\mathcal {X}$ by defining the set of parents ${\varPi _1, \ldots , \varPi _n}$ of each variable. Such a graph induces a joint probability distribution, because of the assumed Markov condition: every variable is conditionally independent of its non-descendant variables given its parent variables.

Different score functions can be used to assess the quality of the DAG; see for example Liu et al. (2012) for a thorough discussion. In this work we adopt the Bayesian Information Criterion ($\mathrm {BIC}$), which is asymptotically proportional to the posterior probability of the DAG. The $\mathrm {BIC}$ score is decomposable, being constituted by the sum of the scores of each variable and its parent set:

$$\begin{aligned}&\mathrm {BIC}(\mathcal {G}) = \sum _{i=1}^{n} \mathrm {BIC}(X_i,\varPi _i)=\sum _{i=1}^n \left( \mathrm {LL}(X_i|\varPi _i) + \mathrm {Pen}(X_i,\varPi _i)\right) , \end{aligned}$$

where $\mathrm {LL}(X_i|\varPi _i)$ denotes the log-likelihood of $X_i$ and its parent set:

$$\begin{aligned}&\mathrm {LL}(X_i|\varPi _i) =\displaystyle \sum \nolimits _{\pi \in \varPi _i, ~ x \in X_i} N_{x,\pi }\log \hat{\theta }_{x|\pi }, \end{aligned}$$

while $\mathrm {Pen}(X_i,\varPi _i)$ is the complexity penalization for $X_i$ and its parent set:

$$\begin{aligned}&\mathrm {Pen}(X_i,\varPi _i) = -\frac{\log N}{2}(|X_i|-1)(|\varPi _i|). \end{aligned}$$

$\hat{\theta }_{x|\pi }$ is the maximum likelihood estimate of the conditional probability $P(X_i=x|\varPi _i=\pi )$; $N_{x,\pi }$ represents the number of times $(X=x\wedge \varPi _i=\pi )$ appears in the data set; $|\cdot |$ indicates the size of the Cartesian product space of the variables given as argument. Thus $|X_i|$ is the number of states of $X_i$ and $|\varPi _i|$ is the product of the number of states of the parents of $X_i$.

By exploiting decomposability, structure learning can be accomplished in two phases. The first phase is to identify a list of candidate parent sets (called parent set identification), which can be done independently for each variable. The second phase is to decide the parent set of each node in order to maximize the score of the resulting DAG (called structure optimization). The ultimate goal is to find

$$\begin{aligned} \mathcal {G}^*\in {{\mathrm{argmax}}}_{\mathcal {G}}\mathrm {BIC}(\mathcal {G}), \end{aligned}$$

where we avoided using the symbol for equality because there might be multiple optima. The usual first step to achieve such a goal is the task of finding the candidate parent sets for a given variable $X_i$ (a candidate parent set cannot contain itself). It regards the construction of $L_i$, the cache of possible parent sets $\varPi _i$ for $X_i$ alongside their scores $\mathrm {BIC}(X_i,\varPi _i)$, which without any restriction has $2^{n-1}$ possible parent sets, since every subset of $\mathcal {X}\setminus \{X_i\}$ is a candidate. This becomes quickly prohibitive with the increase of n. If we apply a bound d on the number of parents that a variable can have (that is, a limit on the in-degree of a node), then the size of

$$\begin{aligned} L_i = \{ \langle \varPi _i, \mathrm {BIC}(X_i,\varPi _i)\rangle ~|~ s(\varPi _i)\le d\} \end{aligned}$$

reduces from $2^{n-1}$ to $\varTheta (n^d)$, which might still be too large and we might be losing optimality (this is the case if any optimal DAG would have more than d parents for $X_i$). $s(\cdot )$ represents the actual cardinality of a set (for instance, $s(\{X_i\})=1$ and $s(\varPi _i)$ is the number of elements in $\varPi _i$).

There is no known manner of avoiding some loss, as this problem is hard itself. The goal is to find the best approximate idea that still keeps in the cache the most promising candidate sets. Pruning based on limiting the number of parents is not enough (nor the most appropriate) if n is large, as we discuss in the next section.

3 Parent set identification

The first objective is to produce a sensible approximation for the cache $L_i$ of each node. The most common approach in the literature is to explore parent sets in sequential order until a certain time-limit is reached: first the empty parent set is included in $L_i$, then all the parent sets of size one, then all the parent sets of size two, and so on and so forth, up to size d, the maximum in-degree. We refer to this approach as sequential exploration. Since the number of candidate parent sets increases exponentially with d, sequential exploration implies the adoption of a low d when n increases, if one wants this method to finish in a reasonable amount of time. For instance, $d=2$ has been used when dealing with more than hundred variables (Bartlett and Cussens 2017; Cussens et al. 2013). This approach prevents detecting higher-scoring parent sets with larger in-degree, while needing the computation of scores for many low-scoring parent sets of low in-degree.

Pruning rules (de Campos et al. 2009) detect sub-optimal parent sets and allow to discard parts of the search space, avoiding to spend time in computing their scores. Although they do reduce the time required to explore the space of parent sets, they are not effective enough and hence do not allow us to deal with much larger in-degrees, in particular when the number of variables is large. Scanagatta et al. (2015) propose an approximate search of candidate parent sets that explores them without limiting a priori the in-degree d. We describe such an approach in the next section. It is worth mentioning that the methods for structure optimization that we discuss in this paper work with any decomposable score function. However, the procedure for efficient exploration of the space of the parent sets of this section exists only for $\mathrm {BIC}$, and it is an open question to devise similar ideas for other score functions.

3.1 Approximate exploration of parent sets

The main idea of Scanagatta et al. (2015) is to quickly identify the most promising parent sets through an approximate scoring function that does not require scanning the data set. Later on, only the scores of the most promising parent sets are computed. The approximate scoring function is called $\mathrm {BIC}^*$. The $\mathrm {BIC}^*$ of a parent set $\varPi = \varPi _{1} \cup \varPi _{2}$ constituted by the union of two non-empty and disjoint parent sets $\varPi _{1}$ and $\varPi _{2}$ is:

$$\begin{aligned} \mathrm {BIC}^*(X, \varPi _{1}, \varPi _{2}) = \mathrm {BIC}(X,\varPi _{1}) + \mathrm {BIC}(X,\varPi _{2}) + \mathrm {inter}(X, \varPi _{1}, \varPi _{2}), \end{aligned}$$

(1)

that is, the sum of the $\mathrm {BIC}$ scores of the two parent sets and of an interaction term, which ensures that the penalty term of $\mathrm {BIC}^*(X, \varPi _{1}, \varPi _{2})$ matches the penalty term of $\mathrm {BIC}(X, \varPi _{1} \cup \varPi _{2})$. In particular, $\mathrm {inter}(X, \varPi _{1}, \varPi _{2}) = \frac{\log N}{2}(|X|-1)(|\varPi _{1}| + |\varPi _{2}| - |\varPi _{1}| |\varPi _{2}| - 1) - \mathrm {BIC}(X,\varnothing )$. The $\mathrm {BIC}^*(X,\varPi )$ score is equal to the $\mathrm {BIC}(X,\varPi )$ score if the interaction information $ii(X; \varPi _{1}; \varPi _{2})$ is zero (Scanagatta et al. 2015). Yet, this condition is generally false; for this reason, $\mathrm {BIC}^*(X,\varPi )$ is an approximate score, but it is efficiently computable. If $\mathrm {BIC}(X,\varPi _{1})$ and $\mathrm {BIC}(X,\varPi _{2})$ are known, then $\mathrm {BIC}^*$ is computed in constant time (with respect to data accesses).

The independence selection algorithm (Scanagatta et al. 2015) exploits $\mathrm {BIC}^*$ to quickly estimate the score of a large number of parent sets. It is described in Algorithm 1. It adopts two lists: (1) open: a list for the parent sets to be explored, ordered by their $\mathrm {BIC}^*$ score; (2) closed: a list of already explored parent sets, along with their actual $\mathrm {BIC}$ score. The algorithm returns the content of the closed list, which becomes $L_i$ for each variable $X_i$. The procedure is repeated for every variable and can be easily parallelized. Independence selection prioritizes the computation of the $\mathrm {BIC}$ score of the most promising parent sets (those with highest $\mathrm {BIC}^*$ score) without constraining the in-degree. It consistently increases the scores achieved by different structure optimization algorithms when compared to sequential ordering (Scanagatta et al. 2015), and thus we adopt it in all our experiments.

4 Structure optimization

The objective of structure optimization is to select the parent set of each node from its cache in order to maximize the score of the resulting DAG. At this stage, all caches of scores are assumed to be available. The number of possible Bayesian networks structures increases super-exponentially with the number of variables, so the task is very hard. When restricted to the available caches, there are still $\prod _{i=1}^n s(L_i)$ graphs to evaluate if it were to use a brute-force approach.

We take the software Gobnilp (Bartlett and Cussens 2017; Cussens 2011) as a benchmark for our evaluations, since it is the state of the art for exact structure learning. It is available from https://www.cs.york.ac.uk/aig/sw/gobnilp/ and is an anytime algorithm. When provided with enough time, it certainly finds the highest-scoring graph, while it provides an approximate solution (provided that a certain amount of time has been given for it to find the first valid graph) whenever it has not yet reached an optimum or has not yet been able to prove it is an optimum. In terms of approximate methods, an effective approach in large domains (thousands of variables) is Acyclic Selection Ordering-Based Search (ASOBS) (Scanagatta et al. 2015). It consistently outperforms Gobnilp on data sets containing more than 500 variables, while Gobnilp generally wins on smaller data sets. In this section we describe ASOBS and then we propose a novel variant named $\hbox {ASOBS}_\mathrm {{ENT}}$, which improves on ASOBS by applying a better scheme to sample orders.

4.1 Acyclic selection ordering-based search

Sampling from the space of orders rather than from the space of structures is certainly appealing since the space of orders is significantly smaller than the space of structures. For any fixed ordering of the n variables, the decomposability of the score enables efficient optimization over all DAGs compatible with the ordering (Cooper and Herskovits 1992). Moreover, identifying the highest-scoring network consistent with a variable order is time-efficient. A network is consistent with the order $\prec$ if $\forall X_i:~ \forall X\in \varPi _i:~ X \prec X_i$; we call this condition the consistency rule. A network consistent with an order is necessarily acyclic. In order to identify the highest-scoring network given an order, we have to choose independently the best parent set for each node $X_i$ among those containing only variables that are antecedent of $X_i$ in that order. Finding the highest-scoring network given the ordering is thus simple and efficient (can be done in linear time in the size of the caches).

The Ordering-Based Search (OBS) algorithm by Teyssier and Koller (2005) learns the highest-scoring network given an order, according to the consistency rule. Then it greedily explores several neighboring orders by considering swaps between variables that are adjacent in the order. Updating the score of the network after swapping two adjacent variables is efficient thanks to score decomposability. ASOBS performs a similar computation but relaxes the consistency rule in order to retrieve higher-scoring DAGs that are inconsistent with the provided order. In particular, it allows arcs from a variable to its successors (back-arcs) if they do not introduce a directed cycle. Scanagatta et al. (2015) prove that, for a given order, ASOBS achieves equal or higher score than OBS. Moreover, ASOBS empirically outperforms OBS in every analyzed data set (Scanagatta et al. 2015).

Table 1 Data sets sorted according to the number n of variables

We recall that $X_j$ is an ancestor of $X_i$ if there is a directed path from $X_j$ to $X_i$. In this case, we equivalently say that $X_i$ is a descendant of $X_j$. The ASOBS algorithm is as follows:

• 1. Build a Boolean square matrix isDescendantOf that tracks the descendants of each node; thus its entry in position $(X_i,X_j)$ is true if and only if $X_i$ is a descendant of $X_j$. All entries of isDescendantOf are initialized as false as we start from an empty structure.

• 2. For each $X_j$ in the order, with $j=n,\ldots ,1$:

  • (a) Select the highest-scoring parent set $\varPi _j$ that contains no descendants of $X_j$, as checked through matrix isDescendantOf.

  • (b) Update matrix isDescendantOf to reflect that:

    • Each variable belonging to $\varPi _j$ is ancestor of $X_j$;

    • Each ancestor of $X_j$ has as descendants $X_j$, the descendants of $X_j$ and any other node in the path between the ancestor and $X_j$.

While the algorithm is quite simple and details about the implementation could be omitted, we would like to point out that a smart representation for the data structure of ancestors/descendants allows us to achieve an overall computational complexity that is asymptotically equal to OBS.

In Scanagatta et al. (2015), ASOBS is implemented by uniformly sampling the space of orders and repeating the above procedure for each sampled order. In the following we introduce a novel approach, which more effectively samples from the space of orders and might be applied to any structure learning algorithm based on ordering search.

4.2 Entropy-based sampling

We investigate which parent sets are especially important for the score of a DAG, with the aim of improving the sampling strategy and thus to cover better regions of the space of orders. To analyze this problem, we introduce the following range statistic:

$$\begin{aligned} \mathrm {range}\left[ \mathrm {BIC}(X_i,\varPi _i)\right] = \mathrm {BIC}(X_i,\varPi _i) - \min _{\varPi '_i \in \mathcal {P}(X_i)}{\mathrm {BIC}}(X_i,\varPi '_i), \end{aligned}$$

(2)

where $\mathcal {P}(X_i)$ denotes the set of the feasible parent sets for $X_i$. Thus the range measures how much the score improves when assigning to $X_i$ the parent set $\varPi _i$ instead of the lowest-scoring parent set (usually the empty parent set). Intuitively, high-entropy variables should achieve higher differences in score when compared to using no parents, since their likelihood (and thus their score) is low without parents. Thus their score can be largely improved through careful selection of their parent set. To verify this intuition, we compute the range score of every parent set of the most entropic and the least entropic variables of different data sets, listed in Table 1.

Results referring to four data sets are given in Fig. 1; note that to understand which variables can most affect the overall score by a more careful selection of their parent sets, we are interested in the highest values of range. High-entropy variables (shown in black, last five boxplots of each graph) yield much higher values of range than low-entropy variables (shown in red, first five boxplots of each graph). For instance, in the data set Reuters-52, high-entropy variables yield ranges that are up to an order of magnitude larger than those of low-entropy variables. Moreover, ranges have a much larger span for high-entropy variables than for low-entropy variables. Again with reference to Reuters-52, the difference between the maximum and the median range is about 500 for high-entropy variables and lower than 25 for low-entropy variables.

Fig. 1

The red boxplots on the left (first five boxplots of each figure) refer to the five least entropic variables of each data set. The black boxplots on the right refer to the five most entropic variables of each data set. Each boxplot represents the distribution of the range statistic, across variables belonging to the same data set (Color figure online)

The results about the range statistic suggest that the choice of the parent sets of high-entropy variables has the largest impact on the eventual score of the DAG. We thus modify ASOBS in order to better assign the parent sets of the high-entropy variables. We do so by putting them at the end of the order provided to ASOBS, so that they are offered plenty of different parent sets to choose from. In particular, we sample the variables of the order in a fashion that is proportional to their entropy. Suppose we have already chosen the first p variables of the ordering ($p= 0,1, \ldots$, n − 1). Without loss of generality, denote a still unselected variable as $X_j$ ($j=p+1,\ldots ,n$). The $(p+1)$th position of the ordering is chosen by assigning to each of the $n-p$ variables not already selected a weight proportional to their entropy:

$$\begin{aligned} \displaystyle w_j = \frac{H(X_j)}{\sum _{i =p+1}^{n} H(X_i)}, \end{aligned}$$

where $H(\cdot )$ denotes the empirical entropy. The next variable of the order is sampled from a discrete distribution, whose probabilities are constituted by the above weights $w_j$. We call $\hbox {ASOBS}_{\mathrm {ENT}}$ this variant of ASOBS, since it is equipped with the entropy-based sampling.

Table 2 Comparison of $\hbox {ASOBS}_{\mathrm {ENT}}$ against ASOBS and Gobnilp

4.3 Experiments

We compare $\hbox {ASOBS}_{\mathrm {ENT}}$, ASOBS and Gobnilp using the twenty data sets of Table 1: such a collection of data sets has been previously used for instance by Rooshenas and Lowd (2014) and by others referenced therein. The data sets are available for instance from https://github.com/arranger1044/awesome-spn#dataset. They contain between 16 and 1556 binary-valued variables. Each data set is split in three subsets, producing a total of 60 structure learning experiments. Moreover, in order to test the algorithms in domains with a large number of variables, we generate further 15 synthetic data sets as follows. Using the BNgenerator package,¹ we generate five networks containing 2000 variables, five networks containing 4000 variables and five networks containing 10,000 variables. From each generated network we then sample a data set of $N=5000$ instances.

In each experiment we run Gobnilp, ASOBS and $\hbox {ASOBS}_{\mathrm {ENT}}$ for one hour, on the same computer and providing them with the same caches of candidate parent sets, which were pre-computed using the $\mathrm {BIC}^*$ approach of Sect. . When computing the caches of parent sets, we allowed one minute per variable with no maximum in-degree. The detailed results of all the experiments (scores obtained by each method in each data set) of this paper are available at: http://ipg.idsia.ch/papers/scanagatta2017b/supplementary.pdf.

We also considered further competitors for structure learning of Bayesian networks. For instance the package urlearning² implements search methods based on Yuan and Malone (2013). Yet, it could not learn from data set containing more than 100 variables; similar limits are indeed acknowledged also by the authors. We also tried WinMine,³ but it failed to provide results within an hour when dealing with more than 500 variables. On smaller data sets, it was anyway outperformed by both Gobnilp and ASOBS-ENT (notice that we ran these experiments using the BDeu score, as WinMine does not support the BIC score). We report the results in the supplementary material.

We analyze the results in Table 2 by separating small data sets ($n \le 200$), large data sets ($200< n < 2000$) and very large data sets ($n\ge 2000$). In each experiment we measure the difference in terms of $\mathrm {BIC}$ scores between $\hbox {ASOBS}_{\mathrm {ENT}}$ and ASOBS, and between $\hbox {ASOBS}_{\mathrm {ENT}}$ and Gobnilp. We denote this difference by $\varDelta \mathrm {BIC}$.

A positive $\varDelta \mathrm {BIC}$ provides evidence in favor of the higher-scoring model. The $\varDelta \mathrm {BIC}$ values can be interpreted as follows (Raftery 1995):

• $\varDelta \mathrm {BIC}>$ 10: extremely positive evidence;

• 6 $<\varDelta \mathrm {BIC}<$ 10: strongly positive evidence;

• 2 $<\varDelta \mathrm {BIC}<$ 6: positive evidence;

• $\varDelta \mathrm {BIC}<$ 2: neutral evidence.

We perform the sign test considering one method as winning over the other when there is a $\varDelta \mathrm {BIC}$ of at least 2 in its favor, and treating as ties the cases in which $|\varDelta \mathrm {BIC}|<$ 2. The statistically significant differences (p value < 0.01) are boldfaced in Table 2. The supplementary material shows in detail the scores obtained by each solver on each data set.

As for the comparison of $\hbox {ASOBS}_{\mathrm {ENT}}$ and ASOBS, $\hbox {ASOBS}_{\mathrm {ENT}}$ performs better in all three categories. Its advantage is more prominent in large and very large data sets: in almost every data set it improves the $\mathrm {BIC}$ score by more than ten points from ASOBS’s values. The number of victories in favor of $\hbox {ASOBS}_{\mathrm {ENT}}$ is significant both in large and very large data sets.

Regarding the comparison of $\hbox {ASOBS}_{\mathrm {ENT}}$ and Gobnilp, Gobnilp is significantly better than $\hbox {ASOBS}_{\mathrm {ENT}}$ in small data sets ($n \le 200$), while in large data sets the situation is reversed: $\hbox {ASOBS}_{\mathrm {ENT}}$ outperforms Gobnilp in all large data sets. When dealing with very large data sets ($n \ge 2000$), Gobnilp failed to provide a solution after one hour of computation.

4.4 Discussion

We further investigate the difference between $\hbox {ASOBS}_{\mathrm {ENT}}$ and ASOBS. We do this by tracking the difference between $\mathrm {BIC}$ scores achieved by $\hbox {ASOBS}_{\mathrm {ENT}}$ and ASOBS on each individual variable $X_i$:

$$\begin{aligned} \varDelta \mathrm {BIC}(X_i,\varPi _i) = \mathrm {BIC}_{\mathrm {ASOBS}_{\mathrm {ENT}}}(X_i,\varPi _i) - \mathrm {BIC}_{\mathrm {ASOBS}}(X_i,\varPi _i). \end{aligned}$$

(3)

We expect $\varDelta \mathrm {BIC}(X_i,\varPi _i)$ to be positive for high-entropy variables and negative for low-entropy variables. For each variable $X_i$, we then compute the following statistic:

$$\begin{aligned} \mathrm {cusum}(\varDelta \mathrm {BIC}(X_i)) = \sum _{X_j: H(X_j) \ge H(X_i)} \varDelta \mathrm {BIC}(X_j,\varPi _j). \end{aligned}$$

This statistic measures the advantage of $\hbox {ASOBS}_{\mathrm {ENT}}$ over ASOBS on the variables that are more than or equally entropic to $X_i$ itself. In Fig. 2, we plot this statistic as a function of $H(X_i)$; it shows that $\hbox {ASOBS}_{\mathrm {ENT}}$ builds a large advantage (largely positive cusum) on high-entropy and medium-entropy variables. This advantage is eventually lost as we reach the least entropic variables, but it remains largely positive in the end. Because of that, $\hbox {ASOBS}_{\mathrm {ENT}}$ yields higher-scoring networks than ASOBS.

Fig. 2

Cusum statistic as a function of $H(X_i)$ for different data sets. The value of the cusum at the end of the curve (i.e., in relation to least entropic variables) equals the difference between the DAG identified by $\hbox {ASOBS}_{\mathrm {ENT}}$ and ASOBS

5 Treewidth-bounded structure optimization

The structure learning approaches discussed so far (including $\hbox {ASOBS}_{\mathrm {ENT}}$) do not bound the treewidth of the DAG. They are therefore a good choice when one wants to learn an expressive model to understand how variables relate to each other. However, it may be important to learn Bayesian networks with bounded treewidth when one needs to do efficient inferences with the model. We discuss this problem in this section. Before we present some ideas and algorithms, we need some background material.

5.1 Treewidth and k-trees

We denote an undirected graph as $U=(V,E)$, where V is the vertex set and E is the edge set. A tree decomposition of U is a pair ($\mathcal {C},\mathcal {T}$) where $\mathcal {C}=\{C_1,C_2,\ldots ,C_m\}$ is a collection of subsets of V and $\mathcal {T}$ is a tree over $\mathcal {C}$, so that:

• $V=\cup _{i=1}^{m} C_i$;

• for every edge that connects the vertices $v_1$ and $v_2$, there is a subset $C_i$ that contains both $v_1$ and $v_2$;

• for all i, j, k in $\{1,2,\ldots , m \}$, if $C_j$ is in the path between $C_i$ and $C_k$ in $\mathcal {T}$, then $C_i \cap C_k \subseteq C_j$.

The width of a tree decomposition is $\max _i s(C_i)-1$, where $s(C_i)$ is the number of vertices in $C_i$. The treewidth of U is the minimum width among all possible tree decompositions of U. Treewidth can be equivalently defined in terms of triangulations of U. A triangulated graph is an undirected graph in which every cycle of length greater than three contains a chord. The treewidth of a triangulated graph is the size of its maximal clique minus one. The treewidth of U is the minimum treewidth over all the possible triangulations of U.

The treewidth of a DAG is characterized with respect to all possible triangulations of its moral graph. The moral graph of a DAG is an undirected graph that includes an edge ($i - j$) for every arc ($i\rightarrow j$) in the DAG and an edge ($p - q$) for every pair of edges ($p\rightarrow i$), ($q\rightarrow i$) in the DAG. The treewidth of a DAG is the minimum treewidth over all the possible triangulations of its moral graph. Thus the maximal clique of any moralized triangulation of G is an upper bound on the treewidth of the model.

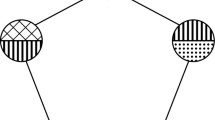
A complete graph is a clique. A clique containing $k+1$ nodes is a ($k+1$)-clique; it has treewidth k. A clique is maximal if it is not a subset of a larger clique. A ($k+1$)-clique thus contains multiple non-maximal k-cliques. An undirected graph is a k-tree if it has treewidth k and the addition of any edge increases its treewidth. A k-tree can be inductively built as follows (Patil 1986). We start with a $(k+1)$-clique. Then we connect a new node to a k-clique of the original graph, obtaining an updated graph. Other nodes can be added one at a time following the same procedure. A partial k-tree is a subgraph of a k-tree; as such, it has treewidth bounded by k. An example of the iterative construction of a k-tree ($k=2$) is given in Fig. 3. We start with the clique over the variables A, B, C. Then we link D to the 2-clique $\{A,B\}$. Then we link E to the 2-clique $\{C,A\}$, and F to the 2-clique $\{C,E\}$. Figure 3 also shows in blue the tree decomposition at each iteration. The nodes of the tree have size three; thus the treewidth is two.

Fig. 3

Iterative construction of a k-tree (white nodes) with treewidth $k=2$. The corresponding tree decomposition is shown alongside (blue nodes) (Color figure online)

5.2 Learning Bayesian networks with bounded treewidth

Learning Bayesian networks with bounded treewidth is very challenging, in particular because treewidth is a global property of the DAG and determining it is already NP-hard. A pioneering approach, polynomial in both the number of variables and the treewidth bound, has been proposed by Elidan and Gould (2008). It incrementally builds the network; at each arc addition it provides an upper-bound on the treewidth of the learned structure. The limit of this approach is that, as the number of variables increases, the gap between the bound and the actual treewidth becomes large, leading to sparse networks.

An exact method has been proposed by Korhonen and Parviainen (2013), which finds the highest-scoring network with the desired treewidth. However, its complexity increases exponentially with the number of variables n and it has been applied in experiments with fewer than 16 variables. Parviainen et al. (2014) adopted an anytime integer linear programming (ILP) approach, called TWILP. If the algorithm is given enough time, it finds the highest-scoring network with bounded treewidth. Otherwise, it returns a sub-optimal DAG with bounded treewidth. Such an ILP problem has an exponential number of constraints in the number of variables; this limits its scalability, even if the constraints can be generated online. Typically it cannot handle data sets containing more than 100 variables. Berg et al. (2014) cast the problem of structure learning with bounded treewidth as a problem of weighted partial maximum satisfiability. They solved the problem exactly through a MaxSAT solver and performed experiments with at most 30 variables. Nie et al. (2014) proposed a more efficient anytime ILP approach with a polynomial number of constraints in the number of variables. Yet, they reported that the quality of the solutions quickly degrades as the number of variables exceeds a few dozens, and that no satisfactory solutions are found with data sets containing more than 50 variables.

To scale to larger domains, one has to resort to approximate approaches. The S2 algorithm (Nie et al. 2015) samples uniformly the space of k-trees; the sampled k-trees are assessed via a heuristic scoring function (called informative score). The DAG is then recovered as a sub-graph of the k-tree with highest informative score. Nie et al. (2016) further refined this idea, obtaining via $\hbox {A}^*$ the k-tree that is guaranteed to maximize the informative score. In Scanagatta et al. (2016), the authors presented the k-G algorithm. It consistently yields higher-scoring networks than S2 for different tested treewidths. The advantage becomes especially important in the largest data sets that contain thousands of variables. An algorithm named k-MAX that follows a similar idea was recently presented in Scanagatta et al. (2018). We describe k-G in the next section, before we present an improvement of it.

5.3 The k-G algorithm

Like ASOBS, k-G is based on sampling orders. In particular, it samples an order and then it greedily (whence the G letter in the name k-G) searches for the highest-scoring DAG with bounded treewidth consistent with the order. The DAG is built iteratively; one variable is added at each iteration while keeping the moral graph of the DAG as a subgraph of a k-tree, which guarantees that the final DAG will have treewidth bounded by k. The algorithm is discussed in the following.

The algorithm starts by choosing an initial k-tree. Such an initial k-tree $\mathcal {K}_{k+1}$ consists of the complete clique over the first $k+1$ variables in the order. Then the initial DAG $\mathcal {G}_{k+1}$ is learned over the same $k+1$ variables. Since $k+1$ often regards a tractable number of variables, we can exactly learn $\mathcal {G}_{k+1}$ adopting a solver such as Gobnilp. Because the moral graph of $\mathcal {G}_{k+1}$ is a subgraph of $\mathcal {K}_{k+1}$, we have that $\mathcal {G}_{k+1}$ has bounded treewidth. We then iteratively add each remaining variable, according to the order. Consider the next variable in the order, $X_{\prec i}$, where $i \in \{ k+2, \ldots , n \}$. Let us denote by $\mathcal {G}_{i-1}$ and $\mathcal {K}_{i-1}$ the DAG and the k-tree that must be updated after adding $X_{\prec i}$. We add $X_{\prec i}$ to $\mathcal {G}_{i-1}$, constraining its parent set $\varPi _{\prec i}$ to be a (subset of a) k-clique in $\mathcal {K}_{i-1}$. This yields the updated DAG $\mathcal {G}_{i}$. We then update the k-tree, connecting $X_{\prec i}$ to such a k-clique. This yields the k-tree $\mathcal {K}_i$; it contains an additional $k+1$-clique compared to $\mathcal {K}_{i-1}$. By construction, $\mathcal {K}_i$ is also a k-tree. Because the moral graph of $\mathcal {G}_i$ cannot have arcs outside this $(k+1)$-clique, it is a subgraph of $\mathcal {K}_i$.

In order to choose the parent set of the variable being added to the graph, k-G chooses the highest-scoring parent set among the feasible ones. We denote the set of existing k-cliques in $\mathcal {K}$ as $\mathcal {K}_C$. Thus k-G chooses as parent set for $X_{\prec i}$ the highest-scoring parent set that is a subset of an existing k-clique in $\mathcal {K}_C$.

$$\begin{aligned} \varPi _{X_{\prec i}} \in {{\mathrm{argmax}}}_{\pi \subset C, C \in \mathcal {K}_C} \mathrm {BIC}(X_{\prec i}, \pi _{\prec i}) . \end{aligned}$$

Thus k-G finds a locally optimal DAG consistent with a given order and whose treewidth is bounded by k (Fig. 4).

Fig. 4

Example of a treewidth-bounded DAG (k=2) being built iteratively. On the left, the DAG at each step (green nodes) is presented, and on the right the resulting k-tree (white nodes). We start with the variables $\{A, B, C\}$ and we add the remaining ones one at a time (D, E and F) (Color figure online)

5.4 Sampling orders for k-G

The insights of Sect. 4.2 about high-entropy and low-entropy variables can be applied also to k-G. We thus modify k-G by applying the entropy-based approach for sampling the orders, as discussed in Sect. 4.2. We call this new approach k-$\hbox {G}_\mathrm {ENT}$ as an extension of the original algorithm k-G.

We compare k-G and k-$\hbox {G}_\mathrm {ENT}$ on small, large and very large data sets already introduced in Sect. 4. We provide each solver with the same cache of candidate parent sets, pre-computed using $\mathrm {BIC}^*$, allowing one minute per variable and no maximum in-degree. Each solver is executed for one hour on the same computer and we track the $\mathrm {BIC}$ score obtained by the two algorithms for treewidths $k \in \{2,4,5,6,8\}$. We summarize the results by again separating small data sets ($n \le 200$, Table 3), large data sets ($200< n < 2000$, Table 4) and very large data sets ($n \ge 2000$, Table 4).

k-$\hbox {G}_\mathrm {ENT}$ performs better than k-G even in small data sets ($n \le 200$). In spite of that, the sign test does not claim significance when analyzing the number of wins and losses of the two methods on such data sets. On the other hand, k-$\hbox {G}_\mathrm {ENT}$ outperforms k-G in almost every large and very large data set; the analysis of the number of wins and losses shows significance for each tested treewidth. In most cases, the obtained $\varDelta \mathrm {BIC}$ is larger than 10, providing very strong evidence in favor of the model learned by k-$\hbox {G}_\mathrm {ENT}$. The difference is significant (sign-test, $p< 0.01$) for every tested treewidth.

Table 3 k-$\hbox {G}_\mathrm {ENT}$ often beats k-G in small data sets, but the number of victories is not statistically significant

Table 4 k-$\hbox {G}_\mathrm {ENT}$ consistently achieves a larger BIC score than k-G in large and very large data sets

Scanagatta et al. (2016) shows that k-G outperforms S2; for the sake of completeness, we have compared k-$\hbox {G}_\mathrm {ENT}$ to S2. It further increases the advantage achieved by k-G over S2. Out of the 75 data sets used in this experiments, of which 36 have are small, 24 are large, and 15 are very large, k-$\hbox {G}_\mathrm {ENT}$ always yields a higher score than S2. In the great majority of cases the improvement is larger than 10; smaller improvements are found only in some data sets with less than 70 variables.

5.5 Inference on real data sets

One of the main reasons to learn Bayesian networks of bounded treewidth is to ensure that their use for inferences later on can be performed exactly and efficiently. In this section we compare the performance (in terms of inferential results between models that were learned with bounded and unbounded treewidths). We consider the 20 real data sets of Table 1. The inference task that we take on is the computation of the probability of evidence P(e) of five randomly selected variables, which we set to random states.

When dealing with large real data sets, the actual value of P(e) may be unknown (since it is a computationally challenging problem). We thus (approximately) assume that the ground-truth is the highest-scoring network of unbounded treewidth that is available to us; that is, we assume that the true networks is either the one obtained by $\hbox {ASOBS}_\mathrm {ENT}$ or by Gobnilp (whichever achieves the best score). We then compute P(e) by performing exact inference on such a network, using the algorithm Iterative Join Graph Propagation (Mateescu et al. 2010) and running it until convergence. This software is available from http://www.hlt.utdallas.edu/~vgogate/ijgp.html.

We assess the difference between P(e) computed using the assumed ground-truth and using the network with bounded treewidth (k=2,4 6,8) learned by k-$\hbox {G}_\mathrm {ENT}$. For each data set, we run 100 queries and we measure the mean absolute error ($\mathrm {mae}$) of the resulting inference for each bounded-treewidth model:

$$\begin{aligned} \mathrm {mae} = \frac{1}{q} \sum _i |P_i(e)-\hat{P}_i(e)| , \end{aligned}$$

where q denotes the total number of queries, $P_i(e)$ and $\hat{P}_i(e)$ are the probability of evidence on the ith query computed by respectively the model assumed as ground-truth and the bounded-treewidth model. We show in Fig. 5 how $\mathrm {mae}$ varies with the treewidth. Overall, the difference in $\mathrm {mae}$ goes down as the treewidth increases, but it almost vanishes at $k=6$ to $k=8$, suggesting that a treewidth larger than 8 should be rarely necessary.

Fig. 5

Distribution of mean absolute errors, for bounded-treewidth models with different treewidths. Each boxplot represents $\mathrm {mae}$ measures taken on 20 data sets

Fig. 6

Distribution of computational times on the 20 data sets in Table 1 for each model. On each of the 20 data sets we record the mean running time of 100 inferences; thus eventually we represent such 20 means for each model with a boxplot

Besides $\mathrm {mae}$, we analyze the time required by the inferences. We report summary results (obtained by averaging over all data sets) in Fig. 6, including also the unbounded model in the comparison. The most striking result is that the bounded-treewidth models are at least one order of magnitude faster than the unbounded-treewidth ones, even with treewidth as large as 8. Such large differences are partially due to the fact that the query involves multiple variables. Smaller differences are observed when computing marginals for these real data sets. Table 5 reports mean inference time and $\mathrm {mae}$ for models with different treewidths. Yet, we show that orders of magnitude of difference in the running time are observed also when computing marginals, when when deal with domains containing thousands of variables, as we study in the next section.

Table 5 Mean inference results on 20 data sets, running 100 queries for each data set

5.6 Inference on synthetic data sets

Now we take on inferential tasks over domains where the true networks is known, so we have access to the true probability of evidence. In this way, we compare inferential results obtained from the networks learned by $\hbox {ASOBS}_{\mathrm {ENT}}$ and by k-$\hbox {G}_{ENT}$, using different treewidths ($k=2,4,6,8$). We consider the 15 very large synthetic data sets ($n\ge 2000$) of Table 1.

Unbounded-treewidth models containing this amount of variables pose serious challenges for inference. Even marginals cannot be computed exactly. In several cases we have had no convergence of the inference after 30 minutes of computation. We thus resorted to approximate inference. Considering that inference with bounded-treewidth models take consistently less than 0.1 seconds (recall that we are computing marginals), we allow one minute (that is, a time superior by two orders of magnitude) of approximate inference for the queries applied to the true unbounded-treewidth models. In these experiments, we do not compute the probability of joint observations, which would even been even more demanding. For each network, we perform inference regarding the marginal probability of 100 different variables. We select the leaves of the network as variables to be queried, as this requires marginalizing out the largest number of variables. This setting should be especially challenging for the accuracy of bounded-treewidth models, which have limited expressiveness. If some intermediate potentials are poorly estimated, errors would propagate. In case the network contains less than 100 leaves, we run the remaining queries on randomly chosen parents of the leaves. We again perform the inferences using Iterative Join Graph Propagation (Mateescu et al. 2010).

Let us denote the true marginal of X by P(X) and the marginal estimated by a model by $\hat{P}(X)$. Let us denote by $\mathcal {Q}$ the set of 100 variables selected for as queries. The mean absolute error ($\mathrm {mae}$) of the marginal query is then:

$$\begin{aligned} \mathrm {mae} = \frac{1}{s(\mathcal {Q})} \sum _{X \in \mathcal {Q} } \frac{1}{|X|} \sum _{x \in {X}} | P(x) - \hat{P}(x) | . \end{aligned}$$

(4)

In order to compare the bounded-treewidth models against the unbounded models learned with $\hbox {ASOBS}_{\mathrm {ENT}}$, we divide $\mathrm {mae}$ of each bounded-treewidth model by the $\mathrm {mae}$ obtained on the same data set by the model learned with $\hbox {ASOBS}_{\mathrm {ENT}}$. We call this measure relative $\mathrm {mae}$. We show in Fig. 7 boxplots of relative $\mathrm {mae}$ for each learned model (with $k=2,4,6,8$). Remarkably, the median of the relative $\mathrm {mae}$ is close to one already for a low treewidth bound of 2, and becomes slightly lower than one for larger treewidths, indicating a slightly better accuracy for the treewidth-bounded models. One might wonder why the treewidth-unbounded models do not yield more accurate inferences than the treewidth-bounded ones, which have lower score. A first conjecture is that we are considering marginal queries, while treewidth-unbounded models might have an advantage in joint queries involving many variables. Another conjecture is that their accuracy might be deteriorated by approximate inference. We leave this type of investigation for future experiments.

Fig. 7

Relative $\mathrm {mae}$ between the bounded-treewidth models and the unbounded-treewidth models learned by $\hbox {ASOBS}_{\mathrm {ENT}}$. Each model performs 100 marginal inferences in each of the 15 very large data sets. We average the results referring to the same data set, obtaining 15 observations for each model. The boxplots visualize such observations

Hence, besides delivering huge computational savings, bounded-treewidth models are competitive with unbounded-treewidth models as for the accuracy of the inference. This corroborates with findings of Elidan and Gould (2008), who pointed out that bounding the treewidth prevents selecting overly complicated structures of dependences, thereby reducing the chance of overfitting.

6 Conclusions

We have presented a set of approximate algorithms for structure learning of Bayesian networks. They include parent set identification, structure optimization and structure optimization under bounded treewidth. Taken together they allow for a remarkable improvement regarding the Bayesian network structure learning task for domains with thousands of variables, both for bounded and unbounded treewidth learning.

We foresee two main directions for future work. From the methodological viewpoint, it would be interesting to extend the procedure of $\mathrm {BIC}^*$ for the preparation of the cache of the parents also to other scoring function for Bayesian networks, such as the Bayesian Dirichlet equivalent uniform (BDeu) score. From the empirical viewpoint, it would be interesting to compare bounded-treewidth Bayesian networks against other probabilistic models that allow tractable inference and scale to thousands of variables, such as sum-product networks, in terms of their computational performance and accuracy of inferences.