Double-diffusive transport and thermodynamic analysis of a magnetic microreactor with non-Newtonian biofuel flow

Abstract

Magnetic microfuel-reforming is a promising method of biofuel processing in diesel engines. However, the complex interactions amongst the non-Newtonian biofuel flow, magnetic field and reactor have hindered understanding of their influences upon the transport phenomena in the system. To resolve this issue, the transport of heat and mass in a porous microreactor containing a Casson rheological fluid and subject to a magnetic field is investigated analytically. The system is assumed to host a homogenous and uniformly distributed endothermic/exothermic chemical reaction. Two-dimensional analytical solutions are developed for the temperature and concentration fields as well as the Nusselt number and local entropy generations, and the results are rigorously validated. It is demonstrated that changes in the non-Newtonian characteristics of the fluid and altering the magnetic and thermal radiation properties can lead to bifurcation of temperature gradient on the surface of the porous medium. The general behaviour of such bifurcation is dominated by the exothermicity (or endothermicity) of the chemical reaction in the fluid phase. It is also shown that variations in the Casson fluid parameter and changes in the intensity and incident angle of the magnetic field can modify the Nusselt number considerably. The extent of these modifications is found to be heavily dependent upon the wall thickness and diminishes as the walls become thicker. Further, the total entropy generation is shown to be highly sensitive to the wall thickness and increases by intensifying the magnetic field, provided that the microreactor walls are thin.

Introduction

Utilisation of biofuels is considered as an important route for decarbonisation of transport and power [1]. Hence, a wide range of biofuels are currently being investigated worldwide for potential use in internal combustion engines [1, 2]. Nonetheless, thermophysical properties of many biologically driven liquid fuels do not allow their direct injection into a diesel engine. As a result, processing of biofuels is receiving an increasing attention [3, 4]. Magnetic reforming of biofuel is an attractive technology with proven high performance and low price [5,6,7]. In magnetic reforming, a flow of biofuel (e.g. pine oil, algae driven oils) is subject to a magnetic field and chemical reactions simultaneously. The physicochemical processes can be hosted by micro- or macrochemical reactors [5, 6]. Often, biofuels have strong non-Newtonian characteristics, and thus the problem includes interactions amongst non-Newtonian fluids, magnetic fields, heat of reactions and transport processes associated with fuel reforming. Further, due to the need for high rates of heat transfer, porous media are commonly used in fuel microreactors [8, 9]. Combination of all these interactions renders a very complicated and largely unknown problem and hinders development of a rigorous physical understanding of the system. The main objective of the current work is to elucidate the fundamental relations between different processes dominating the transport phenomena in magnetic biofuel reformers. This is achieved through development of an analytical model of thermal and concentration fields inside a microchannel as the essential component of microreformers. The thermodynamics of magnetic microreactor and the encountered irreversibilities are also evaluated to provide further insight into the physics of transfer processes.

It has been shown that Casson fluids could represent the non-Newtonian features of some biofuels with an acceptable accuracy [3, 4]. In the following, the existing literature on heat and mass transfer in Casson fluid flows within porous media and/or in the presence of magnetic effects is briefly reviewed. Mustafa et al. [10] investigated stagnation point flow of Casson fluid over a stretching sheet. Their analysis was focused on the heat transfer behaviours of such configuration. These authors introduced similarity parameters and subsequently applied homotopy analysis to solve the resultant ordinary differential equations [10]. Mustafa et al. showed that the velocity and skin friction coefficient were larger for Casson fluid compared to those of viscous fluids. In a separate work, homotopy methods were applied to the MHD (magnetohydrodynamic) flow of Casson fluid over a stretching plate with inclusion of Soret and Dufour effects [11]. This showed that decreasing the Casson parameter could lead to the reduction in temperature and concentration. The boundary layer flow of a Casson nanofluid over a radially stretching cylinder was investigated by Malik et al. [12] through using similarity solutions. MHD boundary layer flow of a Casson nanofluid flow over a stretching plate was also investigated numerically by Nadeem et al. [13]. Through substituting viscous fluids by a Casson fluid, about 5% increase in the value of Nusselt number was reported, and consequently, the temperature dropped in the entire domain [13].

The unsteady natural convection of Casson fluid in a vertical porous plate was investigated by Khalid et al. [14], revealing the decrease in Nusselt number as time elapses. In a theoretical work, Abolbashari et al. [15] modelled entropy generation in a boundary layer flow of Casson fluid flow. Soret effects were considered and the steady transfer of heat and mass from a flat surface was investigated. The authors demonstrated that increasing Casson fluid parameter could slightly thicken the thermal and concentration boundary layers [15]. Further, reducing the value of Casson parameter (i.e. strengthening the non-Newtonian characteristics of the fluid) was shown to intensify the entropy generation within the boundary layer.

In an analytical and numerical work, Hakeem et al. investigated the magnetohydrodynamic boundary layer flow of Casson fluid with thermal radiation [16]. The angle of incidence of the magnetic field could vary, and slip velocity was assumed on the surface of the stretching plate. Hakeem et al. reported increases in skin friction at higher Casson and velocity slip parameters and showed that augmenting these parameters reduces the Nusselt number and thus increases the wall temperature. In another theoretical study, Abbas et al. [17] analysed transport of heat and mass in an unsteady, chemically reactive boundary layer flow on a stretching surface. Temperature-dependent Arrhenius chemical kinetics were included in the analysis, and a linear model of thermal radiation was also added. Increases in Casson fluid parameter (approaching Newtonian fluid) were shown to reduce the thickness of momentum, thermal and concentration boundary layers [17]. It was further demonstrated that thickness of concentration boundary layer decreases by increasing the chemical reaction rate and the temperature difference between the wall and free fluid [17]. Rauf et al. [18] investigated the magnetohydrodynamic, three-dimensional, double-diffusive convection of a reactive boundary layer flow of Casson fluid over a stretching surface. This study showed that enhancement of Casson parameter could increase the friction on the surface [18].

To develop a model for the motion of dusty fluids, Ramesh et al. [19] considered forced convection of Casson fluid over the surface of a stretching cylinder. These authors [19] also investigated the influences of thermal radiation, a secondary particle phase and an imposed magnetic field. Increasing the Casson parameter was shown to reduce the temperature of the investigated phases. In a numerical study, Khan et al. [20] investigated boundary layer flow of a Casson fluid over a stretching surface with catalytic chemical reactions on the surface and a homogenous autocatalytic reaction in the fluid. This study further included the heat of reactions and magnetic effects. It was shown that surface drag grows at larger magnetic intensities. Yet, heat transfer rate decays for higher values of Prandtl number [20]. In a recent work, Rana et al. [21] investigated mixed convection of oblique stagnation flow of Casson fluid. This study included partial slip as well as exothermic heterogeneous and homogenous chemical reactions. Amongst other findings, Rana et al. reported that enhancing the slip parameter decreases the concentration of chemical species on the surface [21]. In another recent study, Rehman et al. [22] analysed MHD of Casson fluid flow over a rotating disc with the inclusion of chemical reactions, exothermicity and thermal diffusion of chemical species. Recently, the non-equilibrium thermodynamics of double-diffusive transport was investigated through employing Lattice–Boltzmann method [23]. Soret and Dufour effects were both considered in this study and temperature and concentration fields were predicted accurately.

It follows from the preceding review of literature that transport of heat and mass in Casson fluids is rather involved and distinctive to that of Newtonian fluids. In particular, the complicated interactions between heat and mass transfer in chemically reactive flow systems including Casson fluids are well demonstrated. Surprisingly, however, so far there has been no investigation of transport phenomena in porous media and microchannels containing Casson fluids (except for Ref. [14]). In line with the goal of understanding the physics of magnetic biofuel reforming, the current study aims to address these issues through a theoretical analysis of heat and mass transfer in a parallel-plate microreactor containing a flow of Casson fluid. The system also includes a homogenous chemical reaction occurring inside a porous medium and is therefore a porous, microstructured chemical reactor [24]. It is further subject to a magnetic field with varying incident angle as pertinent to the design of real magnetic microreformers for biofuels.

Theoretical methods

It is crucial to note that even in the highly simplified model of magnetic microreformer considered in this work, the problem involves multi-physics and is therefore very complex. A large number of parameters describing the effects of non-Newtonian fluid, MHD, heat of reactions, porous media and shape of microreactor influence the transport processes. In practice, design process often involves significant parametric studies and repeating the analysis for many times. Numerical and experimental approaches can become time consuming in such case, while analytical tools remain convenient. Further, analytical solutions are ideal for validation of numerical tools that can consider more sophisticated aspects of the problem. Provision of such solution is a major objective of this work. Towards this goal, the current section develops closed-form analytical solutions for the thermal and concentration fields in a way that different physical interactions can be conveniently added to or eliminated from the system.

Problem configuration and assumptions

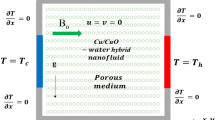
Figure 1 shows a schematic view of the problem under investigation. A uniform flow of an electrically conductive Casson fluid enters an axisymmetric microreactor, which consists of a thick-wall microchannel filled by a porous material. It is noted that practical microreactors include a series of microchannels. However, the current fundamental study considers one microchannel as the building block of the microreformer. Casson fluid is used as a fair model of the non-Newtonian features of the biofuels in magnetic fuel reforming [3, 4]. In general, Casson fluid rheology follows the well-established behaviour described by [25]

$$\tau_{\text{ij}} = \left\{ {\begin{array}{*{20}l} {2\left( {\mu_{\text{b}} + \frac{{p_{\text{y}} }}{{\sqrt {2\pi } }}} \right)e_{\text{ij }} } \hfill & {\quad \pi > \pi_{\text{c}} } \hfill \\ {2\left( {\mu_{\text{b}} + \frac{{p_{\text{y}} }}{{\sqrt {2\pi c} }}} \right)e_{\text{ij}} } \hfill & {\quad \pi < \pi_{\text{c}} } \hfill \\ \end{array} } \right.$$

(1)

Fig. 1

Schematic of the porous microchannel under investigation, as a simplified model of magnetic biofuel microreformers

In Eq. (1), $\tau_{\text{ij}}$ is the (i, j)th component of the stress tensor, $\pi_{\text{ij}} = e_{\text{ij}} e_{\text{ij}}$ and $e_{\text{ij}}$ are the (i, j)th component of the deformation rate. Further, $\pi$ is the product of the component of deformation rate with itself, $\pi_{\text{c}}$ represents a critical value of this product based on the non-Newtonian model, while $\mu_{\text{b}}$ and $p_{\text{y}}$ denote the plastic dynamic viscosity and the yield stress of the considered fluid. The kinematic viscosity suitable for Casson fluid is often given by $\vartheta_{\text{f}} = \frac{{\mu_{\text{b}} }}{\rho }\left( {1 + \beta } \right)$ [25].

In the current work, the Casson fluid is assumed to be electrically conductive and the microchannel is subject to a constant heat flux and a uniform magnetic field with varying angle of incidence. It is important to note that in practice often nanoparticles are added to biofuel to enhance electrical conductivity [26,27,28]. However, to avoid over-complication, nanoparticles have been ignored here. It is further assumed that a homogeneous chemical reaction takes place inside the porous microchannel leading to a forced convection of chemical species. Rosseland approximation and local thermal non-equilibrium (LTNE) [29] are employed to account for radiative heat transfer and local heat exchanges in the porous medium and, thermal diffusion of mass (Soret effect) is considered. It is further assumed that chemical reactions taking place within the fluid phase are exothermic or endothermic, which can be represented by a volumetric source term added to the energy equation [30]. The other assumptions include steady and fully developed fluid flow, homogeneity of the properties of the porous materials, existence of no sharp reaction zones, no gravitational effects and reversibility of the homogenous chemical reaction [31, 32]. The heat of reaction appears as a source term in the energy equation of the fluid phase, similar to that investigated in the previous studies [30].

Governing equations

The Darcy–Brinkman model of transport of momentum provides a hydrodynamic model of Casson fluid flow in the microchannel with MHD effects [33,34,35,36]. That is

$$- \frac{\partial p}{\partial x} + \mu_{\text{eff}} \left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\mu_{\text{b}} \left( {1 + \frac{1}{\beta }} \right)}}{\kappa }u - \sigma B_{\text{o}}^{2} u\sin^{2} \left( \gamma \right) = 0.\quad 0 \le y < h_{1}$$

(2)

Considering the two-equation (LTNE) model of heat transfer in the porous medium in both axial and transversal directions and one-dimensional conduction of heat within the walls of the microchannel, the following equations govern the transport of thermal energy in the system [18, 31, 37, 38]. Here, it is assumed that the fluid is optically thin [30, 39].

$$k_{1} \frac{\partial }{\partial y}\left[ {\frac{{\partial T_{1} }}{\partial y}} \right] = 0,\quad h_{1} < y \le h_{2}$$

(3a)

$$k_{\text{ef}} \frac{{\partial^{2} T_{f} }}{{\partial y^{2} }} + h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) + \sigma B_{\text{o}}^{2} (u\sin^{2} (\gamma ))^{2} + S_{\text{f}} = \rho_{\text{f}} C_{\text{p,f}} u\frac{{\partial T_{\text{f}} }}{\partial x},\quad 0 \le y < h_{1}$$

(3b)

$$k_{\text{es}} \frac{{\partial^{2} T_{\text{s}} }}{{\partial y^{2} }} - h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right) - \left( {\frac{\partial q}{\partial y}} \right) = 0.\quad 0 \le y < h_{1}$$

(3c)

The radiation term in Eq. (3c) is expressed by

$$q = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T_{\text{s}}^{4} }}{\partial y}.$$

(4)

Through applying Rosseland approximation [40], Eq. (4) is transformed to:

$$\frac{\partial q}{\partial y} = \frac{{ - 16\sigma^{*} T_{\text{o}}^{3} }}{{3k^{*} }}\frac{{\partial^{2} T_{\text{s}} }}{{\partial y^{2} }}.$$

(5)

The equations for the transport of heat (Eqs. 3a–c) are associated with the following boundary conditions [28, 41, 42].

$$y = h_{1}: \quad u_{\text{f}} = 0, \quad T_{\text{f}} = T_{\text{s}} = T_{\text{w}} , \quad q_{1} = \left. {k_{\text{ef}} \frac{{\partial T_{\text{f}} }}{\partial y}} \right|_{{{\text{y}} = {\text{h}}_{1} }} + \left. {\left( {k_{\text{es}} + \frac{{16\sigma^{*} T_{\text{o}}^{3} }}{{3k^{*} }}} \right)\frac{{\partial T_{\text{s}} }}{\partial y}} \right|_{{{\text{y}} = {\text{h}}_{1} }} ,$$

(6)

$$y = - h_{1}: \quad u_{\text{f}} = 0, \quad T_{\text{f}} = T_{\text{s}} = T_{\text{w}} , \quad q_{1} = - \left. {k_{\text{ef}} \frac{{\partial T_{\text{f}} }}{\partial y}} \right|_{{{\text{y}} = - {\text{h}}_{1} }} - \,\left. {\left( {k_{\text{es}} + \frac{{16\sigma^{*} T_{\text{o}}^{3} }}{{3k^{*} }}} \right)\frac{{\partial T_{\text{s}} }}{\partial y}} \right|_{{{\text{y}} = - {\text{h}}_{1} }} .$$

(7)

The generation and transport of chemical species in microreactors are governed by the following advection–diffusion–reaction model for a zeroth order, homogenous, temperature indifferent chemical reaction. The model considers the contributions made by the Soret effect to the convection of chemical species [43,44,45,46].

$$u\frac{\partial C}{\partial x} = D\frac{{\partial^{2} C}}{{\partial^{2} y}} - D_{\text{T}} \frac{{\partial^{2} T_{\text{f}} }}{{\partial y^{2} }} + k_{\text{r}} \quad 0 \le y < h_{1}$$

(8)

The boundary conditions imposed to the concentration of chemical species are the followings.

$$x = 0, \quad y = h_{1} , \quad C = C_{0}$$

(9a)

$$y = 0, \quad \frac{\partial C}{\partial y} = 0$$

(9b)

It should be noted that in the current formulation gas rarefaction has been ignored. This is primarily because in microreactors gas pressure is relatively high, and thus, in comparison with other miniaturised devices, rarefication effects are less noticeable [47, 48].

Dimensionless parameters and equations

Next, the governing equations and boundary conditions are non-dimensionalised through introduction of the following dimensionless parameters.

$$\begin{array}{*{20}l} {Da = \frac{\kappa }{{h_{2}^{2} }}} \hfill & {M = \frac{{\mu_{\text{eff}} }}{{\mu_{\text{b}} }}} \hfill & {M_{\text{d}} = \frac{{\sigma B_{0}^{2} h_{2}^{2} }}{{\mu_{\text{b}} }}} \hfill \\ {\theta_{\text{i}} = \frac{{\left( {T_{\text{i}} - T_{\text{w,in}} } \right)k_{\text{es}} }}{{q_{1} h_{2} }}, \quad i = 1,s,f} \hfill & {S = \sqrt {\frac{{\frac{1}{Da}\left( {1 + \frac{1}{\beta }} \right) + M_{\text{d}} \sin^{2} \left( \gamma \right)}}{{\left( {1 + \frac{1}{\beta }} \right)M}}} } \hfill & {U = \frac{u}{{u_{\text{r}} }}, \quad u_{\text{r}} = - \frac{{h_{2}^{2} }}{{\mu_{\text{f}} }}\frac{\partial p}{\partial x}} \hfill \\ {Bi = \frac{{h_{\text{sf}} a_{\text{sf}} h_{2}^{2} }}{{k_{\text{es}} }}} \hfill & {Br = \frac{{\mu_{\text{eff}} \bar{u}^{2} }}{{q_{1} h_{2} }}} \hfill & {k_{\text{e1}} = \frac{{k_{1} }}{{k_{\text{es}} }}} \hfill \\ {k = \frac{{k_{\text{ef}} }}{{k_{\text{es}} }} = \frac{{\varepsilon k_{\text{f}} }}{{\left( {1 - \varepsilon } \right)k_{\text{s}} }}} \hfill & {\omega_{\text{f}} = \frac{{S_{\text{f}} h_{2} }}{{q_{1} }}} \hfill & {R_{\text{d}} = \frac{{16\sigma^{*} T_{\text{o}}^{3} }}{{3k^{*} k_{\text{es}} }}} \hfill \\ {Y = \frac{y}{{h_{2} }}} \hfill & {Y_{1} = \frac{{h_{1} }}{{h_{2} }}} \hfill & {X = \frac{x}{L}} \hfill \\ {Re = \frac{{2h_{2} \rho_{\text{f}} \bar{u}^{2} }}{{\mu_{\text{eff}} }}} \hfill & {\xi = \frac{{h_{2} }}{L}} \hfill & {Pr = \frac{{C_{\text{p,f}} \mu_{\text{eff}} }}{{k_{\text{ef}} }}} \hfill \\ {{{\Phi }} = \frac{C}{{C_{0} }}} \hfill & {Dn = \frac{{k_{\text{r}} h_{1}^{2} }}{{DC_{0} }}} \hfill & {Pe = \frac{{h_{1} \bar{u}}}{D}} \hfill \\ {Sr = \frac{{q_{1} h_{1} D_{\text{T}} }}{{C_{0} k_{\text{f}} D}}} \hfill & {N_{\text{i}} = \frac{{S_{\text{i}}^{\prime\prime\prime} h_{2}^{2} }}{{k_{\text{es}} }}, \quad i = w,s,f, {\text{FF}},{\text{DI}}} \hfill & {\omega = \frac{{q_{1} h_{2} }}{{k_{\text{es}} T_{\text{w,in}} }}} \hfill \\ {\varphi = \frac{{RDC_{\text{o}} }}{{k_{\text{es}} }}} \hfill & {} \hfill & {} \hfill \\ \end{array}$$

(10)

Applying the dimensionless equations, the governing equations renders them dimensionless. For conciseness reasons here only the final form of the dimensionless equations are shown. Further details can be found in Refs. [31, 32]

$$1 + M\left( {1 + \frac{1}{\beta }} \right)\frac{{\partial^{2} U}}{{\partial Y^{2} }} - U\left[ {\frac{1}{Da}\left( {1 + \frac{1}{\beta }} \right) + M_{\text{d}} \sin^{2} \left( \gamma \right)} \right] = 0.\quad 0 \le Y < Y_{1}$$

(11)

The no-slip boundary condition at the solid–porous interfaces are expressed by

$$U\left( {Y_{1} } \right) = U\left( { - Y_{1} } \right) = 0.$$

(12)

Solution of Eq. (11) is given by the following expression

$$U\left( Y \right) = \frac{Da}{{\left( {1 + \frac{1}{\beta }} \right) + DaM_{\text{d}} \sin^{2} \left( \gamma \right)}}\left[ {1 - \frac{{\cosh \left( {SY} \right)}}{{\cosh \left( {SY_{1} } \right)}}} \right].\quad 0 \le Y < Y_{1}$$

(13)

Hence, the dimensionless average flow velocity across the microchannel reduces to

$$\bar{U} = \frac{Da}{{\left( {1 + \frac{1}{\beta }} \right) + DaM_{\text{d}} \sin^{2} \left( \gamma \right)}}\left[ {1 - \frac{{\tanh \left( {SY_{1} } \right)}}{{SY_{1} }}} \right].$$

(14)

Combining Eqs. (13) and (14) leads to the following ratios

$${\raise0.7ex\hbox{$u$} \!\mathord{\left/ {\vphantom {u {\bar{u}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\bar{u}}$}} = {\raise0.7ex\hbox{$U$} \!\mathord{\left/ {\vphantom {U {\bar{U}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\bar{U}}$}} = D_{1} \left[ {\cosh \left( {SY_{1} } \right) - \cosh \left( {SY} \right)} \right].$$

(15)

After some algebraic manipulations, the dimensionless energy equations take the following forms:

$$k_{\text{e1}} \theta_{1}^{\prime\prime} = 0,\quad Y_{1} < Y \le 1$$

(16a)

$$\theta_{\text{f}}^{\prime\prime\prime\prime} - Q_{1} \theta_{\text{f}}^{\prime\prime} + Q_{2} \cosh \left( {2SY} \right) + Q_{3} \cosh \left( {SY} \right) - Q_{4} = 0,$$

(16b)

$$\theta_{\text{s}}^{\prime\prime\prime\prime} - Q_{1} \theta_{\text{s}}^{\prime\prime} - \left[ {Q_{5} \cosh \left( {2SY} \right) + Q_{6} \cosh \left( {SY} \right) + Q_{4} } \right] = 0.$$

(16c)

Analytical expression for the parameters $Q_{1}$ to $Q_{6}$ are provided in “Appendix 1: Closed-form constants”. Specifying the particular solutions of Eqs. (16a–c) requires the boundary conditions given by the followings.

$$\theta_{1} \left( {Y_{1} } \right) = 0, \quad \theta_{1}^{\prime} \left( 1 \right) = \frac{1}{{k_{\text{e1}} }},$$

(17a,b)

$$\theta_{f} \left( {Y_{1} } \right) = \theta_{s} \left( {Y_{1} } \right) = 0$$

(17c)

$$\theta_{f} \left( { - Y_{1} } \right) = \theta_{s} \left( { - Y_{1} } \right) = 0 ,$$

(17d)

$$\theta_{\text{f}}^{\prime\prime} \left( {Y_{1} } \right) = - \frac{1}{k}\left[ {D_{2} \cosh \left( {2SY_{1} } \right) + D_{3} \cosh \left( {SY_{1} } \right) + D_{4} } \right], \quad \theta_{\text{s}}^{\prime\prime} \left( {Y_{1} } \right) = 0,$$

(17e,f)

$$\theta_{\text{f}}^{\prime\prime\prime} \left( 0 \right) = \theta_{\text{s}}^{\prime\prime\prime} \left( 0 \right) = 0,$$

(17g)

where the constants are given in “Appendix 1: Closed-form constants”.

Solutions of momentum, energy and mass transfer equations

Equations (16a–c) are now solved analytically through applying the boundary conditions given by Eqs. (17a–g). This results in the closed-form dimensionless temperature profiles in the transversal direction as:

$$\theta_{1} \left( Y \right) = E_{1} + E_{2} Y,\quad Y_{1} < Y \le 1$$

(18a)

$$\theta_{\text{f}} \left( Y \right) = E_{3} \cosh \left( {2SY} \right) + E_{4} \cosh \left( {SY} \right) + E_{5} \cosh \left( {\alpha Y} \right) + E_{6} Y^{2} + E_{7} Y + E_{8} ,\quad 0 \le Y < Y_{1}$$

(18b)

$$\theta_{\text{s}} \left( Y \right) = E_{9} \cosh \left( {2SY} \right) + E_{10} \cosh \left( {SY} \right) + E_{11} \cosh \left( {\alpha Y} \right) + E_{6} Y^{2} + E_{7} Y + E_{12} ,\quad 0 \le Y < Y_{1}$$

(18c)

in which

$$\alpha = \sqrt {Q_{1} } .$$

(18d)

The two-dimensional temperature fields for the solid and fluid phases are obtained by the addition of the dimensionless axial and transverse temperature profiles and incorporating Eq. (19). The closed-form solutions read as follows.

$$\frac{{{\text{d}}\overline{{\theta_{f} }} }}{{{\text{d}}X}} = \varOmega = \frac{2}{{k\xi Y_{1} PrRe}}\left[ {1 + \omega_{\text{f}} Y_{1} + BrD_{1}^{2} \frac{{M_{\text{d}} }}{M}\sin^{4} \left( \gamma \right)\left( {Y_{1} \cosh^{2} \left( {SY_{1} } \right) + \frac{{SY_{1} - 3\cosh \left( {SY_{1} } \right)\sinh \left( {SY_{1} } \right)}}{2S}} \right)} \right],$$

(19)

$$\theta_{1} \left( {X,Y} \right) = E_{1} + E_{2} Y + \varOmega X,\quad Y_{1} < Y \le 1$$

(20a)

$$\theta_{\text{f}} \left( {X,Y} \right) = E_{3} \cosh \left( {2SY} \right) + E_{4} \cosh \left( {SY} \right) + E_{5} \cosh \left( {\alpha Y} \right) + E_{6} Y^{2} + E_{7} Y + E_{8} + \varOmega X,\quad 0 \le Y < Y_{1}$$

(20b)

$$\theta_{\text{s}} \left( {X,Y} \right) = E_{9} \cosh \left( {2SY} \right) + E_{10} \cosh \left( {SY} \right) + E_{11} \cosh \left( {\alpha Y} \right) + E_{6} Y^{2} + E_{7} Y + E_{12} + \varOmega X.\quad 0 \le Y < Y_{1}$$

(20c)

Once again, the explicit forms of the parameters are given in “Appendix 1: Closed-form constants”.

Following an analytical procedure developed in Refs. [31, 32], the solution of mass transfer equations is given by the following relation.

$$\varPhi \left( {X,Y} \right) = F_{1} \cosh \left( {2SY} \right) + F_{2} \cosh \left( {SY} \right) + F_{3} \cosh \left( {\alpha Y} \right) + F_{4} Y^{2} + F_{5} + \frac{DnX}{{PeY_{1} \xi }},$$

(21)

where constants appearing in the above equations are given in “Appendix 1: Closed-form constants”.

The convection coefficient at the top wall of the microchannel is defined as

$$H_{\text{w}} = \frac{{q_{1} }}{{T_{\text{w}} - \overline{T}_{\text{f}} }},$$

(22)

Nusselt number based on the microchannel height $h_{1}$ is expressed by

$$Nu = \frac{{2H_{\text{w}} h_{1} }}{{k_{\text{ef}} }} = \frac{{2q_{1} h_{1} }}{{k_{\text{ef}} \left( {T_{\text{w}} - \overline{T}_{\text{f}} } \right)}}.$$

(23)

The right-hand side of Eq. (23) can be non-dimensionalised to yield the following Nusselt number relation.

$$Nu_{w} = - \frac{{2Y_{1} }}{{k\overline{\theta }_{\text{f}} }}$$

(24)

The dimensionless mean temperature of the fluid, $\bar{\theta }_{\text{f}}$ is found through the following relation.

$$\overline{\theta }_{\text{f}} = \frac{{D_{1} }}{{Y_{1} }}\mathop \int \limits_{0}^{Y1} \theta_{\text{f}} \left[ {\cosh \left( {SY_{1} } \right) - \cosh \left( {SY} \right)} \right]{\text{d}}Y.$$

(25)

Thermodynamic irreversibilities

To calculate the local rate of entropy generation the velocity, temperature and concentration equations are incorporated into the equations of volumetric local entropy generation given in Refs. [45, 49,50,51,52].

$$S_{\text{w}}^{\prime\prime\prime} = \frac{{k_{1} }}{{T_{1}^{2} }}\left[ {\left( {\frac{{\partial T_{1} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{1} }}{\partial y}} \right)^{2} } \right],$$

(26a)

$$S_{\text{s}}^{\prime\prime\prime} = \frac{{k_{\text{es}} }}{{T_{\text{s}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{s}} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{\text{s}} }}{\partial y}} \right)^{2} } \right] - \frac{{h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right)}}{{T_{\text{s}} }},$$

(26b)

$$S_{\text{f}}^{\prime\prime\prime} = \frac{{k_{\text{ef}} }}{{T_{\text{f}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{f}} }}{\partial x}} \right)^{2} + \left( {\frac{{\partial T_{\text{f}} }}{\partial y}} \right)^{2} } \right] + \frac{{h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{f}} } \right)}}{{T_{\text{f}} }} + \frac{{\sigma B_{\text{o}}^{2} \left( {u\sin^{2} \left( \gamma \right)} \right)}}{{T_{\text{f}} }} + \frac{{S_{\text{f}} }}{{T_{\text{f}} }},$$

(26c)

$$S_{\text{FF}}^{\prime\prime\prime} = \frac{{\mu \left( {1 + \frac{1}{\beta }} \right)}}{{\kappa T_{\text{f}} }}u^{2} + \frac{{\mu_{\text{eff}} \left( {1 + \frac{1}{\beta }} \right)}}{{T_{\text{f}} }}\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} ,$$

(26d)

$$S_{\text{DI}}^{\prime\prime\prime} = \frac{RD}{C}\left[ {\left( {\frac{\partial C}{\partial x}} \right)^{2} + \left( {\frac{\partial C}{\partial y}} \right)^{2} } \right] + \frac{RD}{{T_{\text{f}} }}\left[ {\left( {\frac{\partial C}{\partial x}} \right)\left( {\frac{{\partial T_{\text{f}} }}{\partial x}} \right) + \left( {\frac{\partial C}{\partial y}} \right)\left( {\frac{{\partial T_{\text{f}} }}{\partial y}} \right) } \right],$$

(26e)

In Eq. (26), entropy generation terms have been divided into contributions from different sources of irreversibility. The term ${S}_{\text{w}}^{\prime\prime\prime}$ represents the entropy generation in the thick wall of the microchannel. Entropy generation in the solid phase of the porous medium is shown by ${S}_{\text{s}}^{\prime\prime\prime}$ and ${S}_{\text{f}}^{\prime\prime\prime}$ represents the entropy generation rate in the non-Newtonian fluid phase. Further, the irreversibility in the Casson fluid generated by friction is expressed by ${S}_{\text{FF}}^{\prime\prime\prime}$. The term ${S}_{\text{DI}}^{\prime\prime\prime}$ denotes the entropy generation by mass transfer mechanisms.

The non-dimensionalised forms of Eqs. (26a–e) are as follows.

$$N_{\text{w}} = \frac{{k_{\text{e1}} \omega^{2} }}{{\left( {\omega \theta_{1} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{1} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{1} }}{\partial Y}} \right)^{2} } \right],\quad Y_{1} \le Y < 1$$

(27a)

$$N_{\text{s}} = \frac{{\omega^{2} }}{{\left( {\omega \theta_{\text{s}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{s}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{\text{s}} }}{\partial Y}} \right)^{2} } \right] - \frac{{\omega Bi\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right)}}{{\omega \theta_{\text{s}} + 1}},\quad 0 \le Y < Y_{1}$$

(27b)

$$N_{\text{f}} = \frac{{k\omega^{2} }}{{\left( {\omega \theta_{\text{f}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{f}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{\text{f}} }}{\partial Y}} \right)^{2} } \right] + \frac{{\omega Bi\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right)}}{{\omega \theta_{\text{f}} + 1}} + \frac{{\omega BrM_{\text{d}} \sin^{4} \left( \gamma \right)D_{1}^{2} \left[ {\cosh \left( {SY_{1} } \right) - \cosh \left( {SY} \right)} \right]^{2} }}{{M\left( {\omega \theta_{\text{f}} + 1} \right)}} + \frac{{\omega \omega_{\text{f}} }}{{\omega \theta_{\text{f}} + 1}},\quad 0 \le Y < Y_{1}$$

(27c)

$$N_{\text{FF}} = \frac{{\omega D_{1}^{2} Br\left( {1 + \frac{1}{\beta }} \right)}}{{MDa\left( {\omega \theta_{\text{f}} + 1} \right)}}\left[ {\cosh \left( {SY_{1} } \right) - \cosh \left( {SY} \right)} \right]^{2} + \frac{{\omega D_{1}^{2} S^{2} Br\left( {1 + \frac{1}{\beta }} \right)}}{{\left( {\omega \theta_{\text{f}} + 1} \right)}}\sinh^{2} \left( {SY} \right),\quad 0 \le Y < Y_{1}$$

(27d)

$$N_{\text{DI}} = \frac{\varphi }{\varPhi }\left[ {\xi^{2} \left( {\frac{\partial \varPhi }{\partial X}} \right)^{2} + \left( {\frac{\partial \varPhi }{\partial Y}} \right)^{2} } \right] + \frac{\omega \varphi }{{\omega \theta_{\text{f}} + 1}}\left[ {\xi^{2} \left( {\frac{\partial \varPhi }{\partial X}} \right)\left( {\frac{{\partial \theta_{\text{f}} }}{\partial X}} \right) + \left( {\frac{\partial \varPhi }{\partial Y}} \right)\left( {\frac{{\partial \theta_{\text{f}} }}{\partial Y}} \right)} \right].\quad 0 \le Y < Y_{1}$$

(27e)

Next, the equations for the entropy generation in the non-Newtonian fluid and the solid phases of the porous medium are separated, leading to the following equations for the heat transfer irreversibilities.

$$N_{\text{f,ht}} = \frac{{k\omega^{2} }}{{\left( {\omega \theta_{\text{f}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{f}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{\text{f}} }}{\partial Y}} \right)^{2} } \right],$$

(28a)

$$N_{\text{s,ht}} = \frac{{\omega^{2} }}{{\left( {\omega \theta_{\text{s}} + 1} \right)^{2} }}\left[ {\xi^{2} \left( {\frac{{\partial \theta_{\text{s}} }}{\partial X}} \right)^{2} + \left( {\frac{{\partial \theta_{\text{s}} }}{\partial Y}} \right)^{2} } \right].$$

(28b)

The interphase volumetric entropy generation and those by magnetic effect and internal heat generations can be expressed by [15, 33]:

$$N_{\text{int}} = \frac{{\omega^{2} Bi\left( {\theta_{\text{s}} - \theta_{\text{f}} } \right)^{2} }}{{\left( {\omega \theta_{\text{s}} + 1} \right)\left( {\omega \theta_{\text{f}} + 1} \right)}},$$

(29a)

$$N_{\text{mg}} = \frac{{\omega BrM_{\text{d}} \sin^{4} \left( \gamma \right)D_{1}^{2} \left[ {\cosh \left( {SY_{1} } \right) - \cosh \left( {SY} \right)} \right]^{2} }}{{M\left( {\omega \theta_{\text{f}} + 1} \right)}},$$

(29b)

$$N_{\text{v}} = \frac{{\omega \omega_{\text{f}} }}{{\omega \theta_{\text{f}} + 1}}.$$

(29c)

The volumetric entropy generations in the porous insert, $N_{\text{pm}}$ is the sum of the equations that are applicable to the porous medium.

$$N_{\text{pm}} = N_{\text{f,ht}} + N_{\text{s,ht}} + N_{\text{int}} + N_{\text{mg}} + N_{\text{v}} + N_{\text{FF}} + N_{\text{DI}} .$$

(30)

The total entropy generation is calculated by adding the parts of volumetric entropy generation and integrating over the volume of the microchannel with the inclusion of contributions from the walls. A numerical value for the total entropy generation is therefore produced according to the following equation.

$$N_{\text{Tot}} = 2\int_{0}^{1} {\int_{0}^{1} {\sum {\left( {N_{\text{pm}} + N_{\text{w}} } \right)} } } {\text{d}}X{\text{d}}Y.$$

(31)

Validation

“Appendix 2: Validation” shows that the governing equations and their analytical solutions, developed in “Theoretical methods” section, can be systematically reduced to those in Refs. [31, 53] by setting the magnetic intensity to zero and assigning a large number to Casson fluid parameter ($\beta$). Further, Fig. 2 depicts a comparison between the predicted contours of the dimensionless temperature and concentration as calculated by the current study and those reported in Ref. [30]. The excellent agreement between these two sets of figures confirms the validity of the analytical work presented in “Theoretical methods” section. Table 1 provides the default values of the parameters used in the rest of this study. In setting the values reported in this table, an attempt was made to makes those similar to that already used in the literature in simpler cases [31, 32, 53] to provide a basis for comparison.

Fig. 2

Validation of the analysis a, b contours of fluid phase temperature predicted by the current analysis and calculated by Ref. [31] (right column), c, d contours of porous solid-phase temperature predicted by the current analysis and calculated by Ref. [31] (right column), e, f contours of concentration predicted by the current analysis and calculated by Ref. [31] (right column)

Table 1 The default values of parameters

Results and discussion

Heat and mass transfer

The fluid velocity distribution in the configuration shown in Fig. 1 is well established, see for example [31, 54], the Casson fluid flow differs from that of Newtonian fluid. Nonetheless, for brevity, the flow velocity distribution is not shown here, while the analytical expression for such distribution is provided by Eq. (15). Figures 3 and 4 depict the contours of dimensionless temperature of solid and fluid phases in the microreactor. Temperature is an essential parameter in fuel reforming and therefore special attention is given to the spatial distribution of temperature throughout the microreactor. As a general trend, Figs. 3 and 4 show that there are significant transversal and axial variations in the dimensionless temperature of the fluid phase. However, the temperature distribution in the porous solid phase is essentially axial and features small variations in the transversal direction. This behaviour could be explained by noting that the value of thermal conductivity ratio in Figs. 3 and 4 is much less than unity (see Table 1), and therefore, the solid phase has a much higher thermal conductivity compared to that of the fluid. This reduces the required temperature gradient in the transversal direction to conduct heat within the porous solid phase.

Fig. 3

Dimensionless temperature contours with varying values of magnetic field intensity, M_d—a, c, e the temperature of fluid phase with M_d values of 0, 25 and 50, respectively. b, d, f The temperature of solid phase with M_d values of 0, 25 and 50, respectively

Fig. 4

Dimensionless temperature contours with varying values of the fluid volumetric source term, ω_f—a, c, e the temperature of fluid phase with ω_f values of 0, 1 and 2, respectively. b, d, f The temperature of solid phase with ω_f values of 0, 1 and 2, respectively

The influences of magnetic field upon the dimensionless temperature contours are illustrated in Fig. 3. Clearly, increasing the intensity of the magnetic field does not leave any considerable qualitative effect upon the dimensionless temperature distributions. Yet, it extends the axial and transversal variation of the dimensionless temperatures for both fluid and solid phases. It will be later shown that this is due to the increase in the Nusselt number at higher intensities of the magnetic field. The magnetic term in Eq. (2) appears as a sink of momentum and thus has an effect analogous to that of viscosity. It is well established that in forced convection of heat the dissipation of momentum enhances the rate of heat transfer [43, 55]. It is therefore plausible to expect an increase in the heat transfer to the fluid and consequently a wider transversal range of temperature variation at higher magnetic intensities. Since the solid and fluid temperatures are coupled to each other through internal heat exchanges, an increase in the fluid temperature increases the solid temperature as well. This is well reflected in the dimensionless temperature of the solid phase shown in Fig. 3.

Figure 4 shows the effects of internal heat generation on the contours of non-dimensional temperature inside the microreactor. As expected, internal heat generation imparts significant effects on the dimensionless temperature field. The observed increase in the temperature range by magnifying the internal heat release is simply a consequence of adding more thermal energy to the system through internal heat sources. Also, Fig. 4 implies that by strengthening the internal heat generation, the transversal temperature gradient increases in both fluid and solid phases. In a qualitative sense, increasing the rate of internal heat generation leads to the development of inflection points in the fluid temperature, which in turn results in the so-called bifurcations of temperature gradient. This effect describes a change in the direction of heat flux to or from the porous solid on the surface of the porous medium and solid wall [where the boundary conditions of Eqs. (6) and (7) are applied]. In fuel reformers, direction of heat transfer can significantly influence the chemical composition of the products and hence is of importance [47]. Bifurcation effect was first explained by Yang and Vafai [56] and was later extended to fluid–porous interfaces by Karimi et al. [30] and Dickson et al. [57]. Indeed, all these references assumed flows of Newtonian fluids in the absence of magnetic and radiation effects. Mathematically, the parameter ${{\Sigma }}$ is defined as $\Sigma = \frac{{\left. {\theta_{\text{f}}^{ '} \left( Y \right)} \right| _{{{\text{wall}} - {\text{porous interface}}}} }}{{\left. {\theta_{\text{s}}^{\prime} \left( Y \right)} \right| _{{{\text{wall}} - {\text{porous interface}}}} }}$, where for ${{\Sigma }} < 1$ the heat flux bifurcates [56]. This means that a new route of heat transfer is introduced in which heat is exchanged from the hot phase first to the interface, then from the interface to the cold phase. It is therefore important to predict under which set of parameters the phenomenon of temperature gradient bifurcation can occur. Figures 5 and 6 provide such information, wherein the sign of ${{\Sigma }}$ has been calculated over a k–Bi plane for discrete values of other pertinent parameters.

Fig. 5

Heat flux bifurcation at $\omega_{\text{f}} = - 10$ with varying parameters—a varying Casson fluid parameter, b varying angle of incidence of the magnetic field, c varying magnetic field intensity, d varying radiation parameter. All colours represent ${{\Sigma }} > 0$, indicating no bifurcation

Fig. 6

Bifurcation at $\omega_{\text{f}} = 20$ with varying parameters—a varying Casson fluid parameter, b varying angle of incidence of the magnetic field, c varying magnetic field intensity, d varying radiation parameter. All colours represent ${{\Sigma }} > 0$, indicating no bifurcation

Figure 5 shows that for an endothermic case (heat absorption by the fluid) the numerical values of Casson fluid parameter are immaterial for temperature gradient bifurcation. However, variation in the angle and intensity of the magnetic field can readily cause bifurcation. According to Fig. 5b and c, strengthening the magnetic effect will eventually lead to the bifurcation of temperature gradient. Figure 5d shows that radiation parameter can also contribute to the bifurcation. Yet, unlike magnetic effects, bifurcation is suppressed by intensification of thermal radiation. Changing the internal heat generation from endothermic in Fig. 5 to exothermic in Fig. 6 significantly modifies the bifurcation maps. Most noticeably, in Fig. 6, bifurcation occurs at higher values of Biot number, while in Fig. 5, it is limited to low Biot numbers. Further, for exothermic case in Fig. 6, the temperature gradient bifurcates as the Casson fluid approaches the Newtonian limit. This is an important difference and makes the exothermic case highly susceptible to bifurcation of temperature gradient. The broad colourless regions (indicating bifurcation) in Fig. 6 compared to relatively narrow colourless areas of Fig. 5 confirm this statement. In practice, direction of heat transfer can influence the progress of chemical reaction and thus should be considered in the design of all heat transferring, porous microreactors [48].

The variations of Nusselt number as a function of the non-dimensional height of microchannel (Y₁) have been investigated in Fig. 7. This figure shows that, for all considered cases, reducing the wall thickness results in significant increases in the value of Nusselt number. In explaining this trend, it is noted that the microchannel wall is a thermal resistance, which hinders the process of heat transfer and therefore reduces the heat transfer coefficient. Figure 7a shows that increasing the Casson fluid parameter results in augmentation of Nusselt number. That is the lower values of Casson fluid parameter, and therefore stronger non-Newtonian properties, feature smaller Nusselt numbers compared to those of Newtonian fluids (higher values of Casson fluid parameter). Interestingly, the sensitivity of Nusselt number to variations in the Casson fluid parameter depends upon the wall thickness and is maximised through reducing the wall thickness to zero. It is noted that in real microreformers, variation of the Casson fluid parameter can occur through either of changes in the initial temperature or type of biofuel. Figure 7b illustrates the influences of Biot number or internal heat exchanges upon the Nusselt number. Biot number appears to have major effects on Nusselt number in two different ways. Firstly, increases in Biot number can result in large enhancements of convection coefficient. This is because of the strong heat exchanges between the solid and fluid phases at higher Biot numbers, which increases the capacity of the system to transfer heat from the walls. This result also indicates that the local thermal equilibrium (LTE) assumption, in which the value of Biot number is effectively infinity, can highly overestimate the rate of heat transfer. Secondly, the value of Biot number dominates the sensitivity of Nusselt number to the wall thickness. For low values of Biot number, Nusselt number only slightly depends upon the wall thickness. However, this dependency is greatly intensified at larger values of Biot number. Once again, this observation indicates that LTE assumption, as commonly made in the analysis of microreactors, can lead to the exclusion of important effects such as influences of wall thickness.

Fig. 7

Nusselt Number with varying parameters—a varying Casson fluid parameter, b varying Biot number (top right), c varying magnetic field angle, d varying magnetic field intensity

Figure 7c, d shows the effects of angle and intensity of the magnetic field upon the Nusselt number. According to these figures, increasing the angle and intensity of the magnetic field leads to modest augmentation of Nusselt number (roughly by a value varying between 5 and 10%). As discussed earlier, this is because by strengthening the magnetohydrodynamic forces, the flow loses more momentum. It is known that loss of momentum by the flow in heat convecting flows usually enhances the rate of heat transfer [43]. Similar to that discussed in Fig. 7a, the influence of magnetic intensity and angle of incidence diminishes as the wall thickness increases. Once again, this is due to the growing significance of conduction resistances that overrules the relatively weak magnetohydrodynamic effects. The demonstrated strong dependency of the mechanisms affecting Nusselt number upon the wall thickness is of practical importance in the design of micro thermal and thermochemical systems.

Forced convection of species in the microreactor is governed by Eq. (8). This equation describes the advective–diffusive–reactive nature of transport of mass transfer in the axial and transversal directions. Given that the production of chemical species was assumed to be volumetrically uniform, the mass transfer problem is dominated by the combined actions of advection and mass diffusion. The latter is, itself, through Fickian diffusion of the species as well the thermal diffusion of mass by Soret effect. Figure 8 shows the predicted contours of dimensionless concentration under different values of Biot number and radiation parameters. The general axial increase of concentration in these figures is due to the constant production rate of species, while the transversal gradient is by the combined action of the gradients of flow velocity and temperature fields. Figure 7 shows that increasing Biot number enhances the value of Nusselt number and the rate of heat transfer. As shown in Fig. 8a, c, this reduces the transversal temperature gradient, which in turn weakens the thermal diffusion of mass and leads to smaller concentration of species at the end of the microchannel. Figure 8b, d shows that intensifying the thermal radiation results in a decrease in the transversal gradient of species concentration. Once again, this is due to the partial suppression of thermal diffusion of mass because of the lower temperature gradients at higher radiation rates.

Fig. 8

Contours of dimensionless concentration with varying values of the Biot number (left column) and radiation parameter (right column)—a, c Biot number of 0.1 and 10, respectively. b, dR_d values of 0 and 2, respectively

Entropy generation

Equation (27) showed the non-dimensional entropy generation by different sources of irreversibility including those by heat transfer, mass transfer, fluid friction and various coupling between the sources of irreversibility. The two-dimensional distribution of all these terms were analysed individually. However, for conciseness reasons here, only the most significant sources of irreversibility are shown. Figure 9 illustrates the entropy generation by mass transfer, N_DI, and entropy generation in the porous medium, N_pm (see Eq. 29). This figure shows that by increasing the angle of incidence of the magnetic field, the region with strong mass transfer irreversibility shrinks slightly. This is due to the enhancement of heat transfer by increasing the angle of incidence which in turn reduces the temperature gradients and relaxes the temperature gradients in the fluid domain. As a result, the thermal diffusion of mass, as a highly irreversible process, is partially suppressed and the entropy generation by mass transfer decreases. In contrast to this decrease, entropy generation in the porous medium in Fig. 9 features a small enhancement with increases in the angle of incidence. Given that the heat and mass transfer irreversibilities decrease by increases in the angle of incidence, the intensification of irreversibility can be attributed to the stronger viscous dissipations.

Fig. 9

Contours of dimensionless local entropy generation with varying values of magnetic angle, γ—a, c, eN_DI with γ values of 0, π/6 and π/2, respectively. b, d, fN_pm with γ values of 0, π/6 and π/2, respectively

Changes in the local entropy generation by variations in Casson fluid parameter are investigated in Fig. 10a, c, e and show that increasing this parameter and thus moving towards Newtonian fluid significantly decreases the fluid friction irreversibility (N_FF). This is an anticipated result, as the added viscosity at lower values of Casson fluid parameter causes stronger friction. In the highly non-Newtonian cases (Fig. 10a, b), there is also an irreversible region around the microchannel centreline. This is due to the larger velocity of the viscous flow in this region. The same trend is observed in Fig. 10b, d, f showing the entropy generation in the porous medium. The high level of frictional irreversibility in the vicinity of the top wall of the microchannel, where shear forces are strong, is very noticeable in all subfigures of Fig. 10. Nonetheless, the general behaviour of entropy generation in the porous medium is quite complex. This is because of the influences of Casson fluid parameter upon the Nusselt number (shown in Fig. 7a), which affect both thermal and mass transfer irreversibilities.

Fig. 10

Contours of dimensionless local entropy generation with varying values for Casson fluid parameter, β—a, c, eN_FF with β values of 0.1, 1 and 1000, respectively. b, d, fN_pm with β values of 0.1, 1 and 1000, respectively

Figure 11 shows the distribution of the local entropy generation caused by the magnetic field (defined in Eq. 29b). Intensifying the magnetic field results in the appearance of an irreversibility particularly around the centreline of the microchannel. As shown in Eq. (29b), this mechanism of entropy generation is inversely proportional to the fluid temperature. Increases in the rate of heat transfer by intensifying the magnetic field leads to the reduction of the fluid temperature, which then increases the magnetic irreversibility. Intensification of entropy generation in the porous medium around the centreline region is also depicted in Fig. 11b, d, f. Importantly, a comparison of these figures by their counterparts in Fig. 10 shows that the influences of magnetic field on entropy generation in the porous medium is smaller than that of the Casson fluid parameter. Figure 12 depicts the influences of thermal radiation on entropy generation. According to this figure, intensification of thermal radiation strongly reduces the thermal irreversibility and consequently decreases the entropy generation in the porous medium. Increasing the radiation parameter from 0 to 2 leads to a drop in thermal irreversibility by an order of magnitude. This can be readily explained by noting that increasing the capability of the porous medium to lose heat through radiation decreases the temperature gradients and therefore reduces the thermal irreversibility of the system.

Fig. 11

Contours of dimensionless local entropy generation with varying values of magnetic field intensity, M_d—a, c, eN_mg with M_d values of 0, 25 and 50, respectively. b, d, fN_pm with M_d values of 0, 25 and 50, respectively

Fig. 12

Contours of dimensionless local entropy generation with varying values of radiation parameter R_d—a, c, e contours of local entropy for N_th (fluid phase and solid phase entropy generation) with R_d values of 0, 1 and 2, respectively. b, d, f Contours of local entropy generation for N_pm with R_d values of 0, 1 and 2, respectively

The total irreversibility of the microreactor is investigated in Fig. 13. Evidently, the wall thickness has a pronounced effect on the increase in entropy generation in the microchannel. Figure 13a shows that at low Biot numbers, reducing the wall thickness (increasing Y₁) continues to reduce the total irreversibility for the entire investigated range. However, at higher values of Biot number the decrease in total entropy generation is limited to very thick walls and reaches a plateau at certain wall thicknesses. As shown by Fig. 7b, higher values of Biot number result in larger Nusselt numbers and therefore in reduction in the temperature gradients and thermal irreversibilities. This trend is clearly reflected by Fig. 13a. Figure 13b shows that increasing the thermal conductivity ratio can magnify the total irreversibility of the system. This effect is almost negligible in the limits of thin and very thick walls but becomes considerable for moderate wall thicknesses.

Fig. 13

Total entropy generation with varying parameters—a varying Biot number, b varying thermal conductivity ratio, c varying magnetic field intensity, d varying Soret number

The strong dependency of the rate of heat transfer in porous channels on the value of thermal conductivity ratio is already well demonstrated in the literature [56, 58]. Modification of Nusselt number can readily change the temperature gradients and alter the thermal and mass transfer irreversibilities. As depicted by Fig. 13c, increases in the intensity of the magnetic field increases the total entropy generation within the system. The augmentation is particularly considerable for the case of thin-wall microchannels. As discussed earlier, this is due to the intensification of magnetic irreversibilities by the drop of fluid temperature, which is itself because of thinner walls and slightly larger Nusselt numbers at higher magnetic intensities. Soret number as the representative of thermal diffusion of mass is responsible for a strong entropy generation in the current double-diffusive problem. Figure 13d shows that increase in Soret number can significantly increase the total irreversibility of the microreactor. The dependency of total irreversibility upon Soret number is particularly strong in thick-wall microchannels and mostly disappears in the thin-wall limit, due to the thermal effects of the walls on the fluid phase. For a thick-wall microchannel, the rate of heat transfer is relatively low and thus fluid temperature gradients are strong and consequently the Soret effect is pronounced. As the walls’ thickness declines, the temperature gradients become weaker and the Sort effect and its associated irreversibility decrease.

Conclusions

The main objective of this work was to gain physical understanding of the fundamental processes dominating transport and thermodynamics of magnetic, biofuel microreformers. Casson rheological fluid was used to represent non-Newtonian characteristics of the biofuels. An analytical investigation was conducted on the combined transport of heat and mass in a porous microreactor with a flow of Casson fluid and the influences of an incident magnetic field. It was assumed that the fluid flow inside the microreactor hosts a homogenous chemical reaction with uniformly distributed positive or negative heat of reaction. Further, the concentration and thermal fields were assumed to be coupled through thermal diffusion of mass (Soret effect). The analysis considered the local thermal non-equilibrium and thermal radiation in the porous medium as well as the transversal conduction of heat in the microchannel walls with variable thickness. Two-dimensional, analytical solutions were developed for the temperature and concentration fields and, Nusselt number and entropy generations were also expressed analytically. It was shown that the developed analytical solutions can be systematically reduced to those developed by other authors for simpler configurations [53]. The analysis included a parametric study of transport and thermodynamic irreversibilities in the microreactor. It is emphasised that the closed-form solutions provided in this work allow for isolation of different pieces of physics in the problem. Non-Newtonian fluid, MHD, heat of reactions and porous media effects can be readily added to or removed from the solutions by varying the values of pertinent parameter with no need for resolving. This is an essential and unique feature of the current analytical work which distinguishes it from any numerical solution.

The key physical findings of this work can be summarised as follows.

• In the limit of thin walls, increasing the values of Casson fluid parameter, intensifying the magnetic field and increasing its angle of incidence were shown to increase the Nusselt number considerably. Yet, these effects are almost entirely suppressed as the walls of the microchannel become thicker.

• Changes in the rheological properties of the fluid and modifications in the characteristics of the magnetic field and thermal radiation could lead to the bifurcation of temperature gradient on the contact surface between the walls and the porous insert. Internal heat generations were found to be crucial in determining the general behaviour of this bifurcation.

• If the walls of microchannel are relatively thin, intensification of the magnetic field could noticeably increase the total entropy generation inside the system.

• For thick-wall microchannels, Soret effect is a very strong mechanism of entropy generation. However, the relative importance of Soret effect in the total irreversibility decreases sharply as the walls become thinner.

In closing, it is noted that the presented analytical approach offers two main advantages over an equivalent numerical solution. Firstly, it highly facilitates conduction of parametric studies without the burden of rerunning the computational code. Secondly, and perhaps most importantly, it provides a solid basis for the validation of numerical tools.

Appendices

Appendix 1: Closed-form constants

$$D_{1} = \frac{{SY_{1} }}{{SY_{1} \cosh \left( {SY_{1} } \right) - \sinh \left( {SY_{1} } \right)}}, \quad D_{2} = \frac{{D_{1}^{2} BrM_{\text{d}} }}{2M}\sin^{4} \left( \gamma \right)$$

(32a,b)

$$D_{3} = \frac{{D_{1}^{3} BrM_{\text{d}} }}{{Y_{1} M}}\sin^{4} \left( \gamma \right)\left[ {Y_{1} \cosh^{2} \left( {SY_{1} } \right) + \frac{{SY_{1} - 3\cosh \left( {SY_{1} } \right)\sinh \left( {SY_{1} } \right)}}{2S}} \right] + D_{1} \left( {\frac{1}{{Y_{1} }} + \omega_{\text{f}} } \right) - \frac{{2D_{1}^{2} BrM_{\text{d}} }}{M}\sin^{4} \left( \gamma \right)\cosh \left( {SY_{1} } \right)$$

(32c)

$$D_{4} = \frac{{D_{1}^{2} BrM_{\text{d}} }}{M}\sin^{4} \left( \gamma \right)\left[ {\frac{1}{2} + \cosh^{2} \left( {SY_{1} } \right)} \right] - D_{1} \left( {\frac{1}{{Y_{1} }} + \omega_{\text{f}} } \right)\cosh \left( {SY_{1} } \right) + \omega_{\text{f}} - \frac{{D_{1}^{3} BrM_{\text{d}} }}{{Y_{1} M}}\sin^{4} \left( \gamma \right)\left[ {Y_{1} \cosh^{2} \left( {SY_{1} } \right) + \frac{{SY_{1} - 3\cosh \left( {SY_{1} } \right)\sinh \left( {SY_{1} } \right)}}{2S}} \right]\cosh \left( {SY_{1} } \right)$$

(32d)

$$Q_{1} = \frac{{Bi\left( {1 + k + Rd} \right)}}{{k\left( {1 + Rd} \right)}}, \quad Q_{2} = \frac{{4S^{2} \left( {1 + Rd} \right) - Bi}}{{k\left( {1 + Rd} \right)}}D_{2} , \quad Q_{3} = \frac{{S^{2} \left( {1 + Rd} \right) - Bi}}{{k\left( {1 + Rd} \right)}}D_{3}$$

(33a,b,c)

$$Q_{4} = \frac{{BiD_{4} }}{{k\left( {1 + Rd} \right)}}, \quad Q_{5} = \frac{{BiD_{2} }}{{k\left( {1 + Rd} \right)}}, \quad Q_{6} = \frac{{BiD_{3} }}{{k\left( {1 + Rd} \right)}}$$

(33d,e,f)

$$E_{1} = - \frac{{Y_{1} }}{{k_{\text{e1}} }}, \quad E_{2} = \frac{1}{{k_{\text{e1}} }}$$

(34a,b)

$$E_{3} = - \frac{{Q_{2} }}{{16S_{4} - 4Q_{1} S^{2} }}, \quad E_{4} = - \frac{{Q_{3} }}{{S^{4} - Q_{1} S^{2} }}$$

(34c,d)

$$E_{5} = - \frac{{\left[ {\left( {D_{2} + 4S^{2} E_{3} k} \right)\cosh \left( {2SY_{1} } \right) + \left( {D_{3} + S^{2} E_{4} k} \right)\cosh \left( {SY_{1} } \right) + \left( {D_{4} + 2E_{6} k} \right)} \right]\text{sech} \left( {\alpha Y_{1} } \right)}}{{k\alpha^{2} }}$$

(34e)

$$E_{6} = - \frac{{Q_{4} }}{{2Q_{1} }}, \quad E_{7} = 0$$

(34f,g)

$$E_{8} = - \left[ {E_{3} \cosh \left( {2SY_{1} } \right) + E_{4} \cosh \left( {SY_{1} } \right) + E_{5} \cosh \left( {\alpha Y_{1} } \right) + E_{6} Y_{1}^{2} + E_{7} Y_{1} } \right]$$

(34h)

$$E_{9} = \frac{{Q_{5} }}{{16S^{4} - 4Q_{1} S^{2} }},\quad E_{10} = \frac{{Q_{6} }}{{S^{4} - Q_{1} S^{2} }}$$

(34i,j)

$$E_{11} = - \frac{{\left[ {\left( {4S^{2} E_{9} } \right)\cosh \left( {2SY_{1} } \right) + \left( {S^{2} E_{10} } \right)\cosh \left( {SY_{1} } \right) + 2E_{6} } \right]\text{sech} \left( {\alpha Y_{1} } \right)}}{{\alpha^{2} }}$$

(34k)

$$E_{12} = - \left[ {E_{9} \cosh \left( {2SY_{1} } \right) + E_{10} \cosh \left( {SY_{1} } \right) + E_{11} \cosh \left( {\alpha Y_{1} } \right) + E_{6} Y_{1}^{2} + E_{7} Y_{1} } \right]$$

(34l)

$$F_{1} = \frac{Srk}{{\varepsilon Y_{1} }}E_{3} , \quad F_{2} = \frac{Srk}{{\varepsilon Y_{1} }}E_{4} - \frac{{D_{1} Dn}}{{Y_{1}^{2} S^{2} }}$$

(35a,b)

$$F_{3} = \frac{Srk}{{\varepsilon Y_{1} }}E_{5} , \quad F_{4} = \frac{Srk}{{\varepsilon Y_{1} }}E_{6} + \frac{Dn}{{Y_{1}^{2} }}\left( {\frac{{D_{1} }}{2}\cosh \left( {SY_{1} } \right) - \frac{1}{2}} \right)$$

(35c,d)

$$\begin{aligned} & F_{5} = \frac{Srk}{{\varepsilon Y_{1} }}E_{8} + 1 - \left[ {D_{1} \left( {\frac{{Y_{1}^{2} }}{2}\cosh \left( {SY_{1} } \right) - \frac{{\cosh \left( {SY_{1} } \right)}}{{S^{2} }}} \right) - \frac{{Y_{1}^{2} }}{2}} \right]\frac{Dn}{{Y_{1}^{2} }} - \frac{Srk}{{\varepsilon Y_{1} }}\theta_{\text{f}} \left( {Y_{1} } \right), \\ & {\text{where}}\;\;\theta_{\text{f}} \left( {Y_{1} } \right) = E_{3} \cosh \left( {2SY_{1} } \right) + E_{4} \cosh \left( {SY_{1} } \right) + E_{5} \cosh \left( {\alpha Y_{1} } \right) + E_{6} Y_{1}^{2} + E_{7} Y_{1} + E_{8} \\ \end{aligned}$$

(35e)

Appendix 2: Validation

The mathematical model presented in this paper was validated by reducing to the analytical work of Ting et al. [53] and Hunt et al. [31]. As the magnetic parameter, angle of incidence and the volumetric source term approach zero and the Casson fluid parameter tends to infinity, the model can be compared to those in Refs. [31, 53] without viscous dissipation. Thus, all Casson fluid terms are either set to 0 or infinity, and the volumetric source term is also eliminated. This reduces heat transfer equations to that shown below.

$$\theta_{\text{nf}}^{\prime\prime\prime\prime} - Q_{1}^{\prime} \theta_{\text{nf}}^{\prime\prime} + Q_{3}^{\prime} \cosh \left( {SY} \right) - Q_{4}^{\prime} = 0$$

(36a)

$$\theta_{\text{s}}^{\prime\prime\prime\prime} - Q_{1}^{\prime} \theta_{\text{s}}^{\prime\prime} - \left[ {Q_{6}^{\prime} \cosh \left( {SY} \right) + Q_{4}^{\prime} } \right] = 0$$

(36b)

$$\theta_{\text{nf}} \left( Y \right) = E_{4}^{\prime} \cosh \left( {SY} \right) + E_{5}^{\prime} \cosh \left( {\alpha Y} \right) + E_{6}^{\prime} Y^{2} + E_{7}^{\prime} Y + E_{8}^{\prime} \quad 0 \le Y < Y1$$

(37a)

$$\theta_{\text{s}} \left( Y \right) = E_{10}^{\prime} \cosh \left( {SY} \right) + E_{11}^{\prime} \cosh \left( {\alpha Y} \right) + E_{6}^{\prime} Y^{2} + E_{7}^{\prime} Y + E_{12}^{\prime} \quad 0 \le Y < Y1$$

(37b)

$$\alpha^{\prime} = \sqrt {Q_{1}^{\prime} }$$

(37c)

$$\frac{{{\text{d}}\overline{\theta }_{\text{nf}} }}{{{\text{d}}X}} = \varOmega^{\prime} = \frac{2}{{k\xi Y_{1} PrRe}}$$

(38)

$$\theta_{\text{nf}} \left( {X,Y} \right) = E_{4}^{\prime} \cosh \left( {SY} \right) + E_{5}^{\prime} \cosh \left( {\alpha Y} \right) + E_{6}^{\prime} Y^{2} + E_{7}^{\prime} Y + E_{8}^{\prime} + \varOmega X\quad 0 \le Y < Y1$$

(39a)

$$\theta_{\text{s}} \left( {X,Y} \right) = E_{10}^{\prime} \cosh \left( {SY} \right) + E_{11}^{\prime} \cosh \left( {\alpha Y} \right) + E_{6}^{\prime} Y^{2} + E_{7}^{\prime} Y + E_{12}^{\prime} + \varOmega^{\prime}X\quad 0 \le Y < Y1$$

(39b)

The concentration equation becomes:

$$\varPhi \left( {X,Y} \right) = F_{2}^{\prime} \cosh \left( {SY} \right) + F_{3}^{\prime} \cosh \left( {\alpha Y} \right) + F_{4}^{\prime} Y^{2} + F_{5}^{\prime} + \frac{DnX}{{PeY_{1} \xi }}$$

(40)

where the constants, Q′, E′ and F′ are defined by:

$$D_{1}^{\prime} = \frac{{SY_{1} }}{{SY_{1} \cosh \left( {SY_{1} } \right) - \sinh \left( {SY_{1} } \right)}}, \quad D_{2}^{\prime} = 0$$

(41a,b)

$$D_{3}^{\prime} = \frac{{D_{1}^{\prime} }}{{Y_{1} }},\quad D_{4}^{\prime} = - \frac{{D_{1}^{\prime} }}{{Y_{1} }}\cosh \left( {SY_{1} } \right)$$

(41c,d)

$$Q_{1}^{\prime} = \frac{{Bi\left( {1 + k + Rd} \right)}}{{k\left( {1 + Rd} \right)}}, \quad Q_{2}^{\prime} = 0, \quad Q_{3}^{\prime} = \frac{{S^{2} \left( {1 + Rd} \right) - Bi}}{{k\left( {1 + Rd} \right)}}D_{3}^{\prime}$$

(42a,b,c)

$$Q_{4}^{\prime} = \frac{{BiD_{4}^{\prime} }}{{k\left( {1 + Rd} \right)}}, \quad Q_{5}^{\prime} = 0, \quad Q_{6}^{\prime} = \frac{{BiD_{3}^{\prime} }}{{k\left( {1 + Rd} \right)}}$$

(42d,e,f)

$$E_{4} = - \frac{{Q_{3}^{\prime} }}{{S^{4} - Q_{1}^{\prime} S^{2} }},\quad E_{5} = - \frac{{\left[ {\left( {D_{3}^{\prime} + S^{2} E_{4}^{\prime} k} \right)\cosh \left( {SY_{1} } \right) + \left( {D_{4}^{\prime} + 2E_{6}^{\prime} k} \right)} \right]\text{sech} \left( {\alpha^{\prime}Y_{1} } \right)}}{{k\alpha^{\prime 2} }}$$

(43a,b)

$$E_{6} = - \frac{{Q_{4}^{\prime} }}{{2Q_{1}^{\prime} }}, \quad E_{7} = 0$$

(43c,d)

$$E_{8} = - \left[ {E_{4}^{\prime} \cosh \left( {SY_{1} } \right) + E_{5}^{\prime} \cosh \left( {\alpha^{\prime}Y_{1} } \right) + E_{6}^{\prime} Y_{1}^{2} + E_{7}^{\prime} Y_{1} } \right]$$

(43e)

$$E_{10} = \frac{{Q_{6}^{\prime} }}{{S^{4} - Q_{1}^{\prime} S^{2} }}, \quad E_{11} = - \frac{{\left[ {\left( {S^{2} E_{10}^{\prime} } \right)\cosh \left( {SY_{1} } \right) + 2E_{6}^{\prime} } \right]\text{sech} \left( {\alpha^{\prime}Y_{1} } \right)}}{{\alpha^{\prime 2} }}$$

(43f,g)

$$E_{12} = - \left[ {E_{10}^{\prime} \cosh \left( {SY_{1} } \right) + E_{11}^{\prime} \cosh \left( {\alpha^{\prime}Y_{1} } \right) + E_{6}^{\prime} Y_{1}^{2} + E_{7}^{\prime} Y_{1} } \right]$$

(43h)

$$F_{2}^{\prime} = \frac{Srk}{{\varepsilon Y_{1} }}E_{4}^{\prime} - \frac{{D_{1}^{\prime} Dn}}{{Y_{1}^{2} S^{2} }}, \quad F_{3}^{\prime} = \frac{Srk}{{\varepsilon Y_{1} }}E_{5}^{\prime}$$

(44a,b)

$$F_{4}^{\prime} = \frac{Srk}{{\varepsilon Y_{1} }}E_{6}^{\prime} - \frac{{D_{1}^{\prime} Dn}}{{2Y_{1}^{2} }}\cosh \left( {SY_{1} } \right)$$

(44c)

$$\begin{aligned} & F_{5}^{\prime} = \frac{Srk}{{\varepsilon Y_{1} }}E_{8}^{\prime} + 1 - \left( {\frac{{Y_{1}^{2} }}{2}\cosh \left( {SY_{1} } \right) - \frac{{\cosh \left( {SY_{1} } \right)}}{{S^{2} }}} \right)\frac{{D_{1}^{\prime} Dn}}{{Y_{1}^{2} }} - \frac{Srk}{{\varepsilon Y_{1} }}\theta_{\text{nf}} \left( {Y_{1} } \right), \\ & {\text{where}}\;\; \theta_{\text{f}} \left( {Y_{1} } \right) = E_{4}^{\prime} \cosh \left( {SY_{1} } \right) + E_{5}^{\prime} \cosh \left( {\alpha Y_{1} } \right) + E_{6}^{\prime} Y_{1}^{2} + E_{7}^{\prime} Y_{1} + E_{8}^{\prime} \\ \end{aligned}$$

(44d)

The above coefficients indicate that Eqs. (39a), (39b), and Eq. (40) are identical to the nanofluid and porous solid equations in Ting et al. [53] and Hunt et al. [31] with setting the wall thickness and the heat generation by viscous dissipation to 0.