A comparative study and analysis of natural convection flow of MHD non-Newtonian fluid in the presence of heat source and first-order chemical reaction

Abstract

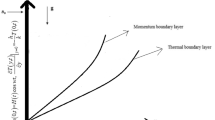
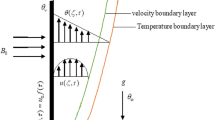
Heat and mass transfer of fractional Jeffrey’s flow over infinite vertical plate moving exponentially with variable temperature and mass diffusion has been detailed. Additionally, first-order chemical reaction, magnetohydrodynamics and rate of heat absorption are also considered. The classical Jeffrey’s fluid model is generalized to a fractional model of non-integer-order ‘α.’ The present problem is solved by two approaches, namely, Caputo and Caputo–Fabrizio. The exact solutions for temperatures, concentrations and velocities have been obtained via Laplace transform method. The corresponding rates of heat, mass and skin friction are also computed. We have drawn a comparison approach between the solutions of two fractional models of Jeffrey’s fluid modeled with Caputo and Caputo–Fabrizio fractional derivatives by means of graphical illustration using MathCad software. Physical impact of fractional parameter ‘α’ on the Sherwood number, Nusselt number and skin friction was presented in a table and found that they are increased by increasing the value of ‘α.’ In comparison, the rates of heat and mass transfer and skin friction of Caputo fractional derivative have greater values than Caputo-Fabrizio.

Appendix

$$L^{ - 1} \left\{ {\frac{1}{q}\exp \left( { - y\sqrt {\frac{q + b}{q + c}} } \right)} \right\} = e^{{ - {\text{at}} - {\text{y}}}} - \frac{{y\sqrt {b - c} }}{2\sqrt \pi }\int\limits_{0}^{\infty } {\int\limits_{0}^{\text{t}} {\frac{{e^{{ - {\text{at}}}} }}{\sqrt t }\exp \left( {at - ct - \frac{{y^{2} }}{4u} - u} \right)} } \times I_{1} \left( {2\sqrt {(b - c)ut} } \right){\text{d}}t{\text{d}}u$$

$$L^{ - 1} \left\{ {\frac{{e^{{ - {\text{aq}}^{\text{b}} }} }}{{q^{\text{c}} }}} \right\} = t^{{{\text{c}} - 1}} \varPhi \left( {c, - b, - at^{{ - {\text{b}}}} } \right)$$

$$L^{ - 1} \left\{ {\frac{{e^{{{\text{a}} - {\text{b}}}} }}{{q^{\text{a}} + c}}} \right\} = t^{{{\text{b}} - 1}} E_{{{\text{a}},{\text{b}}}} \left( { - ct^{\text{a}} } \right)$$

$${\text{If}}\,F(t) = L^{ - } \left\{ {F(q)} \right\} \,{\text{and}}\,g(u,t) = L^{ - 1} \left\{ {e^{{ - {\text{uw}}({\text{q}})}} } \right\}\, {\text{then}}\,L^{ - 1} \left\{ {F[w(q)]} \right\} = \int\limits_{0}^{\infty } {f(u)g(u,t){\text{d}}u}$$

$$\begin{aligned} & \phi_{{1{\text{C}}}} (y,\,t) = L^{ - 1} \left[ {\frac{{q^{\alpha } - \eta_{1} }}{{q^{2} }}} \right] = L^{ - 1} \left[ {\frac{1}{{q^{\alpha - 2} }} - \frac{{\eta_{1} }}{{q^{2} }}} \right] = \frac{{t^{1 - \alpha } }}{\varGamma (2 - \alpha )} - \eta_{1} t, \\ & \phi_{{2{\text{C}}}} = L^{ - 1} \left[ {\frac{1}{{q^{\alpha } - \eta_{1} }}\exp \left( { - y\sqrt {Pr(q^{\alpha } - \eta_{1} )} } \right)} \right] = \int\limits_{0}^{\infty } {{\text{erf}}c\left( {\frac{{y\sqrt {Pr} }}{2\sqrt u }} \right) \cdot e^{{{\text{u}}\eta_{{_{1} }} }} \cdot \frac{1}{t}\psi \left( {0, - \alpha ; - ut^{ - \alpha } } \right)} , \\ \end{aligned}$$

$$\begin{aligned} & \varphi_{{1{\text{C}}}} (y,\,t) = L^{ - 1} \left[ {\frac{{q^{\alpha } + \eta_{2} }}{{q^{2} }}} \right] = L^{ - 1} \left[ {\frac{1}{{q^{\alpha - 2} }} + \frac{{\eta_{2} }}{{q^{2} }}} \right] = \frac{{t^{1 - \alpha } }}{\varGamma (2 - \alpha )} + \eta_{2} t, \\ & \varphi_{{2{\text{C}}}} (y,t) = L^{ - 1} \left[ {\frac{1}{{q^{\alpha } + \eta_{2} }}\exp \left( { - y\sqrt {Sc(q^{\alpha } + \eta_{2} )} } \right)} \right] = \int\limits_{0}^{\infty } {{\text{erfc}}\left( {\frac{{y\sqrt {Sc} }}{2\sqrt u }} \right) \cdot e^{{ - {\text{u}}\eta_{{_{2} }} }} \cdot \frac{1}{t}\psi \left( {0, - \alpha ; - ut^{ - \alpha } } \right)} , \\ \end{aligned}$$