Skip to main content
SpringerLink
Log in

Deterministic Coloring of a Family of Complexes

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

Abstract

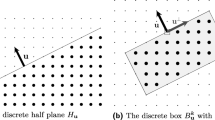
In the famous works “Tilings, substitution systems and dynamical systems generated by them” by S. Mozes and “Matching rules and substitution tilings” by Ch. Goodman-Strauss, important properties of tiling on the plane connecting the language of substitution systems and local rules are investigated. In particular, it is proved that with almost any substitution system of tiles, it is possible to link a system of decorations and local rules to the boundaries of tiles in such a way that any tiling of the plane allowed by the rules will belong to the family generated by this substitution system.

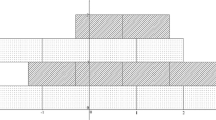
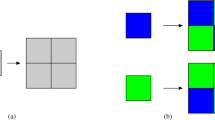
Geometric constructions based on tiling and geometric complexes of glued squares open up new opportunities for the study and construction of algebraic objects. An important property of tiling that allows them to be associated with algebraic objects is determinicity. For square tiles whose sides are painted in a finite number of colors, this property means that the colors of the two adjacent sides of each tile uniquely determine the colors of the other pair of sides. J. Kari and P. Papasoglu constructed a deterministic aperiodic set. Thus, the analogue of the theorems of Goodman-Strauss and Mozes with an additional determinicity condition is an important statement in the theory of aperiodic mosaics. We prove an analog of this statement for a specific fixed substitution system. But its arbitrariness allows us to hope for the possibility of improving the construction for the general case.

This system is important when constructing an infinite finitely presented nilsemigroup, which solves the problem of L. N. Shevrin and M. V. Sapir. The work is also devoted to the construction of a family of geometric complexes and the introduction of coding of vertices and edges on them. For the resulting complex, both properties are fulfilled simultaneously: finiteness of the set of defining local rules and determinicity on paths of length 2 on minimal squares.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. Berger, The Undecidability of the Domino Problem, Ph.D. Thesis, Harvard University (1964).

  2. J. Conway and J. Lagarias, “Tiling with polyminoes and combinatorial group theory,” J. Combin. Theory, Ser. A, 53, No. 2, 183–208 (1990).

  3. B. Durand, L. Levin, and A. Shen, “Local rules and global order, or aperiodic tilings,” Math. Intelligencer, 27, 64–68 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  4. Ch. Goodman-Strauss, “Matching rules and substitution tilings,” Ann. Math. (2), 147, No. 1, 181–223 (1998).

  5. M. Gromov, “Hyperbolic Groups,” in: Essays in Group Theory, S. M. Gersten, ed., MSRI Publ., Vol. 8, Springer (1987), pp. 75–263.

  6. I. A. Ivanov-Pogodaev and A. Ya. Kanel-Belov, “Finitely presented nilsemigroups: complexes with the property of uniform ellipticity,” Izv. Math., 85, No. 6, 1146–1180 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  7. I. Ivanov-Pogodaev, S. Malev, and O. Sapir, “A construction of a finitely presented semigroup containing an infinite squarefree ideal with zero multiplication,” Int. J. Algebra Comput., 28, No. 8, 1565–1573 (2018).

    Article  MATH  Google Scholar 

  8. J. Kari and P. Papasoglu, “Deterministic aperiodic tile sets,” Geom. Funct. Anal., 9, 353–369 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  9. Sh. Mozes, “Tilings, substitution systems, and dynamical systems generated by them,” J. Anal. Math., 53, No. 1, 139–186 (1989).

    Article  MathSciNet  MATH  Google Scholar 

  10. R. M. Robinson, “Undecidability and nonperiodicity for tilings of the plane,” Invent. Math., 12, 177–209 (1971).

    Article  MathSciNet  MATH  Google Scholar 

  11. Wang Hao, “Proving theorems by pattern recognition. II,” Bell System Tech. J., 40, No. 1, 1–41 (1961).

    Article  Google Scholar 

  12. D. Wise, Non-Positively Curved Squared Complexes, Aperiodic Tilings, and Non-Residually Finite Groups, Ph.D. Thesis, Princeton University (1996).

  13. D. Wise, “Cubulating small cancellation groups,” Geom. Funct. Anal., 14, 150–214 (2004).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Moscow Institute of Physics and Technology, Moscow, Russia

    I. A. Ivanov-Pogodaev

  2. Bar-Ilan University, 52900, Ramat Gan, Israel

    A. Ya. Kanel-Belov

  3. Lomonosov Moscow State University, Moscow, Russia

    A. Ya. Kanel-Belov

Authors
  1. I. A. Ivanov-Pogodaev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Ya. Kanel-Belov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. A. Ivanov-Pogodaev.

Additional information

Translated from Fundamentalnaya i Prikladnaya Matematika, Vol. 24, No. 2, pp. 37–180, 2022.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ivanov-Pogodaev, I.A., Kanel-Belov, A.Y. Deterministic Coloring of a Family of Complexes. J Math Sci 275, 403–501 (2023). https://doi.org/10.1007/s10958-023-06691-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-023-06691-9

Search

Navigation