Skip to main content
SpringerLink
Log in

Methods for Control of Dynamical Systems with Delayed Feedback

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

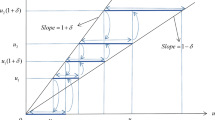
We study the stabilization of linear nonstationary dynamical systems by introducing a linear nonstationary feedback with delay. We obtain sufficient stabilization conditions for the systems and propose a method for constructing stabilizing matrices.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. R. A. Brockett, “A stabilization problem,” In: Open Problems in Mathematical Systems and Control Theory, pp. 75–78, Springer, London (1999).

  2. G. A. Leonov and M. M. Shumafov, Problems of Stabilization of Linear Controlled Systems, St. Petersbg. Univ. Press, St. Petersbg. (2002)

    Google Scholar 

  3. M. M. Shumafov, “Stabilization of linear control systems and pole assignment problem: a survey,” Vestn. St. Petersbg. Univ., Math. 52, No. 4, 349–367 (2019).

  4. I. V. Boykov, “The Brockett stabilization problem,” Autom. Remote Control 66, No. 5, 746–751 (2005).

    Article  MathSciNet  Google Scholar 

  5. G. A. Leonov and M. M. Shumafov, Stabilization Methods for Linear Controlled Systems, St. Petersbg. Univ. Press, St. Petersbg. (2005)

    MATH  Google Scholar 

  6. G. A. Leonov, “The Brockett problem for linear discrete control systems,” Autom. Remote Control 63, No. 5, 777–781 (2002).

    Article  MathSciNet  Google Scholar 

  7. I. V. Boykov, Stability of Solutions to Differential Equations [in Russian], Penza State Univ. Press, Penza (2008).

    Google Scholar 

  8. K. Pyragas, “Continuous control of chaos by selfcontrolling feedback,” Phys. Lett. A 170, 421–428 (1992).

    Article  Google Scholar 

  9. G. A. Leonov and M. M. Shumafov, “Pyragas stabilizability of unstable equilibria by nonstationary time-delayed feedback,” Autom. Remote Control 79, No. 6, 1029–1039 (2018).

    Article  MathSciNet  Google Scholar 

  10. G. A. Leonov, “Pyragas stabilizability via delayed feedback with periodic control gain,” Syst. Control Lett. 69, 34–37 (2014).

    Article  MathSciNet  Google Scholar 

  11. M. M. Shumafov, “Stabilization of the second-order linear time-invariant control systems by a delayed feedback,” Russ. Math. 54. No. 12, 76–78 (2010).

  12. V. Lakshmikantam, S. Lila, and A. A. Martynyuk, Stability of Motion: Comparison Method [in Russian], Naukova Dumka, Kiev (1991).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Penza State University, 40, Krasnaya St, Penza, 440026, Russia

    I. V. Boykov & N. P. Krivulin

Authors
  1. I. V. Boykov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. N. P. Krivulin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to I. V. Boykov.

Additional information

Translated from Problemy Matematicheskogo Analiza 109, 2021, pp. 27-37.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Boykov, I.V., Krivulin, N.P. Methods for Control of Dynamical Systems with Delayed Feedback. J Math Sci 255, 561–573 (2021). https://doi.org/10.1007/s10958-021-05393-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-021-05393-4

Search

Navigation