A Classical WR Model with $q$ Particle Types

Abstract

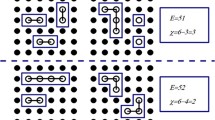
A version of the Widom–Rowlinson model is considered, where particles of $q$ types coexist, subject to pairwise hard-core exclusions. For $q\le 4$, in the case of large equal fugacities, we give a complete description of the pure phase picture based on the theory of dominant ground states.

Appendix: The Polymer Expansion Theorem

Consider a finite or countable set $\Theta$ the elements of which are called (abstract) contours and denoted $\theta ,\theta '$, ets. Fix some anti-reflexive and symmetric relation $\sim$ on $\Theta \times \Theta$ (with $\theta \not \sim \theta$ and $\theta \sim \theta '$ equivalent to $\theta '\sim \theta$). A pair $\theta ,\theta ' \in \Theta \times \Theta$ is called incompatible ($\theta \not \sim \theta '$) if it does not belong to the relation and compatible ($\theta \sim \theta '$) in the opposite case. (In our context, two contours are compatible when they are mutually external and have the same external type.) A collection $\{\theta _j\}$ is called a compatible collection of contours if any two its elements are compatible. Every contour $\theta$ is assigned a (generally speaking) complex-valued statistical weight denoted by $w(\theta )$, and for any finite $\Lambda \subseteq \Theta$ an (abstract) partition function is defined as

$$\begin{aligned} Z(\Lambda )=\sum \limits _{\{\theta _j\}\subseteq \Lambda } \prod _j w(\theta _j), \end{aligned}$$

(6.1)

where the sum is extended to all compatible collections of contours $\theta _i\in \Lambda$. The empty collection is compatible by definition, and it is included in $Z(\Lambda )$ with statistical weight $1$.

A polymer $\Pi =[[\theta _i^{\alpha _i}]]$ is an (unordered) finite collection of different contours $\theta _i \in \Theta$ taken with positive integer multiplicities $\alpha _i$, such that for every pair $\theta ',\ \theta '' \in \Pi$ there exists a sequence $\theta '=\theta _{i_1},\ \theta _{i_2},\ldots , \theta _{i_s}=\theta '' \in \Pi$ with $\theta _{i_j}\not \sim \theta _{i_{j+1}},\ j=1,2,\ldots ,s-1$. The notation $\Pi \subseteq \Lambda$ means that $\theta _i \in \Lambda$ for every $\theta _i \in \Pi$.

With every polymer $\Pi$ we associate an (abstract) graph $G(\Pi )$ which consists of $\sum \limits _i \alpha _i$ vertices labeled by the contours from $\Pi$ and edges joining every two vertices labeled by incompatible contours. As follows from the definition of $\Pi$, graph $G(\Pi )$ is connected. We denote by $r(\Pi )$ the quantity

$$\begin{aligned} r(\Pi )=\prod _i (\alpha _i!)^{-1} \sum \limits _{G' \subseteq G(\Pi )} (-1)^{\sharp \mathcal E(G')} \end{aligned}$$

(6.2)

(the Moebius-type inversion coefficient). Here the sum is taken over all connected subgraphs $G'$ of $G(\Pi )$ containing all $\sum \limits _i \alpha _i$ vertices, and $\sharp \mathcal E(G')$ denotes the number of edges in $G'$. For any $\theta \in \Pi$ we denote by $\alpha (\theta ,\Pi )$ the multiplicity of contour $\theta$ in polymer $\Pi$.

The Polymer expansion theorem (Theorem 6.1 below) is a modification of assertions from [9] (see also [22]) which has been established in [16].

Theorem 6.1

Suppose that there exists a function $a(\theta ):\ \Theta \mapsto {\mathbb R}^{+}$ such that for any contour $\theta$

$$\begin{aligned} \sum \limits _{\theta ':\ \theta '\not \sim \theta } |w(\theta ')| e^{a(\theta ')} \le a(\theta ). \end{aligned}$$

(6.3)

Then, for any finite $\Lambda$,

$$\begin{aligned} \log Z(\Lambda )=\sum \limits _{\Pi \subseteq \Lambda } w(\Pi ), \end{aligned}$$

(6.4)

where the statistical weight of a polymer $\Pi =[\theta _i^{\alpha _i}]$ equals

$$\begin{aligned} w(\Pi )=r(\Pi ) \prod _i w(\theta _i)^{\alpha _i}. \end{aligned}$$

(6.5)

Moreover, the series (6.4) for $\log Z(\Lambda )$ absolutely converges in view of the bound

$$\begin{aligned} \sum \limits _{\Pi :\ \Pi \ni \theta } \alpha (\theta ,\Pi ) |w(\Pi )| \le |w(\theta )| e^{a(\theta )}, \end{aligned}$$

(6.6)

which holds true for any contour $\theta$.