1 Introduction

In normal diffusion processes, the diffusivity can be characterized by the diffusion coefficient in the mean square displacement (MSD). However, many diffusion processes in nature show anomalous diffusion; that is, the MSD does not grow linearly with time but follows a sublinear or superlinear growth with time,

$$\begin{aligned} \langle x_t^2 \rangle \propto t^\beta \quad (\beta \ne 1), \end{aligned}$$
(1)

where \(x_t\) is a position in one-dimensional coordinate, \(t\) is time, and \(\langle \cdot \rangle \) means an ensemble average. In particular, anomalous diffusion in biological systems has been found by single-particle tracking experiments [13, 19, 20, 22, 40, 43, 44]. Thus, the power-law exponent \(\beta \) is one of the most important quantities characterizingthe underlying diffusion process. Especially, anomalous diffusion with \(\beta <1\) is called subdiffusion and that with \(\beta >1\) is called superdiffusion.

Although anomalous diffusion can be characterized by the power-law exponent \(\beta \) in the MSD, the exponent cannot reveal the underlying physical nature in itself. This is because the same power-law exponent in the MSD does not imply that the physical mechanism in the anomalous diffusion is also the same. Therefore, clarifying the origin of anomalous diffusion is an important subject, and many researches on this issue have been conducted extensively [23, 29, 30, 32, 41]. One of the key properties characterizing anomalous diffusion is ergodicity, i.e., time-averaged observables being equal to a constant (the ensemble average). In some experiments [19, 20, 22, 40, 44], (generalized) diffusion coefficients for time-averaged MSDs show large fluctuations, suggesting that ergodicity breaks.

In stochastic models of anomalous diffusion, continuous-time random walk (CTRW) shows a prominent feature called distributional ergodicity [21, 27, 33, 34]; that is, the time-averaged observables obtained from single trajectories do not converge to a constant but the distribution of such time-averaged observables converges to a universal distribution (convergence in distribution). More precisely, the distribution of the time-averaged MSD (TAMSD), which is defined by

$$\begin{aligned} \overline{\delta ^2 (\Delta ; t)} \equiv \frac{1}{t-\Delta } \int _0^{t-\Delta } (x_{t'+\Delta }-x_{t'})^2 dt', \end{aligned}$$
(2)

converges to the Mittag-Leffler distribution of order \(\alpha \) [5, 21]. This statement can be represented by

$$\begin{aligned} \frac{\overline{\delta ^2 (\Delta ; t)}}{\langle \overline{\delta ^2 (\Delta ; t)}\rangle } \Rightarrow M_\alpha \quad \mathrm{as}~t\rightarrow \infty , \end{aligned}$$
(3)

for a fixed \(\Delta \) (\(\ll t\)), where \(M_\alpha \) is a random variable with the Mittag-Leffler distribution of order \(\alpha \). We note that the diffusion coefficients in the TAMSDs are also distributed according to the Mittag-Leffler distribution because the TAMSD shows normal diffusion, i.e, \(\overline{\delta ^2 (\Delta ; t)} \simeq D_t \Delta \) [33, 34], where we refer to \(D_t\) as the diffusion coefficient. In stochastic models, such distributional behavior originates from the divergent mean trapping time. In diffusion in a random energy landscape such as a trap model [11], the trapping-time distribution follows a power law, \(w(\tau ) \propto \tau ^{-1-\alpha }\), if heights of the energy barrier are distributed according to the exponential distribution. The exponent \(\alpha \) smaller than 1 implies a divergence of the mean. In dynamical systems, this divergent mean brings an infinite measure [4]. Thus, such distributional behavior of time-averaged observables is also shown in infinite ergodic theory [1, 5]. Moreover, large fluctuations of time-averaged observables, related to distributional ergodicity, have been observed in biological experiments [19, 20, 22, 40, 44] as well as quantum dot experiments [12, 39].

Recently, we have shown that the distribution of the diffusion coefficients of the TAMSDs in the stored-energy-driven Lévy flight (SEDLF) is different from that in CTRW [6]. The SEDLF is a CTRW with jump lengths correlated with trapping times [24, 26, 28]. One of the most typical examples for such a correlated motion can be observed in Lévy walk [38]. However, Lévy walk and SEDLF are completely different stochastic processes in that a random walker cannot move while it is trapped in SEDLF, whereas it can move with constant velocity in Lévy walk. In other words, in SEDLF, a random walker does not move while storing a sort of energy, and it jumps using the stored energy (see Fig. 1). When the trapping-time distribution follows a power-law, the jump length distribution also follows a power-law, the same as in Lévy flight. Since we consider a power-law trapping-time distribution, we refer to our model as the stored-energy-driven Lévy flight. We note that the MSD does not diverge in SEDLF, whereas it always diverges in Lévy flight. Although the ensemble-averaged MSDs show subdiffusion as well as superdiffusion, the TAMSDs always increase linearly with time in SEDLF [6]. This behavior is completely different from that in Lévy walk [2, 17]. Moreover, the distribution of the TAMSD with a fixed \(\Delta \) converge to a time-independent distribution which is not the same as a universal distribution in CTRW (Mittag-Leffler distribution):

$$\begin{aligned} \frac{\overline{\delta ^2 (\Delta ; t)}}{\langle \overline{\delta ^2 (\Delta ; t)}\rangle } \Rightarrow Y_{\alpha ,\gamma } \quad \mathrm{as}~t\rightarrow \infty , \end{aligned}$$
(4)

where \(Y_{\alpha ,\gamma }\) is a random variable and \(\gamma \) is the coupling parameter between trapping time and jump length. We note that such coupling effects become physically important in turbulent diffusion [38], diffusion of cold atoms [10], and nonthermal systems such as cells [13, 43]. In such enhanced diffusions, it has been known that the coupling between jump lengths and waiting times follows a power-law fashion like SEDLF [10, 38], although a particle is always moving, which is different from SEDLF. Furthermore, it will also be important in complex systems such as finance [31] and earthquakes [14, 25] because jump lengths are correlated with the waiting times in such systems.

Fig. 1
figure 1

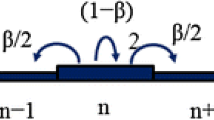
Trajectory of SEDLF in an equilibrium renewal process. A measurement starts at \(t=0\) while the process starts at \(-t_a\). An equilibrium process means a process with \(t_a \rightarrow \infty \) if there exist an equilibrium distribution for the first apparent trapping time and the second moment of the first jump length

Full size image

In terms of an ensemble average, SEDLF exhibits a whole spectrum of diffusion: sub-, normal-, and super-diffusion, depending on the coupling parameter [6, 24, 26, 28].Because distributional behavior of the time-averaged observables such as the diffusion coefficients in SEDLF is different from that in CTRW, it is important to construct a phase diagram in terms of the power-law exponent of the MSD as well as the form of the distribution function of the TAMSD. Here, we provide the phase diagram for the whole parameters range in SEDLF.

2 Model

SEDLF is a cumulative process, which is a generalization of a renewal process [15]. Equivalently, SEDLF is a CTRW with a non-separable joint probability of trapping time and jump length. Therefore, the SEDLF can be defined through the joint probability density function (PDF) \(\psi (x, t)\), where \(\psi (x, t)dx dt\) is the probability that a random walker jumps with length \([x, x+dx)\) just after it is trapped for period \([t, t+dt)\) since its previous jump [11, 37]. Here, we consider the following joint PDF

$$\begin{aligned} \psi (x,t) = w(t) \frac{\delta (x-t^{\gamma }) + \delta (x+t^{\gamma })}{2}, \end{aligned}$$
(5)

where \(w(t)\) is the PDF of trapping times and \(0 \le \gamma \le 1\) is a coupling strength. This kind of coupling has been introduced in [24, 37]. The SEDLF with \(\gamma =0\) is just a separable CTRW. In addition, we consider that the PDF of trapping times follows a power law:

$$\begin{aligned} w(t) \simeq \frac{c_0}{t^{1+\alpha }}, \end{aligned}$$
(6)

as \(t\rightarrow \infty \). Here, \(\alpha \in (0,2)\) is the stable index, a constant \(c_0\) is defined by \(c_0 = {c}/{|\Gamma (-\alpha )|}\) with a scale factor \(c\). We note that the mean trapping time diverges for \(\alpha \le 1\). For \(\gamma >0\), the PDF of jump length also follows a power law:

$$\begin{aligned} l(x) = \int _{0}^{\infty } \psi (x,t) dt = \frac{|x|^{\frac{1}{\gamma }-1}}{2\gamma }w\left( |x|^{\frac{1}{\gamma }}\right) \simeq \frac{c_0}{2\gamma }\frac{1}{|x|^{1+ {\alpha } / {\gamma }}}. \end{aligned}$$
(7)

Thus, the second moment of the jump length diverges for \(2\gamma \ge \alpha \). Because Lévy flight also has a power law distribution of jump length, we call this random walk the stored-energy-driven Lévy flight. In numerical simulations, we set the PDF of the trapping time as \(w(t) = \alpha t^{-1-\alpha }\) \((t\ge 1)\). Thus, the jump length PDF is given by \(l(x) = \alpha /(2\gamma |x|^{1+\alpha /\gamma })\) from Eq. (7), and \(\langle l^2 \rangle = \alpha /(\alpha -2\gamma )\) for \(2\gamma < \alpha \).

Because the mean trapping time is finite for \(\alpha >1\), we consider two typical renewal processes; ordinary renewal process and equilibrium renewal process [15]. Equilibrium renewal process is assumed to start \(-t_a=-\infty \) (see Fig. 1). The PDF of the first jump length \(x\) and the first apparent trapping time (the forward recurrence time) \(t\), \(\psi _0(x, t)\), is given by

$$\begin{aligned} \psi _0(x, t) = \frac{1}{\mu } \int _t^{\infty } w(t') \frac{\delta (x-t'^{\gamma }) + \delta (x + t'^{\gamma })}{2}dt', \end{aligned}$$
(8)

where \(\mu \) is the mean trapping time. See Appendix for the derivation. Generally, the first (true) trapping time is longer than the first apparent trapping time. Integrating Eq. (8) in terms of \(x\), we have the PDF of the first apparent trapping time:

$$\begin{aligned} w_0(t) = \frac{1}{\mu } \int _t^{\infty } w(t')dt'. \end{aligned}$$
(9)

Note that the Eq. (9) is consistent with the result obtained in renewal theory, i.e., the PDF of the forward recurrence time [15]. Thus, the joint PDF of the first jump length and the first apparent trapping time, \(\psi _0 (x, t)\), is not given by the form in Eq. (5). This is because the first jump length \(x\) is determined by the time elapsed since a random walker’s last jump (the first true trapping time) and thus it is not directly related to the first apparent trapping time, i.e., the time elapsed since the beginning of the measurement at \(t=0\). For ordinary renewal process, we just set \(w_0(t)=w(t)\) and \(\psi _0(x,t)=\psi (x,t)\). For \(\alpha \le 1\), we only consider an ordinary renewal process because there is no equilibrium ensemble due to divergent mean trapping time which causes aging [7, 9, 36].

3 Generalized Renewal Equation

The spacial distribution \(P(x,t)\) of SEDLFs with starting from the origin satisfies the generized renewal equations:

$$\begin{aligned} P(x,t)&= \int _{0}^{t} dt' \Psi (t-t') Q(x,t') + \Psi _0(t) \delta (x), \end{aligned}$$
(10)
$$\begin{aligned} Q (x,t)&= \int _{-\infty }^{\infty } dx' \int _{0}^{t} dt' \psi (x', t') Q (x-x', t-t')+ \psi _0 (x, t), \end{aligned}$$
(11)

where \(Q(x,t) dt dx\) is the probability of a random walker reaching an interval \([x,x+dx)\) just in a period \([t, t+dt)\), and \(\Psi (t)\) [\(\Psi _0 (t)\)] is the probability of being trapped for longer than time \(t\) just after a renewal (after the measurement starts at \(t=0\)). \(\Psi (t)\) and \(\Psi _0 (t)\) are defined as follows:

$$\begin{aligned} \Psi (t)&= 1 - \int _{-\infty }^{\infty }dx' \int _{0}^{t} \psi (x', t') dt' = 1 - \int _{0}^{t} w (t') dt',\end{aligned}$$
(12)
$$\begin{aligned} \Psi _0 (t)&= 1 - \int _{-\infty }^{\infty }dx' \int _{0}^{t} \psi _0 (x', t') dt' = 1 - \int _{0}^{t} w_0 (t') dt'. \end{aligned}$$
(13)

Then, the Laplace transforms of these functions are given by

$$\begin{aligned} \hat{\Psi }(s) = \frac{1 - \hat{w} (s)}{s}, \qquad \hat{\Psi }_0(s) = \frac{\mu s -1 +\hat{w}(s)}{\mu s^2}. \end{aligned}$$
(14)

In an ordinary renewal process, \(\psi _0(x,t)\) is the same as \(\psi (x,t)\). On the other hand, the first jump length \(x\) is not determined by the first apparent trapping time \(t\) in an equilibrium renewal process, while the first jump length is not independent of the first apparent trapping time. Fourier-Laplace transform with respect to space and time (\(x\rightarrow k\) and \(t\rightarrow s\), respectively), defined by

$$\begin{aligned} {\hat{P}}(k,s) \equiv \int _{-\infty }^\infty dx \int _0^\infty dt P(x,t) e^{ikx} e^{-st} , \end{aligned}$$
(15)

gives

$$\begin{aligned} {\hat{P}}(k,s)&= \frac{\hat{\Psi } (s)\hat{\psi }_0 (k,s) + \hat{\Psi }_0 (s) [1-\hat{\psi } (k,s)]}{1-{\hat{\psi }}(k,s)}, \end{aligned}$$
(16)

where \(\hat{\psi }_0 (k,s)\) and \(\hat{\psi } (k,s)\) are Fourier-Laplace transforms of \({\psi }_0 (x,t)\) and \({\psi } (x,t)\), respectively. In what follows, we use the notations \(P^{o}(x,t)\) and \(\hat{P}^{o} (k,s)\) for the ordinary renewal process, and \(P^{eq}(x,t)\) and \(\hat{P}^{eq} (k,s)\) for the equilibrium renewal process.

For ordinary renewal process, i.e., \(\psi _0(t)=\psi (t)\) and \(\Psi _0(t)=\Psi (t)\), we have the following generalized renewal equation in the Fourier and Laplace space:

$$\begin{aligned} {\hat{P}}^o(k,s) = \frac{1}{s} \frac{1-\hat{w}(s)}{1-{\hat{\psi }}(k,s)}, \end{aligned}$$
(17)

where we used Eq. (14). For equilibrium renewal process (\(\alpha >1\)), we have

(18)

where we used Eq. (14) and

$$\begin{aligned} \hat{\psi }_0 (k,s) = \frac{\hat{\psi }(k,0) - \hat{\psi }(k,s)}{\mu s}. \end{aligned}$$
(19)

The derivation of Eq. (19) is shown in Appendix.

Thus we expressed \(\hat{P}^{o}(k,s)\) and \(\hat{P}^{eq}(k,s)\) with \(\hat{\psi } (k, t)\) and \(\hat{w}(s)\) [Eqs. (17) and (18)]. Now, we derive the explicit forms of these functions. From Eq. (5), \({\hat{\psi }} (k,s)\) is given by

$$\begin{aligned} {\hat{\psi }} (k,s) = \int _{0}^{\infty } e^{-st} \cos \left( k t^{\gamma }\right) w(t) dt. \end{aligned}$$
(20)

Note that \({\hat{\psi }} (0,s) = \hat{w} (s)\). In addition, from Eq. (6), the asymptotic behavior of the Laplace transform \(\hat{w}(s)\) for \(s\rightarrow 0\) is given by

$$\begin{aligned} \hat{w}(s) = {\left\{ \begin{array}{ll} 1 - c s^{\alpha } +o(s^\alpha ), \quad &{} (0<\alpha <1)\\ 1 + c_0 s \ln s +o(s \ln s), \quad &{} (\alpha =1) \\ 1 - \mu s + cs^{\alpha } +o(s^\alpha ), \quad &{} (1<\alpha <2) \end{array}\right. } \end{aligned}$$

where \(\mu = \left\langle t \right\rangle = \int _0^{\infty } t w(t) dt\).

4 Mean Square Displacement

The asymptotic behavior of the moments of position \(x_t\) for \(t\rightarrow \infty \) can be obtained using the Fourier-Laplace transform \(\hat{P}(k,s)\). Because \(\left. \frac{\partial {\hat{P}} (k,s)}{\partial k}\right| _{k=0} =0\), \(\langle x_t \rangle =0 \) for both renewal processes.

In ordinary renewal process, the Laplace transform of the second moment, i.e., the ensemble-averaged MSD (EAMSD), is given by

(21)

where the ensemble average \(\langle \ldots \rangle _o\) is taken with respect to an ordinary renewal process. For \(\alpha \in (0,1)\), we obtain the EAMSD [6]:

$$\begin{aligned} \langle x^2_t \rangle _o \simeq {\left\{ \begin{array}{ll} \dfrac{\left\langle l^2 \right\rangle }{c \Gamma (1 + \alpha )} t^{\alpha }, &{}\quad \left( 0 < 2\gamma < \alpha \right) \\ \dfrac{1}{|\Gamma (-\alpha )| \Gamma (1 + \alpha )} t^{\alpha } \log t, &{}\quad \left( 2\gamma = \alpha \right) \\ \dfrac{\Gamma (2\gamma -\alpha )}{|\Gamma (-\alpha )| \Gamma (1+2\gamma )} t^{2\gamma }, &{}\quad \left( \alpha < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(22)

where we used \(\left\langle t^{2\gamma } \right\rangle = \left\langle l^{2} \right\rangle = \int _{-\infty } ^\infty x^2 l(x) dx\) when \(\langle l^2 \rangle <\infty \).

For \(\alpha = 1\), the EAMSD is given by

$$\begin{aligned} \langle x^2_t \rangle _o \simeq {\left\{ \begin{array}{ll} \dfrac{\left\langle l^2 \right\rangle }{c_0} \dfrac{t}{ \log t}, &{}\quad \left( 0 < 2\gamma < 1\right) \\ t, &{}\quad \left( 2\gamma = 1\right) \\ \dfrac{\Gamma (2\gamma -1)}{\Gamma (2\gamma +1)} \dfrac{t^{2\gamma }}{ \log t}, &{}\quad \left( 1 < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(23)

Finally, for \(\alpha \in (1,2)\), the EAMSD is given by

$$\begin{aligned} \langle x^2_t \rangle _o \simeq {\left\{ \begin{array}{ll} \frac{\left\langle l^2 \right\rangle }{\mu } t \left[ 1 +\frac{ct^{1-\alpha }}{\mu \Gamma (3-\alpha )} \right] , &{} \left( 0 < 2\gamma < 1\right) \\ \frac{\left\langle l^2 \right\rangle }{\mu } t + \frac{ct^{2-\alpha }}{\mu \Gamma (3 - \alpha )} \left[ \frac{\left\langle l^2 \right\rangle }{\mu } -\alpha \right] , &{} \left( 2\gamma = 1\right) \\ \frac{\left\langle l^2 \right\rangle }{\mu } t + \frac{c_0}{\mu } \frac{\Gamma (2\gamma - \alpha )}{\Gamma (2\gamma - \alpha + 2)} t^{2\gamma -\alpha +1}, &{} \left( 1 < 2\gamma < \alpha \right) \\ \frac{c_0}{\mu } t \log t, &{} \left( 2\gamma = \alpha \right) \\ \frac{c_0\Gamma (2\gamma -\alpha )}{\mu \Gamma (2\gamma -\alpha +2)}t^{2\gamma -\alpha +1}. &{} \left( \alpha < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(24)

These results are consistent with a previous study [24]. We note that the EAMSD for \(\gamma =1\) is smaller than that in Lévy walk, whereas the scaling exponent \(3-\alpha \) is the same as that in Lévy walk [45]. This is because SEDLF is a wait and jump model, while Lévy walk is a moving model.

In equilibrium renewal process (\(\alpha >1\)),

(25)

Eq. (25) is valid only for \(0 < 2\gamma < \alpha -1\), otherwise the second moment of the first jump length diverges, i.e., the EAMSD diverges. This is very different from Lévy walk process because there exists an equilibrium renewal process in Lévy walk with \(\alpha >1\). Because \(\hat{\psi }''(0,0) = \left\langle l^2 \right\rangle \) for \(0 < 2\gamma < \alpha -1\), the EAMSD is given by

$$\begin{aligned} \langle x^2_t \rangle _{eq} = \frac{\langle l^2 \rangle }{\mu } t. \end{aligned}$$
(26)

In SEDLF, the leading order of the EAMSD in an ordinary renewal process is the same as that in an equilibrium renewal process (\(\alpha > 2\gamma +1\)). On the other hand, in Lévy walk, the proportional constant of the EAMSD in a non-equilibrium ensemble such as an ordinary renewal process differs from that in an equilibrium one [16–18, 45]. We note that the TAMSD coincides with the EAMSD in an equilibrium ensemble as the measurement time goes to infinity. Significant initial ensemble dependence of statistical quantity has been also observed in non-hyperbolic dynamical systems [3].

5 Time-Averaged Mean Square Displacement

In normal Brownian motion, the TAMSD defined by Eq. (2) converges to the MSD with an equilibrium ensemble:

$$\begin{aligned} \overline{\delta ^2 (\Delta ; t)} \rightarrow \langle x_{\Delta } ^2 \rangle _{eq}~\mathrm{as}~t\rightarrow \infty . \end{aligned}$$
(27)

Such ergodic property does not hold in various stochastic models of anomalous diffusion such as CTRW and Lévy walk [17, 21, 27]. Here, we derive the TAMSD in the SEDLF. In wait and jump random walks with random waiting times such as CTRW and SEDLF, the TAMSD can be represented using the total number of jumps, denoted by \(N_t\), and \(h_k = \Delta l_k^2 + 2\sum _{m=1}^{k-1}l_kl_m \theta (\Delta - t_k+t_m)\) [6, 34, 35]:

$$\begin{aligned} \overline{\delta ^2 (\Delta ; t)} \simeq \frac{1}{t}\sum _{k=0}^{N_t} h_k\quad (t\rightarrow \infty ), \end{aligned}$$
(28)

where \(l_k\) is the \(k\)-th jump length, \(t_k\) is the time when the \(k\)-th jump occurs, and \(\theta (t)\) is a step function, defined by \(\theta (t)=0\) for \(t<0\) and \(t\) otherwise. For \(\gamma >0\), one can show that \(\sum _{k=0}^{N_t} (h_k - \Delta l^2_k)/\sum _{k=0}^{N_t} l_k^2 \rightarrow 0\) as \(t\rightarrow \infty \) [6]. Therefore, the TAMSD can be written as

$$\begin{aligned} \overline{\delta ^2 (\Delta ; t)} \simeq D_t \Delta \quad (\Delta \ll t ~\mathrm{and}~t\rightarrow \infty ), \end{aligned}$$
(29)

where \(D_t = \sum _{k=0}^{N_t} l^2_k/t\). We note that the relation (28) does not hold if the random walker moves with constant speed as in Lévy walk because \((x_{t+\Delta } - x_t)^2\) is simply zero in SEDLF but not in Lévy walk. In fact, the TAMSD does not increase linearly with time in Lévy walk [16–18].

To investigate an ergodic property of the time-averaged diffusion coefficient \(D_t\), we derive the PDF \(P_2 (z,t)\) of \(Z_t\equiv \sum _{k=0}^{N_t} l^2_k\). Because \(l^2_k\) and \(N_t\) are mutually correlated, we use the generalized renewal equation for \(Z_t\):

$$\begin{aligned} P_2(z,t)&= \int _{0}^{t} dt' \Psi (t-t') Q_2(z,t') + \Psi _0(t) \delta (z), \end{aligned}$$
(30)
$$\begin{aligned} Q_2 (z,t)&= \int _{0}^{\infty } dz' \int _{0}^{t} dt' \phi (z', t') Q_2 (z-x', t-t') + \phi _0 (z, t), \end{aligned}$$
(31)

where the joint PDF \(\phi (z,t)\) is given by

$$\begin{aligned} \phi (z,t) = w(t) \delta (z-t^{2\gamma }) \end{aligned}$$
(32)

The joint PDF of the first squared jump length \(z=l_0^2\) and apparent trapping time \(t\), \(\phi _0 (z,t)\), is given by \(\phi _0 (z,t) = \phi (z,t)\) for the ordinary ensemble, whereas

$$\begin{aligned} \phi _0 (z,t) = \frac{1}{\mu } \int _t^{\infty } dt' w(t') \delta (z-t'^{2\gamma }), \end{aligned}$$
(33)

for equilibrium ensemble, which can be derived in the same way as the derivation of \(\psi _0 (x,t)\) given in Appendix. The double Laplace transform with respect to \(z\) and time \(t\) is defined by

$$\begin{aligned} {\hat{P}}_2(k,s) \equiv \int _{0}^\infty dz \int _0^\infty dt P_2(z,t) e^{-kz} e^{-st}. \end{aligned}$$
(34)

From the generalized renewal equations (30) and (31), we obtain

$$\begin{aligned} {\hat{P}}_2(k,s) = \frac{\hat{\Psi } (s)\hat{\phi }_0 (k,s) + \hat{\Psi }_0 (s) [1-\hat{\phi } (k,s)]}{1-{\hat{\phi }}(k,s)}, \end{aligned}$$
(35)

where the double Laplace transform of \(\phi (z, t)\) is given by

$$\begin{aligned} \hat{\phi } (k,s) = \int _{0}^{\infty } e^{-st} e^{-kt^{2\gamma }} w(t) dt, \end{aligned}$$
(36)

and that of \(\phi _0 (z,t)\) is given by \(\phi _0 (z, t) = \phi (z,t)\) for the ordinary process, and by

$$\begin{aligned} \hat{\phi }_{0} (k,s)&= \frac{\hat{\phi }(k,0) - \hat{\phi } (k, s)}{\mu s}, \end{aligned}$$
(37)

for the equilibrium process. Note that \(\hat{\phi } (0, s) = \hat{w}(s)\).

5.1 Ordinary Renewal Process

In ordinary renewal process, the Laplace transform \({\hat{P}_2}^o(k,s)\) is given by

(38)

Thus, we have the Laplace transform of \(\langle Z_t \rangle _o\) as follows:

(39)

where we used \(- \hat{\phi }'(0,s) = - \hat{\psi }''(0,s)\) and Eq. (21). Then, averaging Eq. (29) over an ordinary ensemble, we have

$$\begin{aligned} \langle \overline{\delta ^2 (\Delta ; t)} \rangle _o \simeq \left\langle D_t \right\rangle _o \Delta = \frac{\langle x_t^2 \rangle _o}{t} \Delta \end{aligned}$$
(40)

Therefore, using Eqs. (22)–(24), we have the leading terms of the mean diffusion coefficient, \(\langle D_t \rangle _o = \langle x_t^2 \rangle _o/t\), for \(t\rightarrow \infty \) as follows:

$$\begin{aligned} \langle D_t \rangle _o&\simeq {\left\{ \begin{array}{ll} \frac{\left\langle l^2 \right\rangle }{c \Gamma (1+\alpha )} t^{\alpha -1} &{} \left( 0 < 2\gamma < \alpha \right) \\ \frac{1}{|\Gamma (-\alpha )| \Gamma (1+\alpha )} t^{\alpha -1} \log t &{} \left( 2\gamma = \alpha \right) \\ \frac{\Gamma (2\gamma -\alpha )}{|\Gamma (-\alpha )| \Gamma (1+2\gamma )} t^{2\gamma -1} &{} \left( \alpha < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(41)

for \(0 < \alpha < 1\),

$$\begin{aligned} \langle D_t \rangle _o \simeq {\left\{ \begin{array}{ll} \frac{\left\langle l^2 \right\rangle }{c_0} \frac{1}{ \log t} +o\left( \frac{1}{\log t}\right) . &{}\quad \left( 0 < 2\gamma < 1\right) \\ 1 + O\left( \frac{1}{\log t}\right) , &{}\quad \left( 2\gamma = 1\right) \\ \frac{\Gamma (2\gamma -1)}{\Gamma (2\gamma +1)} \frac{t^{2\gamma -1}}{ \log t}, &{}\quad \left( 1 < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(42)

for \(\alpha = 1\), and

$$\begin{aligned} \langle D_t \rangle _o \simeq {\left\{ \begin{array}{ll} \frac{\left\langle l^2 \right\rangle }{\mu }\left[ 1 +\frac{ct^{1-\alpha }}{\mu \Gamma (3-\alpha )} \right] , &{} \left( 0 < 2\gamma < 1\right) \\ \frac{\left\langle l^2 \right\rangle }{\mu } + \frac{ct^{1-\alpha }}{\mu \Gamma (3 - \alpha )} \left[ \frac{\left\langle l^2 \right\rangle }{\mu } -\alpha \right] , &{} \left( 2\gamma = 1\right) \\ \frac{\left\langle l^2 \right\rangle }{\mu } + \frac{c_0}{\mu } \frac{\Gamma (2\gamma - \alpha )}{\Gamma (2\gamma - \alpha + 2)} t^{2\gamma -\alpha }, &{} \left( 1 < 2\gamma < \alpha \right) \\ \frac{c_0}{\mu } \log t, &{} \left( 2\gamma = \alpha \right) \\ \frac{c_0\Gamma (2\gamma -\alpha )}{\mu \Gamma (2\gamma -\alpha +2)}t^{2\gamma -\alpha } &{} \left( \alpha < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(43)

for \(1 < \alpha < 2\). It follows that the mean diffusion coefficient diverges as \(t\) goes to infinity for \(1<\alpha <2\) and \(\alpha < 2\gamma < 2\).

Similarly, the Laplace transform of \(\langle Z_t^2 \rangle \) is given by

$$\begin{aligned} \langle Z_s^2 \rangle _o = \frac{1}{s [ 1- \hat{w}(s)]} \left\{ \frac{2\hat{\phi }'(0,s)^2}{1-\hat{w}(s)} + \hat{\phi }{''}(0,s)\right\} . \end{aligned}$$
(44)

It follows that the leading order of the second moment of \(D_t\) is given by

$$\begin{aligned} \langle D^{2}_t \rangle _o \simeq {\left\{ \begin{array}{ll} \frac{2 \left\langle l^2 \right\rangle ^2}{c^2 \Gamma (2 \alpha +1)} t^{2(\alpha -1)}, &{} (0< 2 \gamma < \alpha )\\ \frac{2}{\Gamma (2\alpha + 1) |\Gamma (-\alpha )|} \left( t^{\alpha } \log t\right) ^{2}, &{} (2 \gamma = \alpha ) \\ \frac{\Gamma (4\gamma -\alpha ) |\Gamma (-\alpha )| + 2\Gamma (2\gamma -\alpha )^2}{\Gamma (4\gamma +1)|\Gamma (-\alpha )|^2} t^{4\gamma -2}, &{} (\alpha < 2 \gamma \le 2) \end{array}\right. } \end{aligned}$$
(45)

for \(0 < \alpha <1\),

$$\begin{aligned} \langle D_t^2 \rangle _o \simeq {\left\{ \begin{array}{ll} \frac{\left\langle l^2 \right\rangle ^2}{c_0^2} \frac{1}{(\log t)^2} + o\left( \frac{1}{(\log t)^2}\right) , &{}\quad \left( 0 < 2 \gamma < 1\right) \\ 1 + O\left( \frac{1}{\log t}\right) , &{}\quad (2\gamma = 1)\\ \frac{\Gamma (4\gamma -1)}{\Gamma (4\gamma +1)} \frac{t^{4\gamma -2}}{ \log t}. &{}\quad \left( 1 < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(46)

for \(\alpha = 1\), and

$$\begin{aligned} \langle D^{2}_t \rangle _o \simeq {\left\{ \begin{array}{ll} \frac{\left\langle l^2 \right\rangle ^2}{\mu ^2} + \frac{4c\left\langle l^2 \right\rangle ^2}{\mu ^3} \frac{t^{1-\alpha }}{\Gamma (4 - \alpha )}, &{} \left( 0 < 2\gamma < 1\right) \\ \frac{\left\langle l^2 \right\rangle ^2}{\mu ^2} + \frac{Kt^{1-\alpha }}{\Gamma (4 - \alpha )}, &{} \left( 2\gamma = 1\right) \\ \frac{\left\langle l^2 \right\rangle ^2}{\mu ^2} + \frac{c_0}{\mu } \frac{\Gamma (4\gamma - \alpha )}{\Gamma (4\gamma - \alpha + 2)} t^{4\gamma -\alpha -1}, &{} \left( 1 < 2\gamma < \frac{\alpha +1}{2}\right) \\ \frac{\left\langle l^2 \right\rangle ^2}{\mu ^2} + \frac{c_0}{2\mu }, &{} (2\gamma = \frac{\alpha +1}{2})\\ \frac{c_0 \Gamma (4\gamma -\alpha ) }{\mu \Gamma (4\gamma -\alpha +2)} t^{4\gamma -\alpha -1}, &{} \left( \frac{1+\alpha }{2} < 2\gamma \le 2\right) \\ \end{array}\right. } \end{aligned}$$
(47)

for \(\alpha >1\) \(\left( K := \frac{4\left\langle l^2 \right\rangle c}{\mu ^2} \left\{ \frac{\left\langle l^2 \right\rangle }{\mu } - \alpha \right\} + \frac{c_0 \Gamma (2 - \alpha )}{\mu }\right) \).

Now, we study the relative standard deviation (RSD) of \(D_t\), \(\sigma _\mathrm{EB} (t) \!\equiv \! \sqrt{\langle D_t^2 \rangle - \langle D_t \rangle ^2}/\langle D_t \rangle \) [21, 33, 34], to measure the ergodicity breaking. First, for \(0< \alpha <1\), RSD \(\sigma _{\mathrm {EB}} (t)\) does not converge to zero but to a finite value as \(t\rightarrow \infty \). Therefore, the diffusion coefficients remain random even when the measurement time goes to infinity [6]. Second, for \(\alpha = 1\), we expect usual ergodic behavior for \(0 < 2\gamma \le 1\), because the RSD goes to zero as \(t\rightarrow \infty \). However, for \(1<2 \gamma <2\), the RSD diverges as \(t \rightarrow \infty \):

$$\begin{aligned} \sigma _{\mathrm {EB}}^2 (t) \sim \log t. \end{aligned}$$

Finally, for \(1 < \alpha <2\), we have

$$\begin{aligned} \sigma _{\mathrm {EB}}^2 (t) \sim {\left\{ \begin{array}{ll} t^{1-\alpha }, \qquad &{} \left( 0 < 2\gamma \le 1\right) \\ t^{4\gamma -\alpha - 1}, \qquad &{}\left( 1 < 2\gamma < \frac{\alpha +1}{2}\right) \\ \frac{\mu c_0}{2\left\langle l^2 \right\rangle ^2}, \qquad &{}\left( 2\gamma = \frac{\alpha +1}{2}\right) \\ t^{4\gamma -\alpha - 1}, \qquad &{}\left( \frac{\alpha +1}{2} < 2\gamma < \alpha \right) \\ \frac{t^{\alpha - 1}}{(\log t)^{2}}, \qquad &{}(2\gamma = \alpha )\\ t^{\alpha - 1}, \qquad &{}\left( \alpha < 2\gamma \le 2\right) \end{array}\right. } \end{aligned}$$
(48)

Thus, TAMSDs show ergodic behavior when the parameters satisfy \(0 < 2 \gamma < \frac{\alpha +1}{2}\) because the RSD goes to zero as \(t\rightarrow \infty \). On the other hand, the RSD converges to a finite value for \(\gamma = \frac{\alpha +1}{4}\), and diverges for \(\frac{\alpha +1}{2} < 2 \gamma \le 2\). Numerical simulations suggest that this divergence of the RSD for the case of \(\frac{\alpha +1}{2} < 2 \gamma \le 2\) will be attributed to a power-law with divergent second moment in the PDF of \(D_t/\langle D_t \rangle _o\) (see Fig. 2). Because the RSD is defined using the second moment of \(D_t\), it diverges, whereas the PDF converges to a power-law distribution. Thus, the RSD,\(\sigma _{\mathrm {EB}} (t)\), is not helpful to characterize the ergodicity breaking in this case. Using the relative fluctuation defined by \(R(t) \equiv \langle |D_t -\langle D_t \rangle |\rangle /\langle D_t \rangle \) [8, 42] instead of the RSD, we can clearly see the ergodicity breaking in the case of \(\frac{\alpha +1}{2} < 2 \gamma \le 2\): we numerically found that the relative fluctuation, \(R(t) = \langle |D_t/\langle D_t \rangle _o - 1 |\rangle _o\), converges to a constant as \(t\rightarrow \infty \) because \(D_t/\langle D_t \rangle _o\) does not converge to one but converges in distribution. Thus, the ergodicity in TAMSD breaks down for \(\frac{\alpha +1}{2} \le 2 \gamma \le 2\).

Fig. 2
figure 2

Histograms of the normalized diffusion coefficients \(D\equiv D_t/\langle D_t \rangle \) for different \(\gamma \) and \(\alpha \) (\(t=10^6\)). We calculate \(D_t\) by \(\overline{\delta ^2 (\Delta ; t)}/\Delta \) in numerical simulations with \(\Delta = 10\). The dashed line segments represent power-law distributions with exponent \(-2\) and \(-3\) for reference

Full size image

For \(\alpha >1\), the asymptotic behavior of the Laplace transform of \(\langle Z_t^n \rangle _o\) at \(s\rightarrow 0\) (\(n>1\)) is given by

$$\begin{aligned} \langle Z_s^n \rangle _o \simeq {\left\{ \begin{array}{ll} (-1)^n\dfrac{\hat{\psi }_2^{(n)}(0,s)}{s [ 1- \hat{w}(s)]}, &{} (2\gamma \ge \frac{1+\alpha }{2}) \\ \dfrac{n! \langle l^2 \rangle ^n}{\mu ^n}. &{} (2\gamma < \frac{1+\alpha }{2}) \end{array}\right. } \end{aligned}$$
(49)

It follows that the leading order of the \(n\)th moment of \(D_t\) is given by

$$\begin{aligned} \langle D_t^n \rangle _o \simeq {\left\{ \begin{array}{ll} \dfrac{c_0 \Gamma (4n\gamma -\alpha ) }{\mu \Gamma (4n\gamma -\alpha +2)} t^{2n\gamma -\alpha -1}, &{} (2\gamma \ge \frac{1+\alpha }{2}) \\ \dfrac{n! \langle l^2 \rangle ^n}{\mu ^n}. &{} (2\gamma < \frac{1+\alpha }{2}) \end{array}\right. } \end{aligned}$$
(50)

By numerical simulations, we confirm that the scaled diffusion coefficient \(D_t/\langle D_t \rangle _o\) converges in distribution to a random variable \(S_{\alpha ,\gamma }\):

$$\begin{aligned} \frac{D_t}{\langle D_t \rangle _o} \Rightarrow S_{\alpha ,\gamma } ~\mathrm{as}~t\rightarrow \infty , \end{aligned}$$
(51)

for \(\frac{\alpha + 1}{2} < 2\gamma \le 2\). The distribution depends on \(\gamma \) and \(\alpha \) (see Fig. 2). We note that the distribution obeys a power-law with divergent second moment because all the \(n\)-th moments \((n>1)\) of \(D_t/\langle D_t \rangle _o\) diverge as \(t\) goes to infinity. In fact, as shown in Fig. 2, the power-law exponents are smaller than 3.

For \(\alpha \le 1\), we obtained all the higher moments of \(D_t\) [6]. In particular, for \(2\gamma < \alpha \), all the moments are given by

$$\begin{aligned} \langle D^n_t \rangle _o \simeq \frac{n!\left\langle l^2 \right\rangle ^n }{c^n \Gamma (n+\alpha )} t^{n(\alpha -1)}. \end{aligned}$$
(52)

Therefore, the distribution of the scaled diffusion coefficient converges to the Mittag-Leffler distribution:

$$\begin{aligned} \frac{D_t}{\langle D_t\rangle _o} \Rightarrow M_\alpha ~(t\rightarrow \infty ), \end{aligned}$$
(53)

where

$$\begin{aligned} \langle e^{zM_\alpha } \rangle = \sum _{n=0}^\infty \frac{\Gamma (1+\alpha )^nz^n}{\Gamma (1+n\alpha )}. \end{aligned}$$
(54)

Moreover, for \(2\gamma > \alpha \), the distribution of \( \frac{D_t}{\langle D_t \rangle _o} \) also converges to a time-independent non-trivial distribution as \(t\rightarrow \infty \) [6]:

$$\begin{aligned} \frac{D_t}{\langle D_t\rangle _o} \Rightarrow Y_{\alpha ,\gamma } ~(t\rightarrow \infty ). \end{aligned}$$
(55)

5.2 Equilibrium Renewal Process

In an equilibrium renewal process, i.e., \(1 < \alpha <2\) and \(0< 2\gamma <\alpha -1\), the Laplace transform \({\hat{P}}_{2}^{eq}(k,s)\) is given by

(56)

Thus, we have the Laplace transform of \(\langle Z_{t}\rangle _{eq}\) as follows:

(57)

Averaging Eq. (29) over equilibrium ensemble, we have

$$\begin{aligned} \langle \overline{\delta ^2 (\Delta ; t)} \rangle _{eq} \simeq \left\langle D_t \right\rangle _{eq} \Delta = \frac{\langle Z_t \rangle _{eq}}{t} \Delta = \frac{\left\langle l^2 \right\rangle }{\mu } \Delta , \end{aligned}$$
(58)

where the second moment of the first jump length is finite for \(0<\gamma < \alpha -1\), otherwise the ensemble average of the TAMSD diverges. The second moment of the diffusion constant is also derived in the similar way:

(59)

and thus we have

$$\begin{aligned} \left\langle D_t^2 \right\rangle _{eq} = \frac{\left\langle l^2 \right\rangle ^2}{\mu ^2} + \frac{2c \left\langle l^2 \right\rangle ^2}{\mu ^3 \Gamma (4-\alpha )} t^{1-\alpha }, \end{aligned}$$
(60)

for \(0<\gamma < \alpha -1\). From these results, RSD is given by

$$\begin{aligned} \sigma ^2_{\mathrm {EB}} (t) \simeq \frac{2c}{\mu } \frac{t^{1-\alpha }}{\Gamma (4 - \alpha )}. \end{aligned}$$
(61)

6 Discussion

We have shown the phase diagram based on the power-law exponent of anomalous diffusion and the distribution of TAMSDs in SEDLF. The results are summarized in Fig. 3. Although SEDLF is closely related to CTRW, Lévy walk, and Lévy flight, its statistical properties on anomalous diffusion are different form them. In particular, while the visit points in SEDLF are the same as the turning points of a random walker in Lévy walk [38], a random walker cannot move while it is trapped in SEDLF, which is completely different from Lévy walk. This discrepancy makes the scaling of TAMSD different. In fact, TAMSDs in SEDLF increase linearly with time even when the EAMSD shows superdiffusion. On the other hand, TAMSDs show superlinear scaling (superdiffusion) in Lévy walk. Because a particle is always moving and there is a power-law coupling between waiting times and moving length in turbulent diffusion and diffusion of cold atoms [10, 38], a moving model of SEDLF can be applied to them. On the other hand, a wait and jump model (SEDLF) will be important in finance and earthquakes. In particular, SEDLF will be applied to describe dynamics of energy released in earthquake because energy is gradually accumulated and released in earthquake. Since TAMSDs can not be represented by Eq. (28) in a moving model such as Lévy walk and a moving model of SEDLF, to investigate ergodic properties of TAMSDs in a moving model of SEDLF is left for future work.

Fig. 3
figure 3

Phase diagram of the SEDLF in ordinary and equilibrium renewal processes. Solid lines divide the phase of the EAMSD in the ordinary renewal process. The dashed lines divide the phase of the distribution function of the TAMSD. Only below the dotted line \(2\gamma < \alpha -1\), the equilibrium process exists

Full size image

7 Conclusion

In conclusion, we have shown the phase diagram in SEDLF for a wide range of parameters, where the EAMSD shows normal diffusion, subdiffusion and superdiffusion, and the distribution of the TAMSD depends on the power-law exponent \(\alpha \) of the trapping-time distribution as well as the coupling parameter \(\gamma \). We consider two typical processes: ordinary renewal process and equilibrium renewal process. An equilibrium distribution for the first renewal time (the forward recurrence time) exists in renewal processes when the mean of interoccurrence time between successive renewals does not diverge. However, even when the mean does not diverge, an equilibrium distribution does not exist in the SEDLF because of divergence of the second moment of the first jump length. Therefore, we have found that the TAMSDs remain random in some parameter region even when the mean trapping time does not diverge. In particular, it is interesting to note that this distributional ergodicity is observed even when the EAMSD shows a normal diffusion, i.e., \(\frac{\alpha +1}{2} < 2\gamma < \alpha \) and \(1<\alpha <2\). In this regime, both the mean trapping time and the second moment of jump length are finite. Therefore, this result provides a novel route to the distributional ergodicity, because so far the distributional ergodicity has been found only in systems with the divergent mean trapping time or the divergent second moment of jump length, which break down the law of large numbers.