Beyond Inverse Ising Model: Structure of the Analytical Solution

Abstract

I consider the problem of deriving couplings of a statistical model from measured correlations, a task which generalizes the well-known inverse Ising problem. After reminding that such problem can be mapped on the one of expressing the entropy of a system as a function of its corresponding observables, I show the conditions under which this can be done without resorting to iterative algorithms. I find that inverse problems are local (the inverse Fisher information is sparse) whenever the corresponding models have a factorized form, and the entropy can be split in a sum of small cluster contributions. I illustrate these ideas through two examples (the Ising model on a tree and the one-dimensional periodic chain with arbitrary order interaction) and support the results with numerical simulations. The extension of these methods to more general scenarios is finally discussed.

Appendix: Factorization Property for the One-Dimensional Chain

I show in the following that for a one-dimensional periodic chain defined as in (22), the factorization property

(29)

holds, where Γ _n ={nρ+1,…,nρ+R} and γ _n ={(n+1)ρ+1,…,nρ+R}. To obtain this result, one can consider the auxiliary two-dimensional model defined by the log-probability

(30)

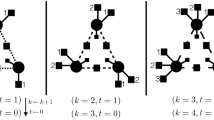
in which the configuration space contains the original degrees of freedom are $s_{i}^{n} \in\{ -1,1\}$ (with n=0,…,N/ρ−1 and i=1+nρ,…,R+nρ) and the auxiliary ones $t_{i}^{n} \in\{ -1,1\}$ (with n=0,…,N/ρ−1 and i=1+(n+1)ρ,…,R+nρ). The relation between the original model and the auxiliary one is sketched in Fig. 6. In particular the coupling λ controls the strength of the bond in the auxiliary dimension (labeled by n), so that the limit λ→∞ describes the original chain with the obvious identification $s^{n}_{i} \to s_{i}$ and $t^{n}_{i} \to s_{i}$. By defining the row variables $\underline{s}^{n} = \{ s_{i}^{n}\}_{i=1+n\rho }^{i=R+n\rho}$ and $\underline{t}^{n} = \{ t_{i}^{n}\}_{i=1+(n+1)\rho }^{i=R+n\rho}$, the log-probability for the two dimensional model can be written as

(31)

Hence the distribution over the degrees of freedom $\underline{s}^{n}$ and $\underline{t}^{n}$ defines a tree, because only successive row of variables interact.¹ The marginals associated with the clusters Γ _n and γ _n can be used in order to express the probability $p^{\lambda}(\underline{s},\underline{t})$ as

(32)

where for the two-dimensional model Γ _n and γ _n are analogously defined. By taking the λ→∞ limit, the identification

(33)

(34)

(35)

allows to recover the factorization property (23).

Fig. 6

Two dimensional auxiliary model p ^λ(s) associated with the original distribution p(s) describing a one-dimensional periodic chain