Tikhonov adaptively regularized gamma variate fitting to assess plasma clearance of inert renal markers

Abstract

The Tk-GV model fits Gamma Variates (GV) to data by Tikhonov regularization (Tk) with shrinkage constant, λ, chosen to minimize the relative error in plasma clearance, CL (ml/min). Using ¹⁶⁹Yb-DTPA and ^99mTc-DTPA (n = 46, 8–9 samples, 5–240 min) bolus-dilution curves, results were obtained for fit methods: (1) Ordinary Least Squares (OLS) one and two exponential term (E ₁ and E ₂), (2) OLS-GV and (3) Tk-GV. Four tests examined the fit results for: (1) physicality of ranges of model parameters, (2) effects on parameter values when different data subsets are fit, (3) characterization of residuals, and (4) extrapolative error and agreement with published correction factors. Test 1 showed physical Tk-GV results, where OLS-GV fits sometimes-produced nonphysical CL. Test 2 showed the Tk-GV model produced good results with 4 or more samples drawn between 10 and 240 min. Test 3 showed that E ₁ and E ₂ failed goodness-of-fit testing whereas GV fits for t > 20 min were acceptably good. Test 4 showed CL _Tk-GV clearance values agreed with published CL corrections with the general result that CL _E1 > CL _E2 > CL _Tk-GV and finally that CL _Tk-GV were considerably more robust, precise and accurate than CL _E2, and should replace the use of CL _E2 for these renal markers.

Introduction

Plasma clearance (CL, ml/min) measurement has multiple clinical uses. Inert markers are routinely employed to calculate CL for triage of chronic renal disease [1], transplant kidney and donor evaluation, and so forth. As one example, the inert markers ⁵¹Cr-EDTA (ethylenediamine tetra-acetic acid) and ^99mTc-DTPA (diethylenetriamine penta-acetic acid) have been used to estimate the Area Under the Curve (AUC) of the plasma concentration of carboplatin and other chemotherapeutic agents to reduce toxicity [2]. The total economic impact of adverse drug events from cancer chemotherapy alone is a 76 billion dollar annual expenditure [3]. Thus, the potential impact of finding efficient, accurate and precise estimates for inert marker CL to avoid toxicity is substantial.

This paper presents detailed results of four tests of three models for estimating CL of intravenously bolus-injected inert markers, which have only been outlined prior as abstracts and patent applications [4–7]. Statistical hypothesis testing of curve fit models (goodness-of-fit testing, lag plotting, etc.) is common practice, e.g., see Trutna et al. Chapter 5 [8]. For hypothesis testing, we examine curve fit suitability for temporal concentration–curves by inspecting (i) fit parameter ranges to see if these values agree with proper physical models, (ii) fits to subsets of the data that include the broadest possible range of mean sample times, (iii) model goodness of fit to see if the model credibly matches the data, and (iv) extrapolation, because only proper extrapolation is likely to conserve mass (Eq. 6).

The historical first model type used for estimating inert marker clearance is the Sums of Exponential Terms model, SETs, which is often fit to concentration curves using Ordinary Least Squares regression, OLS. For most markers, whether metabolized or not, current practice is dominated by fitting the observed concentrations, $C_{obs}$, with SET models using an arbitrary choice of from one to four exponential terms [9]. We call a single exponential term an E ₁ SET model and SET models using 2, 3, 4,$\ldots$, n exponential terms $E_{2} ,E_{3} ,E_{4} , \ldots ,E_{n}$ models. Current recommendations for assessing renal function or drug elimination for nuclear medicine and clinical pharmacology after venous bolus injection are to use $E_{n > 1}$ for fitting marker concentration curves with 8–13 blood samples [9–11]. The use of SET models inspired a physical model of linearly coupled, fast-mixing compartments. The first semiquantitative, graphic methods for E ₂ SET fitting were too inexact for meaningful statistical testing of the quality of the fit, with the first E ₂ SET graphic solution being published in 1944 and predating the general availability of digital computation [12–14]. Some test tools, such as Monte Carlo simulation [15] and bootstrap [16], are more recent and are primarily digital computer techniques. Most criticisms of the unrealistic nature of E ₂ SET modeling [17–20] have fallen on deaf ears [21]. Goodness-of-fit testing was published in 1922 [22], but has seldom been applied to the regression results of SETs, perhaps because of a lack of alternative fit models.

A variation of the SET method of estimating CL uses numerical integration to find AUC of the concentrations of multiple samples at early time and extrapolation of the unmeasured late time behavior using mono-exponential fits to the last 2 h of data [23, 24]. SETs and “AUC plus terminal mono-exponentials” are currently the only bolus models in use for estimating radiometric CL. Using mono-exponential extrapolations, Moore et al. [24] estimated a 10% difference between the 4- and 24-h AUC. Thus, the longer one waits to perform the terminal fit extrapolation with a mono-exponential the less the mono-exponential extrapolation underestimates the actual concentrations.

OLS regression of a gamma variate function is less often used than SETs, and shown here to have a more accurate terminal, or limiting, fit to the data at late times than SET functions. The GV function has been used in two physiologic models: (i) The bolus first-pass blood-flow model, e.g. [25–30] and (ii) The bolus-dose total plasma-clearance model, e.g. [19, 20, 31, 32]. These two physiologic models approximate distinct physical phenomena. Concerning (i), bolus transit models apply to the rapid early-time behavior exhibited by an organ’s vasculature as a source loaded with all the tracer that will empty, and for which there is initially no emptying and a minimum vascular first transit time of several seconds applies [33]. In this case, the system is not in equilibrium, and the GV approximates the temporal behavior of the concentration in one location (e.g., a vein draining the organ). Concerning (ii), a GV renal model uses the dynamic-equilibrium behavior of elimination over several hours, which exhibits gradual changes of concentration in a systemically distributed volume. Here the body acts as a sink for marker and renal GV model shape-parameter values do not overlap with those of the organ-source (i.e., not a sink) first-pass GV model—see the Theory section, below.

Unlike SET models, for which sporadic testing has been performed, to our knowledge, no critical appraisal of GV plasma-clearance models has been presented. Olkkonen et al. [19], using ¹³¹I-hippuran, compared GV fits to E ₂ SET fitting, but did not detect different clearances between models. Wise [20] suggested that the GV be used to model concentration curves and calculate CL of most renal eliminated substances, but did no hypothesis testing. Macheras [31] extended Wise’s [20] work without critical testing. Perkinson et al. found the OLS GV model to fit better than other models, but did not test the GV model itself [32]. We shall find, however, that OLS GV fitting should not be used to find CL and this is at odds with prior work. The gamma variate, GV, model, as presented here, sometimes produces unphysical CL-values when the OLS (ordinary least squares) method is used to fit the data. As we shall see, the problem is that OLS-GV fitting of the concentration versus time is an ill-posed problem. The solution is to introduce regularization. We name this method the Tk-GV method, where “Tk” stands for our implementation of Tikhonov regularization for optimizing CL-values from GV fits to the dilutions curves. The Tk-GV method further selects the shrinkage constant, λ, multiplying the regularization term to minimize the coefficient of variation (CV) of CL. This makes the technique adaptive to the particular data set used and ensures the most reliable result in all cases. This adaptation is unusual in that CL and its errors are not estimated from the fit-data range of times, but from t = 0 to ∞. By finding that GV function that minimizes the CV of CL, as we shall see, the Tk-GV model overcomes the instabilities observed in OLS fitting of the GV function to marker concentrations, and thus provides good CL values.

The Theory section below presents the general relationships governing the dynamic plasma clearance of inert markers. The focus here is on inert Glomerular Filtration Rate, GFR, markers as these produce numerically similar (to within 2 or 3% of ^99mTc-DTPA) CL-values [34, 35]. However, inert markers have different rates of body tissue extraction from plasma for [36], which are likely to be related to the different molecular sizes [17, 37]. Markers for GFR are (i) generally exogenous and not naturally occurring, (ii) metabolically inert, (iii) extracellular markers, (iv) only eliminated by filtration in the renal glomeruli and thus largely lack active transport by the renal tubules, and (v) have poor plasma protein binding. Examples of GFR markers include the DTPA metallic chelates used here, ⁵¹Cr-EDTA, ¹²⁵I-iothalamate, and inulin (an indigestible oligosaccharide). There are occasional quality assurance problems with manufacture of ^99mTc-DTPA, but not ¹⁶⁹Yb-DTPA [38]. As we shall see, GFR is $CL_{urine}$ or renal clearance of plasma measured using urinary collection of a GFR marker and is less than $CL_{total}$, the total plasma-clearance of the GFR marker dosage. For any non-metabolized drug, $CL_{urine}$ corresponds to the rate of drug elimination. However, $CL_{total}$ relates to the systemic effect of (pharmacodynamics), or body exposure to, that drug.

Theory

Measurement systems

Intravenously administered exogenous-marker clearance determinations can be obtained by bolus injection (dynamic) or constant infusion (steady state) methods. An independent classification for clearance determinations arises from the use of either $CL_{total}$, total clearance (a.k.a. input, dose or plasma clearance) or $CL_{urine}$, urinary-clearance (a.k.a. output, renal clearance or glomerular filtration rate; GFR) sampling techniques. For the $CL_{urine}$ technique, two sets of samples, urine and plasma, are assayed. Since the dosage is easy to assay, the majority of papers in the literature, as here, use the total (plasma) clearance method and do not obtain the inconvenient urinary catheterizations for timed urinary collections.

To illustrate the difference between $CL_{total}$ and $CL_{urine}$, let us first consider the steady state (equilibrium) method performed with constant infusion. After several hours of constant infusing, $CL_{total}$ (ml/min) is mg/min of substance infused divided by the constant concentration in plasma in mg/ml, whereas $CL_{urine}$ (ml/min) is the timed urinary output of substance in mg/min divided by the plasma concentration in mg/ml. That the $CL_{total}$ and $CL_{urine}$ sampling techniques yield different estimates was shown by Florijn et al. and others [39]. Florijn et al. constant-infused inulin for 4 h after a loading dose and calculated an 8.3 ml/min/1.73 m² greater $CL_{total}$ than $CL_{urine}$ in humans. This suggests that inulin sequestered itself somewhere in the body at residence times that are substantial in comparison to the duration of their 4-h infusion experiment. Indeed, inulin storage “in a slow compartment” (sic, within the body; the compartmental argument is superfluous) has been invoked to explain same-day repeat-measurement results [40].

For dynamic (bolus) methods there is also an inert marker difference between $CL_{total}$ and $CL_{urine}$ [41]. Radiolabeled DTPA, a smaller molecule than inulin, redistributes more quickly [37]. For an even smaller molecule than labeled DTPA, ⁵¹Cr-EDTA, Moore et al. [24] used the AUC plus terminal mono-exponentials method and found a 7.6% higher 24-h $CL_{total}$ than ${\text{CL}}_{urine}$, and Brochner-Mortensen et al. found 4.5% at 72 h using whole body counting [41].

Thus, both constant infusion experiments, and bolus experiments have shown that $CL_{total} > CL_{urine}$ over long time scales. These results strongly suggest that the difference between $CL_{total}$ and $CL_{urine}$ is a physiologic redistribution (i.e., for inert markers, a clearance) within the body ($CL_{body}$). Thus, one can define

$$ CL_{total} = CL_{body} + CL_{urine} , $$

(1)

such that $CL_{total}$ contains both marker redistribution in the body $\left( {CL_{body} } \right)$ and $CL_{urine}$ over long time scales. $CL_{body}$ is likely a function of the time elapsed during an experiment. For example, during first pass of a ^99mTc-DTPA bolus, the mass extraction of that marker from plasma by the body is approximately 50% and at a maximum rate [36]. Therefore from Eq. 1, $CL_{total}$ is also likely a function of the time elapsed during an experiment.

Theory common to all bolus models of total (plasma) clearance

It is not generally appreciated that plasma clearance (CL) and volume of marker distribution (V) are actually concentration weighted values, i.e., $\left\langle {CL} \right\rangle$ and $\left\langle V \right\rangle$. The common practice is to assume that $CL_{total}$ is a constant. However, this is not reasonable. For one thing, CL varies physiologically in time [42]. Moreover, as per the previous section, $CL_{total}$ likely varies during a bolus experiment. In any case, it is more general to assume that $CL_{total}$ is a function of time, $CL_{total} \left( t \right)$, than a constant, and one can write

$$ D = \int \limits_{0}^{\infty } {CL_{total} \left( t \right)C_{obs} \left( t \right)dt} , $$

(2)

where D is the injected dose (in percent, mg, or Bq) and $C_{obs}$ are the observed concentrations as D (dose units) per ml, as a function of time. With reference to Eq. 2, taken outside of the integral, $CL_{total} \left( t \right)$ becomes a concentration-weighted, time average value, i.e., $\left\langle {CL_{total} } \right\rangle$, allowing Eq. 2 to be rewritten as

$$ D = \left\langle {CL_{total} } \right\rangle \int \limits_{0}^{\infty } {C_{obs} \left( t \right)dt} , $$

or,

$$ \left\langle {CL_{total} } \right\rangle = {\frac{D}{{\int_{0}^{\infty } {C_{obs} \left( t \right)dt} }}}, $$

(3)

where $\left\langle {CL_{total} } \right\rangle$ is concentration weighted for the entire time interval from zero to infinity, and where the term $\int_{0}^{\infty } {C_{obs} \left(t \right)dt}$ is referred to as the Physical AUC, Phy-AUC (in percent dosage-min, mg-min, or Bq-min). Better documented than Eq. 3 is the similarly derived concentration-weighted, average time named the Mean Residence Time, MRT, by Hamilton et al. [43],

$$ MRT = \left\langle t \right\rangle = {\frac{{\int_{0}^{\infty } {t \cdot C_{obs} \left( t \right)dt} }}{{\int_{0}^{\infty } {C_{obs} \left( t \right)dt} }}}. $$

(4)

Finally $\left\langle {V_{total} } \right\rangle$, the concentration-weighted average volume of distribution of the marker, can be defined as the product of MRT and $\left\langle {CL_{total} } \right\rangle$ from Eqs. 3 and 4, i.e.,

$$ \left\langle {V_{total} } \right\rangle = MRT\left\langle {CL_{total} } \right\rangle . $$

(5)

Equations 3 through 5 are common to all bolus models of total plasma clearance. For any specific function used to fit $C_{obs}$, the formulas for that model can be obtained by substituting the fit function into these general equations.

In the following development, when we refer to CL and V values, these should be understood as concentration-weighted, time average values. In practice, using Eq. 3 to evaluate CL is awkward. In particular, one cannot wait infinite time to construct $C_{obs}$ over the required interval from 0 to ∞. Moreover, for discrete blood sampling, one does not have the necessary continuous recording of $C_{obs}$ to apply Eq. 3. One practical solution is to use a continuous function, C(t), to fit the available data and thereby estimate Phy-AUC, i.e., make an Estimated AUC, Est-AUC. The consequences of doing this can be examined by breaking Est-AUC into three pieces: (i) before the earliest plasma concentration measurement time, $t_{1}$ (in min), (ii) during the times the plasma concentration is measured (from $t_{1}$ to $t_{m}$, where $t_{1} ,t_{2} ,t_{3} ,,,t_{m}$ are the sequential sampling times) and (iii) beyond the last measurement time of plasma concentration, $t_{m}$. This yields

$$ CL = {\frac{D}{{Phy{ - }AUC}}} \approx {\frac{D}{{Est{ - }AUC}}} = {\frac{D}{{\int_{0}^{{t_{1} }} {C\left( t \right)dt} + \int_{{t_{1} }}^{{t_{m} }} {C\left( t \right)dt} + \int_{{t_{m} }}^{\infty } {C\left( t \right)dt} }}}, $$

(6)

where C(t) approximates $C_{obs}$ , and where typically both the first and third integrals in the summed denominator are extrapolations, and only the second integral is from interpolation (as in integration of an OLS regression fit function, or occasionally, with numerical integration followed by third integral mono-exponential extrapolation [23, 24]). In practice, one only has a C(t) model that accurately fits the data, $C_{obs}$, over the times for which samples have been collected. The average $\left\langle {CL_{total} } \right\rangle$ derived is consequently in error. To conserve the dose, D, the C(t) fit from $t_{1}$ to $t_{m}$ must also extrapolate correctly over the entire interval from time zero to infinity. Therefore, in order to estimate CL correctly, especially for low renal function when the third integral is much larger (e.g., 50 times larger) than the second, one needs to show that the AUC beyond t _m is correctly estimated. Test 4 below examines this extrapolation process.

Theory specific to SET models

SET models are defined as follows

$$ C\left( t \right) = E_{n} = \sum\limits_{i = 1}^{n} {C_{i} e^{{ - \lambda_{i} \, t}} } ;\,\lambda_{i} > 0, $$

(7)

where $C_{i}$ is in 100 ml⁻¹ (Note, this unit is percent of D per ml, which standardizes D between experiments), MBq/ml or mg/ml, and $\lambda_{i}$ is in min⁻¹. Note that Eq. 7 is used to fit the concentrations from $t_{1}$ to $t_{m}$, and concentration approaches zero rapidly after $t_{m}$, i.e., Eq. 7 may underestimate the third integral of Eq. 6.

Improvements to the E ₂ SET model for better testing. The common expression [44] for an $E_{2}$ SET has the form

$$ C\left( t \right) = C_{1} e^{ - \lambda 1 \, t} + C_{2} e^{ - \lambda 2 \, t} . $$

(8)

This equation has a poorly diagonalized covariance matrix and degraded regression performance. The use of more statistically independent parameters improves convergence. Thus, Eq. 8 was reparameterized (e.g., see [45]) using the substitutions $C_{1} = ka$, and $C_{2} = k$ to yield

$$ C_{obs} \approx E_{2} = k\left( {ae^{ - \lambda 1 \, t} + e^{ - \lambda 2 \, t} } \right), $$

$$ \ln C_{obs} \approx \ln E_{2} = \ln k + \ln \left( {ae^{ - \lambda 1 \, t} + e^{ - \lambda 2 \, t} } \right). $$

(9)

Regression of Eq. 9 yields a more normally distributed ln k (i.e., the concentration measurement errors are proportional to the concentrations) than $C_{1}$ or $C_{2}$ of Eq. 8. While Eqs. 8 and 9 find the same regression solutions, regression of Eq. 9 is more numerically stable with a markedly reduced required number of iterations for convergence.

Once convergence has been achieved, CL is then calculated from this fit using the substitution of Eq. 9 into Eq. 3

$$ CL = {\frac{D}{{\int_{0}^{\infty } {E_{2} dt} }}} = {\frac{D/k}{{a/\lambda_{1} + 1/\lambda_{2} }}}, $$

(10)

where D is the injected dose. Subsequently, Mean Residence Time, MRT, is calculated from substitution of Eq. 9 for $C_{obs}$ in Eq. 4 yielding

$$ MRT = {\frac{{a/\lambda_{1}^{2} + 1/\lambda_{2}^{2} }}{{a/\lambda_{1} + 1/\lambda_{2} }}}. $$

(11)

Then $V = MRT \cdot CL$ gives

$$ V = \frac{D}{k}{\frac{{a/\lambda_{1}^{2} + 1/\lambda_{2}^{2} }}{{\left( {a/\lambda_{1} + 1/\lambda_{2} } \right)^{2} }}}, $$

(12)

from the product of Eqs. 10 and 11.

While reparametrization considerably simplified finding fits to the data, this does not insure convergence, and, for Test 2, constrained global search techniques were applied to $E_{2}$ fitting to guarantee convergence [46–48].

Theory specific to gamma variate models

One might think that a first principles approach to the plasma-clearance marker problem would use a slow-mixing model. One such approach might adapt the Local Density Random Walk (LDRW) function [26, 29]. Specifically, LDRW, which models blood flow with Brownian motion, might be extended to include recirculation. However, and although Brownian motion occurs, turbulent vascular flow [49], core and plug flow of blood [50], delay channels [33] and molecular sieving at capillary walls [14, 51], also occur. Given this complex physiology, (i) use of the term dilution in time is preferred to mixing, and (ii) a dilution in time model derived from first principles may be intractably complicated and position dependent. Fortunately, there is a simple model that approximates the observed marker concentrations, $C_{obs}$, (in Bq per ml or percent dose per ml or mg/ml), in some circumstances, i.e., the GV function,

$$ C_{obs} \approx {\text{GV}}\left( {t;\alpha ,\beta ,K} \right) = C\left( t \right) = Kt^{\alpha - 1} e^{ - \beta t} . $$

(13)

Note that the GV function is described by only three parameters: α, β and K. The parameter α is dimensionless and is called the shape parameter. The rate constant β is used in Eq. 13 rather than its more common reciprocal, θ = 1/β, since β has no discontinuity in the derivative at β = 0. This is important since regression analyses often use gradient techniques (e.g. Levenberg–Marquardt and sequential quadratic programming). And so here, as for the statistical software package SPSS, we adopt the convention of using the rate constant β to describe GV.

The power function multiplier of Eq. 13, $t^{\alpha - 1}$ can assume non-integer powers of time, to have proper physical units, the quantity raised to the α − 1 power must be dimensionless. In other words, Eq. 13 should be understood as meaning, for example, that

$$ C(t) = \kappa \left( {\beta t} \right)^{\alpha - 1} e^{ - \beta t} , $$

(14)

where κ is a constant with units of concentration and the product βt is dimensionless. For equivalence for regression when β ≥ 0 in Eqs. 13 and 14, let $K \equiv \kappa \, \beta^{ \, \alpha - 1}$. Equation 13 is used to fit the data herein, and is the historic form for C(t) (e.g., see [20]). In that form, $Kt^{\alpha - 1}$ has the units of concentration. With these caveats aside, one can derive the formula for CL, the weighted-average rate of total plasma-clearance of dose for the GV model, Eq. 15. After substituting the GV Eq. 13 for $C_{obs}$ in the integral of Eq. 3 and performing the integration, one finds

$$ CL = {\frac{{D\beta^{\alpha } }}{K\Upgamma \left( \alpha \right)}} \, \left( { \equiv {\frac{D\beta }{\kappa \, \Upgamma \left( \alpha \right)}}{\text{ for }}\beta \ge 0} \right), $$

(15)

where $\Upgamma \left( \alpha \right) = \int_{0}^{\infty } {t^{\alpha - 1} e^{ - t} dt}$ is the gamma function and is widely available either as the function itself (e.g., Mathematica) or as its logarithm (Excel and SPSS). Substituting GV from Eq. 13 into Eq. 4 yields

$$ MRT = {\frac{{\int_{0}^{\infty } {t \cdot t^{\alpha - 1} e^{ - \beta t} dt} }}{{\int_{0}^{\infty } {t^{\alpha - 1} e^{ - \beta t} dt} }}} = {\frac{\alpha }{\beta }}. $$

(16)

Indeed, this mean residence time formula has been published for a GV fit to first transit of a bolus through the brain [27], and the form of the equation is identical to that of the CL model, even though the models are physically different. MRT has certain restrictions regarding unbounded integrals [52] that sometimes apply here (see below). To calculate V, the physical volume of the system, one recalls Eq. 5, i.e., $V = MRT \cdot CL$. Thus, Eq. 16 substituted into Eq. 5 yields

$$ V = {\frac{\alpha }{\beta }}CL. $$

(17)

Note that this new expression for V is α times the virtual volume, CL/β, the latter (misleadingly) given by Wise [20] as V. For incrementally small renal function, both CL and β can become small, yet maintain a stable ratio, if the method for extracting the CL/β ratio information is well behaved. So V (Eq. 17) may remain constant even when MRT (Eq. 16) becomes infinite time and CL becomes vanishingly small. As per the Results below, the use of Tk-GV fitting can allow CL/β to be preserved for vanishingly small CL. However, the volume information is indeterminate when CL is exactly zero (and β = 0) as sometimes occurs in β ≥ 0 constrained OLS GV fitting, which latter does not hold CL/β constant.

When C _obs (t) follows a GV law, the rate of change of concentration with time is

$$ {\frac{1}{C(t)}}{\frac{dC\left( t \right)}{dt}} = {\frac{\alpha - 1}{t}} - \beta , $$

(18)

which can be derived from differentiating the GV function with respect to time. The (α − 1)/t term is presumed to be loss of marker to the interstitium and related to ${\text{CL}}_{body}$. The second term, −β, is the more familiar first order kinetic rate constant, herein renal loss only, and as the markers are inert, associated with $CL_{urine}$. So when one uses the AUC method for determining CL with a GV for the concentration, both clearances add up to $CL_{total}$. Indeed, $(\alpha - 1)/t$, hence $CL_{body} (t)$ are time dependent. Hence, $CL_{total} \left( t \right)$ is also time dependent. Hence, we must have $CL_{body} > 0$ and consequently α < 1, or else ${{\left( {\alpha - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\alpha - 1} \right)} t}} \right. \kern-\nulldelimiterspace} t}$ is not a source term (i.e., the sign of the numerator would be positive). Finally since we want positive MRT and volumes of distribution, V, Eqs. 16 and 17 tell us that α > 0 (β is explicitly >0). So finally 0 < α < 1. As presented below, OLS GV fitting produces occasional β < 0 and α > 1 values. This problem is largely solved by adaptively Tikhonov regularizing the GV fit as follows, next.

Introduction to Tikhonov regularization

At the heart of the Tk-GV technique is Tikhonov regularization. Tikhonov regularization is used in a variety of applications to remove solution ambiguity in ill-posed problems [53–55]. The Tk-GV model implements regularization as an adaptive regularizing penalty function that rewards smoother fits to the data. Tk-GV is adaptive because the amount of smoothing is optimized using a controlling variable factor, λ, often called the shrinkage factor. Values for the shrinkage factor can be selected in a variety of ways. However, the goal in this paper is to measure CL. Consequently, the shrinkage factor will be adjusted to minimize the relative error of measuring CL, which error is expressed as the coefficient of variation (CV) of CL, i.e., ${\text{CV}}_{CL} = s_{CL} /CL$, calculated from the propagation of small errors (see the Appendix, Eq. A3).

Tk-GV fitting, unlike OLS fitting, does not minimize the smallest residual interpolation of the concentration data. The Tk-GV fit is biased. In effect, for decreasing renal function, increased regularization (i.e., a higher value of the shrinkage factor) is applied as the relative importance of un-modeled effects extend later and later into the sample measurement times. However, as the shrinkage factor increases, the data becomes increasingly unimportant and eventually is not included in the fit. So results with $\lambda \gg 1$ are suspect. Thus, despite the many expected benefits of the Tk-GV model, it is prudent to examine all aspects of the procedure.

Methods

Methods, data

Forty-one patient studies used here were made available by Dr. Charles D. Russell from a published series [56]. These data are thought to be accurate to within 3% pipetting error [57], contain 8 plasma sample concentrations per case drawn from adults with a wide range of CL-values from very severely impaired to normal. For these studies, 1.85 MBq of ¹⁶⁹Yb-DTPA were injected after which the syringe was flushed with blood. Residual activity in the syringe was less than 2% of the dose. Standards were prepared by dilution from duplicate syringes. Eight blood samples were drawn into standard EDTA anticoagulated vacuum sample tubes at 10, 20, 30, 45, 60, 120, 180, and 240 min after injection, using a vein other than that used for injection. A week after centrifugation, duplicate samples of plasma and standard were pipetted, counted, and the results averaged. The aqueous standard solution of ¹⁶⁹Yb-DTPA was pipetted into counting tubes within 8 h of preparation.

For contrast and completeness, five additional ^99mTc-DTPA patient studies were included. These studies were made available by Barbara Y. Croft, Ph.D. of the Cancer Imaging Program of the National Cancer Institute of the U.S.A. National Institute of Health (private communication, 2007). These patients had 9 blood samples drawn at 5, 10, 15, 20, 60, 70, 80, 90 and 180 min. The CL for these adults ranged from moderate renal failure to normal. Patient weight ranged from 40.6 to 119.5 kg and height from 142 to 188 cm over both data sets.

Methods, numerical methods

In addition to reparametrization as described above, in order to always obtain E ₂ SET results, it proved necessary to use constrained simulated annealing and random search, i.e., regression methods with guaranteed convergence [46–48]. Use of these powerful methods provided converged E ₂-fits under conditions beyond those usually recommended. To ensure that the fit results had converged to the global minimum, two different sets of starting conditions and annealing rates were used for each data set. In addition, constrained random search fits were performed and the least-residual-summed-squares values obtained from the three trials were chosen as the solution. Mathematica ver. 6 global minimization of sum-squared residuals with the simulated annealing option and perturbation scale set to 3, was found to converge fairly rapidly.

The GV fits converged using Mathematica software version 7 and 20 repeat (serial) random applications of the Nelder-Mead algorithm [58] to obtain the global minima for our OLS solutions both with and without constraints. To confirm this, the same results were obtained using repeated applications of simulated annealing [48]. GV fitting can be performed using Multiple Linear Regression (MLR). Writing the logarithm of Eq. 13 yields.

$$ \ln C = \ln K + \left( {\alpha - 1} \right)\ln t - \beta t. $$

(19)

Making the substitutions $Y = \ln C$, $X_{1} = \ln t$ and $X_{2} = t$, one can see that

$$ Y = \ln K + \left( {\alpha - 1} \right)X_{1} - \beta X_{2} , $$

(20)

is linear in Y. This is used for GV and Tk-GV fitting but not for $E_{n \ge 2}$ SET models, the latter of which cannot be usefully transformed into a form for which MLR can be applied.

Tikhonov regularization (Tk) is widely used in ridge regression in statistics [59], and is a standard feature of many statistical packages including SPSS, R and Matlab. The Tk-GV application in Mathematica version 7 has a run time of several seconds for convergence to 16 decimal places. The algorithm was checked against SPSS version 15. Global-optimization-search numerical techniques can enforce convergence [46, 48, 60]. While these methods should find the global minimum (of Eq. A3 of the Appendix), practical implementation may only find a local minimum. To gain confidence that the results presented here are global minima, regressions with multiple random starting conditions were obtained for each sample combination, and this process was carried out for several different regression methods. In difficult cases, i.e., noisy cases from leaving out four samples (L4O), 70,000 regressions were performed with each method. Using L4O, there were 3500 selections of different subsets of the data and each was regressed 20 times to find the best regressions using each of three methods: Nelder-Mead, simulated annealing, and differential evolution. In no single case out of 3500 were the results of any of the three fits methods for a given set of samples different from the other two methods’ fit results to 16 decimal places. To obtain Tk-GV converged solutions to agree within 16 decimal places required a computational precision of more than 32 decimal places, and techniques internally accurate to 40 decimal places were used.

Methods, details of the tests

Only testing can establish that a given functional form fits concentration curves appropriately. The testing performed for SET functions was also applied to the GV function fit using standard OLS methods. However, the OLS-GV fits proved numerically more stable than SET fits. Accordingly, more advanced versions of the tests were used for the OLS-GV model. Testing of the Tk-GV model was refined yet again. The Tk-GV model intrinsically calculates the error in the resulting CL value. The accuracy of the error determination was double-checked with leave one out (LOO), a data holdout method not applicable to less robust models. Four different tests of the suitability of curve fitting were performed.

Test 1, variability of parameters

For the SET and OLS-GV models, Test 1 used bootstrap [16] analysis of variance (ANOVA) to determine whether the parameters of the models are statistically warranted, and whether the values of CL and V (in ml) calculated from those parameters are physical. When fitting the data, when fit parameters take negative values the value of the fit function becomes non-physical, suggesting that the fit quality is not appreciably altered by discarding that variable, i.e., the parameter is unwarranted when the 95% confidence intervals (CIs) include zero. Parameters that have zero magnitude can occur in two scenarios. The first is that the true value of the parameter could be zero (unlikely here). The second is when the parameter is statistically unwarranted. Test 1 used bootstrap resampling and OLS regression to create 1000 values for each parameter for each of the 46 patients. Bootstrap for regression takes the converged model and constructs residuals as the difference between the model and the observed data, in this case the logarithm of concentrations. These residuals are then resampled with replacement, added to the fit curve to form a new synthetic data set, and a new model fit to the new data. In this way, after many resamplings of residuals, a distribution of fit parameters can be constructed. When an equation is fit to the data, the resulting values of the fit parameters may contain zero within the 90% or 95% CIs. Usually, if a model contains parameters that have P(0) > 0.05, those parameters do not contribute to the quality of the fit, and can be removed (set equal to zero) without significantly affecting the fit quality. Bootstrap was done with SPSS 15 Sequential Quadratic Nonlinear Algorithm, SQNA. The 95% CIs were estimated twice. The first estimate was from the SEM (standard error of the mean) of parameters, where SEM =$\sigma /\sqrt n$, σ is the standard deviation and n is 1000 simulations. Even one excessively large value outlier (e.g., 10⁶) would inflate σ. Thus, the mean ± 1.96 SEM, 95% CI is inflated by very far outliers. The second, better CI estimate is to construct 95% CIs using trimming [16]. A trimmed 95% CI is derived by using the 2.5 and the 97.5 percentiles of the bootstrap distribution as its limits.

The bootstrap of GV inclusive of early time data is useful because it can be compared directly to bootstrap of E ₂ SET models for assessment of outliers and CVs for both CL and V using Wilcoxon signed-ranks sums. Outliers were defined as parameter values that lie further than three interquartile ranges away from the median of the population of interest, and are often called far outliers.

Characterization of parameters from Tk-GV fits. Tk fit parameter calculations have a native estimate of the error in CL; the standard deviation, SD, with notation $SD(x) = s_{x}$, as part of the Tk regression process, itself. However, since Tk-GV attempts to minimize ${{s_{CL} } \mathord{\left/ {\vphantom {{s_{CL} } {CL}}} \right. \kern-\nulldelimiterspace} {CL}}$, i.e., an error, it is prudent to crosscheck the intrinsic Tk-GV error calculations. Note that bootstrap regression, which randomizes residuals in time, is not compatible with time-based adaptive fitting. Instead, the Tk-GV parameter errors were crosschecked with LOO (Leave One Out, also called jackknife) analysis of variance for CL and V (373 trials total, resulting from 8 trials for each of the 41, 8-sample patients plus 9 trials for each of 5, 9-sample patients). The resulting jackknife variances are corrected for leaving data out under highly correlated resampling conditions. It is also possible to use L2O (leave two out), L3O, and so forth. To calculate the SD of any parameter of interest, one leaves out data and scales the SD for highly correlated resampling conditions as per [61]. LOO is used only once in Results, Test 1, below. However, leaving out data was also used for testing algorithms, and finding extremes of parameter ranges, as presented next.

Test 2, effects of sample-subset selection on model parameter values

When data is excluded from the fit, parameter values are affected and the errors can become so large as to make a particular procedure unuseful. To explore such effects, a variation of holdout sampling was used that groups the samples into those from the earliest times, all times (the complete set of sample), and samples from the latest times, i.e., (i) fitting the earliest sample times and progressively adding samples from later times until all samples are used, (ii) then dropping samples from early times from the selection in sequence, until only the latest samples remain to be fitted. To still have a statistically independent residual from fitting, the smallest number of samples that can be used for a model with $n_{p}$ parameters is $n_{p} + 1$ samples. There are several motives for using this holdout testing-scheme. One advantage of the holdout technique over bootstrap is not assuming homoscedasticity (uniform variance) of residuals during resampling. Instead, it only uses the actual data (with its native data errors) for testing. Another advantage is that one wants to see what using all samples produces, because that is the usual method of calculating values for an E ₂. Further, one wants to know what happens to the model if the first or last samples are discarded, or the first two or last two samples are discarded, and so forth. Also, this approach includes the recommended times for E ₁ sampling, i.e., 120 to 240 min. Finally, this test examines robustness. These subsets of data were chosen using temporally consecutive samples to span the broadest possible range of mean sampling times. In this way, one can quickly visualize when problems with fitting arise.

A robust model is one that frequently and easily converges to a proper solution. For this test, physically plausible E ₁-fits to the measured data and to simulated data (used as a control) were easy to obtain and E ₁-fits are robust. However, some $E_{2} = k\left( {ae^{ - \lambda 1 \, t} + e^{ - \lambda 2 \, t} } \right)$ fits were problematic, i.e., not robust. Thus, constraints were used to find physically plausible solutions. In specific, the constraints used were $0 \le a \le 5$ and $0 \le \lambda_{2} \le \lambda_{1} \le 2$. Test 2 also examined unconstrained GV fits, ${\text{GV}} = Kt^{\alpha - 1} e^{ - \beta t}$, to the various subsets of sample times. The OLS-GV fitting proved not to be robust. To fix this the constraint β ≥ 0 was imposed. The behavior of OLS-GV and Tk-GV models with respect to the extremes of mean sample times were plotted as the frequency of out of bounds values of α and β for increasing mean sample time. Also of interest is the number of cases for which Tk-GV fits predict vanishingly small CL values. This was examined by leaving out four or fewer samples of the 8 or 9 available for each dilution study.

One can estimate the noise level and the amount of interpolative error contained in fits by plotting an observed variance called the Mean Square Error, MSE. For each patient study, the $MSE = \left( {m - p} \right)^{ - 1} \sum\nolimits_{i = 1}^{m} {R_{i}^{2} }$, where $R_{i}$ is the ith residual (data minus the model value at the ith sample time), m is the number of samples, p is the number of parameters in the fit equation, and m − p adjusts for the number of degrees of freedom. We also performed $E_{1}$ fits to data generated by Monte Carlo simulation of marker concentration data produced by a $E_{1}$ model with a MSE of 0.0009, i.e., from a 3%, 1 SD Gaussian noise error in measuring concentration. Three percent was used as a generous estimate of the SD of the noise, and is larger than the European guidelines suggestion of 3% as an upper limit for error [11].

Finally, one can examine the spread between the MSE from all samples (with possibly the worst interpolative error) with that from fitting the earliest and latest samples (which is closer to noise variance, as any interpolative error present is less severe over shorter ranges). A model that successfully predicts marker concentration over time would have a plot of MSE for temporally increasing mean times of sample time-groupings that is relatively flat and especially should not show systematic trends such as a maximum variance when all of the samples times are used.

Test 3, significance of interpolative error

In Test 3, goodness-of-fit testing of fits to the data was performed for those models that use OLS fitting (i.e., the probability that the error of interpolating marker concentration fitting arose from chance alone). As an average value, the residuals for unconstrained fits should be smaller than for constrained fits as occasionally an unconstrained fit will find a smaller minimum with fit parameters that are outside the region of constraint. Hence, testing the ability of unconstrained fits to fit the data is generally more conservative than testing the constrained fits. Test 3 examines the quality of the interpolative fit, i.e., the middle integral of Eq. 6. This test was done in two ways. The first evaluates the magnitude of the mean residuals for all samples occurring at each sample time-grouping using a one-sample t-test. In general, the one-sample t-test determines the significance of difference in the mean of a sample and a hypothesized mean. A bad fit will have large magnitude t-values and associated probabilities less than 5% for each sample time-group.

The second part of the test measures the goodness of fit of all the samples from the entire study as a group, using Chi-squared. In this case, the probability is the regularized upper incomplete gamma function, ${{\Upgamma \left( {{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2},\chi^{2} } \mathord{\left/ {\vphantom {{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2},\chi^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} \mathord{\left/ {\vphantom {{\Upgamma \left( {{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2},\chi^{2} } \mathord{\left/ {\vphantom {{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2},\chi^{2} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)} {\Upgamma \left( {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}} \right. \kern-\nulldelimiterspace} {\Upgamma \left( {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}$, and is the probability that all the residuals arose merely by chance. A bad fit has a Chi-squared probability of less than 5%.

Characterization of Tk-GV residuals. This examines the structure or temporal trend of the residuals (the differences between the data and the Tk-GV fits) for various Tk smoothings, λ, and renal rate constants, β. In general, one would only expect the mean residuals from ordinary least squares (OLS) regression to be zero for a perfect match between a model and the data. On the other hand, to find a more precise estimate of CL, Tk-GV fitting introduces bias to the otherwise unbiased OLS solution. In other words, for the Tk-GV method, biased residuals from fitting early times are desired given that the terminal GV behavior sought is inappropriate to earlier times. Thus, inspection of these residuals is revealing, and the residuals are examined in some detail in Results, Test 3.

Test 4, extrapolative error

Test 4 evaluates how well the E ₂ model extrapolates beyond the range of the data points. The test used here is the ability of the fit equation to predict future concentration. Extrapolative error, $\varepsilon_{extrap}$, is calculated as follows. Both the fits to the first $m - 1$ and all m samples were performed and evaluated at the time of the mth sample and the concentration difference $E_{2} (m,t_{m} ) - E_{2} (m - 1,t_{m} )$ is called $\varepsilon_{extrap}$. One could as easily have compared $E_{2} (m - 1,t_{m} )$ directly with $C_{obs} (t_{m} )$, but this would include any systemic interpolative error that exists between $E_{2} (m,t_{m} )$ and $C_{obs} (t_{m} )$ and would be a less accurate measure of extrapolative error alone. (See Test 4 for a more graphic presentation.) The extrapolation test yields signed error. The sign of the median error corresponds to a systematic over- or under-estimation of the third integral of Eq. 6. The differences between the logarithms of concentrations from all 46 pairs of fits (to m − 1 and to m samples) were tested for significance with the Wilcoxon signed-ranks sums test. A model with a Wilcoxon $P(\varepsilon_{extrap} ) < 0.05$, is unlikely to extrapolate properly and should be discarded. On the other hand, models with a Wilcoxon $P(\varepsilon_{extrap} ) > 0.05$ might be acceptable, and models with higher P-values correspond to models that are more plausible. The other error measure is precision. The precision for predicting CL and V are measured as the standard deviations of differences between the appropriate m and m − 1 sample functions extrapolated over the interval of t equals 0 to ∞.

Results

Test 1, parameter stability

For OLS $E_{2}$ and GV fits to all data, Test 1 looks at parameter stability using 1000 bootstrap resamplings of each of 46 patient studies. Table 1 shows the breakdown of results for each of the fit parameters from bootstrap as the percentage of parameters that contain zero within their 95% confidence intervals (CIs). Note that for proper parametrization one expects ln k to be quasi-normal and indeed no range estimation problems arose for the constant parameter $\left( {\ln K{\text{ or }}\ln k} \right)$ for any of the models. However, for the $E_{2}$ parameters $a, \, \lambda_{1}$ and $\lambda_{2},$ >50% of the 46 (one per patient study) bootstrap distributions that were fit contained zero within the 95% CI’s as calculated from the SEM (Standard Error of the Mean) for at least one of these parameters. Using SEM to estimate confidence intervals, however, probably over-estimates the frequency for which parameters should be eliminated from the $E_{2}$ model without affecting fit quality. The better, trimmed 95% CI approach suggests a problem only with the distribution of $E_{2}$ renal elimination rate parameter, $\lambda_{2}$, in 19/46 cases. Negative $\lambda_{2}$ implies that concentration increases at late times and is nonphysical. The meaning of this is that the smaller, slower rate constant, $\lambda_{2}$, is the most difficult parameter to detect in a $E_{2}$ model. Perhaps a more direct question would be to ask how frequently one finds $CL \le 0$ from bootstrap, that result being 6.0% of the time or $P = 0.12$, two-tailed. When a parameter does not contribute to the quality of fit of a regression equation, the model is too complex and one would usually discard that parameter (i.e., $\lambda_{2}$). Alternatively, one should constrain $\lambda_{2} > 0$.

Table 1 Test 1. Results for two curve fit models: two exponential terms, E ₂ SET, and gamma variate, GV

As it happens, there is also a problem with the 2.5% trimmed upper tail values of $E_{2}$’s a. The median value of the 2.5% upper tail of a is 7.95. However, the average upper-tail a is 1915, a large number. The frequency of occurrences of $a > 100$ is 12/46 in the 2.5% upper tail. This means that a should be constrained above (i.e., a ≤ 5, see Test 2), or we will allow some models to have $a \gg 100$, i.e., much more initial flow into the deep interstitium than into the central compartment containing the kidneys. This is implausible—see Test 2 Results.

GV’s parameters from bootstrap regression have similar SEM and 5% trimmed ranges. This contrasts to the dissimilarity of the SEM and 5% trimming ranges of the parameters for $E_{2}$—see Table 1. The greater disparity between these measurements in the $E_{2}$ fits results is from a significantly increased number of far outliers for the E ₂ models compared to the GV models. Further, this holds for all of their respective parameters, including CL and V, (P < 0.0001, Table 2). Moreover, CL and V estimated from GV fits are significantly more precise than CL and V estimated from $E_{2}$ (CV, P < 0.0001, Table 2). Note that the CVs for CL and V for $E_{2}$ SET models appear exaggerated compared to the CVs of the GV models. Bootstrap can exaggerate an estimate of CV (just as it does for SEM) due to far outliers and $E_{2}$ SET fitting had significantly more outliers than GV fitting. However, the GV results, which are improved relative to the $E_{2}$ model performance, still yielded β parameter values (renal rate elimination rate) that were statistically indistinguishable from zero one-quarter of the time (Table 1). This is sufficient to reject the OLS GV model as offering a viable procedure with statistically warranted β when all samples are fit. The frequency of inappropriate α and β, GV values changes for different time ranges and this is examined in Test 2.

Table 2 Test 1 results

Characterization of parameters from Tk-GV fits. As per the Methods section, bootstrap is not applicable to the Tk-GV model. Tk-GV’s parameters’ errors are calculated during Tk regularization and were further examined by leaving data out. The most important observation from Table 3 is that the Tk-GV parameters have no silly, nonphysical values and have small measurement errors. For example, the Tk-GV α parameter varied only from 0.59 to 0.99, and no negative (or vanishingly small) β values occurred. Note that ln K is probably normally distributed, P = 0.97, which agrees with an error of measuring K, proportional to K.

Table 3 Test 1, summary of Tk-GV results showing no out-of-bounds, i.e., nonphysical, parameter values. Parameter values do not correspond in adjacent row cells!

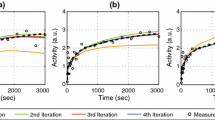
Table 3 does not show a comparison between parameters and for that covariance is examined. The values CL and β covary, and, α closest to 1 and the values of β closest to zero are correlated. This limiting behavior is strong, and otherwise, α and β are not especially related. When the value of CL becomes small, unmodeled dilution increasingly predominates, and it takes more and more regularization to produce a reliable CL estimate (also see Results, Test 3, Characterization of Tk-GV residuals.). Figure 1 shows Tk-GV and E ₂ SETs fits for four cases and a range of CL-values. Tests of these findings under more strenuous conditions are performed in Results, Test 2, Effects of sample-subset selection on Tk-GV model parameters.

Fig. 1

This shows four cases with a range of CL-values. The concentration is in 100/ml or percent (dose) per ml. This allows for comparison between cases. Each sequential case with progressively lower CL is offset to the right in time by a factor of 10ⁱ. For the $i = 0$ case, there is no offset (times 1), and the smoothing, $\lambda$, is 0. The $i = 1,2,3$ cases have $\lambda = 0.0038, \, 0.23, \, 1.6$, respectively, that is, the smoothing increases as CL decreases. Note that for each case $AUC_{E2} < AUC_{\text{Tk-GV}}$ and $CL_{E2} > CL_{\text{Tk-GV}}$

Test 2, effects of sample-subset selection on model parameters

Test 2 uses subsets of actual sample concentrations to build up histograms of parameter values (or derived quantities such as CL and V) when all, or less than all, of the samples are used for fitting. Figure 2 shows results for the $E_{1}$ MSE (mean square error) from 451 trials for the Russell et al. data. Figure 2 also shows MSE when the $E_{1}$ function is fit to Monte Carlo E ₁ simulations with a noise of 0.0009. i.e., a worst case with 3% SD Gaussian noise. This synthetic control data set shows how well the fitting technique perform under ideal conditions, i.e., the underlying truth is a $E_{1}$ and the noise is random and Gaussian. The $E_{1}$ fits to the synthetic data showed an MSE plot that is almost flat for increasing mean fit time and with a recovered MSE that matches (recovers) the known variance of the injected noise. This provides assurance that the fitting techniques and the testing of the variance of fit residuals is working properly. In contrast to this, when 8 samples are included, the $E_{1}$ fits to the actual data (n = 41) from the Russell et al. series have an MSE that is 20 times greater than the simulation, and 2 or 3 times that of the control data when only early- or late-time samples are included. Consequently, the measured variance of $E_{1}$ fits to early- or late-time samples for a large number of cases is not explained by the noise in the data. That is, Fig. 2 shows that $E_{1}$ misfits the data by multiple times the value of a worst-case expected measurement noise.

Fig. 2

Test 2 from the Russell et al. series of 41 patients fit with the logarithm of the SET equations. Behavior of Mean Square Error, MSE, for E ₁ SET (left), and E ₂ SETs, $k\left( {ae^{ - \lambda 1 \, t} + e^{ - \lambda 2 \, t} } \right)$, a and $\lambda_{1}$ parameter behavior (right). Both panels show what happens when data is fit to temporally sequential samples. For example, 1 to 5 on the (left) x-axis means the first through fifth sampling times from 10, 20, 30, 45, 60, 120, 180 and 240 min, i.e., 10 to 60 min. This creates a hump for MSE. The hump is due to a misfit between model and data as illustrated by the circles, which are from 41 Monte Carlo simulations of E ₁ functions with a constant noise of (logarithm) concentration of 0.0009. The histogram (right) from Test 2 (n = 332) shows two populations for the parameters a and $\lambda_{1}$ obtained from constrained regression. One population contained a values ranging from 0.302 to 4.80 with $\lambda_{1}$ values from 0.00276 to 0.312. The second population contained 55 $\lambda_{1} = 5$ with a values ranging from 0.00707 to 2

Interestingly, there were no degenerate fits for either the $E_{1}$ fits to the data or the $E_{1}$ simulations. However, plotting MSE for the E ₂ fits would be misleading given the high frequency of problems with the $E_{2}$ fits (Table 4). For testing the ability of $E_{2}$ models to provide reliable results, we formed a total of 332 subsets from the 46 patient data. These subset included 5 or more samples from each patient study (because $E_{2}$ has 4 parameters).

Table 4 Test 2, results of $E_{2} = k\left( {ae^{ - \lambda 1 \, t} + e^{ - \lambda 2 \, t} } \right) \,$ fit attempts using the constraints $0 \le a \le 5$ and $0 \le \lambda_{2} \le \lambda_{1} \le 2$

For $E_{2}$ model fit attempts, Test 2 used the constraints $0 \le a \le 5$ and $0 \le \lambda_{2} \le \lambda_{1} \le 2$. The constraint $\lambda_{2} \ge 0$ prevented infinite concentration as a limit as time goes to infinity by prohibiting negative $\lambda_{2}$. However, this constraint many times pinned the $\lambda_{2}$ parameter at zero suggesting that this variable should be discarded. That is, the constraint converted the 4.5% negative $\lambda_{2}$ results into $E_{2} \left( {\lambda_{2} = 0} \right)$ $= k\left( {ae^{ - \lambda 1 \, t} + 1} \right)$. In these fifteen $E_{2} \left( {\lambda_{2} = 0} \right)$ out of 332 fits, CL is also zero, i.e., poorly estimated. When this occurred, the magnitude of $\lambda_{1}$ was smaller than usual and closer in magnitude to the usual values for $\lambda_{2}$.

The values of 5 for a and 2 for $\lambda_{1}$ were the upper limit constraint values for those parameters. The degenerate form, $E_{2} \left( {\lambda_{1} = 2} \right) = k\left( {5e^{ - 2t} + e^{ - \lambda 2 \, t} } \right)$, occurred in 11/332 or 3.3% of the fits. All of these occurred when the earliest-time samples included in the data set being fit were the 3rd, 4th or 5th temporal samples. In these cases, the fast exponential term was $< 5 \times 10^{ - 13}$ in magnitude, i.e., not reliably detected without the earliest-time data.

The constraint α < 5 was useful in preventing implausible outliers, and this yielded better extrapolation results (Test 4) than the unconstrained alternative. The lowest a-value detected was a = 0.302, see Fig. 2. However, in agreement with the bootstrap results, there were a number of cases in which high values of a occurred. Figure 2 shows that the a and $\lambda_{1}$ values can be viewed as grouped into two separate populations. These groupings may not really be separate populations. It is just that if a were not tightly constrained from above, there would be numerous very large outlier values of a, and, Eq. 10 would provide poor quality estimates for CL. As per Table 4, including the single $\lambda_{1} = \lambda_{2}$ fit (in effect, an E ₁ fit result), we encountered a grand total of 8.1% or 27/332 problematic E ₂ fits. If one were also to consider all the a = 5 values at the constraint boundary to be implausible, 71/332 or 21.4% of solutions are at least somewhat disturbing. Fortunately, for fits to data with all time samples, or for all time samples save the latest time sample, unconstrained fits converged to physically permitted values. Moreover, for these sample choices, the constrained regressions did not have implausible $\lambda_{1}$-value solutions at the constraint boundaries. Thus, Tests 3 and 4 could be performed without discarding any E ₂ fits for being degenerate.

Test 2, Effects of sample-subset selection on OLS GV and Tk-GV model parameters. Figure 3 shows the frequency of occurrence of problematic values for the parameters α and β from OLS-GV and Tk-GV fits to subsets of samples taken from the 41 cases from the 8 sample Russell et al. data (The 5 cases with 9 samples are not shown to keep it simple.) Each plot presents from left to right, the earliest- to latest-time subsets. For OLS-GV fitting, there are no subsets that do not contain a model with β pinned to the β ≥ 0 boundary or have α > 1. The β = 0 results from OLS fitting constrained by β ≥ 0, would have produced negative β values without the constraint, and are obviously incorrect. As per the Introduction, α > 1 is a non-physical result. Moreover, Fig. 3 shows that the α > 1 frequency increases for OLS fits to late-time data only, just when β = 0 becomes infrequent, which is also problematic. Figure 3 suggests a major improvement in conditioning of the Tk-GV versus the OLS GV models. It is clear that β ≈ 0 occurrences are significantly less frequent for Tk-GV (1/369) than for OLS GV constrained fitting (62/369). From Fig. 3, the Tk-GV versus OLS GV fitting, the frequency of α > 1 (11/369 versus 26/369) is also less for leaving out samples by this method. For Tk-GV fitting, from Fig. 3, the three earliest and the three latest sample subsets contain problematic α > 1 solutions and in one instance a β ≈ 0 solution. If an α ≤ 1 constraint were used this would produce a $E_{1}$, a single exponential term (i.e., low quality, inflated CL estimating) fit would result. Consequently, the best strategy is to include enough sampling time between the first and last samples to avoid an appreciable likelihood of producing an α > 1 fit or, when inappropriate, a β ≈ 0 result.

Fig. 3

Test 2 results from OLS GV function (left) and Tk-GV regression (right) fits to 41 patients from the Russell et al. series of concentration samples. OLS-GV (left) constrained by $\beta \ge 0$ gradually finds fewer $\beta = 0$ (and CL = 0) solutions as the selections are chosen later. This is a maximum of 21/41 or 51% CL = 0 solutions for fits to the 1st through 4th samples and a minimum of 1/41 at the 5th through 8th samples. Also plotted are the numbers of times that $\alpha > 1$ are encountered. Note that $\alpha > 1$ does not occur when all samples are included, or when a maximum of two last samples are left out. From Tk-GV fits (right) the open circles with dashed lines show the frequency of α being out of bounds $\left( {\alpha > 1} \right)$ for subsets of all samples. Problems with detection of CL are shown with solid circles and solid lines, i.e., for β close to zero $\left( {\beta < 1 \cdot 10^{ - 7} , \, CL < 0.001} \right)$. Note that there are no questionable results for α or β when only one sample or no samples are left out, i.e., samples sets 1 to 7, 1 to 8, and 2 to 8

The trend noted in Test 1 above for the Tk-GV model was that as $\alpha \to 1$, $\beta \to 0$. Indeed, $\alpha \to 1$ quickly, and $V \to {{CL} \mathord{\left/ {\vphantom {{CL} \beta }} \right. \kern-\nulldelimiterspace} \beta }$ becomes a constant ratio. To see how this arises, as $\Upgamma \left( 1 \right) = 1$, by using the form of Eq. 14 employing κ, one obtains that for low function ($\alpha \approx 1$), ${{CL} \mathord{\left/ {\vphantom {{CL} \beta }} \right. \kern-\nulldelimiterspace} \beta } \approx {D \mathord{\left/ {\vphantom {D \kappa }} \right. \kern-\nulldelimiterspace} \kappa } \approx V$. Now since concentration is relatively static for low function, and since κ, the concentration constant, is even tamer, then both V and vanishingly small CL should be accurately and simultaneously measurable. This limiting behavior is a result of minimizing the relative error in CL given by Eq. A3, which then effectively acts as an additional constraint equation. So for Tk-GV, if $\mathop {\lim }\limits_{\alpha \to 1} \beta \to 0$, then one should be able to use the Tk-GV method to measure CL and V for patients with very low CL as then ${{CL} \mathord{\left/ {\vphantom {{CL} \beta }} \right. \kern-\nulldelimiterspace} \beta } \approx {D \mathord{\left/ {\vphantom {D \kappa }} \right. \kern-\nulldelimiterspace} \kappa }$ $\approx V$ are constants.

When one has fewer samples to fit, one begins to find $\beta \approx 0$ solutions, which show $\mathop {\lim }\limits_{\alpha \to 1} \beta \to 0$. Amongst the 7963 combinations for leaving out 4 or fewer samples, we encountered trivially small values for β and CL only 9 times (0.11%) and all for the same patient. These occurred for patient 20 when at least the 7th and 8th samples (i.e., the last two) are left out. Using all samples, patient 20 has the smallest CL (1.24 ml/min) of the 46 patients, and a V of 11631 ml, found with a relatively high λ = 1.61 and high α = 0.9895. The median CL for patient 20 with L4O (i.e., from 4 samples) is 1.69 ml/min, (compared to the all–8 sample data set result of 1.24 ml/min.) However, of the 70 L4O trials for patient 20, there are 5 sample combinations (7.14%) with nearly zero renal function. These examples show how remarkably stable the determination of V is for the Tk-GV method. For patient 20, if one leaves out samples 1, 4, 7, and 8 the resulting Tk-GV parameters become α = 1 (exactly to 40 decimal places), $\lambda = 7. 3 4\cdot 1 0^{ 4 1}$ (very high regularization), $CL = 1.71 \cdot 10^{ - 43}$ ml/min, $\beta = 1.53 \cdot 10^{ - 47}$min⁻¹, and V = 11164 ml. This strongly demonstrates that the ratio of CL to β, i.e., V, is preserved by the Tk-GV method even when renal function is vanishingly small. An upper limit of α = 1 was not found in prior works which performed OLS GV fits [20]. However, α ≤ 1 is consistent with $CL_{total} > CL_{urine}$, i.e., total plasma clearance is greater than renal clearance from urinary collection. When α ≈ 1, yielding vanishingly small CL-values, the Tk-GV method found a GV fit with a constant concentration, C(t) ≈ K. So leaving out data can make the data noisier, and cause a problem in detecting already small CL. In that case, the residuals, C _obs (t) − C(t), become $C_{obs} \left( t \right) - K$. This is further explored in Results, Test 3.

In practice, it seems that one needs to include both early and late-time samples to provide good conditioning to the fit in the sense of avoiding α > 1 solutions. For the leave out 4 or fewer samples, there are 7963 different subsets of the data, having a total of 99 fits that produce a value of α greater than 1 (1.24% of all of the trials). For the 4874 trials that included the first sample, there were only 6 with α > 1 (0.12% of the 4874 trials). One should also note the good result that as long as both the 10 and 240 min samples are included, only 4 samples total are needed to obtain a Tk-GV solution. These solutions are not much different than using twice as many samples; see Results, Test 4, Comparison with published values, below.

Test 3, significance of interpolative error

Test 3 examines the goodness of fit of the mean of residuals relative to an expected residual of zero. Test 3 also examined the Chi-squared statistics for the joint probability of a zero mean of residuals for the Russell et al. data of Table 5. For the $E_{1}$ model, the Chi-squared probability would accept the model as plausible (P = 0.2) so long as the recommended 2 to 4 h sampling times are used. However, the $E_{1}$ model had a low probability of fitting each sample correctly as the extreme residuals (at early- and late-times) were significantly positive and the middle residual(s) significantly negative (Sample groups 6 through 8, t-statistics: 2.22, −2.25, 2.25). Not shown in Table 5 is that this curvature mismatch was more pronounced between 60 and 240 min (Sample groups 5 through 8, t-statistics: 5.59, −4.98, −3.77, 5.48), and for all other fits to samples with more sampling times.

Table 5 Test 3 results

Unconstrained $E_{2}$ models were applied to all of the available samples. The unconstrained fits used here often have similar, but sometimes (2/46 with a slightly greater than 5) smaller magnitude residuals than the corresponding constrained fits. Fortunately, using all samples, the resulting unconstrained fits are not unphysical. Thus, it is (slightly) more conservative to use unconstrained, rather than constrained, fitting to generate residuals for this test. Table 3 shows this for the 8 time-sample data from Russell et al., the $E_{2}$ residuals are usually larger than is expected on the basis of random noise. The low probabilities that mean residuals this large (or larger) occur at random shows a significant failure of $E_{2}$ to fit adequately most (6/8) of the data at single sample times, especially the samples with the two earliest times (probability that this occurred randomly is P ≤ 0.0002). The joint probability for the residuals at all sample times was then calculated from the Chi-squared goodness-of-fit statistic, where n is the number of samples times the number of cases or 8 × 41 = 328 degrees of freedom. This probability, as per Table 5, is 0.025, making it unlikely that the misfits of $E_{2}$ models to the data are due to noise alone. Moreover, when the Chi-squared goodness of fit is extended to all 46 patients in both data sets (with 373 degrees of freedom), P = 0.039, or an insignificant chance that the mean residuals at each group of sample times arose from noise alone. These goodness-of-fit test results provide evidence that $E_{2}$ does not interpolate properly. Summarizing both $E_{1}$ and $E_{2}$ SET model results, the Student’s-t probabilities for each group of sample times shows improper interpolation. How can one then expect SETs to do the harder job of extrapolating properly?

Test 3 also examined the GV function goodness-of-fit t-testing and Chi-squared testing for the Russell et al. data of Table 5. Furthermore, for GV fitting, the added disadvantage of using β ≥ 0 constrained fitting was compared to the more liberal unconstrained $E_{1}$ and $E_{2}$ SET fitting to construct Table 5. Despite this additional disadvantage, the GV model clearly outperformed the two SET models. As shown in Table 5, there were no good fits from the $E_{1}$ and $E_{2}$ models, as either the Student’s-t or Chi-squared probabilities or both were insignificant. For the GV model, as long as the data before 20 min was not used, all the t-statistics and Chi-squared values indicated a significantly good fit. Indeed, when only the last four samples times were used, the t-statistics were small, i.e., $\left| {t{\text{ - statistic}}} \right| < 0.2$, indicating a very good fit.

Characterization of Tk-GV residuals. Figure 4 shows the mean residuals from Tk-GV regressions of the 41 Russell et al. cases. These residuals are plotted for LOO fits in 8 equal octiles of increasing shrinkage values having 41 regressions in each octile or 328 in total. When λ = 0, the Tk-GV solution is unbiased and identical to the OLS solution. As can be seen in Fig. 4, when the shrinkage, λ, is very small, the residual function, or difference between the fit and the concentrations, is also small (mean first octile λ = 0.001, and more generally for all 46 LOO series, λ = 0, 17/373 times or 4.6%). This is consistent with the smallest relative errors for measuring CL corresponding to the smallest λ, and the largest CL values. That is, for high normal renal function, the GV model sometimes fits the data without the need for Tk smoothing. Figure 4 confirms that for high renal elimination rates, β, the residuals are small. As the λ values increase in Fig. 4, and the β values decrease, the residuals especially for the earliest sample(s) increase so that the fit then underestimates the concentrations. Moreover, for large λ or low β values, the fit overestimates the concentrations of the late samples. In summary, as the shrinkage increases, so too does the regression bias needed to find the Tk-GV fit with the correct late-time behavior and minimum error in CL. Figure 4 shows graphically how large the bias becomes when estimating very low renal function. In effect, when there is zero renal function, the Tk-GV fit is a flat-line, and the residual concentration reflects unmodeled dilution, with high initial concentration, that decreases with time. On the other hand, when λ = 0 and there is high CL, the Tk-GV fit solutions becomes OLS GV regressions and fit the concentration curves well.

Fig. 4

From Tk-GV applied to the Russell et al. data, residual concentrations (100/ml, not as logarithms) for each of 8 samples from 328 LOO trials are grouped into 8 octiles. Sorted (left) into octiles of increasing shrinkage, λ, are mean residuals and sample number. Note that the residual concentrations are unbiased for low shrinkage, and increasingly biased for progressively larger shrinkage. Sorted (right) into octiles of decreasing renal rate constant β are mean residuals versus β and sample number. Note that the residuals are unbiased for high elimination rates, and more biased for low renal function

Test 4, extrapolative error

Test 4 examined whether the E ₂ SET, GV and Tk-GV models accurately extrapolate beyond the range of the measurement times. For noisy data and good models, extrapolations will produce half of their predictions in the extrapolated range above the actual value and half below. Models whose median extrapolated values do not coincide with the expected value will produce a biased value for Est-AUC.

Extrapolation results are summarized in Table 6. The worst extrapolations were for E ₂ SET models having 31 of 46 extrapolations under-predict the interpolative values from the fit to all the data at the latest sampling time. The Wilcoxon signed-ranks sum test gives this a two-tailed probability of P = 0.0046 of the extrapolated values being an unbiased predictor of the median for unconstrained fits (with less powerful sign test P = 0.026, 2-tailed), and a Wilcoxon P = 0.0071 for constrained fits. Figure 5 shows a typical E ₂ result for the ¹⁶⁹Yb-DTPA data. This is a middle-of-the-road case with midrange renal function, and typical underestimation of future concentration using E ₂. Note that the last data point to the right is also slightly above the interpolative values from the fit to all of the temporal samples. This is the typical result in our fits and is consistent with significant interpolative error at that point (in Table 5, P = 0.037, n = 41). From this test, we learn that E ₂ SETs is a poor model for marker concentration because it too frequently (31/46, sign test P = 0.026) underestimates the last sample value, which in turn suggests that the Est-AUC calculated from E ₂ models will be systematically too small.

Table 6 Test 4 results from extrapolation testing using the Wilcoxon signed-ranks sum test.^a Over- or underestimation of extrapolated ln C(t) values for five fit methods. Note that Tk-GV extrapolated best

Fig. 5

Test 4 example. The y-axis units are ln(100/ml), i.e., logarithm of percentage (of total dose) per ml. Shown is the serious problem of extrapolation to values that are in general lower than the expected concentration. Shown for the 8th data point is the interpolation error (in err) and extrapolation error (ex err). At 240 min, the extrapolation of the fit to the first 7 samples (dashed line) noticeably underestimates both the fit to all samples (solid line) and the 8th sample concentration itself

Test 4 also examined the GV function’s performance for extrapolation. The difference between the concentrations at the time of the mth sample between the fit to m samples and m-1 samples was positive 22 times and negative 24 times. This shows that proper extrapolation cannot be ruled out by the sign test (P = 0.88, 2-tailed) or the Wilcoxon test (P = 0.24, two-tailed). Using β ≥ 0 constrained GV fitting, the Wilcoxon probability becomes P = 0.76 (two-tailed), with no change in the sign test result. In other words, one cannot discard the GV as a properly extrapolating function for the data set used here. (OLS-GV fitting fails Tests 1 and 2.)

Test 4 examined extrapolation of the Tk-GV model. The best extrapolation, from Tk-GV, has a Wilcoxon test probability of 0.91 of the errors being from random noise. Hence, the Tk-GV method offers better assurance that AUC will be correctly estimated than by using the other methods of Table 6. Calculation of CL uses extrapolation of the concentration curve to infinity to find the AUC estimate. Since the Tk-GV method extrapolates better than other methods, the Tk-GV method’s value for CL should be more accurate as well. Fortunately, this can be tested.

CL values were calculated for the first m − 1 samples versus all m samples, and the effects of extrapolation on CL values examined. Table 7 shows this for the Tk-GV model and for the constrained E₂ SET model, which provided the best SET-model performance. From Table 7, one can see that the benefit of waiting another 65 min after the next to last sample to take a last sample is to reduce the value of $CL_{\text{Tk - GV}}$ by about 0.5 ml/min and to reduce constrained $CL_{E2}$ by from 1 to 4 ml/min. Also note that the change in mean CL, i.e., the ΔCL values, the $s_{CL}$ (SD of CL) and CV of CL are all improved for the Tk-GV model versus the constrained E₂ SET model. The $s_{CL}$ were pair-wise tested with Wilcoxon signed-ranks sum test for improvement in performance of the Tk-GV method as compared to constrained fits with an E₂ SET model. This showed that the precision of$CL_{\text{Tk-GV}}$was significantly better than that of$CL_{E2}$ (P = 0.045, two-tailed). Another question is whether the 0.5 ml/min drop in $CL_{\text{Tk-GV}}$ from fits to m rather than m − 1 samples is significant. The Wilcoxon signed-ranks sum test of the 46 paired differences is P = 0.23, two-tailed, or not significant. However, the same calculation for the constrained $CL_{E2}$ is significant (P = 0.0049, two-tailed). Reiterating, $CL_{\text{Tk-GV}}$was not significantly altered and constrained$CL_{E2}$lost significant estimated CL by adding another period of an additional average of 65 min to take a last 8th (or 9th) sample. Not shown in Table 7 are the V results for both models.

Table 7 Test 4 difference between CL (ml/min) values without the last sample (m−1) and with all m samples for the Tk-GV and constrained E ₂ SET models

As calculated from the Tk-GV fit parameters, V was 16378 ± 644 ml (mean ± mean s _V ) with a mean CV of 4.04%. For the constrained E ₂ SET model, V was 15281 ± 1589 ml with a mean CV of 9.49%. This suggests that use of the Tk-GV method represents a major increase in precision in the determination of V and that this reduction in V’s CV is very significant (P = 0.0014, Wilcoxon, two-tailed). Summarizing, the Tk-GV model parameters were significantly less altered by varying the number of samples fit than constrained E ₂ SETs.

Given this evidence that Tk-GV is the superior method, an appropriate question is how this compares to the results from constant infusion of inulin and AUC with exponential extrapolation, which latter are often touted as the gold standards for such measurements. To assess this, one can compare our results to those of methods in the literature. This is done next.

Comparison with published values

Florijn et al. [39] show that use of E ₂ overestimates plasma clearance from constant infusion of inulin and that $CL_{total} > CL_{urine}$. Florijn et al.’s scaling of CL conversion between methods was done by the method of Du Bois and Du Bois [62]: $E\left( {BSA} \right) = 0.007184W^{0.425} H^{0.725}$ in m², where W is patient mass in kg, and H is patient crown-heal height in cm. In short, Florijn et al. give a 5.1 ml/min/1.73 m² greater $CL_{E2}$ than $CL_{total}$. The comparable number from the 46 studies here is 6.1 ml/min/1.73 m², see Table 8. Our $CL_{E2} - CL_{\text{Tk-GV}}$ value is similar to Florijn et al.’s $CL_{E2} - CL_{total}$ result, and the difference observed by Florijn et al.’s is within our 95% CI. If one accepts this result at face value, one concludes that $CL_{\text{Tk-GV}} \approx CL_{total}$, which is significantly more accurate than $CL_{E2}$.

Table 8 Comparison of $CL_{E2}$, $CL_{total}$ and $CL_{urine}$ plasma clearances from three sources. Note that $CL_{\text{Tk-GV}}$ is more accurate than $CL_{E2}$, yet is within the CI for constant infusion and 24 h AUC

Testing of Florijn et al.’s scaling methods was performed with ANOVA (analysis of variance). Note that more precision for a regression formula need not be significantly more precision, when applying the ANOVA requirement that the probability for each model’s parameter(s) partial correlation coefficient achieves significance. Even a comparison of R-values or standard errors adjusted for highly correlated conditions (rarely used correctly) would yield probabilities that have no bearing on the ANOVA requirements for significance. Our result,

$$ {\frac{{CL_{E2} }}{BSA}} = {\frac{{CL_{\text{Tk - GV}} }}{BSA}} + 6.1\, {\text{ml}}/{ \min }/ 1. 7 3 {\text{ m}}^{ 2} , $$

(21)

has a large standard error of estimation for CL of 5.0 ml/min/1.73 m² with R² = 0.9869. However, the exponents of W and H of Eq. 21 (in BSA) are not statistically warranted (P > 0.1, ANOVA). This is expected as catabolism promotes CL and BSA has been shown to be spuriously correlated to CL [63, 64]. To calculate better scaling, one uses the mean $CL_{\text{Tk-GV}}$ value of 74.47 ml/min and the mean $\beta_{\text{Tk-GV}}$ value of 0.003614 s⁻¹, and obtains

$$ CL_{E2} = 1.106 \times 74.47\left( {{\frac{{CL_{\text{Tk-GV}} }}{74.47}}} \right)^{0.9972} \left( {{\frac{{\beta_{\text{Tk-GV}} }}{0.003614}}} \right)^{ - 0.1155} {\text{ml}}/{ \min }, $$

(22)

which reduces the standard error of estimation to 4.2 ml/min, and increases the R² to 0.9919. Note that in Eq. 22, the offset has been dropped as being probably not different from zero (0.1 ml/min, P(offset = 0) = 0.96, two-tailed t-test). Similarly, the $CL_{\text{Tk-GV}}$ 0.9972 exponent could be changed to one without changing the equation significantly. The constant multiplier 1.106 suggests a 10.6% higher $CL_{E2}$ than weighted mean $CL_{\text{Tk-GV}}$ value. Compared to their respective standard methods, the 10% overestimation of CL from 4 h of data from Moore et al. and the 10.6% (95% CI, 8.6% to 12.7%) overestimation by $CL_{E2}$ from Table 8 imply comparable exponential fit underestimations of late AUC values. Thus, the CL _TK-GV-values from 4-h of data correspond to 24-h CL-value estimates from Moore et al. with the difference, 0.6% (0.04 SD), being insignificant.

Equations 21 and 22 are imprecise because the E ₂ SET renal elimination rate parameter is statistically unwarranted (P = 0.12, two-tailed, see Test 1). Using all samples and the E ₁ SET model, one finds a better regression fit,

$$ CL_{E1} = 1.135 \times 74.47\left( {{\frac{{CL_{\text{Tk-GV}} }}{74.47}}} \right)^{1.038} \left( {{\frac{{\beta_{\text{Tk-GV}} }}{0.003614}}} \right)^{ - 0.2102} + 5.967, $$

(23)

where the standard error is 3.4 ml/min., and R² = 0.9947. And, an offset appears probable as P(offset = 0) = 0.005. Eq. 23 does not fail ANOVA t-testing, and is more precise than Eqs. 21 and 22, which do fail ANOVA t-testing in one way or another. However, the E ₁ fit to the data fails t-testing for goodness of fit (Test 3).

Although one can use a formula like Eq. 21 to compare with published values, $CL_{E2}$ is unnecessary for modeling our data. If one has inert marker data enough to calculate a $CL_{E2}$ then the best conversion just calculates the more accurate and precise $CL_{\text{Tk-GV}}$ for that data. Being robust, $CL_{\text{Tk-GV}}$ only needs 4 samples for a solution. For example, if one chooses the 10, 30, 120, and 240 min Russell et al. samples and compares this to using all 8 samples then

$$ CL_{\text{Tk-GV}} ( 4 {\text{ samples)}} = 0.9992 \, CL_{\text{Tk-GV}} ( 8 {\text{ samples)}} $$

(24)

with a standard error of 2.7 ml/min and R² = 0.9965, where a non-zero intercept is unlikely P(offset = 0) = 0.91, and a slope of one is plausible (95% CI, 0.9895–1.0089).

Discussion

The properties of a good model for renal markers are (i) to interpolate $C_{obs}$ accurately over short time intervals, and (ii) yield a terminal or limiting function for the concentration curve with a good fit to the data, i.e., it should extrapolate correctly so that the Est-AUC accurately predicts Phy-AUC. (iii) It should contain as few parameters in number as possible, parameters whose non-degenerate values are physically interpretable and whose errors are small so that plasma clearance and volume of distribution can be precisely calculated.

In otherwise totally unrelated work in children with normal renal function, some of us found that CL-values determined from ^99mTc-DTPA E ₁ SET models scale for body size as approximately proportional to $V^{2/3} W^{1/4}$, where V is volume of distribution, and W is patient mass in kg [63, 64]. In the language of West et al. [65–67], this V, W scaling formula (with V estimated from E ₁ fits) suggested an underlying fractal network as the root of this functional dependency. However, the two propositions, that of an E ₁ (i.e., not scale invariant) and that of fractal (i.e., scale-free) model are somewhat antithetical and hence paradoxical. This prompted a search for a scalable model for DTPA radiochelates that led to the GV function. We are not the first authors to postulate a fractal model for dilution curves [30, 31]. Such structures are scale-free, and must be described by mathematical formulas that are also scale-free, e.g., power functions. Generally, biological fractal structures show self-similarity, e.g., branching structures, independent of magnification down to the small-scale limit (interstitial terminal spaces, in the context of DTPA chelates) of those branching structures. How the body introduces a power function of time in the GV function, which seems to best reflect the late-time concentrations of markers, is a matter of conjecture [e.g., see 20,31]. Moreover, GV functions model require adaptation for practical usage.

The need to impose constraints to control parameter instability is inappropriate for sensible modeling. Imposing constraints, i.e., insisting on physical solutions, in SET modeling is occasionally performed by its proponents. For example Russell et al. [57] use a Bayesian prior approach to E ₂ fitting and Khinkis et al. [68] use constrained optimization techniques. Without constraints, non-physical results may occur as per Table 1. There are no ideal values for the upper constraints for the fast rate constant (λ₁) or the relative first to second exponential initial flow (a). Furthermore, constraints were also imposed on OLS-GV fitting, and the need for this was blatant. That is, negative renal rate constants (β) sometimes occurred.

The typical argument for the use of SETs is that they fit the plasma disappearance curve well. SET models arise naturally from separate, linearly-coupled, fast mixing compartments. The notion of SETs forming a complete basis, i.e., that anything can be described by SETs, is so ingrained that one often neglects the obvious, that not every basis is efficient for every problem. Sine and cosine functions also form a complete basis, and that is insufficient grounds to recommend using that basis to fit marker concentration curves. Concerning efficiency, E ₁ fits to the data have multiple times larger residuals than an E ₁ simulation using exaggerated noise levels (see Fig. 2 and Results, Test 1). E ₁ proved to be an arbitrary model in that it much less efficiently fitted the data than expected for a properly matched two-parameter model/data combination. Test 2 finds that E ₂ models are overly complex and that the increase in fit quality over an E ₁ model provided by adding another exponential term is unwarranted P(λ ₂ = 0) > 0.05. The additional constant multiplier and exponential coefficient of the second exponential term too frequently resulted in degenerate forms (Results, Test 1, and Table 4). There is a clearly identifiable physical model for SETs, which sets an example for physical modeling. The authors are quick to point out, that there is nothing wrong with compartmental theory; SETs just do not fit or span the bolus plasma–dilution curves for DTPA radiochelates properly, and should not be used for that purpose.

SET models underestimate concentrations at late times and are known to underestimate Phy-AUC over the entire range of CL-values, necessitating correction factors to reduce the calculated values for CL for the E ₁ and E ₂ SET (or equivalent) models [10, 11, 24, 39]. Current guidelines suggest that CL from E ₁ SET models should be multiplied by 0.87, called the Chantler correction factor, which implies that AUC is underestimated by a factor of 0.87 [10, 11, 69]. Also, for E ₂ SETs, we are not the first authors to find that they overestimate CL [23, 39]. We may, however, be the first to give a global reason for this occurring. When E ₂ extrapolation was performed, E ₂ was also found to overestimate CL, and in general, E _n overestimates CL. Indeed, the under-extrapolation of AUC is from the native shape of exponentials. Exponentials go to zero too quickly and cannot mimic the true shape of inert marker concentration curves, and this defect cannot easily be eliminated by increasing the number of exponential terms. After observing slow redistribution in nephrectomized dogs, i.e., with $CL_{urine} = 0$, Schloerb warned us to expect SET models to fail [17]. Indeed, the findings of improper extrapolation for E ₂ and mismatched curve shape of E ₁ fits to late data argue (Table 5) against the notion of a “terminal exponential” for the concentration curve. In other words, just because all SETs eventually become a straight line on a plot of logarithm of concentration, does not imply that the logarithm of concentration curves of data become linear with elapsed time. That is, SETs models always converge to zero concentration at a constant rate of dilution for late times, where, physically speaking, a decreasing rate of dilution occurs at late times from Eq. 1: $CL_{total} = CL_{body} + CL_{urine}$, where $CL_{body}$ slowly decreases in time. Larson and Cox [1974, 18] related that an E ₂ fit to plasma ²⁴Na concentrations had different coefficients when fit from data decayed to 1% of the initial value, compared to slower coefficients from a fit containing even more data, and 72 h whole body ⁵¹Cr-EDTA retention has been measured as 4.5% [1969, 41]. So the evidence for $CL_{body}$ slowly decreasing in time has been available for a long time.

One workaround for using SET models is to attempt to optimize the fitting of poorly fitting SET functions (e.g., see [57, 68, 70]). Another workaround for using SET models when renal function is low is to extend the data collection to include very late times. Chantler and Barrett [69] cite Maisey et al. [71] relating that “Though the tracer is substantially equilibrated by 2 h in the normal subject, complete equilibration probably takes much longer. The fraction not equilibrated by 2 h, however, is so small that it cannot be detected in relation to a fast clearance, but in the presence of renal failure (GFR [sic, CL], 15 ml/min per 1.73 m²), the apparent clearance of this small fraction into the tissues becomes more important in relation to the renal clearance and accurate estimates of GFR (sic, CL) require plasma sampling for up to 6 to 8 h.” This comment is optimistic for the E ₁ fit being referred to, and for which we detected a departure from good fitting at 2 h—see Table 5. However, Chantler and Barrett’s observation does apply to the OLS GV-model, which fit 1–4 h concentrations well. That is, with one caveat, namely that these good fits are problematic for finding CL. So, it would seem, the only expedient solution is to use Tk-GV, and let the adaptive smoothing find the correct values for CL when $CL_{body}$ is larger than usual compared to $CL_{urine}$.

For the clearance problem, the OLS-GV model has less wayward assumptions than SET models. For example, the GV model can explain that plasma clearance of a marker is faster than urinary collection of that same marker, because the sense of the body clearance term, (α − 1)/t of Eq. 18, is a loss from plasma that never appears in urine, i.e., that 0 < α ≤ 1. Further, as Table 5 shows, the GV function fits the late samples precisely, where SETs offer only poor fits.

Is the adaptation of the gamma variate, GV, to the plasma clearance of radiolabeled chelates incomplete? For example, Wise [20] and later Macheras [31] merely used power functions, or a GV with β = 0, for those cases or for early data for each case in which the β rate constant was “undetectable” (sic-unphysically negative), and claimed that it is only the last few samples that determine this rate constant. The late samples do not determine detectability. Five of 46 cases had an incorrect β when all samples were used for fitting. In agreement with Table 5, the most plausible explanation for this is that the OLS GV fit procedure is less appropriate for earlier-time data, and thus the GV is an incomplete model. Rather, the use of only late samples avoids modeling earlier dilution that is not related to the GV function (or a power function), the inclusion of which would cause detection of the wrong value of β. Only one of 46 cases (Results; Test 3, above) had an incorrect β value when only the last four blood samples were used for GV fitting. However, as shown in Fig. 3, if only the last four samples are used for OLS GV fitting, then β = 0 becomes infrequent (1/41 and 1/46), just when α > 1 becomes frequent (12/41 and 14/46). Unfortunately, results with α > 1 are implausible, so the OLS-GV model is not useful by itself. What then causes occasional α > 1 results when the latest four samples of the 4-h DTPA data are fit with a GV? In those cases, the GV fit is unstable not in the region of the well-fit data, but at the t-axis intercept where the extrapolated value may have any concentration ranging from 0 to infinity.

In formal language, finding CL from $CL_{\text{GV}} = D\left( {\int_{0}^{\infty } {{\text{GV}}\left( t \right)dt} } \right)^{ - 1}$ is challenging because the integral is ill-posed, i.e., it depends sensitively on the ability of the OLS GV fit to correctly extrapolate (integrals i and iii) in Eq. 6, and these extrapolations depend sensitively on the specifics of the data. The ill-posed nature of $CL_{\text{GV}}$ was solved by introducing $CL_{\text{Tk-GV}}$, i.e., regularizing the fitting procedure and hence stabilizing the method so that it is less sensitive to data specifics. An additional strong benefit is that the Tk-GV regularization also adapts to minimize the relative error of CL. To be useful, this regularization must weight the early- and late-time data in such a way that α and β exhibit ranges that are physical. Notice, however, that the GV model, even when regularized properly, is still an incomplete model.

Tk-GV, a solution for the ill-posed clearance problem

The results show (see Fig. 3) that Tk-GV fits have significantly better performance for predicting α and especially for β than from OLS GV fits. Indeed, β ill-conditioning renders OLS GV fitting useless for determining inert marker CL. As above, marker is always strictly lost to the interstitium, thus α ≤ 1. Moreover, α ≤ 1 results were obtained for Tk-GV fitting at least when the sample times chosen were of sufficient temporal range to allow for good conditioning of those fits. An alternative view is that since the magnitude of the plasma clearance to tissue, (α − 1)/t of Eq. 18, is ever decreasing (it is proportional to 1/t), it only represents loss to parts of the interstitium that are not in rough concentration equilibrium with the plasma. In such a view, portions of the interstitium that are in more intimate contact with the plasma, with fast exchange times ≪ t, readily exchange marker with the plasma. It would then be the less intimate interstitium, which represents a pure sink of marker, which in turn explains why the 1/t term decreases in time. Whatever one’s point of view, inert marker concentration ultimately follows a GV temporal dependency. Figure 4 shows less discordance between the concentration curve and the GV fit function from the Tk-GV method when renal function is high (i.e., when λ is small). When the renal function is good, it takes less time to establish a dynamic-equilibrium concentration than when renal function is poor. The meaning of this is that the GV describes an ultimate dynamic-equilibrium concentration balance with plasma having two marker loss processes, one being loss to urine through the kidneys, i.e., the constant loss rate term $dC\left( t \right)/dt = - \beta C\left( t \right)$, and the other being loss to other parts of the body still not in concentration equilibrium with the plasma, which decreases in time, i.e., $dC\left( t \right)/dt = C\left( t \right)(\alpha - 1)/t$. Thus, the right hand side of Eq. 18 is consistent with a concentration weighted average value interpretation of CL, Eq. 3, in that (i) the rate of CL is variable in time, (ii) the AUC dose method gives a concentration-weighted, average estimate of this variable CL, and (iii) for any bolus inert marker $CL_{total}$ is faster than $CL_{urine}$ [24, 39].

Concerning the volume of distribution, the most useful definition is also an average value, i.e., that based on the concentration-weighted mean residence time as given in Eqs. 4 and 16. Notably, our results show V values to be remarkably stable and to give consistent values even for vanishingly small values of CL. This results from the Tk-GV technique’s minimization of $s_{CL} /CL$, which prevents zero values of CL by enforcing ${{CL} \mathord{\left/ {\vphantom {{CL} \beta }} \right. \kern-\nulldelimiterspace} \beta } \approx {D \mathord{\left/ {\vphantom {D \kappa }} \right. \kern-\nulldelimiterspace} \kappa } \approx V$ for low function (see the Results, Test 3) where D/κ is a very stable concentration ratio. Furthermore, apart from the Tk-GV method, we know of no techniques that are capable of giving reliable estimates of V when CL is very small. In addition, Tk-GV’s α ≤ 1 results, i.e., that plasma definitely leaks inert marker into the body, is suggestive of and consistent with the total plasma clearance being greater than urinary collection of cleared substance, i.e., renal clearance. Finally, the Tk-GV model is extremely stable computationally. Only 4 plasma samples are needed for Tk-GV fit solutions, preferable including one early, e.g., 10 min and one later, 4-h sample. E ₂ SET models, on the other hand, are sometimes degenerate and converge to non-E ₂ functions with a 6% likelihood of this happening using 8 plasma samples.

Precision

Results for Tk-GV method precision were calculated by three methods as in Test 1 and 4, and Tables 3 and 8. Tk-GV offered a significant, improvement in $s_{CL}$ (SD of CL) from constrained E ₂ SET models, P = 0.045, two-tailed, from pair-wise Wilcoxon signed-ranks sum. Test 4 relates a very significant improvement in the relative precision of $V_{\text{Tk - GV}}$ compared to $V_{E2}$, (Wilcoxon P = 0.0007, one-tailed). Thus, the Tk-GV model outperformed the constrained E ₂ SET model with respect to CL and V precision. Test 4 showed that for $CL_{\text{Tk-GV}}$ the decrease in CL from extrapolating 65 min (from ~3 to ~4 h) was insignificant P = 0.23, two-tailed. However, the same calculation for the constrained E ₂ SET model was significant to the P = 0.0049 level. Thus, 3 h is not enough elapsed time to use an E ₂ SET model. But, the same thing cannot be said for the Tk-GV model.

Accuracy

In Table 8 and Results, Comparison with published values, using inulin constant infusion as $CL_{total}$, Florijn et al.’s calculated difference $CL_{E2} - CL_{total}$ is 5.1 ml/min/1.73 m². Moore et al. using ⁵¹Cr-EDTA found a 10% difference between $CL_{4h}$ and $CL_{24h}$. Since the $CL_{E2} - CL_{\text{Tk-GV}}$ difference is 6.1 ml/min/1.73 m² or 10.6%, this largely reconciles the differences and suggests agreement amongst three methods; $CL_{\text{Tk-GV}}$ and two gold standard $CL_{total}$ estimates, i.e., that of total plasma-clearance as $CL_{\text{Tk-GV}}$, as $CL_{total}$ from inulin constant infusion and as $CL_{total}$ from $CL_{24h}$. A more complete validation of the proposed Tk-GV method would require comparison with suitable gold-standard measurements in the same group of subjects. Nevertheless, the comparison with published data provides strong evidence that $CL_{\text{Tk-GV}}$ is accurate to within small errors, and is consistent with agreement among the gold standards themselves.

Moreover, the Tk-GV model clearly outperforms its SETs competitors in many ways. For example, it would be problematic to perform an L2O experiment on E ₂, as E ₂ regression attempts may result in non-E ₂ models—see Table 4 and [57]. So, by process of elimination, the L2O experiment can only be performed using more robust fit-models like Tk-GV or E ₁ SET. There were no failures to find a global minimum converged Tk-GV fit solution for the leave out ≤ 4 samples for 7963 sample combinations, even though a small percentage of those 7963 fits were ill-advised sample choices, i.e., when β ≈ 0 or α > 1, e.g., see Fig. 3. The Tk-GV method only needs 4 samples over 4 h for an accurate solution. This is exceptional performance. Russell, who supplied much of the data used here, suggests that the minimum practical number of samples for our conditions and an E ₂ model is six [72]. Current determinations of CL from bolus techniques are recommended for use with 4 or 5 h of sampling with 8–13 samples [10, 11], up to 6 or 8 h of sampling in renal failure [69, 71] and 24 h of sampling without using correction factors [24].

The Tk-GV model correctly estimates the CL and V values robustly, even when CL is near zero. Even constant infusion cannot achieve this feat, as the infusion is problematic in renal failure. This gives confidence that the Tk-GV method and GV models for marker concentrations have a physiological basis, even though some of the details are unknown. For example, how to diminish inert marker total plasma clearance to estimate urinary clearance cannot, at present, be calculated directly. However, the GV differential equation leak term is consistent with this occurring when α ≤ 1, of which the Tk-GV results provide good assurance, and other models have no such results. Moreover, the leakage can at least be estimated from prior work. Moore et al. estimate this to be 7.6% greater CL from total clearance than urinary clearance, which would correspond to 7% for $CL_{\text{Tk-GV}}$ from Eq. 22. Finally, for certain applications, e.g., drug effects for which plasma concentration in time (AUC of dosage) is the consideration, total plasma-clearance may be more relevant than urinary collection, e.g., methotrexate, carboplatin [2]. Wise [20] pointed out that the majority fits with E ₂ and E ₃ SET functions to drug clearance curves that he surveyed were well fit by GV functions, and he suggested the use of GV functions instead of exponentials to model drug elimination. A GV function is equivalent to a SET model with an infinite number of terms, but with only three parameters instead of an infinite number of parameters. The GV functions from the Tk-GV method afforded curve fits efficient for finding CL of the inert markers examined here. Thus the Tk-GV method provides a key step likely missing for implementation of Wise’s suggestion to use GV functions for CL determinations, namely somewhat paradoxically to extract an accurate terminal fit of marker concentrations from early-time data while at the same time obtaining physiological range plasma leak constants appropriate to inert markers. This is where for i.v. bolused inert markers, the Tk-GV method bridges the gap by allowing for more robust, more versatile, more useful, and more credible total CL estimates. The adaptation of the Tk-GV model for more complex pharmacokinetics, absorption, infusions or multiple-dosing regimens is left for future work.

Conclusions

Modeling tests were constructed and used to examine three models as applied to 46 radiolabeled DTPA bolus concentration curves. Sum of exponential term (SET) models failed the tests for parameter stability, statistically warranted parameters, curve shape, goodness of fit, accuracy and useful extrapolation. Gamma variate (GV) functions fit the late (2 to 4 h) plasma samples with high probability of goodness of fit, but were unreliable for estimating CL. Adaptive Tikhonov (Tk) extraction of the GV functions (Tk-GV) robustly converged to global minima with good evidence of precise (Table 1) and accurate $CL_{\text{Tk-GV}}$ values, which agreed with published corrections of CL from constant infusion of inulin [39] and ⁵¹Cr-EDTA bolus modeling [24] to within insignificant errors (Table 8) without the need for correction factors, constant infusion, overabundant samples, or prolonging the time of data collection from 4 to 24 h. Generally $CL_{E1} > CL_{E2} > CL_{\text{Tk-GV}}$. By design, the Tk-GV method produces CL-values with the smallest CV and consistent values for V for vanishingly small CL, a major achievement. E ₂ and higher models may be replaced for labeled DTPA by Tk-GV, which requires only 4 samples to find solutions (compare to 8 samples for an E ₂ SET). While the Tk-GV method may seem complicated, its use is simpler and more practical than constant infusion, 24-h AUC with mono-exponential extrapolation or E ₂ models. Thus, as far as we can determine, the Tk-GV model results reflect accurate renal function estimates Furthermore, E ₂ SET models sometimes produce nonphysical CL-values, and when physical values occur, they are imprecise and biased. In addition, unlike inulin constant infusion, which is not useful in renal failure and which can cause anaphylaxis [73, 74], or tedious 24 h AUC with mono-exponential extrapolation, Tk-GV provides precise volumes of distribution, V, even when CL is vanishingly small.

Appendix: error adaptive Tikhonov regularization equation section (Next)

For an over-determined system of linear equations, $\mathbf {Ax = b}$, the Tikhonov regularization (Tk) of this problem introduces the penalty function $\Upgamma x$ and seeks to find a solution that minimizes $\left\| {\mathbf {Ax - b}} \right\|^{2} + \left\| {\Upgamma {\mathbf {x}}} \right\|^{2}$. This latter is the square of a norm of the residuals, $\left\| {\mathbf {Ax - b}} \right\|^{2}$, plus the square of a norm of the product of the Tikhonov matrix, Γ, with the x fit parameters (unknowns). The more general $\Upgamma^{\text{T}} \Upgamma$regularizing term is often, as it is here, replaced by $\lambda {\mathbf{I}}$, where I is the identity matrix, and λ is a Lagrange (i.e., constraint) multiplier, also commonly called the shrinkage, Tikhonov or damping factor. There are two points of note. First, although it offers no computational advantage to do so, ridge regression, used here, is Tikhonov regularization with correlation scaling that standardizes λ values. Second, λ = 0 is equivalent to the problem of minimizing the norm $\left\| {\mathbf {Ax - b}} \right\|^{2}$, which is most commonly solved using ordinary least squares (OLS).

A constraint on lnK

A most common constraint for regression is to require the fit function to pass through the data mean point (a.k.a., the centroid, $\bar{x},\bar{y}$). Because the logarithm of concentrations is the more homoscedastic quantity, it is common to fit the logarithms of marker concentrations rather than the concentrations themselves. Thus, for the Tk-GV method, the GV function is written $\ln C = \ln K + (\alpha - 1)\ln t - \beta t$, where the constant term ln K need not be independent, but can be determined from the other fit parameters using a mean value constraint. Taking averages over the data

$$ \ln K \, = \overline{\ln C\left( t \right)} - \left( {\alpha - 1} \right)\overline{\ln t} + \beta \bar{t} \, = \bar{b} - \left( {\alpha - 1} \right)\bar{a}_{1} + \beta \bar{a}_{2} , $$

(A1)

such that $\bar{b}$, $\bar{a}_{1}$ and $\bar{a}_{2}$ are data constants, where $\bar{b}$ is the mean value of the logarithms of the concentrations, $\bar{a}_{1}$ is the mean of the logarithms of the sample times and $\bar{a}_{2}$, is the mean of the sample times. Then, Eq. A1 is used to remove K from the formula for CL formula (Eq. 15), and an expression is derived for the errors in CL with only α and β as independent parameters, as follows

$$ CL = {\frac{{D\beta^{\alpha } }}{{\exp \left( {\bar{b} - \left( {\alpha - 1} \right)\bar{a}_{1} + \beta \bar{a}_{2} } \right)\Upgamma \left( \alpha \right)}}}, $$

(A2)

Error propagation

One applies the well known error propagation formula [75] to Eq. A2 with respect to α and β yielding

$$ \begin{gathered} \left( {{\frac{{s_{CL} }}{CL}}} \right)^{2} = s_{\alpha }^{2} \left( {\bar{a}_{1} + \ln \beta - \Uppsi \left( \alpha \right)} \right)^{2} + s_{\beta }^{2} \left( {{\frac{\alpha }{\beta }} - \bar{a}_{2} } \right)^{2} \, \hfill \\ \, + 2s_{\alpha \beta } \left( {\bar{a}_{1} + \ln \beta - \Uppsi \left( \alpha \right)} \right)\left( {{\frac{\alpha }{\beta }} - \bar{a}_{2} } \right). \hfill \\ \end{gathered} $$

(A3)

where $\Uppsi \left( \alpha \right)$ is the digamma function of α and $\Uppsi \left( \alpha \right) = {{d\left[ {\ln \Upgamma \left( \alpha \right)} \right]} \mathord{\left/ {\vphantom {{d\left[ {\ln \Upgamma \left( \alpha \right)} \right]} {d\alpha }}} \right. \kern-\nulldelimiterspace} {d\alpha }}$ $= {{\Upgamma '\left( \alpha \right)} \mathord{\left/ {\vphantom {{\Upgamma '\left( \alpha \right)} {\Upgamma \left( \alpha \right)}}} \right. \kern-\nulldelimiterspace} {\Upgamma \left( \alpha \right)}}$, the subscripted s variables are the standard deviations of the subscripted quantities, and $\left( {s_{CL} /CL} \right)^{2}$ is the squared coefficient of variation $\left( {\text{CV}} \right)^{2}$ of CL. Minimizing the right hand side of Eq. A3 as a function of the shrinkage, λ, selects a λ value that produces the CL value with the smallest relative error achievable. Also, minimizing the relative error in CL is indispensable for making reliable measures of CL when CL is small.

The variance of V is similarly calculated from application of the propagation of error formula to the substitution of Eq. 17 into Eq. A2 yielding

$$ \begin{gathered} \left( {{\frac{{s_{V} }}{V}}} \right)^{2} = s_{\alpha }^{2} \left( {{\frac{1}{\alpha }} + \bar{a}_{1} + \ln \beta - \Uppsi \left( \alpha \right)} \right)^{2} + s_{\beta }^{2} \left( {{\frac{\alpha }{\beta }} - {\frac{1}{\beta }} - \bar{a}_{2} } \right)^{2} \, \hfill \\ \, + 2s_{\alpha \beta } \left( {{\frac{1}{\alpha }} + \bar{a}_{1} + \ln \beta - \Uppsi \left( \alpha \right)} \right)\left( {{\frac{\alpha }{\beta }} - {\frac{1}{\beta }} - \bar{a}_{2} } \right). \hfill \\ \end{gathered} $$

(A4)

The square root of Eq. A4 is the coefficient of variation, CV, of the individual V values, i.e., $s_{V} /V$.