A Spectrally Accurate Step-by-Step Method for the Numerical Solution of Fractional Differential Equations

Abstract

In this paper we consider the numerical solution of fractional differential equations. In particular, we study a step-by-step procedure, defined over a graded mesh, which is based on a truncated expansion of the vector field along the orthonormal Jacobi polynomial basis. Under mild hypotheses, the proposed procedure is capable of getting spectral accuracy. A few numerical examples are reported to confirm the theoretical findings.

1 Introduction

In recent years fractional differential equation modelling has become more and more frequent—see, for example, the two monographs [20, 37]. In fact the use of fractional models has quite a long history and early applications considered their behaviour in describing anomalous diffusion in a randomly hetergeneous porous medium [31] and in water resources modelling [6]. In mathematical biology, a number of researchers have considered fractional reaction diffusion equations—see, for example, Bueno-Orovio et al. [16] who have studied via a spectral approach the interfacial properties of the Allen-Cahn equation with a quartic double well potential, a model often used for alloy kinetics and the dynamics of phase boundaries. Henry, Langlands and Wearne [27] analysed Turing pattern formation in fractional activator-inhibitor systems. In a computational medicine setting, Henry and Langlands [26] developed fractional cable models for spiny neuronal dendrites. Orsingher and Behgin [36] have considered the dynamics of fractional chemical kinetics for unimolecular systems using time change. The authors in [17] have made a series of arguments based on Riesz potential theory and the wide range of heterogeneous cardiac tissues for the use of fractional models in cardiac electrophysiology, while Cusimano et al. [18] have explored the effects of fractional diffusion on the cardiac action potential shape and electrical propagation. In addition, Magin et al. [34], Hori et al. [28], Bueno-Orovio and Burrage [15] have considered the calibration of fractional cardiac models through a fractional Bloch–Torrey equation.

Due to these application advances there is clearly a need to develop advanced numerical methods for fractional differential equations. In a purely time fractional setting the standard approach has been to use a first order approximation to the Caputo derivative. Lubich [32] has extended this and developed higher order approximations based on an underlying linear multistep method that are convergent of the order of this multistep method.

There are two important issues when designing effective numerical methods for Fractional Differential equations: memory and non-locality. In the case of memory, in principle one needs to evaluate the numerical approximations all the way back to the initial time point at each time step and this becomes very computationally intensive over long time intervals. Techniques such as fixed time windowing have been proposed [37] and more recently a number of approaches have been considered to compute the discrete convolutions to approximate the fractional operator [39, 44]. Zeng et al. [43] developed fast memory-saving time stepping methods in which the fractional operator is decoupled into a local part with fixed memory length and the history part is computed by Laguerre–Gauss quadrature, whose error is independent of the stepsize.

In the second situation the solutions to FDEs are often non-smooth and may have a strong singularity at $t = 0$. In these cases the vector field may inherit this singularity behavior and so a constant stepsize would be very inefficient. Thus graded meshes have been proposed by a number of authors [30, 40, 42]. Lubich [33] on the other hand deals with singularities by introducing certain correction terms. Other approaches have been considered such as Adams methods [21], trapezoidal methods [23] and Bernstein splines [38] while Garrappa [24] has given a survey and software tutorial on numerical methods for FDEs.

In this paper, we consider a major improvement of the recent solution approach described in [2, 9], based on previous work on Hamiltonian Boundary value Methods (HBVMs) [7, 8, 11, 14] (also used as spectral methods in time [3, 5, 12, 13]), for solving fractional initial value problems in the form:

$$\begin{aligned} y^{(\alpha )}(t) = f(y(t)), \quad t\in [0,T], \quad y(0)=y_0\in \mathbb {R}^m, \end{aligned}$$

(1)

where, for sake of brevity, we omit t as a formal argument, at the r.h.s. For the same reason, hereafter the dimension m of the state vector will be also omitted, when unnecessary.

Here, for  $\alpha \in (0,1]$,  $y^{(\alpha )}(t) \equiv D^\alpha y(t)$  is the Caputo fractional derivative:

$$\begin{aligned} D^\alpha g(t) = \frac{1}{\varGamma (1-\alpha )} \int _0^t (t-x)^{-\alpha } \left[ \frac{\textrm{d}}{\textrm{d}x}g(x)\right] \textrm{d}x. \end{aligned}$$

(2)

The Riemann–Liouville integral associated to (2) is given by:

$$\begin{aligned} I^\alpha g(t) = \frac{1}{\varGamma (\alpha )}\int _0^t (t-x)^{\alpha -1} g(x)\textrm{d}x. \end{aligned}$$

(3)

It is known that [37]:

$$\begin{aligned} D^\alpha I^\alpha g(t)= & {} g(t), \quad I^\alpha D^\alpha g(t)=g(t)-g(0), \nonumber \\ I^\alpha t^j= & {} \frac{j!}{\varGamma (\alpha +j+1)}t^{j+\alpha }, \quad j=0,1,2,\dots . \end{aligned}$$

(4)

Consequently, the solution of (1) is formally given by:

$$\begin{aligned} y(t) = y_0 + I^\alpha f(y(t)), \quad t\in [0,T]. \end{aligned}$$

(5)

We shall here generalize the approach given in [2], by defining a step-by-step procedure, whereas the procedure given in [2] was of a global nature. This strategy, when combined with a graded mesh selection, enables better handling of singularities in the derivative of the solution to (1) at the origin, which occur, for example, when f is a suitably regular function. Additionally, our approach partially mitigates issues stemming from the non-local nature of the problem. Indeed, at a given time-step of the integration procedure, it requires the solution of a differential problem within the current time interval along with a finite sequence of pure quadrature problems that account for the contribution brought by the history term.

With this premise, the structure of the paper is as follows: in Sect. 2 we recall some basic facts about Jacobi polynomials, for later use; in Sect. 3 we describe a piecewise quasi-polynomial approximation to the solution of (1); in Sect. 4 the analysis of the new method is carried out; in Sect 5 we report a few numerical tests for assessing the theoretical achievements; at last, in Sect. 6 a few concluding remarks are given.

2 Orthonormal Jacobi Polynomials

Jacobi polynomials form an orthogonal set of polynomials w.r.t. a given weighting function. In more detail, for $r,\nu >-1$:

$$\begin{aligned}{} & {} \bar{P}^{(r,\nu )}_i(x)\in \varPi _i, \quad \left( P_0^{(r,\nu )}(x)\equiv 1\right) \\{} & {} \quad \int _{-1}^1 (1-x)^r(1+x)^\nu \bar{P}_i^{(r,\nu )}(x)\bar{P}_j^{(r,\nu )}(x)\textrm{d}x \\{} & {} \quad = \frac{2^{r+\nu +1}}{2i+r+\nu +1}\frac{\varGamma (i+r+1)\varGamma (i+\nu +1)}{\varGamma (i+r+\nu +1)i!}\delta _{ij}, \quad i,j,=0,1,\dots , \end{aligned}$$

where as is usual, $\varPi _i$ is the vector space of polynomials of degree at most i and $\delta _{ij}$ is the Kronecker symbol. Consequently, the shifted and scaled Jacobi polynomials

$$\begin{aligned} P_i^{(r,\nu )}(c):= & {} \sqrt{(2i+r+\nu +1)\frac{\varGamma (i+r+\nu +1)i!}{\varGamma (i+r+1)\varGamma (i+\nu +1)}}\bar{P}_i^{(r,\nu )}(2c-1), \quad i=0,1,\dots , \end{aligned}$$

are orthonormal w.r.t.

$$\begin{aligned} \int _0^1(1-c)^rc^\nu P_i^{(r,\nu )}(c)P_j^{(r,\nu )}(c)\textrm{d}c = \delta _{ij}, \quad i,j=0,1,\dots . \end{aligned}$$

In particular, hereafter we shall consider the polynomials ¹

$$\begin{aligned} P_i(c) ~:=~ \frac{P_i^{(\alpha -1,0)}(c)}{\sqrt{\alpha }} ~\equiv ~ \frac{\sqrt{2i+\alpha }}{\sqrt{\alpha }}\bar{P}_i^{(\alpha -1,0)}(2c-1), \quad i=0,1,\dots , \end{aligned}$$

(6)

with $\alpha \in (0,1]$ the same parameter in (1), such that:

$$\begin{aligned} P_0(c)~\equiv ~ 1, \quad \alpha \int _0^1(1-c)^{\alpha -1}P_i(c)P_j(c)\textrm{d}c ~=~ \delta _{ij}, \quad i,j=0,1,\dots , \end{aligned}$$

(7)

where we have slightly changed the weighting function, in order that it has a unit integral:

$$\begin{aligned} \alpha \int _0^1(1-c)^{\alpha -1}\textrm{d}c = 1. \end{aligned}$$

(8)

We refer to Gautschi [25] and the accompanying software, for their computation, and for computing the nodes and weights of the Gauss–Jacobi quadrature of order 2k.

Remark 1

As is clear, when in (6)–(8) $\alpha =1$, we obtain the scaled and shifted Legendre polynomials, orthonormal in [0, 1].

As is well known, the polynomials (6) form an orthonormal basis for the Hilbert space $L_2[0,1]$, equipped with the scalar product

$$\begin{aligned} (f,g) = \alpha \int _0^1 (1-c)^{\alpha -1}f(c)g(c)\textrm{d}c, \end{aligned}$$

(9)

and the associated norm

$$\begin{aligned} \Vert f\Vert = \sqrt{(f,f)}. \end{aligned}$$

(10)

Consequently, from the Parseval identity, it follows that any square summable function can be expanded along such a basis, and the corresponding expansion is convergent to the function itself.

That said, with reference to the vector field in (1), let us consider the interval [0, h], and the expansion

$$\begin{aligned} f(y(ch)) ~=~ \sum _{j\ge 0} \gamma _j(y) P_j(c), \quad c\in [0,1], \end{aligned}$$

(11)

with the Fourier coefficients given by:

$$\begin{aligned} \gamma _j(y) ~=~ \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)f(y(ch))\textrm{d}c, \quad j=0,1,\dots . \end{aligned}$$

(12)

Consequently, on the interval [0, h], (1) can be rewritten as

$$\begin{aligned} y^{(\alpha )}(ch) ~=~ \sum _{j\ge 0} \gamma _j(y) P_j(c), \quad c\in [0,1],\quad y(0)=y_0, \end{aligned}$$

(13)

and, by virtue of (3)–(4), one obtains:

$$\begin{aligned} y(ch) ~=~ y_0+h^\alpha \sum _{j\ge 0} \gamma _j(y)I^\alpha P_j(c), \quad c\in [0,1]. \end{aligned}$$

(14)

In particular, due to (7) and (8), one has:

$$\begin{aligned} y(h) ~=~ y_0 + \frac{h^\alpha }{\varGamma (\alpha +1)}\gamma _0(y). \end{aligned}$$

(15)

Remark 2

By considering that $P_0(c)\equiv 1$, from (12) one derives that

$$\begin{aligned} \gamma _0(y) = \alpha \int _0^1 (1-c)^{\alpha -1} f(y(ch))\textrm{d}c. \end{aligned}$$

Consequently, because of (3), (15) becomes

$$\begin{aligned} y(h) = y_0 + I^\alpha f(y(h)), \end{aligned}$$

i.e., (5) with $t=h$. This clearly explains the use of the Jacobi basis for the expansion (11).

Further, we observe that, when $\alpha =1$, one retrieves the approach described in [11] for ODE-IVPs.

We also need the following preliminary results.

Lemma 1

Let  $G:[0,h]\rightarrow V$,  with V a vector space, admit a Taylor expansion at  $t=0$. Then,

$$\begin{aligned} \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)G(ch)\textrm{d}c ~=~ O(h^j), \quad j=0,1,\dots . \end{aligned}$$

Proof

By the hypothesis and (7), one has:

$$\begin{aligned}{} & {} \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)G(ch)\textrm{d}c \\{} & {} \quad =\alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)\sum _{\ell \ge 0}\frac{G^{(\ell )}(0)}{\ell !} (ch)^\ell \textrm{d}c\\{} & {} \quad =\alpha \sum _{\ell \ge 0} \frac{G^{(\ell )}(0)}{\ell !} h^\ell \int _0^1 (1-c)^{\alpha -1}P_j(c)c^\ell \textrm{d}c\\{} & {} \quad = \alpha \sum _{\ell \ge j} \frac{G^{(\ell )}(0)}{\ell !} h^\ell \int _0^1 (1-c)^{\alpha -1}P_j(c)c^\ell \textrm{d}c =O(h^j). \end{aligned}$$

$\square$

Remark 3

Concerning the above result, we observe that, by considering (9)–(10), from the Cauchy–Schwarz theorem one derives that

$$\begin{aligned} \left| \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)c^\ell \textrm{d}c\right| = |(P_j,c^\ell )| \le \Vert P_j\Vert \cdot \Vert c^\ell \Vert \le 1, \quad \forall \ell \ge j\ge 0. \end{aligned}$$

From Lemma 1, one has the following:

Corollary 1

Assume that the r.h.s. of problem (1) admits a Taylor expansion at $t=0$, then the coefficients defined at (12) satisfy:

$$\begin{aligned} \gamma _j(y) = O(h^j). \end{aligned}$$

The result of the previous lemma can be weakened as follows (the proof is similar and, therefore, omitted).

Lemma 2

Let  $G:[0,h]\rightarrow V$,  with V a vector space, admit a Taylor polynomial expansion of degree k with remainder at $t=0$. Then,

$$\begin{aligned} \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)G(ch)\textrm{d}c ~=~ O(h^{\min (j,k)}), \quad j=0,1,\dots . \end{aligned}$$

In such a case, the result of Corollary 1 is weakened accordingly.

Corollary 2

Assume that the r.h.s. of problem (1) admits a Taylor polynomial expansion of degree k with remainder at $t=0$. Then, the coefficients defined at (12) satisfy:

$$\begin{aligned} \gamma _j(y) = O(h^{\min (j,k)}). \end{aligned}$$

However, in general, at $t=0$ the solution may be not regular, since the derivative may be singular (this is, indeed, the case, when f is a regular function). In such a case, we shall resort to the following result.

Lemma 3

Assume that the r.h.s. in (1) is continuous for all $t\in [0,h]$. Then, for a convenient $\xi _t\in (0,t)^m$, one has²:

$$\begin{aligned} y(t) = y_0 + \frac{y^{(\alpha )}(\xi _t)}{\varGamma (\alpha +1)}t^\alpha , \quad t\in [0,h]. \end{aligned}$$

Proof

In fact, from (4), and by using the weighted mean-value theorem for integrals, one has:

$$\begin{aligned} y(t)= & {} y_0 + I^\alpha y^{(\alpha )}(t) ~=~ y_0 + \frac{1}{\varGamma (\alpha )}\int _0^t (t-x)^{\alpha -1} y^{(\alpha )}(x)\textrm{d}x\\= & {} y_0 + \frac{y^{(\alpha )}(\xi _t)}{\varGamma (\alpha )}\int _0^t (t-x)^{\alpha -1}\textrm{d}x ~=~ y_0 + \frac{y^{(\alpha )}(\xi _t)}{\varGamma (\alpha +1)} t^\alpha . \end{aligned}$$

$\square$

As a consequence, we derive the following weaker results concerning the Fourier coefficients (12).

Corollary 3

In the hypotheses of Lemma 3, and assuming f is continuously differentiable in a neighborhood of $y_0$, one has:

$$\begin{aligned} \gamma _0(y) = f(y_0)+ O(h^\alpha ), \quad \gamma _j(y) = O(h^\alpha ), \quad j=1,2,\dots . \end{aligned}$$

Proof

In fact, from Lemma 3, one has:

$$\begin{aligned} f(y(ch)) = f\left( y_0+\frac{y^{(\alpha )}(\xi _{ch})}{\varGamma (\alpha +1)}(ch)^\alpha \right) = f(y_0) + f'(y_0)\frac{y^{(\alpha )}(\xi _{ch})}{\varGamma (\alpha +1)}(ch)^\alpha + o((ch)^\alpha ). \end{aligned}$$

From this relation, and from (12), the statement then follows. $\square$

For later use, we also need to discuss the quadrature error in approximating the first s Fourier coefficients (12) by means of the Gauss–Jacobi formula of order 2k, for a convenient $k\ge s$, whose abscissae are the zeros of $P_k$, as defined in (7), and with weights:

$$\begin{aligned} P_k(c_i)= & {} 0, b_i = \alpha \int _0^1 (1-c)^{\alpha -1}\ell _i(c)\textrm{d}c, \quad \ell _i(c) = \prod _{j=1,\,j\ne i}^k \frac{c-c_j}{c_i-c_j}, \quad i=1,\dots ,k. \nonumber \\ \end{aligned}$$

(16)

That is,

$$\begin{aligned} \gamma _j(y) ~\approx ~ \sum _{i=1}^k b_i P_j(c_j)f(y(c_ih)) ~=:~ \hat{\gamma }_j(y). \end{aligned}$$

(17)

Concerning the quadrature errors

$$\begin{aligned} \varSigma _j^\alpha (y,h) ~:=~ \hat{\gamma }_j(y)-\gamma _j(y),\quad j=0,\dots ,s-1, \end{aligned}$$

(18)

the following result holds true.

Theorem 1

Assume the function $G_{j,h}(c):=P_j(c)f(y(ch))$ be of class $C^{(2k)}[0,h]$. Then, with reference to (18), one has, for a suitable $\xi =(0,1)^m:$

$$\begin{aligned} \varSigma _j^\alpha (y,h) ~=~ K_j\frac{G_{j,h}^{(2k)}(\xi )}{(2k)!} ~=~ O(h^{2k-j}), \quad j=0,\dots ,s-1, \end{aligned}$$

(19)

with the constants $K_j$ independent of both $G_{j,h}$ and h.

Proof

The statement follows by considering that the quadrature is exact for polynomials in $\varPi _{2k-1}$. $\square$

However, as recalled above, when f is a smooth function, the derivative of the solution of problem (1) may have a singularity at $t=0$. In such a case, estimates can be also derived (see, e.g., [19, 41] and [35, Theorem 5.1.8]). However, for our purposes, because of (7), for $j=0,\dots ,s-1$, from Corollary 3 we can easily derive the following one, assuming that $k\ge s$ and (13) hold true:

$$\begin{aligned} \hat{\gamma }_j(y)= & {} \sum _{i=1}^k b_iP_j(c_i)f(y(c_ih)) ~=~ \sum _{i=1}^k b_iP_j(c_i)\sum _{\ell \ge 0} P_\ell (c_i) \gamma _\ell (y)\nonumber \\= & {} \sum _{\ell =0}^{s-1} \underbrace{\left( \sum _{i=1}^k b_i P_j(c_i)P_\ell (c_i)\right) }_{=\,\delta _{j\ell }}\gamma _\ell (y) ~+~ O(h^\alpha )\\\equiv & {} \gamma _j(y) + \varSigma _j(y,h), \quad j=0,\dots ,s-1. \end{aligned}$$

Consequently,

$$\begin{aligned} \varSigma _j(y,h) ~=~ O(h^\alpha ), \quad j=0,\dots ,s-1. \end{aligned}$$

(20)

In order to derive a polynomial approximation to (13), it is enough to truncate the infinite series in (11) to a finite sum, thus obtaining:

$$\begin{aligned} \sigma ^{(\alpha )}(ch) ~=~ \sum _{j=0}^{s-1} \gamma _j(\sigma )P_j(c), \quad c\in [0,1], \quad \sigma (0)=y_0, \end{aligned}$$

(21)

with $\gamma _j(\sigma )$ formally given by (12) upon replacing y by $\sigma$. In so doing, (14) and (15) respectively become:

$$\begin{aligned} \sigma (ch) ~=~ y_0+h^\alpha \sum _{j=0}^{s-1} \gamma _j(\sigma )I^\alpha P_j(c), \quad c\in [0,1], \end{aligned}$$

(22)

and

$$\begin{aligned} \sigma (h) ~=~ y_0 + \frac{h^\alpha }{\varGamma (\alpha +1)}\gamma _0(\sigma ). \end{aligned}$$

(23)

It can be shown that Corollary 1, Corollary 2, Lemma 3, and Corollary 3 continue formally to hold for $\sigma$. Further, by considering the approximation of the Fourier coefficients obtained by using the Gauss–Jacobi quadrature of order 2k,

$$\begin{aligned} \hat{\gamma }_j(\sigma ) ~=~ \sum _{i=1}^k b_i P_j(c_j)f(\sigma (c_ih)) ~\equiv ~ \gamma _j(\sigma ) + \varSigma _j^\alpha (\sigma ,h), \end{aligned}$$

(24)

the result of Theorem 1 continues to hold. Moreover, we shall assume that the expansion

$$\begin{aligned} f(\sigma (ch)) = \sum _{j\ge 0}P_j(c)\gamma _j(\sigma ), \quad c\in [0,1], \end{aligned}$$

(25)

holds true, similarly as (11), from which also (20) follows for the quadrature error $\varSigma _j(\sigma ,h)$, when $\sigma$ has a singular derivative at 0. In the next sections, we shall better detail, generalize, and analyze this approach.

3 Piecewise Quasi-Polynomial Approximation

To begin with, in order to obtain a piecewise quasi-polynomial approximation to the solution of (1), we consider a partition of the integration interval in the form:

$$\begin{aligned} t_n = t_{n-1} + h_n, \quad n=1,\dots ,N, \end{aligned}$$

(26)

where

$$\begin{aligned} t_0=0, \quad \sum _{n=1}^N h_n = T. \end{aligned}$$

(27)

Then, according to (21)–(23), on the first subinterval $[0,h_1]$ we can derive a polynomial approximation of degree $s-1$ to (11), thus getting the fractional initial value problem

$$\begin{aligned} \sigma _1^{(\alpha )}(ch_1) = \sum _{j=0}^{s-1} \gamma _j(\sigma _1) P_j(c), \quad c\in [0,1], \quad \sigma _1(0)=y_0, \end{aligned}$$

(28)

where $\gamma _j(\sigma _1)$ is formally given by (12), upon replacing y by $\sigma _1$ at the right-hand side:

$$\begin{aligned} \gamma _j(\sigma _1) = \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c)f(\sigma _1(ch_1))\textrm{d}c, \quad j=0,\dots ,s-1. \end{aligned}$$

(29)

The solution of (28) is a quasi-polynomial of degree $s-1+\alpha$, formally given by:

$$\begin{aligned} \sigma _1(ch_1) = y_0 + h_1^\alpha \sum _{j=0}^{s-1} \gamma _j(\sigma _1) I^\alpha P_j(c), \quad c\in [0,1]. \end{aligned}$$

(30)

However, in order to actually compute the Fourier coefficients $\{\gamma _j(\sigma _1)\}$, one needs to approximate them by using the Gauss–Jacobi quadrature (16)³:

$$\begin{aligned} \gamma _j^1 ~:=~ \hat{\gamma }_j(\sigma _1) ~=~ \sum _{i=1}^k b_i P_j(c_i)f(\sigma _1(c_ih_1)) ~\equiv ~ \gamma _j(\sigma _1) +\varSigma _j^\alpha (\sigma _1,h_1). \end{aligned}$$

In so doing, (30) now formally becomes

$$\begin{aligned} \sigma _1(ch_1) = y_0 + h_1^\alpha \sum _{j=0}^{s-1} \gamma _j^1 I^\alpha P_j(c), \quad c\in [0,1]. \end{aligned}$$

(31)

Moreover, one solves the system of equations, having (block) dimension s independently of k:

$$\begin{aligned} \gamma _j^1 ~=~ \sum _{i=1}^k b_i P_j(c_i)f\left( y_0+h^\alpha \sum _{\nu =0}^{s-1} \gamma _\nu ^1\, I^\alpha P_\nu (c_i)\right) , \quad j=0,\dots ,s-1. \end{aligned}$$

(32)

This kind of procedure is typical of HBVM(k, s) methods, in the case of ODE-IVPs [7]: the main difference, here, derives from the non-locality of the operator. As is clear [compare with (23)], the approximation at $t=h_1$ will be now given by: ⁴

$$\begin{aligned} \bar{y}_1~:=~\sigma _1(h_1) ~=~ y_0+\frac{h_1^\alpha }{\varGamma (\alpha +1)}\gamma _0^1. \end{aligned}$$

(33)

Remark 4

For an efficient and stable evaluation of the integrals

$$\begin{aligned} I^\alpha P_0(c_i), ~ I^\alpha P_1(c_i), ~\dots ,~ I^\alpha P_{s-1}(c_i), \quad i=1,\dots ,k, \end{aligned}$$

(34)

we refer to the procedure described in [4].

3.1 The General Procedure

We now generalize the previous procedure for the subsequent integration steps. For later use, we shall denote:

$$\begin{aligned} y_n(ch_n) ~:=~ y(t_{n-1}+ch_n), \quad c\in [0,1],\quad n=1,\dots ,N, \end{aligned}$$

(35)

the restriction of the solution on the interval $[t_{n-1},t_n]$. Similarly, we shall denote by $\sigma (t)\approx y(t)$ the piecewise quasi-polynomial approximation such that:

$$\begin{aligned} \sigma |_{[t_{n-1},t_n]} (t_{n-1}+ch_n) ~=:~ \sigma _n(ch_n) ~\approx ~ y_n(ch_n), \quad c\in [0,1], \quad n=1,\dots ,N. \end{aligned}$$

(36)

Then, by using an induction argument, let us suppose one knows the quasi-polynomial approximations

$$\begin{aligned} \sigma _i(ch_i)= & {} \phi ^\alpha _{i-1}(c,\sigma ) + h_i^\alpha \sum _{j=0}^{s-1} \gamma _j^i I^\alpha P_j(c) ~ \approx ~ y_i(ch_i), \quad c\in [0,1],\quad i=1,\dots ,n, \nonumber \\ \end{aligned}$$

(37)

where $\phi ^\alpha _{i-1}(c,\sigma )$ denotes a history term, to be defined later, such that:

• in the first subinterval, according to (31), $\phi _0^\alpha (c,\sigma )\equiv y_0$, $c\in [0,1]$;

• for $i>1$, $\phi _{i-1}^\alpha (c,\sigma )$ only depends on $\sigma _1,\dots ,\sigma _{i-1}$.

The corresponding approximations at the grid-points are given by

$$\begin{aligned} \bar{y}_i~:=~\sigma _i(h_i) ~=~ \phi ^\alpha _{i-1}(1,\sigma )~+~\frac{h_i^\alpha }{\varGamma (\alpha +1)}\gamma _0^i~\approx ~ y_i(h_i)~\equiv ~y(t_i),\quad i=1,\dots ,n, \end{aligned}$$

(38)

and assume we want to compute

$$\begin{aligned} \sigma _{n+1}(ch_{n+1}) := \phi ^\alpha _n(c,\sigma )+h_{n+1}^\alpha \sum _{j=0}^{s-1} \gamma _j^{n+1} I^\alpha P_j(c)~\approx ~y_{n+1}(ch_{n+1}), \quad c\in [0,1]. \end{aligned}$$

(39)

Hereafter, we shall assume that the time-steps in (26) define a graded mesh. In more detail, for a suitable $r>1$:

$$\begin{aligned} h_n ~=~ rh_{n-1} ~\equiv ~ r^{n-1} h_1, \quad n=1,\dots ,N. \end{aligned}$$

(40)

Remark 5

As is clear, in the limit case where $r=1$, (40) reduces to a uniform mesh with a constant time-step  $h=T/N$.

In order to derive the approximation (39), we start computing the solution of the problem in the subinterval $[t_n,t_{n+1}]$. Then, for $t\equiv t_n+ch_{n+1}$, $c\in [0,1]$, one has:

$$\begin{aligned} y(t)\equiv & {} y_{n+1}(ch_{n+1})\\= & {} y_0 ~+~ \frac{1}{\varGamma (\alpha )}\int _0^{t_n+ch_{n+1}} (t_n+ch_{n+1}-x)^{\alpha -1}f(y(x))\textrm{d}x\\= & {} y_0 ~+ \frac{1}{\varGamma (\alpha )}\int _0^{t_n} (t_n+ch_{n+1}-x)^{\alpha -1}f(y(x))\textrm{d}x\\{} & {} ~+\,\frac{1}{\varGamma (\alpha )}\int _{t_n}^{t_n+ch_{n+1}} (t_n+ch_{n+1}-x)^{\alpha -1}f(y(x))\textrm{d}x\\= & {} y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n \int _{t_{\nu -1}}^{t_\nu } (t_n+ch_{n+1}-x)^{\alpha -1}f(y(x))\textrm{d}x\\{} & {} ~+~\frac{1}{\varGamma (\alpha )}\int _{t_n}^{t_n+ch_{n+1}} (t_n+ch_{n+1}-x)^{\alpha -1}f(y(x))\textrm{d}x \\= & {} y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n \int _0^{h_\nu } (t_n-t_{\nu -1}+ch_{n+1}-x)^{\alpha -1}f(y_\nu (x))\textrm{d}x\\{} & {} ~+~\frac{1}{\varGamma (\alpha )}\int _0^{ch_{n+1}} (ch_{n+1}-x)^{\alpha -1}f(y_{n+1}(x))\textrm{d}x \\= & {} y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1\left( \frac{r^{n-\nu +1}-1}{r-1}+cr^{n-\nu +1}-\tau \right) ^{\alpha -1}f(y_\nu (\tau h_\nu ))\textrm{d}\tau \\{} & {} ~+~\frac{h_{n+1}^\alpha }{\varGamma (\alpha )}\int _0^c (c-\tau )^{\alpha -1}f(y_{n+1}(\tau h_{n+1}))\textrm{d}\tau \\\equiv & {} G_n^\alpha (c,y) ~+~ I^\alpha f(y_{n+1}(ch_{n+1})), \end{aligned}$$

having set the history term

$$\begin{aligned}{} & {} G_n^\alpha (c,y) \nonumber \\{} & {} \quad := y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}+cr^{n-\nu +1}-\tau \right) ^{\alpha -1}f(y_\nu (\tau h_\nu ))\textrm{d}\tau , \end{aligned}$$

(41)

which is a known quantity, since it only depends on $y_1,\dots ,y_n$ [see (35)]. Consequently, we have obtained

$$\begin{aligned} y_{n+1}(ch_{n+1}) = G_n^\alpha (c,y) + I^\alpha f(y_{n+1}(ch_{n+1})), \quad c\in [0,1], \end{aligned}$$

(42)

which reduces to (5), when $n=0$ and $t\in [0,h]$. Further, by considering the expansion

$$\begin{aligned} f(y_{n+1}(ch_{n+1})) = \sum _{j\ge 0}\gamma _j(y_{n+1}) P_j(c), \quad c\in [0,1], \end{aligned}$$

(43)

with the Fourier coefficients given by

$$\begin{aligned} \gamma _j(y_{n+1}) = \alpha \int _0^1 (1-c)^{\alpha -1}P_j(c) f(y_{n+1}(ch_{n+1}))\textrm{d}c, \quad j\ge 0, \end{aligned}$$

(44)

one obtains that (42) can be rewritten as

$$\begin{aligned} y_{n+1}(ch_{n+1}) = G_n^\alpha (c,y) + \frac{h_{n+1}^\alpha }{\varGamma (\alpha )}\sum _{j\ge 0}\gamma _j(y_{n+1})I^\alpha P_j(c), \quad c\in [0,1], \end{aligned}$$

(45)

with the value at $t=h$ given by:

$$\begin{aligned} y(t_{n+1}) ~\equiv ~y_{n+1}(h_{n+1}) ~=~ G_n^\alpha (1,y) + \frac{h_{n+1}^\alpha }{\varGamma (\alpha +1)}\gamma _0(y_{n+1}). \end{aligned}$$

(46)

The corresponding approximation is obtained by truncating the series in (42) after s terms, and approximating the corresponding Fourier coefficients via the Gauss–Jacobi quadrature of order 2k,

$$\begin{aligned} \sigma _{n+1}(ch_{n+1}) ~=~ \phi ^\alpha _n(c,\sigma ) ~+~ \frac{h_{n+1}^\alpha }{\varGamma (\alpha )} \sum _{j=0}^{s-1} \gamma _j^{n+1} I^\alpha P_j(c), \quad c\in [0,1], \end{aligned}$$

(47)

and

$$\begin{aligned} \bar{y}_{n+1} ~:=~ \sigma _{n+1}(h_{n+1}) ~=~ \phi ^\alpha _n(1,\sigma ) ~+~ \frac{h_{n+1}^\alpha }{\varGamma (\alpha +1)}\gamma _0^{n+1}, \end{aligned}$$

(48)

with $\phi _n^\alpha (c,\sigma )$ an approximation of $G_n^\alpha (c,y)$ in (41), defined as follows⁵:

$$\begin{aligned}{} & {} \phi _n^\alpha (c,\sigma ) ~\nonumber \\{} & {} \quad :=y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}+cr^{n-\nu +1}-\tau \right) ^{\alpha -1}\sum _{j=0}^{s-1} P_j(\tau ) \gamma _j^\nu \textrm{d}\tau \nonumber \\{} & {} \quad =y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \sum _{j=0}^{s-1}\int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}+cr^{n-\nu +1}-\tau \right) ^{\alpha -1} P_j(\tau )\textrm{d}\tau \gamma _j^\nu \nonumber \\{} & {} \quad \equiv y_0 ~+~ \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \sum _{j=0}^{s-1} J_j^\alpha \left( \frac{r^{n-\nu +1}-1}{r-1}+cr^{n-\nu +1}\right) \gamma _j^\nu , \end{aligned}$$

(49)

having set

$$\begin{aligned} J_j^\alpha (x) := \int _0^1(x-\tau )^{\alpha -1}P_j(\tau )\textrm{d}\tau , \quad j=0,\dots ,s-1,\quad x>1, \end{aligned}$$

(50)

which, as we shall see in Sect. 3.3, can be accurately and efficiently computed.

As is clear, in (49) we have used the approximation

$$\begin{aligned} f(\sigma _\nu (\tau h)) ~=~ \sum _{j=0}^{s-1} P_j(\tau )\gamma _j^\nu ~+~ R_\nu ^\alpha (\tau ), \end{aligned}$$

(51)

with the error term given by [see (17)–(18) and (25)]:

$$\begin{aligned} R_\nu ^\alpha (\tau ):= & {} \sum _{j=0}^{s-1} P_j(\tau )\left[ \gamma _j(\sigma _\nu )-\gamma _j^\nu \right] ~+~ \overbrace{\sum _{j\ge s} P_j(\tau )\gamma _j(\sigma _\nu )}^{=:\,E_\nu ^\alpha (\tau )}\nonumber \\\equiv & {} \underbrace{\sum _{j=0}^{s-1} P_j(\tau ) \varSigma _j^\alpha (\sigma _\nu ,h_\nu )}_{=:\,S_\nu ^\alpha (\tau )}~+~E_\nu ^\alpha (\tau ) ~\equiv ~ S_\nu ^\alpha (\tau ) + E_\nu ^\alpha (\tau ). \end{aligned}$$

(52)

Because of the results of Sect. 2, we shall hereafter assume that

$$\begin{aligned} \left| \varSigma _j^\alpha (\sigma _\nu ,h_\nu )\right| \le \left\{ \begin{array}{cc} O(h_1^\alpha ), &{}\nu =1,\\ O(h_\nu ^{2k-j}), &{}\nu>1,\end{array}\right. \quad \left| E_\nu ^\alpha (\tau )\right| \le \left\{ \begin{array}{cc} O(h_1^\alpha ), &{}\nu =1,\\ O(h_\nu ^s), &{}\nu >1.\end{array}\right. \end{aligned}$$

(53)

Consequently, considering that $k\ge s$, $\alpha \in (0,1)$, and $j=0,\dots ,s-1$, one deduces:

$$\begin{aligned} \left| S_\nu ^\alpha (\tau )\right| \le \left\{ \begin{array}{cc} O(h_1^\alpha ), &{}\nu =1,\\ O(h_\nu ^{s+1}), &{}\nu>1,\end{array}\right. \quad \left| R_\nu ^\alpha (\tau )\right| \le \left\{ \begin{array}{cc} O(h_1^\alpha ), &{}\nu =1,\\ O(h_\nu ^s), &{}\nu >1.\end{array}\right. \end{aligned}$$

(54)

In so doing, see (47), the Fourier coefficients satisfy the system of equations:

$$\begin{aligned} \gamma _j^{n+1}= & {} \sum _{\ell =1}^k b_\ell P_j(c_\ell ) f_{n+1}\left( \phi _n^\alpha (c_\ell ,\sigma )+h_{n+1}^\alpha \sum _{i=0}^{s-1} \gamma _i^{n+1} I^\alpha P_i(c_\ell h)\right) ,\quad j=0,\dots ,s-1, \nonumber \\ \end{aligned}$$

(55)

having (block)-size s, independently of the considered value of k.

Clearly,

$$\begin{aligned} \gamma _j^{n+1}~=~ \gamma _j(\sigma _{n+1}) ~+~ \varSigma _j^\alpha (\sigma _{n+1},h_{n+1}),\quad j=0,\dots ,s-1, \end{aligned}$$

with $\gamma _j(\sigma _{n+1})$ formally defined as in (44), upon replacing $y_{n+1}$ with $\sigma _{n+1}$, and

$$\begin{aligned} \varSigma _j^\alpha (\sigma _{n+1},h_{n+1}) = O(h_{n+1}^{2k-j}), \quad j=0,\dots ,s-1, \end{aligned}$$

the corresponding quadrature errors.

3.2 Solving the Discrete Problems

The discrete problem (55), to be solved at each integration step, can be better cast in vector form by introducing the matrices

$$\begin{aligned} \mathcal{P}_s= & {} \left( \begin{array}{ccc} P_0(c_1) &{} \dots &{} P_{s-1}(c_1)\\ \vdots &{} &{}\vdots \\ P_0(c_k) &{} \dots &{} P_{s-1}(c_k)\end{array}\right) , \quad \mathcal{I}_s^\alpha = \left( \begin{array}{ccc} I^\alpha P_0(c_1)&{} \dots &{}I^\alpha P_{s-1}(c_1)\\ \vdots &{} &{}\vdots \\ I^\alpha P_c(c_k) &{} \dots &{}I^\alpha P_{s-1}(c_k)\end{array}\right) \quad \in \mathbb {R}^{k\times s},\\ \varOmega= & {} \left( \begin{array}{ccc} b_1\\ {} &{}\ddots \\ {} &{}&{}b_k\end{array}\right) , \end{aligned}$$

and the (block) vectors:

$$\begin{aligned} {{\varvec{\gamma }}}^{n+1} = \left( \begin{array}{c} \gamma _0^{n+1}\\ \vdots \\ \gamma _{s-1}^{n+1}\end{array}\right) \in \mathbb {R}^{sm},\quad {{\varvec{\phi }}}_n^\alpha = \left( \begin{array}{c} \phi _n^\alpha (c_1,\sigma )\\ \vdots \\ \phi _n^\alpha (c_k,\sigma )\end{array}\right) \in \mathbb {R}^{km}. \end{aligned}$$

In fact, in so doing (55) can be rewritten as⁶:

$$\begin{aligned} {{\varvec{\gamma }}}^{n+1} = \mathcal{P}_s^\top \varOmega \otimes I_m f\left( {{\varvec{\phi }}}_n^\alpha + h_{n+1}^\alpha \mathcal{I}_s^\alpha \otimes I_m{{\varvec{\gamma }}}^{n+1}\right) , \end{aligned}$$

(56)

This formulation is very similar to that used for HBVMs in the case $\alpha =1$ [10]. The formulation (56) has a twofold use:

• it shows that, assuming, for example, f Lipschitz continuous, then the solution exists and is unique, for all sufficiently small timesteps $h_{n+1}$;

• it induces a straightforward fixed-point iteration:

  $$\begin{aligned} {{\varvec{\gamma }}}^{n+1,0}= & {} {{\varvec{0}}},\nonumber \\ {{\varvec{\gamma }}}^{n+1,\ell }= & {} \mathcal{P}_s^\top \varOmega \otimes I_m f\left( {{\varvec{\phi }}}_n^\alpha + h_{n+1}^\alpha \mathcal{I}_s^\alpha \otimes I_m{{\varvec{\gamma }}}^{n+1,\ell -1}\right) ,\quad \ell =1,2,\dots , \end{aligned}$$

  (57)

  which we shall use for the numerical tests.

Concerning the first point, the following result holds true.

Theorem 2

Assume f be Lipschitz with constant L in in the interval $[t_n,t_{n+1}]$. Then, the iteration (57) is convergent for all timesteps $h_{n+1}$ such that

$$\begin{aligned} h_{n+1}^\alpha L\Vert \mathcal{P}_s^\top \varOmega \Vert \Vert \mathcal{I}_s^\alpha \Vert <1. \end{aligned}$$

(58)

Proof

In fact, one has:

$$\begin{aligned}{} & {} \Vert {{\varvec{\gamma }}}^{n+1,\ell +1}-{{\varvec{\gamma }}}^{n+1,\ell }\Vert \\{} & {} \quad = \Vert \mathcal{P}_s^\top \varOmega \otimes I_m \left[ f\left( {{\varvec{\phi }}}_n^\alpha + h_{n+1}^\alpha \mathcal{I}_s^\alpha \otimes I_m{{\varvec{\gamma }}}^{n+1,\ell }\right) -f\left( {{\varvec{\phi }}}_n^\alpha + h_{n+1}^\alpha \mathcal{I}_s^\alpha \otimes I_m{{\varvec{\gamma }}}^{n+1,\ell -1}\right) \right] \Vert \\{} & {} \quad \le h_{n+1}^\alpha L\Vert \mathcal{P}_s^\top \varOmega \Vert \Vert \mathcal{I}_s^\alpha \Vert \cdot \Vert {{\varvec{\gamma }}}^{n+1,\ell }-{{\varvec{\gamma }}}^{n+1,\ell -1}\Vert , \end{aligned}$$

hence the iteration function defined at (57) is a contraction, when (58) holds true. $\square$

A simplified Newton-type iteration, akin to that defined in [10] for HBVMs, will be the subject of future investigations.

Remark 6

We observe that the discrete problem (56) can be cast in a Runge-Kutta type form. In fact, the vector

$$\begin{aligned} Y^{n+1} ~:=~ {{\varvec{\phi }}}_n^\alpha + h_{n+1}^\alpha \mathcal{I}_s^\alpha \otimes I_m{{\varvec{\gamma }}}^{n+1}, \end{aligned}$$

(59)

in argument to the function f at the r.h.s. in (56), can be regarded as the stage vector of a Runge–Kutta method, tailored for the problem at hand. Substituting (56) into (59), and using $Y^{n+1}$ as argument of f, then gives

$$\begin{aligned} Y^{n+1} ~=~ \phi _n^\alpha + h_{n+1}^\alpha \mathcal{I}_s^\alpha \mathcal{P}_s^\top \varOmega \otimes I_m f(Y^{n+1}). \end{aligned}$$

(60)

It is worth noticing that (60) has (block) dimension k, instead of s. However, by considering that usually $k> s$ (see Sect. 5), it follows that solving (60) is less efficient than solving (56).

This fact is akin to what happens for a HBVM(k, s) method [7, 8, 11], which is the k-stage Runge–Kutta method obtained when $\alpha =1$. In fact, for such a method, the discrete problem can also be cast in the form (56), then having (block) dimension s, independently of k (which is usually much larger than s).

From (59), one easily derives that the Butcher tableau of the Runge–Kutta type method is given by:

$$\begin{aligned} \begin{array}{c|c} {{\varvec{c}}}\, &{} \,\mathcal{I}_s^\alpha \mathcal{P}_s^\top \varOmega \\ \hline \\ &{} {{\varvec{b}}}^\top \end{array} \end{aligned}$$

(61)

where ${{\varvec{b}}},{{\varvec{c}}}\in \mathbb {R}^k$ are the vectors with the Gauss–Jacobi weights and abscissae, respectively. As anticipated above, when $\alpha =1$, (61) becomes the Butcher tableau of a HBVM(k, s) method [7, 8, 11].

Because of what exposed in the previous remark, we give the following definition.

Definition 1

The Runge–Kutta type method defined by (61), with $\alpha \in (0,1)$, will be referred to as a Fractional HBVM(k, s) method or, in short, FHBVM(k, s).

3.3 Computing the Integrals $J_j^\alpha (x)$

From (55) and (49), it follows that one needs to compute the integrals

$$\begin{aligned} J_j^\alpha \left( \frac{r^{n-\nu +1}-1}{r-1}+c_ir^{n-\nu +1}\right) , \quad i=1,\dots ,k,\quad \nu =1,\dots ,n, \end{aligned}$$

(62)

with $\{c_1,\dots ,c_k\}$ the abscissae of the Gauss–Jacobi quadrature (16). As an example, in Fig. 1 we plot the Gauss–Jacobi abscissae for $\alpha =0.5$ and $k=5,10,15,20,25,30$.

Fig. 1

Gauss–Jacobi abscissae for $\alpha =0.5$

Further, there is numerical evidence that a sufficiently high-order Gauss–Legendre formula can compute the integrals (50) up to round-off, when $x\ge 1.5$. Namely,

$$\begin{aligned} J_j^\alpha \left( \frac{r^{n-\nu +1}-1}{r-1}+c_ir^{n-\nu +1}\right) , \quad i=1,\dots ,k,\quad \nu =1,\dots ,n-1, \end{aligned}$$

(63)

and

$$\begin{aligned} J_j^\alpha \left( 1+c_ir\right) , \quad \mathrm{s.t.}\quad c_ir\ge 0.5, \quad j=0,\dots ,s-1. \end{aligned}$$

(64)

However, this is no more the case, when computing:

$$\begin{aligned} J_j^\alpha \left( 1+c_ir\right) , \quad \mathrm{s.t.}\quad c_ir<0.5, \quad j=0,\dots ,s-1. \end{aligned}$$

(65)

Consequently, there is the problem of accurately and efficiently computing these latter integrals.

Remark 7

We observe that the evaluation of the integrals (63)–(64), $j=0,\dots ,s-1$, via a 2p-order Gauss–Legendre formula is inexpensive. As matter of fact, only the values $P_j(\xi _i)$ need to be computed, $j=0,\dots ,s-1$, with

$$\begin{aligned} \{\xi _1, \dots , \xi _p \} \end{aligned}$$

(66)

the Gauss–Legendre abscissae of the considered formula. Further, we observe that, with reference to (62), only the integrals

$$\begin{aligned} J_j^\alpha \left( \frac{r^n-1}{r-1}+c_ir^{n}\right) ,\quad j=0,\dots ,s-1, \quad i=1,\dots ,k, \end{aligned}$$

need to be actually computed: as matter of fact, the remaining integrals,

$$\begin{aligned} J_j^\alpha \left( \frac{r^\nu -1}{r-1}+c_ir^\nu \right) ,\quad j=0,\dots ,s-1, \quad i=1,\dots ,k,\quad \nu =1,\dots ,n-1, \end{aligned}$$

are inherited from the previous steps.

The starting point to derive an efficient algorithm for computing the integrals (65), is that the Jacobi polynomials (6) satisfy, as does any other family of orthogonal polynomials, a three-term recurrence:

$$\begin{aligned} P_{j+1}(c)= & {} (a_jc-b_j)P_j(c) - d_jP_{j-1}(c), \quad j=0,1,\dots ,\nonumber \\ P_0(c)\equiv & {} 1, \quad P_{-1}(c)\equiv 0, \end{aligned}$$

(67)

with prescribed $a_j,b_j,d_j$, $j\ge 0$. In fact, by setting $\phi (c)=c$, and using the scalar product (9), to enforce (7), for $P_0,\dots ,P_{s-1}$, one obtains:

$$\begin{aligned} a_j= & {} \frac{1}{(P_{j+1},\phi \cdot P_j)}, b_j = \frac{(P_j,\phi \cdot P_j)}{(P_{j+1},\phi \cdot P_j)},\quad d_j = \frac{(P_j,\phi \cdot P_{j-1})}{(P_{j+1},\phi \cdot P_j)},\quad j=0,\dots ,s-2. \nonumber \\ \end{aligned}$$

(68)

Consequently, by recalling the definition (50), from (67) one has:

$$\begin{aligned} J_0^\alpha (x) = \frac{x^\alpha - (x-1)^\alpha }{\alpha }, \quad J_{-1}^\alpha (x) = 0, \quad \alpha>0,\quad x>1, \end{aligned}$$

and

$$\begin{aligned} J_{j+1}^\alpha (x)= & {} \int _0^1 (x-\tau )^{\alpha -1} P_{j+1}(\tau )\textrm{d}\tau \\= & {} a_j \int _0^1 (x-\tau )^{\alpha -1}\tau P_j(\tau )\textrm{d}\tau - b_j J_j^\alpha (x) - d_j J_{j-1}^\alpha (x)\\= & {} -a_j\int _0^1(x-\tau )^\alpha P_j(\tau )\textrm{d}\tau +[a_jx-b_j]J_j^\alpha (x) - d_j J_{j-1}^\alpha (x)\\= & {} -a_jJ_j^{\alpha +1}(x)+[a_jx-b_j]J_j^\alpha (x) - d_j J_{j-1}^\alpha (x), \quad j=0,\dots ,j-2. \end{aligned}$$

From the last two formulae, one derives that Jjalfa(a,b,d,alfa,1+ci*r) computes all the integrals in (65) corresponding to the abscissa ci, with Jjalfa the Matlab$^{\copyright }$ function listed in Table 1, and the vectors a,b,d containing the scalars (68). An implementation of the previous function, using the standard variable precision arithmetic (i.e., using vpa in Matlab$^{\copyright }$), allows handling values of s up to 20, at least.

Table 1 Matlab$^{\copyright }$ function Jjalfa

4 Analysis of the Method

From (45) and (47), and with reference to (51)–(54), one derives:

$$\begin{aligned}{} & {} y_{n+1}(ch_{n+1})-\sigma _{n+1}(ch_{n+1})\\{} & {} \quad = \left[ G_n^\alpha (c,y)-\phi _n^\alpha (c,\sigma )\right] ~+~ \frac{h_{n+1}^\alpha }{\varGamma (\alpha )}\sum _{j=0}^{s-1} \left[ \gamma _j(y_{n+1})-\gamma _j^{n+1}\right] I^\alpha P_j(c)\\{} & {} \qquad + \frac{h_{n+1}^\alpha }{\varGamma (\alpha )}\sum _{j\ge s}\gamma _j(y_{n+1}) I^\alpha P_j(c)\\{} & {} \quad = \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}+cr^{n-\nu +1}-\tau \right) ^{\alpha -1} \\{} & {} \qquad \left[ f(y_\nu (\tau h_\nu ))- f(\sigma _\nu (\tau h_\nu ) +R_\nu ^\alpha (\tau )\right] \textrm{d}\tau \\{} & {} \qquad +\frac{h_{n+1}^\alpha }{\varGamma (\alpha )}\sum _{j=0}^{s-1} \left[ \gamma _j(y_{n+1})-\gamma _j(\sigma _{n+1}) +\varSigma _j(\sigma _{n+1},h_{n+1})\right] I^\alpha P_j(c)\\{} & {} \qquad + \frac{h_{n+1}^\alpha }{\varGamma (\alpha )}E_{n+1}^\alpha (c). \end{aligned}$$

Assuming f Lipschitz with constant L in a suitable neighborhood of the solution, and setting

$$\begin{aligned} R_\nu ^\alpha:= & {} \max _{\tau \in [0,1]} |R_\nu ^\alpha (\tau )|,\quad \nu =1,\dots ,N-1,\\ E_{n+1}^\alpha:= & {} \max _{c\in [0,1]} |E_{n+1}^\alpha (c)|,\quad n=1,\dots ,N-1,\\ e_n:= & {} \max _{c\in [0,1]}|y_n(ch_n)-\sigma _n(ch_n)|, \quad n=1,2,\dots ,N, \end{aligned}$$

one then obtains that, for $h_{n+1}^\alpha$ sufficiently small, and a suitable constant $K_1>0$:

$$\begin{aligned} e_{n+1}\le & {} \frac{K_1L}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}-\tau \right) ^{\alpha -1}\textrm{d}\tau \, e_\nu \\{} & {} +\,\frac{K_1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}-\tau \right) ^{\alpha -1}\textrm{d}\tau R_\nu ^\alpha ~+~ g_{n+1}^\alpha ,\quad n=1,\dots ,N-1, \end{aligned}$$

with

$$\begin{aligned} g_{n+1}^\alpha = O(h_{n+1}^{s+\alpha }). \end{aligned}$$

(69)

Considering that

$$\begin{aligned}{} & {} \frac{1}{\varGamma (\alpha )}\int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}-\tau \right) ^{\alpha -1}\textrm{d}\tau \nonumber \\{} & {} \quad =\frac{1}{\varGamma (\alpha +1)}\left[ \left( \frac{r^{n-\nu +1}-1}{r-1}\right) ^\alpha -\left( \frac{r^{n-\nu +1}-r}{r-1}\right) ^\alpha \right] ~\le ~\frac{1}{\varGamma (\alpha +1)},\quad \nu =1,\dots ,n,\nonumber \\ \end{aligned}$$

(70)

and [see (54)]

$$\begin{aligned} h_1^\alpha R_1^\alpha \le O(h_1^{2\alpha }), \quad h_\nu ^\alpha R_\nu ^\alpha \le O(h_\nu ^{s+\alpha }), \quad \nu >1, \end{aligned}$$

so that [see (40)], for a suitable constant $K_2>0$,

$$\begin{aligned} \frac{K_1}{\varGamma (\alpha +1)}\sum _{\nu =1}^n h_\nu ^\alpha R_\nu ^\alpha\le & {} K_2\left( h_1^{2\alpha } + \sum _{\nu =2}^n h_\nu ^{s+\alpha }\right) \\= & {} K_2\left( h_1^{2\alpha } + h_n^{s+\alpha }\sum _{\nu =0}^{n-2} (r^{s+\alpha })^{-\nu }\right) \\\le & {} K_2\left( h_1^{2\alpha } + \frac{h_n^{s+\alpha }}{1-r^{-(s+\alpha )}}\right) , \end{aligned}$$

one eventually obtains:

$$\begin{aligned} e_{n+1}\le & {} \frac{K_1L}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}-\tau \right) ^{\alpha -1}\textrm{d}\tau \, e_\nu ~+~\psi _n^\alpha , \quad n=1,\dots ,N-1, \end{aligned}$$

with [see (40) and (69)]

$$\begin{aligned} \psi _n^\alpha:= & {} K_2\left( h_1^{2\alpha } + \frac{h_n^{s+\alpha }}{1-r^{-(s+\alpha )}}\right) + g_{n+1}^\alpha ~=~ O(h_1^{2\alpha } + h_{n+1}^{s+\alpha }),\quad n=1,\dots ,N-1. \end{aligned}$$

At last, by considering that, for $n=1,\dots ,N-1$,

$$\begin{aligned}{} & {} \frac{1}{\varGamma (\alpha )}\sum _{\nu =1}^n h_\nu ^\alpha \int _0^1 \left( \frac{r^{n-\nu +1}-1}{r-1}-\tau \right) ^{\alpha -1}\textrm{d}\tau \nonumber \\{} & {} \quad =\frac{1}{\varGamma (\alpha +1)} \sum _{\nu =1}^n\left[ h_\nu ^\alpha \left( \frac{r^{n-\nu +1}-1}{r-1}\right) ^\alpha -h_{\nu +1}^\alpha \left( \frac{r^{n-\nu }-1}{r-1}\right) ^\alpha \right] \nonumber \\{} & {} \quad =\frac{1}{\varGamma (\alpha +1)}\left[ \left( h_1\frac{r^n-1}{r-1}\right) ^\alpha -h_{n+1}^\alpha \right] ~\le ~\frac{T^\alpha }{\varGamma (\alpha +1)}, \end{aligned}$$

(71)

setting

$$\begin{aligned} \rho = \exp \left( \frac{K_1LT^\alpha }{\varGamma (\alpha +1)}\right) , \end{aligned}$$

and considering that $e_1\le O(h_1^{2\alpha })$, from the Gronwall lemma (see, e.g., [29]) one eventually obtains, for a suitable $K>0$:

$$\begin{aligned} e_{n+1}\le & {} K\rho \left( h_1^{2\alpha } + \sum _{\nu =1}^n \psi _n^\alpha \right) ~=~ K\rho \left( (n+1)h_1^{2\alpha } + \frac{h_{n+1}^{s+\alpha }}{1-r^{-(s+\alpha )}}\right) \nonumber \\\le & {} K\rho \left( Nh_1^{2\alpha } + \frac{h_N^{s+\alpha }}{1-r^{-(s+\alpha )}}\right) , \quad n=1,\dots ,N-1. \end{aligned}$$

(72)

Considering that [see (27) and (40)] $N = \log _r\left( 1 + T(r-1)/h_1\right)$, the error is optimal when $h_1^{2\alpha }\sim h_N^{s+\alpha }$.

Remark 8

In the case where the vector field of problem (1) is suitably smooth at $t=0$, so that a constant timestep $h=T/N$ can be used, the estimate

$$\begin{aligned} e_n \le O(nh^{s+\alpha }), \quad n=1,\dots ,N, \end{aligned}$$

(73)

can be derived for the error, by using similar arguments as above.

Remark 9

From (72) [or (73)], one deduces that, for a given prescribed accuracy, it is possible to decrease the value of the number N of the time steps, by increasing the degree s of the polynomial approximating the vector field. By considering that, as anticipated in the introduction, one main difficulty in solving the problem (1) stems from the evaluation of the memory terms, reducing N has a welcome impact on the overall complexity of the method.

5 Numerical Tests

We here report a few numerical tests to illustrate the theoretical findings. For all tests, when not otherwise specified, we use $k=30$ for the Gauss–Jacobi quadrature (16), and $p=30$ for the Gauss–Legendre quadrature formula (66). Also, the following values of s will be considered:

$$\begin{aligned} s\in \{1,2,3,4,5,6,7,8,9,10,20\}. \end{aligned}$$

All the numerical tests have been performed in Matlab$^{\copyright }$ (Rel. 2023b) on a Silicon M2 laptop with 16GB of shared memory. As anticipated, we use the fixed-point iteration (57) to solve the generated discrete problems (56). The iteration is carried out until full machine accuracy is gained.

5.1 Example 1

The first problem, taken from Garrappa [24], is given by:

$$\begin{aligned} y^{(0.6)} = -10 y, \quad t\in [0,5], \quad y(0) = 1, \end{aligned}$$

(74)

whose solution is given by the following Mittag–Leffler function⁷:

$$\begin{aligned} E_{0.6}(-10 t^{0.6}) = \sum _{j\ge 0} \frac{(-10 t^{0.6})^j}{\varGamma (0.6j+1)}. \end{aligned}$$

In Table 2, we list the obtained results, in terms of maximum error, when using different values of s and $h_1$, with $h_N$ fixed, in order to ascertain the contribution of the first term of the error in the bound (72). In order to satisfy the requirements:

$$\begin{aligned} t_N = h_1\frac{r^N-1}{r-1}\approx 5, \quad h_N\approx 0.05, \end{aligned}$$

for all combinations of $h_1$ and N, we use the value $r=1.01$ in (40), and the number of timesteps N is chosen in order that $t_N$ is the closest point to the end of the integration interval. The ***, in the line corresponding to $s=1$, means that the solution is not properly evaluated: this is due to the failure of the fixed-point iteration (57) in the last integration steps (the same notation will be used in the subsequent tables). As is expected from (72), the error decreases as s increases and the initial timestep $h_1$ decreases. Further, having a large value of s is not effective, if $h_1$ is not suitably small, and vice versa (again from the bound (72)). Remarkably, by choosing s large enough and $h_1$ suitably small, full machine accuracy is gained (cf. the last 4 entries in the last column of the table, having the same error).

In Table 3 we list the results obtained by using $k=s$, which is the minimum value allowed for k. In such a case, the accuracy is generally slightly worse, due to the fact that the quadrature error is of the same order as the truncation error. It is, however, enough choosing k only slightly larger than s, to achieve a comparable accuracy, as is shown in Table 4 for $k=s+5$. Nevertheless, it must be stressed that choosing larger values of k is not an issue, since the discrete problem (56), to be solved at each integration step, has (block) size s, independently of k.

Table 2 Maximum error for Problem (74), $r=1.01$ and $k=30$

Table 3 Maximum error for Problem (74), $r=1.01$ and $k=s$

Table 4 Maximum error for Problem (74), $r=1.01$ and $k=s+5$

5.2 Example 2

The next problem that we consider is from Diethelm et al. [21] (see also [24]):

$$\begin{aligned} y^{(0.5)}= & {} -|y|^{1.5} +\frac{40320}{\varGamma (8.5) }t^{7.5} - 3\frac{\varGamma (5.25)}{\varGamma (4.75)}t^{3.75} + \left( \frac{3}{2}t^{0.25} - t^4 \right) ^3 + \frac{9}{4}\varGamma (1.5),\nonumber \\{} & {} t\in [0,1], \quad y(0)=0, \end{aligned}$$

(75)

whose solution is

$$\begin{aligned} y(t) = t^8-3\,t^{4.25}+\frac{9}{4}\,t^{0.5}. \end{aligned}$$

(76)

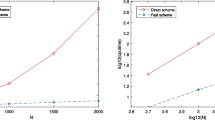
According to Garrappa [24], “this problem is surely of interest because, unlike several other problems often proposed in the literature, it does not present an artificial smooth solution, which is indeed not realistic in most of the fractional-order applications.” Despite this, a constant timestep $h=1/N$ turns out to be appropriate since, unlike the solution (76), the vector field (75) is very smooth at the origin, as one may see in Fig. 2. In Table 5 we list the maximum error by using different values of N: as is clear, by using $s\ge 8$, only 32 steps are needed to gain full machine accuracy for the computed solution. Further, in Fig. 3 is the work-precision diagram (i.e., execution time ⁸ vs. computed accuracy) for the following methods, used on a uniform grid with $N+1$ points, with $N=2^\nu$, as below specified:

• FHBVM(30,1), $\nu = 5,6,\dots ,12$;

• FHBVM(30,2), $\nu = 4,5,\dots ,12$;

• FHBVM(30,5), $\nu = 2,3,\dots ,8$;

• HFBVM(30,10), $\nu = 2,3,4,5$;

• FHBVM(30,20), $\nu = 2,3$;

• the BDF-2 method implemented in the Matlab code flmm2 [23],⁹$\nu = 6,\dots ,20$.

The rationale for this choice is to use FHBVMs both as spectral methods and not, with a further comparison with a state-of-art numerical code. In the plots, the computed accuracy (ca) is measured as follows: if $e_i$ is the absolute error at the i-th grid point, then

$$\begin{aligned} \texttt {ca} = -\log _{10}\max _{i=1,\dots ,N} |e_i|. \end{aligned}$$

From the obtained results, one concludes that:

• low-order FHBVMs are less competitive than high-order ones;

• high-order FHBVMs require less time steps and are, therefore, able to obtain a fully accurate solution;

• when used as spectrally accurate methods in time, FHBVMs are very effective, and competitive with existing methods.

Fig. 2

solution (continuous line) and vector field (dashed line) for problem (75)

Table 5 Maximum error for Problem (75), constant timestep $h=1/N$

Fig. 3

Work-precision diagram for Problem (75)

5.3 Example 3

We now consider the following problem taken from Satmari [38],

$$\begin{aligned} y^{(1/3)} = \frac{t}{10} \left[ y^3 - (t^{2/3}+1)^3\right] + \frac{\varGamma (5/3)}{\varGamma (4/3)} t^{1/3}, \quad t\in [0,1], \quad y(0) = 1, \end{aligned}$$

(77)

whose solution is $y(t) = t^{2/3}+1$. We solve it by using $h_1=10^{-11}$ and $r=1.2$. In such a case, $N=130$ timesteps are needed to cover approximately the integration interval, with $h_N\le 0.2$. The obtained results, by considering increasing values of s, are listed in Table 6. Also in this case, we obtain full accuracy starting from $s=8$.

Remark 10

Concerning the choice of the parameters $h_1$, r, and N for the graded mesh, one has to consider that, in principle [see (72)]:

$$\begin{aligned} T \equiv t_N = h_1\frac{r^N-1}{r-1}, \quad h_N = h_1 r^{N-1}, \quad h_1^{2\alpha }\sim h_N^{s+\alpha }. \end{aligned}$$

It is then important to properly choose $h_1$, and arrange the other parameters accordingly. In such a case, one may reduce the number N of time steps by increasing s, as observed in Remark 9. The optimal choice of such parameters, however, deserves to be further investigated.

Table 6 Maximum error for Problems (77) and (79), $r=1.2$ and $h_1=10^{-11}$

5.4 Example 4

Next, we consider the following problem, again taken from [38],

$$\begin{aligned} y^{(1/3)} = \frac{1}{3}\left( y^3 - t^4\right) + \varGamma (7/3)t, \quad t\in [0,1], \quad y(0) = 0, \end{aligned}$$

(78)

whose solution is $y(t) = t^{4/3}$. We solve this problem by using a constant timestep $h=1/N$: in fact, the vector field can be seen to be a polynomial of degree 1. The obtained results are listed in Table 7: an order 1 convergence can be observed for $s=1$ [which is consistent with (73)], whereas full machine accuracy is obtained for $s\ge 2$, due to the fact that, as anticipated above, the vector field of problem (78) is a polynomial of degree 1 in t and, consequently, (13) and (21) coincide, for all $s\ge 2$.

Table 7 Maximum error for Problem (78), constant timestep $h=1/N$

5.5 Example 5

Finally, we reformulate the two problems (77) and (78) as a system of two equations, having the same solutions as above, as follows:

$$\begin{aligned} y_1^{(1/3)}= & {} \frac{t}{10} \left[ y_1^3 - (y_2^{1/2}+1)^3\right] + \frac{\varGamma (5/3)}{\varGamma (4/3)} t^{1/3}, \quad y_1(0) = 1,\nonumber \\ y_2^{(1/3)}= & {} \frac{1}{3}\left( y_2^3 - (y_1-1)^6\right) + \varGamma (7/3)t, ~~\quad y_2(0) = 0, \quad t\in [0,1]. \end{aligned}$$

(79)

We solve Problem (79) by using the same parameters used for Problem (77): $h_1=10^{-11}$, $r=1.2$, and 130 timesteps. The obtained results are again listed in Table 6: it turns out that they are similar to those obtained for Problem (77) and, also in this case, we obtain full accuracy starting from $s=8$.

6 Conclusions

In this paper we have devised a novel step-by-step procedure for solving fractional differential equations. The procedure, which generalizes that given in [2], relies on the expansion of the vector field along a suitable orthonormal basis, here chosen as the shifted and orthonormal Jacobi polynomial basis. The analysis of the method has been given, along with its implementation details. These latter details show that the method can be very efficiently implemented. A few numerical tests confirm the theoretical findings.

It is worth mentioning that systems with FDEs of different orders can be also solved by slightly adapting the previous framework: as matter of fact, it suffices using different Jacobi polynomials, corresponding to the different orders of the FDEs. This, in turn, allows easily managing fractional differential equations of order $\alpha >1$, by casting them as a system of $\lfloor \alpha \rfloor$ ODEs, coupled with a fractional equation of order $\beta :=\,\alpha -\lfloor \alpha \rfloor \in (0,1)$.

As anticipated in Sect. 3.2, a future direction of investigation will concern the efficient numerical solution of the generated discrete problems, which is crucial when using larger stepsizes. Also the optimal choice of the parameters for the methods will be further investigated, in particular those for generating the graded mesh, as well as the possibility of adaptively defining it. Further, the parallel implementation of the methods could be also considered, following an approach similar to [1].