Abstract
Additional grid points are often introduced for the higher-order polynomial of a numerical solution with curvilinear elements. However, those points are likely to be located slightly outside the domain, even when the vertices of the curvilinear elements lie within the curved domain. This misallocation of grid points generates a mesh error, called geometric approximation error. This error is smaller than the discretization error but large enough to significantly degrade a long-time integration. Moreover, this mesh error is considered to be the leading cause of conservation error. Two novel schemes are proposed to improve conservation error and/or discretization error for long-time integration caused by geometric approximation error: The first scheme retrieves the original divergence of the original domain; the second scheme reconstructs the original path of differentiation, called connection, thus retrieving the original connection. The increased accuracies of the proposed schemes are demonstrated by the conservation error for various partial differential equations with moving frames on the sphere.
Similar content being viewed by others
1 Introduction
The curvilinear mesh has been widely welcomed for various computational simulations. A curvilinear mesh consists of curved elements that are larger than the regular elements having straight edges in a highly curved boundary or domain. A larger curved element computationally allows a larger time step and a better approximation of the domain to yield better accuracy and efficiency for the numerical scheme. Thus, curvilinear elements or curved elements are widely used, particularly in the weak formulation of high-order schemes. For example, the modern Earth system model adapts weak formulations in the context of a continuous Galerkin method (also known as the spectral element method) or discontinuous Galerkin method such as the Energy Exascale Earth System Model(E3SM) [1], Nonhydrostatic Unified Model of the Atmosphere (NUMA) [2], Korea Meteorological Administration’s KIM [3], and the Met Office’s LFRic [4]. For models that involve a long-time integration, such as climate models, conservation properties become important. Several models such as E3SM [5, 6] and LFRic [7,8,9] employ compatible or mimetic schemes, which use discrete operators that mimic the key mathematical properties of the divergence, gradient, and curl operators of the continuous governing equations [10] to ensure better conservation properties.
One critical issue of the curvilinear mesh in a weak formulation is that the internal grid points may not be exactly in the domain, even when the vertices and edges are exactly located in the original domain. Consider a curved line element with two vertices, \(\mathbf {x}_A\) and \(\mathbf {x}_B\). A mesh for this element creates the grid points \(\mathbf {x}_i,~ 1 \le i \le p-1\), for a solution of polynomial order p. Consider the Lagrangian polynomial expansion on this curved line element as follows.
where the range of \(\xi \) is \(0 \le \xi \le \xi _m\) for the collocation points \(\xi _m\). The ith order Lagrangian polynomial basis \(\ell _i\) is defined as
Suppose that the vertices are exactly in the domain, as \(\mathbf {x}_0 = \mathbf {x}_A\) and \(\mathbf {x}_p = \mathbf {x}_B\). The locations of the internal grid points are not analytically allocated but should be approximated in the weak formulation. Note that the internal grid points significantly affect the accuracy and stability of the weak formulation. Many schemes have been proposed to effectively place the internal grid points on a curved line in the weak formulation, such as the Galerkin projection [11] or isoparametric representation [11, 12]. However, the exact allocation of the internal grid points is challenging. This misallocation of the internal grid points produces a relatively small error, called geometric approximation error [13], defined as follows.
where \(\mathbf {x}_i^{exact}\) is the ith point’s exact location on the domain. Note that the mesh error is the summation of geometric approximation error and the vertex error defined as \( (1/\sqrt{2}) [ \Vert \mathbf {x}_0 - \mathbf {x}_0^{exact} \Vert \) + \(\Vert \mathbf {x}_p - \mathbf {x}_p^{exact} \Vert ]\) for the curved line element.
The geometric approximation error is not significant for all the numerical schemes. The finite difference scheme with a spherical coordinate axis and corresponding metric tensor does not generate significant geometric approximation error. This is because the finite difference scheme a priori requires the construction of all the discrete grid points. Moreover, the analytically-known metric tensor specifies the path between the discrete grid points. Thus, all the geometric information is completely determined. This contrasts with the weak formulation where the additional grid points should be located in a curved domain depending on the polynomial order of the solution. Moreover, the Piola-transformation type numerical schemes [14,15,16] are also free from geometric approximation error.
The weak formulations of high-order methods, such as spectral methods and (continuous/discontinuous) Galerkin methods, have gained broad attention for solving partial differential equations (PDEs) on curved surfaces for their distinctive advantages such as geometric flexibility, long-time stability/accuracy, and computational efficiency for a given accuracy threshold. However, it has recently been revealed that the geometric approximation error, which is unique in the weak formulation with curvilinear mesh, may degrade the overall accuracy, particularly in long-time integration [13]. Moreover, it has been reported that the geometric approximation error significantly affects the conservation error of mass and energy. This is because the geometric approximation error modifies the surface normal vector to change the differential operator and consequently degrades the Jacobian for accurate integration [13].
One possible solution for removing the geometric approximation error is to use a high-order mesh. In the study by [13], a high-order mesh, known as NekMesh [17,18,19], was introduced to demonstrate the trivial geometric approximation error of a curvilinear spherical mesh. The mesh error of NekMesh converges exponentially as p increases. Briefly speaking, NekMesh deforms the CAD-based low-order linear mesh of the surface to conform to the original geometry. NekMesh reallocates the interior grid points through energy-based optimization for optimal nodal sets. However, the problem is that the high-order mesh could be challenging to construct for a domain that is more complex than the sphere. Consider the diverse curved elements of a sphere having quadrilateral or hexagonal patches. A high-order mesh may not always be available with specific geometric constraints, even for the sphere. This is the case for the majority of finite-difference or finite-volume schemes on the sphere. These schemes generally show second-order convergence with grid systems that do not use the latitude-longitude grid (e.g., triangular, hexagonal, or cubed-sphere grids). This phenomenon occurs because of the lack of grid orthogonality, a tradeoff that comes to avoid pole singularity for better parallel scalability, which consequently makes high-order schemes difficult to formulate.
This paper proposes two novel schemes to significantly reduce the conservation error caused by geometric approximation error, particularly in a mesh with non-negligible geometric approximation error. The first scheme retrieves the original magnitude of the covariant divergence, and the second scheme retrieves the path of differentiation for the original covariant divergence. By covariant divergence, we mean the divergence on general curved surfaces where the vector differentiation should be considered with respect to the varying axes on the surface.
The introduced schemes can be applied to any arbitrary curved surface. However, theoretical and test examples generally use the sphere for validation convenience. Mathematical symbols introduced in this paper is summarized in Table 1. Moving frames have been demonstrated to be accurate and efficient geometric tools for the numerical solution of various PDEs on general curved surfaces [20,21,22,23]. Moving frames provide a convenient change of differentiation to constitute original and deformed connections. However, the error related to the different directions of moving frames on the sphere is considered negligible in this paper. This is made possible by using a sufficient number of curved elements and grid points for the domain, as described in refs. [20, 21].
The content of this paper is organized as follows. Sections 2 and 3 explain the changes in divergence and flux by geometric approximation error of a slightly deformed domain. In Sect. 4, divergence/connection preservation schemes are proposed to improve the conservation error of the numerical schemes for general PDEs with divergence. Section 5 provides explanations about how to construct LOCAL and LOCSPH moving frames on an arbitrary curved domain. Section 6 presents numerical tests of static divergence and curl on the sphere and corresponding partial differential equations such as conservational laws and Maxwell’s equations. Section 7 displays several numerical tests for shallow water equations (SWEs) to show the accuracy of the proposed scheme, particularly for the conservation of mass and energy. A discussion follows in Sect. 8.
2 Divergence on a Slightly Deformed Domain
Consider a smoothly curved original domain \(\Omega ^{0}\) without any mesh error. A tessellation of the domain is obtained as \(\Omega ^{0} = \cup _e \Omega _e^{0}\) where \(\Omega _i^{0} \cap \Omega _j^{0} = \emptyset \) when \(i \ne j\). For a velocity vector \(\mathbf {v}\) defined on a curved element \(\Omega _e^{0}\), the divergence theorem holds,
where the superscript 0 indicates that the corresponding quantity is defined on the original domain \(\Omega ^0\). For an element of the domain that has a slightly deformed from the original domain, let \(\varepsilon \) be the angle between the surface normal vector of the original domain and that of the deformed domain. Denote the deformed element as \(\Omega ^{\varepsilon }_e\) to indicate the quantitative deformation magnitude of \(\varepsilon \). We use the superscript \(\varepsilon \) to represent a vector or a differential operator that lies on \(\Omega ^{\varepsilon }_e\). The divergence theorem still holds for the vector \(\mathbf {v}^{\varepsilon }\) with the corresponding differential operator defined on \(\Omega ^{\varepsilon }_e\) as
On a slightly deformed surface \(\Omega _e^{\varepsilon }\) with a geometric approximation error, the source and sink of the flow is conserved, respectively. The flux that enters through the boundaries of the domain is the divergence of the vector, which is often identified as the source of the flow. When the surrounding space outside the domain, known as the ambient space, is absent, every vector is projected into the domain \(\Omega _e^{\varepsilon }\). Thus, the projection of the vector is generally achieved instantaneously.
The projection of the divergence operator \(\nabla \cdot \) is critical because the path on a curved surface determines the vector differentiation between discrete grid points. To obtain accurate vector differentiation on a surface, the exact metric tensor should be provided. This means that the path between the grid points should be computed accurately. Another option is to use moving frames lying on the domain [20,21,22,23]. The projection of the divergence operator \(\nabla ^{\varepsilon } \cdot \) is instantly obtained without computing the metric tensor of the new curved domain \(\Omega _e^{\varepsilon }\). In the moving frames, the divergence operator \(\nabla ^{\varepsilon } \cdot \) can be conveniently constructed on the domain \(\Omega _e^{\varepsilon }\).
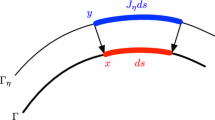
Illustrations of the geometric components of an one-dimensional domain \(\Omega _e^0\) and \(\Omega _e^{\varepsilon }\), respectively. The definition of geometric components for two dimensional domain is similar along a curved line. Surface normal vectors \(\mathbf {k}^{\varepsilon }\) and \(\mathbf {k}\) is orthogonal to edge normal vector \(\mathbf {n}^{\varepsilon }\) and \(\mathbf {n}\), respectively. Thus, the angle between them is the same as \(\varepsilon \). The mesh error between \(\Omega _e^0\) and \(\Omega _e^{\varepsilon }\) is denoted by \(\delta \)
The divergence theorems in Eq. (2) and Eq. (3) holds respectively. However, this does not necessarily mean that the two equalities are the same, i.e.,
The divergence on a surface can be changed due to the changes in the domain. For example, consider a spherical shell of radius r with the metric \(ds^2 = r^2 d \theta ^2 + r^2 \sin ^2 \theta d \phi ^2\). This implies that \(x = r \sin \theta \cos \phi \), \(y = r \sin \theta \sin \phi \), \(z = r \cos \theta \), where \(\phi \) and \(\theta \) are the azimuthal and polar angle, respectively. Consider a velocity vector \(\mathbf {v}^0\) on this sphere such that the velocity is expanded by the spherical coordinate axis of the sphere as
where \(\varvec{\phi }\) and \(\varvec{\theta }\) represent the tangent vectors of the axis \(\phi \) and \(\theta \), respectively. The divergence of this vector on \(\Omega \) is computed as
In the domain \(\Omega ^{\varepsilon }_e\), suppose that the inner grid points lie slightly outside the sphere of radius r. For simplicity, suppose that only the \(\theta \) component changes. The velocity vector \(\mathbf {v}^{\varepsilon }\) on \(\Omega ^{\varepsilon }_e\) is then expressed as
The new unit axis \(\theta '\) for \(\Vert \varvec{\theta '} \Vert = 1\) is constructed as \(\varvec{\theta '} = \sin \varepsilon \mathbf {r} + \cos \varepsilon \varvec{\theta }\) where \(\varepsilon \) is the angle between \(\theta \) and \(\theta '\). Note that the velocity coefficient difference \(\Vert {v}_{\theta } - {v}_{\theta '} \Vert \) corresponds to the projection error of the velocity vector and is approximately proportional to \(\mathcal {O}(\varepsilon ^2)\). The grid points have a small variable of radius dependent on \(\theta \) such that \(r' = r + \sin \varepsilon (\theta ')\) where \(x = r' \sin \theta ' \cos \phi \), \(y = r' \sin \theta ' \sin \phi \), \(z = r' \cos \theta '\). Then, the divergence of the velocity vector on \(\Omega ^{\varepsilon }_e\) is approximately given as
Suppose that \(\varepsilon \) is sufficiently small such that \(\theta \approx \theta '\). Then, for the projected velocity vector \(\mathbf {v}^{\varepsilon }\), the difference between the two different divergence operator Eqs. (5) and (7) is given as
Equation (8) shows the changes in divergence, or the source term, by geometric approximation error. The change in divergence occurs due to the curvedness of the domain. Thus, it depends on the direction of the velocity vector. A slight modification of flux magnitude along a specific axis, for example, \(v_{\theta '}\) in Eq. (8), dramatically changes the divergence of the flux. However, any modification of magnitude along another axis, for example, \(v_{\phi }\) in Eq. (8), does not affect the divergence of the flux. The divergence also remains the same if the right-hand side of Eq. (8) is zero. The change in surface area by the deformed domain causes further changes in Eq. (8).
3 Flux on a Slightly Deformed Domain
Equation (8) indicates that the slightly deformed domain \(\Omega ^{\varepsilon }_e\) yields a change in the divergence of the projected vector \(\mathbf {v}^{\varepsilon }\), in comparison with the divergence of the vector \(\mathbf {v}^0\) in \(\Omega _e^0\). Then, the inequality Eq. (4) corresponds to
Note that the left and right integrand have the same magnitude. For example, consider the edge normal vector and the velocity vector lying on the sphere \(\mathbf {v}\) as
Consider a slightly deformed domain \(\Omega ^{\varepsilon }_e\) with an angle of \(\varepsilon \), as defined previously. For simplicity, suppose that deformation occurs only along the \(\theta \)-axis. Similar conclusion can be drawn for the general case. Then, the unit tangent vector and the velocity vector are modified as
Simple calculus yields the same flux as
Therefore, the only other reason for the inequality in Eq. (9) is the length difference between the lines \(\partial \Omega ^{\varepsilon }_e\) and \(\partial \Omega _e^0\).
Let \(\mathbf {k}^0\) and \(\mathbf {k}^{\varepsilon }\) be the surface normal vector of \(\Omega ^0\) and \(\Omega ^{\varepsilon }\), respectively, as illustrated in Fig. 1. Let \(\varepsilon \) be the angle between \(\mathbf {k}^0\) and \(\mathbf {k}^{\varepsilon }\). Note that \(\mathbf {k}^0\) and \(\mathbf {k}^{\varepsilon }\) are orthogonal to \(\mathbf {n}^0\) and \(\mathbf {n}^{\varepsilon }\), respectively. Thus, the angle between the corresponding edge normal vector \(\mathbf {n}^0\) and \(\mathbf {n}^{\varepsilon }\) is also \(\varepsilon \). For simplicity, suppose that there is no deformation along the direction orthogonal to the edge normal vector, equivalently \(\mathbf {t}^0 = \mathbf {t}^{\varepsilon }\). A similar conclusion could be reached for the general case where deformation occurs both for \(\mathbf {n}\) and \(\mathbf {t}\). Define the edge length h of the element as follows:
The boundaries \(\partial \Omega ^{\varepsilon }_e\) and \(\partial \Omega _e^0\) become flatter as the edge length h becomes smaller. Suppose that h is sufficiently small. Note that the curvature of the lines in Fig. 1 is exaggerated but it is common to have thousands of curved elements or more for a sphere of radius r. Thus, every line on each element is close to a straight line. Moreover, the angle \(\varepsilon \) is sufficiently small because we assume that the geometric approximation error is relatively smaller than the discretization error. Let the mesh error, which is defined as the radius difference between \(\partial \Omega ^{\varepsilon }_e\) and \(\partial \Omega _e^0\), be denoted by \(\delta \). Then, the mesh error \(\delta \) is expressed as follows under the above assumption:
This means that the mesh error is the first order function of the angle \(\varepsilon \). With the assumption of sufficiently small h, the ratio of the length between \(\partial \Omega ^{\varepsilon }_e\) and \(\partial \Omega _e^0\) is approximated as follows:
Particularly, if \(\varepsilon \) is approximately constant within the domain, then we have
Thus, we have the following change of flux for the slightly deformed domain \(\Omega ^{\varepsilon }_e\):
Equations (12) and (13) explains the inequality in Eq. (9). Therefore, from Eqs. (4) and (12), we reach the following proposition.
Proposition 1 A small geometric approximation error can generate a small change in the divergence of the flow on a curved domain.
This proposition suggests that the flow in a curved surface is caused by the geometric shape of the domain, particularly when the domain is curved. Consequently, the change of the shape of the domain may have a direct impact on the divergence of the flow.
Consequently, the goal is to accurately compute the original divergence of the flux in the deformed domain with the geometric approximation error. Thus, the proposed scheme should identify the original divergence from the modified divergence of the deformed domain. This scheme computes the divergence caused by the geometric approximation error and use it to compute the original divergence of the velocity vector. For this purpose, the curl theorem is used.
4 Divergence/Connection Preservation Scheme
Consider that the differential operator \(\nabla ^{\varepsilon }\) lies on \(\Omega ^{\varepsilon }_e\). For example, if differentiation is obtained on the discrete points on \(\Omega ^{\varepsilon }_e\), then the differential operator in the scheme is \(\nabla ^{\varepsilon }\). Construction of such a differential operator with moving frames will be explained in the next section. Consider a vector \(\mathbf {F}\) lying on the curved element \(\Omega ^{\varepsilon }_e\) with geometric approximation error. Then, Stokes theorem is expressed with \(\mathbf {F}\) in \(\Omega ^{\varepsilon }_e\) as follows:
On the curved element \(\Omega ^{\varepsilon }_e\), two orthonormal basis vectors can be chosen such as \(\mathbf {e}_{\varepsilon }^1\) and \(\mathbf {e}_{\varepsilon }^2\) which lie on the tangent plane. The surface normal vector for \(\Omega ^{\varepsilon }_e\) can be defined as \(\mathbf {k}^{\varepsilon } = \mathbf {e}^{\varepsilon }_1 \times \mathbf {e}^{\varepsilon }_2\). Then, the curl operator can be defined on \(\Omega ^{\varepsilon }_e\) such that the differential operator is expanded in \(\mathbf {e}_{\varepsilon }^1\) and \(\mathbf {e}_{\varepsilon }^2\), similar to the following gradient operator:
4.1 Divergence Preservation Scheme
Define the vector \(\mathbf {F} \) in Eq. (15) as follows:
Note that the surface normal vector \( \mathbf {k}^{0}\) of the original domain \(\Omega _e\) is used, instead of \(\mathbf {k}^{\varepsilon }\). Substituting it into Eq. (15), we obtain
The function \(\mathcal {G}\) is defined as follows:
The function \(\mathcal {G} \) measures the variation in \(\mathbf {v} \) with respect to \(\mathbf {k} \) along the paths of \(\nabla \), known as the connection. Note that \(\mathcal {G}(\mathbf {k}^0,\nabla ^{\varepsilon },\mathbf {v}^{\varepsilon }) \) is always zero if \(\mathbf {k}^{\varepsilon }\) is used instead of \(\mathbf {k}^{0}\) in Eq. (17). Generally speaking, if \(\mathbf {k}\), \(\mathbf {v}\), and \(\nabla \) lie on the same domain, then \(\mathcal {G}\) is always zero and, consequently, the conservation laws hold in Eq. (16). The definition of \(\mathbf {F}^{0\varepsilon }\) yields the change of the flux in Eq. (16), compared with the flux with \(\mathbf {F}^{\varepsilon \varepsilon } = \mathbf {k}^{\varepsilon } \times \mathbf {v}^{\varepsilon }\). Consider that \(\mathbf {n}^{0} \cdot \mathbf {v}^{\varepsilon } = \cos \varepsilon ( \mathbf {n}^{\varepsilon } \cdot \mathbf {v}^{\varepsilon } )\).
From Eq. (14), we observe that \(\mathcal {G}(\mathbf {k}^0,\nabla ^{\varepsilon },\mathbf {v}^{\varepsilon })\) is the divergence difference of the velocity vector between the original domain and the deformed domain. Thus, we obtain
Thus, we call Eq. (18) the divergence preservation scheme. Consequently, we have the following corollary.
Corollary 1 The original divergence of the velocity vector \(\mathbf {v}^0\) can be approximately obtained by adding \(- \iint _{\Omega ^{\varepsilon }_e } \mathcal {G}(\mathbf {k}^0,\nabla ^{\varepsilon },\mathbf {v}^{\varepsilon }) d A \), defined in Eq. (17), from the modified divergence \(\iint _{\Omega ^{\varepsilon }_e} ( \nabla ^{\varepsilon } \cdot \mathbf {v}^{\varepsilon } ) d A\) on the deformed domain to the geometric approximation error.
4.2 Connection Preservation Scheme
As an alternative scheme to approximately compute the original divergence, the differential operator \(\nabla ^0\) of the original domain can be used with the curl theorem. Define the vector \(\mathbf {F}^{\varepsilon \varepsilon } \) in Eq. (15) as follows
Substituting this vector into the curl theorem in Eq. (15), we obtain
The differential operator \(\nabla ^0\) is constructed from the original domain \(\Omega _e^0\). Thus, \( \mathcal {G}(\mathbf {k}^{\varepsilon },\nabla ^{0},\mathbf {v}^{\varepsilon }) \) is not always zero and can be non trivial. Eq. (19) makes it possible to compute the divergence of \(\nabla ^0 \cdot \mathbf {v}^{\varepsilon }\) which does not hold conservation properties, i.e.,
The negative gradient is used to construct a divergence form similar to that in Eq. (18). In summary, we have the following corollary.
Corollary 2 The original divergence \(\iint _{\Omega ^{0}_e} ( \nabla ^{0} \cdot \mathbf {v}^{\varepsilon } ) d A \) of the vector \(\mathbf {v}^{\varepsilon }\) can be approximately obtained by adding \(\iint _{\Omega ^{\varepsilon }_e } \mathcal {G}(\mathbf {k}^{\varepsilon },\nabla ^{0},\mathbf {v}^{\varepsilon }) d A \) to the modified divergence \(\iint _{\Omega ^{\varepsilon }_e} ( \nabla ^{0} \cdot \mathbf {v}^{\varepsilon } ) d A\) on the deformed domain with geometric approximation error.
4.3 Computation of \(\mathcal {G}\)
The modifications of the divergence shown in Eqs. (18) and (20) can be written as the approximation of the original divergence in the deformed domain \(\Omega ^{\varepsilon }_0\) as follows.
where \(\mathcal {G}\) is defined in Eq. (17). The computation of the spurious divergence \(\mathcal {G}\) requires a novel numerical scheme to compute material derivative, or convective operator, which is mathematically expressed as \((\mathbf {A} \cdot \nabla ) \mathbf {B}\). Consider a two-dimensional orthogonal curved domain with the constant magnitude of tangent vectors. Then, the material divergence on this domain is given as follows [24].
where \(g_{kk}\) is the metric tensor and \(\xi _i\) is the orthogonal curved axis. The subscript i implies that the corresponding quantity is the vector expansion along the ith axis. Construct moving frames such that \(g_{kk} = 1, ~ 1 \le k \le 3\) everywhere. Expand the vectors \(\mathbf {A}\) and \(\mathbf {B}\) on the frames \(\mathbf {e}^i,~ 1 \le i \le 3\) such that
Then, the numerical scheme with moving frames to compute the material derivative in Eq. (21) is given as follows.
Then, the spurious divergence \(\mathcal {G}\) is computed as follows:
Note that if \(\mathbf {k}\) is orthogonal to \(\mathbf {e}^1\) and \(\mathbf {e}^2\), then the spurious divergence \(\mathcal {G} =0\). However, \(\mathcal {G}\) can be significant. For a nontrivial \( \mathcal {G}(\mathbf {k}^0,\nabla ^{\varepsilon },\mathbf {v}^{\varepsilon })\), \(\mathbf {k}^0\) should not be orthogonal to \(\mathbf {e}^1_{\varepsilon }\) and \(\mathbf {e}^2_{\varepsilon }\). For a nontrivial \( \mathcal {G}(\mathbf {k}^{\varepsilon },\nabla ^{0},\mathbf {v}^{\varepsilon }) \), \(\mathbf {k}^{\varepsilon }\) should not be orthogonal to \(\mathbf {e}^1_{0}\) and \(\mathbf {e}^2_{0}\).
5 Constructing \(\nabla ^0\) or \(\nabla ^{\varepsilon }\) with Moving Frames
To construct two types of differential operators, i.e., \(\nabla ^0\) or \(\nabla ^{\varepsilon }\), the local orthonormal basis sets, called moving frames, are used. Suppose \(\mathbf {e}^i, ~ 1 \le i \le 3,\) is an orthonormal basis set defined on every grid point such that
where \(\delta ^i_j\) is the Kronecker delta. Let the basis vector, also called as frame, \(\mathbf {e}^1\) and \(\mathbf {e}^2\) lie on the tangent plane of the domain. Consequently, the third frame \(\mathbf {e}^3\) is aligned along the surface normal vector. The gradient operator expanded on this moving frame is defined as follows
where \( f_i = \nabla f \cdot \mathbf {e}^i\) for \(i =1,~2\). Similar definitions are applied to other differential operators. Moving frames are directly related to the direction of differentiation. By defining the domain where \(\mathbf {e}^1\) and \(\mathbf {e}^2\) lie, \(\nabla ^{\varepsilon }\) and \(\nabla ^{0}\) can be fully represented by moving frames.
5.1 Constructing Moving Frames for \(\nabla ^{\varepsilon }\)
The differential operator \(\nabla ^{\varepsilon }\) is based on the orthonormal bases that lie on the tangent plane of the surface, which are called LOCAL moving frames [25]. Consider the element-wise mapping from the standard element to the curved element of the domain. Then, construction of these bases can be easily achieved by using a differentiation of the map as follows. For a more detailed description of construction, please refer to [20, 21].
Denote \(\Omega _{st}\) as a standard triangular element having unit length. Suppose r and s are the two independent axes of \(\Omega _{st}\) as shown in Fig. 2. Consider a mapping \(\mathbf {X}(r, s)\) from \(\Omega _{st}\) to a curved element \(\Omega ^{\varepsilon }_e\). The mapping \(\mathbf {X}(r, s)\), represented as a polynomial of two variables r and s, displays the coordinate of the curved element \(\Omega ^{\varepsilon }_e\) where the Jacobian is not constant. In this mapping, the grid points and the tangent vectors of \(\Omega _{st}\) correspond to the grid points and the tangent vectors of \(\Omega ^{\varepsilon }_e\), respectively. The tangent vector of the domain \(\Omega _{st}\) is denoted by \(\partial / \partial r\) or \(\partial / \partial s\). Then, the mapping \(\mathbf {X}(r, s)\) also maps these tangent vectors onto \(\Omega ^{\varepsilon }_e\) as follows:
where the equality holds by the law of vector mapping. The above equation implies that the tangent vector of the curved element is obtained by differentiating the map \(\mathbf {c}(r, s)\) with respect to the axis. The derived two tangent vectors are not necessarily orthonormal. Thus, the orthonormalization of the two vectors yields the local orthonormal basis vectors \(\mathbf {e}^1\) and \(\mathbf {e}^2\). The differentiability of these bases is guaranteed by sufficient smoothness of the map \(\mathbf {X}(r,s)\). The third basis \(\mathbf {e}^3\) is obtained by the curl of the two basis vectors. The obtained LOCAL moving frames are generally discontinuous across the interfaces of the elements. An additional process could be applied, though it is not necessary, to construct a more Euclidean-like moving frames by comparing the divergence of \(\mathbf {e}^1\) along each edge direction [25]. The LOCAL moving frames coincide with the local shape of the surface. Thus, any differential operator using LOCAL moving frames is \(\nabla ^{\varepsilon }\).
5.2 Constructing Moving Frames for \(\nabla ^{0}\)
Deriving the differential operator \(\nabla ^{0}\) defined on the original domain is also conveniently obtained by using moving frames. The only adjustment needed from LOCAL moving frames is to align \(\mathbf {e}^3\) along the surface normal vector of the original domain \(\Omega ^0\) and reorthornomalize the frames. The first step is to replace the third frame \(\mathbf {e}^3\) with the unit surface normal vector of \(\Omega ^0\), or \(\mathbf {k} / \Vert \mathbf {k} \Vert \). The second step is to project \(\mathbf {e}^1\) and \(\mathbf {e}^2\) onto the new tangent space to form a new orthonormal set \(\mathbf {e}^i~1, \le i \le 3\). Another orthonormalization of the basis vectors creates a set of LOCAL moving frames without geometric approximation error. When the surface normal vector is the same as that of a sphere with unit length, moving frames are called LOCSPH (short for LOCAL SPHERE) moving frames in this paper. The third moving frame \(\mathbf {e}^3\) of LOCSPH is the same as the surface normal vector of the sphere. However, major difference is that LOCSPH is discontinuous across the interfaces of elements, in contrast to the continuous spherical coordinate system. Consequently, no geometric singularity exists for LOCSPH. A quick summary of the three different moving frames is given in Table. 2
6 Numerical Tests
For the test problems, the following spherical mesh known as ProjMesh [26] is used. The cube edges of unit length are equidistantly dissected according to a user-defined edge length. As ProjMesh projects the mesh of the cube onto a perfect sphere, the vertices of the derived edges are exactly on the sphere. Vertex and node distributions are uniform. However, the edges of triangular elements are inaccurately represented. Consequently, the inaccurate edges yields inaccurate locations for internal grid points by isoparametric representation [11, 12].
Consider the definition of mesh error and surface normal vector error in \(L_2\) as follows. Let \(r^{\text {0}}\) and \( \mathbf {k}^{\text {0}}\) be the radius and surface normal vector of the original domain, respectively. For all the indices i of the total N grid points in the slightly deformed domain \(\Omega ^{\varepsilon }\), we have
and
The distribution of mesh error and the surface normal vector are displayed in Fig. 3. The maximum edge length is \(h=0.4\) with 480 curved elements. Each edge has the maximum polynomial order of three. Table 3 shows the convergence of mesh error as p. Observe that there is little convergence for the \(p\ge 3\) of mesh error due to geometric approximation error.
In the remainder of this section, the numerical scheme with LOCAL moving frames with \(\mathcal {G}=0\) in Eq. (18) is referred the SD0 scheme. The divergence preservation scheme in Eq. (18) and the connection preservation scheme in Eq. (20) are referred the SD1 and SD2 scheme, respectively. For the SWEs, the connection preservation scheme is modified. Thus, Eqs. (43)–(45) are referred the SD2 scheme for the SWEs.
For error convergence, the relative error is often used in this section because the difference between the schemes is relatively small compared to the total error range. The relative error is defined as follows. Suppose that a is the error of the standard scheme, for example, SD0 in this paper. Suppose that b is the error of a proposed scheme, for example, the SD1 or SD2 scheme. The relative error of b with respect to a can be computed as follows.
If the relative error is negative, the corresponding scheme’s accuracy is better than the standard scheme. Otherwise, the corresponding scheme shows inferior accuracy compared to the standard scheme.
6.1 Divergence Test
Consider the following static divergence test on a sphere of unit length. Let \((x,y,z)=(\sin \theta \cos \phi ,\sin \theta \sin \phi ,\cos \theta )\). Expand the velocity vector along spherical coordinate axes, as \(\mathbf {v} = v_{\theta } \varvec{\theta } + v_{\phi } \varvec{\phi }\). For the velocity vector, consider the Rossby-Haurwitz flow defined as
where \(\omega = K = 7.848 \times 10^{-6}~ s^{-1}\). The divergence of the Rossby-Haurwitz flow on the sphere is zero such as
By using Eq. (16), a discontinuous Galerkin scheme for the above divergence with respect to a test function \(\varphi \) is expressed as
where \(*\) represents the corresponding quantity that is the numerical flux at the interfaces. Upwind flux is chosen for accurate integration.
Figure 4 demonstrates enhanced accuracy of the SD1 scheme in \(L_2\) and \(L_{\infty }\) error, compared with the scheme having LOCAL moving frames. SD2 scheme does not show any corresponding advantage for \(L_2\) and \(L_{\infty }\) error. There is no improvement in the accuracy of the SD2 scheme because the weak formulation of the divergence in Eq. (27) does not require any covariant differentiation. Only divergence compensation increases the accuracy of the numerical scheme noticeably. This result is expected as the SD1 scheme is optimized for accurate divergence computation.
Relative \(L_2\) and \(L_{\infty }\) error in static divergence test problem. The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
6.2 Time-dependent Advection
For a velocity vector \(\mathbf {v}\) on the sphere (\(S^2\)), the following conservation law is considered.
Then, the weak formulation of the above conservation law is obtained as
A smooth cosine bell is advected around the sphere to test the above conservation law. Refer to [20, 27, 28] for a detailed description of the test The test problem is to passively advect the cosine bell one revolution around the sphere. Time is marched using a step size of \(10^{-4}\) by an explicit fourth-order Runge-Kutta scheme. The cosine bell is advected at an angle of \(\pi /4\) with respect to the axes of the poles.
Figure 5 presents an error convergence similar to that of the divergence test in Fig. 4. For \(L_2\) error, the SD1 scheme is significantly more accurate than the scheme having LOCAL moving frames or the SD2 scheme. For \(L_{\infty }\) error, the SD1 scheme’s solution fluctuates for a low order p, but converges to show better accuracy for \(p\ge 6\). Again, this result is expected as advection is purely driven by divergence.
Relative \(L_2\) and \(L_{\infty }\) error in time-dependent advection test problem. The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
6.3 Curl Test
The cur test problem for the curl with respect to the surface normal direction \(( \nabla \times \mathbf {v} ) \cdot \mathbf {k}\) is similar to the divergence test. For the test, a flipped Rossby Haurwitz flow between the \(\theta \)-axis and \(\phi \) axis is used, and it is defined as
where \(\omega \) and K are the same as that of the divergence test. Then, the both flows are curl-free to have the following equality
The geometric effects on \(( \nabla \times \mathbf {v} ) \cdot \mathbf {k}\) are more complicated than the divergence of a vector because the magnitude of the curl is measured only along the surface normal vector. For example, the LOCAL and LOCSPH have different surface normal directions when their tangent planes are different. A discontinuous Galerkin scheme to compute Eq. (30) is given as
where \(\tilde{\mathbf {v}}^c \equiv - (\mathbf {v} \cdot \mathbf {e}^1) \mathbf {e}^2 + (\mathbf {v} \cdot \mathbf {e}^2) \mathbf {e}^1\).
Figure 6 demonstrates superior accuracy of the connection preservation scheme for the curl operator than that of the conservation preservation scheme. For \(L_2\) error, the SD2 scheme is significantly more accurate than the scheme having LOCAL moving frames or the SD1 scheme. However, the difference between the two schemes becomes smaller as p increases. For \(L_{\infty }\) error, the SD1 scheme shows similar accuracy up to \(p=5\). For \(p \ge 6\), the SD2 scheme shows smaller error than the SD1 scheme. Overall, the SD1 scheme shows better accuracy than the scheme having LOCAL moving frames with no \(\mathcal {G}\), particularly as p increases. However, the best accuracy is obtained by the SD2 scheme. This is due to the covariant differentiation term, i.e., \(\nabla \times \mathbf {e}^3\), which significantly contributes to the overall error of the curl operator in Eq. (31). Thus, error caused by wrong connection is greater than that caused by wrong divergence in the overall error. Consequently, retrieving the original connection improves the accuracy of the scheme. This phenomenon is more apparent at a lower p because the connection error diminishes as p increases.
Relative \(L_2\) and \(L_{\infty }\) error in static curl test problem. The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
6.4 Time-dependent Maxwell’s Equations
For time-dependent PDEs with the curl operator, the following Maxwell’s equations are chosen:
where \(\mathbf {E}\) and \(\mathbf {H}\) are the electric field and h-field, respectively. \(\hat{\varepsilon }\) and \(\hat{\mu }\) are the permittivity and permeability tensors, respectively. Consider transverse magnetic (TM) mode such that \(\mathbf {H} = H^1 \mathbf {e}^1 + H^2 \mathbf {e}^2\) and \(\mathbf {E} = E^3 \mathbf {e}^3\). The transverse electric (TE) mode would yield similar results. Then, the weak formulation of Maxwell’s equations in Eq. (32) in the context of discontinuous Galerkin methods is given as follows: For \(i=1,2\), we have
where \(\mathbf {E} = E^3 \mathbf {e}^3\) and \(\mathbf {E}^*_i = {E}^3 \mathbf {e}^{3i} = E^3 ( \mathbf {e}^3 \times \mathbf {e}^i )\). The tilde sign implies that the corresponding quantity is an approximated value at the boundary, called numerical flux. The permeability tensor is also decomposed into two frames \(\mathbf {e}^1\) and \(\mathbf {e}^2\) as \(\hat{\mu } = \mu ^1 \mathbf {e}^1 + \mu ^2 \mathbf {e}^2\). The electric field is updated as follows.
where \(\mathbf {H}^i = H^i \mathbf {e}^i\) and \(\mathbf {H}^*_i = {H}^i \mathbf {e}^{i3} = H^i ( \mathbf {e}^i \times \mathbf {e}^3 )\).
For the test problem, consider the initial shock of the electromagnetic pulse and energy conservation error during the extremely low frequency (ELF) propagation on the sphere. The TM mode is chosen. A shock is initiated at \((1/\sqrt{2},0,1/\sqrt{2})\) to propagates infinitely between the initial point and antipode without losing energy. Figure 7 presents the difference in the energy conservation error for the two schemes versus time. The SD2 scheme noticeably shows better conservation error than does the SD1 scheme. Similar to the static curl operator test, the covariant derivative component \(\nabla \times \mathbf {e}^3\) is computed more accurately in the connection preservation scheme than the divergence preservation scheme for the deformed domain.
Energy conservation error of the ELF propagation on the sphere. The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
7 Application to Shallow Water Equations
As an application of the proposed scheme, SWEs is chosen on the sphere as the governing equation is given as follows:
where \(\eta \) and \(\mathbf {u}\) represent the free surface elevation and the depth-averaged velocity, respectively. \(H_0\) is the still water depth and \(H= H_0 + \eta \) is the total water depth. f and g are the Coriolis parameter and the gravitational constant, respectively. The divergence preservation scheme is obtained similarly as for other PDEs. However, the connection preservation scheme requires further modifications in the SWEs because of the (1) zero tendency condition, (2) gradient computation, and (3) differentiation of different vectors.
7.1 Zero Tendency Condition
Let \(\mathbf {e}^i\) be moving frames that are constructed at each point on the sphere. Consider \(\mathbf {u} = u \mathbf {e}^1 + v \mathbf {e}^2\). Multiply \(\mathbf {e}^i\) with Eq. (36) to obtain the following expression:
The above equations are obtained by assuming the following zero tendency condition:
If moving frames are aligned in a more Euclidean connection, the tendency is closer to zero. In other words, if the moving frames’ curvature within an element is closer to zero, the left hand side in Eq.(39) is also closer to zero. For the Williamson’s tests, the zero tendency of the spherical coordinate is assumed to be satisfied, even when the left hand side in Eq.(39) is not necessarily zero along the spherical coordinate axis. the left hand side in Eq.(39) is implicitly assumed to be zero or at least approximately negligible compared with discretization error. Because any Euclidean axis or spherical coordinate axis provides zero tendency conditions, only LOCAL and LOCSPH satisfy the zero-tendency condition.
7.2 Gradient Computation
Another problem pertains to formulating the gradient in the SWEs for the divergence/connection conservation scheme. In the SWEs, two gradients emerge: \( (g/2) \nabla H^2\) and \(g H \nabla H_0\) in Eq.(36). In most numerical schemes [29,30,31,32], the gradient of \(H^2\), or \(\nabla H^2\), is computed in the weak formulation. For the given moving frames \(\mathbf {e}^i\), the weak formulation of \(\nabla H^2\) can be computed similarly to the divergence as follows.
Note that spurious divergence is not added to the weak formulation of the gradient, even though the integration by parts of its weak formulation is similar to that of divergence. We assume that no spurious divergence is generated for the gradient in the slightly deformed domain. Several computational tests have confirmed this claim but are not included in the paper.
Another gradient, or \(g H \nabla H_0\), is computed directly because the integration of part for \(H \nabla H_0\) is impossible when \(H_0\) is not a constant. We observed that the existence of this direct computation of the gradient causes deteriorated accuracy for moving frames other than LOCAL moving frames.
7.3 Differentiation of Vectors
In the SWEs in Eqs. (35) and (36), two different differentiations of a vector occur: the first occurs for divergence computations such as
The second occurs for rotation effect to yield the following component non-trivial in Eqs. (37)–(38).
The derivative \(\partial \mathbf {e}^i / \partial t\) is another direct differentiation with respect to moving frames \(\mathbf {e}^i\) such as
where \(\mathbf {x}^k\) is the kth Cartesian frame. For the computation of Eqs. (41) and (42), the choice of moving frames should be theoretically independent. However, this is not true for a slightly deformed domain \(\Omega ^{\varepsilon }\). Adopting LOCAL moving frames for \(\Omega ^{\varepsilon }\) reflects the current geometry, or connection. For the connection preservation scheme, LOCSPH moving frames, which are the original connection of \(\Omega ^0\), are adopted for the expansion of the vector in Eqs. (41) and (42).
7.4 Divergence/Connection Preservation Scheme
Considering the aforementioned three factors for the improved accuracy of the numerical scheme, the following weak formulation with moving frames is proposed for SWE equations in the context of the discontinuous Galerkin method.
where
and
and
The moving frames \(\mathbf {d}^i\) are also orthonormal vectors. However, they are not necessarily the same as \(\mathbf {e}^i\). The moving frames \(\mathbf {d}^i\) preserve the original connection of the original domain \(\Omega ^0\). In our scheme, \(\mathbf {e}^i\) is chosen as LOCAL moving frames and \(\mathbf {e}^i_c\) is chosen as LOCSPH moving frames. For example we have the following equality in any domain.
Without the spurious divergence, the numerical scheme in Eqs. (43)–(45) is exactly the same as the typical numerical scheme with moving frames, as used in ref. [22]. Note that the \(\mathcal {G}\) component has a different velocity vector as indicated in the parentheses. If LOCAL is used for \(\mathbf {d}^i \), then the numerical scheme is a divergence preservation scheme, the same as in Eq. (18). If LOCSPH is used for \(\mathbf {d}^i \), then the numerical scheme is both a divergence and a connection preservation scheme. We call this scheme as divergence/connection preservation scheme, as described in detail as follows.
Consider a velocity vector that lies on the slightly deformed mesh \(\Omega ^{\varepsilon }\), but is expanded by LOCSPH, denoted by \( {\mathbf {v}}^{0}_{\Vert \varepsilon }\). The subscript \(\Vert \varepsilon \) implies that the corresponding quantity is projected onto \(\Omega ^{\varepsilon }\). Similarly, the del operator is expanded by LOCSPH. This means that the differentiation occurs in the direction of the LOCSPH frame and is projected at the same time because the grid points lie on the slightly deformed domain \(\Omega ^{\varepsilon }\). By substituting \(\mathbf {F} = \mathbf {k}^{\varepsilon } \times {\mathbf {v}}^{0}_{\Vert \varepsilon }\) into the following Stokes theorem, we obtain
Eq. (46) is fundamentally a divergence preservation scheme because it retrieves the original divergence \(\nabla ^0 \cdot \mathbf {v}^0\). At the same time, the use of the original connection \(\nabla ^0\) preserves the original differentiation connection.
For the numerical tests in the following subsections, the Lax-Friedrich flux is used for the numerical flux. The classical explicit fourth-order Runge-Kutta scheme with a sufficiently small \(\Delta t\) is used for time marching. The details of the numerical flux and scheme are well described in ref. [23]. The numeric test problems are also described in ref. [23, 28], thus they are not presented in this paper.
Steady zonal flow: Initial condition of \(\eta \) and velocity vector, overall relative \(L_2\) error, and mass conservation error for \(3 \le p \le 7\). \(h=0.4\) with 480 elements. Computed up to T=5 (days). The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
7.5 Steady Zonal Flow
The first test is the steady zonal test with constant free surface elevation and velocity vector over time. The angle of the velocity vector with respect to the polar axis is set to \(\pi /4\). The still water depth (\(H_0\)) is chosen as 1.0 and \(\nabla H_0 = 0\). Error is measured at \(T=5.0\) (days).
Figure 8 displays the overall relative \(L_2\)/\(L_{\infty }\) error and the mass/energy conservation error compared with the initial mass and energy. The overall errors are saturated for \(p \ge 4\) in all the schemes. However, the overall \(L_2\) error for the SD2 scheme is significantly smaller than those of the SD0 and SD1 schemes. Figure 8a shows that the relative error of the SD2 scheme in comparison with the SD1 scheme is significantly smaller than that of the SD1 scheme. The overall error increases as T increases.
Similarly, mass and energy conservation error are both saturated for \(p \ge 4\) in all the schemes. Conservation error is more severe than the overall error. The SD2 scheme shows noticeably smaller errors in comparison with the SD0 and SD1 schemes. For mass conservation error, the difference between the SD2 scheme and the SD0/SD1 scheme is approximately \(3.00 \times 10^{-7}\) at \(T=5\) for \(p\ge 4\). The error difference is small but significant when the mesh error is approximately in the range of \(2.00 \times 10^{-5} \sim 3.00 \times 10^{-4}\). However, this small difference contributes to a meaningful deterioration of the overall error in long time integration.
7.6 Unsteady Zonal Flow
Contrary to the steady zonal test, the unsteady zonal test in the Williamson’s test suites uses a variable still surface elevation of \(H_0\) as follows.
where \(r_a\) is the radius of the earth, g is the gravitational constant, and \(\Omega _f\) is the Earth’s rotational frequency. Note that \(g H \nabla H_0 \cdot \mathbf {e}^i\) should be computed directly because it cannot be computed in a weak form by integration by part. Thus, the divergence/connection scheme cannot be applied to \(H \nabla H_0\).
Similar to the error plot of the steady zonal test in Figs. 8, 9 presents the overall error and mass conservation error for the SD0, SD1, and SD2 schemes. The overall errors are also saturated for \(p \ge 4\) in all the schemes. The overall \(L_2\) error for the SD2 scheme is slightly better than those of the SD0 and SD1 schemes because of the relatively short time integration up to 0.5(days). The mass conservation error difference is approximately \(3.30 \times 10^{-7}\) at \(T=5\) for \(p\ge 4\), similar to the result of the steady zonal flow test. Adopting LOCAL moving frames for \(\mathbf {e}^i\) seems to be the primary reason for the accuracy maintained for the direct derivative of the non-constant \(H_0 (\theta )\), regardless of \(\mathbf {d}^i\).
Unsteady zonal flow: Initial condition of \(\eta \) and velocity vector, overall relative \(L_2\) error, and mass conservation error for \(3 \le p \le 7\). \(h=0.4\) with 480 elements. Computed up to T=5 (days). The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
7.7 Rossby–Haurwitz Flow
The third test problem is the Rossby–Haurwitz flow on the sphere. There is no exact solution to this problem. However, the periodic distribution of the free surface elevation (\(\eta \)) and the velocity vector (\(\mathbf {u}\)) along the \(\phi \)-axis rotate around the axis of the sphere. The conservation error of mass and energy is considered the most important measure for demonstrating the accuracy of the implemented numerical schemes. The initial distribution of \(\eta \) and \(\mathbf {u}\) is more complicated than those of the steady zonal flow, as shown in Fig. 10. Let \(H_0\) be constant, set to 1.0, and \(\nabla H_0\) be zero. Thus, the LOCSPH with the \(\mathcal {G}\) scheme can be implemented for better accuracy. The SWEs equations are computed up to \(T=15\) days.
Figure 10 demonstrates the mass and energy conservation error versus time. The SD2 scheme clearly shows better accuracy both in mass and energy conservation error than do the SD0 and SD1 schemes. The SD1 scheme’s mass and energy conservation errors are more accurate than those of the SD0 scheme by \(1.09\times 10^{-06}\) and \(1.51\times 10^{-06}\), respectively. The SD2 scheme’s mass and energy conservation errors are more accurate than those of the SD0 scheme by \(1.45\times 10^{-05}\) and \(2.02\times 10^{-05}\), respectively. The SD2’s improved accuracy is significant in comparison with the mesh error in the range of \(2.00 \times 10^{-5} \sim 3.00 \times 10^{-4}\).
7.8 Steady Jet Flow
As the last test problem with the constant \(H_0\), the jet flow simulation is known to be one of the most challenging tests as the initial condition is presented in Fig. 11a. One difficulty is that a very fine spatial resolution should be provided for accurate computation. For the weak formulation, it is known that the edge of curved elements should be less than h=0.1. Consequently, the number of curved triangular elements for a sphere should be at least more than 10, 000 for most numerical schemes. For our simulation, 10752 curved elements are used with \(p=5\), equivalent to approximately \(4.5\times 10^5\) grid points. Perturbed jet simulations require more space resolutions. Figure 11b demonstrates the improved accuracy in mass conservation in a steady jet flow simulation up to \(T=6\) (days). At \(T=6\), the mass conservation error of the SD1 scheme is \(99.97\%.\) compared to that of the SD0 scheme. However, the mass conservation error of the SD2 scheme is only \(75.87\%\) compared to that of the SD0 scheme. Results are similar for perturbed jet simulations for increased spatial resolution for \(p>5\). Thus, this result is omitted in the paper.
7.9 On Ellipsoids
The Williamson’s test cases were derived for the sphere of the normalized radius [28]. Thus, the test cases should be numerically solved on the sphere for the convergence of numerical error and conservation error. Moreover, the divergence preservation scheme and divergence/connection preservation scheme can be effectively implemented using the exact geometry of the sphere. On the other hand, the SD1 and SD2 schemes cannot be tested on a domain other than the sphere. The solution of the SWEs cannot be derived and maybe the conservation may not hold on the non-sphere domain.
Suppose that the spherical domain is an ellipsoid, which is slightly deformed from the unit sphere. No solution is provided on this ellipsoid. However, the connection of the exact ellipsoid can be closer to the connection of the unit sphere than the connection of the approximated ellipsoidal domain. Thus, the divergence preservation and divergence/connection preservation scheme may provide a lesser error in conservation error.
Consider the following normalized ellipsoid such that the z-axis is aligned along the north and south pole.
Consider an ellipsoid similar to the ratio of the earth such that \(a = b = 1.003364\). The axis’s length along the north and south poles is \(6.37122 \times 10^6~m\). The other axes’s length is \(6.39265 \times 10^6~m\). Figure 12 demonstrates that the SD1 and SD2 schemes show better accuracy in the conservation of mass than the SD0 scheme. Particularly, the SD2 scheme shows the best accuracy among the three schemes, similar to the convergence tests on the sphere. We suppose that the error caused by non-unit a and b is significantly smaller than the improvement by more accurate divergence and connection.
Moreover, another ellipsoid can be considered with a larger deformation from the sphere such that \(a = b = 1.2\). Interestingly, the SD1 scheme consistently shows better accuracy in mass conservation for \( p > 2\) as shown in Fig. 13. However, the convergence of the SD2 scheme is erratic, and its accuracy is worse than the SD0 scheme at some ps for \(h=0.3\). Thus, the convergence of the SD2 scheme does not have much meaning and is excluded in Fig. 13. This result seems to imply that the connection is more sensitive to the overall error and conservation error than the divergence.
Rossby-Haurwitz wave on an earth-like ellipsoid of \(x^2/a^2 + y^2/b^2 + z^2 = 1\) for \(a=b=1.003364\). \(h=0.3\). The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
Rossby-Haurwitz wave on an earth-like ellipsoid of \(x^2/a^2 + y^2/b^2 + z^2 = 1\) for \(a=b=1.2\). \(h=0.3\). The relative error is computed by Eq. (26). Lower relative errors are better and negative relative error indicates better accuracy with respect to SD0
8 Discussion
This paper proposes two novel schemes to improve the overall accuracy and the conservation properties in a slightly deformed curved surface. The improvements in accuracy are achieved by retrieving the divergence or connection from the exact domain, not the approximated domain by computational tessellation. For this purpose, we introduce the exact surface normal vector or the exact del operator or connection. When the discretization error is sufficiently small, the proposed schemes significantly improve the overall error and mass/energy conservation error accuracy. The main drawback of the proposed schemes is that extra computational costs are required to compute the spurious divergence \(\mathcal {G}\) at every time step. Accuracy gain seems to be relatively small compared to the additional computational costs. However, the improved accuracy seems to identify the source of the mysterious conservation error by a slightly-deformed domain. Moreover, the proposed schemes can significantly improve the overall error in long-time integration where conservation is critical such as in climate simulations.
This paper shows that the two novel schemes show better accuracy in a slightly-deformed domain than the numerical scheme without any preservation compensation. The connection preservation (SD2) scheme shows better accuracy than the divergence preservation (SD1) scheme in the static curl test, Maxwell’s equations, and the shallow water test cases. The results suggest that retrieving the exact divergence could be less critical than retrieving the exact connection when the surface domain is approximated from the exact domain. However, the SD1 shows better accuracy for the static divergence test and time-dependent advection problems. We consider that this phenomenon occurs because the connection is not critical for the divergence computation in weak formulation.
In other words, the source of errors for a slightly modified domain is more affected by the changes in the path for the differentiation of vectors or the so-called covariant derivative of vectors. Retrieving the exact connection requires prior knowledge of the domain, such as the surface normal vector \(\mathbf {k}^0\) or the \(\nabla \) operator \(\nabla ^0\). This result can be applied to various applications, for example, in divergence computation in data science, where the original information is slightly modified, but a theoretical configuration exists.
Data Availability
Enquiries about data availability should be directed to the authors.
References
Energy Exascale Earth System Model (DOE E3SM Atmosphere). https://e3sm.org/model/e3sm-model-description/v1-description/v1-atmosphere/
The nonhydrostatic unified model of the atmosphere (NUMA). https://frankgiraldo.wixsite.com/mysite/numa
Choi, S.-J., Hong, S.-Y.: A global non-hydrostatic dynamical core using the spectral element method on a cubed-sphere grid. Asia-Pacific J. Atmosph. Sci. 52, 291–307 (2016)
LFRic - a modelling system fit for future computers. https://www.metoffice.gov.uk/research/approach/modelling-systems/lfric
Taylor, M.A., Fournier, A.: A compatible and conservative spectral element method on unstructured grids. J. Comput. Phys. 229, 5879–5895 (2010). https://doi.org/10.1016/j.jcp.2010.04.008
Taylor, M.A., Guba, O., Steyer, A., Ullrich, P.A., Hall, D.M., Eldrid, C.: An energy consistent discretization of the nonhydrostatic equations in primitive variables. J. Adv. Model. Earth Syst. (2020). https://doi.org/10.1029/2019MS001783
Cotter, C.J., Shipton, J.: Mixed finite elements for numerical weather prediction. J. Comput. Phys. 231(21), 7076–7091 (2012). https://doi.org/10.1016/j.jcp.2012.05.020
Cotter, C.J., Thuburn, J.: A finite element exterior calculus framework for the rotating shallow-water equations. J. Comput. Phys. 257, 1506–1526 (2014). https://doi.org/10.1016/j.jcp.2013.10.008
Melvin, T., Benacchio, T., Shipway, B., Wood, N., Thuburn, J., Cotter, C.: A mixed finite-element, finite-volume, semi-implicit discretization for atmospheric dynamics: Cartesian geometry. Q. J. R. Meteorol. Soc. 145(724), 2835–2853 (2019). https://doi.org/10.1002/qj.3501
Thuburn, J., Cotter, C.J.: A primal-dual mimetic finite element scheme for the rotating shallow water equations on polygonal spherical meshes. J. Comput. Phys. 290, 274–297 (2015). https://doi.org/10.1016/j.jcp.2015.02.045
Karniadakis, G.E., Sherwin, S.J.: Spectral/hp element methods for CFD (2005)
Ergatoudis, I., Irons, B.M., Zienkiewicz, O.C.: Curved, isoparametric, qadrilateral elements for finite element analysis. Int. J. Solids Struct. 4, 31–42 (1968)
Chun, S., Marcon, J., Peiró, J., Sherwin, S.J.: Reducing errors due to geometrical inaccuracy in high-order moving frames simulations. submitted (2021)
Natale, A., Shipton, J., Cotter, C.J.: Compatible finite element spaces for geophysical fluid dynamics. Dyn. Sta. Clim. Sys., 1–31 (2016)
Taylor, M.A., Fournier, A.: A compatible and conservative spectral element method on unstructured grids. J. Compt. Phys. 229, 5879–5895 (2010)
Thuburn, J., Ringler, T.D., Skamarock, W.C., Klemp, J.B.: Numerical representation of geostrophic modes on arbitrarily structured c-grids. J. Compt. Phys. 228, 8321–8335 (2009)
Turner, M., Moxey, D., Sherwin, S.J., Peiró, J.: Eccomas congress 2016: Vii european congress on computational methods in applied sciences and engineering, 428–443 (2016)
Sherwin, S.J., Peiró, J.: Mesh generation in curvilinear domains using high-order elements. Int. J. Numer. Meth. Eng. 53, 207–223 (2002)
Turner, M.: High-order mesh generation for CFD solvers. PhD thesis, Imperial College London (2017)
Chun, S.: Method of moving frames to solve conservation laws on curved surfaces. J. Sci. Comput. 53(2), 268–294 (2012)
Chun, S.: Method of moving frames to solve (an)isotropic diffusion equations on curved surfaces. J. Sci. Comput. 59(3), 626–666 (2013)
Chun, S., Eskilsson, C.: Method of moving frames to solve the shallow water equations on arbitrary rotating curved surfaces. J. Compt. Phys. 333, 1–23 (2017)
Chun, S.: Method of moving frames to solve the time-dependent Maxwell’s equations on anisotropic curved surfaces: applications to invisible cloak and ELF propagation. J. Compt. Phys. 340, 85–104 (2017)
Eric W. Weisstein: Convective Operator. [From MathWorld-A Wolfram Web Resource]. https://mathworld.wolfram.com/ConvectiveOperator.html
Chun, S.: High-order covariant differentiation in application to helmholtz-hodge decomposition on curved surfaces. submitted (2020)
Risser, L.: personal communication
Pudykiewicz, J.A.: On numerical solution of the shallow water equations with chemical reactions on icosahedral geodesic grid. J. Comput. Phys. 230, 1956–1991 (2011)
Williamson, D.L., Drake, J.B., Hack, J.J., Jakob, R., Swarztrauber, P.N.: A standard test set for numerical approximations to the shallow water equations in spherical geometry. J. Comput. Phys. 102(1), 211–224 (1992)
Bernard, P.-E., Remacle, J.-F., Comblen, R., Legat, V., Hillewaert, K.: High-order discontinuous Galerkin schemes on general 2D manifolds applied to shallow water equations. J. Comput. Phys. 228(17), 6514–6535 (2009)
Giraldo, F.X., Warburton, T.: A nodal triangle-based spectral element method for the shallow water equations on the sphere. J. Comput. Phys. 207, 129–150 (2005)
Läuter, M., Giraldo, F.X., Handorf, D., Dethloff, K.: A discontinuous Galerkin method for the shallow water equations in spherical triangular coordinates. J. Comput. Phys. 227, 10226–10242 (2008)
Nair, R.D., Thomas, S.J., Loft, R.D.: A discontinuous Galerkin global shallow water model. Mon. Wea. Rev. 133, 876–888 (2005)
Acknowledgements
This research was supported by the National Research Foundation of Korea (NRF-2021R1A2C109297811). The second author is supported by the R &D project “Development of a Next-generation Operational System by the Korea Institute of Atmospheric Prediction Systems (KIAPS)”, funded by the Korea Meteorological Administration (KMA2020-02213).
Funding
The authors have not disclosed any funding.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have not disclosed any competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chun, S., Oh, T. Divergence/Connection Preservation Scheme in the Curvilinear Domain with a Small Geometric Approximation Error. J Sci Comput 92, 15 (2022). https://doi.org/10.1007/s10915-022-01865-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-01865-0