A New Functional Iterative Algorithm for the Regularized Long-Wave Equation Using an Integral Equation Formalism

Abstract

A fundamental question in computational nonlinear partial differential equations is raised to discover if one could construct a functional iterative algorithm for the regularized long-wave (RLW) equation (or the Benjamin–Bona–Mahony equation) based on an integral equation formalism? Here, the RLW equation is a third-order nonlinear partial differential equation, describing physically nonlinear dispersive waves in shallow water. For the question, the concept of pseudo-parameter, suggested by Jang (Commun Nonlinear Sci Numer Simul 43:118–138, 2017), is introduced and incorporated into the RLW equation. Thereby, dual nonlinear integral equations of second kind involving the parameter are formulated. The application of the fixed point theorem to the integral equations results in a new (semi-analytic and derivative-free) functional iteration algorithm (as required). The new algorithm allows the exploration of new regimes of pseudo-parameters, so that it can be valid for a much wider range (in the complex plane) of pseudo-parameter values than that of Jang (2017). Being fairly simple (or straightforward), the iteration algorithm is found to be not only stable but accurate. Specifically, a numerical experiment on a solitary wave is performed on the convergence and accuracy of the iteration for various complex values of the pseudo-parameters, further providing the regions of convergence subject to some constraints in the complex plane. Moreover, the algorithm yields a particularly relevant physical investigation of the nonlinear behavior near the front of a slowly varying wave train, in which, indeed, interesting nonlinear wave features are demonstrated. As a consequence, the preceding question may be answered.

1 Introduction

As a starting point of this paper, a fundamental (as well as theoretical) question is raised with regard to computational partial differential equations: is it possible to construct a functional iterative algorithm for the regularized long-wave (RLW) equation (also termed the Benjamin–Bona–Mahony equation) [1]

$$\begin{aligned} \eta _{t} +c_{0}{\eta }_{x} +\frac{3c_{0}}{2h_{0} }\eta \eta _{x} -\frac{h_{0}^{2}}{6}\eta _{xxt} =0 \end{aligned}$$

(1.1)

through an integral equation formalism? Here, $\eta$ and $c_0$ denote wave elevation and characteristic velocity (of the square root of the product of gravitational acceleration g and water depth $h_{0} )$

$$\begin{aligned} c_{0} =\sqrt{gh_{0} }, \end{aligned}$$

(1.2)

respectively.

Physically, the nonlinear partial differential equation (1.1) models a one-way wave propagation of water waves over a horizontal bottom valid for (weakly) nonlinear and fairly long waves, being widely studied and frequently used for simulating nonlinear dispersive waves in shallow water in applied sciences and coastal engineering. Being an alternative model to the Korteweg–de Vries (KdV) equation, the RLW (1.1) was firstly used by Peregrine for its advantages in numerical computations [2] and examined extensively by Benjamin et al. [3]. Here, the term “regularized” is used, because of the much better nature of the dispersion relation between frequency $\omega _\mathrm{{BBM}}$ and wave number k

$$\begin{aligned} \omega _\mathrm{{BBM}} =\frac{c_{0} {k}}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}, \end{aligned}$$

(1.3)

when compared to that of the KdV equation. This is the main reason why (1.1) is much more referred for a one-way propagation model.

There exists only few about the analytical studies on the nonlinear equation (1.1); e.g., Benjamin et al. [3] found the analytical solution for the equation just under the restricted initial and boundary conditions [3]. Thus, finding its numerical solutions is of practical importance and the availability of accurate and efficient numerical methods is essential [4]. Over the last few decades, significant efforts have been made for developing useful numerical procedures for (1.1). The finite difference approach would be the most typical numerical scheme, approximating (1.1) with difference equations. For instance, Eilbeck and McGuire [5] investigated numerical solitary wave solutions of the RLW equation to show that they exhibit true soliton behavior, being stable on collision with other solitary waves [5]. Bhardwaj and Shankar [6] employed quintic spline technique and splitting method to develop a new-finite difference method, which is used to model solitary wave motion and undular bore development [6]. Cai [7] derived a 6-point multisymplectic Preissman scheme from its Bridges’ multisymplectic form, where backward error analysis is implemented and the performance and the efficiency of the new scheme are illustrated by solving several test examples [7]. However, finite element schemes also have been one of the most commonly used numerical methods, which are extensively employed in the area of computational partial differential equations. Challenging issues are found; for example, Gardner et al. [8] used a B-spline finite element method to solve the RLW equation numerically, which is involved with a Galerkin method with quadratic B-spline finite elements [8]. Dağ et al. [9] applied Cubic B-spline functions to develop a collocation method for the nonlinear numerical solutions, which is used to model solitary waves, undular bore development and wave generation [9].

Now we return to the question at the beginning about how to construct a functional iterative algorithm of the RLW equation based on an integral equation formalism. For that, we will introduce the notion of pseudo-parameter proposed by Jang [10], which is incorporated into (1.1), for establishing a nonlinear integral formalism involving the parameter. This enables us to obtain dual nonlinear integral equations, equivalent to (1.1). Here, it is pointed out that the integral equations are not singular but regular, which inherently differ from not only the boundary integral equations resulted from boundary element methods but also the weak integral formulations from finite element methods. We then apply Banach fixed point theorem [10, 11] to the integral equations and derive a (required) functional iteration algorithm for integrating (1.1), implying that the answer to the question may be found.

The iteration algorithm derived in this paper is semi-analytic and derivative-free, which provides a fast convergence speed for achieving highly accurate numerical solutions as is illustrated in the numerical experiment on moving solitary waves. The numerical results are also compared to those of the conventional excellent methods. Here, it should be emphasized that the derived algorithm works even for a much wider range of pseudo-parameter values than that of Jang [10]; e.g., the pseudo-parameter can be a complex number (rather than a real number), in the present study. Thus, a complex (numerical) calculation is naturally required for performing the iteration, which leads to a complex numerical solution. This point is in sharp contrast to the previous article by Jang [10], where pseudo-parameter values were only restricted to some part of the real numbers and thus a real (not complex) numerical calculation was required. This may be best illustrated by showing the regions of convergence (ROCs) subject to some constraints in the complex plane, presented in numerical experiment section. In particular, for a further relevant investigation for nonlinear dispersive water waves, the algorithm is also found to be useful at observing the nonlinear behavior near a wave train front. Here, the nonlinear feature of the front wave is confirmed; i.e., the front wave has more peaked crests and flatter troughs, as it becomes steep, and the wave moves faster with larger amplitude.

2 Integral Formalism

Here, we will present an integral formalism which corresponds to the RLW equation (1.1). We first modify the governing equation (1.1), following the concept of pseudo-parameter [10]. To be specific, we introduce a pseudo-parameter $\alpha \in \mathbb {C}$ in the present study, where $\mathbb {C}$ denotes the set of complex numbers, and add the product of $\alpha \cdot \eta$ to both sides of (1.1), leading to

$$\begin{aligned} \eta _{t} +c_{0}{\eta }_{x} -\frac{h_{0}^{2} }{6}\eta _{xxt} +\alpha \cdot \eta =\varphi . \end{aligned}$$

(2.1)

The forcing term $\varphi$ in (2.1) involves $\eta$ as well as its derivative $\eta _x$, i.e.,

$$\begin{aligned} \varphi (\eta ,\eta _{x} )\equiv -\frac{3c_{0} }{2h_{0} }\eta \eta _{x} +\alpha \cdot \eta . \end{aligned}$$

(2.2)

It immediately follows that (2.1), combined with (2.2), is still equivalent to the original Eq. (1.1), regardless of complex values of $\alpha$.

The parameter $\alpha$ introduced above will play a crucial role in formulating an integral formalism for (1.1), which is necessary for obtaining a system of nonlinear integral equations, as shall be discussed later. We begin with applying two successive integral transforms.

2.1 Integral Transformations

Here, associated with (2.1), we aim to find the successive Fourier and Laplace transforms of $\eta$. First of all, we apply Fourier integral transform to both sides of the partial differential equation of (2.1) to find an ordinary differential equation. We denote by $\bar{{\eta }}$ the Fourier transform ${\mathfrak {F}}$ of $\eta$ with respect to space x as [10, 12]

$$\begin{aligned} {\mathfrak {F}}(\eta )\equiv \int _{-\infty }^\infty {\eta (x,t)} \cdot e^{ikx}dx\equiv \bar{{\eta }}(k,t) \end{aligned}$$

(2.3)

for a parameter k. Then, the inverse Fourier transform ${\mathfrak {F}}^{-1}$ is expressed as

$$\begin{aligned} \eta (x,t)={\mathfrak {F}}^{-1}(\bar{{\eta }})=\frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}(k,t)} \cdot e^{-ikx}dk. \end{aligned}$$

(2.4)

If we assume a localized wave motion of $\eta$ in x, i.e.,

$$\begin{aligned} \eta ,\;\eta _{x} \rightarrow 0, \text {as}\, x\rightarrow \pm \infty , \end{aligned}$$

(2.5)

we have the (well known) differentiation properties of Fourier transform

$$\begin{aligned} {\mathfrak {F}}(\eta _{x} )=(-ik)\bar{{\eta }}, {\mathfrak {F}}(\eta _{xx})=(-ik)^{2}\bar{{\eta }}. \end{aligned}$$

(2.6)

This allows (2.1) to be converted into an (first order) ordinary differential equation for $\bar{{\eta }}$,

$$\begin{aligned} \frac{d\bar{{\eta }}}{dt}+c_{0} {(-ik)}\bar{{\eta }}-\frac{h_{0}^{2} }{6}\frac{d}{dt}\left[ {(-ik)^{2}\bar{{\eta }}} \right] +\alpha \bar{{\eta }}=\bar{{\varphi }}. \end{aligned}$$

(2.7)

Next, the Laplace transform ${\mathfrak {L}}$ of $\bar{{\eta }}$ is to be performed on (2.7) with respect to time t, denoted by $\bar{{\eta }}^{{*}}$, i.e.,

$$\begin{aligned} {\mathfrak {L}}(\bar{{\eta }})\equiv \int _{0}^\infty {\bar{{\eta }}(k,t)} \cdot e^{-st}dt\equiv \bar{{\eta }}^{{*}}(k,s) \end{aligned}$$

(2.8)

for a parameter s [10, 12]. This results simply in an algebraic equation for $\bar{{\eta }}^{{*}}$ (i.e., ${\mathfrak {L}}\left[ {\mathfrak {F}}(\eta ) \right] )$,

$$\begin{aligned} \left( {s\bar{{\eta }}^{{*}}-\bar{{\eta }}_1 } \right) +c_{0} {(-ik)}\bar{{\eta }}^{{*}}-\frac{h_{0}^{2} }{6}\left[ {(-ik)^{2}(s\bar{{\eta }}^{{*}}-\bar{{\eta }}_{1} )} \right] +\alpha \bar{{\eta }}^{{*}}=\bar{{\varphi }}^{{*}} \end{aligned}$$

or

$$\begin{aligned} \bar{{\eta }}^{{*}}\left[ {s\left( {1-\frac{h_{0}^{2} }{6}(-ik)^{2}} \right) +c_{0} {(-ik)}+\alpha } \right] =\bar{{\varphi }}^{{*}}+\bar{{\eta }}_{1} \left( {1-\frac{h_{0}^{2} }{6}(-ik)^{2}} \right) . \end{aligned}$$

(2.9)

Here, the Laplace-transform property of differentiation is employed together with initial condition;

$$\begin{aligned} (d\bar{{\eta }}/dt)^{{*}}=s\bar{{\eta }}^{{*}}-\bar{{\eta }}(k,0)=s\bar{{\eta }}^{{*}}-\bar{{\eta }}_1 , \end{aligned}$$

(2.10)

in which $\eta _{1}$ designates an initial wave profile, i.e., $\eta _{1} (x)=\eta (x,0)$. (2.9) is readily solved for $\bar{{\eta }}^{{*}}$ to give

$$\begin{aligned} \bar{{\eta }}^{{*}}= & {} \frac{1}{ 1-\frac{h_{0}^{2} }{6}(-ik)^{2}}\cdot \frac{\bar{{\varphi }}^{{*}}+\bar{{\eta }}_{1} \left( {1-\frac{h_{0}^{2} }{6}(-ik)^{2}} \right) }{s+\frac{c_{0} {(-ik)}+\alpha }{1-\frac{h_{0}^{2} }{6}(-ik)^{2}}}\nonumber \\= & {} \frac{1}{ \;1+\frac{h_0^2 k^{2}}{6}\;}\cdot \frac{\;\bar{{\varphi }}^{{*}}+\bar{{\eta }}_{1} \left( {1+\frac{h_{0}^{2} k^{2}}{6}} \right) }{s-i\frac{(c_{0} {k}-\alpha /i)}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}}. \end{aligned}$$

(2.11)

With the definition of a (complex-valued) function ${\tilde{\omega }}_\mathrm{{BBM}}$ such that

$$\begin{aligned} {\tilde{\omega }}_\mathrm{{BBM}} (k)\equiv \frac{c_{0} {k}-\alpha /i}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}, \end{aligned}$$

(2.12)

the expression (2.11) may be further shortened; (2.11) admits the partial fractions representation in the simple form in terms of the ${\tilde{\omega }}_\mathrm{{BBM}}$

$$\begin{aligned} \bar{{\eta }}^{{*}}=\frac{\bar{{\eta }}_{1} }{\;s-i\tilde{\omega }_\mathrm{{BBM}} \;}+\frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_{0} {k}-\alpha /i\;}\cdot \frac{\bar{{\varphi }}^{{*}}}{\;s-i\tilde{\omega }_\mathrm{{BBM}} \;}. \end{aligned}$$

(2.13)

Remark 1

The newly defined ${\tilde{\omega }}_\mathrm{{BBM}}$ in (2.12) converges to $\omega _\mathrm{{BBM}}$ in (1.3) of the RLW equation (1.1), as the pseudo-parameter $\alpha \in {\mathbb {C}}$ tends to zero: i.e.,

$$\begin{aligned} {\tilde{\omega }}_\mathrm{{BBM}} \rightarrow \omega _\mathrm{{BBM}} , \text {as}\, \alpha \rightarrow 0. \end{aligned}$$

(2.14)

2.2 Inverse Integral Transformations

We start with taking the inverse Laplace transform ${\mathfrak {L}}^{-1}$ on the first term of the right hand side of (2.13), which is

$$\begin{aligned} {\mathfrak {L}}^{-1}\left[ {\frac{\bar{{\eta }}_1 (k)}{\;s-i\tilde{\omega }_\mathrm{{BBM}} \;}} \right]= & {} \bar{{\eta }}_1 (k)\cdot {\mathfrak {L}}^{-1}\left[ {\frac{1}{\;s-i\tilde{\omega }_\mathrm{{BBM}} \;}} \right] \nonumber \\= & {} \bar{{\eta }}_{1} (k)\cdot \left[ {\exp \left( {i{\tilde{\omega }}_\mathrm{{BBM}} \cdot t} \right) } \right] \end{aligned}$$

(2.15)

because $1/(s-a)={\mathfrak {L}}\left[ {\exp (at)} \right]$ for $a\in \mathbb {C}$ from table [10, 12]. Performing further the inverse Fourier transform ${\mathfrak {F}}^{-1}$ on the above result, being denoted by $\hbox {I}_{1}$, would lead to

$$\begin{aligned} {\hbox {I}}_1 (x,t)\equiv & {} \, {\mathfrak {F}}^{-1}\left\{ {\bar{{\eta }}_{1} (k)\cdot \left[ {\exp \left( {i{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right) } \right] } \right\} \nonumber \\= & {} \left\{ {\mathfrak {F}}^{-1}\left[ {\bar{{\eta }}_{1} (k)} \right] \right\} {*}\left\{ {\mathfrak {F}}^{-1}\left[ {\exp \left( {i{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right) } \right] \right\} \end{aligned}$$

(2.16)

by Fourier convolution theorem, where the notation ${*}$ means Fourier convolution.

$\hbox {I}_{1}$ in (2.16) can be calculated as

$$\begin{aligned} \mathrm{I}_1= & {} \left\{ {\eta _1 (x)} \right\} {*}\left\{ {\frac{1}{2\pi }\int _{-\infty }^\infty {\exp \left[ {i{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right] \cdot \exp (-ikx)dk} } \right\} \nonumber \\= & {} \left\{ {\eta _1 (x)} \right\} {*}\left\{ {\frac{1}{2\pi } \int _{-\infty }^\infty {e^{-i\left[ {kx-{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right] }dk} } \right\} \nonumber \\= & {} \frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {e^{-i\left[ {k(x-\xi )-{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right] }\cdot \eta _1 \left( \xi \right) d\xi dk} } , \end{aligned}$$

(2.17)

owing to the formula of inverse Fourier transform (2.4), definition of Fourier convolution and the identities

$$\begin{aligned} {\mathfrak {F}}^{-1}\bar{{\eta }}_{1} =({\mathfrak {F}}^{-1}{\mathfrak {F}})\eta _{1} =\eta _{1} (x). \end{aligned}$$

(2.18)

If we define the (complex) pseudo-phase function

$$\begin{aligned} {\tilde{\theta }}(x,t;k)\equiv kx-{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t. \end{aligned}$$

(2.19)

(2.17) then may be simplified into

$$\begin{aligned} \mathrm{I}_1 (x,t)=\frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_{1} (k)\cdot } e^{-i{\tilde{\theta }}(x,t;k)}dk, \end{aligned}$$

(2.20)

which describes physically the superposition of (complex) elementary wave solutions $e^{-i{\tilde{\theta }}(x,t;k)}$ with a wave spectrum $\bar{{\eta }}_{1}$, i.e., the Fourier transform of the initial profile $\eta _{1} (x)$;

$$\begin{aligned} \bar{{\eta }}_{1} (k)={\mathfrak {F}}(\eta _{1} (x))=\int _{-\infty }^\infty {\eta _1 \left( \xi \right) \cdot e^{ik\xi }d\xi } . \end{aligned}$$

(2.21)

Next, we move on to the inverse Laplace transform ${\mathfrak {L}}^{-1}$ on the second term of (2.13),

$$\begin{aligned} {\mathfrak {L}}^{-1}\left[ {\frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_{0} k-\alpha /i\;}\cdot \frac{\bar{{\varphi }}^{{*}}}{\;s-i{\tilde{\omega }}_\mathrm{{BBM}} \;}} \right]= & {} \frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_{0} k-\alpha /i\;}\cdot {\mathfrak {L}}^{-1}\left[ {\frac{1}{\;s-i{\tilde{\omega }}_\mathrm{{BBM}} \;}\cdot {\mathfrak {L}} {\bar{{\varphi }}}} \right] \nonumber \\= & {} \frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_{0} k-\alpha /i\;}\cdot {\mathfrak {L}}^{-1} \left[ {\mathfrak {L}}\left[ {\exp \left( {i{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right) } \right] \cdot {\mathfrak {L}} {\bar{\varphi }} \right] \nonumber \\= & {} \frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_0 k-\alpha /i\;}\cdot \exp \left[ {i{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right] \circ \bar{{\varphi }}\nonumber \\= & {} \frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_0 k-\alpha /i\;}\int _{0}^{t} {\exp \left[ {i\tilde{\omega }_\mathrm{{BBM}} (k)\cdot (t-\tau )} \right] } \cdot \bar{{\varphi }}(k,\tau )d\tau ,\nonumber \\ \end{aligned}$$

(2.22)

where the formula $1/(s-a)={\mathfrak {L}}\left[ {\exp (at)} \right]$ for $a\in {\mathbb {C}}$ and Laplace convolution theorem are used [10, 12]. And we take the inverse Fourier transform ${\mathfrak {F}}^{-1}$ on the above result, giving a triple integral $\hbox {I}_2$,

$$\begin{aligned} \mathrm{I}_2 (x,t)\,\equiv&\,\, {\mathfrak {F}}^{-1}\left\{ {\frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_{0} {k}-\alpha /i\;}\int _{0}^{t} {\exp \left[ {i\tilde{\omega }_\mathrm{{BBM}} (k)\cdot (t-\tau )} \right] } \cdot \bar{{\varphi }}(k,\tau )d\tau } \right\} \nonumber \\ =&\,\frac{1}{2\pi }\int _{-\infty }^\infty \left\{ \frac{\tilde{\omega }_\mathrm{{BBM}} }{ \;c_{0} {k}-\alpha /i\;}\cdot \int _{0}^{t} {\exp \left[ {i{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot (t-\tau )} \right] } \right. \nonumber \\&\qquad \qquad \left. \cdot \left( {\int _{-\infty }^\infty {\varphi \left( {\xi ,\tau } \right) \cdot e^{ik\xi }d\xi } } \right) d\tau \right\} \cdot e^{-ikx}dk\nonumber \\ =&\,\frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\exp \left[ {i\tilde{\omega }_\mathrm{{BBM}} (k)\cdot (t-\tau )} \right] \nonumber \\&\qquad \qquad \cdot e^{ik\left( {\xi -x} \right) }\cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau \nonumber \\ =&\,\frac{1}{2\pi }\int _0^t {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot e^{-i\tilde{\theta }(x-\xi ,t-\tau ;k)}\cdot \varphi \left( {\xi ,\tau } \right) d\xi } } dkd\tau } \end{aligned}$$

(2.23)

by the use of Fourier formula (2.3), its inverse (2.4) and (2.12).

Remark 2

The integral $\hbox {I}_2$ of (2.23) can be also expressed as a single integral in the form

$$\begin{aligned} \mathrm{I}_2 (x,t)=\frac{1}{2\pi }\int _{0}^{t} {\zeta (x,t,\tau ;\varphi )d\tau } . \end{aligned}$$

(2.24)

Then, the integrand $\zeta$ physically represents the superposition of elementary wave solutions $e^{-i{\tilde{\theta }}(x,t-\tau ;k)}$ with time shift $\tau$, which has a wave spectrum $\bar{{\varphi }}(k,\tau )/(1+h_{0}^{2} k^{2}/6)$ parametrized by the $\tau$:

$$\begin{aligned} \zeta (x,t,\tau ;\varphi )\equiv \int _{-\infty }^\infty {\frac{\bar{{\varphi }}(k,\tau )}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot e^{-i{\tilde{\theta }}(x,t-\tau ;k)}dk} \end{aligned}$$

(2.25)

2.3 Establishing Integral Formalism

This subsection is devoted to the realization of an integral formalism from the results in the previous subsection. This is simply achieved by recalling that $\eta$ is recovered by taking the two successive inverse Fourier and Laplace transforms on both sides of (2.13), i.e., for a pseudo-parameter $\alpha \in {\mathbb {C}}$, $\eta$ is symbolically represented as

$$\begin{aligned} \eta= & {} ({\mathfrak {F}}^{-1}{\mathfrak {L}}^{-1})\bar{{\eta }}^{{*}}=\mathrm{I}_1 +\mathrm{I}_{2}\nonumber \\= & {} \frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_{1} (k)} \cdot e^{-i{\tilde{\theta }}(x,t;k)}dk \nonumber \\&+\frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)} \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau \end{aligned}$$

(2.26)

from (2.20) and (2.23). The relation (2.26) may be considered as our integral formalism which corresponds to (1.1), where $\varphi$ is directly related with $\eta$ and its derivative through (2.2).

3 Derivation of Functional Iteration Algorithm

In this section, we shall derive a new functional iteration algorithm for solving the RLW equation (1.1). To this end, (1.1) is transformed into a system of nonlinear integral equations by using the results of the previous section. And then, we employ Banach contraction theorem [10, 11], applied to the system of integral equations, which makes us derive an (numerical) iterative strategy (i.e., a functional iteration algorithm for (1.1)).

3.1 Dual Integral Equations

With the integral formalism (2.26) established in Sect. 2.3, we will obtain nonlinear integral equations. For that, let us substitute (2.2) into (2.26) to find

$$\begin{aligned} \eta (x,t)= & {} \frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_1 (k)} \cdot e^{-i{\tilde{\theta }}(x,t;k)}dk \nonumber \\&-\frac{1}{2\pi }\int _{0}^{t} {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{\frac{3c_{0}}{2h_{0} }}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)}\cdot \eta (\xi ,\tau )\cdot \psi (\xi ,\tau )d\xi dkd\tau } } } \nonumber \\&+\frac{\alpha }{2\pi }\int _0^t {\int _{-\infty }^\infty {\int _{-\infty }^{\infty } {\frac{1}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot e^{-i{\tilde{\theta }}(x-\xi , t-\tau ;k)}\cdot \eta (\xi ,\tau )d\xi dkd\tau } } } \end{aligned}$$

(3.1)

where $\psi$ indicates a new variable, corresponding physically to wave slope $\eta _{x}$. And, we differentiate the above with respect to x, giving

$$\begin{aligned} \psi (x,t)= & {} \frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_{1} (k) \cdot \frac{\partial }{\partial x}} e^{-i{\tilde{\theta }}(x,t;k)}dk \nonumber \\&-\frac{1}{2\pi }\int _{0}^{t} \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{\frac{3c_{0}}{2h_{0}}}{1+\frac{h_{0}^{2} k^{2}}{6}}\cdot \frac{\partial }{\partial x}e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)}\cdot \eta (\xi ,\tau )\cdot \psi (\xi ,\tau )d\xi dkd\tau \nonumber \\&+\frac{\alpha }{2\pi }\int _{0}^{t} {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot \frac{\partial }{\partial x} e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)}\cdot \eta (\xi ,\tau )d\xi dkd\tau } } } . \end{aligned}$$

(3.2)

The pair of (3.1) and (3.2) then constitutes two coupled nonlinear integral equations of second kind for the two unknown functions of $\eta$ and $\psi$.

The integral equations of the form (3.1) and (3.2) may be abbreviated, with some preliminaries of background material of function spaces. Denote by ${\text{ B }}_T$ the collection of complex-valued continuous and bounded functions defined on ${\mathbb {R}}\times [0,T]$ for $T>0$, where $\mathbb {R}$ is the set of real numbers. Analogously, let ${\text{ B }}_{0}$ be the collection of real-valued continuous and bounded functions defined on ${\mathbb {R}}$. Then, associated with (3.1) and (3.2), we can define an integral operator $\hbox {J}:{\mathrm{B}}_{0} \rightarrow {\mathrm{B}}_{T}$ such that

$$\begin{aligned} \hbox {J}[\eta _{1} ](x,t)\equiv \frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_{1} (k)\cdot } e^{-i{\tilde{\theta }}(x,t;k)}dk \end{aligned}$$

(3.3)

for any $\eta _1 \in {\text{ B }}_{0}$. In a similar way, we define $\hbox {K}:\hbox {B}_{T} \rightarrow \hbox {B}_{T}$ such that

$$\begin{aligned} \hbox {K}[\eta ](x,t)\equiv \frac{1}{2\pi }\int _0^t {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)}\cdot \eta (\xi ,\tau )d\xi dkd\tau } } } \end{aligned}$$

(3.4)

for any $\eta \in \hbox {B}_{T}$.

By virtue of the integral operators $\hbox {J}$ in (3.3) and $\hbox {K}$ in (3.4), we can write (3.1) as

$$\begin{aligned} \eta =\hbox {J}[\eta _{1} ]-\frac{3c_{0}}{2h_{0}} \hbox {K}[\eta \cdot \psi ]+\alpha \hbox {K}[\eta ] \end{aligned}$$

(3.5)

and (3.2) as

$$\begin{aligned} \psi =\hbox {J}_{x} [\eta _1 ]-\frac{3c_{0} }{2h_{0} }\hbox {K}_x [\eta \cdot \psi ]+\alpha \hbox {K}_{x} [\eta ]. \end{aligned}$$

(3.6)

The two operator equations of (3.5) and (3.6) can be considered as an abbreviated form for the integral equations described by (3.1) and (3.2). Here, the new operators $\hbox {J}_{x}$ and $\hbox {K}_{x}$ have the expressions

$$\begin{aligned}&\hbox {J}_{x} [\eta _{1} ](x,t)\equiv \frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_{1} (k)\cdot } \frac{\partial }{\partial x}e^{-i{\tilde{\theta }}(x,t;k)}dk \quad \text {for } \, \eta _1 \in \hbox {B}_{0} \end{aligned}$$

(3.7)

and

$$\begin{aligned} \hbox {K}_{x} [\eta ](x,t)&\equiv \frac{1}{2\pi }\int _{0}^{t} {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot \frac{\partial }{\partial x}e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)}\cdot \eta (\xi ,\tau )d\xi dkd\tau } } }\nonumber \\&\qquad \qquad \qquad \qquad \quad \qquad \qquad \text {for} \quad \eta \in \hbox {B}_{T} , \end{aligned}$$

(3.8)

respectively.

3.2 Deriving Functional Iterative Algorithm

In this subsection, we present the derivation of a functional iteration algorithm to solve (1.1) by means of the integral equations obtained in the previous subsection.

Let us define a (integral) nonlinear operator

$$\begin{aligned} \hbox {T}[\eta ,\psi ]\equiv \hbox {J}[\eta _{1} ]-\frac{3c_{0} }{2h_{0} } \hbox {K}[\eta \cdot \psi ]+\alpha \hbox {K}[\eta ] \end{aligned}$$

(3.9)

for any $\eta , \hbox { }\psi \in \mathrm{B}_T$, so that (3.5) can be more shortened into

$$\begin{aligned} \eta = \hbox {T}[\eta ,\psi ]. \end{aligned}$$

(3.10)

Then, the integral equations (3.1) and (3.2) are much more abbreviated as

$$\begin{aligned} {\varvec{\eta }} =\mathbf{T}[{\varvec{\eta }}]. \end{aligned}$$

(3.11)

Here, the nonlinear operator $\mathbf{T}$ has the form (the superscript t denotes the transpose)

$$\begin{aligned} \mathbf{T}[{\varvec{\eta }} ]\equiv \left( {\hbox {T}}[\eta ,\psi ],{\hbox {T}}_{x} [\eta ,\psi ] \right) ^\mathrm{t} \end{aligned}$$

(3.12)

in terms of a new variable ${\varvec{\eta }}=(\eta ,\psi )^\mathrm{t}$, in which the operator $\hbox {T}_{x}$ stands for the right hand side of (3.6), i.e.,

$$\begin{aligned} \hbox {T}_{x} [\eta ,\psi ]=\hbox {J}_{x} [\eta _{1} ]-\frac{3c_{0}}{2h_{0} }{\hbox {K}}_{x} [\eta \cdot \psi ]+\alpha {\hbox {K}}_{x} [\eta ]. \end{aligned}$$

(3.13)

Based on the fact that ${\varvec{\eta }}$ is invariant under the mapping $\mathbf{T}$ in (3.11), we would like to propose a functional iteration algorithm for ${\varvec{\eta }}_n \equiv (\eta _{n} ,\psi _{n} )^\mathrm{t}$, where $\eta _{n} , \psi _{n} \in {\hbox {B}}_{T}$,

$$\begin{aligned} {\varvec{\eta }}_{n+1} =\mathbf{{T}}[{{\varvec{\eta }} }_{n} ]\quad \text {for} \quad n=0,1,2,... \end{aligned}$$

(3.14)

with the initial guess

$$\begin{aligned} {{\varvec{\eta }}}_{0} \equiv (0,0)^\mathrm{t} \end{aligned}$$

(3.15)

by appealing to Banach fixed point theorem [10, 11]. That is, (3.14) is a recurrence relation which recursively defines a functional sequence $\left\{ {{{\varvec{\eta }}}_{n} } \right\}$, $n=0,1,2,...$.

Remark 3

Being semi-analytic and derivative-free iterative strategy, the iteration (3.14) yields a solution $\eta$ of (1.1) as well as its derivative $\eta _x (= \psi )$ as a bonus, as the number of iteration n increases, provided that (3.14) converges.

We recall that the model (1.1) physically describes a one-way wave propagation of nonlinear dispersive waves $\eta (x,t)$ over a horizontal bottom as discussed in Introduction, where $\eta (x,t)$ is real-valued, if a real-valued initial condition $\eta _1 (x)=\eta (x,0)$ is taken into account. Suppose that $\eta$ is a (real-valued) wave solution of the initial value problem for (1.1) with the real-valued initial condition. Then, the $\eta$ should also satisfy the $\alpha$-parameterized partial differential equations of (2.1) and (2.2) together with the initial condition, for any pseudo-parameter $\alpha \in {\mathbb {C}}$, due to the fact that (2.1) and (2.2), for $\alpha \in {\mathbb {C}}$, are equivalent to (1.1) as mentioned at the beginning of Sect. 2. And, the $\eta$ even further should satisfy the system of integral equations (3.1) and (3.2), or alternatively, the integral operator equation (3.11), because (3.1) and (3.2) describe an (equivalent) integral equation formulation for (1.1) combined with the initial condition.

If $\mathbf{{T}}$ in the integral operator equation (3.11) has a contractive nature, the $\eta$ then may be expressed as a limit of a sequence $\left\{ {\eta _{n} } \right\}$, $n=0,1,2,...$, generated by (3.14) (recalling that ${\varvec{\eta }}$ is invariant under $\mathbf{{T}})$ and the sequence converges (See Banach fixed point theorem [11]). The sequence is a Cauchy sequence, which has a unique limit in a Banach space (such as our solution space), because every Banach space is topologically a Hausdorff space (Roman [11]); i.e.,

$$\begin{aligned} \eta _n \rightarrow \eta \quad \text {as} \quad n\rightarrow \infty . \end{aligned}$$

(3.16)

Remark 4

(3.16) indicates that a limit of a sequence $\left\{ {\eta _{n} } \right\}$, $n=0,1,2,...$by (3.14) is unique and real-valued, if a real-valued initial condition $\eta _{1} (x)=\eta (x,0)$ is imposed. However, if n is finite, the output $\eta _{n}$ may be complex-valued, whose real part converges to the true solution of (1.1) as $n\rightarrow \infty$, while its imaginary part goes to zero. That is,

$$\begin{aligned} \hbox {Re}\left( {\eta _{n} } \right) \rightarrow \eta \quad \text {and}\quad \hbox {Im} \left( {\eta _{n}} \right) \rightarrow 0 \quad \text {as} \quad n\rightarrow \infty , \end{aligned}$$

(3.17)

followed by the fact that $\eta _{n} =\mathrm{Re}\left( {\eta _{n} } \right) +i\cdot \hbox {Im}\left( {\eta _{n} } \right) \rightarrow \eta$ as $n\rightarrow \infty$ by (3.16) and the limit $\eta$ is real-valued.

3.3 Iterative Algorithm for the Special Case $\alpha =0$

Notice that it is a complex value that the pseudo-parameter $\alpha$ of the iteration (3.14) involves. This demands that the output of the numerical iteration (3.14) should be complex-valued for a finite n. However, if we set $\alpha =0$ in (3.14), the output becomes real-valued.

Suppose that the pseudo-parameter $\alpha \in \mathbb {C}$ vanishes in (3.14). Then, I$_{1}$ in (2.17) or (2.20) reduces to

$$\begin{aligned} (\hbox {I}_1 )_{\alpha =0}= & {} \frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {e^{-i\left[ {k(x-\xi )-\omega _\mathrm{{BBM}} (k)\cdot t} \right] } \cdot \eta _1 \left( \xi \right) d\xi dk} }\nonumber \\= & {} \frac{1}{\pi }\int _0^\infty {\int _{-\infty }^\infty {\cos \left[ {\theta (x-\xi ,t;k)} \right] \cdot \eta _1 \left( \xi \right) d\xi dk} } \end{aligned}$$

(3.18)

where $\theta$ represents the phase function $\tilde{\theta }$ in (2.19) when $\alpha =0$, i.e.,

$$\begin{aligned} \theta (x,t;k)\equiv & {} {\tilde{\theta }}_{\alpha =0} (x,t;k)\nonumber \\= & {} kx-\omega _\mathrm{{BBM}} (k)\cdot t. \end{aligned}$$

(3.19)

Here, the kernel in (3.18) results from the Euler formula

$$\begin{aligned} e^{-i\theta }=\cos \theta -i\sin \theta \end{aligned}$$

(3.20)

and the anti-symmetric property

$$\begin{aligned} \sin \left[ {\theta (x-\xi ,t;-k)} \right]= & {} \sin \left[ {-\theta (x-\xi ,t;k)} \right] \nonumber \\= & {} -\sin \left[ {\theta (x-\xi ,t;k)} \right] \end{aligned}$$

(3.21)

because $\omega _\mathrm{{BBM}}$ and (thus) $\theta$ are odd in k.

Similarly, from (2.23)

$$\begin{aligned} (\hbox {I}_{2} )_{\alpha =0}= & {} \frac{1}{2\pi }\int _0^t {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot e^{-i\theta (x-\xi ,t-\tau ;k)} \cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau } } }\nonumber \\= & {} \frac{1}{\pi }\int _0^t {\int _0^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cos \left[ {\theta (x-\xi ,t-\tau ;k)} \right] \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau } } } ,\qquad \quad \end{aligned}$$

(3.22)

because of the anti-symmetry (in k)

$$\begin{aligned} \sin \left[ {\theta (x-\xi ,t-\tau ;-k)} \right]= & {} \sin \left[ {-\theta (x-\xi ,t-\tau ;k)} \right] \nonumber \\= & {} -\sin \left[ {\theta (x-\xi ,t-\tau ;k)} \right] . \end{aligned}$$

(3.23)

Therefore, (3.14) becomes

$$\begin{aligned} \eta _{n+1} (x,t)= & {} \frac{1}{\pi }\int _0^\infty {\int _{-\infty }^\infty {\cos \left[ {\theta (x-\xi ,t;k)} \right] \cdot \eta _1 \left( \xi \right) d\xi dk} }\nonumber \\&-\frac{1}{\pi }\int _{0}^{t} \int _0^\infty \int _{-\infty }^\infty {\frac{\frac{3c_0}{2h_{0} }}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot \cos \left[ {\theta (x-\xi ,t-\tau ;k)} \right] }\nonumber \\&\quad \qquad \qquad \qquad \qquad \cdot \eta _n (\xi ,\tau )\cdot \psi _n (\xi ,\tau )d\xi dkd\tau \end{aligned}$$

(3.24)

and

$$\begin{aligned} \psi _{n+1} (x,t)= & {} \frac{1}{\pi }\int _0^\infty {\int _{-\infty }^\infty {\frac{\partial }{\partial x}\cos \left[ {\theta (x-\xi ,t;k)} \right] \cdot \eta _{1} \left( \xi \right) d\xi dk} }\nonumber \\&-\frac{1}{\pi }\int _0^t \int _0^\infty \int _{-\infty }^\infty {\frac{\frac{3c_{0}}{2h_{0} }}{\;1+\frac{h_{0}^{2} k^{2}}{6}\;}\cdot \frac{\partial }{\partial x}\cos \left[ {\theta (x-\xi ,t-\tau ;k)} \right] }\nonumber \\&\quad \qquad \qquad \qquad \qquad \cdot \eta _n (\xi ,\tau )\cdot \psi _n (\xi ,\tau )d\xi dkd\tau \end{aligned}$$

(3.25)

for $n=0,1,2,...$, respectively, due to (3.18) and (3.22), when $\alpha =0$; with emphasis on that $\hbox {I}_{1}$ in (2.17) and I$_{2}$ in (2.23) remain pure real. It is clear that the functional iteration consisting of (3.24) and (3.25) derived above is a recurrence relation which does not involve a pseudo-parameter $\alpha \in {\mathbb {C}}$ at all (i.e., it is pseudo-parameter free.) and thus both $\eta _n$ and $\psi _{n}$ are real-valued. That is, the output of the iteration of (3.24) and (3.25) is real-valued, as mentioned above in this subsection.

Remark 5

As a special case of (3.14), the pair of (3.24) and (3.25), which corresponds to $\alpha =0$, is the simplest (or the most efficient) recurrence relation among our $\alpha$-parameter family of (3.14); in fact, the pair is an iterative strategy whose output is real-valued. Even though the pair is the simplest, it produces the highest levels of accuracy in the present iterative strategy (3.14), as can be seen later (see Sect. 4).

4 Numerical Experiments

4.1 Numerical Performance

This subsection concerns numerical experiments performed on solitary wave propagations to examine whether the functional iteration algorithm (3.14) works. Thereby, we will investigate the effect of the pseudo-parameter $\alpha \in {\mathbb {C}}$ introduced in Sect. 2 on the numerical performance of the iteration (e.g., the iteration’s convergence speed and accuracy).

We first introduce three appropriate dimensionless variables, defined by

$$\begin{aligned} \eta ^{*}=\frac{3\eta }{2h_{0} }, \quad t^{*}=t\sqrt{\frac{6g}{h_{0} }}, \quad x^{*}=\frac{\sqrt{6}}{h_{0} }x. \end{aligned}$$

(4.1)

Then, the (original) physical partial differential equation (1.1) is transformed into a dimensionless RLW equation [13] (see “Appendix A”)

$$\begin{aligned} \eta _{{t}^{*}}^*+\eta _{x^{*}}^*+\eta ^{*}\eta _{x^{*}}^*-\eta _{x^{*}x^{*}t^{*}}^*=0. \end{aligned}$$

(4.2)

It is well known that (4.2) allows a solitary wave (or soliton) moving to the right in the form [13]

$$\begin{aligned} \eta _\mathrm{{ex}}^*\left( {x^{*},t^{*}} \right) =3d\cdot \hbox {sech}^{2}\left[ {\kappa \left( {x^{*}-vt^{*}-x_0^*} \right) } \right] , \end{aligned}$$

(4.3)

where 3d indicates dimensionless amplitude, v wave velocity($=d+1$), and 2$\pi$/$\kappa$ wave width:

$$\begin{aligned} \kappa =\sqrt{d/4v} \end{aligned}$$

(4.4)

In original physical variables, (4.3) may be re-expressed as

$$\begin{aligned} \eta _\mathrm{{ex}} \left( {x,t} \right) =2h_{0} d\cdot \hbox {sech}^{2}\left[ {\frac{\kappa \sqrt{6}}{h_{0} }\left( {x-v\sqrt{gh_{0} }t-x_{0} } \right) } \right] . \end{aligned}$$

(4.5)

By iterating the recursion of (3.14) together with the (zero) initial guess (3.15), we now numerically simulate the solitary wave of (4.3) or (4.5) using the initial condition imposed by

$$\begin{aligned} \eta _{1}^{*} \left( {x^{*}} \right) =\eta ^{*}\left( {x^{*},0} \right) =3d\cdot \hbox {sech}^{2}\left[ {\kappa \left( {x^{*}-x_0^*} \right) } \right] \end{aligned}$$

(4.6)

or

$$\begin{aligned} \eta _{1} \left( x \right) =\eta \left( {x,0} \right) =2h_{0} d\cdot \hbox {sech}^{2}\left[ {\frac{\kappa \sqrt{6}}{h_{0} }\left( {x-x_{0} } \right) } \right] . \end{aligned}$$

(4.7)

Recall that (3.14) involves the pseudo-parameter $\alpha$ which is in general complex. For this reason, a complex domain calculation is generally demanded for the numerical simulation as was discussed before. However, we start with the simplest case of (3.24) and (3.25) (when $\alpha =0$).

4.1.1 Simulations for $\alpha =0$

We iterate the pair of (3.24) and (3.25), corresponding to case $\alpha =0$, with the initial condition (4.6) or (4.7) to obtain the solitary wave solution of (4.3) or (4.5). For the simulation, the dimensionless amplitude 3d is chosen as 0.3, and gravitational acceleration g and water depth $h_{0 }$ as $9.80665\,\hbox {m/s}^{2}$ and 1.0 m, respectively. Here, the usual Simpson integration rule is used to estimate the integrals appearing in the pair (but, with the trapezoidal rule in time), where we discretize dimensionless temporal interval $0<t^{*}<T$ into $(N-1)$ equal length-parts $\Delta t^{*}=T/(N-1)$ and dimensionless spatial interval $a<x^{*}<b$ into $(M-1)$ equally spaced panels $\Delta x^{*}=(b-a)/(M-1)$, giving $x_i^*$ (these points will be used for error estimation later) for positive integers i ($1\le i\le M)$,

$$\begin{aligned} x_{i}^{*} =a+\left( {i-1} \right) \frac{\left( {b-a} \right) }{M-1}. \end{aligned}$$

(4.8)

Fig. 1

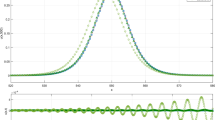
Plot of the moving solitary wave (4.3)

Fig. 2

Convergence behavior of the proposed iteration for the solitary wave solution (4.3): $\alpha =0$, $\Delta x^{*} =1/8$ and $\Delta t^{*} =0.1$

Fig. 3

Convergence behavior of Fig. 2 at fixed dimensionless time $t^{*}=20$

Fig. 4

Two errors of $Err_{2}$ in (4.9) and $Err_{\infty }$ in (4.10) at $t^{*}=10$, 20: $\alpha =0$, $\Delta x^{*}=1/8$ and $\Delta t^{*} =0.1$

Figures 1 and 2 show the numerical plot of the solitary wave (4.3) and its numerical convergence behavior, respectively, where dimensionless spatial and temporal computational domains are taken as $-40<x^{*} <60$ and $0<t^{*} <20$ respectively, with their increments of $\Delta x^{*} =1/8$ and $\Delta t^{*} =0.1$; i.e., $a=-40$, $b=60$, $T=20$, $M=801$, $N=201$. A reasonable wave solution can be observed by only the first iteration when $t^{*}$ is small and there appears to be an almost converged solution valid for the whole time interval when $n=12$, as demonstrated in Fig. 2. With dimensionless time fixed ($t^{*}=20$), the numerical convergence behavior is depicted in Fig. 3.

Figure 4 illustrates that the discrete root mean square norm Err $_{2}$ and the maximum error Err $_{\infty }$[14] decay rapidly as the number of iterations n increases;

$$\begin{aligned} Err_{2} (t^{*} )=\left\| {\eta _\mathrm{{ex}}^*(x^{*} ,t^{*} )-\eta _n^*(x^{*} ,t^{*} )} \right\| _2 =\sqrt{\Delta x^{*}\cdot \sum _{i=1}^M {\left| {\eta _\mathrm{{ex}}^*(x_{i}^{*} ,t^{*} )-\eta _{n}^{*} (x_{i}^{*} ,t^{*} )} \right| ^{2}} } \end{aligned}$$

(4.9)

and

$$\begin{aligned} Err_{\infty } \left( {t^{*} } \right) =\left\| {\eta _\mathrm{{ex}}^{*} \left( {x^{*},t^{*} } \right) -\eta _{n}^{*} \left( {x^{*},t^{*} } \right) } \right\| _\infty =\mathop {\max }\limits _{i=1,..,M} \left| {\eta _{\mathrm{{ex}}}^*\left( {x_{i}^{*} ,t^{*} } \right) -\eta _{n}^{*} \left( {x_{i}^{*} ,t^{*} } \right) } \right| , \end{aligned}$$

(4.10)

where two norms $\left\| { \cdot } \right\| _2$ and $\left\| { \cdot } \right\| _\infty$ are taken over the $x^{*}$ variable only, with dimensionless time $t^{*}$ being kept fixed ($t^{*} =10,20)$. The values of errors are tabulated in Table 1 for various specified dimensionless times. Note that the order of accuracy is of $10^{-6}$, being accurate. They are also compared to other results of the conventional excellent methods as is Table 2.

Table 1 Numerical values given by the proposed iteration for $Err_{ 2}$ in (4.9), $Err_{\infty }$ in (4.10) and invariants in (4.11–4.13) for various dimensionless times: $\alpha =0$, $\Delta x^{*}=1/8$, $\Delta t^*=0.1$

Table 2 Numerical values given by the proposed iteration and other conventional excellent methods for Err $_{2}$ in (4.9), $Err_{ \infty }$ in (4.10) and invariants in (4.11–4.13) at specified dimensionless time $t^{*}=20$: $\alpha =0$

It may be worth estimating numerical values for the following three conservative (invariant) quantities corresponding to mass, momentum and energy [14, 15]:

$$\begin{aligned} C_{1} \left( {t^{*} } \right)= & {} \int _{-40}^{60} {\eta _{n}^*\left( {x^{*}, t^{*} } \right) dx^{*}} \simeq \Delta x^{*}\sum _{i=1}^M {\eta _{n}^{*} \left( {x_{i}^*,t^{*} } \right) }, \end{aligned}$$

(4.11)

$$\begin{aligned} C_{2} \left( {t^{*} } \right)= & {} \int _{-40}^{60} {\eta _{n}^{*_ {2}} \left( {x^{*},t^{*} } \right) +\left( {\frac{\partial \eta _{n}^{*} }{\partial x^{*}}} \right) ^{2}\left( {x^{*},t^*} \right) dx^{*}}\nonumber \\\simeq & {} \Delta x^{*}\sum _{i=1}^{M} {\left\{ {\eta _{n}^{*2}\left( {x_{i}^*, t^{*} } \right) +\left( {\frac{\partial \eta _{n}^{*} }{\partial x^{*}}} \right) ^{2}\left( {x_{i}^{*} ,t^{*} } \right) } \right\} }, \end{aligned}$$

(4.12)

and

$$\begin{aligned} C_{3} \left( {t^{*} } \right)= & {} \int _{-40}^{60} {\eta _{n}^{*3} \left( {x^{*},t^{*} } \right) +3\eta _{n}^{*2}\left( {x^{*}, t^{*} } \right) dx^{*}} \simeq \Delta x^{*}\sum _{i=1}^M {\left\{ {\eta _{n}^{*3}\left( {x_{i}^*,t^*} \right) +3\eta _{n}^{*2}\left( {x_{i}^{*} ,t^{*} } \right) } \right\} } ,\nonumber \\ \end{aligned}$$

(4.13)

where, we review that (1.1) is known to have exactly the three conservation laws (4.11–4.13). Being compared to the analytical results, the numerical values of the invariants of $C_{1}$, $C_{2}$, $C_{3}$ in (4.11–4.13) by the proposed iteration of (3.24) and (3.25) are shown for various dimensionless times in Table 1. For other two types of increments, e.g., $\Delta x^{*}=\Delta t^{*}=0.50$ and $\Delta x^{*}=\Delta t^{*}=0.25$, the corresponding errors and invariants are presented as well in Table 2.

4.1.2 Simulations for $\alpha$ Other than Zero

In Sect. 4.1.1, we examined the special case of the iterative algorithm (3.14), i.e., the pair of (3.24) and (3.25) which corresponds to (3.14) when $\alpha =0$, for the numerical experiment on a solitary wave. However, in the present subsection, we extend the pseudo-parameter $\alpha$ to complex numbers (of course, which include real numbers) to explore its effect on the numerical results. Using the same integration numerical rules as was employed in Sect. 4.1.1, we perform (3.14) together with the initial condition (4.6) or (4.7) to simulate again the solitary wave solution of (4.3) or (4.5). Here, the dimensionless computational domains are chosen to be $-35<x^{*}<35$ and $0<t^{*}<4$ respectively, but with the larger increments of $\Delta x^{*}=0.5$ and $\Delta t^{*}=0.2$ (than before).

It should be noted that, for non-zero complex numbers $\alpha$, the iterative solutions $\eta _n (x,t)$ for finite integers n produced by (3.14) are in general complex-valued (as was pointed out in Sect. 3.2), because the (two) concerning operators $\hbox {J}$ in (3.3) and $\mathrm{K}$ in (3.4) are complex-valued. So, generally, the real parts of iterative solutions converge to a true solution as the number of iteration n increases, while the imaginary parts of iterative solutions converge to zero (See Remark 4).

However, we find it interesting to observe an exceptional case, where the iterative solutions $\eta _n (x,t)$ for finite integers n produced by (3.14) are proved to be all real-valued (not complex-valued), especially when $\alpha$ is pure real (because the iteration (3.14) becomes essentially a real-valued (recurrence) equation if $\alpha$ is real. See “Appendix B”). Bearing in mind this, the iterative algorithm (3.14) yields Fig. 5, which exhibits only convergence behaviors of the real parts of $\eta _n (x,t)$, when the pseudo-parameter is selected to be pure real; $\alpha =1$. Here, the real parts of the iterative solutions converge to a true solution as the number of iteration n increases.

Fig. 5

Convergence behavior (real part) of the proposed iteration for the solitary wave solution (4.3): $\alpha =1$, $\Delta x^{*}=0.5$, $\Delta t^{*}=0.2$

Figures 6 and 7 present the convergence characteristics of (3.14) for the pure imaginary case, $\alpha =i$. The convergence behavior (real part) of Fig. 6 is analogous to that of the previous case of $\alpha =1$ in Fig. 5, and the imaginary parts of the iterative solutions are seen to converge to zero in Fig. 7. Figures 8 and 9 account for the nature of solution convergence for $\alpha$ =1+i. Figures 10, 11 and 12 plot the iterative solitary wave profiles with dimensionless time kept fixed ($t^{*}$=4). Here, note again that Fig. 10 only shows convergence behaviors of the real parts, because the iterative solutions are real-valued with $\alpha$ pure real, as was discussed above.

Fig. 6

Convergence behavior (real part) of the proposed iteration for the solitary wave solution (4.3): $\alpha =i$, $\Delta x^{*}=0.5$, $\Delta t^{*}=0.2$

Fig. 7

Convergence behavior (imaginary part) of the proposed iteration for the solitary wave solution (4.3): $\alpha =i$, $\Delta x^{*}=0.5$, $\Delta t^{*}=0.2$

Fig. 8

Convergence behavior (real part) of the proposed iteration for the solitary wave solution (4.3): $\alpha =1+i$, $\Delta x^{*}=0.5$, $\Delta t^{*}=0.2$

Fig. 9

Convergence behavior (imaginary part) of the proposed iteration for the solitary wave solution (4.3): $\alpha =1+i$, $\Delta x^{*}=0.5$, $\Delta t^{*}=0.2$

Fig. 10

Convergence behaviors (real part) of the proposed iteration for the solitary wave solution (4.3) when $t^{*}=4: \alpha =1$, $\Delta x^{*}=0.5, \Delta t^{*}=0.2$

Fig. 11

Convergence behaviors (real and imaginary parts) of the proposed iteration for the solitary wave solution (4.3) when $t^{*}=4: \alpha =i, \Delta x^{*}=0.5, \Delta t^{*}=0.2$

Fig. 12

Convergence behaviors (real and imaginary parts) of the proposed iteration for the solitary wave solution (4.3) when $t^{*}=4:\alpha =1+i$, $\Delta x^{*}=0.5, \Delta t^{*}=0.2$

Fig. 13

Convergence characteristics of the proposed iteration against n depending on $\alpha$, when $t^{*}=4: \Delta x^{*}=0.5, \Delta t^{*}=0.2$

As was discussed earlier, the pseudo-parameter $\alpha$ was artificially introduced at the beginning of this study and it may be crucial in that it affects the nature of convergence and accuracy of the iteration (3.14) derived (or proposed) in this paper. Indeed, Fig. 13 reveals the characteristics of convergence and accuracy depending on the parameter $\alpha$ for a fixed dimensionless time $t^{*}=4$, where the real and imaginary parts of errors are defined as

$$\begin{aligned} (Err_{2} )_\mathrm{{real}}= & {} \left\| \eta _\mathrm{{ex}}^*-\hbox {Re} (\eta _n^*) \right\| _2 , \end{aligned}$$

(4.14)

$$\begin{aligned} \left( {Err_{2} } \right) _\mathrm{{imag}}= & {} \left\| { 0 - \hbox {Im}(\eta _n^*)} \right\| _2. \end{aligned}$$

(4.15)

Here, $\eta _\mathrm{{ex}}^{*}$ is the exact solution of the moving solitary wave of (4.3). It is interesting to see that the smaller the norm of $\alpha$ tends to contribute to the faster iteration’s convergence and more accurate solutions.

Fig. 14

Two shaded regions of pseudo-parameters $\alpha$ satisfying the performance requirement (4.16) with tolerance $\varepsilon =0.1$; Specifically, for a dimensionless amplitude $3d_1 =0.3$, an enlarged rectangle is inserted, containing 10 red-colored points which correspond to the pseudo-parameters $\alpha$ used in Sect. 4.1.2 Similarly, an enlarged rectangle is inserted as well for b dimensionless amplitude $3d_2 =1.2$, where the 10 red-colored points are also depicted

Fig. 15

Convergence characteristics of the proposed iteration where the pseudo-parameters $\alpha$ lie in the real axis ${\mathbb {R}}$ but inside the shaded regions of $\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$ in Fig. 14; In particular, for a $3d_{1} =0.3$ and b $3d_{2} =1.2$, the points of $\alpha =13.5$ and $\alpha =9.5$ lie on the boundaries of $\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$, respectively

4.1.3 Region of $\alpha \in {\mathbb {C}}$ Satisfying Requirement

We have, so far, performed the numerical simulation of a solitary wave to find the numerical performances of the algorithm, when given a specified $\alpha$. However, in this subsection, we would like to look for inversely pseudo-parameters $\alpha$ which satisfy a (planned) performance requirement of the algorithm through the numerical simulation. In practice, this would be an issue of clear engineering importance.

With the use of the same computational condition as that of Sect. 4.1.2, Fig. 14 depicts the two shaded regions of $\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$ of pseudo-parameters $\alpha \in {\mathbb {C}}$ satisfying (cf. see (4.14))

$$\begin{aligned} \left\| \eta _\mathrm{{ex}}^*-\mathrm{Re}{(\eta _{n}^{*} )} \right\| _{2}<\varepsilon , \end{aligned}$$

(4.16)

which is an inequality of a performance requirement with a tolerance $\varepsilon$. The two regions ($\varepsilon =0.1)$, plotted in the complex plane ${\mathbb {C}}$ as in Fig. 14a, b, respectively, both look symmetric with respect to the real axis ${\mathbb {R}}$ and similar. In addition, the former is bigger than the latter. This is because the algorithm produces a less accurate solution with higher dimensionless amplitude, when given a computational (discretization) condition; therefore, ultimately, there may exist an empty space which satisfies (4.16) for a (very) high dimensionless amplitude. Here, it is also observed that the $\alpha \in {\mathbb {C}}$, considered for the numerical experiment in the above subsections, are inside the two regions (i.e., $\alpha \in \mathfrak {R}_1 , \mathfrak {R}_2 )$, which, in fact, are located near the origin in the complex plane ${\mathbb {C}}$ (see the enlarged images in Fig. 14).

Fig. 16

Typical convergence behavior of the proposed iteration (3.24) and (3.25) for a slowly varying wave train due to the Maxwellian initial condition; $A_{3}=0.27, B=0.1$

The regions can be also considered as the ROCs subject to the constraint (4.16), due to the fact that they clearly show parts of ROCs of the present iterative algorithm. If $\alpha$ were limited to real numbers as was done in Jang [10], then, the corresponding ROCs subject to the constraint (4.16) would be the intersections of $\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$ with the real axis ${\mathbb {R}}$. Because $\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$ are much larger than the intersections, the present algorithm is shown to have much wider ranges of the ROCs subject to the constraint (4.16) than those of Jang [10].

It would be instructive to investigate convergence characteristics of the proposed iteration, when $\alpha$ lies (very) close to the boundaries of the shaded regions. Figure 15 gives the convergence characteristics corresponding to $\alpha$ which remain strictly real but inside the shaded regions (including the boundaries). As was pointed out in Sect. 4.1.2, we also observe that the smaller the (real) values of $\alpha$ contribute to the faster convergence and more accurate results.

4.2 Nonlinear Behavior Near Wave Train Front

In this subsection, we will explore the nonlinear behavior near the front of a slowly varying wave train due to a local disturbance by using the present algorithm. This is a fascinating matter in water waves, in fact, which has been significantly examined in the past (e.g., in relation with tsunami). However, the classical (theoretical) study was restricted essentially to the linear approximation; cf. see Kajiura [21] who found the leading wave (linear) solution in the form of an Airy function [21].

For simulating a wave train, we first consider an initial value problem of the governing equation (1.1) and the initial conditions

$$\begin{aligned} \eta _1^*=A_i \cdot \exp \left[ {-B x^{*2}} \right] , \quad i=1,2,3, \end{aligned}$$

(4.17)

or, alternatively,

$$\begin{aligned} \eta _{1} =\frac{2h_{0} A_{i} }{3}\cdot \exp \left[ {-\frac{6B}{h_{0}^{2} }x^{2}} \right] , \quad i=1,2,3, \end{aligned}$$

(4.18)

for constants $A_{i}>0$ and $B>0$, which are known as the Maxwellian conditions [22]. And then, the algorithm (3.24) and (3.25), which corresponds to $\alpha =0$, is iterated to solve the above initial value problem for three different $A_i >0$, i.e., $A_{1}=0.01$, $A_{2}=0.20$ and $A_{3}=0.27$, where the concerning computational domains are selected as $20\hbox {m}<x<140\,\hbox {m}$ $(M=481, \Delta x=1/3\,\hbox {m})$ and 0sec$<t<35$sec ($N=211, \Delta t=1/6\,\hbox {sec})$; equivalently, -49$<x^{*}<343 (\Delta x^{*}\approx 0.82)$, 0$<t^{*}<T=268 (\Delta t^{*}\approx 1.28)$ in dimensionless form.

Figure 16 indicates a typical convergence behavior of the algorithm, say for $A_{3}=0.27$, in which, similarly as in the previous subsection (e.g., in Fig. 2), qualitatively reasonable iterative solutions $\eta _{n}^{*}$ are found to be achieved at the early stage of iteration. Furthermore, it is clearly seen that the Maxwellian profile (4.17) propagates into space and time in a dispersive manner.

We will next determine where to stop the (iterative) algorithm (3.24) and (3.25), based on the norm difference e between $\eta _{n+1}^*$ and $\eta _n^*$ in this study; we would like to stop the iteration of the algorithm, if e satisfies the inequality

$$\begin{aligned} e=\left\| {\eta _{n+1}^*(x^*, T)-\eta _{n}^{*} (x^*, T)} \right\| _2 <\delta \end{aligned}$$

(4.19)

with a (tolerance) bound $\delta$ and an end time Tin numerical experiment ($=268$, see the (just) above). Figure 17 uncovers plots of e against iteration n for $A_i >0$, $i=1,2,3$, which illustrates that smaller amplitudes $A_{i}$ make e decay much more rapidly, as n increases.

If we set, say $\delta =O(10^{-9})$ in (4.19), we then stop the iteration algorithm at $n=6$ for $A_{1}=0.01$, because e has order $O(10^{-9})$ at $n=6$ for $A_{1}=0.01$ as shown in Fig. 17. Similarly, we stop the iteration at $n=25$ for $A_{2}=0.20$ and at $n=32$ for $A_{3}=0.27$, respectively, where $e=O(10^{-9})$ for both cases $A_{2}$ and $A_{3}$ (see Fig. 17). These results imply that our numerically converged solutions become $\eta _{6}^*$, $\eta _{25}^{*}$ and $\eta _{32}^{*}$ for $A_{1}=0.01$, for $A_{2}=0.20$ and $A_{3}=0.27$, respectively, if $\delta =O(10^{-9})$ is chosen for (4.19).

Fig. 17

Plots of e in (4.19) against iteration n for three different cases of $A_{i} >0(i=1,2,3); B=0.1$

Fig. 18

Development of slowly varying wave train fronts caused by the Maxwellian conditions (4.17); $A_{i}>0, (i=1, 2, 3)$, $B=0.1$

Remark 6

No analytical solution of the present initial value problem has been found, so there may be no way to estimate quantitative errors of the iterative solutions such as (4.9) and (4.10).

Figure 18 shows the numerically converged solutions of the $\eta _6^*$, $\eta _{25}^*$ and $\eta _{32}^*$ for three different amplitudes, $A_i >0$, $i=1,2,3$. These describe physically the development of nonlinear wave train fronts. Here, we clearly observe the nonlinear behaviors near wave train fronts (within blue-colored rectangles), which are compared to the linear result,

$$\begin{aligned} \eta _\mathrm{{linear}} (x,t)=\frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_{1} (k)} \cdot e^{-i{\tilde{\theta }}(x,t;k)}dk. \end{aligned}$$

(4.20)

$\eta _\mathrm{{linear}}$ in (4.20) denotes the closed form of solution for the linearized version of the RLW equation (1.1), being resulted from (2.13) when $\bar{{\varphi }}^{{*}}$ vanishes.

It is found that the nonlinear behavior of the leading wave (or the wave front) is in a good agreement with the linear one, when the smallest amplitude, i.e., $A_{1}=0.01$, of (4.17) is considered, as expected. However, there is a sensible discrepancy between them for the other amplitudes. Especially, the nonlinear feature of the leading wave (or the wave front within blue-colored rectangles) is most revealed for the case $A_{3}=0.27$, where we can find steep waves with peaked crests and flat troughs like a cnoidal wave. And we further discover the interesting nonlinear phenomenon that high-amplitude waves move faster than waves of low amplitude.

5 Concluding Remarks

The basic idea underlying this paper may be characterized by the question which concerns how to construct a functional iterative algorithm for the RLW equation via an integral equation formalism. For resolving the question, we have introduced the pseudo-parameter concept [10], merged into the original RLW equation. This provides the (pseudo-parameterized) dual regular integral equations, making us derive a recurrence relation using fixed point iteration. It is a (required) new functional iterative algorithm for integrating the RLW equation.

The functional iterative algorithm derived in this paper is semi-analytic and derivative-free, which is straightforward to apply in that the only thing required is just the use of regular numerical integration in every iterative process (because the concerning integral equations are regular). For checking the algorithm’s performance, we have made a numerical experiment with solitary wave propagations to examine not only the convergence properties and accuracy characteristics but also the ROCs subject to some constraints in the complex plane. Notably, the algorithm is also shown to be good at investigating the evolution of a slowly varyng nonlinear wave train and the nonlinear behavior near the front of the wave train, which demonstrates fundamental and interesting physical phenomena of nonlinear dispersive water waves.

It is noted that the pseudo-parameter, artificially introduced here, may be regarded as an important parameter, which has several roles. For the first, it connects the original RLW equation with the dual integral equations. Second, it is related with the iteration’s performance, e.g., the convergence speed and accuracy of the iteration algorithm. Finally, we would like to close this paper by stressing the point that the values of the pseudo-parameter in this paper extend over a much wider range than those in the previous study in Jang [10]. This may be clearly confirmed by presenting diagrams showing the ROCs subject to some constraints plotted in the complex plane.

Appendices

Appendix A: Derivation of (4.2)

With the chain differentiation rule

$$\begin{aligned} \frac{\partial }{\partial t}=\frac{\partial }{\partial t^{*}}\frac{dt^{*}}{dt}, \quad \frac{\partial }{\partial x}=\frac{\partial }{\partial x^{*}}\frac{dx^{*}}{dx} \end{aligned}$$

we have

$$\begin{aligned} \frac{\partial }{\partial t}\left( {\frac{\partial }{\partial t}} \right)= & {} \frac{\partial }{\partial t}\left( {\frac{\partial }{\partial t^{*}}\frac{dt^{*}}{dt}} \right) =\frac{\partial ^{2}}{\partial t^{*2}}\left( {\frac{dt^{*}}{dt}} \right) ^{2}=\frac{6g}{h_0 }\frac{\partial ^{2}}{\partial t^{*2}}, \end{aligned}$$

(A.1)

$$\begin{aligned} \frac{\partial }{\partial x}\left( {\frac{\partial }{\partial x}} \right)= & {} \frac{\partial }{\partial x}\left( {\frac{\partial }{\partial x^{*}}\frac{dx^{*}}{dx}} \right) =\frac{\partial ^{2}}{\partial x^{*2}}\left( {\frac{dx^{*}}{dx}} \right) ^{2}=\frac{6}{h_0^2 }\frac{\partial ^{2}}{\partial x^{*2}}. \end{aligned}$$

(A.2)

because $dt^{*}=dt\sqrt{6g/h_0 }$ and $dx^{*}=dx\sqrt{6}/h_0$ from (4.1). This enables us to obtain

$$\begin{aligned} \frac{\partial }{\partial t}\eta= & {} \left( {\sqrt{\frac{6g}{h_0 }}\frac{\partial }{\partial t^{*}}} \right) \left( {\frac{2h_0 }{3}\eta ^{*}} \right) =\frac{2\sqrt{6gh_0 }}{3}\eta _{t^{*}}^*, \end{aligned}$$

(A.3)

$$\begin{aligned} \frac{\partial }{\partial x}\eta= & {} \left( {\frac{\sqrt{6}}{h_0 }\frac{\partial }{\partial x^{*}}} \right) \left( {\frac{2h_0 }{3}\eta ^{*}} \right) =\frac{2\sqrt{6}}{3}\eta _{x^{*}}^*, \end{aligned}$$

(A.4)

$$\begin{aligned} \eta \frac{\partial }{\partial x}\eta= & {} \left( {\frac{2h_0 }{3}\eta ^{*}} \right) \left( {\frac{2\sqrt{6}}{3}\eta _{x^{*}}^*} \right) =\frac{4h_0 \sqrt{6}}{9}\eta ^{*}\eta _{x^{*}}^*\end{aligned}$$

(A.5)

and

$$\begin{aligned} \frac{\partial ^{3}}{\partial x^{2}\partial t}\eta =\left( {\frac{6}{h_0^2 }\frac{d^{2}}{dx^{*2}}} \right) \left( {\sqrt{\frac{6g}{h_0 }}\frac{d}{dt^{*}}} \right) \left( {\frac{2h_0 }{3}\eta ^{*}} \right) =\frac{4}{h_0 }\sqrt{\frac{6g}{h_0 }}\eta _{x^{*}x^{*}t^{*}}^*\end{aligned}$$

(A.6)

from (A.1) and (A.2). Finally, we substitute (A.3–A.6) to (1.1) to arrive at

$$\begin{aligned} \frac{2\sqrt{6gh_{0} }}{3}\eta _{t^{*}}^{*} +c_{0}\left( {\frac{2\sqrt{6}}{3}\eta _{x^{*}}^*} \right) +\frac{3c_0 }{2h_{0} }\left( {\frac{4h_0 \sqrt{6}}{9}\eta ^{*}\eta _{x^{*}}^*} \right) -\frac{h_0^2 }{6}\left( {\frac{4}{h_0 }\sqrt{\frac{6g}{h_0 }}\eta _{x^{*}x^{*}t^{*}}^*} \right) =0,\nonumber \\ \end{aligned}$$

(A.7)

where $c_0 =\sqrt{gh_0 }$ from (1.2). It immediately follows that (A.7) is equivalent to (4.2).

Appendix B: Proof that the Iteration (3.14) is Essentially a Real-Valued (Recurrence) Equation if $\alpha$ is Real

Recall that (3.1) is equivalent to (2.26), which can be written as

$$\begin{aligned} \eta =\mathrm{I}_1 +\mathrm{I}_2 \end{aligned}$$

(B.1)

where

$$\begin{aligned} \mathrm{I}_1 =\frac{1}{2\pi }\int _{-\infty }^\infty {\bar{{\eta }}_1 (k)} \cdot e^{-i\tilde{\theta }(x,t;k)}dk \end{aligned}$$

(B.2)

and

$$\begin{aligned} \mathrm{I}_2 =\frac{1}{2\pi }\int _0^t {\int _{-\infty }^\infty {\int _{-\infty }^\infty {\frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot e^{-i\tilde{\theta }(x-\xi ,t-\tau ;k)}\cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau } } } . \end{aligned}$$

(B.3)

From (2.17),

$$\begin{aligned} \hbox {I}_{1} =&\frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {e^{-i\left[ {k(x-\xi )-{\tilde{\omega }}_\mathrm{{BBM}} (k)\cdot t} \right] }\cdot \eta _1 \left( \xi \right) d\xi dk} } \nonumber \\ =&\frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {\eta _1 (\xi )\cdot \exp \left[ {-i\left\{ {k\left( {x-\xi } \right) -\frac{c_0 k-\alpha /i}{1+h_0^2 k^{2}/6}\cdot t} \right\} } \right] d\xi dk} } \nonumber \\ =&\frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {\exp \left[ {\frac{-\alpha t}{1+h_0^2 k^{2}/6}} \right] \cdot \eta _1 (\xi )\cdot \exp \left[ {-i\left\{ {k\left( {x-\xi } \right) -\frac{c_0 kt}{1+h_0^2 k^{2}/6}} \right\} } \right] d\xi dk} } \nonumber \\ =&\frac{1}{2\pi }\int _{-\infty }^\infty \int _{-\infty }^\infty \exp \left[ {\frac{-\alpha t}{1+h_0^2 k^{2}/6}} \right] \cdot \eta _1 (\xi )\cdot \left[ \cos \left[ {k\left( {x-\xi } \right) -\frac{c_0 kt}{1+h_0^2 k^{2}/6}} \right] \right. \nonumber \\&\qquad \qquad \qquad \left. -i\sin \left[ {k\left( {x-\xi } \right) -\frac{c_0 kt}{1+h_0^2 k^{2}/6}} \right] \right] d\xi dk \nonumber \\ =&\frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {\exp \left[ {\frac{-\alpha t}{1+h_0^2 k^{2}/6}} \right] \cdot \cos \left[ {k\left( {x-\xi } \right) -\frac{c_0 kt}{1+h_0^2 k^{2}/6}} \right] \cdot \eta _1 (\xi )d\xi dk} } \nonumber \\&-i\frac{1}{2\pi }\int _{-\infty }^\infty {\int _{-\infty }^\infty {\exp \left[ {\frac{-\alpha t}{1+h_0^2 k^{2}/6}} \right] \cdot \sin \left[ {k\left( {x-\xi } \right) -\frac{c_0 kt}{1+h_0^2 k^{2}/6}} \right] \cdot \eta _1 (\xi )d\xi dk} } . \end{aligned}$$

(B.4)

where pseudo-dispersion relation (2.12) and pseudo-phase function (2.19) are used.

Similarly as above, from (2.23),

$$\begin{aligned} \hbox {I}_2= & {} \frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot e^{-i{\tilde{\theta }}(x-\xi ,t-\tau ;k)} \cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau \nonumber \\= & {} \frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot \exp \left[ {-i\left\{ {k\left( {x-\xi } \right) -\frac{c_0 k-\alpha /i}{1+h_0^2 k^{2}/6}\cdot \left( {t-\tau } \right) } \right\} } \right] \nonumber \\&\qquad \qquad \qquad \qquad \cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau \nonumber \\= & {} \frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot \exp \left[ {\frac{-\alpha }{1+h_0^2 k^{2}/6}\cdot \left( {t-\tau } \right) } \right] \nonumber \\&\cdot \exp \left[ {-i\left\{ {k\left( {x-\xi } \right) -\frac{c_0 k}{1+h_0^2 k^{2}/6} \cdot \left( {t-\tau } \right) } \right\} } \right] \cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau \nonumber \\= & {} \frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot \exp \left[ {\frac{-\alpha }{1+h_0^2 k^{2}/6}\cdot \left( {t-\tau } \right) } \right] \nonumber \\&\qquad \qquad \qquad \qquad \cdot \cos \left[ {k\left( {x-\xi } \right) -\frac{c_0 k}{1+h_0^2 k^{2}/6}\cdot \left( {t-\tau } \right) } \right] \cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau \nonumber \\- & {} i\frac{1}{2\pi }\int _0^t \int _{-\infty }^\infty \int _{-\infty }^\infty \frac{1}{\;1+\frac{h_0^2 k^{2}}{6}\;}\cdot \exp \left[ {\frac{-\alpha }{1+h_0^2 k^{2}/6}\cdot \left( {t-\tau } \right) } \right] \nonumber \\&\cdot \sin \left[ {k\left( {x-\xi } \right) -\frac{c_0 k}{1+h_0^2 k^{2}/6}\cdot \left( {t-\tau } \right) } \right] \cdot \varphi \left( {\xi ,\tau } \right) d\xi dkd\tau . \end{aligned}$$

(B.5)

Bear in mind that (3.2) can be written as

$$\begin{aligned} \psi =\frac{\partial \mathrm{I}_1 }{\partial x}+\frac{\partial \mathrm{I}_2 }{\partial x}. \end{aligned}$$

(B.6)

From (B.4),

(B.7)

In the same way as above, differentiating (B.5) yields

(B.8)

The imaginary parts of (B.4–B.8) all vanish, if $\alpha$ is real, because the integrands of the imaginary parts of (B.4–B.8) are odd in k. Thus, the pair of (3.1) and (3.2) are all real-valued equations, which implies the iteration (3.14) is essentially a real-valued (recurrence) equation, since (3.11) is identical with the pair. This completes the proof.