1 Introduction and Motivation

Smoothness-increasing accuracy-conserving (SIAC) filtering has demonstrated its effectiveness in raising the convergence rate for discontinuous Galerkin solutions from order \(k+\frac{1}{2}\) to order 2k+1 for specific types of translation invariant meshes [7–9]. Additionally it improves the weak continuity in the discontinuous Galerkin method to k−1 continuity. Typically this improvement has a positive impact on the error quantity in the sense that it also reduces the absolute errors in the solution. However, not enough emphasis has been placed on the difference between superconvergent accuracy and improved errors. This distinction is particularly important when it comes to interpreting the interplay introduced through meshing, between geometry and filtering. The underlying mesh over which the DG solution is built is important because the tool used in SIAC filtering—convolution—is scaled by the geometric mesh size. This scaling heavily contributes to the effectiveness of the post-processor. Although the choice of this scaling is straightforward when dealing with a uniform mesh, it is not clear what the impact of either a global or local scaling will be on either the absolute error or on the superconvergence properties of the post-processor. In this paper, we present a study of the mesh scaling used in the SIAC filter and how it factors into the theoretical errors. To accomplish the large volume of post-processing necessary for this study, commodity streaming multiprocessors in the form of graphical processing units (GPUs) were used; we demonstrate that when applied to structured meshes, up to a 50× speed up in the computational time over traditional CPU implementations of the SIAC filter can be achieved. This shows that it is feasible for SIAC filtering to be inserted into the post-processing pipeline as a natural stage between simulation and further evaluation such as visualization.

The typical application of SIAC filters has been to discontinuous Galerkin solutions on translation invariant meshes. The most typical means of generating translation invariant meshes is by constructing a base tessellation of size H and repeatedly tiling in a non-overlapping fashion the base tessellation until the volume of interest is filled [1, 2]. The effectiveness of such a translation invariant filter for discontinuous Galerkin solutions of linear hyperbolic equations was initially demonstrated by Cockburn, Luskin, Shu and Süli [7]. A computational extension to smoothly-varying meshes as well as random meshes, where a scaling equal to the largest element size was used, was given in [8]. For smoothly-varying meshes, the improvement to order 2k+1 was observed. For random meshes there was no clear order improvement, which could be due to an incorrect kernel scaling. These results were theoretically and numerically extended to translation invariant structured triangular meshes in [9]. However, the outlook for triangular meshes is actually much better than those presented in [9]. Indeed, the order improvement was not clear for filtering over a Union-Jack mesh when a filter scaling equal \(\frac{H}{2}\) was used (see Fig. 11). In this paper, we revisit the Union-Jack mesh case, as well as a Chevron triangular mesh and demonstrate that it is indeed possible to obtain superconvergence of order 2k+1 for these mesh types when the proper scaling of the filter, related to the translation invariant properties of the mesh, are employed. Furthermore we also introduce theoretical proof that these results can be extended to adaptive meshes that are constructed in a hierarchical manner—in particular, adaptive meshes whose elements are defined by hierarchical (integer) splittings of elements of size H, where H represents both the macro-element spacing used in the generation of the mesh and the minimum scaling used for the SIAC filter.

To accomplish this study and revisit some of the previous results, we were required to run exhaustive tests over many meshes with different scaling parameters. Though conceptually possible using traditional CPU-based solutions, the task of sweeping through the large number of simulations necessary for such a systematic study seemed daunting. In light of this, we focused our efforts on the development of a streaming commodity architecture—graphical processing unit (GPU) version of our SIAC filter. By exploiting the structured nature of our meshes and the streaming SIMD (single-instruction-multiple-data) nature of available hardware, we were able to achieve nearly 50× speed up over our traditional CPU implementation—making the tests presented herein computationally tractable. All results presented here were run on an NVIDIA C2050 Tesla card using full double-precision. It consists of 14 Streaming MultiProcessors (SMs), each of which has 32 cores for a total of 448 cores. Each core runs at 1.15 GHz.

This paper addresses these issues in the following manner: in Sect. 2, the necessary background for the discontinuous Galerkin method and the smoothness-increasing accuracy-conserving filter is given; Sect. 3 contains the theoretical extension to adaptive meshes; Sect. 4 discusses the GPU implementation of the post-processor that was used to generate the results in Sect. 4.2. In that section, an emphasize on the difference between order improvement and error improvement is discussed through presenting various numerical examples. Finally, in Sect. 5 we conclude the paper.

2 Background

In this section we discuss the required background necessary to implement the smoothness-increasing accuracy-conserving (SIAC) filter. This method is specifically applied to discontinuous Galerkin (DG) methods in this paper, which is why it is important to review the important features of this method and how the solution can be improved. A review summary of the SIAC filter is then presented.

2.1 Discontinuous Galerkin Methods (DG)

The studies included in this paper concentrate on the linear hyperbolic equation

(1)

where x∈Ω⊂ℝd, and t∈ℝ. We note that it is possible to extend the studies contained in this paper to variable coefficient equations as given in [9].

The effectiveness of the SIAC filter was initially established for finite element methods [5] and extended to discontinuous Galerkin methods in [7]. For an overview of DG methods see [6]. Here a review of the important properties of the DG solution is given. First, the discontinuous Galerkin method uses an approximation space of piecewise polynomials of degree less than or equal to k,

$$V_h=\bigl\{v\in L_2(\Omega): v|_{K}\in \mathbb{P}^k(K),\ \forall K \in \mathcal{T}_h\bigr\},$$

where \(\mathcal{T}_{h}\) is a tessellation of the domain Ω and \(K\in\mathcal{T}_{h}\). Using such an approximation space, the order of the approximation is \(k+\frac{1}{2}\) and k+1 in special cases. Second, the DG method is based upon a variational formulation given by

$$\int_{\tau_e}\frac{\partial{u}_{h}}{\partial t}{ v}_{h}\, d\mathbf{x}-\sum_{i=1}^d\, \int_{\tau_e}\, f_i(\mathbf{x},t)\frac{\partial v_{h}}{\partial x_i}\, d\mathbf{x} + \int _{\tau_e}\, A_0u_h(\mathbf{x},t)v_h(\mathbf{x},t)\, d\mathbf{x} + \sum_{i=1}^d\, \int_{\partial\tau_e}\hat{f}_i\hat{n}_i {v}_{h}\, ds=0, $$
(2)

where f i (x,t)=A i u h (x,t), i=1,…,d. Lastly, it is important to note that in this formulation, there is only weak continuity imposed at the element interfaces.

2.2 Smoothness-Increasing Accuracy-Conserving (SIAC) Filtering

It is observable that the errors in the discontinuous Galerkin solution are highly oscillatory. We are able to smooth out these oscillations and increase the order of accuracy through the use of a smoothness-increasing accuracy-conserving (SIAC) filter. Indeed, the smoothness will increase to \(\mathcal{C}^{k-1}\) and the order will improve to \(\mathcal{O}(h^{2k+1})\). This is possible due to the superconvergence of the DG solution in the negative-order norm, which gives an indication of the oscillatory nature of the errors. Because the error estimates for the DG solution in the negative-order norm are of higher order than the L 2-error estimates, applying this SIAC filter to the DG solution at the final time increases the order of the solution in the L 2-norm. This post-processor was introduced for DG by Cockburn, Luskin, Shu, and Süli [7] based on the ideas for finite element methods of Bramble and Schatz [5] and Mock and Lax [11]. Background on the SIAC filter can be found in [7, 14] and implementation details in [10].

To introduce the SIAC filter, it is enough to consider the one-dimensional case as the multi-dimensional kernel is a tensor product of the one-dimensional case. The kernel works in the following way: Let u h be the discontinuous Galerkin solution at the final time. The symmetric SIAC filtered solution, used in the interior of the domain, is given by

$$u^{\star}(x) = \bigl(K^{2(k+1),k+1}_h \star u_h(\cdot,T)\bigr) (x), $$
(3)

where the convolution kernel is defined as

$$K_h^{2(k+1),k+1}(x)=\frac{1}{h}\sum _{\gamma=0}^{2k} c_\gamma^{2(k+1),k+1}\psi^{(k+1)} \biggl(\frac{x}{h}-k+\gamma \biggr), $$
(4)

where ψ (k+1) represents a B-spline of order k+1 and c γ are the kernel coefficients. This dependence on B-Splines to form the kernel gives it a local support, which also makes it computationally efficient to implement. Additionally, the coefficients of the kernel are chosen such that the kernel reproduces polynomials of degree less than or equal to 2k. This ensures that the post-processed solution maintains the current level of accuracy. As the filtered solution is based on convolution, it inherits the continuity from the B-Splines, which is \(\mathcal{C}^{k-1}\). In the interior of the domain, a symmetric kernel consisting of 2k+1 B-Splines is used and near the boundary 4k+1 B-Splines are used. In the transition regions, a convex combination of these kernels ensures a smooth transition between the two kernels,

$$u^{\star}_h({x}) = \underbrace{\theta({x})\underbrace{u^{\star}_{h, 2k+ 1}({x})}_{\mathrm{filtering\ with}\ 2k + 1\ \mathrm{B}\mbox{-}\mathrm{splines}} + \bigl(1- \theta ({x})\bigr) \underbrace{u^{\star}_{h, 4k+1}({x}),}_{\mathrm{filtering\ with}\ 4k + 1\ \mathrm{B}\mbox{-}\mathrm{splines}}}_{\mathrm{smooth\ convex\ combination}}$$
(5)

where θ(x)∈[0,1] and has the proper continuity (see [14]).

For a uniform, translation invariant mesh, the kernel is scaled by the uniform element size, h:

$$u^{\star}(x) = \bigl(K^{2(k+1),k+1}_h \star u_h(\cdot,T)\bigr) (x) = \frac{1}{h} \sum _{I_i} \sum_{K_b} \int K \biggl(\frac{y-x}{h} \biggr)u_h(y)\, dy.$$
(6)

This makes the ideal application of this SIAC filter to uniform quadrilateral or hexahedral meshes, or structured triangle meshes as shown in [9].

As mentioned previously, for the multi-dimensional kernel, the kernel is given by a tensor product of the one-dimensional kernel,

$$K_h(x_1,x_2,\ldots,x_d)=\prod _{n=1}^d\, K_h(x_n). $$
(7)

The filtered solution in 2D is then

$$u^\star(\bar{x},\bar{y}) = \int\int_{\mathbb{R}^2} K \biggl(\frac {x_1-\bar{x}}{\triangle x_1},\frac{x_2-\bar{y}}{\triangle x_2} \biggr) u_h(x_1,x_2)\, dx_1dx_2,$$
(8)

where

$$K(x_1,x_2) = K(x_1)\cdot K(x_2) = \sum_{\gamma_1} \sum _{\gamma_2}\, c_{\gamma_1}c_{\gamma_2}\,\psi^{(k+1)}(x_1-x_{\gamma_1})\psi^{(k+1)}(x_2-x_{\gamma_2}).$$
(9)

Notice that the kernel scaling in the x 1 and x 2 directions need not be the same. The scaling only has to be uniform for a given coordinate direction.

3 Theoretical Kernel Scaling

In this section a proof of the superconvergence of the DG solution through SIAC filtering for \(h=\frac{1}{\ell}H\) where ℓ is a multi-integer is given. The main theorem is the following:

Theorem 3.1

Let u h be the DG solution to

where A i , i=0,…,d are constant coefficients, Ω⊂ℝd. The approximation is taken over a mesh whose elements are of size \(h=\frac{1}{\ell} H\) in each coordinate direction where ℓ is a multi-integer (of dimension equal to the number of elements along one coordinate direction) and H represents the macro-element size of which any particular element is generated by hierarchical integer partitioning of the macro-element. Given sufficient smoothness in the initial data,

$$\| u-K_H\star u_h\|_\Omega\leq CH^{2k+1},$$

where K H is the post-processing kernel given in Eq. (7) scaled by H.

Remark 3.1

This theorem is more about geometry than the issues of superconvergence. Indeed the difference between this estimate and the estimate in [7] has to do with the kernel scaling, H.

Proof

The general estimate for a uniform mesh was proven in [7]. Here, we repeat the important points for this extension.

First, the error is split into two parts—the error from the design of the filter and the error from the approximation method used:

$$\| u-K_H\star u_H\|_\Omega\leq\underbrace{\|u-K_H\star u\|_\Omega }_{\mathrm{Filtering\ exact\ solution}} + \underbrace{\bigl \Vert K_H\star (u-u_h)\bigr \Vert _\Omega.}_{\mathrm{Filtering\ of\ approximation}}$$
(10)

The first part of this error estimate simply uses the fact that the kernel reproduces polynomials of degree less than or equal to degree 2k as well as a Taylor expansion. Details are given in [7]. Note that it is possible to make the estimate of the first term of arbitrarily high order. It is therefore the second term, the post-processed approximation, that dominates the error estimate.

One key aspect of the second error estimate is a property of the B-Splines. That is,

$$ D^\alpha\bigl(K_H\star(u-u_h)\bigr)=\widetilde{K}_H\star\partial_H^\alpha(u-u_h),$$
(11)

where K H is the kernel using B-splines of order k+1+α, \(\widetilde{K}_{H}\) is the kernel using B-splines of order k+1, and the operator \(\partial^{\alpha}_{H}\) denotes the differencing operator as defined in [5]. Another important factor in obtaining the bound on the approximation is the estimate by Bramble and Schatz [5] that bounds the L 2-error by the superconvergent error in the negative-order norm:

$$ \bigl\|K_H\star(u-u_h)\bigr\|_\Omega \leq C \sum_{\alpha\leq|\ell|} \bigl\|D^\alpha\bigl(K_H\star(u-u_h)\bigr)\bigr\|_{-\ell} \leq C \sum_{\alpha\leq|\ell|} \bigl\|\partial^\alpha_H (u-u_h)\bigr\|_{-\ell} \leq C H^{2k+1}.$$
(12)

This superconvergence in the negative-order norm was proven by Cockburn et al. in [7] for a uniform translation invariant mesh. This is a consequence of the B-Spline property that allows derivatives to be expressed as divided difference quotients. The divided difference quotient relationship as expressed in Eq. (11) is only possible for an H-translation invariant mesh or those meshes in which the mesh element spacings are integer multiples of the characteristic length H. This occurs automatically for uniform quadrilateral or hexahedral meshes as well as structured triangular meshes. However, extension to adaptive meshes is possible by constructing the element spacing h as an integer partitioning of the fundamental characteristic size, \(h=\frac {1}{\ell} H, \ell\) a multi-integer. When this is the case, one can observe that the translation operator as defined in [5] specified with respect to H can be related to translation with respect to the actual element size h, i.e. over the DG mesh, as follows:

$$T_H^m v(\mathbf{x}) = v(\mathbf{x}+mH)=v(\mathbf{x}+m\ell h)=T_h^{m\ell}v(\mathbf{x}).$$
(13)

The error estimate therefore follows as the divided difference operator in Eq. (12), originally expressed in terms of H can be expressed in terms of its integer multiples. The constant C in the right-most expression encapsulates the impact of the (integer multiple) adaptive spacing. □

Remark 3.2

Particular emphasis should be placed on the fact that this makes the SIAC filter applicable to adaptive meshes, provided the scaling is taken in the correct manner.

4 Kernel Scaling Results

In this section we outline the extension of the smoothness-increasing accuracy-conserving (SIAC) filter for computing using GPUs. This is an important step as it speeds up computational costs, allowing for exploring more complicated mesh structures. This extension allows for a true study of the kernel mesh scaling for various mesh geometries, which in turn leads to placing emphasis on the distinction between higher-order convergence and reduced errors.

4.1 Efficient Computing Using GPUs

The upward trends in graphics processor (GPU) performance are impressive, even relative to progressively more powerful, conventional CPUs [13]. A variety of forces in manufacturing, marketing, and applications are driving this upward trend, but the growing consensus is that the streaming architecture embodied in most modern graphics processors has inherent advantages in scalability.

Stream processing simplifies hardware by restricting the parallel computations that can be performed. Given a set of data (a stream), stream processors apply a series of operations (kernel functions) to each element in the data stream with often one kernel function being applied to all elements in the stream (uniform streaming). This paradigm allows kernel functions to be pipelined, and local on-chip memory and data transmission is reused to minimize external memory needs. This design paradigm virtually eliminates the need for cache hierarchies, which allows more space on each chip to be allocated to processing and also allows for very high bandwidth between processors (e.g. ALUs) and memory used for data streams.

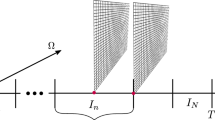
Most current streaming processors rely on a SIMD (single-instruction-multiple-data) programming model in which a single kernel is applied to a very large number of data items with no data dependencies among streams. This paradigm is very amenable to the SIAC filtering as presented in Sect. 2.2 and as demonstrated in [10] when OpenMP parallelization was applied. In [10], nearly embarrassingly parallel speed-up was attainable by partitioning the elements to be post-processed amongst the various processors available. Using that same strategy, we can exploit the massively SIMD programming model of the GPU. For each element that requires post-processing, we are able to use the kernel footprint to determine the neighboring elements needed in the post-processing, and then isolate this computation so that it can be done in an embarrassingly parallel fashion as illustrated in Fig. 1. In the case of a structured mesh in which the operations being accomplished to post-process an element are independent of its position in the mesh and in which the collection of operations are identical (with only changes in the data on which those operations are accomplished), GPU parallelization is straightforward.

Fig. 1
figure 1

Each element to be post-processed and the neighborhood of elements dictated by the geometric footprint of the kernel can be allocated to a GPU core in an embarrassingly parallel fashion

Full size image

In Table 1 we present a comparison of the post-processing times (in milliseconds) required by our CPU and GPU implementations of the SIAC filter for various structured quadrilateral meshes at different polynomial orders under the assumption of periodic boundary conditions. The CPU machine used in this comparison was an Intel Xeon X7542 running at 2.67 GHz.

Table 1 Wall-clock times (ms) required to post-process a DG solution for various mesh sizes and polynomial orders. For the GPU case, three different integer multiples m of the kernel scaling parameter H are provided
Full size table

The following observations can be made based upon the data presented in Table 1:

  • There is a static amount of overhead associated with running a process on the GPU. This gives a false impression as to the scaling of computation times at lower mesh resolutions. The overhead will be hardware/implementation dependent. In this case the trend becomes more clear for computations that take at least five or more seconds to complete on the GPU.

  • The majority of the computation times were spent on memory access. As the footprint of the kernel increases, more neighboring data must be accessed to compute the post-processed solution at a given evaluation point. Judicious memory layout patterns were key to achieving significantly improved performance on the GPU.

  • As the kernel spacing increases, the GPU wall-clock time increases. This increase comes as a consequence of the increased width of the kernel footprint induced by the increased scaling factor. As an increased number of elements surrounding an element are needed in order to generate the post-processed solution for a particular element, the number of floating-point operations increases (and hence the total wall clock time).

  • The increase in the kernel spacing also dictates how much data from the region surrounding an element is necessary to accomplish the post-processing. This increased memory usage decreases the efficiency of computation per core as more loads/stores are required to facilitate computation on a GPU core.

Remark 4.1

A multi-GPU version of our SIAC filter was implemented for comparison. Given the initial cost of initializing multiple GPUs and moving data from main memory down to the individual GPU memory, we found that only for large meshes was the multi-GPU implementation profitable in terms of wall-clock time. We were able to see over a three times speed-up over our single GPU performance when using four GPUs for meshes larger than 1602 elements.

4.2 Numerical Results

In this section we discuss the importance of geometric mesh assumptions for obtaining improved errors versus improved order of accuracy. This is done by inspecting one equation for different mesh types. That is,

An investigation of the filtered DG solution will be performed for meshes that include the uniform quadrilateral mesh, an adaptive mesh, a structured triangular mesh, a Union-Jack mesh, and a Chevron mesh. Additionally, for the first time, three-dimensional results over a hexahedral mesh are also given. Note that similar behavior has been observed for variable coefficient equations, as predicted by the theory [9]. A particular emphasis will be placed on the distinction between reduced errors and higher order accuracy for a given scaling of the SIAC filter.

4.2.1 Uniform Quadrilateral Mesh

The first example presented is a study of the scaling for the SIAC filter for a uniform quadrilateral mesh as shown in Fig. 2.

Fig. 2
figure 2

Example of uniform quadrilateral mesh (a) and diagram of filter spacing used (b)

Full size image

The theory of [7] establishes that the scaling H used by the post-processor should be the same as used to construct the mesh (i.e. the mesh is of uniform spacing H). However, according to Theorem 3.1, a scaling of any integer multiple, mH should also produce superconvergent accuracy. Indeed, in Table 2 the numerical results using different values of m for the kernel scaling are presented. It can be seen that as long as m≥1 accuracy of order 2k+1 is obtained. Examining the errors closely, it becomes obvious that the errors are actually increasing as the kernel scaling becomes greater, even with this 2k+1 convergence. A plot of absolute error versus different scalings is given in Fig. 3. This plot demonstrates that the minimal error actually occurs with a SIAC filter scaling a bit less than the element spacing H and after this scaling the errors begin increasing, although maintaining the 2k+1 convergence rate. In Fig. 4, contour plots of the errors for N=40 for ℙ2 and ℙ3 polynomial approximations are presented for scalings of 0.5H, H and 2H. The plots demonstrate that the errors get much smoother as we increase the scaling from 0.5H to H. The errors using 2H scaling are also smooth, however, the magnitude of the errors are larger.

Fig. 3
figure 3

Plots of error versus scaling (m) used in the SIAC filter for a uniform quadrilateral mesh for ℙ2 (left) and ℙ3 (right) polynomial approximations

Full size image
Fig. 4
figure 4

Contour plots using a scaling of 0.5H (left) and H (middle) and 2H (right) for a uniform quadrilateral mesh such as the one in Fig. 2. Top row: ℙ2, Bottom row: ℙ3

Full size image
Table 2 Table of L 2-errors for various scalings used in the SIAC filter for a uniform quadrilateral mesh
Full size table

4.2.2 Quadrilateral Cross Mesh

In this example we consider a variable-spacing quadrilateral mesh. The mesh was designed in the following manner: let \(H=\frac{2}{N}\), where N is the total number of elements in one direction used in the approximation. We first divide the mesh into a collection of evenly-spaced quadrilateral macro-elements of size H. In order to generate the final mesh, we further split some of these quadrilateral elements (more towards the middle of the mesh) into two, four or more quadrilateral sub-elements, i.e., each element of the new mesh is created by subdividing the macro-element of size H by some integer partition. This type of scaling gives an adaptive cross mesh as shown in Fig. 5. Note that although this mesh is not uniformly-spaced, the mesh construction proposed does meet a local hierarchical partitioning property which we have proven to be sufficient for observing superconvergence when applying the SIAC filter with a scaling of H.

Fig. 5
figure 5

Example of a variable-spacing quadrilateral (cross) mesh (a) and diagram of filter spacing used (b)

Full size image

In Table 3 the errors for mH where m=0.25,0.5,1.0,1.5,2.0 are given. Notice that one begins to see the correct superconvergent rate of order 2k+1 for a scaling of m=1.0, as expected. The “x’s” given in the table denote regions in which the chosen scaling of the kernel makes the kernel support wider than the mesh used in the approximation. In Fig. 6, a plot of error versus m is given. Observe that the minimum error and the correct convergence rate occurs at H (m=1) as predicted by the theory. In Fig. 7, contour error plots are shown for different scalings of the SIAC filter. Additional tests not reported here in which we split the quadrilateral-based adaptive mesh into an adaptive structured triangle mesh yield similar results to those reported here; a filter scaling of size H yields the optimal results in terms of absolute error.

Fig. 6
figure 6

Plots of error versus various scalings (m) used in the SIAC filter for a variable-spacing cross mesh for ℙ2 (left) and ℙ3 (right) polynomial approximations

Full size image
Fig. 7
figure 7

Contour plots using a scaling of 0.5H (left), H (middle), and 1.5H (right) for a variable-spacing cross quadrilateral mesh such as the one in Fig. 5. Top row: ℙ2, Bottom row: ℙ3

Full size image
Table 3 Table of L 2-errors for various scalings used in the SIAC filter for a variable-spacing cross mesh
Full size table

4.2.3 Structured Triangular Mesh

Once it has been established that superconvergence occurs for various scalings of quadrilateral meshes, it is then interesting to test whether these ideas extend to structured triangular meshes, as these meshes are also translation invariant. Below are the numerical results for three different types of structured triangular meshes: a uniform structured triangular mesh, a Union-Jack mesh and a Chevron mesh.

The uniform structured triangular mesh as shown in Fig. 8 is first examined to ensure the extension of the main ideas of Theorem 3.1 to this type of mesh. The DG errors together with the filtered errors were first presented in [9]. Table 4 presents the ratio of the kernel size to mesh size for various kernel scalings of mH, m=0.5,1,2,3,4. It demonstrates that the ratio becomes larger for increasing polynomial order or increased m values, which means that the foorprint of the post-processor requires more elements in the computation and becomes less local. Moreover, Table 5 presents the L 2-errors for various scalings. It can be seen that the superconvergent accuracy of order 2k+1 occurs for scalings of mH, m≥1 although the errors increase with increasing m. This is also shown in Fig. 9. In Fig. 10, contour plots of the errors for scalings of m=0.5,1,2 are also shown. A scaling of 0.5H and 2H produce worse errors than that of H. Although scalings of H and 2H also produce smoothness in the errors.

Fig. 8
figure 8

Example of structured triangular mesh (a) and diagram of filter spacing used (b)

Full size image
Fig. 9
figure 9

Plots of error versus various scalings (m) used in the SIAC filter for a structured triangular mesh for ℙ2 (left) and ℙ3 (right) polynomial approximations

Full size image
Fig. 10
figure 10

Contour plots using a scaling of 0.5H (left), H (middle) and 2H (right) for a structured triangular mesh such as the one in Fig. 8. Top row: ℙ2, Bottom row: ℙ3

Full size image
Table 4 Kernel to mesh ratios for the structured triangular mesh cases (uniform, Jack and Chevron). N 2 represents the number of quadrilateral elements
Full size table
Table 5 Table of L 2-errors for various scalings used in the SIAC filter for a structured triangle mesh
Full size table

4.2.4 Union-Jack Mesh

In [9], error results for the Union-Jack mesh were presented with a scaling of \(\frac{H}{2}\) equal to the uniform spacing of the base quadrilateral mesh. It was noted at the time that the correct convergence order was not obtained (and from the theory was not expected to be obtained), but error improvement was observed. However, as Babuška et al. noted in [2–4, 12], this mesh is translation invariant in H, as seen in Fig. 11.

Fig. 11
figure 11

Example of a Union-Jack mesh (a) and diagram of filter spacing used (b)

Full size image

In Table 6 errors for scaling of mH, where m=0.5,1,1.5,2 are presented. It is clearly seen that the superconvergence is observed for scalings of mH where m≥1. It is interesting to note that the mesh is not translation invariant in 1.5H but we see the superconvergence of order 2k+1. Additionally, the errors begin to worsen after the scaling of H. This is also seen in Fig. 12 (m=1). Additionally, in Fig. 13 the differences in the errors between 0.25H scaling, 0.5H, and H are shown. We obtain a much smoother contour plot with the H scaling.

Fig. 12
figure 12

Plots of error versus various scalings used in the SIAC filter for a Union Jack mesh for ℙ2 (left) and ℙ3 (right) polynomial approximations

Full size image
Fig. 13
figure 13

Contour plots using a scaling of 0.25H (left), 0.5H (middle) and H (right) for a Union-Jack mesh such as the one in Fig. 11. Top row: ℙ2, Bottom row: ℙ3

Full size image
Table 6 Table of L 2-errors for various scalings used in the SIAC filter for a Union-Jack mesh
Full size table

4.2.5 Chevron Mesh

In this example, the structured Chevron mesh presented in Fig. 14 is examined. Note that the mesh is translation invariant for H=2h in the x 1-direction and H=h in the x 2-direction where h denotes the spacing of the base quadrilateral mesh. For simplicity in the calculations, the kernel scaling for the x 1 and x 2 directions have been taken to be the same and equal to H=2h. In Table 7, the errors are presented for various choices of m. The table shows mixed results in convergence order for a scaling of m=0.5, but clear improvement to the theoretical order for m=1 and larger. In Fig. 15, the errors versus different scalings are presented similar to previous examples. Figure 16 depicts the contour plots.

Fig. 14
figure 14

Example of a Chevron mesh (a) and diagram of filter spacing used (b). H represents the minimum translation invariance of the mesh. This value is not necessarily the same for each direction as it is shown in (b)

Full size image
Fig. 15
figure 15

Plots of error versus various scalings used in the SIAC filter for a Chevron mesh for ℙ2 (left) and ℙ3 (right) polynomial approximations

Full size image
Fig. 16
figure 16

Contour plots using a scaling of 0.25H (left), 0.5H (middle) and H (right) for a Chevron mesh such as the one in Fig. 14. Top row: ℙ2, Bottom row: ℙ3

Full size image
Table 7 Table of L 2-errors for various scalings used in the SIAC filter for a Chevron mesh
Full size table

4.2.6 Hexahedral Mesh

The last example that we present is the first example of the extension of this SIAC filter to three-dimensions. The extension is for a uniform hexahedral mesh of spacing H. In Table 8, the errors for the discontinuous Galerkin solution of a three-dimensional DG projection problem are given along with the improved errors using the SIAC filter for various scalings mH. We can see that the added dimension does not reduce the order of convergence, and a superconvergent rate of 2k+1 is obtained. This is in agreement with the theory [7].

Table 8 Table of L 2-errors for various scalings used in the SIAC filter for a uniform hexahedral mesh
Full size table

5 Conclusions

By implementing smoothness-increasing accuracy-conserving filtering, the errors for the DG solution can usually be improved from order k+1 to order 2k+1 for linear hyperbolic equations. Additionally, due to the nature of the convolution kernel used in this SIAC filter, the smoothness of the solution is also improved from only having weak continuity to having continuity of k−1. However, care has to be taken with the mesh geometry and correct kernel scalings must be used. The emphasis of this paper has been on the difference between error improvement versus order improvement in terms of geometry. In all our numerical examples it has been demonstrated that it is possible to obtain superconvergence with the correct kernel scaling. However, if the scaling becomes too large the errors worsen and can become worse than the original DG errors while maintaining superconvergence. We further note that when the mesh size is large enough, filtering with the true scaling parameter H yields the optimal results in terms of the magnitude of the error. Moreover, GPU implementation of this SIAC filter was also given. Using GPUs, up to a 50× reduction in computational costs can be obtained for these translation invariant mesh types. Care must be taken with the programming of the GPUs to obtain such a reduction. Lastly, numerical results showing the effectiveness of the SIAC filter for a three-dimensional DG projection problem was presented. For this equation, superconvergence of order 2k+1 was obtained, showing that adding a dimension did not reduce the achieved convergence rate.