1 Introduction

Two-dimensional (2D) ion pools exist under the surface of bulk liquid helium [1,2,3]. An electron inside liquid He forms an otherwise empty void volume or bubble in which it is trapped [4]. This state is referred to as an electron bubble, with a radius of about 17 Å under a saturated vapor pressure (SVP). A positive ion or a snowball is a solid He sphere, at least for the first approximation, formed around a \(^4\)He\(_{2}^+\) ion core, caused by an increase in local pressure induced by electrostriction. The positive ion radius is about 6 Å under SVP [5]. Electron bubbles and positive ions are the most studied ion species in liquid He [6], particularly those trapped at the He surface. Inside liquid He, a charged object receives a repulsive image force from the surface. 2D charge pools can be trapped under the free surface of liquid He by applying a perpendicular pressing electric field, which produces a potential well together with the repulsion from the surface. Although a 2D ion pool of electron bubbles is metastable in the presence of the pressing electric field, an experimental condition can be found such that the pool persists sufficiently long in practice at low temperatures [7]. Many ion species are known to exist in liquid He, for example, ions of He, alkaline, or alkaline-earth elements [8,9,10,11], and charged metallic clusters [12,13,14]. 2D ion pools of electron bubbles and positive ions are used by Poitrenaud and Williams to directly determine the ionic masses in superfluid \(^4\)He [15]. Ott-Rowland et al. [16] and Hannahs and Williams [17, 18] investigated plasma resonances of 2D ion pools of positive ions. Later on, Vinen’s group in Birmingham carried out the most vigorous investigations on the ion pools [3, 19,20,21,22]: mobility [23,24,25,26], plasmons [27], edge magnetoplasmons [28,29,30,31,32], novel oscillation modes of the Wigner solid [33,34,35,36,37,38,39,40], and so forth [41, 42].

Inspired by the mobility measurements of ion pools under the superfluid \(^4\)He surface by Vinen’s group, we came up with an idea to study the nucleation phenomena of quantized vortices [43, 44] by moving ions. The ion vortex ring complex was first discovered by Rayfield and Reif [45, 46]. They suggested that after the nucleation of a quantized vortex, an ion is trapped by the vortex ring, the velocity of which is inversely proportional to the vortex ring radius. Therefore, the larger the associated energy of the ion vortex ring complex, the lower the velocity. Careri et al. showed a clear transition taking place at a critical driving electric field \(E_\textrm{c}\), from a vortex-free flow state to that with vorticity [47]. The \(E_\textrm{c}\) is signaled by an abrupt velocity drop. The maximum ion velocity in the vortex-free flow regime right below \(E_\textrm{c}\) is referred to as the critical velocity \(v_\textrm{c}\). Below \(E_\textrm{c}\), the ion velocity is controlled by the driving electric field, whereas above \(E_\textrm{c}\), it is predominated by the attached vortex ring. The mechanism of nucleation of quantized vortices by moving ions has attracted the interest of researchers [48]. Schwartz and Jang [49] and Muirhead et al. [50] considered the scenario where the nucleation is impeded by the potential barrier, which can be reduced by increasing velocity [51]. Vortex nucleation occurs either through quantum tunneling under the barrier at low temperatures or thermal activation over the barrier at higher temperatures.

In the context of quantum vortex nucleation, ion transport was experimentally verified by researchers in Lancaster [52,53,54]. They measured the vortex nucleation rate by determining the time evolution of displacement current due to the moving ions in isotopically purified \(^4\)He. A similar detection scheme is also used in a time-of-flight (TOF) method with an appropriate grid configuration. The obtained nucleation rate is constant below 250 mK. This is interpreted as quantum tunneling through the barrier. At higher temperatures, the nucleation rate increases rapidly, which is ascribed to a thermal activation process. An activation energy of around 3 K was obtained, which is in agreement with the model proposed by Muirhead et al. [50]. In these measurements at low temperatures, the ion mobility becomes so high that it is difficult to control the electric field below \(E_\textrm{c}\). To overcome this difficulty, the mobility is suppressed by introducing roton emission at appropriate pressures above 1.2 MPa or introducing \(^3\)He impurities [52,53,54,55,56,57].

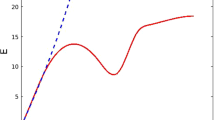
This technical issue can be overcome by employing the transport measurement technique for 2D ion pools. We can measure ion velocity even at electric field intensities below 0.01 Vm\(^{-1}\). In this paper, we report our experimental results on transitions from the vortex-free state to the ion vortex complex state in a 2D positive ion pool. Positive ions are much more stable than electron bubbles. Electron bubbles may disappear when the 2D ion pool is driven too hard. In short our main results are as follows. We observed that the critical velocity increased as a function of temperature from 50 mK to 500 mK as shown in Fig. 7a. This behavior implies a decrease in nucleation rate, and hence, the result is contrary to the thermal activation process. In Sec. 2, we describe the experimental setup used. In Sec. 3, we present our experimental results and discussion, where we argue that the temperature dependence of critical velocity is consistent with the “superohmic” case of the Caldeira–Leggett (CL) theory [58,59,60]. In Sec. 4, we summarize this study and provide some future prospects.

2 Experiment

Fig. 1
figure 1

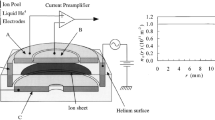
(Color online). a Schematic view of the experimental cell. To store positive ions under the free surface of superfluid \(^4\)He, the upper, lower, and side walls of the cell are appropriately biased with DC potentials. The upper wall consists of two concentric electrodes of equal area, which are used as the exciter and detector electrodes. b Equivalent circuit of the system. The ion pool of resistance R is capacitively coupled to the central exciter electrode (terminal 1) and the peripheral detector electrode (terminal 3) through capacitor \(C_0\). The ion pool is also coupled to the AC ground of bottom electrodes through capacitor \(C_1\). Because the areas of the inner and outer electrodes are equal, the capacitors are symmetric with respect to resistor R

Full size image

The critical velocity of a positive ion is investigated by the transport measurement of a 2D positive ion pool below the surface of superfluid \(^4\)He. The experimental cell is schematically shown in Fig. 1a. The cell is cylindrical, with ions held below the surface by the potential generated by the top, bottom, and guard electrodes. The top electrode assembly consists of a pair of concentric electrodes with the inner radius \(r_\textrm{i}=6.3\) mm and outer radius \(r_\textrm{o}=9.0\) mm separated by a 0.1 mm gap, so that the areas of the inner and outer electrodes are equal. The bottom electrode is a circular plate. The distance between the top and bottom electrodes is set at 3.0 mm, and the surface of liquid He is located 1.74 mm above the bottom electrode. Positive ions are injected from a tungsten tip by field ionization [61] and held below the surface by a DC electric field \(E_{\bot }\) produced by a positive voltage applied to the bottom electrode and the ground-level potential of the top electrodes. The guard ring of 10.0 mm radius is biased positively to radially confine positive ions. The radius of the ion pool, which is numerically estimated [62], is adjusted to be 9.0 mm for any \(E_{\bot }\) by varying the voltage on the guard ring. The depth of the positive ion \(z_{i}\) from the surface is adjustable between 20 and 40 nm by varying \(E_{\bot }\) from 10 to 6 kVm\(^{-1}\) [25]. Here, we present only the data obtained at \(z_\textrm{i}=37.6\) nm. The density n of positive ions is determined by the frequency of plasma resonance [25, 62]. The data presented here were obtained at \(n=6.6\times 10^{11}\) m\(^{-2}\). The (Wigner) solidification temperature for this ion density is estimated as 185 mK. Even above this temperature, the ions are strongly correlated, so that each ion is well separated from others. The average distance between nearest-neighbor ions is more than 1 \(\mu\)m, which is much larger than the ion radius or the size of vortices produced immediately after the nucleation. In the present temperature range, therefore, we may regard nucleation processes as independent, and neglect collective effects.

The Sommer–Tanner method is employed to measure the transport properties of a positive ion pool [63]. An AC voltage \(V_\textrm{i}=V_\textrm{ac}\sin \omega t\) applied to the inner electrode induces a current in the ion pool, and the induced current is detected on the outer electrode. In our electrode geometry, the ion current is radial. The current density profile may be obtained on the basis of a 2D transmission line model [64,65,66]. The profile is nearly triangular, zero at both the center and the peripheral edge, and has a maximum over the gap region. The maximum is not sharp but appears similarly to a rounded peak in the radial direction with a width comparable to the distance between the upper electrode assembly and the ion pool (1.26 mm), where the positive ion velocity is almost uniform. The detected current on the outer electrode is proportional to the maximum current density integrated along the azimuthal path over the gap. The data presented here were obtained at a frequency of \(f = 50.02\) kHz.

The relationship between the driving AC voltage \(V_\textrm{i}\) and the output current detected on the outer electrode \(I_\textrm{o}\) is essentially determined by the impedance analysis of the lumped parameter circuit shown in Fig. 1b. Because the areas of the inner and outer electrodes of the top electrode assembly are equal, the capacitors in the diagram are symmetric. First, when we connect an AC voltage source between terminals 1 and 2 and a current meter between terminals 3 and 4 shown in Fig. 1b to measure \(I_\textrm{o}\), terminals 3 and 4 are effectively shunted. The relationship between the current I flowing through resistor R and the detected current \(I_\textrm{o}\) is expressed as \(I=I_\textrm{o}(1+C_1/C_0)\). The maximum velocity v of ions is obtained by dividing the current density \(I/2\pi r_\textrm{i}\) by the ion charge density ne, where e is the elementary charge, so that it is given straightforwardly from the detected current \(I_\textrm{o}\) by

$$v=I_\textrm{o}\left( 1+\frac{C_1}{C_0}\right) \frac{1}{2\pi r_\textrm{i}ne}.$$

Here, \(C_0\) (\(C_1\)) may be regarded as the capacitance per unit area between the ion pool and the top (bottom) electrode.

Fig. 2
figure 2

(Color online). a Resonance curves of plasmon of ion pool of positive ions at different temperatures. b Temperature dependence of positive ion mobility under the free surface of isotopically pure superfluid \(^4\)He. Solid circles indicate the mobility determined by impedance analysis, whereas open circles indicate the mobility obtained from plasmon damping. Above 0.5 K, the mobility is predominated by roton scattering, and below 0.5 K, phonons predominate over rotons. At the lowest temperature region below \({\sim }\)200 mK, ripplons reveal themselves

Full size image

To determine the mobility of ions in a pool, we need to conduct impedance analysis on the basis of either the lumped parameter circuit

$$\frac{I_\textrm{o}}{V_\textrm{i}}=i\omega {}C_0\frac{C_0}{C_0+C_1}\frac{1}{2+i\omega (C_0+C_1)R}$$

or the 2D transmission line model [64,65,66]. When the mobility is very high so that \(i\omega (C_0+C_1)R\ll {}1\), the output current \(I_\textrm{o}\) is insensitive to R. Under such conditions, the line width or damping \(\tau ^{-1}\) of plasma resonance, as shown in Fig. 2a, and the expression for the mobility \(\mu =e\tau /m\) should be used to determine the positive ion mobility, where m is the positive ion mass. As shown in Fig. 2b, the observed mobility of positive ions agrees with that obtained by Barenghi et al. in isotopically pure \(^4\)He [25] and is considerably higher below 300 mK than that in the natural \(^4\)He containing 200 ppb \(^3\)He impurity. Our measurement is performed in isotopically pure \(^4\)He with less than 1 ppb \(^3\)He.

3 Results and Discussion

3.1 Critical Velocity and Single Vortex Nucleation

Fig. 3
figure 3

(Color online). Positive ion velocity as a function of driving voltage measured for \(z_\textrm{i}=37.6\) nm. Downward and upward arrows correspond to the upward and downward sweeps of \(V_\textrm{ac}\), respectively. Horizontal arrows indicate the critical velocity, \(v_\textrm{c}\). Note that the slope of the velocity against \(V_\textrm{ac}\) does not reflect the mobility of ions because the current is limited by the capacitance between the ion sheet and the electrodes

Full size image

Figure 3 shows the maximum velocity of positive ions as a function of \(V_\textrm{ac}\) at several temperatures measured at a positive ion depth of 37.6 nm. In this measurement, \(I_\textrm{o}\) is recorded over increasing or decreasing \(V_\textrm{ac}\) in fine steps at intervals of 20 s. At a low \(V_\textrm{ac}\), the velocity increases proportionally to \(V_\textrm{ac}\). In this low-velocity regime, the superfluid flow around the ions exhibits a pure potential flow and the drag force is only due to scattering predominantly by thermally excited rotons, phonons, and surface capillary waves (ripplons), depending on the temperature range as shown in Fig. 2b; these observations are in agreement with the previous study by Barenghi et al. [25]. At a higher \(V_\textrm{ac}\), the velocity shows an abrupt drop at \(18-32\) ms\(^{-1}\). This threshold velocity increases with temperature. We attribute the drop to a large drag force generated by the formation of a vortex loop on the positive ions. This attribution is not only based on the previous studies [45,46,47], but it is also a common understanding in superfluid hydrodynamics. The phenomenon involves the transition from the nondissipative to a dissipative flow regime in superfluid \(^4\)He, which is referred to as quantum turbulence, for which Vinen has long led the field [67]. This is not due to the emission of rotons by the moving ions because roton emission occurs at a much higher velocity around the Landau critical velocity (\({\sim }57\) ms\(^{-1}\) at SVP), and the velocity is merely expected to saturate [68]. When \(V_\textrm{ac}\) decreases to a smaller \(V_\textrm{ac}\), it again restores a linear behavior.

The hysteretic behavior strongly suggests that the nucleated vortex loop evolves into a vortex tangle. The loop is stretched by the moving ion and the vortex lines repeatedly reconnect. The hysteretic behavior indicates that the lifetime of the tangle state should be sufficiently longer than the period of ac excitation. The hysteretic behavior is similar to the transition between the laminar and turbulent states developing from remnant vortices observed for oscillating macroscopic objects [69,70,71]. As discussed below, however, the critical velocity is too high to be explained by the remnant vortices. When the velocity of nucleated vortex loop is different from the instant velocity of positive ion, then the loop is stretched and develops into the turbulence [71, 72]. While reducing the driving voltage, the transition from the turbulent flow to the laminar flow occurs at a velocity lower than \(v_\textrm{c}\), giving rise to the hysteretic behavior.

Hence, we attribute the observed \(v_\textrm{c}\) to the nucleation event of the quantized vortex loop attached to the positive ion. We may exclude the remnant vortex from the origin of \(v_\textrm{c}\) by the following argument. If it originates from the remnant vortices, which bridge between ions and experimental cell walls, the Glaberson–Donnelly instability critical velocity may be the origin of \(v_\textrm{c}\) [73]. However, according to the Glaberson–Donnelly instability critical velocity, \(v_\textrm{c}=(\kappa /2\pi {}l_\textrm{v})[\ln (4l_\textrm{v}/\textrm{a})-1/4]\), the estimated vortex length \(l_\textrm{v}\) is on the order of nm. Here, \(\kappa\) and a are the quantized circulation and core radius of the vortex of \({\sim }0.1\) nm, respectively. This length scale is very small compared with any characteristic length of the experimental cell. This observation strongly suggests that the nucleation is associated with the superfluid flow only in the vicinity of each positive ion. The present experimental observations are reproduced after recharging positive ions or refilling liquid \(^4\)He, also strongly suggesting that the observed phenomena are not associated with the remnant vortices. Hereafter, we focus on the threshold velocity \(v_\textrm{c}\) on increasing \(V_\textrm{ac}\).

3.2 Smallness of the Applied Electric Field

Fig. 4
figure 4

(Color online). Positive ion drift velocity \(v_{\text{d}}\) below \(v_\textrm{c}\) as a function of the driving electric field E for \(z_\textrm{i}=37.6\) nm. The electric field is obtained from the mobility \(\mu\) and \(v_{\text{d}}\) as \(E=v_{\text{d}}/\mu\). As for the data at \(T<350\) mK, \(\mu\) is determined by the plasmon damping, which corresponds to the linear-regime value. The behavior is almost linear up to \(v_\textrm{c}\). At \(T\ge {}350\) mK, \(\mu\) is determined for each data point, and the drift velocity tends to level off before reaching \(v_\textrm{c}\)

Full size image

Note that the smallness of the critical electric field \(E_\textrm{c}\) as low as \(10^{-2}\) Vm\(^{-1}\) reported here has so far never been reached. This value is extremely lower than those obtained in previous studies, which were typically \({>}100\) Vm\(^{-1}\) [55,56,57, 74,75,76,77]. The electric field applied to the positive ion can be estimated from the independently measured mobility. The electric field is given by \(E=v_{\text{d}}/\mu\), where \(v_{\text{d}}\) is the drift velocity of the positive ion and \(\mu\) is the mobility. Figure 4 shows the drift velocity \(v_{\text{d}}\) of the positive ion against the applied electric field only below \(v_\textrm{c}\). Below 350 mK, the mobility is determined by plasmon damping, which corresponds to the ohmic-regime value. As for the data at \(T\ge {}350\) mK, \(\mu\) is determined for each data point, and the drift velocity tends to level off before reaching \(v_\textrm{c}\). With our present method, lower driving electric fields of even \(<10^{-2}\) Vm\(^{-1}\) are possible. This advantage makes it possible to accurately measure \(v_\textrm{c}\) at low temperatures (\(T\le {}500\) mK) in isotopically pure liquid \(^4\)He.

3.3 Nonlinear Plasma Resonance and Present Observation

Here, we comment on the pronounced nonlinearity and velocity jump observed in plasma resonance curves. This nonlinearity was experimentally studied by Ott-Rawland et al. [16]. At a sufficiently high amplitude of plasma oscillation, the nonlinear term of plasma motion, \((\textbf{v}\cdot \nabla )\textbf{v}\), cannot be neglected. Therefore, the resonance curve behaves similarly to the so-called Duffing oscillator, showing an amplitude jump and hysteresis. Figure 5 shows such resonance curves measured at 70 and 100 mK. The driving ac voltage is fixed and the frequency is swept. The trace at 100 mK shows typical characteristics of the Duffing oscillator. On the other hand, at 70 mK, the positive ion velocity is higher than that at 100 mK because of the mobility increase at lower temperatures, and we observed further drop of the positive ion velocity, as indicated by the arrow in Fig. 5, where the velocity is around \({\sim }17\) m/s. This value corresponds to the \(v_\textrm{c}\) observed in the off-resonant measurement, as shown in Fig. 3; hence, we attribute this to vortex nucleation. This kind of phenomenon was mentioned by Barenghi et al. as a possible explanation for the loss of electron bubbles above a certain critical velocity [23]. From our observation, however, we conclude that although such a phenomenon certainly exists, it may not be an adequate explanation for the ion loss mechanism because we observed no charge loss for positive ions.

Fig. 5
figure 5

(Color online). Nonlinear behavior of the plasma resonance of the positive ion pool in natural \(^4\)He at 100 mK and 70 mK at an ion depth of 37.6 nm. The ac driving voltage is 1 mV\(_{\textrm{pp}}\). The anomaly indicated by the arrow is ascribed to the same critical velocity shown in Fig. 3

Full size image

3.4 Temperature Dependence of Critical Velocity

The critical velocity \(v_\textrm{c}\) shown in Fig. 3 shows a stochastic behavior, \(v_\textrm{c}\) varies from one \(V_\textrm{ac}\) sweep to another. This observation is in accordance with the vortex nucleation process. Vortex nucleation occurs when a potential barrier is overcome either by thermal activation or quantum tunneling, which is stochastic in nature. Data analysis requires a probabilistic treatment. Varoquaux and Avenel carefully analyzed their vortex nucleation data [78]. They observed single vortex nucleation events using a flow through a microaperture, the characteristic length of which was about 1 \(\mu\)m, and they obtained a critical velocity of about 6 ms\(^{-1}\). Although the magnitude of the critical velocity and the characteristic length of the system are different from those in the microaperture experiment, we analyzed our data by using their formulae because the sinusoidal temporal variation of flow velocity and the sweep of flow velocity are common. According to Eqs. (30) and (31) in Ref. [78], we employ the following fitting function:

$$\begin{aligned} P(v)=1-\exp \left[ -\ln {}2\,\exp \left( \frac{2(v-v_\textrm{c})}{\Delta v_\textrm{c} \ln {}2}\right) \right] . \end{aligned}$$
(1)

Here, \(v_\textrm{c}\) and \(\Delta {}v_\textrm{c}=(\partial {}P/\partial {}v)\vert _{v=v_\textrm{c}}^{-1}\) are the fitting parameters. The function P(v) is a cumulative probability to observe a nucleation event below a certain positive ion velocity v. Since the positive ion velocity increases stepwise by about 0.14 ms\(^{-1}\) with a waiting time of 20 s, the obtained \(v_\textrm{c}\) may be smaller than the true value by about 0.3 ms\(^{-1}\). However, here we neglect this difference for simplicity. Figure 6 shows an example of such a fitting.

Fig. 6
figure 6

(Color online). Cumulative probability distribution to observe a vortex nucleation event below a certain value of positive ion velocity. The solid line is the fitting result with Eq. (1). Data are for the positive ion pool trapped 37.2 nm below the surface and at \(T=200\) mK

Full size image

The temperature dependences of \(v_\textrm{c}\) and \(\Delta {}v_\textrm{c}\) are summarized in Fig. 7. The error bars show the standard deviation resulting from the fitting. As for \(\Delta {}v_\textrm{c}\), the data scatter and some points have large error bars. This is because of insufficient statistical data points. Nevertheless, we briefly discuss the origin of \(\Delta {}v_\textrm{c}\) here. \(\Delta {}v_\textrm{c}\) corresponds to the full width of the probability density function. In the maximum-velocity region (\(r_\textrm{i}=6.3\) mm, width \(={\sim }1\) mm), there are \(N_{max}\) (\(\sim {}2.6\times {}10^{7}\)) positive ions. If the observed \(\Delta {}v_\textrm{c}\) on the order of 1 ms\(^{-1}\) reflects the width of the probability distribution of average quantity of \(N_{\max }\) particles, the ions in the maximum-velocity region should have an unreasonably large distribution of \(v_\textrm{c}\) according to the law of large numbers (\(\sim \Delta {}v_\textrm{c}\sqrt{N_{\max }}\)). Therefore, it seems that the velocity drop event that we observed originates from a single nucleation event, and then it is amplified by the evolution of the vortex line by an oscillating object [79]. In the present experiment, roughly at \(v_\textrm{c}\), the probability to encounter the event in 20 s for \(N_{max}\) sites is 0.5; hence, the nucleation rate should be on the order of \(1\times {}10^{-9}\) s\(^{-1}\). The critical velocity \(v_\textrm{c}\) should depend on the positive ion density if the present argument is correct. The statistical properties should be verified by systematic studies on the positive ion density dependence.

Fig. 7
figure 7

(Color online). a Temperature dependence of the critical velocity \(v_\textrm{c}\). The error bar is smaller than the symbol size. b Temperature dependence of the width of critical velocity \(\Delta {}v_\textrm{c}\). Data are for the positive ion pool trapped at a depth of 37.6 nm

Full size image

The prominent properties in the temperature dependence of the critical velocity are the leveling off of the critical velocity below 250 mK and the obvious increase in critical velocity as a function of temperature. These trends of \(v_\textrm{c}\) imply that the vortex nucleation rate decreases as a function of temperature since the energy barrier for the vortex nucleation decreases as a function of flow velocity, that is, the vortex nucleation is suppressed by increasing temperature. It opposes a thermal activation process, suggesting quantum tunneling nucleation of quantized vortices. Although we were not able to measure \(v_\textrm{c}\) above 500 mK, previous studies suggest a decrease in critical velocity in the higher-temperature region [75]. This aspect should be investigated in the future.

This type of temperature dependence, that is, the suppression of nucleation by increasing temperature, was observed in previous studies, for example, in the decay of metastable states in a \(^3\)He–\(^4\)He liquid mixture at ultralow temperatures studied by Satoh et al. [80]. They argued for the critical supersaturation below 10 mK by mentioning quantum tunneling, but they provided no specific nor conclusive mechanism that explains the increase of the supersaturation above 10 mK. In a microaperture experiment [78], a similar temperature dependence of the vortex nucleation rate was also observed, although the signature was much weaker than that in the present work. The interpretation of the dip in the nucleation rate was based on the CL theory extended for finite temperatures, that is, Eq. (7) in Ref. [78]. However, this formula is for the case of weak ohmic damping in the CL theory, and the temperature effect is to increase the rate. To interpret the dip, it was necessary to assume the originally positive constant \(\alpha\) associated with the dissipation to be negative. Hendry et al. reported a very similar temperature dependence of the vortex nucleation rate to our present observation at pressures higher than 15 bars [54]. They argued that the reduction in the nucleation rate is due to the reduction in the tunneling rate caused by phonon scattering, intuitively shown by Muirhead et al. [50]. Under the experimental conditions of Ref. [54], however, rotons were intentionally excited to reduce the ion velocity, and the system might be in strongly non-equilibrium. In a system other than helium, a similar temperature dependence was also observed. For example, Rall et al. observed a similar temperature dependence in the nuclear spin–spin relaxation time of HD impurities in solid hydrogen [81]. The relaxation time is controlled by the motion of impurities, in which vacancies play an essential role. All these processes involve three energy scales, the creation energy of vacancies and two energy barriers for the vacancy and impurity motion. The dip in the temperature dependence of relaxation time is interpreted by the interplay among competing thermal activation processes in addition to constant quantum tunneling contributions at \(T=0\). In all the above-mentioned studies, the temperature-independent rate is due to quantum tunneling. The appearance of the dip in the temperature dependence of the rate, on the other hand, remains as issue.

As for the present observations, one may think of the following two different processes: the nucleation of quantized vortices and the detrapping of ions from quantized vortices. On the basis of a previous study [82], the depth of trapping potential for a positive ion by the vortex core is estimated as about \(-17\) K and the width is on the order of the ion size. Therefore, the positive ion is immediately trapped by the nucleated vortex. The trapped ion can escape from the vortex by thermal agitation. According to previous studies, however, the half-life of trapped ions below 0.5 K is much longer than 1 s [83,84,85]. Therefore, in our present temperature range, such an escape event is negligible, and we need an intrinsic interpretation for the temperature dependence based on only the nucleation process.

To interpret our observation, we try to present an argument on the basis of the CL theory of macroscopic quantum coherence at finite temperatures [60]. The environment in isotopically pure superfluid \(^4\)He is simple and well defined. The internal degree of freedom of a positive ion can be neglected. The lowest vibration frequency of solid helium of the size of the positive ion is given by \(C_\textrm{t}\pi /R_0\), where \(C_\textrm{t}\) is the transverse phonon speed and \(R_0\) is the positive ion radius (\({\sim }0.6\) nm). \(C_\textrm{t}\) can be as low as 75 ms\(^{-1}\) [86], and then the corresponding vibration frequency is \({\sim }4\times {}10^{11}\) s\(^{-1}\). In the presence of electrostriction, the positive ion is harder than a bulk solid helium, and the corresponding frequency is even higher. Since this frequency is much higher than that corresponding to our experimental temperature, the internal degree of freedom of the positive ion can be safely neglected. Then, we only have a superfluid condensate and elementary excitations, phonons, rotons, and, in our case, maybe also ripplons. There are no solid walls near the positive ion, so that no bulk excitation has to be considered. Since the positive ion is a kind of defect in this system, we may consider quasilocalized phonons in addition to bulk elementary excitations, if necessary [87]. As a result, we have only one energy barrier for the vortex nucleation and the field of quasiparticles as the environment. First, note that our process of vortex nucleation by the positive ion very much resembles the case of defect (or electron) tunneling in a solid with coupling to a (three-dimensional) acoustic phonon bath. In the CL theory, this case is categorized into the “superohmic” case [60].

Leggett et al. [60] dealt with the two-state system described by the tunneling in a double-well potential. The strength of the tunneling is represented by the energy level splitting \(\hbar \Delta\) between the symmetric and asymmetric states. We naively expect that the quantum nucleation rate in our case is proportional to \(\Delta\). As for the superohmic case, the level splitting renormalized by the environment is given by Eq. (6.35) in Ref. [60]

$$\tilde{\Delta }(\beta )=\Delta \exp \left[ -A\int _0^{\infty }\frac{d\omega }{\omega ^2}J(\omega ) \coth \frac{\beta \hbar \omega }{2}\right] ,$$

where \(\beta =1/k{_\textrm{B}}T\), A is a positive constant, and \(J(\omega )\) is the spectral density, which is proportional to \(\omega ^s\) with \(s>2\) for small \(\omega\) and decays to zero at large \(\omega\). In the limit of \(x\rightarrow \infty\), the \(\coth (x)\) function approaches unity to give the level splitting that is suppressed by the environment at \(T=0\). With increase in temperature, \(\coth (\beta \hbar \omega /2)\) increases and the formula results in further suppression of level splitting, implying the suppression of tunneling rate. At further higher temperatures, the formula should eventually merge into the thermal activation regime; hence, the rate shows the dip around the crossover temperature between the quantum and classical regimes. In our case, this dip corresponds to the maximum critical velocity. Accordingly, our observation can be naturally adopted to the CL theory, although a quantitative verification is required. Further theoretical development is desired to quantitatively compare the theoretical results with the experimental data. In addition, for further discussion, we might need more statistics, particularly for \(\Delta {}v_\textrm{c}\).

Note that the previous observation of optical absorption spectra of a zero phonon line (ZPL) of a Dy atom embedded in superfluid helium [12] showed that the line width of ZPL is much larger than that in vacuum and increases with temperature. The temperature dependence is qualitatively interpreted as the phase decoherence caused by the bombardment of phonons and rotons. The optical transition has a much higher energy scale than ambient temperature, and the CL theory is not adequate in this case. However, there seem to be many similarities between these different phenomena.

4 Conclusions

We observed the critical velocity \(v_\textrm{c}\) of the 2D positive ion system below isotopically pure superfluid \(^4\)He by transport measurements. The critical velocity \(v_\textrm{c}\) is well defined by the jump of the positive ion velocity caused by the drag force generated by quantized vortex nucleation. We successfully determined in detail the temperature dependence of \(v_\textrm{c}\) down to very low temperatures, where the nucleation is due to macroscopic quantum tunneling. For such measurements, an electric field of less than 0.01 V/m is essential, which is three orders of magnitude smaller than those used in previous measurements by the TOF method. The stochastic nature of \(v_\textrm{c}\) is discussed on the basis of the statistical model presented by Varoquaux and Avenel [78]. We argued that the temperature dependence of \(v_\textrm{c}\) can be qualitatively interpreted by the standard theory of quantum friction by Caldeira and Leggett, assuming the superohmic case [60].

The present experimental technique used to determine the critical velocity for the nucleation of quantized vortices is versatile. The positive ion velocity can be directly controlled by setting the appropriate external experimental condition. We can keep the velocity constant as long as possible, which enables us to wait until the nucleation event occurs. By doing so, we can directly obtain the nucleation rate. The rate is more straightforward to be compared with theoretical results. By controlling the frequency, amplitude, \(V_\textrm{ac}\) waveform, positive ion density, positive ion pool shape, and so on, we can carry out various unique measurements in the future. Our environment is well defined and, particularly for ripplons, the coupling to the positive ion system is tunable. However, in Fig. 7, data only at a depth of 37.6 nm are presented, because at the other depths, a number of data points are not sufficient to draw a conclusion. Hence, detailed verifications of theoretical predictions in the future are particularly interesting.

5 Dedication to Joe Vinen

In addition to the present study, we collaborated with Joe Vinen on many other aspects of low-temperature helium physics. His work on the nonlinear transport of the Wigner solid on a He surface [88] yielded particularly fruitful outcomes [65, 66, 89,90,91,92]. He also inspired us to perform ion pool experiments in superfluid \(^3\)He [93,94,95,96,97]. We have benefited greatly from the collaboration with Joe, which brought many good memories.