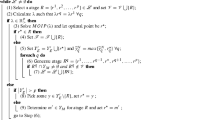Skip to main content
SpringerLink
Log in

On the hierarchical structure of Pareto critical sets

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

In this article we show that the boundary of the Pareto critical set of an unconstrained multiobjective optimization problem (MOP) consists of Pareto critical points of subproblems where only a subset of the set of objective functions is taken into account. If the Pareto critical set is completely described by its boundary (e.g., if we have more objective functions than dimensions in decision space), then this can be used to efficiently solve the MOP by solving a number of MOPs with fewer objective functions. If this is not the case, the results can still give insight into the structure of the Pareto critical set.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Brockhoff, D., Zitzler, E.: Objective reduction in evolutionary multiobjective optimization: theory and applications. Evolut. Comput. 17(2), 135–166 (2009)

    Article  Google Scholar 

  2. De Melo, W.: On the structure of the Pareto set of generic mappings. Bull. Braz. Math. Soc. 7(2), 121–126 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  3. Degiovanni, M., Lucchetti, R., Ribarska, N.: Critical point theory for vector valued functions. J. Convex Anal. 9, 415–428 (2002)

    MathSciNet  MATH  Google Scholar 

  4. Dellnitz, M., Schütze, O., Hestermeyer, T.: Covering pareto sets by multilevel subdivision techniques. J. Optim. Theory Appl. 124(1), 113–136 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  5. di Pierro, F., Khu, S.T., Savic, D.A.: An investigation on preference order ranking scheme for multiobjective evolutionary optimization. IEEE Trans. Evolut. Comput. 11(1), 17–45 (2007)

    Article  Google Scholar 

  6. Ehrgott, M.: Multicriteria Optimization. Springer, Berlin (2005)

    MATH  Google Scholar 

  7. Enrico, M., Elena, M., Matteo, R.: A Morse-type index for critical points of vector functions. Economics and quantitative methods, Department of Economics, University of Insubria (2007). URL https://EconPapers.repec.org/RePEc:ins:quaeco:qf0702. Accessed 9 Jan 2019

  8. Giorgi, G., Guerraggio, A.: On the notion of tangent cone in mathematical programming. Optimization 25(1), 11–23 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hillermeier, C.: Nonlinear Multiobjective Optimization: A Generalized Homotopy Approach. Springer, Birkhäuser, Basel (2001)

    Book  MATH  Google Scholar 

  10. Ishibuchi, H., Tsukamoto, N., Nojima, Y.: Evolutionary many-objective optimization: a short review. In: Proceedings of the 2008 IEEE Congress on Evolutionary Computation, pp. 2419–2426 (2008)

  11. Kuhn, H.W., Tucker, A.W.: Nonlinear programming. In: Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, pp. 481–492. University of California Press, Berkeley (1951)

  12. Lange, K.: Optimization, 2nd edn. Springer, New York (2013)

    Book  MATH  Google Scholar 

  13. Lee, J.: Introduction to Smooth Manifolds. Springer, New York (2012)

    Book  Google Scholar 

  14. López Jaimes, A., Coello Coello, C.A., Chakraborty, D.: Objective reduction using a feature selection technique. In: Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, GECCO ’08, pp. 673–680. ACM (2008)

  15. Lovison, A.: Singular continuation: generating piecewise linear approximations to pareto sets via global analysis. SIAM J. Optim. 21(2), 463–490 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lovison, A., Pecci, F.: Hierarchical Stratification of Pareto Sets. arXiv:1407.1755 (2014)

  17. Lowe, T.J., Thisse, J.F., Ward, J.E., Wendell, R.E.: On efficient solutions to multiple objective mathematical programs. Manag. Sci. 30, 1346–1349 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  18. Malivert, C., Boissard, N.: Structure of efficient sets for strictly quasi convex objectives. J. Convex Anal. 1(2), 143–150 (1994)

    MathSciNet  MATH  Google Scholar 

  19. Miettinen, K.: Nonlinear Multiobjective Optimization. Springer, New York (1998)

    Book  MATH  Google Scholar 

  20. Miglierina, E., Molho, E., Rocca, M.: Critical points index for vector functions and vector optimization. J. Optim. Theory Appl. 138(3), 479–496 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  21. Mueller-Gritschneder, D., Graeb, H., Schlichtmann, U.: A successive approach to compute the bounded pareto front of practical multiobjective optimization problems. SIAM J. Optim. 20(2), 915–934 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  22. Peitz, S.: Exploiting structure in multiobjective optimization and optimal control. In: Ph.D. Thesis, Paderborn University, Paderborn(2017)

  23. Popovici, N.: Pareto reducible multicriteria optimization problems. Optimization 54(3), 253–263 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  24. Saxena, D.K., Duro, J.A., Tiwari, A., Deb, K., Zhang, Q.: Objective reduction in many-objective optimization: linear and nonlinear algorithms. IEEE Trans. Evolut. Comput. 17(1), 77–99 (2013)

    Article  Google Scholar 

  25. Schütze, O., Lara, A., Coello Coello, C.A.: On the influence of the number of objectives on the hardness of a multiobjective optimization problem. IEEE Trans. Evolut. Comput. 15(4), 444–455 (2011)

    Article  Google Scholar 

  26. Shoval, O., Sheftel, H., Shinar, G., Hart, Y., Ramote, O., Mayo, A., Dekel, E., Kavanagh, K., Alon, U.: Evolutionary trade-offs, pareto optimality, and the geometry of phenotype space. Science 336(6085), 1157–1160 (2012)

    Article  Google Scholar 

  27. Singh, H.K., Isaacs, A., Ray, T.: A pareto corner search evolutionary algorithm and dimensionality reduction in many-objective optimization problems. IEEE Trans. Evolut. Comput. 15(4), 539–556 (2011)

    Article  Google Scholar 

  28. Smale, S.: Global analysis and economics I: Pareto optimum and a generalization of Morse theory. In: Dynamical Systems, pp. 531–544. Academic Press, Cambridge (1973)

  29. Smale, S.: Optimizing several functions. In: Proceedings of International Conference on Manifolds and Related Topics in Topology, pp. 69–75. University of Tokyo, Tokyo (1975)

  30. Sun, J.Q., Xiong, F.R., Schütze, O., Hernández, C.: Cell Mapping Methods. Springer, New York (2018)

    MATH  Google Scholar 

  31. Wan, Y.: Morse theory for two functions. Topology 14(3), 217–228 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  32. Witting, K.: Numerical algorithms for the treatment of parametric multiobjective optimization problems and applications. In: Ph.D. Thesis, Paderborn University, Paderborn (2012)

Download references

Acknowledgements

This research was funded by the DFG Priority Programme 1962 ”Non-smooth and Com-plementarity-based Distributed Parameter Systems”.

Author information

Authors and Affiliations

  1. Chair of Applied Mathematics, Paderborn University, Warburger Str. 100, 33098, Paderborn, Germany

    Bennet Gebken, Sebastian Peitz & Michael Dellnitz

Authors
  1. Bennet Gebken
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sebastian Peitz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Michael Dellnitz
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bennet Gebken.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gebken, B., Peitz, S. & Dellnitz, M. On the hierarchical structure of Pareto critical sets. J Glob Optim 73, 891–913 (2019). https://doi.org/10.1007/s10898-019-00737-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10898-019-00737-6

Keywords

Search

Navigation