Skip to main content
SpringerLink
Log in

The Geometry of the Solution Set of Nonlinear Optimal Control Problems

  • Published:
Journal of Dynamics and Differential Equations Aims and scope Submit manuscript

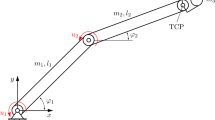
In an optimal control problem one seeks a time-varying input to a dynamical systems in order to stabilize a given target trajectory, such that a particular cost function is minimized. That is, for any initial condition, one tries to find a control that drives the point to this target trajectory in the cheapest way. We consider the inverted pendulum on a moving cart as an ideal example to investigate the solution structure of a nonlinear optimal control problem. Since the dimension of the pendulum system is small, it is possible to use illustrations that enhance the understanding of the geometry of the solution set. We are interested in the value function, that is, the optimal cost associated with each initial condition, as well as the control input that achieves this optimum. We consider different representations of the value function by including both globally and locally optimal solutions. Via Pontryagin’s maximum principle, we can relate the optimal control inputs to trajectories on the smooth stable manifold of a Hamiltonian system. By combining the results we can make some firm statements regarding the existence and smoothness of the solution set.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bardi M., Capuzzo-Dolcetta I. (1997). Optimal Control and Viscosity Solugions of Hamilton Jacobi Bellman Equations. Birkhäuser, Boston

    Google Scholar 

  2. Buttazzo G., Giaquinta M., Hildebrandt S. (1998). One-Dimensional Variational Problems. Oxford University Press, New York

    MATH  Google Scholar 

  3. Cesari L. (1983). Optimization – Theory and Applications: Problems with Ordinary Differential Equations. Springer-Verlag, New York

    Google Scholar 

  4. Dacorogna B. (1989). Direct Methods in the Calculus of Variations. Springer-Verlag, New York

    MATH  Google Scholar 

  5. Day M.V. (1998). On Lagrange manifolds and viscosity solutions. J. Math. Syst, Estimation Control 8(3): 369–372

    MATH  MathSciNet  Google Scholar 

  6. Hauser, J., and Osinga, H. M. (2001). On the geometry of optimal control: the inverted pendulum example. In Proceedings Amer. Control Conference, Arlington VA, pp. 1721–1726.

  7. Jadbabaie, A., Yu, J., and Hauser, J. (1999). Unconstrained receding horizon control: Stability region of attraction results. In Proceedings Conference on Decision and Control, No. CDC99-REG0545, Phoenix, AZ.

  8. Jadbabaie A., Yu J., Hauser J. (2001). Unconstrained receding horizon control of nonlinear systems. IEEE Trans. Autom. Control 46(5): 776–783

    Article  MATH  MathSciNet  Google Scholar 

  9. Krauskopf B., Osinga H.M. (2003). Computing geodesic level sets on global (un)stable manifolds of vector fields. SIAM J. Appl. Dyn. Syst. 2(4): 546–569

    Article  MATH  MathSciNet  Google Scholar 

  10. Krauskopf B., Osinga H.M., Doedel E.J., Henderson M.E., Guckenheimer J., Vladimirsky A., Dellnitz M., Junge O. (2005). A survey of methods for computing (un)stable manifolds of vector fields. Int. J. Bifurcation Chaos 15(3): 763–791

    Article  MATH  MathSciNet  Google Scholar 

  11. Lee E.B., Markus L. (1967). Optimization – Theory and Applications: Problems with Ordinary Differential Equations. Wiley, New York

    Google Scholar 

  12. Lukes D.L. (1969). Optimal regulation of nonlinear dynamical systems. SIAM J. Control 7(1): 75–100

    Article  MATH  MathSciNet  Google Scholar 

  13. Malisoff M. (2002). Viscosity solutions of the Bellman equation for exit time optimal control problems with vanishing Lagrangians. SIAM J. Control Optim. 40(5): 1358–1383

    Article  MATH  MathSciNet  Google Scholar 

  14. Malisoff M. (2003). Further results on the Bellman equation for optimal control problems with exit times and nonnegative Lagrangians. Syst. & Control Lett. 50, 65–79

    Article  MathSciNet  Google Scholar 

  15. Malisoff M. (2004). Bounded-from-below solutions of the Hamilton-Jacobi equation for optimal control problems with exit times: vanishing Lagrangians, eikonal equations, and shape-from-shading. Nonlinear Diff. Eq. Appl. 11(1): 95–122

    Article  MATH  MathSciNet  Google Scholar 

  16. Osinga H. M., and Hauser, J. (2005). Multimedia supplement with this paper; available at http://www.enm.bris.ac.uk/anm/preprints/2005r28.html.

  17. Palis J., de Melo W. (1982). Geometric Theory of Dynamical Systems. Springer-Verlag, New York

    MATH  Google Scholar 

  18. Pontryagin L.S., Boltyanski V.G., Gamkrelidze R.V., Mischenko E.F. (1962). The Mathematical Theory of Optimal Processes. Wiley, New York

    Google Scholar 

  19. Van der Schaft A.J. (2000). L 2-Gain and Passivity Techniques in Nonlinear Control. 2nd edn. Springer-Verlag, New York

    MATH  Google Scholar 

  20. Sontag E.D. (1998). Mathematical Control Theory: Deterministic Finite Dimensional Systems, 2nd edn. Texts in Applied Mathematics 6, Springer-Verlag, New York

    Google Scholar 

  21. Sussmann H.J., Willems J.C. (1997). 300 years of optimal control: From the brachystochrone to the maximum principle. IEEE Control Syst. Maga. 17(3): 32–44

    Article  Google Scholar 

  22. Sussmann H.J. (1998). Geometry and optimal control. In: Baillieul J., Willems J.C. (eds). Mathematical Control Theory. Springer-Verlag, New York, pp. 140–198

    Google Scholar 

  23. Zelikin M.I., Borisov V.F. (1994). Theory of Chattering Control with Applications to Astronautics, Robotcs, Economics, and Engineering. Birkhäuser, Boston

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Engineering Mathematics, University of Bristol, Bristol, BS8 1TR, UK

    Hinke M. Osinga

  2. Department of Electrical and Computer Engineering, University of Colorado at Boulder, Boulder, CO, 80309-0425, USA

    John Hauser

Authors
  1. Hinke M. Osinga
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. John Hauser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hinke M. Osinga.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Osinga, H.M., Hauser, J. The Geometry of the Solution Set of Nonlinear Optimal Control Problems. J Dyn Diff Equat 18, 881–900 (2006). https://doi.org/10.1007/s10884-006-9051-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10884-006-9051-0

Keywords

AMS Subject Classifications

Search

Navigation