Abstract
A semiorganic nonlinear optical (NLO) single crystal of bis(thiourea) manganese chloride (BTMC) is grown successfully by slow cooling technique using water as solvent at temperature 45 °C. The optically good quality crystal of BTMC was grown with dimension up to 8 × 8 × 2 mm3 in a period of 2–3 weeks. The grown crystal crystallizes in orthorhombic crystal system which was confirmed by single crystal X-ray diffraction analysis. The various functional groups of BTMC were identified through FT-IR spectroscopic analysis. The lower cut-off wavelength of 280 nm was revealed from optical transmittance spectrum of UV. The mechanical behavior of BTMC crystal was analyzed by Vicker’s microhardness study and also the various mechanical parameters were determined. Vickers micro hardness test revealed, the titular crystal belongs to harder material category. The SHG efficiency is estimated from Kurtz-Perry powder method and it found to be 0.33 times than the reference material. The dielectric behavior, photo conducting nature and surface properties have been analyzed for grown BTMC crystal. The presence of synthesized elements was confirmed by EDAX study. The third order nonlinear optical susceptibility \(\chi^{\left(3 \right)}\) of the material is measured using Z-scan technique and it is found to be 5.1202 × 10−14 esu.
Similar content being viewed by others
1 Introduction
Nowadays, nonlinear optical (NLO) single crystals are focusing by modern technology like electronic industry, photonic industry and fiber optical communication because of their capable for frequency conversion [1]. Single crystals are in solid form with highly periodic arrangement of atoms which allow the transmission of light without any scattering. Hence, single crystals with perfection are acting a major role in recent science and technology applications.
Material researches are given more concentration on the materials which are exhibiting large NLO property with higher stability. Choosing of material not only depends on lasing condition but also on conversion efficiency, transparency and mechanical stability. The materials have been synthesis and formed as inorganic, organic and semi-organic NLO materials. Generally, organic crystals possess high optical nonlinearity but poor mechanical strength, thermal stability and low laser damage threshold whereas an inorganic possess better mechanical strength and high thermal stability although they show relatively low nonlinearity due to the shortfall of extended π-electron delocalization [2].The problems can be overcome by new type of compound called semiorganic. Literature elucidate that semiorganic material shows the properties of high non-linearity of organics with better mechanical and thermal stability of the inorganic [3,4,5,6,7,8,9,10,11]. Hence, semi-organic materials are made an attention by material researchers. Particularly thiourea based semiorganic NLO crystals possess high SHG efficiency which was got from recently reported semi-organic materials. [12,13,14,15,16]. Thiourea (NH2CSNH2) based crystals are capable for frequency doubling because thiourea molecule is an attractive inorganic matrix converter with large dipole moment which able to form an extensive network of hydrogen bonds. The reality of reaction is that the centrosymmetric thiourea molecule mixed with inorganic salt yield non-centrosymmetric complex which is the key factor for NLO properties [17,18,19]. Metal complex of thiourea have low UV cutoff wavelength hence they have obtained great attention in the field of optical storage industry. Literature pointed out that the significant of thiourea based semiorganic compounds owing to their high NLO properties. In recent years, there are many thiourea based materials are reported with high second harmonic efficiency (SHG) than the commercial material potassium dihydrogen phosphate (KDP). The SHG efficiency of reported materials are bis(thiourea) ammonium nitrate (1.52 times > KDP) [3], bis(thiourea) cadmium formate (2 times > KDP) [20], bis(thiourea) zinc acetate (2 times > KDP) [21], bis(thiurea) zinc chloride (1.75 times > KDP) [22] and bis(thiourea) strontium chloride (BTSC) (1.54 times > KDP) [23].
With this attractive property of thiourea leads to do research work in thiourea complex. Therefore, in the present work we concentrate on thiourea complex semiorganic crystal of bis(thiourea) manganese chloride (BTMC). This work is differed from earlier work in terms of growth technique hence we adopted the slow cooling technique to grow crystal with bulk size, transparency, defect less. Also, the motivation of this work was to improve the SHG efficiency, mechanical stability and optical transparency. In addition, the important optical parameters, mechanical parameters were determined. The obtained results from spectroscopic analysis, optical, mechanical, electrical, surface, second and third order NLO properties are discussed in this manuscript. The BTMC crystal has good transparency with UV cut off wavelength 280 nm, SHG efficiency 1.33 times KDP, good mechanical stability, third order nonlinear absorption coefficient (3.4460 14 × 10−9 m/W) and third order on linear optical susceptibility (5.1202 × 10−14 esu) which are shows the novelty of the grown crystal BTMC. Therefore, authors are strongly suggests that the grown BTMC crystal should be a commercial candidate for device applications.
2 Experimental procedure
2.1 Synthesis
Bis(thiourea) manganese chloride (BTMC) was synthesized using thiourea (AR grade) and manganese chloride (AR grade) in double distilled water at room temperature. The thiourea and manganese chloride was taken in 2:1 molar ratio and mixed together using magnetic stirrer for more than 7 h to obtain the homogenous saturated solution. The following chemical reaction was taken to obtain the BTMC crystal (Fig. 1).
2.2 Growth of BTMC
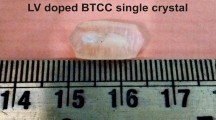
The saturated solution (pH 5) was then filtered using Whatmann filter paper to remove the suspended particles. The filtered solution was taken in a beaker and covered with thin perforated polythene paper with more number of minute holes. This solution was then kept in constant temperature bath (accuracy ± 0.01) at 45 °C to controlled evaporation of solution. The temperature was maintained for 3 days after that the temperature was reduced 0.3 °C/day. The defect free, colorless, good quality crystal of BTMC was harvested in a period of 2–3 weeks with dimension 8 × 8 × 2 mm3 by slow cooling method. The as grown crystal of BTMC is shown in the Fig. 2. The optimized growth conditions of BTMC are given in the Table 1.
3 Results and discussion
3.1 Single crystal X-ray diffraction analyses
The well developed BTMC crystal is chosen for single crystal X-ray diffraction analyses. The harvested BTMC crystal exists in orthorhombic crystal system. The cell parameters were measured as a = 5.48 Å, b = 7.68 Å, c = 8.53 Å, \(\alpha = \beta = \gamma = 90^\circ\) and the cell volume is found to be 359.47 Å3. The obtained parameters are well matches with reported values [1].
3.2 FT-IR spectral analyses
The various essential functional groups present in the BTMC crystal are identified using FT-IR analysis. Figure 3 shows the recorded FTIR spectrum. The FT-IR spectrum was recorded in the wave number range between 4000 and 400 cm−1 is shown in the Fig. 3. The peak observed at 3369 cm−1 and 3270 cm−1 are the characteristic of the titular compound which are due to NH2 stretching and N–H symmetric stretching vibrations. This implies that the existence of thiourea molecule in the grown crystal. The peaks at 2921 cm−1 is due to C–H stretching vibration. The NH2 bending vibration was observed around at 1604 cm−1. The N–C–N stretching vibration was validated at 1468 cm−1. The peak at 1405 cm−1 have been confirmed the C=S stretching vibration. The NH2 rocking vibration was identified at 1080 cm−1. The C–H deformation was observed at 667 cm−1. The C–Cl stretching produced at broad intense signal at 552 cm−1. The (N–C–S) deformation was observed at 521 cm−1. The observed wave number and corresponding assignments of BTMC crystal are compared with thiourea and details assignments are given in the Table 2.
3.3 UV–Visible spectral analyses
The optical property of BTMC crystal was analyzed using UV–Vis NIR analysis in the wavelength range of about 200–1100 nm and the recorded transmittance spectrum is shown in the Fig. 4. It is observed from transmission spectrum that the lower cut-off wavelength of the BTMC is 280 nm which implies that the suitability of crystal for device fabrications and other NLO application. The UV cut off wavelength BTMC crystal compared with other bis(thiourea) metallic compound are given in the Table 3.
3.4 Determination of optical parameters
Generally, the optical properties of the materials related to their atomic structure, electronic band structure and electrical properties. An accurate measurement of optical properties in terms of optical parameters such as absorption coefficient (α), band gap (Eg), reflectance (R), refractive index (n), extinction coefficient (K) and electrical susceptibility are essential towards the application point of view. Therefore, from the optical transmission spectrum the optical parameters are determined.
The optical band gap can be calculated by using the following equations and these equations are proposed by Ashour et al. in the year of 1995 [29].
where, T is the transmittance and t is the thickness of the crystal, Eg is the optical band gap and α is the optical absorption coefficient (α).
The band gap of BTMC crystal was estimated by plotting (αhυ)2 versus hυ as shown in the Fig. 5a. The value of bandgap was found to be 5.1 eV. The wide band gap of the BTMC crystal confirms the large transmittance in the visible region [30] and this crystal can be suitable for the optoelectronic devices like laser diode [31]. Extinction coefficient (K) can be obtained from the following equation
The extinction coefficient as a function of absorption coefficient (α) is shown in Fig. 5b. The transmittance (T) is given by
The reflectance (R) in terms of the absorption coefficient can be obtained from the above equation. Hence,
The refractive index (n) can be determined from reflectance data using the equation.
The absorption coefficient versus reflectance is shown in the Fig. 5c. Figure 5d represents the variation of refractive index as a function of wavelength. The refractive index (n) decrease with increase in wavelength indicates that the grown sample absorbs at lower wavelength region. The relation between n and K values with respect to wavelength exposes the interaction of photon with electron. The refractive index ‘n’ is 1.42 at 1000 nm and the refractive index is strongly dependent on wavelength.
The electrical susceptibility (\(\chi_{\text{c}}\)) can be calculated using the following relation,
hence, susceptibility = 1.02.
Since electrical susceptibility is greater than 1, the material can be easily polarized when high intense light incident on the material.
3.5 Micro hardness test
The mechanical behaviour of a material can be analyzed by microhardness test in terms of measuring hardness number (Hv), elastic stiffness constant (C11), yield strength (σy), fracture toughness (kc), Brittleness index (Bi) and tensile strength (Y) [32]. Generally mechanical properties of materials mainly depend on the crystal structure, number of bonds per unit volume and the composition of crystalline solid [33,34,35]. Particularly, materials could be utilized for device application may depend on mechanical stability. Therefore, it is necessary to analyse the mechanical behavior of grown crystal. Hence, BTMC crystal was subjected to Vickers’s microhardness test. The Vicker’s hardness (Hv) of each load was calculated using the expression,
where, p—applied load in (g), d—diagonal length (mm), 1.8574 is a constant related to geometrical factor of diamond pyramid indenter. The plot between Hv and (P) are depicted in Fig. 6. From the plot, it is viewed that the hardness number (Hv) increases with increase in load (P). This type of behaviour is called reverse indentation size effect (RISE) [36]. The maximum hardness value obtained as 86.2 kg/mm2 at 100 g. In order to know the category of the materials, the work hardening coefficient could be calculated. The n can be calculated by plotted the graph between log p versus log d. The graph of log p versus log d is shown in the Fig. 7 and from the graph n has been calculated as 1.1734 by linear fit method. According to Onitsch, if an ‘n’ lie between 1 and 1.6, then the grown crystal belongs to a harder material and it is more than 1.6 called soft materials [37]. Since, the calculated value of ‘n’ is less than 1.6, therefore the grown crystal comes under the category of hard material.
3.5.1 Yield strength
The yield strength refers to the maximum stress that can be applied on a crystal at which the crystal gets deform permanently. The yield strength can be estimated using the following relation. A graph had been plotted in between applied load P and yield strength (σy) shown in Fig. 8.
where n’ = n+2.
3.5.2 Elastic stiffness constant
Stiffness constant (or) elastic stiffness constant explains about the bonding nature of atoms [38]. It can be calculated using Wooster’s empirical formula. The variation of stiffness constant with applied load is shown in the Fig. 9.
The higher the value of stiffness constant C11 denotes that the binding forces between ions are quite stronger.
3.5.3 Fracture toughness
Fracture toughness gives information about, the ability of a material to resist fracture. This parameter may decide many design application of the materials. The fracture toughness can be estimated using the following relation.
where, β—indenter constant, for Vickers’s diamond pyramid indenter (β = 7). The average of two crack length for each indentation is considered as crack length (l).
3.5.4 Brittleness index
The Brittleness is a property that deals with the mechanical behaviour of a crystal and controls fracture without any considerable deformation. The value of the Brittleness index (Bi) is estimated using the following relation [39].
The mechanical parameters like hardness number (Hv), yield strength (σy), elastic stiffness constant (C11), Fracture toughness (Kc) and Brittleness constant (Bi) were determined for various load P and the estimated values are tabulated in Table 4.
3.6 Dielectric studies
The variation of dielectric constant (ε′) versus logarithm of the applied frequency is shown in the Fig. 10. The dielectric constant is high at the low frequency area and decreases with frequency. Dielectric constant (ε′) is 170 at 100 Hz at the temperature 308 K. The large value of ε′ at low frequencies is assigning to the presence of space charge polarization which depends on pureness and perfection of the sample. Displacement of ions from an equilibrium position is equivalent to the placing of the dipole at the state with the ion in equilibrium [40]. The plot of dielectric loss decreasing with the increase in temperature. The plot between log f and dielectric loss is shown in Fig. 11. This is clear from the plot the dielectric loss is strongly based on the applied frequency [41]. This indicates the grown BTMC crystal has lesser defects and good optical properties suit for electro-optic applications.
3.7 Photoconductivity studies
The dark currents as well as the photocurrent measurements on the BTMC single crystal were recorded using a Keithley 485 Picoammeter in the field applied from 5 to 50 V. The dark current was recorded with the sample unexposed by radiation and photo current were measured in the presence of radiation. A plot is plotted as a function of dark current and photo current with the applied field. From the plot (Fig. 12), it is observed that the photo current is always less than the dark current. The photoconductivity analysis reveals the BTMC crystal exhibits negative photoconductivity [42]. The negative photoconductivity exhibited by the crystal because when the crystal subjected to radiation (exposing the radiation by halogen lamp with a power of 100 W) the number of charge carriers or their lifetime decrease. Due to this the current produced by the crystal is less in the presence of radiation than the absence of radiation.
3.8 SEM analysis
A careful study of surface feature of a crystal can expose the growth condition. The surface morphology of the crystal can be viewed by scanning electron microscope (SEM). The SEM pictures were taken in three magnifications × 292, × 684 and × 728 which are shown in the Fig. 12a–c respectively. It is observed from Fig. 13a, the surface of the crystal has layered pattern whereas the magnification increased to × 684 (Fig. 12b), the surface shows that the pits are randomly distributed and the alignment of pits orientated in the particular direction. From the Fig. 12c (magnification × 728), it is observed that the surface has dendrites pattern which means surface has treelike structure. The development of dendrite structures on the surface of the crystal due to rise in growth temperature hence the concentration of the solution increase rapidly due to faster evaporation of solvent. This caused in a higher degree of supersaturation and faster growth in the later stages [43, 44].
3.9 EDAX analyses
The elements presence in the grown crystal is analyzed using Oxford INCA EDAX analyser. The real concentration of Mn in BTMC is 1.29% consistent with nominal composition. The presence of chlorine (4.44%), sulphur (12.74%) and nitrogen (81.51%) are identified by scanning several points. The EDAX spectrum of BTMC crystal having the peaks endorsed to Cl, S, N and Mn at different energies exposed in the Fig. 14. The presence of elements in the sample in atomic and weight percentage are given in Table 5.
3.10 Etching study
In view of applications of crystals, the surface must be a good quality without any defects. The defects in the crystal surface which leads to change the properties of the crystal [45, 46]. Therefore, the analysis of the surface is most important for the crystal. The one of the methods to analysis of the crystal surface is etching with suitable solvent. The Etch pattern of BTMC crystal is shown in Fig. 15. The grown crystal of BTMC is subjected to etching with etchants (water) for 20 s at room temperature. The surface of the crystal has been changed from smooth to rectangular etch pits which shows the layer growth of the crystal.
3.11 Second harmonic generation (SHG) studies
The intense of second harmonic generation (SHG) efficiency of BTMC crystal was determined as per the principle of Kurtz and Perry technique [47]. This analysis was carried out using Nd: YAG laser as source with a fundamental wavelength of 1064 nm with a laser pulse width of 8 ns on the BTMC crystal powder. The radiation of laser should fall on the grown sample then the sample absorbed the laser radiation and emits the high intense green radiation. This implies the confirmation of SHG efficiency of BTMC crystal. By analyzing the SHG output from the sample, the output power was found to be 31.92 mV for the input energy of 1 mV. The similar practice is repeated for the reference KDP crystal and the obtained output was 24 mV for the same input. Comparing the result the BTMC crystal was 1.33 times greater than the KDP crystal.
3.12 Z-scan studies
To determine the third order nonlinear parameters like nonlinear refractive index (n2) and nonlinear absorption coefficient (β) the grown crystal of BTMC was subjected to Z-scan technique. The Z-scan study was carried out using a He–Ne laser with an output of power 100 mW is used as a source with wavelength of 532 nm with a beam diameter 2.8 mm. A Gaussian filter is use to convert the input beam as a polarize Gaussian beam and focus the beam using a convex lens of focal length of 10.3 cm on the sample of thickness of 1 mm. The sample holder can able to move along positive and negative directions of Z axis in the path of laser beam. The transmitted intensity of the sample was recorded using a photo detector along with a graph on a computer using an appropriate software of Z-scan. The recorded graph is consisting of two ways namely closed aperture and open aperture. In closed aperture method, a pre-determined aperture with fixed radius is places in front detector. The incident beam intensity was depends upon the radius of the aperture.
In open aperture method, the laser beam intensity will be maximum on the sample material because the beam is focused directly on the sample without any aperture in order to find out the nonlinear absorption co-efficient (β). The BTMC crystals Z-scan graphs of open and closed aperture are shown in Figs. 16a,b.
The refractive index and absorption co-efficient of the sample is depends up on the intensity of the laser beam. The alteration in transmittance between peak and valley was a self-focusing method for closed aperture [48].The nonlinear absorption co-efficient in open aperture can be calculated [49].
The nonlinear refractive index (n2) is calculated using the following equation.
where Δφ is the axis phase shift, k is the wave number, I0 is the monochromatic source intensity at the focus and Leff is the thickness of the sample. The axis phase shift Δφ is calculated using the following equation.
here ΔTp-v is the difference value between the normalized and valley transmittance peak of the closed aperture. The linear transmittance aperture S is calculated using the following formula [50].
where ra is the radius of the aperture and ωa is the beam radius at aperture. The wave number k is calculated using the following equation.
here λ is the monochromatic source wavelength. The intensity I0 is calculated using the following the equation.
where P is the power of the laser source, A is the area of the monochromatic. The area A of the monochromatic beam is obtained from the following equation.
where r is the radius of the beam on aperture, the beam diameter is obtained using the following equation.
where f is the focal length of the lens and the calculated diameter is found to be 2.493 × 10−5. The effective thickness Leff is calculated using the following equation.
where α is the linear absorption co-efficient, L is the thickness of the sample (1 mm). The nonlinear absorption co-efficient β is calculated using the following equation.
The third order NLO susceptibility \(\chi^{\left(3 \right)}\) can be calculated using the above parameters. To calculate the third order NLO susceptibility \(\chi^{\left(3 \right)}\) for real and imaginary parts the following equations are used [49].
where ε0 is the permittivity of free space 8.854 × 10−12 C2N−1m−2, c is the velocity of light in vacuum, n0 refractive index of the sample. Using the following formula we can able to calculate the third order nonlinear susceptibility \(\chi^{\left(3 \right)}\) for the crystal.
Third-order NLO parameters such as nonlinear refractive index (n2) and nonlinear absorption coefficient (β) and NLO susceptibility \(\chi^{\left(3 \right)}\) of the BTMC were evaluated successfullyby Z-scan analyses and the self-defocusing nature of the material was confirmed. The calculated parameters and their results are tabulated in Table 6.
4 Conclusion
A semiorganic optical single crystal of bis (thiourea) manganese chloride (BTMC) has been grown by slow cooling technique with dimension 8 × 8 × 2 mm3. The BTMC crystallize in orthorhombic crystal system with cell parameters a = 5.48 Å b = 7.68 Å and c = 8.53 Å, \(\alpha = \beta = \gamma = 90^\circ\) which was confirmed from Single crystal XRD analyses. The presents of functional groups are verified by FTIR analysis. The lower UV cut off wavelength 280 nm of grown crystal was evaluated from UV–Visible transmission spectrum. The Vickers’s microhardness study proves that BTMC belongs to hard material category which obeys the reverse indentation size effect (RISE) for the applied loads. The BTMC crystal exhibits a SHG efficiency of about 1.33 times than that of the reference KDP crystal. Third-order NLO parameters of the BTMC were calculated and the self-defocusing nature of the material was successfully revealed by Z-scan analysis. The Nonlinear refractive index (n2) (1.14 × 10−15 m3/W) Nonlinear absorption co-efficient (β) (3.4460 × 10−9 m/W) Third-order NLO susceptibility (χ(3)) (5.1202 × 10−14 esu) have been determined. The surface aspect of BTMC crystal was indentified by SEM and etching studies. The presence of elements like Mn, N, S, Cl were confirmed from EDAX spectrum. All the results confirm that the grown crystal is potential candidate for the fabrication of various optoelectronic devices.
References
C. Ramachandraraja, R.S. Sundararajan, V. Krishnakumar, FTIR, FT Raman and thermal studies of bis(thiourea) manganese chloride—an organo metallic crystal. Spectrochim. Acta A 71, 1634–1637 (2009)
K. Mahendra, A. D’Souza, N.K. Udayashankar, Synthesis, structural, optical and electrical (DC) properties of a semiorganic thiourea barium chloride (TBC) single crystal. Optik 145, 436–447 (2017)
A. Anbarasi, S.M. Ravikumar, G.J. Shanmuga Sundar, M. Allen Moses, M. Packiya Raj, M. Prabhakaran, R. Ravisankar, R. Gunaseelan, Investigation on synthesis, growth and physicochemical properties of semi-organic NLO crystal bis(thiourea) ammonium nitrate for nonlinear frequency conversion. Phys. B 522, 31–38 (2017)
N. Bhuvaneswari Arvind, K. Baskar, R. Dhanasekaran, Growth and characterization of tris thiourea magnesium zinc sulphate single crystals. Optik 126, 3731–3736 (2015)
S. Gowri, K. Hemalatha, Influence of picric acid on organometallic bisthiourea manganese chloride crystals. Int. J. Tech. Res. Appl. 38, 65–68 (2016)
R. Manickam, C. Babu, G. Srinivasan, Single crystal: bisthiourea doped manganese chloride, synthesis, growth and characterization. Int. J. Eng. Sci. Invent. 2319–6726, 18–20 (2017)
M. Anis, S.S. Hussaini, A. Hakeem, M.D. Shirsat, G.G. Muley, Synthesis, growth and optical studies of novel organometallic NLO crystal: calcium bis-thiourea chloride. Optik 127, 2137–2142 (2016)
M. Packiya Raj, S.M. Ravi Kumar, D. Sivavishnu, T. Kubendiran, A. Anbarasi, S.E. Allen Moses, Synthesis, growth and optical, mechanical, electrical and surface properties of an inorganic new nonlinear optical crystal: sodium cadmium tetra chloride (SCTC). Cryst. Res. Technol. 1700271, 1–8 (2018)
J.H. Joshi, K.P. Dixit, K.D. Parikh, H.O. Jethva, D.K. Kanchan, S. Kalainathan, M.J. Joshi, Effect of Sr +2 on growth and properties of ammonium dihydrogen phosphate single crystal. J. Mater. Sci. 29, 5837–5852 (2018)
J.H. Joshi, G.M. Joshi, M.J. Joshi, H.O. Jethva, K.D. Parikh, Raman, photoluminescence, A.C. electrical studies of pure and l-serine doped ammonium dihydrogen phosphate single crystals: the understanding of defect chemistry in hydrogen bonding. New J. Chem. 21, 17227–17249 (2018)
J.H. Joshi, S. Kalainthan, D.K. Kanchan, M.J. Joshi, K.D. Parikh, Effect of l-threonine on growth and properties of ammonium dihydrogen phosphate crystal. Arab. J. Chem. 6, 1555–1558 (2017)
A. Vijayakumar, A. Kala, Thermal and dielectric studies on bis (thiourea) nickel chloride NLO single crystals. Mater. Today 5, 8818–8823 (2018)
A. Subashini, K. Rajarajan, S. Sagadevan, Synthesis, growth, spectral, optical and thermal studies of thiourea family crystal: TTPB. Mater. Res. Express 4, 026202 (2017)
R. Thirumurugan, B. Babu, K. Anitha, J. Chandrasekaran, Synthesis, growth, characterization and quantum chemical investigations of a promising organic nonlinear optical material: thiourea-glutaric acid. J. Mol. Struct. 1171, 915–925 (2018)
S.E. Allen Moses, S. Tamilselvan, S.M. Ravi Kumar, J. Johnson, Synthesis, growth and characterization of semi-organic nonlinear optical l-threnoninum sodium fluoride (LTSF) crystal for photonics application. Chin. J. Phys. 58, 294–302 (2019)
G. Ramasamy, S. Meenakshi sundram, Synthesis, growth characterization and crystal structure of zinc cadmium thioure complex Zn0.625Cd1.375(CS(NH2)2)9·4(SO2). J. Cryst. Growth 377, 197–202 (2013)
S. Annie Roshan, C. Joseph, M.A. Ittachen, Matter. Lett. 49, 299–302 (2001)
R.R. Hajiyani, C.K. Chauhan, M.J. Joshi, Growth, thermal and spectroscopic studies of bis-thiourea nickel barium chloride single crystals. Asian J. Chem. 30(2), 257–259 (2018)
R.R. Hajiyani, D.J. Dave, C.K. Chauhan, P.M. Vyas, M.J. Joshi, Growth and characterization of bis-thiourea strontium chloride single crystals. Mod. Phys. Lett. B 24, 735–747 (2010)
S. Selvakumar, S.M. Ravi Kumar, K. Rajarajan, A.J.A. Pragasam, S.A. Rajasekar, K. Thamizharasn, P. Sagayaraj, Growth and characterization of a novel organometallic nonlinear optical crystal: bis(thiourea) cadmium formate. Cryst. Growth Des. 6, 2607–2610 (2006)
L.R. Nirmala, J.T.J. Prakash, Effect of lithium chloride on spectral, optical, thermal and mechanical behaviour of bis thiourea zinc acetate crystals. Spectrochim. Acta A 97, 673–677 (2012)
K. Parasuraman, K.S. Murugesan, R. Uthrakumar, J.J. Das, B. Boaz, Growth, optical, mechanical and dielectric studies on NLO active pure and metal ion doped single crystals of bis-thiourea zinc chloride. Phys. B 406, 3856–3860 (2011)
K. Rajagopalan, P. Krishnamoorthy, K. Jayamoorthy, M. Austeria, Bis (thiourea) strontium chloride as promising NLO material: an experimental and theoretical study. Karbala Int. J. Mod. Sci. 2, 219–225 (2016)
K. Muthu, S.P. Meenakshisundaram, Synthesis, growth, structure and characterization of a new semiorganic crystal: tetrakis(thiourea)zinc(II) picrate. Mater. Lett. 84, 56–58 (2012)
N. Sivakumar, V. Jaisankar, G. Chakkaravarthi, G. Anbalagan, Synthesis, crystal structure, optical, thermal and mechanical characterization of poly bis(thiourea) silver(I) nitrate single crystals synthesized at room temperature. Mater. Lett. 132, 298–301 (2014)
M.L. Carolinea, S. Vasudevan, Growth and characterization of bis thiourea cadmium iodide: a semiorganic single crystal. Mater. Chem. Phys. 113, 670–674 (2009)
R. Hanumantharao, S. Kalainathan, Growth spectroscopic investigation, optical, mechanical, chemical etching and nonlinear optical studies of semi-organic crystal: bis (thiourea) zinc formate. Spectrochim. Acta A 106, 86–90 (2013)
S. Selvakumar, K. Rajarajan, S.M. Ravi Kumar, I.V. Potheher, D.P. Anand, K. Ambujam, P. Sagayaraj, Growth and characterization of pure and metal doped bis(thiourea) zinc chloride single crystals. Cryst. Res. Technol. 41(8), 766–770 (2006)
A. Ashour, N. El-Kadry, S.A. Mahmoud, On the electrical and optical properties of CdS films thermally deposited by modified source. Thin Solid Films 269, 117–120 (1995)
V. Vasudevan, R.R. Babu, G. Bhagavannarayana, K. Ramamurth, Effect of metal and aminoacid dopants on the growth and properties of l-lysine monohydrochloride dihydrate single crystal. Mater. Chem. Phys. 124, 681–688 (2010)
Y. Zhou, W.H. Nelson, Phys. Chem. 79, 479–489 (2010)
P. Jayaprakash, P. Sangeetha, C.R. Thayakumara, M.L. Caroline, Investigation on the growth, spectral, lifetime, mechanical analysis and third-order nonlinear optical studies of l-methionine admixture d-mandelic acid single crystal: a promising material for nonlinear applications. Phys. B 518, 1–12 (2017)
N. Durairaj, S. Kalainathan, M.V. Krishnaiah, Investigation on uniderctional growth of 1,3,5-triphenylbenzene by Sankaranarayanan-Ramasamy method and its characterizeation of lifetime, thermal analysis, hardness and etching studies. Mater. Chem. Phys. 181, 529–537 (2016)
B.W. Mott, Micro Hardness Indentation Testing (Butterworths, London, 1956)
J.H. Westbrook, H. Conrad, The Science of Hardness Testing (American Society for Metals, Metals Park, 1971)
K. Sangwal, M. Hordyjewicz, B. Surowska, Microindentation hardness of SrLaAlO4 and SrLaGaO4 single crystals. J. Optoelectron. Adv. Mater. 4, 875–882 (2002)
E.M. Onitsch, The present status of testing the hardness of materials. Mikroskopie 95, 12–14 (1956)
P. Jayaprakash, M.P. Mohamed, M.L. Caroline, Growth, spectral and optical characterization of a novel nonlinear optical organic material: d-alanine dl-mandelic acid single crystal. J. Mol. Struct. 1134, 67–77 (2017)
Suresh Sagadevan, Priya Murugasen, Mechanical behavior of nonlinear optical (NLO) single crystal. Int. J. ChemTech Res. 6, 5604–5607 (2014)
I. Bunget, M. Popescu, Physics of Solid Dielectrics (Elsevier, New York, 1984)
J.C. Owens, Anharmonicity and millimeter-wave absorption in alkali halide crystals. Phys. Rev. 181, 1228–1236 (1969)
V.N. Joshi, Photoconductivity (Marcel Dekker, New York, 1990)
Binay Kumar, Nidhi Sinha, Micromorphology of pure and PbI2-doped CdI2 dendritic single crystals. Cryst. Res. Technol. 40, 887–892 (2005)
N. Sinha, B.K. Singh, K. Kumar, N. Singh, M.K. Gupta, G.C. Budakoti, B. Kumar, Solution growth and comparative characterization of L-HFB single crystals. Cryst. Res. Technol. 44, 167–172 (2009)
K. Sangwal, Etching of Crystals Theory, Experiment and Application (Elsevier Science, Burlington, 2012)
S. Amelinckx, The Direct Observation of Dislocations (Academic Press, New York, 1964)
S.K. Kurtz, T.T. Perry, A powder technique for the evaluation of nonlinear optical materials. J. Appl. Phys. 39, 3798–3813 (1968)
I. Bhattacharyya, S. Priyadarshi, D. Goswami, Molecular structure-property correlations from optical nonlinearity and thermal-relaxation dynamics. Chem. Phys. Lett. 469, 104–109 (2009)
E.W. Van Stryland, M. Sheik-Bahae, Z-scan measurements of optical nonlinearities. Charact. Tech. Tabul. Org. Nonlinear Mater. 60, 655–692 (1998)
S. Shettigar, G. Umesh, K. Chandrasekharan, B. Kalluraya, Third order nonlinear optical properties and two photon absorption in newly synthesized phenyl syndrome doped polymer. Synth. Met. 157, 142–146 (2007)
Acknowledgements
The Corresponding author sincerely thanks to Science & Engineering Research Board (SERB) (a statutory body of the Department of Science & Technology, Government of India) for funding research project (NO.EEQ/2016/000451) and also acknowledge Department of Physics, B.S. Abdurrahman University, Chennai for NLO test and Department of Physics, St. Joseph College, Tiruchirapalli for providing microhaness test.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kubendiran, T., Ravi Kumar, S.M., Allen Moses, S.E. et al. Second and third order nonlinear optical, mechanical, surface characteristics of bis(thiourea) manganese chloride (BTMC) grown by slow cooling technique used for frequency conversion applications. J Mater Sci: Mater Electron 30, 17559–17571 (2019). https://doi.org/10.1007/s10854-019-02105-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10854-019-02105-2