Deep Convolutional Neural Networks with Spatial Regularization, Volume and Star-Shape Priors for Image Segmentation

Abstract

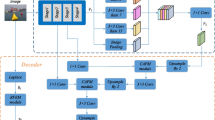
Deep Convolutional Neural Networks (DCNNs) can well extract the features from natural images. However, the classification functions in the existing network architecture of CNNs are simple and lack capabilities to handle important spatial information as have been done by many well-known traditional variational image segmentation models. Priors such as spatial regularization, volume prior and shapes priors cannot be handled by existing DCNNs. We propose a novel Soft Threshold Dynamics (STD) framework which can integrate many spatial priors of the classic variational models into the DCNNs for image segmentation. The novelty of our method is to interpret the softmax activation function as a dual variable in a variational problem, and thus many spatial priors can be imposed in the dual space. From this viewpoint, we can build a STD based framework which can enable the outputs of DCNNs to have many special priors such as spatial regularization, volume preservation and star-shape prior. The proposed method is a general mathematical framework and it can be applied to any image segmentation DCNNs with a softmax classification layer. To show the efficiency of our method, we applied it to the popular DeepLabV3+ image segmentation network, and the experiments results show that our method can work efficiently on data-driven image segmentation DCNNs.

Appendices

Calculating Subgradient of ${\mathcal {R}}$

Since ${\mathcal {R}}$ is smooth and thus $\partial {\mathcal {R}}(\varvec{u})=\{\delta {\mathcal {R}}(\varvec{u})\}$. Let us first calculate the directional derivative

$$\begin{aligned} \begin{array}{rl} \frac{\text {d} {\mathcal {R}}(\varvec{u}+\tau \varvec{v})}{\text {d}\tau }\Big |_{\tau =0}&{}=\lambda \langle e\varvec{v}, k*(1-\varvec{u})\rangle - \lambda \langle e\varvec{u}, k*\varvec{v}\rangle \\ &{}=\lambda \langle \varvec{v}, (k*(1-\varvec{u}))e-{\hat{k}}*(e\varvec{u})\rangle \\ &{}=\lambda \langle \varvec{v}, (k*(1-\varvec{u}))e-k*(e\varvec{u})\rangle . \end{array} \end{aligned}$$

Here ${\hat{k}}$ is the conjugate function of k and the last equation follows by the fact that ${\hat{k}}=k$ when k is a symmetric kernel function $k(x)=k(-x)$ such as Gaussian kernel. Therefore $\delta {\mathcal {R}}(\varvec{u})= \lambda ((k*(1-\varvec{u}))e-k*(e\varvec{u}))$ according to the variational equation $\frac{\text {d} {\mathcal {R}}(\varvec{u}+\tau \varvec{v})}{\text {d}\tau }\Big |_{\tau =0}=\langle \varvec{v}, \delta {\mathcal {R}}(\varvec{u})\rangle$. Therefore $p=\lambda ((k*(1-\varvec{u}))e-k*(e\varvec{u})).$

Proof of Theorem 1

Proof

According to (7)

$$\begin{aligned} {\mathcal {F}}({\varvec{u}}^{t_1+1})+\langle \varvec{p}^{t_1},{\varvec{u}}^{t_1+1} \rangle \le {\mathcal {F}}({\varvec{u}}^{t_1})+\langle \varvec{p}^{t_1},{\varvec{u}}^{t_1} \rangle , \end{aligned}$$

and thus

$$\begin{aligned} {\mathcal {F}}({\varvec{u}}^{t_1+1})-{\mathcal {F}}({\varvec{u}}^{t_1})\le \langle \varvec{p}^{t_1},{\varvec{u}}^{t_1}-{\varvec{u}}^{t_1+1} \rangle . \end{aligned}$$

Since ${\mathcal {R}}(\varvec{u})$ is concave, by the definition of subgradient for a concave function, $\forall \varvec{p}^{t_1}\in \partial {\mathcal {R}}(\varvec{u}^{t_1}),$ one can have

$$\begin{aligned} {\mathcal {R}}({\varvec{u}}^{t_1+1})-{\mathcal {R}}({\varvec{u}}^{t_1})\le \langle \varvec{p}^{t_1},{\varvec{u}}^{t_1+1}-{\varvec{u}}^{t_1} \rangle . \end{aligned}$$

Therefore,

$$\begin{aligned} \begin{array}{rl} &{}{\mathcal {F}}({\varvec{u}}^{t_1+1})-{\mathcal {F}}({\varvec{u}}^{t_1}) +{\mathcal {R}}({\varvec{u}}^{t_1+1}) -{\mathcal {R}}({\varvec{u}}^{t_1})\\ &{}\quad \leqslant \langle \varvec{p}^{t_1},{\varvec{u}}^{t_1}-{\varvec{u}}^{t_1+1} \rangle +\langle \varvec{p}^ {t_1},{\varvec{u}}^{t_1+1}-{\varvec{u}}^{t_1} \rangle =0,\\ \end{array} \end{aligned}$$

which completes the proof. $\square$

Proof of Proposition 3

Proof

By introducing Lagrangian multipliers $\varvec{q}, \widehat{\varvec{q}}$ associated to the constraints $\int _{\Omega }u_i(x){\text {d} x}=V_i$ and $\sum _{i=1}^I u_{i}(x)=1,\forall x\in \Omega$, we have the related Lagrangian function

$$\begin{aligned} \begin{aligned}&{\mathcal {L}}({\varvec{u}},\varvec{q},\widehat{\varvec{q}})\\&\quad =\sum _{i=1}^I \int _{\Omega } (-o_i(x)+p_i^{t_1}(x)+\varepsilon \ln u_i(x))u_i(x){\text {d} x}\\&\qquad +\sum \limits ^I_{i=1} q_i(V_i-\int _{\Omega }u_i(x){\text {d} x})+\int _{\Omega } {\widehat{q}}(x)(1-\sum \limits ^I_{i=1}u_i(x)){\text {d} x}. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \underset{\varvec{u}\in {\mathbb {U}}_{\varvec{V}}}{\min }\left\{ {\mathcal {F}}(\varvec{u})+\hat{{\mathcal {R}}}(\varvec{u})\right\} =\underset{\varvec{u}}{\min }~\underset{\varvec{q},\widehat{\varvec{q}}}{\max }~{\mathcal {L}}({\varvec{u}},\varvec{q},\widehat{\varvec{q}}). \end{aligned}$$

The derivative of ${\mathcal {L}}$ with respect to $u_i$

$$\begin{aligned}\frac{\partial {\mathcal {L}}}{\partial u_i}=-o_i+p_i^{t_1}-q_i-{\widehat{q}}+\varepsilon \ln u_i+\varepsilon =0, \end{aligned}$$

therefore, by the first order optimization condition

$$\begin{aligned} \widetilde{u}_i(x)=e^{\frac{o_i(x)-p_i^{t_1}(x)+q_i+{\widehat{q}}(x)}{\varepsilon }-1}, \end{aligned}$$

Furthermore, using the condition

$$\begin{aligned} \sum \limits ^I_{i=1}u_i(x)=e^\frac{{\widehat{q}}(x)}{\varepsilon }\sum \limits ^I_{i=1}e^{\frac{o_i(x)-p_i^{t_1}(x)+q_i}{\varepsilon }-1}=1, \end{aligned}$$

we can obtain

$$\begin{aligned} {\widetilde{u}}_i(x)=\frac{e^{\frac{o_i(x)-q_i^{t_1}(x)+\widetilde{ q}_i(x)}{\varepsilon }}}{\sum \limits ^I_{{\hat{i}}=1}e^{\frac{o_{{\hat{i}}}(x)-q_{{\hat{i}}}^{t_1}(x)+{\widetilde{q}}_{{\hat{i}}} (x)}{\varepsilon }}}, \end{aligned}$$

Substituting this into the saddle problem of ${\mathcal {L}}(\varvec{u},\varvec{q},\widehat{\varvec{q}})$, we can obtain

$$\begin{aligned} \begin{aligned}&{\mathop {max}\limits _{\varvec{q}}}\left\{ \sum \limits ^I_{i=1}q_iV_i-\varepsilon \int _{\Omega }\mathrm {\ln }\sum \limits ^I_{i=1}e^{\frac{o_i(x)-p_i^{t_1}(x)+q_i}{\varepsilon }}{\text {d} x}-|\Omega |\varepsilon \right\} \\&\quad ={\mathop {max}\limits _{\varvec{q}}}\left\{ \langle \varvec{q},\varvec{V}\rangle +\langle \varvec{q}^{c,\varepsilon },\varvec{1}\rangle -|\Omega |\varepsilon \right\} , \end{aligned} \end{aligned}$$

which completes the proof. $\square$

Proof of Theorem 2

Proof by contradiction. Suppose $u^{-1}[\gamma ,+\infty )$ is not a star-shaped domain.

Then $\exists y\in \partial u^{-1}[\gamma ,+\infty )$, $\exists \zeta _1\in (0,1)$, s.t. $z=(1-\zeta _1)y+\zeta _1c\notin u^{-1}[\gamma ,+\infty )$ according to the definition of star-shaped domain. It implies $u(z)<\gamma$ by the definition of the $\gamma$-super level set.

Let $f(\zeta )=u((1-\zeta )y+\zeta c), \zeta \in [0,1)$, then $f\in C^1$ and $f^{'}(\zeta )=\langle \nabla u((1-\zeta )y+\zeta c) , c-y\rangle$.

Since $\langle \nabla u(x),\varvec{s}(x)\rangle \geqslant 0$ for all x, we have $\langle \nabla u((1-\zeta )y+\zeta c),c-[(1-\zeta )y+\zeta c]\rangle \geqslant 0$ by taking $x=(1-\zeta )y+\zeta c$ and $\varvec{s}(x)=c-[(1-\zeta )y+\zeta c]$. Arranging the above formulation, one can get $\langle \nabla u((1-\zeta )y+\zeta c),(1-\zeta )(c-y)\rangle \geqslant 0$.

So $\langle \nabla u((1-\zeta )y+\zeta c),c-y\rangle \geqslant 0$ since $1-\zeta >0$. It implies $f^{'}(\zeta )\geqslant 0$ for $\zeta \in [0,1)$. Here $f^{'}(0)$ stands for $f^{'}_{+}(0)$.

Therefore, we can conclude that $f(\zeta )$ is monotone increasing when $\zeta \in [0,1)$. However, $f(0)=u(y)\geqslant \gamma$, $f(\zeta _1)=u(z)<\gamma , 0<\zeta _1<1$. This is a contradiction with $f(\zeta )$ is monotone increasing. The proof is completed.