Introduction

The cyclic decapeptide antamanide, cycl[-Val(1)-Pro(2) -Pro(3)-Ala(4)-Phe(5)-Phe(6)-Pro(7)-Pro(8)-Phe(9)-Phe(10)-], C64H78N10O10, see Scheme 1, consists entirely of l-amino acids. Antamanide was isolated from the poisonous mushroom Amanita phalloides and it has the unique property of counteracting the toxin phalloidin, produced by the mentioned mushroom. Furthermore, the antamanide was also prepared by synthetic way [1, 2]. Moreover, it should be noted that various conformations of this electroneutral decapeptide compound have been reported [3,4,5].

Scheme 1
scheme 1

Structural formula of antamanide

Full size image

Cyclic peptides are also somewhat more “rigid” compared to the corresponding linear peptides, and this attribute promotes binding by removing the “entropic penalty” [5]. Falvo et al. found strong intramolecular hydrogen bonding network in the molecule of antamanide [4].

Antamanide forms 1:1 complexes with a variety of metal cations [6,7,8,9]. In our previous works, we dealt with the complexes of antamanide with univalent [10,11,12,13,14] and divalent cations [15,16,17]. The structures of antamanide complexes have been studied by the quantum mechanical DFT calculations. It was found that the cations are embedded in the cavity of antamanide. Univalent cations H+, K+, Tl+ and H3O+ are bonded by four bonds to four oxygens of antamanide molecule, while the divalent Ca2+, Sr2+ and Ba2+ are bonded by six bonds to the six antamanide oxygens.

Fig. 1
figure 1

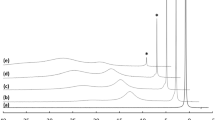
Mass spectrum in the negative ESI mode of a mixture of antamanide (5*10− 6 mol/L) and TBA+NO3− (2.5*10− 4 mol/L) in chloroform/methanol, 1:1 (ν/ν). Anionic complex of antamanide with NO3− in the ratio 1/1, [C64H78N10O10 + NO3]−, provides ion cluster at m/z 1208.6. The insets show (a) the zoomed view of the measured ion cluster and (b) the isotope model of the ion cluster of the complex, respectively. Very intense ion cluster at m/z 366.3 belongs to complex of TBA+ with two nitrate anions

Full size image

Zhu et al. [18] and Becherer et al. [19] investigated the formation of anionic complexes of various macrocycles. Reviews of the complex formation of macrocycles with anions published Kubik [20] and Elmes and Jolliffe [21]. The latter authors pointed out that the large peptides proteins give the possibility of numerous H-bonding interactions available from the different amino acids that are present in the peptide molecule. Kubik reported macrocyclic complexes of halides, nitrate, hydrogensulfate, and dihydrogenphosphate anions [20].

However, up to now, the investigation of the antamanide H-bonding with the anions has not been made. So, in the current work, electrospray ionization mass spectrometry (ESI-MS) was used for the investigation of the interaction between the univalent nitrate anion and the antamanide ligand in the gas phase. Further, employing quantum mechanical DFT calculations, the most probable structure of this experimentally proven anionic complex in the gas phase was predicted.

Experimental

Antamanide was supplied by the Padua Unit of the IBCCNR, Italy. Other chemicals used (Lachema, Brno, Czech Republic) were of reagent grade purity.

Fig. 2
figure 2

Enhanced product ion mass spectrum of [C64H78N10O10 + NO3]−. Loss of neutral molecule HNO3 is evident. The fragment was obtained with nitrogen as collision gas at collision energy of -45 eV

Full size image

The experiments were provided with a 3200 Q TRAP (AB Sciex, Canada) mass spectrometer fitted with an electrospray ion source. Antamanide and tetrabutylammonium nitrate (TBA+NO3−) were dissolved in chloroform/methanol, 1:1 (ν/ν). Final concentration of antamanide was 5*10− 6 mol/L and that of TBA+NO3− 2.5*10− 4 mol/L. The dissolved mixture was introduced into the ESI source via a PEEK capillary at a flow rate of 10 µL/min. Nitrogen was used as a nebulizer and collision gas. The operating conditions for the mass spectrometer were set as follows: ionspray voltage − 4.5 kV; curtain gas 10, ion source gas(1) 18, and ion source gas(2) 0 psig; ion source temperature ambient; declustering potential − 60 V, entrance potential − 10 V.

Fig. 3
figure 3

DFT optimized structure of free ligand

Full size image

The theoretical calculations have been performed in the frame of the density functional theory with hybrid density functional, “Becke, 3-parameter, Lee-Yang-Parr” (B3LYP) version [22]. Gaussian 16 set of programs was used for all calculations [23]. In order to stabilize self-consistent field procedure, the scaled steepest descent algorithm was used during optimization. The optimization itself was unconstrained. LanL2DZ (Los Alamos National Laboratory 2 double ζ) basis set [24, 25] was used for the respective calculations.

The interaction energies between antamanide and the nitrate anion was calculated with basis set super position error correction. The counterpoise method, as it is implemented in Gaussian 16 package program, was used. The convergence energy criteria were set to E < 10− 9 hartree.

The Gaussian keyword “integral(ultrafinegrid)” was used in order to increase the numerical accuracy and to reduce oscillations during the molecular geometry optimization. So, two-electron integrals and their derivatives were calculated by using the pruned (99,590) integration grid, having 99 radial shells and 590 angular points per shell.

Results and discussion

Figure 1 shows an ESI spectrum obtained in negative mode for a mixture of antamanide with TBA+NO3- in chloroform/methanol mixture (1:1, ν/ ν). The ion cluster at m/z 1208.6 belongs to the anionic complex of antamanide with nitrate anion, [C64H78N10O10 + NO3]-. Very intense ion cluster at m/z 366.3 belongs to complex of TBA+ with two nitrate anions. The insets in Fig. 1 represent the zoomed view of the measured ion cluster and the appropriate model spectrum, respectively. As can be seen the measured ion cluster and a theoretical one are very close. The heights of the peaks correspond to the content of 13 C in natural carbon (1.1%) and to 64 carbon atoms in the molecule of antamanide.

The existence of the above mentioned 1/1 complex of antamanide with NO3- was further proofed by a tandem mass spectrometry experiment.

Figure 2 shows enhanced product ion spectrum of the precursor m/z 1208.6, [C64H78N10O10 + NO3]-. In the spectrum, it is possible to distinguish a signal related to the presence of the original precursor. The other signal obtained by collision induced dissociation (CID) relates to a loss of HNO3 from the precursor leading to the fragment possessing the structure [C64H78N10O10-H]-.

So, the anionic complex of antamanide with one nitrate anion has been proved by mass spectrometry.

The most probable conformations of the antamanide – NO3- complex has been determined based on the thorough conformational analysis (i.e., six very different initial mutual positions of the ligand and the nitrate anion were considered during the geometry optimization) and the respective vibrational frequency calculations, analogously as in our previous articles [11,12,13,14,15,16,17]. The molecular geometries of the free ligand and its complex with NO3- were optimized. The optimized conformation of this free ligand is given in Fig. 3.

In Fig. 4, the structure obtained by the full DFT optimization of the antamanide-NO3- complex is depicted, together with the lengths of the corresponding bonds (in Å). In the resulting anionic complex species, which is most energetically favored, the three oxygens of the “central” anion NO3- is bound by seven hydrogen bonds to the respective seven hydrogen atoms of the parent antamanide ligand.

Fig. 4
figure 4

DFT optimized structure of the complex of NO3− with antamanide molecule; distances / Å

Full size image

The interaction between the atoms of nitrate anion and others closest atoms is described in the frame of the Wiberg bond index [26] after deduction of mutual bonds in NO3- (Table 1).

Table 1 Wiberg indices for NO3− after deduction of mutual bonds in NO3− That is, the size of the “bond” between the NO3− atoms and the ligand
Full size table

Furthermore, the interaction energy, E(int), of the antamanide-NO3- complex [calculated as the respective difference between the pure electronic energies of the respective complex and isolated antamanide and NO3- species: E(int) = [E(complex) – E(antamanide) – E(NO3-)] was calculated. Energies were calculated in optimized geometry from B3LYP/LanL2DZ approach. For these calculations, we used B3LYP functional with LanL2DZ resp. Def2TZVP basis sets and M06 functional with Def2TZVP basis sets, with and without the dispersion correction [27,28,29,30,31]. The results are summarized in Table 2.

Table 2 Calculated energies of antamanide – NO3−interaction
Full size table

It is clear from Table 2 that the calculated interaction energies for the B3LYP functional are almost the same despite the basis set used, while the M06 functional gives slightly higher interaction energy values. The introduction of the dispersion correction always leads to a little bit higher values ​​of the calculated interaction energy.

Conclusion

In this work, we have shown that the combination of theoretical DFT calculations and an experimental ESI-MS method can provide relevant data on the noncovalent bonding interactions of the nitrate anion NO3− with the antamanide ligand. By using this experimental method, the anionic antamanide – NO3− complex has been evidenced quite unambiguously. An anionic complex of antamanide has been here described for the first time. Applying DFT calculations, the most probable structure of this complex was derived. In this anionic complex, the NO3− anion is embedded in the molecule of antamanide. Two or three bonds to the hydrogen atoms of antamanide molecule bond each oxygen atom of this anion. The interaction energy, E(int), of the antamanide-NO3− complex has been calculated as -175.9 kJ/mol.