Abstract
Linear temporal logic (\(\textsf{LTL}\,\)) and its variant interpreted on finite traces (\(\textsf{LTL}_{\textsf{f}\,}\)) are among the most popular specification languages in the fields of formal verification, artificial intelligence, and others. In this paper, we focus on the satisfiability problem for \(\textsf{LTL}\,\)and \(\textsf{LTL}_{\textsf{f}\,}\)formulas, for which many techniques have been devised during the last decades. Among these are tableau systems, of which the most recent is Reynolds’ tree-shaped tableau. We provide a SAT-based algorithm for \(\textsf{LTL}\,\)and \(\textsf{LTL}_{\textsf{f}\,}\)satisfiability checking based on Reynolds’ tableau, proving its correctness and discussing experimental results obtained through its implementation in the BLACK satisfiability checker.
Similar content being viewed by others
1 Introduction
Linear temporal logic (\(\textsf{LTL}\,\)) [44] is the de-facto standard language for the specification of system properties in the fields of formal verification and artificial intelligence. \(\textsf{LTL}\,\)is a modal logic usually interpreted over infinite and discrete linear orders, but recently its variant interpreted over finite traces (\(\textsf{LTL}_{\textsf{f}\,}\)) has gained traction, especially in the artificial intelligence community [16, 18]. Satisfiability checking, that is, the problem of deciding whether a given formula admits a satisfying model, is one of the most important computational tasks associated with the logic, and one of the first that have been carefully studied [48]. Tableau systems are among the first methods that have been proposed to solve the satisfiability checking problem for \(\textsf{LTL}\,\)[55]. Classic tableau systems for \(\textsf{LTL}\,\)[39, 55] are graph-shaped and two-passes, that is, they build a graph structure, that represents all tentative paths of the transition system described by the input formula, and then traverse it, in a second pass, to find a suitable model for the formula. In contrast, the alternative tableau system recently devised by Reynolds [45] is tree-shaped and one-pass, since it builds a tree structure where a single pass is required to build a given branch and simultaneously decide whether it corresponds to a model for the formula. Reports on early implementations of Reynolds tableau [4, 42] highlights how propositional reasoning is the bottleneck for this kind of procedures, since the search for solutions of the propositional part of temporal formulas is basically done by brute force.
To overcome this limitation, in this paper we join Reynolds’ tableau with Boolean satisfiability (SAT) solvers, by providing a SAT-based satisfiability checking procedure for \(\textsf{LTL}\,\)and \(\textsf{LTL}_{\textsf{f}\,}\)based on Reynolds’ tableau. In our procedure, the tableau is never built explicitly. Instead, suitable SAT formulas representing all the branches of the tableau tree up to a given depth k are solved, for increasing values of k. If a successful branch (i.e. a model for the formula) is found within the given bound, the formula is satisfiable, otherwise k is incremented and the procedure continues. In contrast to similar approaches \(\grave{a}\, la\,\)bounded model checking, our procedure guarantees completeness and termination both for satisfiable and unsatisfiable formulas, without the need to precompute unsatisfiability thresholds, thanks to the pruning rule of Reynolds’ tableau.
The modularity of Reynolds’ tableau and of its encoding allows our procedure to support both future and past temporal modalities, interpreted on both finite and infinite traces. On the one hand, past temporal modalities do not add expressive power to the logic, but do increase its succinctness [41] and allow many properties to be expressed in a more natural way [40]. Independently of the set of temporal modalities and the considered class of models, our procedure is also able to output a model for satisfiable formulas.
We describe the procedure, prove its correctness, and evaluate its performance. To this aim, the procedure has been implemented in the BLACKFootnote 1 satisfiabilty checker, whose architecture we describe here as well. To assess the performance of the tool, we compare it with several state-of-the-art tools that support satisfiability checking for \(\textsf{LTL}\,\)over a benchmark set of thousands of formulas gathered from various sources. The results show that our technique is competitive for many classes of benchmark formulas.
The paper is structured as follows. After reviewing the relevant literature in Sect. 2, we recall the needed background in Sect. 3, including Reynolds’ one-pass and tree-shaped tableau. Then, in Sect. 4, we describe in detail our SAT-based procedure, including full proofs of soundness, completeness, and termination. Section 5 discusses the implementation of BLACK, with a particular attention to design choices. Finally, Sect. 6 experimentally compares the tool with other state-of-the-art solvers. Section 7 concludes with some final remarks and a discussion of future developments.
2 Related Work
Shortly after its introduction [44], Linear Temporal Logic has become the de-facto standard language for specification of temporal properties both in formal verification [15] and in artificial intelligence [2]. The satisfiability problem for \(\textsf{LTL}\,\)has been proved to be  -complete [48]. Despite such a theoretically high computational complexity, many techniques and tools have been developed to solve it, ranging from tableau systems [1, 4, 39, 45, 47, 54] to reduction to model checking [10], from temporal resolution [24, 25, 33], to labelled superposition [51], to automata-theoretic techniques [36].
-complete [48]. Despite such a theoretically high computational complexity, many techniques and tools have been developed to solve it, ranging from tableau systems [1, 4, 39, 45, 47, 54] to reduction to model checking [10], from temporal resolution [24, 25, 33], to labelled superposition [51], to automata-theoretic techniques [36].
Tableau methods were among the first techniques to be proposed. Born in the context of propositional and first-order logic [5], tableaux are quite easy to extend to the non-classical setting. Most tableaux for \(\textsf{LTL}\,\)are graph-shaped [39, 55], as they build a graph structure which is then traversed in a second pass to find a suitable model for the formula. Since in many cases the built structure is really huge, various techniques have been proposed to improve the efficiency of the procedure. As an example, in incremental tableaux [35], only those parts of the graph that are actually involved in the search for the model are built. In contrast, tree-shaped tableaux try to avoid building the entire structure altogether, focusing instead on its paths. The first such tableau was proposed by Schwendimann [47], followed by Reynolds’ tableau [45]. In this paper, we focus on the latter. Even if both tableaux are tree-shaped and can be regarded as being one-pass, Reynolds’ one has the advantage of expanding each branch of the tree completely independently from the others, as each branch corresponds to a distinct tentative model for the formula. In contrast, Schwendimann’s tableau needs to keep track of multiple branches in order to accept or reject a given subtree. The possibility of such an independent exploration of branches has been heavily exploited by an early implementation of Reynolds’ tableau [4] and its later parallelization [42]. As a matter of fact, the SAT-based procedure shown in this paper would not be possible for Schwendimann’s tableau exactly because of this difference. In addition to that, the modular, rule-based structure of Reynolds’ tableau system allowed it to be extended to various logics beyond standard \(\textsf{LTL}\,\). In particular, support for past modalities has been added, as well as for more expressive logics like the real-time Timed Propositional Temporal Logic (TPTL ) [28].
An important property of \(\textsf{LTL}\,\)is that satisfiability checking can be easily reduced to model checking: to establish whether a formula is satisfiable, its negation is model checked against the complete transition system, with any counterexample being a model of the original formula. Hence, any model checking technique can be seen as an alternative satisfiability checking technique. In this perspective, the procedure presented here is similar in spirit to bounded model checking techniques [6, 12]: a counterexample (here, a tableau branch) of length (tree depth) up to k, for increasing values of k, is found by encoding the paths of the structure (the branches of the tree) up to length (depth) k into a SAT formula. However, bounded model checking techniques are usually incomplete, since the computation of the diameter of the graph, which witnesses the exploration of all paths, is usually a very hard task (requiring, e.g., to solve the satisfiability problem of a quantified Boolean formula [6]). Here, instead, our algorithm is complete thanks to the encoding of the  rule of Reynolds’ tableau (see Sect. 3). In addition to that, the encoding of past modalities, coming from the tableau rules, is much simpler than the virtual unrollings technique used to support past modalities in bounded model checking approaches [7]. In our encoding, support for past modalities comes almost for free. This was surprising at first, since support for past modalities (sketched by Gigante et al. [31] and finalized by Geatti et al. [28]) is a bit more involved in the explicit construction of Reynolds’ tableau.
rule of Reynolds’ tableau (see Sect. 3). In addition to that, the encoding of past modalities, coming from the tableau rules, is much simpler than the virtual unrollings technique used to support past modalities in bounded model checking approaches [7]. In our encoding, support for past modalities comes almost for free. This was surprising at first, since support for past modalities (sketched by Gigante et al. [31] and finalized by Geatti et al. [28]) is a bit more involved in the explicit construction of Reynolds’ tableau.
Although \(\textsf{LTL}\,\)has been historically defined over infinite traces, the finite-trace semantics has recently gained popularity in the artificial intelligence [16] and business process modelling fields [17]. Although the computational complexity of all the main problems remain the same, the manipulation of finite state automata on finite words, instead of Büchi automata on infinite words, guarantees a notable speed-up in practice. This led to much work revisiting, for example, model checking and synthesis [18], and the use of LTL on finite traces as specification language for non-Markovian rewards in Markov Decision Processes [9], for restraining specifications in reinforcement learning applications [19], and for specifications of temporally extended goals in fully observable nondeterministic planning [8].
The approach presented here would not be sensible without the use of efficient SAT solvers as the backend. The satisfiability problem for propositional logic is the canonical  -complete problem and one of the most studied problems in computer science. For this reason, the efficiency of modern SAT solvers has grown beyond the best expectations. BLACK, the tool we developed to evaluate our procedure, supports different solvers as backend in order to be able to exploit the advantages of each. In addition to the classic, but now outdated, MiniSAT [21], we support CryptoMiniSAT [49], a modern, parallelized and very flexible SAT solver. In addition to that, we support two Satisfiability Modulo Theories (SMT) solvers, Z3 [20], cvc5 [3], and MathSAT [14]. For \(\textsf{LTL}\,\)satisfiability, we do not make use of any SMT feature, but the two SMT solvers proved to be very competitive backends also for purely propositional problems.
-complete problem and one of the most studied problems in computer science. For this reason, the efficiency of modern SAT solvers has grown beyond the best expectations. BLACK, the tool we developed to evaluate our procedure, supports different solvers as backend in order to be able to exploit the advantages of each. In addition to the classic, but now outdated, MiniSAT [21], we support CryptoMiniSAT [49], a modern, parallelized and very flexible SAT solver. In addition to that, we support two Satisfiability Modulo Theories (SMT) solvers, Z3 [20], cvc5 [3], and MathSAT [14]. For \(\textsf{LTL}\,\)satisfiability, we do not make use of any SMT feature, but the two SMT solvers proved to be very competitive backends also for purely propositional problems.
The present paper is an extension of previous work [27, 29], which presented the SAT-based procedure and later extended it to past modalities. Support for finite-trace semantics has never been presented before.
3 Reynolds’ One-Pass and Tree-Shaped Tableau System
In this section, we recall the syntax and semantics of \(\textsf{LTL}\,\)and of its extension with past operators, \({\mathsf {LTL{+}Past}}\,\). Then, we describe the rules of Reynolds’ tableau, that is the subject of the encoding presented in Sect. 4.
3.1 Syntax and Semantics of \({\mathsf {LTL{+}Past}}\,\)
Let us consider an alphabet \(\varSigma \) of proposition letters (or propositions). Then, the syntax of an \({\mathsf {LTL{+}Past}}\,\)formula \(\phi \) over \(\varSigma \) can be defined as follows:

where
\(p\in \varSigma \) and
\(\phi \),
\(\phi _1\), and
\(\phi _2\) are
\({\mathsf {LTL{+}Past}}\,\)formulas. The (future-only) fragment
\(\textsf{LTL}\,\)only uses Boolean connectives and future operators. One can define the standard shorthands and derived operators as usual, e.g.,
\(\top \equiv p \vee \lnot p\), for some
\(p \in \varSigma \),
\(\bot \equiv \lnot \top \),
 ,
,
 ,
,
 ,
,
 . Given a temporal operator op, a formula is an op formula if the top-level operator of the formula is op (e.g.
. Given a temporal operator op, a formula is an op formula if the top-level operator of the formula is op (e.g.
 is a tomorrow formula).
is a tomorrow formula).
Given a set of symbols A, we denote as
\(A^*\) the set of finite words over A, and as
\(A^\omega \) the set of infinite words over A. Given a word \(w\in A^*\), we denote as  the length of w, while we set
the length of w, while we set  for \(w\in A^\omega \).
\({\mathsf {LTL{+}Past}}\,\)is interpreted over finite or infinite state sequences, i.e. words
\({\bar{\sigma }}\in (2^\varSigma )^*\) or
\({\bar{\sigma }}\in (2^\varSigma )^\omega \). Given a (finite or infinite) state sequence
for \(w\in A^\omega \).
\({\mathsf {LTL{+}Past}}\,\)is interpreted over finite or infinite state sequences, i.e. words
\({\bar{\sigma }}\in (2^\varSigma )^*\) or
\({\bar{\sigma }}\in (2^\varSigma )^\omega \). Given a (finite or infinite) state sequence
 , the satisfaction of a formula
\(\phi \) by
\({\bar{\sigma }}\) at a time point
\(i\ge 0\), denoted as
\({\bar{\sigma }},i\models \phi \), is defined as follows:
, the satisfaction of a formula
\(\phi \) by
\({\bar{\sigma }}\) at a time point
\(i\ge 0\), denoted as
\({\bar{\sigma }},i\models \phi \), is defined as follows:

A state sequence
\({\bar{\sigma }}\) satisfies
\(\phi \), written \({\bar{\sigma }}\models \phi \), if \({\bar{\sigma }},0\models \phi \). Observe that some operators can be derived from a smaller set of so-called “primitive” ones. In particular, the \(\wedge \) connective, the release operator ( ), the triggered operator (
), the triggered operator ( ), and the weak yesterday operator (
), and the weak yesterday operator ( ) can be defined in terms of the \(\vee \) connective, the until operator (
) can be defined in terms of the \(\vee \) connective, the until operator ( ), the since operator (
), the since operator ( ), and the yesterday operator (
), and the yesterday operator ( ), respectively. However, here we consider them as primitive operators as well, since this allows us to put any formula into negation normal form (NNF), i.e. with the negations applied only to propositions, which will be useful later. Moreover, note that state sequences have a definite starting point, hence the past is bounded, and we need to distinguish between the yesterday operator
), respectively. However, here we consider them as primitive operators as well, since this allows us to put any formula into negation normal form (NNF), i.e. with the negations applied only to propositions, which will be useful later. Moreover, note that state sequences have a definite starting point, hence the past is bounded, and we need to distinguish between the yesterday operator  (\(\phi \) holds at the previous state) and the weak yesterday operator
(\(\phi \) holds at the previous state) and the weak yesterday operator  (\(\phi \) holds at the previous state, if it exists). Similarly, when the logic is interpreted over finite state sequences, we have to distinguish between the tomorrow operator
(\(\phi \) holds at the previous state, if it exists). Similarly, when the logic is interpreted over finite state sequences, we have to distinguish between the tomorrow operator  (\(\phi \) holds at the next state) and the weak tomorrow operator
(\(\phi \) holds at the next state) and the weak tomorrow operator  (\(\phi \) holds at the next state, if it exists). When the logic is interpreted over infinite state sequences, the semantics of the tomorrow and weak tomorrow operators coincide. We nevertheless keep them separated for uniformity. When interpreted over finite state sequences, the logic is often referred to as \(\textsf{LTL}_{\textsf{f}\,}\).
(\(\phi \) holds at the next state, if it exists). When the logic is interpreted over infinite state sequences, the semantics of the tomorrow and weak tomorrow operators coincide. We nevertheless keep them separated for uniformity. When interpreted over finite state sequences, the logic is often referred to as \(\textsf{LTL}_{\textsf{f}\,}\).
The notion of closure of a formula will be useful later. It is defined as follows.
Definition 1
(Closure of an \({\mathsf {LTL{+}Past}}\,\) formula) Let \(\psi \) be an \({\mathsf {LTL{+}Past}}\,\)formula built over \(\varSigma \). The closure of \(\psi \) is the smallest set of formulas \({{\,\mathrm{{\mathcal {C}}}\,}}(\psi )\) satisfying the following properties:
-
1.
\(\psi \in {{\,\mathrm{{\mathcal {C}}}\,}}(\psi )\);
-
2.
for each sub-formula \(\psi '\) of \(\psi \), \(\psi ' \in {{\,\mathrm{{\mathcal {C}}}\,}}(\psi )\);
-
3.
for each \(p \in \varSigma \), \(p \in {{\,\mathrm{{\mathcal {C}}}\,}}(\psi )\) if and only if \(\lnot p \in {{\,\mathrm{{\mathcal {C}}}\,}}(\psi )\);
-
4.
if
 , then
, then  ;
; -
5.
if
 , then
, then  ;
; -
6.
if
 , then
, then  ;
; -
7.
if
 , then
, then  .
.
It is worth pointing out that Item 3 of Definition 1 only applies to proposition letters because formulas will be assumed to be in NNF.
3.2 The One-Pass and Tree-Shaped Tableau for \({\mathsf {LTL{+}Past}}\,\)
In this subsection we will describe the tableau system for \({\mathsf {LTL{+}Past}}\,\)introduced by Geatti et al. [28]. This extends the tableau system for \(\textsf{LTL}\,\)by Reynolds [45], and will be used as the basis for the direct encoding discussed in Sect. 4. As presented by Geatti et al. [28], the tableau rules only handle \({\mathsf {LTL{+}Past}}\,\)interpreted over infinite state sequences. However, the modifications to support finite state sequences are straightforward, as will be shown in Sect. 4.
Every \({\mathsf {LTL{+}Past}}\,\)formula can be trivially transformed in NNF, therefore, for ease of exposition, we will assume formulas to be in NNF. A tableau for a formula \(\phi \) is a tree where each node u is labeled by a set of formulas  , with the root \(u_0\) labeled by
, with the root \(u_0\) labeled by  . This tree is built step-wise: at each step, a set of rules is applied to a leaf, until all branches have been either accepted or rejected. A tableau where this is the case is called complete.Footnote 2 Each rule either (i) adds one or more children to the current leaf or (ii) either accepts or rejects the current branch. Given a branch
. This tree is built step-wise: at each step, a set of rules is applied to a leaf, until all branches have been either accepted or rejected. A tableau where this is the case is called complete.Footnote 2 Each rule either (i) adds one or more children to the current leaf or (ii) either accepts or rejects the current branch. Given a branch  , the sequence of nodes
, the sequence of nodes  , for some \(0\le i \le j \le n\), is denoted by
, for some \(0\le i \le j \le n\), is denoted by  .
.
One node is selected at each time step and it is subject to a number of expansion rules. These rules select a formula of the node label and expand the tableau according to its semantics, as shown in Table 1. Each expansion rule creates one or two children depending on the selected formula. When a formula \(\phi \) of one of the types shown in the table is found in the label  of a node u, one or two children \(u'\) and \(u''\) are created with the same label as u, but replacing \(\phi \) by the formulas from \(\varGamma _1(\phi )\) and \(\varGamma _2(\phi )\), respectively. Only one child is created if \(\varGamma _2(\phi )\) is empty. An elementary formula is either a proposition, a negated proposition, or a tomorrow, weak tomorrow, yesterday, or weak yesterday formula. The expansion rules in Table 1 always decompose formulas into their subformulas or elementary formulas. Hence, after repeated applications of the expansion rules, sooner or later a node that only contains elementary formulas is obtained. We call such a node a poised node. Elementary formulas of the form
of a node u, one or two children \(u'\) and \(u''\) are created with the same label as u, but replacing \(\phi \) by the formulas from \(\varGamma _1(\phi )\) and \(\varGamma _2(\phi )\), respectively. Only one child is created if \(\varGamma _2(\phi )\) is empty. An elementary formula is either a proposition, a negated proposition, or a tomorrow, weak tomorrow, yesterday, or weak yesterday formula. The expansion rules in Table 1 always decompose formulas into their subformulas or elementary formulas. Hence, after repeated applications of the expansion rules, sooner or later a node that only contains elementary formulas is obtained. We call such a node a poised node. Elementary formulas of the form  are called
are called  . An
. An  is a formula that, intuitively, requests something to be fulfilled later. Given an
is a formula that, intuitively, requests something to be fulfilled later. Given an 
 , \(\phi \) is said to be requested in a node u if
, \(\phi \) is said to be requested in a node u if  , and it is said to be fulfilled in a node u if
, and it is said to be fulfilled in a node u if  . An
. An  is fulfilled in a subsequence of a branch is it is fulfilled in at least one node of the subsequence.
is fulfilled in a subsequence of a branch is it is fulfilled in at least one node of the subsequence.
The tableau advances through time by making temporal steps. To do that, the following rules are applied to poised nodes  .
.
 :
:-
A child
 is added to
is added to  , with:
, with: 
 :
:-
Let

For each subset \(G_n'\subseteq G_n\) (including \(\emptyset \)), a child
 is added to
is added to  such that
such that  . This is done once and only once before every application of the
. This is done once and only once before every application of the  rule.
rule.
The  rule advances the construction of the current branch to the subsequent temporal state. The
rule advances the construction of the current branch to the subsequent temporal state. The  is essential to the well-functioning of the rule dealing with past, as it adds a number of branches that nondeterministically guess formulas that may be needed to fulfil past requests coming from future states. For details on the
is essential to the well-functioning of the rule dealing with past, as it adds a number of branches that nondeterministically guess formulas that may be needed to fulfil past requests coming from future states. For details on the  rule, we refer the reader to Geatti et al. [28].
rule, we refer the reader to Geatti et al. [28].
Since the  rule is not applied to all the poised nodes (to some of which the
rule is not applied to all the poised nodes (to some of which the  rule is applied instead), we need the following definition.
rule is applied instead), we need the following definition.
Definition 2
(Step node) In a complete tableau for an \({\mathsf {LTL{+}Past}}\,\)formula, a poised node  is a step node if it is either a poised leaf or a poised node to which the
is a step node if it is either a poised leaf or a poised node to which the  rule was applied.
rule was applied.
Before applying the  rule though, poised nodes are subject to the application of a few termination rules, that is, rules that decide whether the construction has to continue or the current branch has to be either rejected or accepted.
rule though, poised nodes are subject to the application of a few termination rules, that is, rules that decide whether the construction has to continue or the current branch has to be either rejected or accepted.
Let u be a node. We define \(u^*\) as the closest ancestor of u that is a child of a step node, if any.  is the union of the labels of the nodes from u to \(u^*\) or to the root, if \(u^*\) does not exist. Given a branch
is the union of the labels of the nodes from u to \(u^*\) or to the root, if \(u^*\) does not exist. Given a branch  , with
, with  a step node, the termination rules are the following ones, which are checked in the following order.
a step node, the termination rules are the following ones, which are checked in the following order.
 :
:-
If
 , for some \(p\in \varSigma \), then
, for some \(p\in \varSigma \), then  is rejected.
is rejected.  :
:-
If
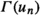 does not contain tomorrow or weak tomorrow formulas, then
does not contain tomorrow or weak tomorrow formulas, then  is accepted.
is accepted.  :
:-
If
 , then the branch
, then the branch  is rejected if either
is rejected if either  does not exist or
does not exist or  , where
, where  .
.  :
:-
If
 , then
, then  is rejected if
is rejected if  exists and
exists and  , where
, where  .
.  :
:-
If there exists a position \(i<n\) such that
 and all the
and all the  requested in
requested in  are fulfilled in
are fulfilled in  , then
, then  is accepted.
is accepted.  :
:-
If there exist two positions i and j such that \(i<j < n\),
 , and all the
, and all the  requested in these nodes which are fulfilled in
requested in these nodes which are fulfilled in  are also fulfilled in
are also fulfilled in  , then
, then  is rejected.
is rejected.
Intuitively, the  ,
,  , and
, and  rules reject branches that contain some contradiction, either a propositional one or because of some unfulfilled past request. The
rules reject branches that contain some contradiction, either a propositional one or because of some unfulfilled past request. The  rule accepts a branch devoid of contradictions where there is nothing left to do, while the
rule accepts a branch devoid of contradictions where there is nothing left to do, while the  one accepts a looping branch where all the
one accepts a looping branch where all the  are proposed again and fulfilled at every repetition of the loop. This scenario can be seen in Fig. 1a, that depicts the tableau for the satisfiable formula
are proposed again and fulfilled at every repetition of the loop. This scenario can be seen in Fig. 1a, that depicts the tableau for the satisfiable formula  . Finally, the
. Finally, the  rule, which was the main novelty of the system when introduced by Reynolds [45], rejects a branch that, otherwise, is going to be infinitely unrolled because of an
rule, which was the main novelty of the system when introduced by Reynolds [45], rejects a branch that, otherwise, is going to be infinitely unrolled because of an  impossible to fulfil. This happens in the tableau of the formula
impossible to fulfil. This happens in the tableau of the formula  depicted in Fig. 1b, where the
depicted in Fig. 1b, where the 
 is never going to be fulfilled, hence the rightmost branch is closed by the
is never going to be fulfilled, hence the rightmost branch is closed by the  rule.
rule.
The following has been proved to hold.
Proposition 1
(Termination, soundness and completeness of Reynolds’ tableau [28]) Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. The complete tableau for \(\phi \) is finite. Moreover, it contains an accepted branch if and only if \(\phi \) is satisfiable.
Besides what Proposition 1 states, it is useful to build an intuition of the correspondence between accepted branches of the tableau and models of the formulas. In particular, the proof of Proposition 1 [26] shows how to effectively build a model of the formula from an accepted tableau. This is accomplished by simply stating that any proposition appearing in the label of the i-th node of the branch holds at the i-th state of the model.
3.3 Adapting the \({\mathsf {LTL{+}Past}}\,\)Tableau to Finite Traces
We conclude the section by briefly discussing the finite-trace case. First of all, we observe that Reynolds’ tableau, as presented above, assumes an infinite-trace semantics, and treats tomorrow and weak tomorrow formulas exactly in the same way (as they have exactly the same semantics in the infinite-trace case).
Adapting Reynolds’ tableau to the finite-trace semantics is done as follows:
-
1.
Remove the
 rule;
rule; -
2.
Change the
 rule as follows:
rule as follows:  :
:-
If
 does not contain tomorrow formulas, then
does not contain tomorrow formulas, then  is accepted.
is accepted.
-
3.
Optionally, change the
 rule as follows:
rule as follows:  :
:-
If there is a \(j < n\) such that
 , then
, then  is rejected.
is rejected.
Intuitively, by removing the  rule, we ignore infinite periodic models, which end up being rejected by the
rule, we ignore infinite periodic models, which end up being rejected by the  rule instead. In this way, we focus only on finite models accepted by the
rule instead. In this way, we focus only on finite models accepted by the  rule, which is changed to accept branches with pending weak tomorrow requests, thus respecting the semantics of the weak tomorrow operator on finite traces. The
rule, which is changed to accept branches with pending weak tomorrow requests, thus respecting the semantics of the weak tomorrow operator on finite traces. The  rule can optionally be used instead of the
rule can optionally be used instead of the  one. Completeness is ensured in either case, but
one. Completeness is ensured in either case, but  can amount to a considerable speedup, because it can prune branches much earlier.
can amount to a considerable speedup, because it can prune branches much earlier.
The proofs of termination, soundness and completeness of the tableau given in [28] (Proposition 1) work pretty much unchanged in the finite-trace case with the above changes. In particular:
-
1.
termination is unaffected, since the same argument (see [28], Theorem 1) applies to both the
 and the
and the  rules: the number of labels is finite, and therefore, sooner or later, a label will repeat in any long-enough branch. The
rules: the number of labels is finite, and therefore, sooner or later, a label will repeat in any long-enough branch. The  rule has to wait this to happen twice, while the
rule has to wait this to happen twice, while the  can reject the branch straightaway.
can reject the branch straightaway. -
2.
soundness is unaffected, since the same arguments that worked for the
 and the
and the  rule work now for the
rule work now for the  rule (see [28], Theorem 2);
rule (see [28], Theorem 2); -
3.
the arguments required to show completeness are unaffected if the
 rule is used (see [28], Theorem 3). If the
rule is used (see [28], Theorem 3). If the  is used, completeness is much easier to show. If a branch
is used, completeness is much easier to show. If a branch  has a position \(j<n\) such that
has a position \(j<n\) such that  , then the whole subtree obtained by expanding
, then the whole subtree obtained by expanding  will also be found as the subtree of
will also be found as the subtree of  . Hence, any successful branch obtained by expanding
. Hence, any successful branch obtained by expanding  can also be obtained by expanding
can also be obtained by expanding  , hence the search can stop at
, hence the search can stop at  and
and  can be rejected.
can be rejected.
Note that the argument at Item 3 above does not work for infinite traces, i.e.  would break completeness in that setting, because infinite traces may have to periodically fulfill multiple eventualities (e.g.
would break completeness in that setting, because infinite traces may have to periodically fulfill multiple eventualities (e.g.  ), and partially fulfilling loops can still be valuable. See the counterexample shown by Geatti et al. [26] in their Fig. 2.
), and partially fulfilling loops can still be valuable. See the counterexample shown by Geatti et al. [26] in their Fig. 2.
In the following, we will assume to work with the  rule when looking for finite traces.
rule when looking for finite traces.
4 A SAT-Based Procedure Based on Reynolds’ Tableau
This section describes our SAT-based \(\textsf{LTL}\,\)satisfiability checking procedure based on Reynolds’ tableau. The procedure exploits SAT solvers to find suitable branches of the tableau tree without expanding the tableau nodes explicitly. This exploration is performed up to a given depth k, for increasing values of k (bounded). The procedure is reported in Algorithm 1. The five formulas \(\llbracket \phi \rrbracket ^k\), \(|\phi |^k\), \(|\phi |_{\text {fin}}^k\), \(|\phi |_T^k\), and \(|\phi |_{T, fin }^k\) encode different rules of the tableau. Note that, at Line 7 of Algorithm 1, \(|\phi |^k\) has to be used to solve the formula for the infinite-trace semantics, while \(|\phi |_{\text {fin}}^k\) has to be used for the finite-trace semantics. A similar distinction applies to Line 10.
Let us start with some notation. Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula in NNF over the alphabet \(\varSigma \). We define the following sets of formulas:

The encoding formulas are defined over an extended alphabet \({\bar{\varSigma }}\), which includes:
-
1.
any proposition letter from the original alphabet \(\varSigma \);
-
2.
the set
 of propositions that are the surrogate version of the corresponding
of propositions that are the surrogate version of the corresponding  -,
-,  -, and
-, and  -formulas;
-formulas; -
3.
a stepped version \(p^k\) of all the proposition letters defined in items 1 and 2, with \(k \in \mathbb {N}\) and \(p^0\) identified as p.
Intuitively, different stepped versions of the same proposition letter p are used to represent the value of p at different states. Thus, when \(p^i\) holds, it means that p belongs to the label of the i-th step node of the branch, i.e. the i-th state of the model.
Moreover, given \(\psi \in {{\,\mathrm{{\mathcal {C}}}\,}}(\phi )\), we denote by \(\psi _S\) the formula where all the  -,
-,  -,
-,  - and
- and  -formulas are replaced by their surrogate version. Similarly, given \(\psi \in {{\,\mathrm{{\mathcal {C}}}\,}}(\phi )\), we denote by \(\psi ^k\) the formula in which all proposition letters are replaced by their k stepped version. We write \(\psi _S^k\) to denote \((\psi _S)^k\).
-formulas are replaced by their surrogate version. Similarly, given \(\psi \in {{\,\mathrm{{\mathcal {C}}}\,}}(\phi )\), we denote by \(\psi ^k\) the formula in which all proposition letters are replaced by their k stepped version. We write \(\psi _S^k\) to denote \((\psi _S)^k\).
The formula \(\llbracket \phi \rrbracket ^k\) is called the k-unraveling of \(\phi \), and it encodes the expansion of the tableau tree. To define it, we need an encoding of the expansion rules of Table 1.
Definition 3
(Stepped normal form) Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula in NNF. Its stepped normal form, denoted by \({{\,\textrm{snf}\,}}(\phi )\), is defined as follows:

The stepped normal form is the extension to past operators of the next normal form used by Geatti et al. [28]. It easily follows from the expansion rules of each operator in Table 1. We can now define the k-unraveling of \(\phi \) recursively as follows:
where

The \(T_k\), \(Y_k\) and \(Z_k\) formulas encode, respectively, the  ,
,  , and
, and  rules of the tableau, while the base case of the 0-unraveling ensures that yesterday formulas are false and weak yesterday formulas are true at the first state. The
rules of the tableau, while the base case of the 0-unraveling ensures that yesterday formulas are false and weak yesterday formulas are true at the first state. The  rule of the tableau is implicitly encoded by the fact that only satisfying assignments of the formula are considered. Similarly, the
rule of the tableau is implicitly encoded by the fact that only satisfying assignments of the formula are considered. Similarly, the  rule does not need to be explicitly encoded: the intrinsic nondeterminism of the SAT solving process accounts for the nondeterministic choices implemented by the rule.
rule does not need to be explicitly encoded: the intrinsic nondeterminism of the SAT solving process accounts for the nondeterministic choices implemented by the rule.
Intuitively, if \(\llbracket \phi \rrbracket ^k\) is unsatisfiable, all the branches of the tableau for \(\phi \) (either the one for finite or infinite traces) are rejected before \(k+1\) steps, as formally stated by the next lemma.
Lemma 1
Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. Then, \(\llbracket \phi \rrbracket ^k\) is unsatisfiable if and only if all the branches of the complete tableau for \(\phi \) are rejected by the  or
or  rules and contain at most \(k+1\) step nodes.
rules and contain at most \(k+1\) step nodes.
Proof
We prove the contrapositive, i.e. that \(\llbracket \phi \rrbracket ^k\) is satisfiable if and only if the complete tableau for \(\phi \) has at least a branch that is either accepted, rejected by  or
or  , or longer than \(k+1\) step nodes. To do that, we establish a connection between truth assignments of \(\llbracket \phi \rrbracket ^k\) and suitable branches of the tableau.
, or longer than \(k+1\) step nodes. To do that, we establish a connection between truth assignments of \(\llbracket \phi \rrbracket ^k\) and suitable branches of the tableau.
From branches to assignments. Let  be a branch that is either accepted, rejected by
be a branch that is either accepted, rejected by  (or
(or  ), or longer than \(k+1\) step nodes. Let
), or longer than \(k+1\) step nodes. Let  be the sequence of its step nodes. We define a truth assignment \(\nu \) for \(\llbracket \phi \rrbracket ^k\) as follows. Since \(\llbracket \phi \rrbracket ^k\) contains stepped propositions from \(p^0\) until \(p^{k}\), for any given p, we need at most \(k+1\) step nodes from
be the sequence of its step nodes. We define a truth assignment \(\nu \) for \(\llbracket \phi \rrbracket ^k\) as follows. Since \(\llbracket \phi \rrbracket ^k\) contains stepped propositions from \(p^0\) until \(p^{k}\), for any given p, we need at most \(k+1\) step nodes from  , which, however, can be shorter if it is accepted or rejected by the
, which, however, can be shorter if it is accepted or rejected by the  or
or  rules. Hence, let \(\ell =\min \{m,k\}\). Moreover, let \(p_U\) be p, if \(p\in \varSigma \), and \(\psi \), if \(p=\psi _S\), for some
rules. Hence, let \(\ell =\min \{m,k\}\). Moreover, let \(p_U\) be p, if \(p\in \varSigma \), and \(\psi \), if \(p=\psi _S\), for some  -,
-,  -,
-,  -, or
-, or  -request \(\psi \), i.e. \((\cdot )_U\) is the inverse of the \((\cdot )_S\) operation. Then, for \(0\le i\le \ell \), we set \(\nu (p^i)=\top \) if and only if
-request \(\psi \), i.e. \((\cdot )_U\) is the inverse of the \((\cdot )_S\) operation. Then, for \(0\le i\le \ell \), we set \(\nu (p^i)=\top \) if and only if  . Then, we complete the assignments for positions \(m<j\le k+1\) (if any) as follows:
. Then, we complete the assignments for positions \(m<j\le k+1\) (if any) as follows:
-
1.
if the branch has been accepted by the
 or the
or the  rule, the evaluation of any proposition \(p^j\) with \(j>m\) can be chosen arbitrarily;
rule, the evaluation of any proposition \(p^j\) with \(j>m\) can be chosen arbitrarily; -
2.
if the branch has been accepted by the
 rule or rejected by the
rule or rejected by the  or
or  rules, then there is a position w such that
rules, then there is a position w such that  , and we continue by filling the truth assignment considering the successor of \(\pi _w\) as a successor of \(\pi _m\).
, and we continue by filling the truth assignment considering the successor of \(\pi _w\) as a successor of \(\pi _m\).
It can be easily checked that the truth assignment built in this way satisfies \(\llbracket \phi \rrbracket ^k\).
From assignments to branches. Let \(\nu \) be a truth assignment for \(\llbracket \phi \rrbracket ^k\). We use \(\nu \) as a guide to navigate the tableau tree to find a suitable branch which is either accepted, rejected by  or
or  , or has more than \(k+1\) step nodes. To do that, we build a sequence of branch prefixes
, or has more than \(k+1\) step nodes. To do that, we build a sequence of branch prefixes  where at each step we obtain
where at each step we obtain  by choosing
by choosing  among the children of
among the children of  , until we find a leaf or we reach \(k+1\) step nodes. During the descent, we build a partial function \(J:\mathbb {N}\rightarrow \mathbb {N}\) that maps positions j in
, until we find a leaf or we reach \(k+1\) step nodes. During the descent, we build a partial function \(J:\mathbb {N}\rightarrow \mathbb {N}\) that maps positions j in  to indexes J(j) such that, for all \(\psi \), it holds that
to indexes J(j) such that, for all \(\psi \), it holds that  if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(j)}\), i.e. we build a relationship between positions in the branch and steps in \(\nu \). As the base case, we put
if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(j)}\), i.e. we build a relationship between positions in the branch and steps in \(\nu \). As the base case, we put  and \(J(0)=0\) so that the invariant holds since
and \(J(0)=0\) so that the invariant holds since  and \(\nu \models {{\,\textrm{snf}\,}}(\phi )^0_S\) by the definition of \(\llbracket \phi \rrbracket ^k\). Then, depending on the rule that was applied to
and \(\nu \models {{\,\textrm{snf}\,}}(\phi )^0_S\) by the definition of \(\llbracket \phi \rrbracket ^k\). Then, depending on the rule that was applied to  , we choose
, we choose  among its children as follows.
among its children as follows.
-
1.
If the
 rule has been applied to
rule has been applied to  , then there is a unique child that we choose as
, then there is a unique child that we choose as  , and we define \(J(i+1)=J(i)+1\). Now, for all
, and we define \(J(i+1)=J(i)+1\). Now, for all  or
or  , we have
, we have  by construction of the tableau. Note that
by construction of the tableau. Note that  and
and  , hence we know by construction that
, hence we know by construction that  (or
(or  ). Then, by definition of \(\llbracket \phi \rrbracket ^k\), we know that \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(j)+1}\), i.e. \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(i+1)}\). For the other direction, if \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(i+1)}\), then by definition of \(\llbracket \phi \rrbracket ^k\) we have both
). Then, by definition of \(\llbracket \phi \rrbracket ^k\), we know that \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(j)+1}\), i.e. \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(i+1)}\). For the other direction, if \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(i+1)}\), then by definition of \(\llbracket \phi \rrbracket ^k\) we have both  and
and  , hence
, hence  and
and  , and thus
, and thus  and
and  , so by construction of the tableau it holds that
, so by construction of the tableau it holds that  . Hence the invariant holds.
. Hence the invariant holds. -
2.
If the
 rule has been applied to
rule has been applied to  , then there are n children
, then there are n children  such that
such that  for all \(1\le m\le n\). Now, we set \(J(i+1)=J(i)\) and we choose
for all \(1\le m\le n\). Now, we set \(J(i+1)=J(i)\) and we choose  as a child
as a child  with a label
with a label  such that, for any \(\psi \),
such that, for any \(\psi \),  if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i+1)}\). Note that at least one such child exists, because at least one child has the same label as
if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i+1)}\). Note that at least one such child exists, because at least one child has the same label as  . Thus the invariant holds by construction.
. Thus the invariant holds by construction. -
3.
If an expansion rule has been applied to
 , then there are one or two children. In both cases, we set \(J(i+1)=J(i)\). Then, we proceed as follows.
, then there are one or two children. In both cases, we set \(J(i+1)=J(i)\). Then, we proceed as follows. -
(a)
If there is only one child, then it is chosen as
 . In such a case, the applied rule is necessarily the
. In such a case, the applied rule is necessarily the  one, applied to a formula \(\psi \equiv \psi _1\wedge \psi _2\), and thus
one, applied to a formula \(\psi \equiv \psi _1\wedge \psi _2\), and thus  . By construction, \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i)}\), and thus \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i+1)}\). Since \({{\,\textrm{snf}\,}}(\psi _1\wedge \psi _2)={{\,\textrm{snf}\,}}(\psi _1)\wedge {{\,\textrm{snf}\,}}(\psi _2)\), it holds that \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) and \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\). As for the other direction, if \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) and \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\), then \(\nu \models {{\,\textrm{snf}\,}}(\psi _1\wedge \psi _2)_S^{J(i+1)}\), and thus \(\nu \models {{\,\textrm{snf}\,}}(\psi _1\wedge \psi _2)_S^{J(i)}\). Then, by construction, it holds that
. By construction, \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i)}\), and thus \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i+1)}\). Since \({{\,\textrm{snf}\,}}(\psi _1\wedge \psi _2)={{\,\textrm{snf}\,}}(\psi _1)\wedge {{\,\textrm{snf}\,}}(\psi _2)\), it holds that \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) and \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\). As for the other direction, if \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) and \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\), then \(\nu \models {{\,\textrm{snf}\,}}(\psi _1\wedge \psi _2)_S^{J(i+1)}\), and thus \(\nu \models {{\,\textrm{snf}\,}}(\psi _1\wedge \psi _2)_S^{J(i)}\). Then, by construction, it holds that  , and thus
, and thus  . Hence, the invariant holds.
. Hence, the invariant holds. -
(b)
If there are two children
 and
and  , then let us suppose the applied rule is the
, then let us suppose the applied rule is the  rule (similar arguments hold for the other rules). In this case, the rule has been applied to a formula \(\psi \equiv \psi _1\vee \psi _2\), and thus
rule (similar arguments hold for the other rules). In this case, the rule has been applied to a formula \(\psi \equiv \psi _1\vee \psi _2\), and thus  and
and  . We know that \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i)}\), and hence \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i+1)}\). Since \({{\,\textrm{snf}\,}}(\psi _1\vee \psi _2)={{\,\textrm{snf}\,}}(\psi _1)\vee {{\,\textrm{snf}\,}}(\psi _2)\), it holds that either \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) or \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\). Now, we choose
. We know that \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i)}\), and hence \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i+1)}\). Since \({{\,\textrm{snf}\,}}(\psi _1\vee \psi _2)={{\,\textrm{snf}\,}}(\psi _1)\vee {{\,\textrm{snf}\,}}(\psi _2)\), it holds that either \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) or \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\). Now, we choose  accordingly, so to respect the invariant. Note that if both nodes are eligible, which one is chosen does not matter. The other direction of the invariant holds as well, since if either \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) or \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\), then \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i)}\) or \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i)}\), and thus \(\nu \models {{\,\textrm{snf}\,}}(\psi _1\vee \psi _2)_S^{J(i)}\). Hence,
accordingly, so to respect the invariant. Note that if both nodes are eligible, which one is chosen does not matter. The other direction of the invariant holds as well, since if either \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i+1)}\) or \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i+1)}\), then \(\nu \models {{\,\textrm{snf}\,}}(\psi _1)_S^{J(i)}\) or \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^{J(i)}\), and thus \(\nu \models {{\,\textrm{snf}\,}}(\psi _1\vee \psi _2)_S^{J(i)}\). Hence,  , and then either
, and then either  or
or  .
.
-
(a)
Let  be the branch prefix built as above explained, and let
be the branch prefix built as above explained, and let  be the sequence of its step nodes. As already pointed out, the descent stops when \(\pi _n\) is a leaf or when \(n=k+1\). Note that any leaf is a step node, so
be the sequence of its step nodes. As already pointed out, the descent stops when \(\pi _n\) is a leaf or when \(n=k+1\). Note that any leaf is a step node, so  . In case we find a leaf, it is not possible that it has been rejected by the
. In case we find a leaf, it is not possible that it has been rejected by the  rule. Otherwise, we would have
rule. Otherwise, we would have  , which would mean \(\nu \models p^{J(i)}\) and \(\nu \models \lnot p^{J(i)}\), which is not possible. Moreover, it is not possible that it has been rejected by the
, which would mean \(\nu \models p^{J(i)}\) and \(\nu \models \lnot p^{J(i)}\), which is not possible. Moreover, it is not possible that it has been rejected by the  rule, as that would mean there is some
rule, as that would mean there is some  , with
, with  , and we know that
, and we know that  , and then
, and then  , since
, since  . Then, by definition of \(\llbracket \phi \rrbracket ^k\), we know that \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(i)-1}\). Since
. Then, by definition of \(\llbracket \phi \rrbracket ^k\), we know that \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(i)-1}\). Since  is a step node, \(J(i)-1=J(j)\), for some j such that
is a step node, \(J(i)-1=J(j)\), for some j such that  , and thus \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(j)}\), and by construction we know that
, and thus \(\nu \models {{\,\textrm{snf}\,}}(\alpha )_S^{J(j)}\), and by construction we know that  , which conflicts with the hypothesis that the
, which conflicts with the hypothesis that the  rule rejected the branch. By a similar argument, we can conclude that it is not possible that it has been rejected by the
rule rejected the branch. By a similar argument, we can conclude that it is not possible that it has been rejected by the  rule. Hence, we found a branch that either is longer than \(k+1\) step nodes, or has been accepted, or has been rejected by the
rule. Hence, we found a branch that either is longer than \(k+1\) step nodes, or has been accepted, or has been rejected by the  or
or  rules.\(\square \)
rules.\(\square \)
The formulas \(|\phi |^k\) and \(|\phi |_{\text {fin}}^k\) are called respectively the base encoding and the finite base encoding of \(\phi \) and, in addition to the k-unraveling, include the encoding of the  and
and  rules (in \(|\phi |^k\)), and of the
rules (in \(|\phi |^k\)), and of the  rule (in \(|\phi |_{\text {fin}}^k\)). These are the rules that accept the branches. The two formulas are defined as follows:
rule (in \(|\phi |_{\text {fin}}^k\)). These are the rules that accept the branches. The two formulas are defined as follows:
where the formulas \(E_k\) and \({\widetilde{E}}_k\), that together encode the  and
and  rules, are defined as follows:
rules, are defined as follows:

and the formula \(L_k\), that encodes the  rule, is defined as follows:
rule, is defined as follows:
where

Intuitively, \(_lR_k\) encodes the presence of two nodes whose labels contain the same requests for the next and the previous nodes. Note that the  rule demands the two nodes to have the same labels, while here we are checking something looser. Hence, we need \(_lG_k\) to be sure that the two nodes can be used to loop, and in particular, that the past requests at the step \(l+1\) are fulfilled at step k. This turns out to be sufficient (see Lemma 3 below). Then, \(_lF_k\) checks that all the
rule demands the two nodes to have the same labels, while here we are checking something looser. Hence, we need \(_lG_k\) to be sure that the two nodes can be used to loop, and in particular, that the past requests at the step \(l+1\) are fulfilled at step k. This turns out to be sufficient (see Lemma 3 below). Then, \(_lF_k\) checks that all the  are fulfilled between those nodes. The following result shows that \(|\phi |^k\) encodes tableau trees where at least one branch is accepted in \(k+1\) steps.
are fulfilled between those nodes. The following result shows that \(|\phi |^k\) encodes tableau trees where at least one branch is accepted in \(k+1\) steps.
Lemma 2
Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. If the complete tableau for infinite-trace (resp. for finite-trace) semantics for \(\phi \) contains an accepted branch of \(k+1\) step nodes, then \(|\phi |^k\) (resp. \(|\phi |_{\text {fin}}^k\)) is satisfiable.
Proof
Suppose that the complete tableau (either for finite- or infinite-trace semantics) for \(\phi \) contains an accepted branch of \(k+1\) step nodes, so let  be such a branch, and let
be such a branch, and let  be the sequence of its step nodes. By Lemma 1, \(\llbracket \phi \rrbracket ^k\) is satisfiable. We can then build a truth assignment \(\nu \), in the same way as in the proof of Lemma 1, such that \(\nu \models \llbracket \phi \rrbracket ^k\). Remember that this means that we set \(\nu (p^i)=\top \) if and only if
be the sequence of its step nodes. By Lemma 1, \(\llbracket \phi \rrbracket ^k\) is satisfiable. We can then build a truth assignment \(\nu \), in the same way as in the proof of Lemma 1, such that \(\nu \models \llbracket \phi \rrbracket ^k\). Remember that this means that we set \(\nu (p^i)=\top \) if and only if  , for all \(0\le i\le k\). Thus, depending on the semantics we have to prove that \(\nu \) satisfies either \(E_k\wedge {\widetilde{E}}_k\) or \(L_k\) (for the infinite-trace semantics) or just \(E_k\) (for the finite-trace semantics). To this end, we need to preliminarily show that
, for all \(0\le i\le k\). Thus, depending on the semantics we have to prove that \(\nu \) satisfies either \(E_k\wedge {\widetilde{E}}_k\) or \(L_k\) (for the infinite-trace semantics) or just \(E_k\) (for the finite-trace semantics). To this end, we need to preliminarily show that  if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^i\). Such a statement can be proved by induction on the structure of \(\psi \), by exploiting the definition of the expansion rules of the tableau.
if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^i\). Such a statement can be proved by induction on the structure of \(\psi \), by exploiting the definition of the expansion rules of the tableau.
Now, we distinguish three cases, depending on which rule accepted the branch.
-
1.
If, in the tableau for infinite-trace semantics, the branch was accepted by the
 rule, then
rule, then  does not contain tomorrow or weak tomorrow formulas. By definition of \(\nu \), it follows that \(\nu \models \lnot \psi _S^k\), for any
does not contain tomorrow or weak tomorrow formulas. By definition of \(\nu \), it follows that \(\nu \models \lnot \psi _S^k\), for any  , and thus \(E_k\) and \({\widetilde{E}}_k\) are satisfied.
, and thus \(E_k\) and \({\widetilde{E}}_k\) are satisfied. -
2.
If, in the tableau for finite-trace semantics, the branch was accepted by the
 rule, a similar reasoning implies that \(E_k\) is satisfied.
rule, a similar reasoning implies that \(E_k\) is satisfied. -
3.
If the branch was accepted by the
 rule, then there exists a node \(\pi _l\) such that
rule, then there exists a node \(\pi _l\) such that  . By definition of \(\nu \), it holds that \(\nu \models \psi _S^l\) if and only if \(\nu \models \psi _S^k\), for any
. By definition of \(\nu \), it holds that \(\nu \models \psi _S^l\) if and only if \(\nu \models \psi _S^k\), for any  , and thus \(_lR_k\) is satisfied. Moreover, since
, and thus \(_lR_k\) is satisfied. Moreover, since  , any past request
, any past request  or
or  contained in
contained in  , that by construction is fulfilled in \(\pi _l\), is also fulfilled in \(\pi _k\), hence \(_lG_k\) is satisfied as well. Then, we know that for any
, that by construction is fulfilled in \(\pi _l\), is also fulfilled in \(\pi _k\), hence \(_lG_k\) is satisfied as well. Then, we know that for any 
 requested in
requested in  , \(\psi \) has been fulfilled between \(\pi _l\) and \(\pi _k\), i.e. there exists \(l<j\le k\) such that
, \(\psi \) has been fulfilled between \(\pi _l\) and \(\pi _k\), i.e. there exists \(l<j\le k\) such that  . Hence, it holds that \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^j\), and thus \(_lF_k\) is satisfied. Then, \(_lR_k \wedge {}_lG_k \wedge {}_lF_k\) is satisfied for at least one l, so \(L_k\) is satisfied.\(\square \)
. Hence, it holds that \(\nu \models {{\,\textrm{snf}\,}}(\psi _2)_S^j\), and thus \(_lF_k\) is satisfied. Then, \(_lR_k \wedge {}_lG_k \wedge {}_lF_k\) is satisfied for at least one l, so \(L_k\) is satisfied.\(\square \)
Lemma 3
Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. If \(|\phi |^k\) (resp. \(|\phi |_{\text {fin}}^k\)) is satisfiable, then the complete tableau for \(\phi \) for infinite-trace (resp. finite-trace) semantics contains an accepted branch.
Proof
Suppose that \(|\phi |^k\) (resp. \(|\phi |_{\text {fin}}^k\)) is satisfiable. Hence, there exists a truth assignment \(\nu \) such that \(\nu \models |\phi |^k\) (resp. \(\nu \models |\phi |_{\text {fin}}^k\)). Then, \(\llbracket \phi \rrbracket ^k\) is satisfiable, and we know from Lemma 1 that the complete tableau for \(\phi \) has a branch that is either accepted, rejected by  (or
(or  ), or longer than \(k+1\) step nodes. Let
), or longer than \(k+1\) step nodes. Let  be the branch prefix found as shown in the proof of Lemma 1, and let
be the branch prefix found as shown in the proof of Lemma 1, and let  be the sequence of its step nodes. By construction, there exists a function \(J:\mathbb {N}\rightarrow \mathbb {N}\) fulfilling the invariant:
be the sequence of its step nodes. By construction, there exists a function \(J:\mathbb {N}\rightarrow \mathbb {N}\) fulfilling the invariant:  if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i)}\). We now show that indeed
if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^{J(i)}\). We now show that indeed  is accepted or is the prefix of an accepted branch. Now we distinguish whether we are talking about \(|\phi |^k\) or \(|\phi |_{\text {fin}}^k\):
is accepted or is the prefix of an accepted branch. Now we distinguish whether we are talking about \(|\phi |^k\) or \(|\phi |_{\text {fin}}^k\):
-
1.
If \(|\phi |^k\) is satisfiable, either \(E_k\wedge {\widetilde{E}}_k\) or \(L_k\) are satisfiable as well. We distinguish the two cases:
-
(a)
If \(E_k\wedge {\widetilde{E}}_k\) is satisfiable, then \(\nu \models \lnot \psi _S^k\) for each
 . Since \(\psi \) is an
. Since \(\psi \) is an  - or
- or  -request, \({{\,\textrm{snf}\,}}(\psi )\equiv \psi \), and thus \(\nu \not \models {{\,\textrm{snf}\,}}(\psi )_S^k\). Here, \(k=J(j)\), for some j, and, from the invariant, it follows that
-request, \({{\,\textrm{snf}\,}}(\psi )\equiv \psi \), and thus \(\nu \not \models {{\,\textrm{snf}\,}}(\psi )_S^k\). Here, \(k=J(j)\), for some j, and, from the invariant, it follows that  . Hence,
. Hence,  does not contain any
does not contain any  - or
- or  -request, triggering the
-request, triggering the  rule that accepts the branch.
rule that accepts the branch. -
(b)
If \(L_k\) is satisfiable, so are \(_lR_k\), \(_lG_k\) and \(_lF_k\), for some \(0\le l < k\). From \(_lR_k\), we have that \(\nu \models \psi _S^l\) if and only if \(\nu \models \psi _S^k\) for all
 , that is, \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^l\) if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^k\), because \(\psi \) is an
, that is, \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^l\) if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )_S^k\), because \(\psi \) is an  -,
-,  -,
-,  -, or
-, or  -request. Here, \(l=J(i)\) and \(k=J(j)\), for some i and some j. Since the value of the function J increments at each step node, w.l.o.g. we can assume that
-request. Here, \(l=J(i)\) and \(k=J(j)\), for some i and some j. Since the value of the function J increments at each step node, w.l.o.g. we can assume that  and
and  are step nodes, and by the invariant it holds that
are step nodes, and by the invariant it holds that  if and only if
if and only if  , that is,
, that is,  and
and  have the same
have the same  -,
-,  -,
-,  -, and
-, and  -requests. Similarly, the fact that \(\nu \models {}_lF_k\) tells us that all the
-requests. Similarly, the fact that \(\nu \models {}_lF_k\) tells us that all the  requested in
requested in  are fulfilled between
are fulfilled between  and
and  . The
. The  rule requires two identical labels in order to trigger, but
rule requires two identical labels in order to trigger, but  and
and  only have the same requests. However, since they have the same
only have the same requests. However, since they have the same  -requests, we know that
-requests, we know that  . Then, there is a step node
. Then, there is a step node  , grandchild of
, grandchild of  , such that
, such that  and the segment of the branch between
and the segment of the branch between  and
and  is equal to the segment between
is equal to the segment between  and
and  , hence all the
, hence all the  requested in
requested in  and
and  , fulfilled between
, fulfilled between  and
and  , are fulfilled between
, are fulfilled between  and
and  as well, and the
as well, and the  rule can apply to
rule can apply to  , accepting the branch.
, accepting the branch.
-
(a)
-
2.
If \(|\phi |_{\text {fin}}^k\) is satisfiable, then \(E_k\) is satisfiable, and the same reasoning applied above for \(E_k\wedge {\widetilde{E}}_k\) applies, to conclude that the
 has accepted the branch.\(\square \)
has accepted the branch.\(\square \)
Finally, the formula \(|\phi |_T^k\) and \(|\phi |_{T, fin }^k\), called the termination encoding and the finite termination encoding, and encode the  and the
and the  rule, respectively. The formulas are defined as follows:
rule, respectively. The formulas are defined as follows:
where

It can be shown that \(|\phi |_T^k\) or \(|\phi |_{T, fin }^k\) are unsatisfiable if the tableau for \(\phi \), for infinite or finite traces respectively, contains only rejected branches.
Lemma 4
Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. If \(|\phi |^k_T\) (resp. \(|\phi |_{T, fin }^k\)) is unsatisfiable, then the complete tableau for \(\phi \) for infinite traces (resp. finite traces) contains only rejected branches.
Proof
We prove the contrapositive, that is, if the complete tableau for \(\phi \) contains an accepted branch, then \(|\phi |^k_T\) (or \(|\phi |_{T, fin }^k\)) is satisfiable. Let  be such a branch, and let
be such a branch, and let  be the sequence of its step nodes. By Lemma 1, we know \(\llbracket \phi \rrbracket ^k\) is satisfiable, thus we can obtain a truth assignment \(\nu \) such that \(\nu \models \llbracket \phi \rrbracket ^k\). We can build \(\nu \) as in the proof of Lemma 1, that is, such that \(\nu (p^i)=\top \) if and only if
be the sequence of its step nodes. By Lemma 1, we know \(\llbracket \phi \rrbracket ^k\) is satisfiable, thus we can obtain a truth assignment \(\nu \) such that \(\nu \models \llbracket \phi \rrbracket ^k\). We can build \(\nu \) as in the proof of Lemma 1, that is, such that \(\nu (p^i)=\top \) if and only if  for all \(0\le i\le k\). Similarly to the proof of Lemma 2, it holds that
for all \(0\le i\le k\). Similarly to the proof of Lemma 2, it holds that  if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )^i_S\). Now, since the branch is accepted, neither the
if and only if \(\nu \models {{\,\textrm{snf}\,}}(\psi )^i_S\). Now, since the branch is accepted, neither the  nor the
nor the  rule can be applied to it. This has the following consequences, depending on whether we are dealing with infinite or finite traces:
rule can be applied to it. This has the following consequences, depending on whether we are dealing with infinite or finite traces:
-
1.
for infinite traces, it means that either (i) there are no three nodes \(\pi _u\), \(\pi _v\), \(\pi _w\) such that
 , or (ii) these three nodes exist, but there is an
, or (ii) these three nodes exist, but there is an  \(\psi \), requested in
\(\psi \), requested in  , which is fulfilled between \(\pi _u\) and \(\pi _v\) and not between \(\pi _v\) and \(\pi _w\). In case (i), this means that \(_uR_v\wedge {}_vR_w\) does not hold for any u and v. In case (ii), \(_uR_v\wedge {}_vR_w\) holds, but \(_uP_v^w\) does not. In both cases, it follows that \(\lnot P^i\) holds for any \(0\le i \le k\), and thus \(|\phi |^k_T\) is satisfied;
, which is fulfilled between \(\pi _u\) and \(\pi _v\) and not between \(\pi _v\) and \(\pi _w\). In case (i), this means that \(_uR_v\wedge {}_vR_w\) does not hold for any u and v. In case (ii), \(_uR_v\wedge {}_vR_w\) holds, but \(_uP_v^w\) does not. In both cases, it follows that \(\lnot P^i\) holds for any \(0\le i \le k\), and thus \(|\phi |^k_T\) is satisfied; -
2.
for finite traces, it means that there are no two nodes \(\pi _u\), \(\pi _w\) such that
 . A similar reasoning as above concludes that \(|\phi |_{T, fin }^k\) is satisfied.\(\square \)
. A similar reasoning as above concludes that \(|\phi |_{T, fin }^k\) is satisfied.\(\square \)
Together with the soundness and completeness results for the underlying tableau (Proposition 1), the above Lemmata allow us to prove the soundness and completeness of Algorithm 1.
Theorem 1
(Soundness and completeness) Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. Algorithm 1 always terminates and answers SATon \(\phi \) if and only if \(\phi \) is satisfiable.
Proof
As for the left-to-right direction, suppose that the procedure at Algorithm 1 answers SATon the formula \(\phi \). Then, it means there is a \(k\ge 0\) such that \(|\phi |^k\) is satisfiable. By Lemma 3, the complete tableau for \(\phi \) has an accepting branch. By the soundness of the tableau, \(\phi \) is satisfiable.
As for the right-to-left direction, suppose that the formula \(\phi \) is satisfiable. By the completeness of the tableau, the complete tableau for \(\phi \) has an accepting branch. Let us suppose that such a branch has \(k+1\) step nodes, for some \(k\ge 0\). Then, we have to show that the procedure eventually answers SAT. Let \(i<k\) be any earlier iteration of the main loop of the algorithm. By Lemma 1, \(\llbracket \phi \rrbracket ^i\) is satisfiable because there is a branch longer than \(i+1\) step nodes. Similarly, by Lemma 4, \(|\phi |^i_T\) (or \(|\phi |_{T, fin }^i\)) is satisfiable because not all the branches of the tableau are rejected. Hence, the algorithm does not answer UNSATat step i. At step k, \(|\phi |^k\) is satisfiable by Lemma 2, because the tableau has an accepted branch of \(k+1\) step nodes, and thus the algorithm answers SAT.
To see the guarantee of termination, consider that if the formula is satisfiable, then by the above soundness argument we get a SAT answer, hence the algorithm terminates. Otherwise, the termination argument for the tableau ensures us that at some depth k all the branches will be closed by  (or
(or  ), hence \(|\phi |^k_T\) (or \(|\phi |_{T, fin }^k\)) will be unsatisfiable, and the algorithm will return UNSAT.\(\square \)
), hence \(|\phi |^k_T\) (or \(|\phi |_{T, fin }^k\)) will be unsatisfiable, and the algorithm will return UNSAT.\(\square \)
4.1 Incremental Algorithm
Algorithm 1 can be improved to better exploit the incrementality features of modern SATsolvers. We describe here how to do that in the case of infinite traces. The finite-traces case is very similar. Most solvers give the possibility to ask multiple related satisfiability queries without discarding the learnt clauses between subsequent calls. Depending on the cases, performance can dramatically increase in this way. Algorithm 2 is a variant of Algorithm 1 that shows how to exploit the incrementality of the underlying solver, making use of an assumption-based interface. With such an interface, supported by all major SATand \({\textsf{SMT}}\,\)solvers (see e.g. [21]), the satisfiability of multiple assertions can be asked, each time maintaining the clauses learnt from older assertions. Moreover, the satisfiability of the current set of assertions can be asked multiple times with a different set of assumptions, where learnt clauses that follow from the current assumption are discarded at the following satisfiability query. In this way, the procedure maintains learnt clauses in the SATsolvers between multiple iteration steps, allowing the solver to build a rich understanding of the tableau tree that is maintained step after step.
We will now define the assumption-based interface that we assume a SAT solver to support in order to make Algorithm 2 work correctly. Many solvers support this style of interfacing. An incremental solver supports these four operations:
-
1.
Initialization The expression new Solver (used at Line 3 of Algorithm 2) returns a new object, say s, that keeps track of the state of the solver, that includes A(s), a Boolean formula called the current assertion of the solver. After the initialization, \(A(s)=\top \), initially.
-
2.
Assertion Given a solver object s and a Boolean formula \(\phi \), a call to \(s.\text {assert}(\phi )\) conjuncts \(\phi \) to the current assertion, i.e. \(A(s)\leftarrow A(s) \wedge \phi \).
-
3.
Solving Given a solver object s, a call to \(s.\text {solve()}\) asks the solver to solve the satisfiability problem for the current assertion. That is, the call returns SATif A(s) is satisfiable, or UNSATotherwise.
-
4.
Solving with assumptions Given a solver object s and a Boolean formula \(\phi \), a call to \(s.\hbox { solve-assuming}\ (\phi )\) asks the solver to solve the satisfiability problem for the current assertion set conjuncted with \(\phi \). That is, the call returns SATif \(A(s)\wedge \phi \) is satisfiable, or UNSATotherwise. Note that the current assertion is not modified by the call.
The semantics of the above operations do not talk about what happens under the hood. In practice, a solver implementing these operations will keep as much information as possible between subsequent calls to \(\text {solve()}\) and \(\text {solve-assuming}()\), to waste as little work as possible. This can dramatically speed up SAT based algorithms in many cases [22, 43].
Assuming the underlying SATsolver correctly implements the above interface, we can prove the correctness of Algorithm 2.
Theorem 2
(Incremental algorithm) Let \(\phi \) be an \({\mathsf {LTL{+}Past}}\,\)formula. Algorithm 2 always terminates and answers SAT if and only if \(\phi \) is satisfiable.
Proof
Let \(\phi \) be an \(\textsf{LTL}\,\)formula. At first, let us track the evolution of A(s) through the execution of the algorithm. We track the calls to \(s.\text {assert}()\), which is called at Line 4 (i.e. before the loop), at Line 12, and at Line 17 (at the end of the loop). It is easy to see that at each iteration k, at the beginning of the loop (Line 6), the current assertion is as follows:
Note, instead, that after Line 12, at each iteration k, the assertion is as follows:
Now, suppose Algorithm 2 returns SATat some iteration \(k\ge 0\). This can only happen at Line 9. Then, the call to \(s.\text {solve-assuming}((E_k \wedge {\widetilde{E}}_k) \vee L_k)\) returned SAT. This means \(A(s)\wedge ((E_k \wedge {\widetilde{E}}_k) \vee L_k)\) is satisfiable. Notice that this implies \(|\phi |^k\) is satisfiable, hence by Lemma 3, \(\phi \) is satisfiable.
Conversely, suppose \(\phi \) is satisfiable. By the completeness of the tableau, the complete tableau for \(\phi \) has an accepting branch. Let us suppose that such a branch has \(k+1\) step nodes, for some \(k\ge 0\). For all iterations \(i\le k\), by Lemma 1, \(\llbracket \phi \rrbracket ^i\) is satisfiable, and by Lemma 4, \(|\phi |^k_T\) is satisfiable. Hence, neither Line 7 nor Line 14 returns UNSATat any iterations \(i<k\). Instead, by Lemma 2, we know \(|\phi |^k\equiv \llbracket \phi \rrbracket ^k\wedge (E_k \wedge {\widetilde{E}}_k) \vee L_k\) is satisfiable, hence Line 10 correctly returns SAT.
Termination is proved along the lines of Theorem 1, considering that Line 13 effectively tests the satisfiability of \(|\phi |^k_T\) at each iteration.\(\square \)
4.2 Extraction of Models
We conclude the section by briefly describing an additional feature of the proposed encoding and algorithm: they can be used not only to decide the satisfiability of \({\mathsf {LTL{+}Past}}\,\)formulas, but also to extract a model for satisfiable ones.
Such an extraction consists of two steps. First of all, one has to ask the SAT solver to return the values of the proposition letters \(p^t\) from the assignment to \(|\phi |^k\). These proposition letters tell the truth value of the proposition p at each time step t.
Next, in the case of infinite-state semantics, one has to extract the starting state of the loop of the periodic model identified by the  rule, if any. To this end, a few propositions \(\ell _{l,k}\) are introduced, for some k and some \(l<k\), and the formula \(L_k\), which is used in the base encoding \(|\phi |^k\), is modified as follows:
rule, if any. To this end, a few propositions \(\ell _{l,k}\) are introduced, for some k and some \(l<k\), and the formula \(L_k\), which is used in the base encoding \(|\phi |^k\), is modified as follows:
It is clear that this formulation of \(L_k\) is equisatisfiable to the formulation of \(L_k\) that has been presented above. However, in this way, for a satisfiable formula \(\varphi \), the first \(\ell _{l,k}\) that turns out to be true tells us that the loop starts at time \(t=l\). If no one of them holds, the branch was closed by the  rule and the model can be regarded as looping through its last state (if we are looking for an infinite model).
rule and the model can be regarded as looping through its last state (if we are looking for an infinite model).
5 Implementation
In order to perform the experimental evaluation described in the next section, the proposed algorithm has been implemented in a tool that has been called BLACK(Bounded Ltl sAtisfiability ChecKer). To ease reproducibility of the results, the tool is portable across all major platforms and runs on Windows, Linux, and macOS, and easy-to-install binary packages are provided for all the supported platforms. Developed over the course of a few years, BLACKevolved beyond being a simple prototype to test our algorithm. For this reason, this section describes BLACK’s internal architecture and its main features.
5.1 BLACK’s Library
An important feature of the tool is its embeddability into third-party applications: BLACKis implemented as a shared library, written in C++20, that can be linked by any client application, with a well-defined API that provides access to BLACK’s solver and more. The tool itself is then just a thin command-line wrapper over the library. We will call BLACK’s library \({\textsf{libblack}}\,\), and the BLACKtool black, to distinguish them from BLACKthe project as a whole. A high-level account of the architecture of BLACKis given in Fig. 2.
The \({\textsf{libblack}}\,\)library provides several facilities besides the solver itself:
-
1.
basic supporting data structures and metaprogramming utilities;
-
2.
mechanisms to create, parse, and manipulate \(\textsf{LTL}\,\)and propositional formulas;
-
3.
an abstraction layer over the supported SAT solver backends.
The mechanisms to handle \(\textsf{LTL}\,\)formulas inside the library merit their own discussion. To ease memory management (one of the primary source of bugs in C++ programs), formulas are represented by objects whose lifetime is exclusively handled by a central alphabet object whose purpose is to create and keep track of created formulas. Formulas are created by asking the alphabet object to create new (objects representing) propositional symbols, and then combining such symbols with logical and temporal operators to obtain more complex formulas. All formulas are destroyed when the lifetime of the parent alphabet object ends. In order to save memory, equal formulas are reused. This means that creating twice the same formula (say, \(p \wedge q\)), will not create two different objects, but the same object is returned. This deduplicating mechanism, implemented through the use of an efficient hash table, ensures that checking equality of formulas (for example to implement memoization of recursive procedures) can be done in \({\mathcal {O}}(1)\) time with a simple and very fast pointer comparison. On top of that, formulas can of course also be created by parsing strings or text files.
The above structure is similar to the API of many SMT solvers (such as Z3 [20] or MathSAT [14]), but there are two key differences. The first regards how propositional letters are labelled. In similar APIs, the name of a propositional symbol or variable is usually a string of some kind ("p", "q", etc.). Instead, \({\textsf{libblack}}\,\)allows objects of any type to be used as the label of propositional letters. This means that labels of such symbols can carry complex information, and, in particular, propositional letters can be labelled by other formulas. Thanks to this particular feature, the surrogating transformation of a formula \(\phi \) into its corresponding grounded symbol \(\phi _S\), used in the encoding described in Sect. 4, is essentially a no-op: the object representing \(\phi _S\) is just a propositional symbol whose label is \(\phi \).
The second key ingredient is how formulas can be handled once they are created. In order to ease the implementation of several parts of the solver (the NNF, the stepped normal form, the encoding, etc.) the \({\textsf{libblack}}\,\)library provides facilities to manipulate formulas using a functional-style pattern matching approach, instead of complex visitor patterns usually required for such scenarios in classical object-oriented approaches. As an example, the snippet of code shown in Fig. 3 computes the depth of a formula.
Besides the unavoidable noise introduced by the C++ syntax, the above snippet shows a clear connection with the formal definition of depth of a formula (which we do not need to recall here). Note that the burden of implementing this mechanism of formula manipulation is on the library, since the language does not natively support functional-style pattern matching on objects.
Thanks to these particular features, the whole encoding and solver algorithm are implemented in just over 400 lines of readable source code. Note that this formula manipulation layer works for both \(\textsf{LTL}\,\)and propositional formulas (which are just a subset of \(\textsf{LTL}\,\)formulas) and is useful beyond its use of feeding formulas to the solver, making \({\textsf{libblack}}\,\)a flexible basic block for any application that needs to create, parse, and manipulate \(\textsf{LTL}\,\)formulas.
The second major purpose of the library is to provide access to the SAT solver backends. As already mentioned, \({\textsf{libblack}}\,\)supports MiniSAT [21], CryptoMiniSAT [49], Z3 [20], cvc5 [3], and MathSAT [14] as backends. Supporting additional backends is a matter of implementing a few functions to plug into the abstraction layer. Support for further backends is planned for the future. The major difference in the API of MiniSAT and CryptoMiniSAT on one side, and Z3 and MathSAT on the other, is that the former two solvers accept input in conjunctive normal form (CNF), while the latter two accept free-form Boolean formulas. In order to support the CNF-based solvers, \({\textsf{libblack}}\,\)implements a CNF conversion utility based on the classic Tseitin encoding. This is all hidden behind an abstraction layer that allows the client application to just create a generic sat::solver object, feed it with propositional formulas, and get the result of the SAT solving process.
It is also worth mentioning that BLACKsupports a first-order extension of \(\textsf{LTL}_{\textsf{f}\,}\)called \(\textsf{LTL}_{\textsf{f}\,}\) modulo theories (\(\textsf{LTL}_\textsf{f}^{\textsf{MT}}\,\)). The description of this logic is beyond the scope of this paper, but readers are redirected to the relevant literature [30].
6 Experimental Evaluation
In this section, we describe the experimental evaluation of BLACKagainst other state-of-the-art tools for the satisfiability of \(\textsf{LTL}\,\), \({\mathsf {LTL{+}Past}}\,\), and \(\textsf{LTL}_{\textsf{f}\,}\)formulas. Benchmarks consist of a set of input formulas (see later for a detailed account) over which the different tools have been run to measure their solving speed. All the benchmarks have been run on a 16-core AMD EPYC 7281 processor with 64GB of RAM, with a timeout of five minutes and a memory limit of 3GB for each formula. All the benchmark formulas and the supporting scripts are available in BLACK’s source code repository.Footnote 3 In all the tests described here, BLACKhas been run using the Z3 backend [20], which is the default backend included in BLACK’s binary distributions.
Cactus plots for \(\textsf{LTL}\,\)over infinite traces (top row), \({\mathsf {LTL{+}Past}}\,\)(middle row), and \(\textsf{LTL}\,\)over finite traces (bottom row). The total number of formulas in the third column is higher than the sum of SAT and UNSAT formulas. This is because some formulas are not solved by any of the tools, i.e. we don’t know if they are SAT or not. Therefore they are counted only when aggregating all the results
6.1 \(\textsf{LTL}\,\)Over Infinite Traces
To evaluate BLACK’s performance on \(\textsf{LTL}\,\)over infinite traces, we compared it with the following tools:
-
1.
the \({\textsf{nuXmv}}\,\)[11] model checker, both in SBMC and K-Liveness modesFootnote 4;
-
2.
Aalta 2 [37], a tool based on an explicit graph-shaped tableau built with the help of a SAT solverFootnote 5;
-
3.
ls4 [51], version 1.1,Footnote 6 a solver based on labelled superposition; we used the ltl2snf conversion tool to put the formulas in the required separated normal form [34]Footnote 7;
-
4.
pltl, a tableau-based tool that implements both a graph-shaped tableau [1] and a tree-shaped tableau \(\grave{a}\, la\,\)Schwendimann [47];
-
5.
Leviathan [4], a tool that directly implements the construction of Reynolds’ tableau [45].Footnote 8
Of these, \({\textsf{nuXmv}}\,\)in SBMC mode and Leviathan are the most similar to BLACK, in different ways. The former implements an iterative model checking procedure that looks for counter-examples to the specification of length at most k, for increasing values of k, with a completeness check that ensures termination for unsatisfiable formulas [32]. Note that this means we do not need to specify a maximum value for k in SBMC mode. The latter is the first implementation of Reynolds’ tableau, which is the tableau underlying BLACK’s SAT encoding and algorithm, that Leviathan constructs explicitly. All the tools are run with their default options. In particular, they do not offer tuning options nor anything that can affect the result of the evaluation except for the operating mode of \({\textsf{nuXmv}}\,\)(SBMC vs. K-Liveness) and pltl (graph- vs. tree-shaped tableau).
These tools have been tested on a total of 4181 formulas, which have been obtained from two different sources:
-
1.
the formulas collected by Schuppan and Darmawan [46], which include the acacia, alaska, anzu, forobots, rozier, trp, and schuppan setsFootnote 9;
-
2.
a set of formulas coming from the \(\textsf{LTL}\,\)encoding of the temporal description logic TDL-lite, as described by Tahrat et al. [52], which are referred to in the plots as the tdllite set.
The results are shown in the scatter plots of Figs. 4, 5, 6, in the cactus plot of Fig. 9, and in the bar charts of Fig. 10. In the comparison with \({\textsf{nuXmv}}\,\), it can be seen that BLACKoutperforms it in SBMC mode, which is the most similar approach to BLACK. With respect to \({\textsf{nuXmv}}\,\)in K-Liveness mode, BLACKperforms better over satisfiable formulas and suffers over unsatisfiable formulas. This is a pattern that repeats also in the comparison with Aalta. This suffering in unsatisfiable formulas can be explained with the cubic growth in size of the termination encoding \(|\phi |^k_T\) at increasing values of k. On the other hand, in the comparison with the tableau-based tools Leviathan and pltl, it can be seen that BLACKperforms considerably better both on satisfiable and unsatisfiable formulas. It is worthwhile to note that BLACKperforms particularly well on the tdllite set, followed by Aalta and ls4.
6.2 \({\mathsf {LTL{+}Past}}\,\)
To evaluate BLACKover \({\mathsf {LTL{+}Past}}\,\)formulas, we compared it with \({\textsf{nuXmv}}\,\)[11] which, as far as we know, is the only other tool available that directly supports past operators. As there are no readily available benchmark sets for \({\mathsf {LTL{+}Past}}\,\)in the literature, we came up with our own. The benchmark formulas consist of two sets:
-
1.
the random set, which consists of 1300 randomly generated formulas of varying size, generated in a straightforward way, similarly to what was shown by Tauriainen and Heljanko [53] (269 UNSAT, 1011 SAT, 20 unknown);
-
2.
the crscounter set, which consists of 240 formulas resulted from the adaptation to the satisfiability problem of a benchmark set for model checking provided by Cimatti et al. [13] (112 UNSAT, 101 SAT, 27 unknown).
The second family needs some explanations. In the original benchmark set for model checking, a Kripke structure called Counter(N), where N is a power of two, is introduced. Counter(N) works as follows: it starts at \(c = 0\), counts up to \(c = N\), jumps back to \(c = N/2\), and then loops, counting up to \(c = N\) and jumping back to \(c = N/2\), forever. Afterwards, they evaluated, on top of that Kripke structure, some parametric properties of the form:

The value i identifies the number of nested once operators, while the structure of such properties requires that the loop of length N/2 in the model is traversed backwards several times in order to reach a counterexample.
Since these benchmarks were introduced in the context of model checking, we made a reduction from the model checking problem to the satisfiability checking one for \({\mathsf {LTL{+}Past}}\,\): we built the \({\mathsf {LTL{+}Past}}\,\)formulas \(\phi _{Counter(N)}\) and \(\phi _{P(i)}\) encoding the above elements. In this way, \(\lnot (\phi _{Counter(N)} \rightarrow \phi _{P(i)})\) is UNSATif and only if \(Counter(N) \models P(i)\). With this framework, we were able to obtain both SAT(\(i \le \frac{N}{2}\)) and UNSAT(\(i > \frac{N}{2}\)) formulas. Moreover, this family of formulas stresses the ability to process past operators and find short counterexamples, and thus it specifically challenges BLACK’s performance.
The results are shown in the scatter plots of Fig. 7, in the cactus plot of Fig. 9, and in the bar charts of Fig. 10. As can be seen, again BLACKoutperforms \({\textsf{nuXmv}}\,\)in SBMC mode, and is competitive with \({\textsf{nuXmv}}\,\)in K-Liveness mode. The performance gain is more visible in satisfiable formulas, as in the future-only formulas of the previous sections. In general, BLACK’s performance is better on random formulas. Note that, while for \(\textsf{LTL}\,\)(finite or infinite traces), most of the solvers solve most of the formulas in short time, general times needed to solve \({\mathsf {LTL{+}Past}}\,\)formulas are higher. The reason for this behaviour is that for the \({\mathsf {LTL{+}Past}}\,\)we have formulas (both the random and the crscounter sets) of increasing size. This translates into a slightly more uniform distribution of formulas over time with respect to the other cases where formulas tend to be fixed to a specific size.
6.3 \(\textsf{LTL}\,\)Over Finite Traces
Finally, we compared BLACKagainst two state-of-the-art tools for \(\textsf{LTL}\,\)over finite traces, namely Aaltaf [38],Footnote 10 which implements an algorithm, called Conflict-Driven \(\textsf{LTL}_{\textsf{f}\,}\) Satisfiability Checking, where a SAT-aided explicit tableau construction is paired with the extraction of unsatisfiable cores to prune the search space, and LTL2SAT [23],Footnote 11 a tool which employs a SAT-based reduction, but with specific heuristics for particular classes of formulas.
We compared the tools against the following sets of formulas:
-
1.
all the formula sets from the infinite traces case as described above, but interpreted over finite traces;
-
2.
a set of 1875 formulas particularly crafted for finite traces, referred to as LiEtAl2020 in the plots, taken from Li et al. [38] (1301 UNSAT, 567 SAT, 7 unknown).
The results are shown in the scatter plots of Fig. 8, in the cactus plot of Fig. 9, and in the bar charts of Fig. 10. The finite traces setting is the one where BLACKsuffers the most. As usual, the performance is better on satisfiable formulas. As in the infinite trace setting, it is worthwhile to note that BLACKperforms comparably particularly well on the tdllite set. It is worthwhile to note that, even though LTL2SAT generally has very good performance, it seems to suffer from some correctness problems since, in a non-negligible number of cases,Footnote 12 it reports results different from those reported by BLACKand Aaltaf.
7 Conclusions
In this paper, we presented a new SAT-based satisfiability checking technique for \(\textsf{LTL}\,\), \({\mathsf {LTL{+}Past}}\,\), and \(\textsf{LTL}_{\textsf{f}\,}\), inspired by the one-pass and tree-shaped tableau by Reynolds [45]. We provided full correctness proofs and an extensive experimental evaluation of the performance of its implementation, included in the BLACKsatisfiability checker, whose architecture has also been described. Performance-wise, the evaluation shows that our implementation of the technique is competitive with other state-of-the-art tools in most circumstances, especially on satisfiable formulas.
Many future developments are possible. From the point of view of the performance, it would be interesting to find heuristics to optimize the application of the  rule of the tableau in order to speed up the execution on unsatisfiable formulas. In particular, a linear-size encoding (similar to the ones for Bounded Model Checking introduced by Biere et al. [7]) would arguably provide a great speed-up in such cases.
rule of the tableau in order to speed up the execution on unsatisfiable formulas. In particular, a linear-size encoding (similar to the ones for Bounded Model Checking introduced by Biere et al. [7]) would arguably provide a great speed-up in such cases.
Reynolds’ tableau has been extended to other logics beyond \(\textsf{LTL}\,\), such as TPTL . A similar SAT (or SMT) encoding for the TPTL tableau would allow BLACKto support this real-time logic as well. Similar extensions are being investigated for first-order extensions of \(\textsf{LTL}\,\), e.g. \(\textsf{LTL}\,\) modulo theories [30].
As far as the tool itself is concerned, many improvements are possible, such as the support of more SAT backends, the improvement of the efficiency of the current CNF translation, the stabilization and documentation of the library API, the integration of more input and/or output formats. Moreover, the modular structure of the tool and of the library is not at all tied to the specific algorithm and encoding presented here, hence the implementation of different satisfiability checking approaches is possible and would provide a nice portfolio-based solver able to cope with even more application scenarios.
Notes
BLACKcan be downloaded from https://github.com/black-sat/black.
Of course, when checking the satisfiability of a formula, the tableau construction can stop as soon as a single accepted branch is found.
The original set contained also the negations of all the formulas but the benchmark set we used was downloaded from the StarExec platform [50], where the negations are not included.
Precisely, 468 formulas out of 6113.
References
Abate, P., Goré, R., Widmann, F.: An on-the-fly tableau-based decision procedure for PDL-satisfiability. Electron. Notes Theor. Comput. Sci. 231, 191–209 (2009). https://doi.org/10.1016/j.entcs.2009.02.036
Bacchus, F., Kabanza, F.: Planning for temporally extended goals. Ann. Math. Artif. Intell. 22(1–2), 5–27 (1998)
Barbosa, H., Barrett, C.W., Brain, M., Kremer, G., Lachnitt, H., Mann, M., Mohamed, A., Mohamed, M., Niemetz, A., Nötzli, A., Ozdemir, A., Preiner, M., Reynolds, A., Sheng, Y., Tinelli, C., Zohar, Y.: cvc5: a versatile and industrial-strength SMT solver. In: Fisman, D., Rosu, G. (eds.) Tools and Algorithms for the Construction and Analysis of Systems-28th International Conference, TACAS 2022, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2022, Munich, Germany, April 2-7, 2022, Proceedings, Part I, Lecture Notes in Computer Science, vol. 13243, pp. 415–442. Springer (2022). https://doi.org/10.1007/978-3-030-99524-9_24
Bertello, M., Gigante, N., Montanari, A., Reynolds, M.: Leviathan: a new LTL satisfiability checking tool based on a one-pass tree-shaped tableau. In: Proceedings of the 25th International Joint Conference on Artificial Intelligence, pp. 950–956. IJCAI/AAAI Press (2016)
Beth, E.W.: Semantic entailment and formal derivability. Sapientia 14(54), 311 (1959)
Biere, A., Cimatti, A., Clarke, E.M., Strichman, O., Zhu, Y.: Bounded model checking. Adv. Comput. 58, 117–148 (2003). https://doi.org/10.1016/S0065-2458(03)58003-2
Biere, A., Heljanko, K., Junttila, T.A., Latvala, T., Schuppan, V.: Linear encodings of bounded LTL model checking. Log. Methods Comput. Sci. (2006). https://doi.org/10.2168/LMCS-2(5:5)2006
Brafman, R.I., De Giacomo, G.: Planning for LTLf/LDLf goals in non-markovian fully observable nondeterministic domains. In: Kraus, S. (ed.) Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 1602–1608 (2019). https://doi.org/10.24963/ijcai.2019/222
Brafman, R.I., De Giacomo, G., Patrizi, F.: LTLf/LDLf non-markovian rewards. In: S.A. McIlraith, K.Q. Weinberger (eds.) Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, pp. 1771–1778. AAAI Press (2018)
Cavada, R., Cimatti, A., Dorigatti, M., Griggio, A., Mariotti, A., Micheli, A., Mover, S., Roveri, M., Tonetta, S.: The nuXmv symbolic model checker. In: Computer Aided Verification, pp. 334–342. Springer (2014). https://doi.org/10.1007/978-3-319-08867-9_22
Cavada, R., Cimatti, A., Dorigatti, M., Griggio, A., Mariotti, A., Micheli, A., Mover, S., Roveri, M., Tonetta, S.: The nuXmv symbolic model checker. In: Proceedings of the 26th International Conference on Computer Aided Verification, pp. 334–342. Springer (2014)
Cimatti, A., Roveri, M., Sheridan, D.: Bounded verification of past LTL. In: Proceedings of the 5th International Conference on Formal Methods in Computer-Aided Design, pp. 245–259. Springer (2004)
Cimatti, A., Roveri, M., Sheridan, D.: Bounded Verification of Past LTL. In: Formal Methods in Computer-Aided Design, LNCS, pp. 245–259. Springer (2004). https://doi.org/10.1007/978-3-540-30494-4_18
Cimatti, A., Griggio, A., Schaafsma, B.J., Sebastiani, R.: The MathSAT5 SMT solver. In: Piterman, N., Smolka, S.A. (eds.) Proceedings of the 19th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Lecture Notes in Computer Science, vol. 7795, pp. 93–107. Springer (2013). https://doi.org/10.1007/978-3-642-36742-7_7
Clarke, E.M., Grumberg, O., Peled, D.A.: Model Checking. MIT Press, Cambridge (2001)
De Giacomo, G., Vardi, M.Y.: Linear temporal logic and linear dynamic logic on finite traces. In: Rossi, F. (ed.) Proceedings of the 23rd International Joint Conference on Artificial Intelligence, pp. 854–860. IJCAI/AAAI (2013)
De Giacomo, G., De Masellis, R., Grasso, M., Maggi, F.M., Montali, M.: Monitoring business metaconstraints based on LTL and LDL for finite traces. In: Sadiq, S.W., Soffer, P., Völzer, H. (eds.) Proceedings of the 12th International Conference on Business Process Management, Lecture Notes in Computer Science, vol. 8659, pp. 1–17. Springer (2014). https://doi.org/10.1007/978-3-319-10172-9_1
De Giacomo, G., Vardi, M.Y.: Synthesis for LTL and LDL on finite traces. In: Yang, Q., Wooldridge, M.J. (eds.) Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, pp. 1558–1564. AAAI Press (2015)
De Giacomo, G., Iocchi, L., Favorito, M., Patrizi, F.: Foundations for restraining bolts: Reinforcement learning with LTLf/LDLf restraining specifications. In: Benton, J., Lipovetzky, N., Onaindia, E., Smith, D.E., Srivastava, S. (eds.) Proceedings of the Twenty-Ninth International Conference on Automated Planning and Scheduling, pp. 128–136. AAAI Press (2019)
de Moura, L.M., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) Proceedings of the 14th International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Lecture Notes in Computer Science, vol. 4963, pp. 337–340. Springer (2008). https://doi.org/10.1007/978-3-540-78800-3_24
Eén, N., Sörensson, N.: An extensible sat-solver. In: Selected Revised Papers of the 6th International Conference on Theory and Applications of Satisfiability Testing, pp. 502–518 (2003). https://doi.org/10.1007/978-3-540-24605-3_37
Eén, N., Sörensson, N.: An extensible sat-solver. In: International conference on theory and applications of satisfiability testing, pp. 502–518. Springer (2003)
Fionda, V., Greco, G.: LTL on finite and process traces: complexity results and a practical reasoner. J. Artif. Intell. Res. 63, 557–623 (2018). https://doi.org/10.1613/jair.1.11256
Fisher, M.: A resolution method for temporal logic. In: Mylopoulos, J., Reiter, R. (eds.) Proceedings of the 12th International Joint Conference on Artificial Intelligence, pp. 99–104. Morgan Kaufmann (1991)
Fisher, M.: A normal form for temporal logics and its applications in theorem-proving and execution. J. Logic Comput. 7(4), 429–456 (1997). https://doi.org/10.1093/logcom/7.4.429
Geatti, L., Gigante, N., Montanari, A., Reynolds, M.: One-pass and tree-shaped tableau systems for TPTL and TPTLb+Past. In: Orlandini, A., Zimmermann, M. (eds.) Proceedings 9th International Symposium on Games, Automata, Logics, and Formal Verification, EPTCS, vol. 277, pp. 176–190 (2018). https://doi.org/10.4204/EPTCS.277.13
Geatti, L., Gigante, N., Montanari, A.: A SAT-Based encoding of the one-pass and tree-shaped tableau system for LTL. In: Cerrito, S., Popescu, A. (eds.) Proceedings of the 28th International Conference on Automated Reasoning with Analytic Tableaux and Related Methods, Lecture Notes in Computer Science, vol. 11714, pp. 3–20. Springer (2019). https://doi.org/10.1007/978-3-030-29026-9_1
Geatti, L., Gigante, N., Montanari, A., Reynolds, M.: One-pass and tree-shaped tableau systems for TPTL and TPTL${}_{\text{ b }}Past. Inf. Comput. 278, 104599 (2021). https://doi.org/10.1016/j.ic.2020.104599
Geatti, L., Gigante, N., Montanari, A., Venturato, G.: Past matters: Supporting LTL+Past in the BLACK satisfiability checker. In: Proceedings of the 28th International Symposium on Temporal Representation and Reasoning (2021)
Geatti, L., Gianola, A., Gigante, N.: Linear temporal logic modulo theories over finite traces. In: L.D. Raedt (ed.) Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, IJCAI 2022, Vienna, Austria, 23–29 July 2022, pp. 2641–2647. ijcai.org (2022). https://doi.org/10.24963/ijcai.2022/366
Gigante, N., Montanari, A., Reynolds, M.: A one-pass tree-shaped tableau for LTL+Past. In: Proc. of 21st International Conference on Logic for Programming, Artificial Intelligence and Reasoning, EPiC Series in Computing, vol. 46, pp. 456–473 (2017)
Heljanko, K., Junttila, T., Latvala, T.: Incremental and complete bounded model checking for full PLTL. In: Proceedings of the 17th International Conference on Computer Aided Verification, pp. 98–111. Springer (2005)
Hustadt, U., Konev, B.: TRP++2.0: A temporal resolution prover. In: Proceedings of the 19th International Conference on Automated Deduction, LNCS, vol. 2741, pp. 274–278. Springer (2003). https://doi.org/10.1007/978-3-540-45085-6_21
Hustadt, U., Nalon, C., Dixon, C.: Evaluating pre-processing techniques for the separated normal form for temporal logics. In: B. Konev, J. Urban, P. Rümmer (eds.) Proceedings of the 6th Workshop on Practical Aspects of Automated Reasoning co-located with Federated Logic Conference 2018 (FLoC 2018), Oxford, UK, July 19th, 2018, CEUR Workshop Proceedings, vol. 2162, pp. 34–48. CEUR-WS.org (2018)
Kesten, Y., Manna, Z., McGuire, H., Pnueli, A.: A decision algorithm for full propositional temporal logic. In: Proc. of the 5th International Conference on Computer Aided Verification, LNCS, vol. 697, pp. 97–109. Springer (1993). https://doi.org/10.1007/3-540-56922-7_9
Li, J., Yao, Y., Pu, G., Zhang, L., He, J.: Aalta: an LTL satisfiability checker over infinite/finite traces. In: Cheung, S., Orso, A., Storey, M.D. (eds.) Proceedings of the 22nd ACM SIGSOFT International Symposium on Foundations of Software Engineering, pp. 731–734. ACM (2014). https://doi.org/10.1145/2635868.2661669
Li, J., Zhu, S., Pu, G., Zhang, L., Vardi, M.Y.: Sat-based explicit LTL reasoning and its application to satisfiability checking. Formal Methods Syst. Des. 54(2), 164–190 (2019). https://doi.org/10.1007/s10703-018-00326-5
Li, J., Pu, G., Zhang, Y., Vardi, M.Y., Rozier, K.Y.: Sat-based explicit LTLF satisfiability checking. Artif. Intell. 289, 103369 (2020). https://doi.org/10.1016/j.artint.2020.103369
Lichtenstein, O., Pnueli, A.: Propositional temporal logics: decidability and completeness. Logic J. IGPL 8(1), 55–85 (2000). https://doi.org/10.1093/jigpal/8.1.55
Lichtenstein, O., Pnueli, A., Zuck, L.D.: The Glory of the Past. In: Procedings of the Logics of Programs Conference, LNCS, vol. 193, pp. 196–218. Springer (1985). https://doi.org/10.1007/3-540-15648-8_16
Markey, N.: Temporal logic with past is exponentially more succinct. Bull. EATCS 79, 122–128 (2003)
McCabe-Dansted, J.C., Reynolds, M.: A parallel linear temporal logic tableau. In: Bouyer, P., Orlandini, A., Pietro, P.S. (eds.) Proceedings of the 8th International Symposium on Games, Automata, Logics and Formal Verification, EPTCS, vol. 256, pp. 166–179 (2017)
Moskewicz, M.W., Madigan, C.F., Zhao, Y., Zhang, L., Malik, S.: Chaff: Engineering an efficient sat solver. In: Proceedings of the 38th annual Design Automation Conference, pp. 530–535 (2001)
Pnueli, A.: The Temporal Logic of Programs. In: Proceedings of the 18th Annual Symposium on Foundations of Computer Science, pp. 46–57. IEEE Computer Society (1977). https://doi.org/10.1109/SFCS.1977.32
Reynolds, M.: A New Rule for LTL Tableaux. In: Proceedings of the 7th International Symposium on Games, Automata, Logics and Formal Verification, EPTCS, vol. 26, pp. 287–301 (2016). https://doi.org/10.4204/EPTCS.226.20
Schuppan, V., Darmawan, L.: Evaluating LTL satisfiability solvers. In: Proceedings of the 9th International Symposium on Automated Technology for Verification and Analysis, pp. 397–413 (2011)
Schwendimann, S.: A new one-pass tableau calculus for PLTL. In: Proceedings of the 7th International Conference on Automated Reasoning with Analytic Tableaux and Related Methods, LNCS, vol. 1397, pp. 277–292. Springer (1998). https://doi.org/10.1007/3-540-69778-0_28
Sistla, A.P., Clarke, E.M.: The complexity of propositional linear temporal logics. J. ACM 32(3), 733–749 (1985). https://doi.org/10.1145/3828.3837
Soos, M., Nohl, K., Castelluccia, C.: Extending SAT solvers to cryptographic problems. In: O. Kullmann (ed.) Proceedings of the 12th International Conference on Theory and Applications of Satisfiability Testing, Lecture Notes in Computer Science, vol. 5584, pp. 244–257. Springer (2009). https://doi.org/10.1007/978-3-642-02777-2_24
Stump, A., Sutcliffe, G., Tinelli, C.: Starexec: A cross-community infrastructure for logic solving. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) Automated Reasoning—7th International Joint Conference, IJCAR 2014, Held as Part of the Vienna Summer of Logic, VSL 2014, Vienna, Austria, July 19–22, 2014. Proceedings, Lecture Notes in Computer Science, vol. 8562, pp. 367–373. Springer (2014). https://doi.org/10.1007/978-3-319-08587-6_28
Suda, M., Weidenbach, C.: A PLTL-prover based on labelled superposition with partial model guidance. In: Proceedings of the 6th International Joint Conference on Automated Reasoning, LNCS, vol. 7364, pp. 537–543. Springer (2012). https://doi.org/10.1007/978-3-642-31365-3_42
Tahrat, S., Braun, G., Artale, A., Ozaki, A.: Abstracting temporal aboxes in TDL-Lite. In: Proceedings of the 34th International Workshop on Description Logics (2021)
Tauriainen, H., Heljanko, K.: Testing LTL formula translation into Büchi automata. Int. J. Softw. Tools Technol. Transf. 4(1), 57–70 (2002). https://doi.org/10.1007/s100090200070
Wolper, P.: Temporal logic can be more expressive. Inf. Control 56(1/2), 72–99 (1983). https://doi.org/10.1016/S0019-9958(83)80051-5
Wolper, P.: The tableau method for temporal logic: an overview. Logique et Analyse 28, 119–136 (1985)
Funding
Open access funding provided by Libera Università di Bolzano within the CRUI-CARE Agreement. Nicola Gigante acknowledges the support of the TOTA project (Temporal Ontologies and Tableau Algorithms) funded by the Free University of Bozen-Bolzano. Luca Geatti, Nicola Gigante, and Angelo Montanari would also like to acknowledge the support from the GNCS project: “Strategic reasoning and automatic synthesis of multi-agent systems”. Gabriele Venturato acknowledges the partial support of the KU Leuven Research Fund (C14/18/062).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the realisation of this manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests affecting this manuscript.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Geatti, L., Gigante, N., Montanari, A. et al. SAT Meets Tableaux for Linear Temporal Logic Satisfiability. J Autom Reasoning 68, 6 (2024). https://doi.org/10.1007/s10817-023-09691-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10817-023-09691-1


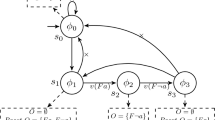


 , then
, then  ;
; , then
, then  ;
; , then
, then  ;
; , then
, then  .
. :
: is added to
is added to  , with:
, with: 
 :
:
 is added to
is added to  such that
such that  . This is done once and only once before every application of the
. This is done once and only once before every application of the  rule.
rule. :
: , for some
, for some  is rejected.
is rejected. :
: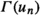 does not contain tomorrow or weak tomorrow formulas, then
does not contain tomorrow or weak tomorrow formulas, then  is accepted.
is accepted. :
: , then the branch
, then the branch  is rejected if either
is rejected if either  does not exist or
does not exist or  , where
, where  .
. :
: , then
, then  is rejected if
is rejected if  exists and
exists and  , where
, where  .
. :
: and all the
and all the  requested in
requested in  are fulfilled in
are fulfilled in  , then
, then  is accepted.
is accepted. :
: , and all the
, and all the  requested in these nodes which are fulfilled in
requested in these nodes which are fulfilled in  are also fulfilled in
are also fulfilled in  , then
, then  is rejected.
is rejected.
 and
and  rules. Dashed edges represent subtrees collapsed to save space, bold arrows represent the application of a
rules. Dashed edges represent subtrees collapsed to save space, bold arrows represent the application of a  rule to a poised label
rule to a poised label rule;
rule; rule as follows:
rule as follows:  :
: does not contain tomorrow formulas, then
does not contain tomorrow formulas, then  is accepted.
is accepted. rule as follows:
rule as follows:  :
: , then
, then  is rejected.
is rejected. and the
and the  rules: the number of labels is finite, and therefore, sooner or later, a label will repeat in any long-enough branch. The
rules: the number of labels is finite, and therefore, sooner or later, a label will repeat in any long-enough branch. The  rule has to wait this to happen twice, while the
rule has to wait this to happen twice, while the  can reject the branch straightaway.
can reject the branch straightaway. and the
and the  rule work now for the
rule work now for the  rule (see [
rule (see [ rule is used (see [
rule is used (see [ is used, completeness is much easier to show. If a branch
is used, completeness is much easier to show. If a branch  has a position
has a position  , then the whole subtree obtained by expanding
, then the whole subtree obtained by expanding  will also be found as the subtree of
will also be found as the subtree of  . Hence, any successful branch obtained by expanding
. Hence, any successful branch obtained by expanding  can also be obtained by expanding
can also be obtained by expanding  , hence the search can stop at
, hence the search can stop at  and
and  can be rejected.
can be rejected. of propositions that are the surrogate version of the corresponding
of propositions that are the surrogate version of the corresponding  -,
-,  -, and
-, and  -formulas;
-formulas;
 or the
or the  rule, the evaluation of any proposition
rule, the evaluation of any proposition  rule or rejected by the
rule or rejected by the  or
or  rules, then there is a position w such that
rules, then there is a position w such that  , and we continue by filling the truth assignment considering the successor of
, and we continue by filling the truth assignment considering the successor of  rule has been applied to
rule has been applied to  , then there is a unique child that we choose as
, then there is a unique child that we choose as  , and we define
, and we define  or
or  , we have
, we have  by construction of the tableau. Note that
by construction of the tableau. Note that  and
and  , hence we know by construction that
, hence we know by construction that  (or
(or  ). Then, by definition of
). Then, by definition of  and
and  , hence
, hence  and
and  , and thus
, and thus  and
and  , so by construction of the tableau it holds that
, so by construction of the tableau it holds that  . Hence the invariant holds.
. Hence the invariant holds. rule has been applied to
rule has been applied to  , then there are n children
, then there are n children  such that
such that  for all
for all  as a child
as a child  with a label
with a label  such that, for any
such that, for any  if and only if
if and only if  . Thus the invariant holds by construction.
. Thus the invariant holds by construction. , then there are one or two children. In both cases, we set
, then there are one or two children. In both cases, we set  . In such a case, the applied rule is necessarily the
. In such a case, the applied rule is necessarily the  one, applied to a formula
one, applied to a formula  . By construction,
. By construction,  , and thus
, and thus  . Hence, the invariant holds.
. Hence, the invariant holds. and
and  , then let us suppose the applied rule is the
, then let us suppose the applied rule is the  rule (similar arguments hold for the other rules). In this case, the rule has been applied to a formula
rule (similar arguments hold for the other rules). In this case, the rule has been applied to a formula  and
and  . We know that
. We know that  accordingly, so to respect the invariant. Note that if both nodes are eligible, which one is chosen does not matter. The other direction of the invariant holds as well, since if either
accordingly, so to respect the invariant. Note that if both nodes are eligible, which one is chosen does not matter. The other direction of the invariant holds as well, since if either  , and then either
, and then either  or
or  .
. rule, then
rule, then  does not contain tomorrow or weak tomorrow formulas. By definition of
does not contain tomorrow or weak tomorrow formulas. By definition of  , and thus
, and thus  rule, a similar reasoning implies that
rule, a similar reasoning implies that  rule, then there exists a node
rule, then there exists a node  . By definition of
. By definition of  , and thus
, and thus  , any past request
, any past request  or
or  contained in
contained in  , that by construction is fulfilled in
, that by construction is fulfilled in 
 requested in
requested in  ,
,  . Hence, it holds that
. Hence, it holds that  . Since
. Since  - or
- or  -request,
-request,  . Hence,
. Hence,  does not contain any
does not contain any  - or
- or  -request, triggering the
-request, triggering the  rule that accepts the branch.
rule that accepts the branch. , that is,
, that is,  -,
-,  -,
-,  -, or
-, or  -request. Here,
-request. Here,  and
and  are step nodes, and by the invariant it holds that
are step nodes, and by the invariant it holds that  if and only if
if and only if  , that is,
, that is,  and
and  have the same
have the same  -,
-,  -,
-,  -, and
-, and  -requests. Similarly, the fact that
-requests. Similarly, the fact that  requested in
requested in  are fulfilled between
are fulfilled between  and
and  . The
. The  rule requires two identical labels in order to trigger, but
rule requires two identical labels in order to trigger, but  and
and  only have the same requests. However, since they have the same
only have the same requests. However, since they have the same  -requests, we know that
-requests, we know that  . Then, there is a step node
. Then, there is a step node  , grandchild of
, grandchild of  , such that
, such that  and the segment of the branch between
and the segment of the branch between  and
and  is equal to the segment between
is equal to the segment between  and
and  , hence all the
, hence all the  requested in
requested in  and
and  , fulfilled between
, fulfilled between  and
and  , are fulfilled between
, are fulfilled between  and
and  as well, and the
as well, and the  rule can apply to
rule can apply to  , accepting the branch.
, accepting the branch. has accepted the branch.
has accepted the branch. , or (ii) these three nodes exist, but there is an
, or (ii) these three nodes exist, but there is an 
 , which is fulfilled between
, which is fulfilled between  . A similar reasoning as above concludes that
. A similar reasoning as above concludes that 








