Bisequent Calculus for Four-Valued Quasi-Relevant Logics: Cut Elimination and Interpolation

Abstract

We present a uniform syntactical characterisation of the class of quasi-relevant logics which are four-valued extensions of the basic relevant logic B of Meyer and Routley. All these logics are obtained by the addition of suitable quasi-relevant implications to the four-valued logic of First Degree Entailment FDE. So far they were characterised axiomatically and semantically in several ways but did not obtain a special proof-theoretic treatment. To this aim a generalised form of sequent calculus called bisequent calculus (BSC) is applied. In BSC rules operate on the ordered pairs of ordinary sequents. It may be treated as the weakest kind of system in the rich family of generalised sequent calculi operating on items which are some collections of ordinary sequents, like hypersequents or nested sequents. It is shown that all logics under consideration have cut-free characterisation in BSC which satisfies the subformula property and yields decidability. It is also shown that the interpolation theorem holds for these logics if their language is enriched with additional negation.

1 Introduction

Many-valued logics were characterised by means of a variety of proof systems of different kinds so far (see e.g. Hähnle [17], or Baaz, Fermüller and Salzer [6] for a survey). The most direct and popular approach to construction of many-valued sequent calculi (SC) or tableau systems is based on the idea of syntactic representation of n values either by means of n-sided sequents or by n labels attached to formulae or sets of formulae. This solution was presented by many authors, starting with the works of Schröter [33] and later, independently, of Takahashi [38] and Rousseau [31]. Those n-sequent based approaches were succesfully developed in a general way by many authors, with constructive cut elimination theorems established (see e.g. Baaz, Fermüller and Zach [5]). Dual approach, based on the tableau systems with n labels added to formulae, was also independently developed by several authors (see e.g. Surma [36], Suchoń [35], Carnielli [12]). These methodologies of formalisation of many-valued logic, despite their generality and popularity, have some drawbacks (see [20] for discussion). Significant improvement in the construction of efficient SC or tableau systems for many-valued logic was proposed independently by Doherty [14] and Hähnle [17]. It is based on the idea that labels should correspond not to single values but to their (selected) sets. Such an approach was developed in several variants also in the setting of SC. In particular, for several three-valued logics it allows to develop an almost standard form of SC (see Avron [4]).

The aim of this paper is to present yet another approach to many-valued logics, a simple form of cut-free generalised sequent calculus called bisequent calculus (BSC). It was introduced by Indrzejczak [21]¹ to obtain a cut-free BSC for several variants of first-order modal logic S5. BSC has strictly syntactical character, i.e. no labels or other external devices are required. Rules are defined on ordered pairs of sequents, so it may be treated as the weakest kind of system in the rich family of generalised sequent calculi operating on items being some collections of ordinary sequents and called many-sequent calculi in [20]. All these generalised kinds of SC, like hyper- or nested sequent calculi have shown a great utility in applications to several non-classical logics.² However it seems that in some cases a reasonably modest generalisation of standard sequent calculus is sufficient. In particular, if we use structures which consist of two sequents only we obtain a limiting case of either hypersequent or nested sequent calculi.

This is where BSC enters and in case of some classes of logics it allows us to obtain simpler and more direct formalisation than the uniform approach based on n-sequents. In this paper we focus on the interesting class of so called quasi-relevant logics (simply R4-logics) determined by four-valued matrices. They are quasi-relevant in the sense explicated e.g. in Avron, Arieli and Zamansky [2]: every implicational thesis has either some variable common to its arguments, or both the negation of the antecedent and the succedent is a thesis. The matrices determining these logics are obtained by the addition of several implication operation to the well-known matrix B4 introduced for FDE—the logic of First Degree Entailment proposed by Belnap [7] and Dunn [15] (see also [8] or [1]). The important position of FDE in the research on relevant and paraconsistent logics is well known and established (see e.g. [26] in the special issue of Studia Logica devoted to FDE). The connection of R4-logics to relevant logics is even stronger since all R4-logics are also axiomatic extensions of the basic relevant logic B of Meyer and Routley. Since both FDE and B play a crucial role in the study of relevant logics, the examination of those logics which are at the same time (implicational) expansions of FDE, (axiomatic) extensions of B, and are in a sense relevant, is surely interesting. All these logics are also paraconsistent and paracomplete in the sense that sentences may be evaluated as having both values or neither. Thus the laws of noncontradiction and of the excluded middle fail.

Incidentally we will characterise also some other (non-relevant) implicational expansions of FDE but the main interest is in the proof-theoretic characterisation of R4-logics. It was shown recently by Lopez that this class contains exactly 8 logics, of which two - BN4 and E4 were identified and investigated earlier. BN4 was introduced by Brady [11] as the four-valued logic of the relevant conditional. It can be seen as an extension of RW, the contractionless version of the well-known relevant logic R, and its implication is sometimes claimed as the most naturally associated with FDE (see e.g. [30]). E4 was introduced by Robles and Mendez [29] and is related to E, the well-known logic of entailment, in a similar way, as BN4 is related to R. Namely, it is a four-valued extension of Er, the reductioless version of E. Both logics were presented as axiomatic calculi and proved complete also with respect to relational semantics. Robles and Mendez [29] described 6 other logics of this type and Lopez [23] showed that there are no other quasi-relevant logics which share B and are determined by the four-valued matrix. She provided also their axiomatization and semantic characterisation by means of relational models in [24].

The aim of this paper is twofold: to provide a uniform characterisation of these logics by means of BSC and to use this framework for proving interpolation theorems for negational expansions of all considered logics. In Sect. 2 we describe briefly the logics under consideration. In the next section we provide rules for the connectives of the logics introduced in Sect. 2. Section 4 presents a constructive proof of cut elimination for these systems and Sect. 5 shows how BSC can be applied to prove interpolation for their negational expansions, i.e. after addition of a different kind of negation to the language and suitable rules to the calculus. We will close the paper with some concluding remarks and comparison with other approaches.

2 Logics

Fig. 1

B4

Fig. 2

Implication operations

We will examine propositional logics determined by four-element matrices which are implicational expansions of the well-known matrix B4 due to Dunn and Belnap. Generally a matrix $M = \langle \mathcal{A}, D\rangle$ for a propositional language $\mathcal{L}$ is an algebra $\mathcal{A} =\langle A, O\rangle$ similar to $\mathcal{L}$, and D is a nonempty subset of designated elements of its carrier. B4 is a matrix with $A=\{0, \bot , \top , 1\}$, $D=\{1, \top \}$ and O containing a unary operation $\underline{\lnot }:A\longrightarrow A$ and binary operations $\odot : A\times A\longrightarrow A$, where $\odot \in \{\underline{\wedge }, \underline{\vee } \}$. Informally $\bot$ stands for a gap (no value) and $\top$ for a glut (both values). Operations are defined in Fig.1 where we have added also a characterisation of three additional negations: boolean $\sim$ and two cyclic negations: $\circlearrowright$ (see Ruet [32]) and $\circlearrowleft$, called also demi-negation (see Humberstone [18]). As we will see the addition of at least one of them will be necessary for proving the interpolation theorem.

Languages of our logics are freely generated algebras $\langle For, \lnot , \wedge , \vee , \rightarrow \rangle$ similar to the underlying algebra of B4 enriched with some additional implication operation $\underline{\rightarrow _i}$ with suitable index i. Logics are interpreted by homomorphisms from the language to algebra of values such that $h(c^n(\varphi _1, \ldots , \varphi _n))= \underline{c}(h(\varphi _1), \ldots , h(\varphi _n))$ for every $n-$argument connective c and the corresponding operation $\underline{c}$. For any matrix M we define a relation of matrix consequence in the following way: $\varGamma \models _M\varphi$ iff for any homomorphism h: if $h(\varGamma )\subseteq D$, then $h(\varphi )\in D$, where $h(\varGamma )=\{h(\psi ):\psi \in \varGamma \}$. In what follows the logics under consideration are identified with suitable matrix consequences.

Although FDE is formulated in the language without implication, a lot of implications have been considered as a reasonable expansion, in particular those which are listed in the first row of Fig. 2. In the first case b is for boolean, since it is material implication definable in terms of boolean negation and disjunction (see Omori and Wansing [26]). The second is mixed implication which is a joint extension of three-valued implications of Kleene’s logic K3 and Priest’s LP (with taking Kleene’s third value as $\bot$ and Priest’s third value as $\top$) (see Degauquier [13]). The next is extensional implication which is the most popular implication considered in the context of extended FDE (see Avron [4]). The next one is an interesting case of connexive implication (see Omori and Wansing [26]).

Neither of these four implications is relevant in any sense. Also their proof-theoretic characterisation in terms of BSC does not raise any problem. The situation is different and more demanding with the remaining 8 logics whose implications are defined in the last two positions of the first and in the second row of Fig. 2. The two four-valued quasi-relevant logics proposed as expansions of FDE are Brady’s BN4 ($\rightarrow _B$ for Brady) and Robles’ E4 ($\rightarrow _R$ for Robles). Both are axiomatic extensions of the basic relevant logic B of Meyer and Routley. In particular $\rightarrow _B$ is a joint extension of three-valued implications of Łukasiewicz’s L3 and the implication of three-valued relevant logic MR3. Although neither BN4 nor E4 is relevant in the strict sense of satisfying the variable-sharing property, they both satisfy the weaker quasi-relevance property: For every theorem of the form $\varphi \rightarrow \psi$ either $AT(\varphi )\cap AT(\psi ) \ne \varnothing$ or $\lnot \varphi$ and $\psi$ are theorems ($AT(\varphi )$ denotes the set of atoms, i.e. propositional variables, occurring in $\varphi$).

The following six implications listed in the second row of Fig.2 are the remaining ones that on the basis of FDE yield quasi-relevant logics which are the four-valued extensions of B. The nomenclature is taken from Lopez and the missing $\underline{\rightarrow _1}$ and $\underline{\rightarrow _5}$ are just $\underline{\rightarrow _B}$ and $\underline{\rightarrow _R}$ respectively. All these 8 logics are quasi-relevant, paraconsistent and paracomplete. They were characterised semantically not only by means of matrix semantics but also in terms of Belnap-Dunn semantics (Lopez [23]) and Routley-Meyer’s ternary relational semantics (Lopez [24]). However, in syntactical terms they obtained only standard Hilbert-style axiomatisation. In what follows we provided a proof-theoretic characterisation in terms of BSC which is cut-free and analytic, in the sense of enjoying the subformula property. These features yield decidability of all considered logics. Moreover, after enriching the set of rules with rules for boolean or circular negation, we obtain a calculus which yields a constructive proof of the Craig’s interpolation property for the expansions of these logics with respective negation.

Fig. 3

BSC-FDE

3 Bisequent Calculus

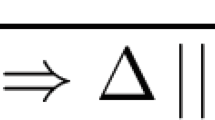
Our proof-theoretic tool is a generalised form of sequent calculus using bisequents which are ordered pairs of sequents $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$, where $\varGamma , \varDelta , \varPi , \varSigma$ are finite (possibly empty) multisets of formulae. We will call the elements of a bisequent as 1- and 2-sequent respectively. Bisequents with all elements being atomic will be also called atomic.

What is the rationale behind the bisequents? In a deep sense the notion of a bisequent is implicitly based on the so called Suszko’s thesis [37] according to which there are only two “real" truth values corresponding to sets of designated and nondesignated values in the characteristic matrix. This view, and a way of its interpretation, is a matter of philosophical dispute³ but technically, Suszko’s thesis may serve as a convenient basis for one of the possible introductions of SC into the realm of many-valued logics, and BSC is one of the possible frameworks for the development of this idea. More precisely, this fundamental bivalence is expressed by 1-sequent; its antecedent refers to designated values, and its succedent to nondesignated ones. Therefore to show that the bisequent is falsified we must show that all elements of the antecedent of 1-sequent are true or $\top$, and all elements of the succedent of 1-sequent are false or $\bot$. The 2-sequent has rather auxiliary character; its arguments refer to the remaining combinations of truth values, namely 1, $\bot$ for the antecedent and 0, $\top$ for the succedent.

Thus, in the sense of semantical motivation, BSC is rather far from n-sided approach, where each part of the n-sequent corresponds to a unique truth value. If we look for a semantic motivation it is rather closer to Hähnle’s sets-as-signs approach [17] using labels representing sets of truth values. It is clear that BSC and sets-as-signs tableaux realise essentially the same idea when we consider a semantic interpretation of bisequents suggested above. As a result it makes possible to simulate BSC rules in the setting of Hähnle’s system. On the other hand, BSC is different in many respects from Hähnle’s approach since it is a purely proof-theoretic system with rules constructed to satisfy standard desiderata and enabling constructive proofs of admissibility of cut and interpolation. Similar solutions but developed by means of different kinds of generalised sequents can be found in Degauquier [13] and Indrzejczak [20].

This idea allows for defining a uniform and simple framework having several nice properties. The set of axioms is fixed for all considered calculi: a bisequent $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ is axiomatic iff it has nonempty $\varGamma \cap \varDelta$ or $\varPi \cap \varSigma$. The set of rules characterising the operations of the B4 consists of the schemata listed in Fig. 3. Let us call this calculus BSC-FDE. We have included here also the rules for additional negations which will be of interest in Sect. 5. The formulae displayed in the schemata are called active; in particular those in the premisses are side formulae, whereas the one in the conclusion is the principal formula. The remaining formulae are parametric and together form a context.

Fig. 4

Basic implications

Fig. 5

E4

Boolean and mixed implication are characterised by the rules in Fig. 4. Note that all rules for $\rightarrow _b$ are uniform in the sense that all active formulae are in the same sequent, either 1- or 2-sequent, in a similar way as in the case of $\wedge , \vee , \sim$, whereas in case of $\rightarrow _m$ rules are mixed having always one side formula (namely the antecedent of implication) in the opposite sequent than the principal formula. To obtain a calculus for FDE with extensional implication we do not need any new rules—it is given by BSC-FDE with $({\Rightarrow }{\rightarrow _b}\mid ), ({\rightarrow _b}{\Rightarrow }\mid ), ({\mid \Rightarrow }{\rightarrow _m}), ({\mid \rightarrow _m}{\Rightarrow })$. It follows from the fact that a distribution of $1, \top$ and $0, \bot$ is the same in the tables for $\rightarrow _b$ and $\rightarrow _e$, whereas a distribution of $1, \bot$ and $0, \top$ are the same for $\rightarrow _m$ and $\rightarrow _e$. Since in the case of $\rightarrow _c$ a distribution of $1, \top$ and $0, \bot$ is also the same as in the table for $\rightarrow _b$ one pair of rules is identical to $({\Rightarrow }{\rightarrow _b}\mid ), ({\rightarrow _b}{\Rightarrow }\mid )$. We need only two new rules listed in Fig. 4.

Fig. 6

Quasi-relevant implications

To get a calculus for E4 we need the rules for $\rightarrow _R$ listed in Fig. 5. However, to obtain a calculus for BN4 we do not need new rules for $\rightarrow _B$ again. The respective rules are: $({\mid \Rightarrow }{\rightarrow _m})$, $({\mid \rightarrow _m}{\Rightarrow })$, $({\Rightarrow }{\rightarrow _R}\mid )$ and $({\rightarrow _R}{\Rightarrow }\mid )$. In the first case identical rules follow from the fact that a distribution of $1, \bot$ and $0, \top$ is the same in the tables for $\underline{\rightarrow _m}$ and $\underline{\rightarrow _B}$. In the second case it is a consequence of the same distribution of $1, \top$ and $0, \bot$ in the tables for $\underline{\rightarrow _R}$ and $\underline{\rightarrow _B}$.

Now note that for all the remaining implications a distribution of $1, \top$ and $0, \bot$ are also the same as in the tables for $\underline{\rightarrow _R}$, hence for all these implications we have the same rules, namely $({\Rightarrow }{\rightarrow _R}\mid )$ and $({\rightarrow _R}{\Rightarrow }\mid )$. What we need are only special rules for $({\mid \Rightarrow }{\rightarrow _i})$ and $({\mid \rightarrow _i}{\Rightarrow })$ listed in Fig. 6.

To facilitate orientation in the construction of all considered logics as BSC calculi we provide a description of their rules in Fig. 7. Note that all considered calculi are rule-extensions of BSC-FDE which means that all share the same axioms and all rules for $\lnot , \wedge , \vee$ from Fig 3. The only difference is the set of four rules for $\rightarrow$ which are specified in the table.

Fig. 7

BSC for considered logics

One may easily notice that all rules satisfy the subformula property and other desirable properties of well-behaved SC, like explicitness, symmetry, separation (see [20]). In particular, since no rules are constrained with any side conditions they are context independent in the sense that validity-preservation of rules is intact by deletion or addition of the same parameters in the premisses and conclusion. This feature will be of special importance for the proof of admissibility of important structural rules, including cut, in Sect. 4, and for the proof of the interpolation theorem in Sect. 5. One may easily observe that in case of rules for $\wedge , \vee , \sim$ and boolean $\rightarrow$ we have just standard G3 rules but repeated in both components. Rules for $\lnot , \circlearrowright , \circlearrowleft$ and the remaining kinds of $\rightarrow$ have different character since side and principal formulae are in different sequents in most cases.

A proof in BSC-L, where L is one of the logics under consideration, is defined as a tree where each leaf is axiomatic, the root is a bisequent B of the form $\varGamma \Rightarrow \varDelta \mid \Rightarrow$ and all nodes are generated by the rules defined for BSC-L.

Slightly more general notion is that of a proof-search tree for B, where leaves are not necessarily axiomatic. If moreover, all leaves are atomic bisequents, it is called a complete proof-search tree. The height of a proof-search tree (a proof in particular) is defined as the length of the maximal branches. A simple consequence of the subformula property of rules is:

Proposition 1

Every proof-search tree is extendible to a finite complete proof-search tree.

To show the adequacy of all systems we use the following falsifying interpretation of bisequents: $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ is falsified by h (in L) iff all elements of $\varGamma$ are designated (either true or $\top$), all elements of $\varDelta$ are not designated (either false or $\bot$), all elements of $\varPi$ are either true or $\bot$ and all elements of $\varSigma$ are either false or $\top$. Otherwise, $\varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma$ is satisfied by h (in L). If it is satisfied by every h we say that it is valid in L.

Obviously, all axiomatic bisequents are valid for any logic L. As for the rules they are not only sound (i.e. validity-preserving) but also invertible; namely it holds:

Theorem 1

For all rules of BSC-L, all premisses are L-valid iff the conclusion is L-valid.

Proof

By simple but tedious calculation. It is easier to prove it by contraposition, i.e. that for every rule the conclusion is falsified by some h iff at least one premiss is falsified by the same h. For illustration consider $(\rightarrow _R\Rightarrow \mid )$. In one direction assume that the conclusion is falsified by some h. Hence $h(\varphi \rightarrow \psi )\in \{1, \top \}$ and the same holds for all elements of $\varGamma$, whereas every element of $\varDelta$ is either false or $\bot$, every element of $\varPi$ is either true or $\bot$ and every element of $\varSigma$ is either false or $\top$. Since the values of all parametric formulae under h remain fixed we need to check only the values of side formulae, and there are four cases: a) $h(\varphi )=0$ or b) $h(\psi )=1$ or c) $h(\varphi )=h(\psi )=\top$ or d) $h(\varphi )=h(\psi )=\bot$. In the first case h falsifies the rightmost premiss. Similarly, case b), c), d) falsifies the third, the second and the first (leftmost) premiss respectively. In the second direction, assume that some premiss is falsified by some h. Take the leftmost one where $h(\varphi )\in \{0, \bot \}, h(\psi )\in \{1, \bot \}$. But if $h(\varphi )=0$ or $h(\psi )=1$, then $h(\varphi \rightarrow \psi )=1$ and if $h(\varphi )=h(\psi )=\bot$, then $h(\varphi \rightarrow \psi )=\top$. In any case $h(\varphi \rightarrow \psi )\in \{1, \top \}$ and this falsifies the conclusion. The remaining three premisses, when assumed to be falsified, lead to the same result. $\square$

Theorem 2

(Soundness) If BSC-L $\vdash \varGamma \Rightarrow \varphi \mid \Rightarrow$, then $\varGamma \models _{L}\varphi$

Proof

It follows from Theorem 1 by induction on the height of the proof. $\square$

Invertibility of all rules implies that proof search process is confluent, i.e. that the order of applications of rules does not affect the result. In particular, a bisequent B is provable iff every proof-search tree may be extended to obtain a proof.

Theorem 3

(Completeness) If $\varGamma \models _{L}\varphi$, then BSC-L $\vdash \varGamma \Rightarrow \varphi \mid \Rightarrow$

Proof

Assume that $\varGamma \models _{L}\varphi$ but BSC-L $\nvdash \varGamma \Rightarrow \varphi \mid \Rightarrow$. Moreover, since all rules satisfy the subformula-property, by Proposition 1 every proof-search is terminating. Hence in every complete proof-search tree for $\varGamma \Rightarrow \varphi \mid \Rightarrow$ there is at least one branch starting with nonaxiomatic atomic bisequent falsified by some h. Since all rules inherit this valuation, then the root is also falsified, contrary to our assumption. $\square$

As a simple consequence we obtain also a decision procedure for every L under consideration. Another by-product of our proof is that the structural rules of weakening, contraction and cut from Fig. 8 are admissible in BSC-L. One may easily check that all of them are validity-preserving, hence by soundness and completeness theorem, they are also admissible.

Fig. 8

Structural Rules

4 Cut Elimination

Moreover we can constructively prove that all structural rules introduced in the previous section are admissible. The most suitable strategy is that developed by Dragalin and applied for standard sequent calculus G3 in Negri and von Plato [25]. It is convenient to use for this task a version of BSC where active formulae in axioms are restricted to atomic ones. In order to show that this variant is equivalent to the one introduced in the previous section it is sufficient to prove:

Proposition 2

Axiomatic sequents with arbitrary formulae are provable in BSC with restricted axioms.

Proof

By induction on the complexity of active formulae. We provide one case for illustration. Consider $\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varPi \Rightarrow \varSigma$ proven in BSC-E4.

From: 1. $\varphi , \varGamma \Rightarrow \varDelta , \psi , \varphi \mid \psi , \varPi \Rightarrow \varSigma$, 2. $\psi , \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma , \varphi$

3. $\psi , \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \psi , \varPi \Rightarrow \varSigma$ and 4. $\varphi , \varGamma \Rightarrow \varDelta , \psi , \varphi \mid \varPi \Rightarrow \varSigma , \varphi$

we obtain by $(\rightarrow _R \Rightarrow \mid )$: a. $\varphi \rightarrow \psi , \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varPi \Rightarrow \varSigma$.

From 5. $\varGamma \Rightarrow \varDelta , \varphi \mid \psi , \varphi , \varPi \Rightarrow \varSigma , \psi$, 6. $\psi , \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma , \psi , \varphi$

7. $\psi , \varGamma \Rightarrow \varDelta \mid \psi , \varphi , \varPi \Rightarrow \varSigma , \psi$ and 8. $\varGamma \Rightarrow \varDelta , \varphi \mid \varphi , \varPi \Rightarrow \varSigma , \psi , \varphi$

we obtain by $(\rightarrow _R \Rightarrow \mid )$: b. $\varphi \rightarrow \psi , \varGamma \Rightarrow \varDelta \mid \varphi , \varPi \Rightarrow \varSigma , \psi$.

From a and b by $(\Rightarrow \rightarrow _R\mid )$ we obtain the result. All sequents 1–8 are provable by the induction hypothesis. $\square$

The remaining results in this section are proven for the version with restricted axioms, although for some of them this difference does not matter.

Proposition 3

Weakening rules are height-preserving admissible.

Proof

By induction on the height of the proof of the premiss, and context independence of all rules. $\square$

Proposition 4

All primitive (logical) rules are height-preserving invertible.

Proof

By induction on the height of the proof of the conclusion for each rule r. In the basis the considered bisequent is an axiom, hence the complex formula which we take as the principal formula of the respective rule r cannot be active in this axiom. Hence, by the context independence, it may be replaced with side formula(e). Otherwise this sequent is derived and either the complex formula in question is indeed principal or not. In the former case we have a proof of the premiss(es) directly above. In the latter case this formula belongs to the context and by the context independence and the induction hypothesis we derive the proof of the required premiss. $\square$

Proposition 5

Contraction rules are height-preserving admissible.

Proof

It follows by induction on the height of the proof of the premiss, context independence and invertibility of all rules. $\square$

Theorem 4

Both cut rules are admissible.

Proof

We prove their admissibility simultaneously by double induction on the complexity of cut-fromula and on the sum of heights of the proofs of the premisses of cut. The cases where at least one premiss of cut is axiomatic or has a parametric cut-formula are trivial. The latter follows from the context independence of all rules. The only interesting points are where both cut-formulae are principal. In case of formulae which are not implications, or implications derived by rules for $\rightarrow _b, \rightarrow _m, \rightarrow _e, \rightarrow _c$, the proofs are like in the classical logic, so we only examine the cases of rules for quasi-relevant implications. Consider the following application of cut:

$(Cut\mid )$$\dfrac{\varGamma \Rightarrow \varDelta , \varphi \rightarrow \psi \mid \varLambda \Rightarrow \varTheta \qquad \varphi \rightarrow \psi , \varPi \Rightarrow \varSigma \mid \varXi \Rightarrow \varOmega }{\varGamma , \varPi \Rightarrow \varDelta , \varSigma \mid \varLambda , \varXi \Rightarrow \varTheta , \varOmega }$

where the left premiss is derived by $(\Rightarrow \rightarrow _R\mid )$ from:

$a: \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varLambda \Rightarrow \varTheta$

$b: \varGamma \Rightarrow \varDelta \mid \varphi , \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\rightarrow _R\Rightarrow \mid )$ from:

1: $\varPi \Rightarrow \varSigma , \varphi \mid \psi , \varXi \Rightarrow \varOmega$

2: $\psi , \varPi \Rightarrow \varSigma \mid \varXi \Rightarrow \varOmega , \varphi$

3: $\psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

4: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

and:

By $(\mid Cut)$ on $\psi$ and contractions we obtain $\varGamma , \varPi \Rightarrow \varDelta , \varSigma \mid \varLambda , \varXi \Rightarrow \varTheta , \varOmega$. Since all cuts were performed on subformulae of the original cut-formula they are admissible by the induction hypothesis. Note that this is a solution correct for all 8 R4-logics.

Now we must examine the second cut for every logic. For BN4 it is obvious. For E4:

$(\mid Cut)$$\dfrac{\varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \varphi \rightarrow \psi \qquad \varPi \Rightarrow \varSigma \mid \varphi \rightarrow \psi , \varXi \Rightarrow \varOmega }{\varGamma , \varPi \Rightarrow \varDelta , \varSigma \mid \varLambda , \varXi \Rightarrow \varTheta , \varOmega }$

where the left premiss is derived by $(\mid \Rightarrow \rightarrow _R)$ from:

1: $\varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varLambda \Rightarrow \varTheta$

2: $\varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

3: $\varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varLambda \Rightarrow \varTheta$

4: $\varGamma \Rightarrow \varDelta \mid \varphi , \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\mid \rightarrow _R\Rightarrow )$ from:

$a: \varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

$b: \psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

and

which both by $(Cut \mid )$ on $\psi$ and contractions yield the result.

For $\rightarrow _2$ let the left premiss be derived by $(\mid \Rightarrow \rightarrow _2)$ from:

$a: \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varLambda \Rightarrow \varTheta$

$b: \varGamma \Rightarrow \varDelta \mid \varphi , \varLambda \Rightarrow \varTheta , \psi$

$c: \varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\mid \rightarrow _2\Rightarrow )$ from:

1: $\varPi \Rightarrow \varSigma , \varphi \mid \psi , \varXi \Rightarrow \varOmega$

2: $\psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

3: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

and

which both by $(Cut \mid )$ on $\psi$ and contractions yield the result.

For $\rightarrow _3$ where the left premiss is derived by $(\mid \Rightarrow \rightarrow _3)$ from:

$a: \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varLambda \Rightarrow \varTheta$

$b: \varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\mid \rightarrow _3\Rightarrow )$ from:

1: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega$

2: $\psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

For $\rightarrow _4$ where the left premiss is derived by $(\mid \Rightarrow \rightarrow _4)$ from:

$a: \varGamma \Rightarrow \varDelta \mid \varphi , \varLambda \Rightarrow \varTheta , \psi$

$b: \varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\mid \rightarrow _4\Rightarrow )$ from:

1: $\varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

2: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

For $\rightarrow _6$ let the left premiss be derived by $(\mid \Rightarrow \rightarrow _6)$ from:

$a: \varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varLambda \Rightarrow \varTheta$

$b: \varGamma \Rightarrow \varDelta \mid \varphi , \varLambda \Rightarrow \varTheta , \psi$

$c: \varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\mid \rightarrow _6\Rightarrow )$ from:

1: $\varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega , \varphi$

2: $\psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

3: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

For $\rightarrow _7$ let the left premiss be derived by $(\mid \Rightarrow \rightarrow _7)$ from:

$a: \varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varLambda \Rightarrow \varTheta$

$b: \varphi , \varGamma \Rightarrow \varDelta , \psi \mid \varLambda \Rightarrow \varTheta$

$c: \varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

and the right premiss by $(\mid \rightarrow _7\Rightarrow )$ from:

1: $\psi , \varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega$

2: $\psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

3: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

For $\rightarrow _8$ where the left premiss is derived by $(\mid \Rightarrow \rightarrow _8)$ from:

$a: \varphi , \varGamma \Rightarrow \varDelta \mid \varLambda \Rightarrow \varTheta , \psi$

$b: \varGamma \Rightarrow \varDelta , \psi \mid \varphi , \varLambda \Rightarrow \varTheta$

and the right premiss by $(\mid \rightarrow _8\Rightarrow )$ from:

1: $\psi , \varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega$

2: $\varPi \Rightarrow \varSigma , \varphi \mid \varXi \Rightarrow \varOmega , \varphi$

3: $\psi , \varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega$

4: $\varPi \Rightarrow \varSigma \mid \psi , \varXi \Rightarrow \varOmega , \varphi$

Using cuts on several occurrences of $\varphi , \psi$ and contractions we obtain:

and

which by $(Cut\mid )$ on $\varphi$ and contractions yields the desired effect. $\square$

5 Interpolation

We present a constructive proof of the Craig interpolation theorem for all discussed logics. However, it does not hold for these logics as formulated in the original language $\mathcal{L}$; we consider instead their variants in the language $\mathcal{L}_\sim$, with added boolean negation $\sim$. If some other proof leads to the result for these logics in L is an open problem. Perhaps, the original language is not expressive enough and interpolation does not hold for the original formulation. Our strategy is based on the proof by Muskens and Wintein [39] originally applied in the tableau setting for $\mathbf{B_4}$ and three-valued logics $\mathbf{K_3}$ and LP. Here we demonstrate that BSC can be also used for showing that interpolation holds for all 12 logics under consideration, since in the proof only the rules common to all calculi in the extended version with $\sim$ are applied. A close analysis of our proof demonstrates that interpolation holds for any logic which is adequately characterised by cut-free and terminating BSC such that it contains invertible and context independent rules. Indeed it is sufficient if it contains the rules for $\wedge , \vee , \lnot , \sim$, since only these rules are used in the proof. $AT(\varGamma )$ extends to multisets the notion which was used to denote the set of propositional variables in $\varphi$.

Theorem 5

For any formulae $\varphi , \psi$ such that neither $\varphi \models$ nor $\models \psi$ holds, if $\varphi \models \psi$, then we can construct an interpolant on the basis of proof-search trees for $\varphi \Rightarrow \mid \Rightarrow$ and $\Rightarrow \psi \mid \Rightarrow$.

Proof

Since $\varphi \models \psi$ then, by completeness we have a cut-free proof of $\varphi \Rightarrow \psi \mid \Rightarrow$. Now produce complete proof-search trees for $\varphi \Rightarrow \mid \Rightarrow$ and $\Rightarrow \psi \mid \Rightarrow$. Since neither $\varphi \models$, nor $\models \psi$ hold, these proof-search trees have some nonaxiomatic leaves. Let $\varGamma _1\Rightarrow \varDelta _1\mid \varPi _1\Rightarrow \varSigma _1, \ldots , \varGamma _k\Rightarrow \varDelta _k\mid \varPi _k\Rightarrow \varSigma _k$ be the list of nonaxiomatic atomic leaves of the proof-search tree for $\varphi \Rightarrow \mid \Rightarrow$ and $\varTheta _1\Rightarrow \varLambda _1\mid \varXi _1\Rightarrow \varOmega _1, \ldots , \varTheta _n\Rightarrow \varLambda _n\mid \varXi _n\Rightarrow \varOmega _n$ such a list taken from the proof-search tree for $\Rightarrow \psi \mid \Rightarrow$. It holds:

Claim (1). For any $i\le k$ and $j\le n$, $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \varLambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ is an axiomatic atomic bisequent.

This is a straightforward observation. Consider a proof-search tree for $\varphi \Rightarrow \mid \Rightarrow$ and add $\psi$ to succedents of all 1-sequents in the tree. Due to context independence of all rules it is a correct proof-search tree. Now for each leaf $\varGamma _i\Rightarrow \varDelta _i, \psi \mid \varPi _i\Rightarrow \varSigma _i$ append a tree of $\Rightarrow \psi \mid \Rightarrow$ but with $\varGamma _i$ added to each antecedent and $\varDelta _i$ added to each succedent of 1-sequents, and similarly with $\varPi _i$ and $\varSigma _i$ in all 2-sequents. In the resulting proof-search tree we have leaves of the form $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \varLambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ for all $i\le k$ and $j\le n$. If at least one of them is not axiomatic, then $\nvdash \varphi \Rightarrow \psi \mid \Rightarrow$. $\square$

Next for every $\varGamma _i\Rightarrow \varDelta _i\mid \varPi _i\Rightarrow \varSigma _i, i\le k$, define the following sets:

$\varGamma _i' = \varGamma _i\cap \bigcup _{j\le n}\varLambda _j$

$\varDelta _i' = \varDelta _i\cap \bigcup _{j\le n}\varTheta _j$

$\varPi _i' = \varPi _i\cap \bigcup _{j\le n}\varOmega _j$

$\varSigma _i' = \varSigma _i\cap \bigcup _{j\le n}\varXi _j$

Since every $\varGamma _i\Rightarrow \varDelta _i\mid \varPi _i\Rightarrow \varSigma _i$ is not axiomatic but every $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \varLambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ is axiomatic we are guaranteed that $\varGamma _i'\cup \varDelta _i'\cup \varPi _i'\cup \varSigma _i'\ne \varnothing$. Note also that $AT(\varGamma _i'\cup \varDelta _i'\cup \varPi _i'\cup \varSigma _i') \subseteq AT(\varphi )\cap AT(\psi )$.

Now define an interpolant $Int(\varphi , \psi )$ as a formula of the following form:

$\bigwedge \varGamma _1' \wedge \bigwedge \lnot \varSigma _1'\wedge \bigwedge \sim \varDelta _1'\wedge \bigwedge \sim \lnot \varPi _1' \ \vee \ldots \vee \ \bigwedge \varGamma _k' \wedge \bigwedge \lnot \varSigma _k'\wedge \bigwedge \sim \varDelta _k'\wedge \bigwedge \sim \lnot \varPi _k'$,

where $\bigwedge \varPi$ denotes the conjunction of all elements of $\varPi$ and $\lnot \varPi , \sim \varPi , \sim \lnot \varPi$ denote sets of suitable negations (double negations) of all elements in $\varPi$.

We can show that:

Claim (2). $Int(\varphi , \psi )$ is an interpolant for $\varphi \models \psi$. $\square$

Proof

Since for every $\bigwedge \varGamma _i'\wedge \bigwedge \lnot \varSigma _i'\wedge \bigwedge \sim \varDelta _i'\wedge \bigwedge \sim \lnot \varPi _i'$ all (negated) atoms are by definition taken from $AT(\varphi )\cap AT(\psi )$ we must only prove that $\vdash \varphi \Rightarrow Int(\varphi , \psi )\mid \Rightarrow$, and $\vdash Int(\varphi , \psi ) \Rightarrow \psi \mid \Rightarrow$. Again take a complete proof-search tree for $\varphi \Rightarrow \mid \Rightarrow$ and add $Int(\varphi , \psi )$ to every succedent of 1-sequent. For every $\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )\mid \varPi _i\Rightarrow \varSigma _i$ which is not axiomatic apply $(\Rightarrow \vee \mid )$ to get $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \varGamma _i'\wedge \bigwedge \lnot \varSigma _i'\wedge \bigwedge \sim \varDelta _i'\wedge \bigwedge \sim \lnot \varPi _i', Int(\varphi , \psi )^{-i} \mid \varPi _i\Rightarrow \varSigma _i$, where $Int(\varphi , \psi )^{-i}$ is the multiset of the remaining disjuncts (if any). Applying $(\Rightarrow \wedge \mid )$ we obtain the following bisequents:

(a) $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \varGamma _i', Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$

(b) $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \lnot \varSigma _i', Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$

(c) $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \sim \varDelta _i', Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$

(d) $\varGamma _i\Rightarrow \varDelta _i, \bigwedge \sim \lnot \varPi _i', Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$

Systematically applying $(\Rightarrow \wedge \mid )$ to (a) we obtain $\varGamma _i\Rightarrow \varDelta _i, p, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varGamma _i'$ and since $\varGamma _i'\subseteq \varGamma _i$ they are all axiomatic. Similarly with (b) but now we first obtain $\varGamma _i\Rightarrow \varDelta _i, \lnot p, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varSigma _i'$. After the application of $(\Rightarrow \lnot \mid )$ we obtain $\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid p, \varPi _i\Rightarrow \varSigma _i$ which is axiomatic since $\varSigma _i'\subseteq \varSigma _i$. In the similar way from (c) by the application of $(\Rightarrow \wedge \mid )$ and $(\Rightarrow \sim \mid )$ we obtain $p, \varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i$ for each $p\in \varDelta _i'$ which is axiomatic since $\varDelta _i'\subseteq \varDelta _i$. Finally for (d) we succesively apply $(\Rightarrow \wedge \mid )$, $(\Rightarrow \sim \mid )$ and $(\lnot \Rightarrow \mid )$ to obtain $\varGamma _i\Rightarrow \varDelta _i, Int(\varphi , \psi )^{-i}\mid \varPi _i\Rightarrow \varSigma _i, p$ for each $p\in \varPi _i'$ which is axiomatic since $\varPi _i'\subseteq \varPi _i$. In this way we obtain a proof of $\varphi \Rightarrow Int(\varphi , \psi )\mid \Rightarrow$.

We have to do the same with a complete proof-search tree for $\Rightarrow \psi \mid \Rightarrow$ but now adding $Int(\varphi , \psi )$ to every antecedent of all 1-sequents in the tree. For every nonaxiomatic leaf $Int(\varphi , \psi ), \varTheta _j\Rightarrow \varLambda _j\mid \varXi _j\Rightarrow \varOmega _j$ we apply $(\vee \Rightarrow |)$ to each disjunct of $Int(\varphi , \psi )$ until we get leaves: $\bigwedge \varGamma _1'\wedge \bigwedge \lnot \varSigma _1'\wedge \bigwedge \sim \varDelta _1'\wedge \bigwedge \sim \lnot \varPi _1', \varTheta _j\Rightarrow \varLambda _j\mid \varXi _j\Rightarrow \varOmega _j$ ...$\bigwedge \varGamma _k'\wedge \bigwedge \lnot \varSigma _k'\wedge \bigwedge \sim \varDelta _k'\wedge \bigwedge \sim \lnot \varPi _k', \varTheta _j\Rightarrow \varLambda _j\mid \varXi _j\Rightarrow \varOmega _j$. To each such leaf we apply $(\wedge \Rightarrow \mid )$ obtaining bisequents of the form $\varGamma _i', \lnot \varSigma _i', \sim \varDelta _i', \sim \lnot \varPi _i', \varTheta _j\Rightarrow \varLambda _j\mid \varXi _j\Rightarrow \varOmega _j$ for $i\le k, j\le n$. In each case the successive applications of $(\lnot \Rightarrow \mid )$ to $\lnot \varSigma _i'$, $(\sim \Rightarrow \mid )$ to $\sim \varDelta _i'$ and $(\sim \Rightarrow \mid )$ and then $(\Rightarrow \lnot \mid )$ to $\sim \lnot \varPi _i'$ yield in the effect leaves of the form $\varGamma _i', \varTheta _j\Rightarrow \varLambda _j, \varDelta _i'\mid \varPi _i', \varXi _j\Rightarrow \varOmega _j, \varSigma _i'$. Since for every $i\le k, j\le n$, $\varGamma _i, \varTheta _j\Rightarrow \varDelta _i, \varLambda _j\mid \varPi _i, \varXi _j\Rightarrow \varSigma _i, \varOmega _j$ is axiomatic these primed versions are axiomatic too. This follows from definition of primed sets, since they contain just these atoms which occur also in their complementary sets, for example if some $p\in \varGamma _i\cap \varLambda _j$, then $p\in \varGamma _i'$ as well. $\square$

It is worth noting that this theorem may be also proved in the same way for the versions with added cyclic negation. The only difference is that the interpolation formulae now have the shapes:

$\bigwedge \varGamma _1' \wedge \bigwedge \lnot \varSigma _1'\wedge \bigwedge \circlearrowright \varPi _1'\wedge \bigwedge \circlearrowright \lnot \varDelta _1' \ \vee \ldots \vee \ \bigwedge \varGamma _k' \wedge \bigwedge \lnot \varSigma _k'\wedge \bigwedge \circlearrowright \varPi _k'\wedge \bigwedge \circlearrowright \lnot \varDelta _k'$.

$\bigwedge \varGamma _1' \wedge \bigwedge \lnot \varSigma _1'\wedge \bigwedge \lnot \circlearrowleft \varDelta _1'\wedge \bigwedge \lnot \circlearrowleft \lnot \varPi _1' \ \vee \ldots \vee \ \bigwedge \varGamma _k' \wedge \bigwedge \lnot \varSigma _k'\wedge \bigwedge \lnot \circlearrowleft \varDelta _k'\wedge \bigwedge \lnot \circlearrowleft \lnot \varPi _k'$.

Interested reader is invited to provide a proof. What is even more interesting both cyclic negations may be used instead of $\lnot$, and each is sufficient to prove interpolation. It follows from the fact that the rules $(\mid \circlearrowright \Rightarrow ), (\mid \Rightarrow \circlearrowright )$ and $(\circlearrowleft \Rightarrow \mid ), (\Rightarrow \circlearrowleft \mid )$ are identical with respective rules for $\lnot$. The alternative interpolants look like this:

$\bigwedge \varGamma _1' \wedge \bigwedge \circlearrowright \varPi _1'\wedge \bigwedge \circlearrowright \circlearrowright \varDelta _1'\wedge \bigwedge \circlearrowright \circlearrowright \circlearrowright \varSigma _1' \ \vee \ldots \vee \ \bigwedge \varGamma _k' \wedge \bigwedge \circlearrowright \varPi _k'\wedge \bigwedge \circlearrowright \circlearrowright \varDelta _k'\wedge \bigwedge \circlearrowright \circlearrowright \circlearrowright \varSigma _k'$.

$\bigwedge \varGamma _1' \wedge \bigwedge \circlearrowleft \varSigma _1'\wedge \bigwedge \circlearrowleft \circlearrowleft \varDelta _1'\wedge \bigwedge \circlearrowleft \circlearrowleft \circlearrowleft \varPi _1' \ \vee \ldots \vee \ \bigwedge \varGamma _k' \wedge \bigwedge \circlearrowleft \varSigma _k'\wedge \bigwedge \circlearrowleft \circlearrowleft \varDelta _k'\wedge \bigwedge \circlearrowleft \circlearrowleft \circlearrowleft \varPi _k'$.

Perhaps this result is not so surprising in light of the fact that Ruet’s [32] cyclic negation was shown to be functionally complete (see [26]). Since this kind of connective is sometimes considered as doubtful (see e.g. Humberstone [18]) this result may be seen as another evidence for the usefulness of cyclic negation and another contribution to the study of these interesting connectives recently investigated by several researchers.⁴

6 Conclusion

BSC is a relatively simple generalization of standard form of sequent calculus which can be of great utility in the field of many-valued logics. It is not a general framework which can be used for characterisation of arbitrary many-valued logics, like n-sequents, or n-labelled approaches mentioned in the introduction. However for some classes of many-valued logics it offers simpler calculi than those covered by these more prevalent methodologies. The class of logics considered in this paper is important but rather small, nonetheless the applicability of BSC is wider. In [19] we show that in the case of three-valued logics BSC can be applied universally, in the sense that arbitrary connectives of such propositional logics can be characterised by means of bisequent rules. When the number of values is four or higher the situation is not so clear. In this work we have shown how BSC works for the specific class of such four-valued logics. Investigation on other types of non-classical logics is an open problem.

Despite of the signalled limitations of BSC framework its simplicity in the considered case is appealing. It lies in the fact that two sequents are sufficient for encoding all situations which are relevant for searching of proof/falsification in the case where precisely two values are accepted/rejected. Rules of BSC are not computed on the basis of any normal (disjunctive or conjunctive) form, like in other approaches, but directly based on the tabular representation of the respective connective. Geometrical insights are appropriate here: to establish the premisses for the rule with the principal formula in one of the four positions in a bisequent, we just examine the tabular representation of this connective. For example, if indicated values of the arguments form a rectangle, one premiss is enough, in case of more complex shapes, two or three or even four premisses are required.

Since the process of construction of rules on the basis of tables is not deterministic we do not propose any algorithm for that aim. However, an analysis of some example shall make it clear how the rules were constructed and can help the reader to apply this strategy to their favourite logics. Let us consider the case of $(\rightarrow _R\Rightarrow \mid )$. The principal formula is placed in the antecedent of the 1-sequent which means that it is designated (either 1 or $\top$). In the table for $\underline{\rightarrow _R}$ from Fig 2 a distribution of these values is not very regular: (a) the leftmost column, (b) the last row, plus the single cels for both arguments being either (c) $\top$ or (d) $\bot$. The case (a) shows that the implication is designated if the succedent is 1 and this yields the third premiss where $\psi$ is in both antecedents. Since the first means that $\psi$ is either 1 or $\top$, and the second that $\psi$ is either 1 or $\bot$, such placement means that $\psi$ is simply 1. Similarly the case (b) means that the implication is designated if the antecedent is just 0. Hence it dictates the fourth premiss where $\varphi$ is in both succedents, hence simply false. How to deal with cases (c) and (d)? One may note that the leftmost half of the second row with the leftmost half of the last row gives us the rectangle having only designated values and including the cell (c). This rectangle is determined by $\varphi$ being $\top$ or 0, and $\psi$ being 1 or $\top$. This determines the placement of $\varphi$ and $\psi$ in the second premiss. Similarly, the bottom halves of the first and the third column give us a rectangle capturing cell (d) and containing only designated values. This rectangle is determined by $\varphi$ being $\bot$ or 0, and $\psi$ being 1 or $\bot$, which dictates the placement of $\varphi$ and $\psi$ in the first premiss.

Note that the interpretation of bisequents together with this technique of analysing the table for the connective does not dictate the shape of the rules in a deterministic way. Very often several possibilities are at hand. For example in the analysed case we could keep the premiss one and two but for the third and fourth just consider the remaining cells with designated values; the upper rightmost (with $\varphi$ and $\psi$ being 1) and the lowest rightmost (with $\varphi$ and $\psi$ being 0). Such a choice gives premisses where both formulae $\varphi , \psi$ are put in the places which are originally occupied only by $\psi$ in the third premiss and by $\varphi$ in the fourth premiss. Alternatively we can keep the third and fourth premiss intact but try to provide premisses one and two which uniquely describe cells c) and d). This yields the first premiss of the shape $\varGamma \Rightarrow \varDelta , \varphi , \psi \mid \varphi , \psi , \varPi \Rightarrow \varSigma$ (case d) and the second of the shape $\varphi , \psi , \varGamma \Rightarrow \varDelta \mid \varPi \Rightarrow \varSigma , \varphi , \psi$ (case c). Such rules are however more redundant and may lead to more complex proof-search trees.

While constructing rules on the basis of tables we made an effort to select these choices which led to the simplest possible rules allowing us to carry the proofs of proof-theoretic results. As a result the rules of BSC are proof-theoretically well-behaved, similar to standard sequent rules, satisfying properties of explicitness, separation, symmetry (see [20]), the subformula-property and admissibility of structural rules, including cut. Moreover, for negation expansions, with $\sim$ or with $\circlearrowright$ or $\circlearrowleft$, we have the algorithm for construction of interpolants. In the future work we are going to extend the application of BSC to many-valued first-order logics.