1 Introduction

It is well known that any realistic quantum systems interact inevitably with their surrounding environments, which introduce quantum noise into the systems. As a result, the quantum systems will lose their energy (dissipation) and/or coherence (dephasing). Quantum entanglement [1], as a main physical resource, plays a important role in quantum information processing (QIP). The unavoidable coupling of a quantum system with its surrounding environment leads to finite-time disentanglement [2], or even entanglement sudden death (ESD) [3]. In addition, for many tasks of quantum information processing, such as teleportation [4], dense coding [5], quantum cryptography [6], remote-state preparation [7, 8], quantum remote control [9] and distributed quantum computation [10], distant entanglement is the basic ingredient. However, before entanglement distribution the whole quantum system of interest is usually stored for some time inside a quantum register or memory. Therefore, protecting entanglement in a common environment before entanglement distribution will be a precondition for actual application.

On the other hand, the notion of weak measurement, first introduced by Aharonov, Albert, and Vaidman [11], has attracted much interests. The weak measurement satisfies two key requirements, i.e., controllable strength of the measurement and no coherence lost from the system being gently perturbed, and has been proven to be general in any measurement [12]. That is to say, for weak measurements, the information extracted from the quantum system’s is deliberately limited, thereby keeping the measured systems state from randomly collapsing towards an eigenstate. Thus, it would be possible to reverse the initial state by some operations [13, 14]. More recently, the WM and QMR approach have also been widely applied to various aspects of quantum information processing. It found that the WM and QMR approach can effectively protect quantum entanglements of two qubits and qutrits from amplitude-damping decoherence [15,16,17]. More interestingly, the famous ESD can be avoided by the WM and QMR approach [18]. Moreover, in Ref. [19], the authors investigated the generation of the concurrence of assistance from tripartite to bipartite entanglement by the WM and QMR. In Ref. [20], the authors investigated entanglement amplification via local weak measurements. In Ref. [21], the authors discussed the improvement of the fidelity of teleportation through a noisy channel using the WM and QMR. The robust state transfer and entanglement distribution in a single linear open ended spin-1/2 isotropic Heisenberg chain using the WM and QMR was also discussed in Ref. [22]. Moreover,It found that the WM and QMR approach can effectively protect quantum entanglements of two qubits from amplitude-damping decoherence [23, 24]. Up to now, to our best knowledge, the majority of previously publications focused on entanglement manipulation in amplitude damping decoherence via WM and QMR, we have not seen any report for entanglement protecting in other decoherence environment (such as, phase decoherence) using WM and QMR.

Motivated by the idea that the WM and QWR can protect quantum entanglements from the amplitude-damping decoherence. In this paper, we would like to extend to use WM and QMR to preserve the quantum entanglement of two initially entangled qubits which suffer a common phase decoherence environment. We study the quantum entanglement of a two uncoupled qubits system interacting with a common surrounding environments, we show explicitly that the quantum entanglement can be obviously protected by means of the proper WM and QMR. In particular, it is found that there is a specific initial state parameter region, the entanglement ratio, which is determined only by the initial state parameter and independent of the form of the spectral density of the reservoir.

The paper is structured as follows: In Section 2, we present our physical model and its solution. In Section 3, the detailed scheme of entanglement protection based on the WM and QMR and a brief discussion of the experimental feasibility is given. Finally, we give a brief discussion of our scheme and summarize our conclusions in Section 4.

2 Basic Theory

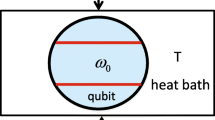
Before describing our scheme, we take a brief review of the physics model. We consider two uncoupled qubit, qubit A and qubit B, interacting with a common environment. The Hamiltonian of the whole system can be written as (ℏ = 1):

$$ H=H_{S}+H_{E}+H_{I} $$
(1)

where the first term \(H_{S}=\frac {1}{2}\omega _{A}{\sigma _{A}^{z}}+\frac {1}{2}\omega _{B}{\sigma _{B}^{z}}\) is the Hamiltonians of the two qubits, the ωA(B) is the energy separation, and \(\sigma _{A(B)}^{z}=|0\rangle _{A(B)}\langle 0|-|1\rangle _{A(B)}\langle 1|\) is the Pauli operator with |0〉A(B) and |1〉A(B) being the excited and ground states of the qubit A(B), respectively. The second term \(H_{E}={\sum }_{k}\omega _{k}b^{\dagger }_{k}b_{k}\) is the Hamiltonian of the environment, the ω k is the frequency of the kth harmonic oscillator depicted by the usual bosonic creation and annihilation. operators \(b^{\dagger }_{k}\) and b k , satisfying the commutative relation \([b_{k}, b^{\dagger }_{k}]= 1\). The last term \(H_{I}=H_{S}\otimes {\sum }_{k}g_{k}(b^{\dagger }_{k}+b_{k})\) describes the interaction Hamiltonian between the system and the kth harmonic oscillator of the heat bath, the g k is the coupling constant. It is obvious that [H S , H I ] = 0, which means that there is no energy transfer between the system and the environment, energy of the system is conservative, so that what interaction between the system and environment describes is the phase decoherence effect.

According to [25, 26], the total density operator of the system plus the heat bath can be expressed as

$$ \rho_{T}(t)=e^{-iH_{S}t}U^{-1}e^{-iH_{E}t}U\rho_{T}(0)U^{-1}e^{iH_{E}t}Ue^{iH_{S}t} $$
(2)

where the unitary transformation \(U=\exp {\left [H_{S}\otimes {\sum }_{k}g_{k}(b^{\dagger }_{k}-b_{k})\right ]}\), with ρ T (0) being the initial total density operator. We assume that the system and reservoir are initially in thermal equilibrium and uncorrelated, so that ρ T (0) = ρ S (0) ⊗ ρ R (0), where ρ S (0) and ρ R (0) are the initial density operator of the system and the reservoir, respectively. We can obtain the reduced density operator of the system, denoted by ρ(t) = Tr R [ρ T (t)]. Its matrix elements in the eigenrepresentation of H S (with the four dressed eigenstates {|00〉, |01〉, |10〉, |11〉} can be written as

$$\begin{array}{@{}rcl@{}} \rho_{(l^{\prime}_{A},l^{\prime}_{B})(l_{A},l_{B})}(t)&=&\rho_{(l^{\prime}_{A},l^{\prime}_{B})(l_{A},l_{B})}(0)R_{(l^{\prime}_{A},l^{\prime}_{B})(l_{A},l_{B})}(t) \\ &\times&e^{{-i}[E(l^{\prime}_{A},l^{\prime}_{B})-E(l_{A},l_{B})]t} \end{array} $$
(3)

where \(E(l_{A},l_{B}) (E(l^{\prime }_{A},l^{\prime }_{B}))\) is the eigenvalue of the operator H S with the corresponding eigenstate \(|l_{A},l_{B}\rangle (|l^{\prime }_{A},l^{\prime }_{B}\rangle )\) and the the expression of E(l A , l B ) is \(E(l_{A},l_{B})=[(-1)^{l_{A}}\omega _{A}+(-1)^{l_{B}}\omega _{B}]/2\). The reservoir dependent part \(R_{(l^{\prime }_{A},l^{\prime }_{B})(l_{A},l_{B})}(t)\) is

$$\begin{array}{@{}rcl@{}} R_{(l^{\prime}_{A},l^{\prime}_{B})(l_{A},l_{B})}(t)&=& e^{-i[E^{2}(l^{\prime}_{A},l^{\prime}_{B})-E^{2}(l_{A},l_{B})]Q_{1}(t)} \\ &\times& e^{-i[E(l^{\prime}_{A},l^{\prime}_{B})-E(l_{A},l_{B})]^{2}Q_{2}(t)} \end{array} $$
(4)

Here the two reservoir-dependent functions are

$$\begin{array}{@{}rcl@{}} Q_{1}(t)&=&{\int}_{0}^{\infty}d\omega J(\omega)\frac{g^{2}(\omega)}{\omega^{2}}\sin(\omega t) \\ Q_{2}(t)&=&2{\int}_{0}^{\infty}d\omega J(\omega)\frac{g^{2}(\omega)}{\omega^{2}}\sin^{2}(\frac{\omega t}{2})\coth(\frac{\beta\omega}{2}) \end{array} $$
(5)

Here we have taken the continuum limit of the reservoir modes: \({\sum }_{k}\rightarrow {\int }_{0}^{\infty }d\omega J(\omega )\), where J(ω) is the spectral density of the reservoir, g(ω) is the corresponding continuum expression for g k and β = 1/T (with the Boltzmann constant k B = 1).

Next,let us review briefly the notion of the WM and QMR [27]. The WM involved in our discussion is a null weak measurement or partial-collapse measurement, which can be performed by a device that indirectly monitors a qubit. If the device has no signal (namely, the null result case), the qubit was only partially collapsed and let it evolve, which is the so-called WM. If the device has a signal, we discard the result. The corresponding map of WM on the qubit can be expressed as WM(p)|n〉 → (1 − p)n/2|n〉(n = 0, 1), where p (0 ≤ p < 1) is the strength of WM. Equivalently, the map of WM in the computational basis |0〉,|1〉 can also be written as \(M_{w}=\texttt {diag}(1,\sqrt {1-p})\). Obviously, the effect of WM is a reduction of the weight of the excited state |1〉, so that the excited state |1〉 will undergo less influence of decoherence. Conversely, the corresponding map of QMR has the following form QMR (q)|n〉→ (1 − q)(n⊕1)/2|n〉(n = 0, 1), where ⊕ stands for an addition mod 2 and q (0 ≤ q < 1) is the strength of QMR. Likewise, the map of QMR in the computational basis |0〉, |1〉 can also be represented as \(M_{r}=\texttt {diag}(\sqrt {1-q},1)\). Thus, the effect of QMR is restoration of the weight of the excited state |1〉. As the weak measurement and quantum measurement reversal are non-unitary operations, our scheme naturally has less than unity success probability.

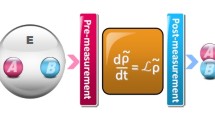
Our entanglement protecting scheme includes following three steps for comparision (as shown in Fig. 1): (1) Before interacting with the common phase decoherence environment, the two initial quantum qubits were implemented with WM, respectively; (2) the quantum qubits of implementing the WM interacts with the heat bath; (3) after interacting with the heat bath, the QMR was applied to the corresponding quantum qubits.

Fig. 1
figure 1

(Color online) Schemes for protecting entanglement from decoherence using weak measurement and weak measurement reversal: A prior weak measurement is applied before the two entangled qubits interact with the common phase decoherence environment and then a weak measurement reversal is performed

Full size image

Here, We assume that the two qubits are initially prepared in a class of state with the maximally mixed marginals described by the three-parameter X-type density matrix

$$\begin{array}{@{}rcl@{}} \rho(0)&=&\frac{1}{4}\left( I_{AB}+\sum\limits_{i = 1}^{3}c_{i}{\sigma_{A}^{i}}{\otimes\sigma_{B}^{i}}\right) \\ &=&\frac{1}{4}\left( \begin{array}{cccc} 1+c_{3} & 0 & 0 & c_{1}-c_{2} \\ 0 & 1-c_{3} & c_{1}+c_{2} & 0 \\ 0 & c_{1}+c_{2} & 1-c_{3} & 0 \\ c_{1}-c_{2} & 0 & 0 & 1+c_{3} \end{array} \right) \end{array} $$
(6)

where I A B is the identity operator in the Hilbert space of the two qubits, \({\sigma _{A}^{i}}\) and \({\sigma _{B}^{i}}\) (i = 1, 2, 3 mean x, y, z, respectively) are the Pauli operators of qubit A and qubit B, respectively, and c i (|c i | ∈ [0, 1]) are the real numbers satisfying the unit trace and positivity conditions of the density operator. The density operator ρ(0) includes the Werner states and the Bell states as two special cases. In general, (6) represents an entangled state and the initial entanglement may be assessed by concurrence [28] as \(C(\rho (0))=\frac {1}{2}\texttt {max}\{0,|c_{1}+c_{2}|-(1+c_{3}),|c_{1}-c_{2}|-(1-c_{3})\}\). Under the phase decoherence environment, the evolution of the density operator ρ(t) initially prepared in (6) can be obtained according to (3). Its explicit form at time t is

$$\begin{array}{@{}rcl@{}} \rho(t)=\frac{1}{4}\left( \begin{array}{cccc} 1+c_{3} & 0 & 0 & \mu e^{i{\Delta}_{1}} \\ 0 & 1-c_{3} & \nu e^{i{\Delta}_{2}} & 0 \\ 0 & \nu e^{-i{\Delta}_{2}} & 1-c_{3} & 0 \\ \mu e^{-i{\Delta}_{1}} & 0 & 0 & 1+c_{3} \end{array} \right) \end{array} $$
(7)

where we have introduced the following parameters:

$$\begin{array}{@{}rcl@{}} &&{\Delta}_{1}=(\omega_{A}+\omega_{B})t, {\Delta}_{2}=(\omega_{A}-\omega_{B})t, \\ &&\mu(t)=(c_{1}-c_{2})\gamma_{1}(t), \nu(t)=(c_{1}+c_{2})\gamma_{2}(t), \\ &&\gamma_{1}(t)=e^{-(\omega_{A}+\omega_{B})^{2}Q_{2}(t)}, \gamma_{2}(t)=e^{-(\omega_{A}-\omega_{B})^{2}Q_{2}(t)} \end{array} $$
(8)

In the following article, we consider the two qubits are identical, i.e. ω A = ω B , from (9) we have Δ2 = 0, γ2 = 1 and ν = c1 + c2. Then the final concurrence of the ρ(t) can be calculated as \(C(\rho (t))=\frac {1}{2}\texttt {max}\{0,|c_{1}+c_{2}|-(1+c_{3}),|(c_{1}-c_{2})\gamma _{1}(t)|-(1-c_{3})\}\). We can easily find out that, i.e. c1 = c2 and c3 = 0, the initial entanglement is equivalent to the final amount, that means there exists a decoherence-free subspace with two basis state |01〉 and |10〉 for the phase dechoherence,

3 Entanglement Protection Scheme

In what follows, we will consider the entanglement protection using the WM and QMR. Taking the initial state ρ(0), at the beginning, we individually perform both WMs with the same strength p on each qubit before they experience the phase decoherence. After two WMs on the qubit pair, the state of the qubits becomes

$$\begin{array}{@{}rcl@{}} \rho(p,t)=\frac{1}{P(p)}\left( \begin{array}{cccc} \rho_{11} & 0 & 0 & \rho_{14} \\ 0 & \rho_{22} & \rho_{23} & 0 \\ 0 & \rho_{23}^{*} & \rho_{33} & 0 \\ \rho_{14}^{*} & 0 & 0 & \rho_{44}) \end{array} \right) \end{array} $$
(9)

where ρ11 = 1 + c3, ρ22 = (1 − p)(1 − c3), ρ33 = (1 − p)(1 − c3), ρ44 = (1 − p)2(1 + c3), ρ14 = (1 − p)(c1 − c2), ρ23 = (1 − p)(c1 + c2), and P(p) = (p − 2)2 + p2c3 is the WM success probability.

After the phase decoherence and we apply two QMRs with the same strength q on each qubit. The final state is given by

$$\begin{array}{@{}rcl@{}} \rho(p,q,t)=\frac{1}{P(p,q)}\left( \begin{array}{cccc} \rho_{11}^{\prime} & 0 & 0 & \rho_{14}^{\prime} \\ 0 & \rho_{22}^{\prime} & \rho_{23}^{\prime} & 0 \\ 0 & \rho_{23}^{\prime*} & \rho_{33}^{\prime} & 0 \\ \rho_{14}^{\prime*} & 0 & 0 & \rho_{44}^{\prime} \end{array} \right) \end{array} $$
(10)

where \(\rho _{11}^{\prime }=(1-q)^{2}(1+c_{3})\), \(\rho _{22}^{\prime }=(1-p)(1-q)(1-c_{3})\), \(\rho _{33}^{\prime }=(1-p)(1-q)(1-c_{3})\), \(\rho _{44}^{\prime }=(1-p)^{2}(1+c_{3})\), \(\rho _{14}^{\prime }=(1-p)(1-q)(c_{1}-c_{2})\gamma _{1}(t)e^{i{\Delta }_{1}}\), \(\rho _{23}^{\prime }=(1-p)(1-q)(c_{1}+c_{2})\), and P(p, q) = (p + q − 2)2 + (p − q)2c3 is the QMR success probability. After some straightforward calculations, we can derive the concurrence of the ρ(p, q, t) as

$$\begin{array}{@{}rcl@{}} C(\rho(p,q,t))=\frac{X}{P(p,q)} \end{array} $$
(11)

where \(X=\frac {1}{2}(1-p)(1-q)\texttt {max}\{0,|c_{1}+c_{2}|-(1+c_{3}),|c_{1}-c_{2}|-(1-c_{3})\}\)

To quantify the effect of the WM and QMR, we define entanglement protection rate η = C(ρ(p, q, t))/C(ρ(t)), where η > (<)1 means that WM and QMR does (not) work. In order to obtain the optimal entanglement protection scheme, we try to find the optimal condition between the p and q, which maximizes the entanglement protection. To this end, we turn to the following equations:

$$\begin{array}{@{}rcl@{}} \frac{\partial C(\rho(p,q,t))}{\partial q}= 0 and \frac{\partial^{2} C(\rho(p,q,t))}{\partial^{2} q}<0 \end{array} $$
(12)

where we choose q as the variable. So with this optimal value of q, after some straightforward calculations, the optimal success probability and entanglement protection rate of the ρ(p, q, t) are given by, respectively,

$$\begin{array}{@{}rcl@{}} &&q^{opt}= 1-\frac{p}{1+{c_{3}^{2}}(1-p^{2})} \\ &&P^{opt}= 4(1-p)^{2}c_{3} \\ &&\eta^{opt}=\frac{1}{4c_{3}} \end{array} $$
(13)

From (13), we can see that, when we choose optimal condition, the optimal entanglement rate is only depend the state parameter c3, and independent of the spectral density of the reservoir. More importantly, when choosing c3 ∈ (0, 0.25), the ηopt can always greater than 1 at any time, meaning the WM and QMR operation indeed helps for protecting entanglement from phase decoherence.

However, the trend relationship of the success rate and entanglement rate is just reverse, as shown in the optimal success probability Popt of the (13). In other words, the high entanglement comes at the expense of the success rate. As we can see, the larger the weak measurement p and the smaller the state parameter c3, the less the success probability Popt. In the limit p → 1, we may have the success probabilities Popt → 0. There is hence a trade-off between success rate and degree of entanglement, such that the desirable value of c3 and p depends on the practical consideration for the balance between the success rate and entanglement.

It is necessary to give a brief discussion of some key problems which are related to experimental implementation of our scheme. Our WM and QMR operation can be immediately tested using current laboratory techniques, such as the operations on polarization-entangled states of the photons. The operations on the single-photon polarization qubit can be implemented by Brewster-angle glass plates (BPs) and half-wave plates (HWPs) [15]. As the BP rejects the vertical polarization (i.e., the state |1〉) with a probabilistic reflection p, but completely transmits the horizontal polarization (i.e.,|0〉), the appearance of a single-photon polarization qubit behind the BP implies a weak measurement. Moreover, the reversing operation M r can be rewritten as

$$ M_{r}=\left( \begin{array}{cc} \sqrt{1-q} & 0 \\ 0 & 1 \end{array} \right)=\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right)\left( \begin{array}{cc} 1 & 0 \\ 0 & \sqrt{1-q} \end{array} \right)\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), $$
(14)

which is equivalent to a weak measurement sandwiched by two bit-flip operations. This requires two HWPs, in addition to a BP, where the WMR strengths p and q can be adjusted by changing the number of the BPs employed.

4 Conclusions

In conclusion, we have demonstrated that WM and QMR can indeed be useful for protecting entanglement from the phase decoherence. More interestingly, it has been shown that, for X-type states, there is a specific initial state parameter region, the entanglement ratio, which is determined only by the initial state parameter and independent of the form of the spectral density of the reservoir. We have also studied the relationship between the concurrence, success probability and the weak measurement strength or the quantum measurement reversal strength. Unlike the majority of previously publications focused on entanglement protecting in amplitude damping decoherence via WM and QMR, The results of our study focus on phase decoherence environment may extends the applicable scope of the WM and QMR approach.