Finsler pp-waves and the Penrose limit

Abstract

We extend the notion of a Lorentzian pp-wave to that of Finsler spacetimes by providing a coordinate-independent definition of a Finsler pp-wave with respect to the Chern connection; our definition also includes the special case of a plane wave. This treatment introduces suitable lightlike coordinates, in analogy with the Lorentzian case, and utilizes the anisotropic calculus recently developed by one of the authors. We then extend Penrose’s “plane wave limit” to the setting of Finsler spacetimes. New examples of such Finsler pp-waves are also presented.

1 Introduction

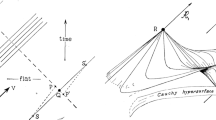
Among R. Penrose’s many accomplishments in general relativity are two foundational results on plane waves, a distinguished class of spacetimes modeling radiation propagating at the speed of light. These metrics have a long and rich history within the field of general relativity; they sit inside the more general family of pp-wave spacetimes introduced by Ehlers and Kundt [1], which themselves comprise an important subclass of the family of so called Brinkmann spacetimes due to H. W. Brinkmann [2], that contain a parallel (covariantly constant) lightlike vector field. A very comprehensive recent survey of plane waves can be found in [3]; pp-waves are now also studied purely in a mathematical context (see, e.g., [4,5,6,7,8]), in addition to their continued usage in gravitational physics (see, e.g., [9, 10]). Of their many properties both physical and mathematical, two of the most noteworthy were discovered by Penrose himself. The first of these, [11], is that plane waves are never globally hyperbolic: this is “remarkable”, to borrow Penrose’s own description, all the more so since plane waves are known to be geodesically complete. The second result, [12], no less remarkable, is that every spacetime has a plane wave in a certain well defined limit, a local construction now known as Penrose’s “plane wave limit,” perhaps the most important realization of a more general notion of “spacetime limit” due to Geroch [13].

Given the distinguished position that plane waves occupy—and especially in light of Penrose’s result that every Lorentzian metric admits one as a limit—it is worthwhile to ask whether there exist analogues of them in other geometries of indefinite signature, and, if so, whether Penrose’s plane wave limit carries over to such settings as well. A natural direction in which to take this question is that of Finsler geometry of Lorentzian signature, the setting of so called Finsler spacetimes, especially in light of their many recent physical applications; see, e.g., [14,15,16,17,18,19,20] and the references therein. Indeed, there are already examples of “Finsler pp-waves” in the literature (see, e.g., [21, 22]). In pursuing our question, we are less motivated by the connection between pp-waves, gravitational radiation, and Einstein’s equation—indeed, there is no agreed upon analogue of the latter in Finsler geometry—and more by the fact that, via Penrose’s limit, plane waves play a central role in Lorentzian geometry per se. What role may they play in Finsler geometry?

In this paper we attempt an answer to this question by first introducing a general definition of Finsler pp-wave, a definition that subsumes the isolated examples of Finsler pp-waves already in the literature; indeed, in Sect. 6 below we introduce additional examples of Finsler pp-waves in accord with our definition. Second, we show that there does exist a notion of “plane wave limit” in the Finslerian setting. These two facts, we argue, make them worthy of study as Finslerian objects. Throughout our paper, at every step of construction, we carefully present the modifications required to pass from Lorentzian to Finslerian geometry: this includes introducing the Chern connection and its corresponding Chern curvature tensor (Sect. 2), as well as presenting the Finsler analogue of lightlike coordinates (see, e.g., [23]), the Finsler analogue of the invariant definition of pp-wave in terms of the Riemann curvature tensor (see, e.g., [6]), and, finally, the Finsler analogue of the construction of Penrose’s plane wave limit itself. Let us stress that while the notions of lightlike coordinates and parallel lightlike vector fields in Finsler spacetimes depend only on the nonlinear connection, the definition of Finsler pp-waves requires the use of Chern connection. Finally, we note that, while for ease of presentation we have restricted our attention to dimension 4, our definition of Finsler pp-wave extends to all dimensions with only minor modification.

2 Preliminaries

Let M be a (connected) manifold, TM its tangent bundle, and $\pi :TM\rightarrow M$ the natural projection. Let us consider a connected open subset $A\subset TM\setminus \textbf{0}$ which is conic, namely, satisfying the property that $\lambda v\in A$ for all $v\in A$ and $\lambda >0$. Let us further assume that A has smooth boundary, that each $A_p=A\cap T_pM$ is nonempty for all $p\in M$, and denote ${\bar{A}}$ its closure in $TM\setminus {\textbf{0}}$. Then, given a function $L:{\bar{A}} \subseteq TM \rightarrow [0,\infty )$, we say that (M, L) is a Finsler spacetime if

• i. L is a smooth function that is positive homogeneous of degree 2 when restricted to each ${\bar{A}}_p {:}{=}T_pM\cap {\bar{A}}$,

• ii. its fundamental tensor g, defined for any $v\in {\bar{A}}$ and $u,w\in T_{\pi (v)}M$ by

  $$\begin{aligned} g_{v}(u,w) {:}{=}\frac{1}{2}\frac{\partial ^2}{\partial s\partial t} L(v+tu+sw)\bigg |_{t=s=0}, \end{aligned}$$

  (1)

  has signature $(+-\dots -)$,

• iii. the boundary of ${\bar{A}}$ in $TM\setminus \textbf{0}$ coincides with ${\mathcal {C}}{:}{=}L^{-1}(0)$, called the lightcone of L.

Observe that in this case, ${\bar{A}}_p$ is convex and salient for every $p\in M$ and the indicatrix $\varSigma {:}{=}L^{-1}(1)$ is a strongly convex hypersurface when restricted to each $T_pM$; i.e., each $\varSigma _p=\varSigma \cap T_pM$ is strongly convex. We will say that a vector $v\in TM$ is timelike if $v\in A$ and lightlike if $v\in {\mathcal {C}}$, both of which are always non-zero. Observe that we only consider the future cone in the definition of Finsler spacetime, so we will not distinguished future and past causal vectors.

Observe that there are quite a few subtleties in the definition of a Finsler spacetime, but we will adopt the one firstly considered in [24]. Amongst the subtleties to bear in mind we can point out that

• in some definitions, beginning with that of Beem [25], L is defined in the whole TM. Observe that as explained in [14], for an observer $v\in \varSigma$ one can consider as a positive definite metric in its restspace, without any need of considering L defined away from the causal cone.

• In others, some non-smooth directions are allowed [20, 26,27,28] or they must be smooth up to some power [19] (relevant in the lightlike directions),

• there are others that do not consider the lightlike directions as a part of the model [29],

• there are some models which appear in other contexts with slightly different properties [17, 18].

Associated with the Lorentz-Finsler metric L, there is another anisotropic tensor, usually called the Cartan tensor, defined as

$$\begin{aligned} C_{v}(u,w,z)=\frac{1}{4}\left. \frac{\partial ^3}{\partial r\partial s\partial t} L(v+tu+sw+rz)\right| _{t=s=r=0}, \end{aligned}$$

(2)

for any $v\in {\bar{A}}$ and $u,w,z\in T_{\pi (v)}M$. This symmetric anisotropic tensor is what makes different Finsler spacetimes from the classical Lorentzian geometry. It is straightforward to check that

$$\begin{aligned} C_{v}(v,u,w)=C_{v}(u,v,w)=C_{v}(u,w,v)=0, \end{aligned}$$

(3)

for any $v\in {\bar{A}}$ and $u,w\in T_{\pi (v)}M$. Moreover, the Levi-Civita–Chern anisotropic connection is a very useful tool for the study of Finsler spacetimes (see [30,31,32] for more details about anisotropic connections and calculus). Recall that an anistropic connection can be thought as a connection which depends on directions. This means that for every $v\in {\bar{A}}$ and $X,Y\in {\mathfrak {X}}(M)$, one obtains a different value $\nabla ^{v}_XY\in T_{\pi (v)}M$. In particular, given a chart $({\mathscr {U}},\varphi )$, the Christoffel symbols are functions $\varGamma ^k_{ij}:{\bar{A}}\cap T{\mathscr {U}}\rightarrow {\mathbb {R}}$ which are homogeneous of degree zero and $\nabla ^{v}_{\partial _i}\partial _j=\varGamma ^k_{ij}(v)\partial _k$, where $\partial _1,\ldots ,\partial _n$ are the partial vector fields of the chart. If we fix a vector field $V\in {{\mathfrak {X}}}({\mathscr {U}})$ which is ${\bar{A}}$-admissible, that is to say, taking values in ${\bar{A}}$, we obtain then an affine connection in ${\mathscr {U}}$ with Christoffel symbols $\varGamma ^i_{jk}\circ V$. The Levi-Civita–Chern connection can be characterized in terms of the associated affine connections . Indeed, it is the only one such that

• 1. is torsion-free, namely, for every $X, Y\in {{\mathfrak {X}}}({\mathscr {U}})$,

• 2. is almost g-compatible, namely

  

  where $X,Y,Z\in {{\mathfrak {X}}}({\mathscr {U}})$ and and are the classical tensors obtained when (1) and (2) are evaluated in the vector field V.

Observe that almost g-compatibility is equivalent to $\nabla g=0$ when this tensor derivative is computed using the anisotropic calculus developed in [30, 31]. Moreover, there is also a Koszul formula that determines :

(4)

Let us recall that we say that a causal vector field V is parallel, or a parallel observer (see [32]) when for all $X\in {\mathfrak {X}}({\mathscr {U}})$. Observe that when V is parallel, then the above Koszul formula coincides with the Koszul formula for . This means that when V is parallel, the Levi-Civita–Chern connection of L coincides with the Levi-Civita connection of —this crucial fact is what enables our definition of Finsler pp-wave in Definition 1in a manner analogous to that of the Lorentzian version. Let us say more about this here. To begin with, even if it is not always possible to choose a parallel extension of a vector $v\in {\bar{A}}$, one can still find a pointwise parallel vector field, as follows: if $p=\pi (v)$, then there exists an extension $V\in {\mathfrak {X}}({\mathscr {U}})$ on a certain neighborhood ${\mathscr {U}}\subseteq M$ of p such that for all $X\in {\mathfrak {X}}({\mathscr {U}})$ (see [31, Prop. 2.13]). Indeed, such extensions allow one to easily compute the Chern curvature tensor $R_v$ of L: if $R_v(X,Y)Z$ is the value of the Chern curvature tensor (an anisotropic tensor) for $v\in {\bar{A}}$ and $X,Y,Z\in {\mathfrak {X}}(M)$, then, choosing a pointwise parallel extension V of v as above, it follows that

where is the curvature tensor of . The reason for this equality is that, in the general expression of the Chern curvature tensor computed using , there are additional tensorial terms apart from of the form (see [31, Prop. 2.5]) which vanish when V is parallel. So, in this case, the curvature tensor of the Levi-Civita connection of coincides with the Chern curvature tensor evaluated at V.

A function $f:M\rightarrow {\mathbb {R}}$ admits a gradient with respect to L, denoted $\nabla \!f$, if there exists a vector field metrically equivalent to df, namely, which satisfies

for all $X\in {{\mathfrak {X}}}(M)$. Moreover, in this case the Hessian of f is defined as the anisotropic tensor $H^f(X,Y)=\nabla _{\!X}{d f}(Y)$, where $\nabla$ is the Levi-Civita–Chern connection of L. Observe that there is a dependence on $v\in A$ in the sense that

Let us see that $H^f$ is symmetric as

and (the Levi-Civita–Chern connection is torsion-free), it follows that

(5)

This follows from the above formula, because using the almost-compatibility of $\nabla$ with g,

(the Cartan term vanishes because homogeneity (3)). Let us observe that even if the Hessian is always well-defined for all real functions, the gradient is not. In the classical case of positive definite Finsler metrics, the gradient is well-defined up to the critical points of the function, where it could continuously be extended as zero. In Finsler spacetimes there are more restrictions.

Lemma 1

A smooth function $f:M\rightarrow {\mathbb {R}}$ admits a gradient with respect to a Finsler spacetime (M, L) if and only if $df|_A>0$. Moreover, in this case the gradient is unique.

Proof

For the implication to the right, observe that if $\nabla \!f$ is lightlike at $p\in M$, this means that the kernel of $df_p$ is tangent to ${\mathcal {C}}_p$. As $A_p$ is convex, it remains on one side of the hyperplane $\ker (df_p)$, and as is a Lorentzian-type metric (with index $n-1$) it follows that $df_p|_A>0$, because the lightlike cone of remains on the same side of $\ker (df_p)$. If $\nabla \!f$ is timelike at $p\in M$, then $\ker (df_p)$ does not touch ${\bar{A}}_p$ and as , it follows that $df_p|_A>0$.

For the implication to the left, we know that $\ker (df)\cap A=\emptyset$. If $\ker (df_p)$ is tangent to ${\mathcal {C}}_p$, then there exists $v\in {\mathcal {C}}_p\cap \ker (df)$. Then it is easy to see that

$$\begin{aligned} df_p=\lambda g_{v}(v,\cdot )=g_{\lambda v}(\lambda v,\cdot ) \end{aligned}$$

(6)

and therefore $\nabla \!f=\lambda v$. If $\ker (df_p)$ is not tangent to ${\mathcal {C}}_p$, then there exists $v\in \varSigma _p$ where the minimum distance between $\ker (df_p)$ and $\varSigma _p$ is attained. Then (6) holds for some $\lambda$. This also shows that the gradient is unique, because the strict convexity of $\varSigma _p$ implies that the distance is attained in a unique point. $\square$

Lemma 2

If a function $f:M\rightarrow {\mathbb {R}}$ has a gradient field with constant L-norm, then its flow is given by geodesics.

Proof

As the gradient field has constant L-norm, it follows that $X(L(\nabla \!f))=0$ and then

and as this holds for all $X\in {{\mathfrak {X}}}(M)$, it follows that and $\nabla \!f$ is geodesic. $\square$

3 Lightlike coordinates and their properties

Although lightlike coordinates exist in all dimensions, we present them here in dimension 4, for convenience. In the following, when a chart $({\mathscr {U}},\varphi )$ is fixed, we will denote by $g_{ij}:{\bar{A}}\cap T{\mathscr {U}}\rightarrow {\mathbb {R}}$ the coordinates of the fundamental tensor g in (1), namely, .

Lemma 3

(Lightlike coordinates) Let (M, L) be a Finsler spacetime and f a smooth function defined on an open subset ${\mathscr {U}} \subseteq M$. If $N {:}{=}\nabla \!f$ is a lightlike vector field, then there exist coordinates $({\tilde{x}}^0,{\tilde{x}}^1,{\tilde{x}}^2,{\tilde{x}}^3)$ with $N=\frac{\partial }{\partial {\tilde{x}}^0}$ about any point in ${\mathscr {U}}$ in which the metric has components

$$\begin{aligned} (g_{ij}(N)) = \left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} g_{11}(N) &{} g_{12}(N) &{} g_{13}(N)\\ 0 &{} g_{21}(N) &{} h_{22} &{} h_{23}\\ 0 &{} g_{31}(N) &{} h_{32} &{} h_{33} \end{array} \right) , \end{aligned}$$

(7)

with $(h_{ij})$ a positive-definite $2 \times 2$ matrix.

Proof

Of course, “lightlike” means that N is nowhere vanishing yet satisfies $L(N)= 0$; the former implies that the level sets ${\mathcal {S}}_c {:}{=}f^{-1}(c)$ are embedded hypersurfaces, while the latter implies that N has geodesic flow, , where is the Levi-Civita–Chern connection of L (recall Lemma 2). At any $p \in {\mathcal {S}}_c$, $g_{\scriptscriptstyle N_p}({N_p},{N_p}) = 0$ implies that the induced metric by $g_{N_p}$ on ${\mathcal {S}}_c$ is degenerate. Let $(x^0,x^1,x^2,x^3)$ denote coordinates within ${\mathscr {U}}$ in which $N = \partial _0$. Then by the almost compatibility of g and $\nabla$ and the fact that

by (3), we have that

so that each $c_i{:}{=}g_{0i}(N)$, $i=0,1,2,3$, is independent of $x^0$. Of course, at least one of these $c_i$’s must be nonzero, otherwise each $N_p^{\perp }$ would be four-dimensional. Let us assume that $c_1 \ne 0$. Thus at the moment our metric in the coordinates $(x^0,x^1,x^2,x^3)$ takes the form

with the function f satisfying

(8)

These coordinates, however, are not slice coordinates for the level sets ${\mathcal {S}}_c$; to make them so, simply define new coordinates $(\tilde{x}^0,\tilde{x}^1,\tilde{x}^2,\tilde{x}^3)$ by

$$\begin{aligned} \left\{ \begin{array}{ll} \tilde{x}^0 = x^0,\\ \tilde{x}^1 = f(x^1,x^2,x^3),\\ \tilde{x}^2 = x^2,\\ \tilde{x}^3 = x^3.\end{array} \right. \end{aligned}$$

These new coordinates satisfy $\nabla \tilde{x}^1 = \partial /\partial \tilde{x}^0$, and they are indeed slice coordinates for ${\mathcal {S}}_c$:

$$\begin{aligned} {\mathcal {S}}_c = \left\{ q \in {\mathscr {U}}:\,\tilde{x}(q) = \left( \tilde{x}^0(q),c,\tilde{x}^2(q),\tilde{x}^3(q)\right) \right\} \cdot \end{aligned}$$

Thus each $N_q^{\perp } = T_q{\mathcal {S}}_c = \text {span}\,\{\partial /\partial \tilde{x}^0|_q,\partial /\partial \tilde{x}^2|_q,\partial /\partial \tilde{x}^3|_q\}$, with

for $i=2,3$, and $\partial /\partial \tilde{x}^0$ has a nice relationship with the other coordinate basis vectors:

The metric in the new coordinates $(\tilde{x}^0,\tilde{x}^1,\tilde{x}^2,\tilde{x}^3)$ is now precisely in the form of (7). Finally, note that since $\partial /\partial \tilde{x}^2$ and $\partial /\partial \tilde{x}^3$ are both orthogonal to the lightlike vector $\partial /\partial \tilde{x}^0$, they must satisfy $g_{22}(N)> 0, g_{33}(N) > 0$. It follows that each embedded 2-submanifold defined by

(9)

with induced metric , is Riemannian; indeed, since has negative determinant,

(10)

Together with the fact that $g_{22} > 0$, it follows that the two leading submatrices of the $2 \times 2$ matrix $\begin{pmatrix}g_{22}(N)&{}g_{23}(N)\\ g_{32}(N)&{}g_{33})N) \end{pmatrix}$ have positive determinant; thus this submatrix is positive definite. Renaming each $g_{ij}(N)$ to $h_{ij}$ for $i,j=2,3$, the proof is complete.

$\square$

Lemma 4

Given an arbitrary lightlike vector $v_0$ of a Finsler spacetime (M, L), it is possible to extend it to a lightlike gradient vector field in a certain neighborhood of $\pi (v_0)$.

Proof

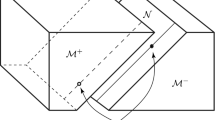
First, consider a local splitting $I\times B$ of M with $I\subset {\mathbb {R}}$ in such a way that $\{t_0\}\times B$ is spacelike for all $t_0\in I$ and $\partial _t$ is timelike. Then consider a surface $S_0$ in B diffeomorphic to $S^2$ which contains $\pi (v_0)$ and is orthogonal to $v_0$, with $v_0$ pointing to the exterior region of $I\times S_0$. Observe that the cylinder $I\times S_0$ is a hypersurface and that it admits a smooth lightlike vector field N along it with the following property: for any $(t_0,p_0)\in I\times S_0$, $N_{(t_0,p_0)}$ is orthogonal to $\{t_0\}\times S_0$. By the Inverse Function Theorem, the exponential map restricted to the bundle generated by N along $S_0$ is a local diffeomorphism. In particular, one can construct local coordinates around $\pi (v_0)$ using product coordinates in $I\times S_0$ and then the one of the exponential map $s\rightarrow \exp _{(t,p)}(sN)$. All this together implies that the projection onto I in these coordinates provides a function $f:{\mathscr {U}}\subset M\rightarrow {\mathbb {R}}$ whose level sets $f^{-1}(t_0)$ are the hypersurfaces obtained as the union of all the lightlike geodesics passing through the points $(t_0,p)$ with $p\in S_0$ and with velocity $N_{(t_0,p)}$. Reducing ${\mathscr {U}}$ if necessary, we can assume that these hypersurfaces are a piece of the horismos $E^+(\{t_0\}\times S_0)\cup E^-(\{t_0\}\times S_0)$. Therefore, they are degenerate and the gradient vector field $\nabla \!f$ must be lightlike. $\square$

Observe that the last lemma can be interpreted in the following way. The lightlike gradient vector field can be thought of as the vector field tangent to the light rays departing orthogonally from a given spacelike surface and its temporal cylinder of a given interval of a universal time. In [23, p. 60], there is a sketch of a very similar argument for Lorentzian manifolds.

There is a direct relationship between the domain of validity of lightlike coordinates and the existence of focal points along the geodesic integral curves of N. First, define $\varDelta _4 {:}{=}\sqrt{-\text {det}\,g_{ij}(N)}$ and

$$\begin{aligned} \varDelta {:}{=}\left| \begin{array}{cc} h_{22} &{} h_{23}\\ h_{32} &{} h_{33} \end{array} \right| ^{\frac{1}{2}}, \end{aligned}$$

and observe that $\varDelta _4 = \varDelta$. Then the relationship is as follows:

Lemma 5

In lightlike coordinates, a point $p \in {\mathscr {U}}$ is a focal point of (9) along the geodesic integral curve of N through p if and only if $\varDelta |_p = 0$.

Proof

Let $(x^0,x^1,x^2,x^3)$ be lightlike coordinates as in Lemma 3, with $N = \partial _0$, and let $\varLambda$ be a Riemannian 2-submanifold as in (9). We begin by observing that $\partial _0,\partial _1,\partial _2,\partial _3$ are all Jacobi fields along any geodesic integral curve $\gamma (x^0)$ of N starting in $\varLambda$. Indeed, setting $J {:}{=}\partial _i$, and noting that $[J,N] = 0$ and , we have that

where $R_{\scriptscriptstyle N}$ is the (1, 3)-Chern curvature tensor. Now suppose that $\varDelta |_p = 0$ at a point p along $\gamma$. Then $\partial _2|_p,\partial _3|_p$ must be linearly dependent, hence some nontrivial linear combination of the two gives the zero vector at p. If we extend this linear combination as is to a vector field $J(x^0)$ along $\gamma$, then J will be a Jacobi field. In fact it is a $\varLambda$-Jacobi field, since $J(0) \in T_{\gamma (0)}\varLambda$ and since (see, e.g., [33, Def. 3.12]); we thus conclude that p is a focal point of $\varLambda$ along $\gamma$. Now for the converse. Suppose that p is a focal point of $\varLambda$ along the geodesic integral curve $\gamma (x^0)$ of N, with $\gamma (b) = p$; let $J:[0,b] \longrightarrow {\mathscr {U}}$ denote the corresponding $\varLambda$-Jacobi field, with J(b) its (zero) value at p:

$$\begin{aligned} J(b) = f^i(b)\partial _i\big |_{p} = 0. \end{aligned}$$

(In fact $f^1$ is identically zero, since J is orthogonal to $\gamma$.) If the $f^i(b)$’s are not all zero, then we are done, since we would thus have a nontrivial linear combination of the $\partial _i|_p$’s equalling zero, which can happen only if $\varDelta _4|_p = \varDelta |_p = 0$. Thus, assume that each $f^i(b) = 0$, in which case

where at least one of ${\dot{f}}^i(b)$ is nonzero, for otherwise $J(b) = J'(b) = 0$ and so J would have to be trivial. Next, because each $\partial _i$ is a Jacobi field, and because any two $\varLambda$-Jacobi fields V, W along a geodesic satisfy (see, e.g., [33, Prop. 3.18]), we have that

the latter because $J(b) = 0$. Thus we’ve arrived at the system of equations

$$\begin{aligned} g_{ji}(N_p){\dot{f}}^i(b) = 0, \end{aligned}$$

with the ${\dot{f}}^i(b)$’s not all zero. This can only happen if $\varDelta _4|_p = 0$, in which case $\varDelta _p = 0$ and the proof is complete. $\square$

4 Finsler pp-waves and Brinkmann coordinates

We begin first of all by providing a coordinate-independent definition of a Finsler pp-wave spacetime (in dimension 4), analogous to the Lorentzian version to be found in [6]; then, in Theorem 1 below, we show the existence of canonical (Brinkmann) coordinates [2] for any Finsler pp-wave, once again in analogy with the Lorentzian case. In the following, given an ${\bar{A}}$-admissible N defined in some open subset ${\mathscr {U}}\subset M$, we will use the notation $\varGamma (N^{\perp })$ for the space of vector fields $X\in {\mathfrak {X}}({\mathscr {U}})$ such that .

Definition 1

(pp-waves) Let (M, L) be a 4-dimensional Finsler spacetime with a parallel lightlike gradient vector field N. Then (M, L) is a pp-wave if its Chern curvature tensor satisfies

(11)

for all $X, Y, Z \in \varGamma (N^{\perp })$. If, in addition to (11), it is also the case that

(12)

for all $X \in \varGamma (N^{\perp })$, then (M, L) is a plane wave.

Remark 1

Let us observe that the definition of parallelism used above depends only on the nonlinear connection associated with L, whose coefficients can be obtained from the Christoffel symbols of the Chern connection as $N^i_j(w)=w^k\varGamma ^i_{kj}(w)$. Indeed, in coordinates, . However, conditions (11) and (12) are specific to the Chern connection, and using the curvature tensor of the Berwald connection, one would obtain different equations. Recall that the difference between the Chern and Berwald connections can be written in terms of the Landsberg connection, and using [31, Cor. 2.17], one can compute the difference between the curvature tensors of both connections, which is not zero in general. As we will see in Theorem 1, both conditions (11) and (12) admit a very simple characterization in coordinates, which does not seem available for the Berwald connection. This reinforces the Chern connection as the best one to measure the stress-energy tensor in a Finsler spacetime (see [32, 34] for more details).

Before proceeding to a coordinate version of Definition 1, we will first need the following

Lemma 6

A lightlike gradient vector field $N=\nabla \!f$ is parallel if and only if all components of the metric (7) are independent of $\tilde{x}^0$.

Proof

Assume that for all $X\in {\mathfrak {X}}(M)$. Consider the partial vectors $N=\partial _0,\partial _1,\partial _2,\partial _3$ of the coordinates $({\tilde{x}}^0,{\tilde{x}}^1,{\tilde{x}}^2,{\tilde{x}}^3)$ in Lemma 3, and observe that by (7), we know that if $2\le i\le 3$ and . By the Koszul formula (4), taking into account that $N=\partial _0$ and all the Lie Brackets will vanish,

which implies that for all $i,j= 1,2, 3$, namely, the coefficients $g_{ij}(N)$ do not depend on the coordinate $\tilde{x}^0$.

Assume now that all the $g_{ij}(N)$ do not depend on ${\tilde{x}}^0$. Let us see first that . Using the Koszul formula (4),

for any $j= 0,1,2,3$, which implies that . Using this identity and the Koszul formula once more,

for any $i,j=0,1,2,3$, which implies that . $\square$

Remark 2

Observe that the above lemma implies in particular that a parallel lightlike gradient vector field N is Killing for the Lorentzian metric , but not necessarily for L, as this metric could have a dependence on $\tilde{x}^0$. Indeed, we can modify L away from the direction of N without losing the parallel lightlike gradient vector field N, but still losing all the global symmetries.

Theorem 1

(pp-waves; [6]) A 4-dimensional Finsler spacetime (M, L) is a pp-wave if and only if there exist local coordinates (v, u, x, y) in which (7) takes the form

$$\begin{aligned} (g_{ij}(N)) = \left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} H &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) , \end{aligned}$$

(13)

where $g_{uu}(N) {:}{=}H(u,x,y)$. Furthermore, (M, L) is a plane wave if and only if H(u, x, y) is quadratic in x, y.

Proof

Consider each embedded 2-submanifold given by (9), with its corresponding induced Riemannian metric

(Since by Lemma 6 each $g_{ij}(N)$ is independent of $\tilde{x}^0$, the components $h_{ij}$ are $\tilde{x}^0$-independent.) By the Gauss Equation ([35, Theorem 8.5, p. 230]), we know that the (single) component of the curvature tensor of is related to that of by

(14)

where is the second fundamental form of ; observe that as N is parallel, the curvature tensor of coincides with $R_{\scriptscriptstyle N}$. But when $N=\partial _0$ is parallel, this equation simplifies considerably, because in such a case the vector field has no $\partial _1$-component,

(15)

for some smooth functions $\alpha ,\beta ,\gamma$ (here use that

because $\partial _0=N$ is parallel and the compatibility of $\nabla$ and ). Thus, since $\partial _0$ is orthogonal to ,

(16)

where, as N is parallel, we observe that is the Levi-Civita connection of ; likewise for and .¹ Thus, as $\partial _0$ is lightlike, (14) simplifies to

(17)

In other words, each Riemannian submanifold is flat, which means that there exist local coordinates on each with respect to which the induced metric takes the form

At each $\tilde{x}^1 = c$, we thus have the triple ; considering if necessary, we may also assume that each is positively oriented (namely, is positively oriented with the natural orientation of the chart). We now put these together to form a smooth coordinate chart $(\tilde{x}^0,\tilde{x}^1,x,y)$, as follows. First, at each point , rotate each so that points in the direction of $\partial _2$ (i.e., ); these rotated ’s thus comprise a smooth vector field $V {:}{=}\frac{1}{\sqrt{h_{22}}}\partial _2$ on the submanifold $\varSigma {:}{=}\{(\tilde{x}^0,\tilde{x}^1,0,0)\}$. As each is orthogonal to its corresponding and since an orientation has been fixed, the ’s thus also comprise a smooth vector field W on $\varSigma$, namely, the unique unit length vector field orthogonal to V and such that $\{V,W\}$ is positively oriented. Next, at each , parallel transport V, W along the integral curve $\gamma ^{(p)}$ of through p, via the connection compatible with the induced metric ; then, at each point along $\gamma ^{(p)}$, parallel transport along the integral curve of on ; by abuse of notation, let V, W denote the resulting vector fields, now smoothly defined on ${\mathscr {U}}$. By the Gauss Formula (see, e.g., [35, Theorem 8.2, p. 228]) and the flatness condition (17), we have, on each , that

similarly for , and . But just as in (16), each must point solely in the direction of $\partial _0$. Finally, define the orthonormal pair

which pair is now orthogonal to $\partial _0,\partial _1$. It follows that all of the Lie brackets of the frame $\{\partial _0,\partial _1,X,Y\}$ will have only a $\partial _0$-component, which collectively yields that and will be closed; indeed, for any pair of vector fields $A,B \in \{\partial _0,\partial _1,X,Y\}$,

likewise with $dY^{\flat }$. By the Poincaré Lemma, both 1-forms are locally exact: $X^{\flat } = dx$ and $Y^{\flat } = dy$, for some smooth functions x, y. With respect to the coordinate chart $(\tilde{x}^0,\tilde{x}^1,x,y)$, the ambient Lorentzian metric thus takes the form

$$\begin{aligned} (g_{ij}(N)) = \left( \begin{array}{cccc} 0 &{} 1 &{} 0 &{} 0\\ 1 &{} g_{11}(N) &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) , \end{aligned}$$

which is precisely (13). (This argument generalizes to dimensions $> 4$.) Conversely, suppose that local coordinates (v, u, x, y) exist in which the metric takes this form, with $N = \partial _v = \nabla u$. Then the nonvanishing Christoffel symbols of such a metric are determined by

where $H_u$, $H_x$, $H_y$ denote, respectively, the partial derivatives of H with respect to u, x and y, from which it follows that $R_{\scriptscriptstyle N}(\partial _x,\partial _y)\partial _x = R_{\scriptscriptstyle N}(\partial _x,\partial _y)\partial _y = 0$; this is precisely the curvature condition (11). Actually something else vanishes, too:

so that $R_{\scriptscriptstyle N}(X,Y)W = 0$ for all $X,Y \in \varGamma (N^{\perp })$ and $W \in {\mathfrak {X}}({\mathscr {U}})$. Finally, if (12) is also true for all $X \in \varGamma (N^{\perp })$, then for any choice $i,j \in \{x,y\}$,

which yields $H_{xji} = H_{yij} = 0$. As the above covariant derivatives of are the only non-vanishing ones up to symmetries with respect to vector fields in $\varGamma (N^{\perp })$, we conclude that H(u, x, y) is quadratic in x, y if and only if for all $X \in \varGamma (N^{\perp })$, completing the proof of Theorem 1. $\square$

We will give some examples of Finsler pp-waves in Sect. 6, but let us observe that the examples of Finsler pp-waves already present in literature can be included in the definition of Theorem 1 up to some interpretations. In both cases, [21, 22], the Lorentz-Finsler metric is not smooth on the lightlike parallel vector field N, but as these Finsler spacetimes are of Berwald type, there is an available affine connection which makes N parallel. Moreover, the role of -orthogonality to N can be played by the tangent space to the lightcone at N. In both cases, it coincides with the tangent space to the lightlike cone of a Lorentzian metric which is already a pp-wave with N as parallel vector field. Therefore, the conditions of Theorem 1 are satisfied also for the Berwaldian Finsler pp-waves of [21, 22].

5 The quotient bundle of a Finsler pp-wave

Theorem 2

([7, 37]) Let (M, L) be a Finsler spacetime and $N = \nabla \!f$ a lightlike, parallel gradient vector field defined in an open subset ${\mathscr {U}}\subseteq M$, with orthogonal complement $N^{\perp } \subseteq T{\mathscr {U}}$. Then the vector bundle $N^{\perp }/N$ admits a positive-definite inner product $\bar{g}$,

and a corresponding linear connection ${\overline{\nabla }}:{\mathfrak {X}}({\mathscr {U}})\times \varGamma (N^{\perp }/N) \longrightarrow \varGamma (N^{\perp }/N)$,

This connection is flat if and only if $({\mathscr {U}},L|_{{\mathscr {U}}})$ is a Finsler pp-wave.

Proof

The metric $\bar{g}$ will be well defined, and positive definite, whenever N is lightlike; indeed, every $X \in \varGamma (N^{\perp })$ not proportional to N is necessarily spacelike, so that $\bar{g}$ is nondegenerate (and positive-definite), and if $[X] = [X']$ and $[Y] =[Y']$, so that $X' = X +fN$ and $Y' = Y+kN$ for some smooth functions f, k, then

On the other hand, the connection ${\overline{\nabla }}$ requires N to be parallel or else it is not well defined: if N is parallel, in which case

That ${\overline{\nabla }}$ is indeed a linear connection follows easily. Now, if this connection is flat, then by definition its curvature endomorphism

$$\begin{aligned}{} & {} \overline{\text {R}}:{\mathfrak {X}}({\mathscr {U}}) \times {\mathfrak {X}}({\mathscr {U}}) \times \varGamma (N^{\perp }/N) \rightarrow \varGamma (N^{\perp }/N),~\text {given by}\\{} & {} \overline{\text {R}}(U,W)[X] {:}{=}{\overline{\nabla }}_{\!V}[{\overline{\nabla }}_{\!W}[X]] - {\overline{\nabla }}_{\!W}[{\overline{\nabla }}_{\!U}[X]] - \overline{\nabla }_{\![U,W]}{[X]} \end{aligned}$$

vanishes, for any section $[X] \in \varGamma (N^{\perp }/N)$ and vector fields $U,W \in {\mathfrak {X}}({\mathscr {U}})$. Using the metric $\bar{g}$, this flatness condition is equivalent to

$$\begin{aligned} \bar{g}(\overline{\text {R}}(U,W)[X],[Y]) = 0\text {for all}U,W \in {\mathfrak {X}}({\mathscr {U}}),[X],[Y] \in \varGamma (N^{\perp }/N). \end{aligned}$$

But if we unpack the definitions of ${\overline{\nabla }}$ and $\bar{g}$, we see that

(18)

It follows that $\overline{\text {R}} = 0$ if and only if $R_{\scriptscriptstyle N}(X,Y)W = 0$ for all $X,Y \in \varGamma (N^{\perp })$ and $W \in {\mathfrak {X}}({\mathscr {U}})$; by (11), this is precisely the condition to be a Finsler pp-wave. $\square$

6 Examples

6.1 Parallel lightlike vector field

Let us choose a Finsler metric F on $M={\mathbb {R}}^2\times S$ with v, u the coordinates of ${\mathbb {R}}^2$ and such that $\partial _v$ is a Killing field, namely, F does not depend on v. Define a one-form $\omega$ such that

where z is tangent to S and $N{:}{=}\partial _v$. Then the Lorentz-Finsler metric defined by

$$\begin{aligned} L(w){:}{=}\omega (w)^2-F(w)^2 \end{aligned}$$

(19)

for any $w\in TM$, admits N as a lightlike parallel vector field (here we are using the fact that if $A=\{w\in TM: L(w)>0\}$ is nonempty, then L determines a Finsler spacetime on M, see [16, Theorem 4.1]). To check this, observe that the fundamental tensor of L is given by

where g is the fundamental tensor of F. By the definition of $\omega$, it follows that the coefficients , form a matrix as in (7). This implies in particular that N is the L-gradient of the function $f:M={\mathbb {R}}^2\times S \rightarrow {\mathbb {R}}$ defined as $f(v,u,p)=u$. By Lemma 6, recalling that F has been chosen independent of v and that $\omega$ has been constructed from F, we conclude that N is parallel.

6.2 Finsler pp-waves

Let us give a particular example of Finsler pp-wave on $M={\mathbb {R}}^2\times {\mathbb {R}}^2$. Let (v, u, x, y) be the canonical coordinates of ${\mathbb {R}}^4$ and choose a parametric family of Minkowski norms F on ${\mathbb {R}}^2$ smoothly depending on the last three coordinates of ${\mathbb {R}}^4$, (u, x, y). Moreover, define the one-form in ${\mathbb {R}}^2$ determined by

where $N=\partial _v$, then

$$\begin{aligned} L=\omega ^2-F^2-dx^2-dy^2 \end{aligned}$$

(20)

is a Finsler pp-wave defined in the region $A=\{w\in TM: L(w)\ge 0\}$. Observe that the matrix of (the fundamental tensor of L), for $N=\partial _v$, is of the form (13). Moreover, this metric is smooth on A, because it is not smooth in the vectors $(0,w)\in T({\mathbb {R}}^2\times {\mathbb {R}}^2)$ with $w\in T{\mathbb {R}}^2$ but in this case, $L(0,w)=-w_1^2-w^2_2<0$ if $w\not =0$. Even if this metric is not of the same type as (19), it is very similar. Indeed, in this case, the role of the metric F in (19) is played by $\sqrt{F^2+dx^2+dy^2}$, which is not a regular Finsler metric because of the smoothness issues, but the proof of [16, Theorem 4.1]) still works to guarantee that (20) determines a Finsler spacetime. Moreover, as in the last subsection, one can check that L admits $N=\partial _v$ as a parallel and lightlike vector field, and the coordinates of are of the form (13), which concludes by Theorem 1, that L is a Finsler pp-wave.

7 Penrose’s construction

With the generalizations of lightlike coordinates and pp-waves to Finsler spacetimes in Sects. 3 and 4, respectively, we are now ready to consider the extension of Penrose’s “plane wave limit” [12]. Again, consider a 4-dimensional Finsler spacetime (M, L) and N a lightlike gradient vector field such that locally in lightlike coordinates $({\tilde{x}}^0,{\tilde{x}}^1,{\tilde{x}}^2,{\tilde{x}}^3)$, $g_{\scriptscriptstyle N}$ takes the form

$$\begin{aligned} (g_{ij}(N)) {:}{=}\begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} g_{11}(N) &{} g_{12}(N) &{} g_{13}(N) \\ 0 &{} g_{21}(N) &{} h_{22} &{} h_{23} \\ 0 &{} g_{31}(N) &{} h_{32} &{} h_{33} \end{pmatrix}, \end{aligned}$$

being $N=\frac{\partial }{\partial \tilde{x}^0}$. Recall that lightlike gradient vector fields always exist at least locally (see Lemma 4). Penrose’s construction now proceeds as follows. Define another coordinate system $(x^0,x^1,x^2,x^3)$ via the diffeomorphism $\varphi$ given by

$$\begin{aligned} (\tilde{x}^0,\dots ,\tilde{x}^3) \overset{\varphi }{\mapsto } (\tilde{x}^0,\varOmega ^{-2}\tilde{x}^1,\varOmega ^{-1} \tilde{x}^2,\varOmega ^{-1} \tilde{x}^3) {:}{=}({x}^0,\dots ,{x}^3), \end{aligned}$$

(21)

where $\varOmega > 0$ is a constant. Next, define the following metric $h_{\scriptscriptstyle \varOmega }$ in the new coordinates $({x}^0,\dots ,{x}^3)$,

$$\begin{aligned} \big ((h_{\scriptscriptstyle \varOmega })_{ij}\big ) {:}{=}\underbrace{\,\begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} \varOmega ^2g_{11}(N) &{} \varOmega g_{12}(N) &{} \varOmega g_{13}(N) \\ 0 &{} \varOmega g_{21}(N) &{} h_{22} &{} h_{23} \\ 0 &{} \varOmega g_{31}(N) &{} h_{32} &{} h_{33} \end{pmatrix}\,}_{\text {defined in the coordinates}~({x}^0,{x}^1,{x}^2,{x}^3)}, \end{aligned}$$

where each component $(h_{\scriptscriptstyle \varOmega })_{ij}$ is (strategically) defined as follows,

(22)

(23)

and similarly with the others. Note that as $\varOmega \rightarrow 0$,

similarly with the others. The crucial fact is the following:

Lemma 7

The metric $h_{\scriptscriptstyle \varOmega }$ is conformal to .

Proof

Use the fact that

as well as (21), to obtain

and so on, which clearly yields the relationship

(24)

This completes the proof. $\square$

In particular, setting , observe that the homothety (24) means that the Levi-Civita connections of $h_{\scriptscriptstyle \varOmega }$ and $\tilde{g}$ are equal: $\nabla ^{\scriptscriptstyle \varOmega } = \nabla ^{\scriptscriptstyle \tilde{g}}$. Taking the limit

thus yields the metric

$$\begin{aligned} \underbrace{\,\begin{pmatrix} 0 &{} 1 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} h_{22}({x}^0,0,\dots ,0) &{} h_{23}({x}^0,0,\dots ,0) \\ 0 &{} 0 &{} h_{32}({x}^0,0,\dots ,0) &{} h_{33}({x}^0,0,\dots ,0) \end{pmatrix}\,}_{\text {defined in the coordinates}~({x}^0,\dots ,{x}^3)}, \end{aligned}$$

which is clearly a metric in so-called Rosen coordinates of Lorentzian geometry, also referred to as Baldwin-Jeffery-Rosen coordinates (e.g. [38]) due to the pioneering paper [39] by Baldwin and Jeffery. So, finally, we need to confirm that this can indeed be interpreted as a Finsler pp-wave in Brinkmann coordinates as discussed before. Following the standard coordinate transformation as described e.g. by Blau and O’Loughlin [40], we introduce a matrix Q such that

$$\begin{aligned} h_{ij}({x}_0)Q^i_k({x}^0) Q^j_l({x}^0)=\delta _{kl}, \end{aligned}$$

satisfying the symmetry property

$$\begin{aligned} h_{ij} {\dot{Q}}^i_k Q^j_l = h_{ij}Q^i_k {\dot{Q}} ^j_l, \end{aligned}$$

with $2\le i,j,k\le 3$ labelling the transverse coordinates, and the dot denoting differentiation with respect to ${x^0}$. Since $h_{ij}$ depends smoothly on ${x}^0$, such a matrix Q can always be found for sufficiently small ${x}^0$ (e.g. [9]). Then the transformation

$$\begin{aligned} {x}^0&=u\,, \\ {x}^1&=v-\frac{1}{2}h_{ij}{\dot{Q}}^i_k Q^j_l {\hat{x}}^k {\hat{x}}^l\,,\\ {x}^i&=Q^i_j{\hat{x}}^j\,, \end{aligned}$$

gives rise to the metric in Brinkmann coordinates $(v,u,{\hat{x}}^i)$ with

$$\begin{aligned} H=-(h_{ij} {\dot{Q}}^i_k\dot{)} Q^j_l {\hat{x}}^k {\hat{x}}^l \end{aligned}$$

as the uu-component of in (13).

Remark 3

Observe that the Finslerian Penrose limit depends only on the initial geodesic $\gamma$, the one with all the coordinates zero, except ${\tilde{x}}^0$. This can be seen using the covariance characterisation of the Penrose limit in [41]. As a first observation, the Finslerian Penrose limit is a classical Penrose limit for the Lorentzian metric . Then in [41, Section 2], the authors show that the Penrose limit depends only on the parallel transport and the curvature tensor of along $\gamma$. As this parallel transport is the one of (which is both the Levi-Civita connection of and the Chern connection of L in the direction N) and the curvature tensor of is , the Chern curvature tensor, it turns out that the Finslerian Penrose limit depends only on $\gamma$ and not on the considered extension N.

8 Concluding remarks

The first main result of this article is the construction of a lightlike gradient vector field N in Finsler spacetimes (see Lemma 4) yielding a particular chart for , as given in Lemma 3. Secondly, after establishing a condition for N to be parallel, we extend the notion of pp-waves, as given by [6], to Finsler spacetimes in Theorem 1. New examples of such Finsler pp-waves are found in Sect. 6, and we also show their quotient bundle structure in Sect. 5. Finally, Penrose’s plane wave limit is adapted to Finsler pp-waves in Sect. 7.

In closing, let us note that Lorentzian spacetimes with a parallel lightlike vector field are also known as Bargmann manifolds. These have proven useful for studying kinematical groups, in particular the Carroll group of plane waves (notably in [38]), thus raising the question of the kinematical group structure associated with Finsler pp-waves. The optical properties of Finsler pp-waves may offer another worthwhile avenue for future work, as Lorentzian plane waves are well-known to exhibit some remarkable lensing effects (e.g., [42]). Indeed, it may be interesting to see whether Finsler pp-waves can also be regarded as members of a Kundt class generalized to Finsler spacetimes.