Topological and dynamical properties of Torelli groups of partitioned surfaces

Abstract

Putman introduced a notion of a partitioned surface which is a surface with boundary with decoration restricting how the surface can be embedded into larger surfaces, and defined the Torelli group of the partitioned surfaces. In this paper, we study some topological and dynamical aspects of the Torelli groups of partitioned surfaces. More precisely, first we obtain upper and lower bounds on the cohomological dimension of Torelli groups of partitioned surfaces and show that those two bounds coincide when at most three boundary components are grouped together in the partition of the boundary. Second, we study the asymptotic translation lengths of Torelli groups of partitioned surfaces on the corresponding curve complexes. We show that the minimal asymptotic translation length asymptotically behaves almost like the reciprocal of the Euler characteristic of the surface. This generalizes the previous result of the first and second authors on Torelli groups for closed surfaces.

1 Introduction

Let S be a connected orientable surface of finite type. When it is closed with genus g, we denote it by $S_g$. In this paper, we will also consider surfaces with punctures or boundary components but not both at the same time. For notation, we use $S_{g}^n$ to denote the surface of genus g with n boundary components, and $S_{g,n}$ to denote the surface of genus g with n punctures. In any case, we will always assume that $\chi (S) < 0$ and $g \ge 2$. The mapping class group of S, denoted by ${{\,\textrm{Mod}\,}}(S)$, is the group of homotopy classes of orientation-preserving homeomorphisms of S. For a surface $S_g^n$ with boundary components, ${{\,\textrm{Mod}\,}}(S_g^n)$ consists of orientation-preserving homeomorphisms up to homotopy fixing boundary pointwise.

For a closed surface $S_g$, one of the important proper normal subgroups of ${{\,\textrm{Mod}\,}}(S)$ is the Torelli group ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g)$, which is the kernel of the following symplectic representation

$$\begin{aligned} \Psi : {{\,\textrm{Mod}\,}}(S_g) {{\,\mathrm{\rightarrow }\,}}{{\,\textrm{Sp}\,}}(2g,{{\,\mathrm{{\mathbb {Z}}}\,}}). \end{aligned}$$

This homomorphism is induced by the action on the first homology $H_1(S_g,{{\,\mathrm{{\mathbb {Z}}}\,}})$ and the algebraic intersection number gives a symplectic structure. For more discussion on the Torelli group, see [9] or [14].

For a surface $S_g^n$ with boundary components, if $n>1$, the algebraic intersection number becomes degenerate. Hence there is no such symplectic representation and the analogous definition of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n)$ does not work. In [19], Putman introduced the notion of a partitioned surface to develop a “Torelli functor” on the category of partitioned surfaces and extend the usual definition of Torelli group of a closed surface. For a surface $S_g^n$ with a partition P of boundary components, let ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ be the Torelli group for the pair $(S_g^n,P)$ in the sense of Putman. When $\partial S = \{b_1, \ldots , b_n\}$, we set notations for two extreme cases for P as $P_{\max }=\{\{b_1\}, \{b_2\}, \ldots , \{b_n\}\}$ and $P_{\min }=\{ \{ b_1, b_2, \ldots , b_n \} \}.$ For the definition and review of basic facts, see Sect. 2 or [19].

For any partition P, we compute bounds for the cohomological dimension of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. In [1], the authors showed that the cohomological dimension of the Torelli group of a closed surface is equal to $3g -5$. The fact that $3g -5$ is a lower bound for the cohomological dimension was already shown long ago by Mess in an unpublished paper [16]. He used the theory of Poincaré duality groups for constructing, by induction, a subgroup of the wanted dimension. The authors of [1] then showed that $3g -5$ is an upper bound by using the action of the Torelli group on the complex of reduced cycles that they defined in the same paper.

We will deduce a lower bound from the lower bound for the closed surface case and a generalized Birman exact sequence for Torelli groups of partitioned surfaces. For the upper bound, we will extend the Poincaré duality groups of Mess by some free abelian subgroup for bridging the gap between the closed case and the boundary case.

Let $S_g^n$ be a surface of genus g with n boundary components. Let P be a partition of its boundaries. We define $P^1:= \{ p \in P \mid |p| = 1 \}$ and $P^2:= \{ p \in P \mid |p| = 2 \}$. Our main theorem about cohomological dimension is

Theorem 1.1

Let $n \ge 1$, and let |P| denote the cardinality of P. Then

$$\begin{aligned} 3g -4 + 3|P|-|P^1| \le {{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}_g^n,P) \le 3g -4 +n +(|P^1| + |P^2|) \end{aligned}$$

We remark that this lower bound and upper bound coincide if the partition P contains only elements of cardinality at most 3, giving a precise formula for those cases.

Next, we discuss the least asymptotic translation length of proper normal subgroups of ${{\,\textrm{Mod}\,}}(S_g^n)$ on the curve graph. This is motivated by the action of the Torelli group of a closed surface $S_g$ on the curve graph ${{\,\mathrm{{\mathcal {C}}}\,}}(S_g)$. Let ${{\,\mathrm{{\mathcal {C}}}\,}}(S_g)$ be the curve graph of $S_g$ with path metric $d_{{{\,\mathrm{{\mathcal {C}}}\,}}}(\cdot ,\cdot )$, i.e., each edge in ${{\,\mathrm{{\mathcal {C}}}\,}}(S_g)$ has length 1. Let $\ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f)$ be the asymptotic translation length of $f \in {{\,\textrm{Mod}\,}}(S_g)$ defined by

$$\begin{aligned} \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}} (f) = \liminf _{j {{\,\mathrm{\rightarrow }\,}}\infty } \frac{d_{{{\,\mathrm{{\mathcal {C}}}\,}}}(\alpha , f^j(\alpha ))}{j}, \end{aligned}$$

where $\alpha$ is an element in ${{\,\mathrm{{\mathcal {C}}}\,}}(S)$. Note that $\ell _{C}(f)$ is independent of the choice of $\alpha$. For any $H \subset {{\,\textrm{Mod}\,}}(S_g)$, define

$$\begin{aligned} L_{{{\,\mathrm{{\mathcal {C}}}\,}}}(H) = \min \{ {{\,\mathrm{\ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}}\,}}(f): \, f \in H, \ \text {pseudo-Anosov} \}. \end{aligned}$$

In [5], the first and second authors proved that

$$\begin{aligned} L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g)) \asymp \frac{1}{g}, \end{aligned}$$

that is, there are constants $C_1$ and $C_2$, independent of g, such that

$$\begin{aligned} \frac{C_1}{g} \le L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g)) \le \frac{C_2}{g}. \end{aligned}$$

On the contrary, Gadre–Tsai [12] showed that $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g)) \asymp 1/g^2$. Hence the minimal asymptotic translation lengths from ${{\,\textrm{Mod}\,}}(S_g)$ and ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g)$ approach 0 at a different rate, $1/g^2$ and 1/g, respectively.

This is analogous to the previous results of [18] and [7] regarding the stretch factor $\lambda$ of pseudo-Anosov mapping classes. For any $H \subset {{\,\textrm{Mod}\,}}(S_g)$, let us define

$$\begin{aligned} L(H) = \min \{ \log (\lambda (f)): \, f \in H \ \text {is pseudo-Anosov} \}. \end{aligned}$$

Notice that $L({{\,\textrm{Mod}\,}}(S_g))$ can be thought of as the length spectrum of the moduli space of genus g Riemann surfaces. Penner [18] proved that $L({{\,\textrm{Mod}\,}}(S_g)) \asymp 1/g$. On the contrary, Farb–Leininger–Margalit [7] showed that $L({{\,\mathrm{{\mathcal {I}}}\,}}(S_g)) \asymp 1$, and that for level m congruence subgroup ${{\,\textrm{Mod}\,}}(S_g)[m]$, $L({{\,\textrm{Mod}\,}}(S_g)[m]) \asymp 1$ with $m \ge 3$. Later, Lanier–Margalit [15] generalized this result and showed that for any proper normal subgroup N of ${{\,\textrm{Mod}\,}}(S_g)$, $L(H) > \log (\sqrt{2})$ for $g >3$.

Inspired by previous works, we generalize the result of [5] about Torelli groups to the case of surfaces with boundary components. Our main result along this line is

Theorem 1.2

We have

$$\begin{aligned} \frac{1}{|\chi (S_g^n)|} \lesssim L_{{{\,\mathrm{{\mathcal {C}}}\,}}} ({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)) \lesssim \frac{1}{|\chi (S_g^n)| -(n-|P|)}. \end{aligned}$$

In particular, $L_{{{\,\mathrm{{\mathcal {C}}}\,}}} ({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)) \asymp \frac{1}{|\chi (S_g^n)|}$.

Note that Gadre–Tsai proved that

$$\begin{aligned} L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g^n)) > \frac{1}{18(2g-2+n)^2+30(2g-2+n)-10n}. \end{aligned}$$

Hence it is natural to ask if $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g^n)) \asymp \frac{1}{|\chi (S_g^n)|^2}.$ We show that it is not the case.

Theorem 1.3

Suppose $g < (1/4 - \epsilon ) n$ for arbitrarily small $\epsilon > 0$. Then $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g^n)) \asymp 1/|\chi (S_{g,n})|$.

It would be interesting to know if we have $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g^n)) \asymp 1/|\chi (S_{g,n})|$ without any restriction on (g, n).

In Sect. 2, we review the notion of partitioned surfaces and Putman’s construction of Torelli groups for partitioned surfaces. In section 3, we obtain bounds on the cohomological dimensions of Torelli groups for partitioned surfaces in the sense of Putman. In Sect. 4, we obtain the lower bound for Theorem 1.2. In Sect. 5, we complete the proof of Theorem 1.2 by obtaining the upper bound. In Sect. 6, we discuss the current state of the art and prove Theorem 1.3.

2 Preliminaries

2.1 Cohomological dimension of groups

We first recall the definition of cohomological dimension, even though we will not actually make any use of the concrete definition.

Definition 2.1

Let G be a group. The cohomological dimension of G, denoted ${{\,\textrm{cd}\,}}(G)$, is the smallest integer n such that

• (1) for any G-module M and for every $i > n$, we have $H^i(G,M) = 0$

• (2) There exists some G-module M with $H^n(G,M) \ne 0$

More importantly, we will repeatedly use two key properties of cohomological dimensions that we list here. The next two results are the content of [4, Chapter VIII, Proposition 2.4]

Proposition 2.2

(Monotonicity) Let $H \subset G$ be a subgroup. Then ${{\,\textrm{cd}\,}}(H) \le {{\,\textrm{cd}\,}}(G)$.

Proposition 2.3

(Subadditivity) Let

be a short exact sequence of groups. Then, we have that ${{\,\textrm{cd}\,}}(G) \le {{\,\textrm{cd}\,}}(H) + {{\,\textrm{cd}\,}}(Q)$.

We will also need to use some theory about Poincaré duality groups. For defining Poincaré duality groups, we first need one definition about a finiteness property of groups.

Definition 2.4

A group G is of type FP if there exists a resolution of ${\mathbb {Z}}$ of finite length by finitely generated ${\mathbb {Z}}G$-modules:

$$\begin{aligned} 0 \rightarrow P_n \rightarrow \cdots \rightarrow P_0 \rightarrow {\mathbb {Z}} \rightarrow 0 \end{aligned}$$

such that each $P_i$ is projective.

A Poincaré duality group is a group G of type FP whose cohomology groups satisfy some additional structure. More precisely:

Definition 2.5

A group G is a Poincaré duality group of dimension n if

• (1) G is of type FP

• (2) $H^i(G,{{\,\mathrm{{\mathbb {Z}}}\,}}G) = 0$ if $i \ne n$ and $H^n(G,{{\,\mathrm{{\mathbb {Z}}}\,}}G) = {{\,\mathrm{{\mathbb {Z}}}\,}}$

They key feature of Poincaré duality groups we will make use of is that they improve the subadditivity of cohomological dimension.

Proposition 2.6

[6] Let

be a short exact sequence of groups such that H and Q are Poincaré duality groups. Then G is also a Poincaré duality group and ${{\,\textrm{cd}\,}}(G) = {{\,\textrm{cd}\,}}(H) + {{\,\textrm{cd}\,}}(Q)$.

Finally, we need to be able to recognise some Poincaré duality group when we encounter them.

Proposition 2.7

The fundamental group of a closed, aspherical n-manifold and free abelian groups of rank n are both Poincaré duality group of dimension n.

2.2 Putman’s Construction of Torelli groups for surfaces with boundary

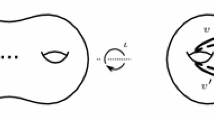
Let $S_g^n$ be a surface of genus g with n boundary components, say with the labels $\{b_1, \ldots , b_n\}$. Let P be a partition of the set of boundary components of $S_g^n$, then we call the pair $(S_g^n, P)$ a partitioned surface. For instance, one can think of an example where $n = 7$ and $P = \{ \{b_1, b_2, b_3\}, \{b_4, b_5\}, \{b_6\}, \{b_7\} \}$ (See Fig. 1).

Let $(S_g^n, P)$ be a partitioned surface. As in [19], we define a capping of $(S_g^n, P)$ as an embedding where the set of the sets of boundary components of the connected components of $S_{g'} {\setminus } S_g^n$ is exactly the partition P. The Torelli group ${\mathcal {I}}(S_g^n, P)$ of the partitioned surface ${\mathcal {I}}(S_g^n, P)$ is defined by

$$\begin{aligned} {\mathcal {I}}(S_g^n, P):= \iota _*^{-1} ({\mathcal {I}}_{g'}) < {{\,\textrm{Mod}\,}}(S_g^n). \end{aligned}$$

for any capping . Putman proved that this definition is independent of the choice of capping $\iota$.

Fig. 1

A capping of $S_2^7$ with $P = \{ \{b_1, b_2, b_3\}, \{b_4, b_5\}, \{b_6\}, \{b_7\} \}.$

In this paper, we will need special types of curves for constructing pseudo-Anosov maps belonging to ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. A curve $\gamma$ on $S_g^n$ is said to be P-separating if it is separating on $S_{g'}$ where is any capping respecting the partition P. A pair of curves $\gamma _1$ and $\gamma _2$ on a surface S is said to be a bounding pair if $\gamma _1$ and $\gamma _2$ represent different homotopy classes of curves but the same non trivial homology class. This means that neither $\gamma _1$ nor $\gamma _2$ are separating, but that if we cut S along $\gamma _1$ and $\gamma _2$, we obtain two disjoint surfaces. A bounding pair map is then the product $T_{\gamma _1} T^{-1}_{\gamma _2}$ of the positive Dehn twist around $\gamma _1$ and the negative Dehn twist around $\gamma _2$, where $\gamma _1$ and $\gamma _2$ form a bounding pair. A pair of curves is then a P-bounding pair if the two curves form a bounding pair on $S_{g'}$ where is any capping respecting the partition P. A P-bounding pair map is then a bounding pair map where the defining curves form a P-bounding pair.

2.3 Action on Homology groups

Putman defined some version of homology group $H_1^P(S_g^n)$ depending only on the surface and the partition P. For completion, we describe the definition of $H_1^P(S_g^n)$ here (see [19] for detail).

Consider a partitioned surface (S, P) and enumerate the partition P as

$$\begin{aligned} P=\{ \{ b_1^1, \ldots , b_{k_1}^1\}, \cdots , \{b_1^m, \ldots , b_{k_m}^m \} \}. \end{aligned}$$

Orient the boundary components $b_i^j$ so that $\sum _{i,j}[b_i^j] = 0$ in $H_1(S)$. Define

$$\begin{aligned} \partial H_1^P( S)&= \langle [b_1^1]+\cdots +[b_{k_1}^1], \cdots , [b_1^m]+ \cdots + [b_{k_m}^m] \rangle \subset H_1(S) \end{aligned}$$

Let Q be a set containing one point from each boundary component of S. Define $H_1^P(S)$ to be equal to the image of the following submodule of $H_1(S,Q)$ in $H_1(S,Q)/\partial H_1^P(S)$:

$$\begin{aligned} \langle \{ [h] \in H_1(S,Q) | \ {}&\text {either { h} is a simple closed curve or { h} is a properly}\\&\text {embedded arc from }q_1\text { to }q_2\text { with }q_1, q_2 \in Q\text { lying}\\&\hbox {in boundary components} b_1 \hbox {and} b_2 \text { with }\{b_1, b_2\} \subset p\\&\hbox { for some}\ p\in P \} \rangle . \end{aligned}$$

Putman proved that an element of ${{\,\textrm{Mod}\,}}(S_g^n)$ belongs to ${\mathcal {I}}(S_g^n, P)$ if and only if it acts trivially on $H_1^P(S_g^n)$. In particular, this shows that ${\mathcal {I}}(S_g^n, P)$ is well-defined, not depending on the choice of the capping $\iota$.

3 Estimates on the cohomological dimension

We begin by a brief discussion on the arguments used in [1] for computing the cohomological dimension of the Torelli group of a surface with only one boundary component, as the ideas used for the general case are somewhat similar. The authors in [1] first prove that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g)) = 3g -5$. Then, the Birman exact sequence

immediately yields that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^1)) \le 3(g+1) -5$. Here, $US_g$ is the unit tangent bundle of $S_g$ and is therefore a closed 3-manifold, and has cohomological dimension 3. We thus get the desired inequality by subadditivity of cohomological dimensions.

The inequality in the other direction uses Poincaré duality groups and was first proven in [16]. It was also shown in [1] that ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g)$ contains a Poincaré duality group $\Gamma$ of cohomological dimension $3g -5$. Restricting the Birman exact sequence to $\Gamma$, we get

where $\Gamma '$ is the preimage of $\Gamma$ under the capping homomorphism. By proposition 2.7, $\pi _1(US_g)$ also is a Poincaré duality group. Hence, using proposition 2.6, we get that ${{\,\textrm{cd}\,}}(\Gamma ') = 3g - 5 +3 = 3(g+1) -5$. Since $\Gamma '$ is a subgroup of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^1)$, we deduce that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^1)) \ge 3(g+1)-5$. Therefore, this proves that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^1)) = 3(g+1) -5$.

Since here $P = P^1$ and $= |P| = |P^1| = n = 1$, both the lower and upper bound of theorem 1.1 are equal to $3\,g -4 +2 = 3(g+1) -5$, concluding the case $n=1$.

3.1 The upper bound

Let $S_g^n$ be a surface of genus g with n boundary components and consider $S_g$ to be obtained from $S_g^n$ by gluing a disk to each boundary. We then have a map ${{\,\textrm{Cap}\,}}_n :{{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{Mod}\,}}(S_g)$ obtained by extending mapping classes in ${{\,\textrm{Mod}\,}}(S_g^n)$ by the identity on each of the glued disks.

We would like to understand the kernel of ${{\,\textrm{Cap}\,}}_n$ as well as the kernel of the restriction of ${{\,\textrm{Cap}\,}}_n$ to ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. The case of the map ${{\,\textrm{Cap}\,}}:{{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{Mod}\,}}(S_g^{n-1})$ is already well understood. Indeed, the Birman exact sequence shows that the kernel of ${{\,\textrm{Cap}\,}}$ is isomorphic to the fundamental group of the unitary tangent bundle of $S_g^{n-1}$ and the kernel of the restriction of ${{\,\textrm{Cap}\,}}$ to ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ was investigated in [19]. We carry a similar investigation for ${{\,\textrm{Cap}\,}}_n$ here.

To understand the kernel of ${{\,\textrm{Cap}\,}}_n$, we need to introduce the notions of configuration spaces and framed configuration spaces and their fundamental groups.

The n dimensional configuration space of a space X, denoted ${{\,\textrm{CG}\,}}_n(X)$, is the set $\{(p_1,\cdots ,p_n) \in X^n \mid p_i \ne p_j \forall i \ne j \}$. In other words, ${{\,\textrm{CG}\,}}_n(X)$ is the set of all n-tuples of distinct points in $X^n$. The pure braid group on n strands over X, denoted $PB_n(X)$ is defined to be the fundamental group of ${{\,\textrm{CG}\,}}_n(X)$.

We define the framed configuration space of a space X, denoted by ${{\,\textrm{FCG}\,}}(X)$, to be the set $\{(p,v_1, \cdots ,v_n) \in CG(X) \times (S^1)^n\}$ where $S^1$ is the unit circle. We think of it as the space of embeddings of n distinct points into X, with a unit tangent vector at each point. The pure framed braid group on n strands over X, denoted by ${{\,\textrm{PFB}\,}}_n(X)$, is the fundamental group of ${{\,\textrm{FCG}\,}}(X)$.

Armed with these new concepts, we can describe the kernel of ${{\,\textrm{Cap}\,}}_n :$ ${{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{Mod}\,}}(S_g)$. We note that this is proven in [2], but we recall the proof here for completeness.

Theorem 3.1

The kernel of ${{\,\textrm{Cap}\,}}_n :{{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{Mod}\,}}(S_g)$ can be identified with ${{\,\textrm{PFB}\,}}_n(S_g)$. Hence, the following sequence is exact

$$\begin{aligned} 1 \rightarrow {{\,\textrm{PFB}\,}}_n(S_g) \rightarrow {{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{Mod}\,}}(S_g) \rightarrow 1 \end{aligned}$$

Proof

We consider $S_g$ to be obtained from $S_g^n$ by gluing a disk on each boundary component and we let $p_1, \cdots , p_n$ be n points, one in each disk we glued. We also choose a unit tangent vector $v_i$ at each $p_i$. Let ${{\,\textrm{Diffeo}\,}}^+(S_g)$ be the group of orientation preserving diffeomorphisms of $S_g$ and define $\psi :{{\,\textrm{Diffeo}\,}}^+(S_g) \rightarrow {{\,\textrm{FCG}\,}}(S_g)$ by $\psi (f) = (f(p_1), \cdots , f(p_n), f_*(v_1),\cdots , f_*(v_n))$. Then $\psi$ is a fiber bundle with fiber the group of diffeomorphisms of $S_g$ fixing $\{p_1, \cdots , p_n\}$ pointwise and fixing a unit tangent vector at each of these points. Thus, these diffeomorphisms fix the regular neighborhoods of each of the $p_i$’s. We can thus identify the fiber with ${{\,\textrm{Diffeo}\,}}^+(S_g^n)$. We then get the desired result by looking at the long exact sequence of homotopy groups associated to this fiber bundle. $\square$

Remark 3.2

It is shown in [2] that ${{\,\textrm{PFB}\,}}_n(S_g)$ is a semidirect product of ${{\,\textrm{PB}\,}}_n(S_g)$ with ${\mathbb {Z}}^n$. This means that we have a short exact sequence

$$\begin{aligned} 1 \rightarrow {\mathbb {Z}}^n \rightarrow {{\,\textrm{PFB}\,}}_n(S_g) \xrightarrow {\hbox { }\ \pi } {{\,\textrm{PB}\,}}_n(S_g) \rightarrow 1 \end{aligned}$$

We now investigate the kernel of the restriction of ${{\,\textrm{Cap}\,}}_n$ to ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. Let us define $P^1 = \{p \in P \mid |p| = 1\}$ and $P^2 = \{p \in P \mid |p| = 2\}$.

Theorem 3.3

The kernel K of ${{\,\textrm{Cap}\,}}_n :{{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P) \rightarrow {{\,\mathrm{{\mathcal {I}}}\,}}(S_g)$ fits in a short exact sequence

$$\begin{aligned} 1 \rightarrow {\mathbb {Z}}^m \rightarrow K \rightarrow K'\rightarrow 1 \end{aligned}$$

where $K'$ is $\pi (K)$, where $\pi$ is the projection from ${{\,\textrm{PFB}\,}}_n(S_g)$ to ${{\,\textrm{PB}\,}}(S_g)$, and $m = |P^1| + |P^2|$.

Proof

We have a short exact sequence

$$\begin{aligned} 1 \rightarrow {\mathbb {Z}}^n \rightarrow {{\,\textrm{PFB}\,}}_n(S_g) \rightarrow {{\,\textrm{PB}\,}}_n(S_g) \rightarrow 1 \end{aligned}$$

and K is a subgroup of ${{\,\textrm{PFB}\,}}_n(S_g)$. Hence, we want to understand the rank of ${\mathbb {Z}}^n \cap K$. The generators of ${\mathbb {Z}}^n$ are represented, as elements of ${{\,\textrm{Mod}\,}}(S_g^n)$, by the Dehn twists around the boundary components of $S_g^n$. We thus only need to check which compositions of these Dehn twists are in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. Clearly, for any $p \in P$ of cardinality 1, the corresponding Dehn twist is in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ since it is a P-separating twist. Also, for any $p = \{ b_i,b_j\}$, we have that $T_{b_i}T_{b_j}^{-1}$ also is in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ since it is a P-bounding pair. We now show that the only elements in ${\mathbb {Z}}^n \cap K$ are words in these P-separating twists and in these P-bounding pairs.

For proving that no other composition of such Dehn twists is in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$, we will look at their action on some arcs, which are elements of $H_1^P(S_g^n)$. Suppose that f is a product of powers of Dehn twists around the boundaries of $S_g^n$. If $T_{b_1}^{k_1}T_{b_2}^{k_2}$ appears in f with $k_1 + k_2 \ne 0$ for some $\{b_1,b_2\} \in P$, then we choose any arc a from $b_1$ to $b_2$ and note that $f_*([a]) = T_{b_1}^{k_1}T_{b_2}^{k_2}([a]) \ne [a]$. Similarly, if $T_b^k$ appears in f for some $b \in p \in P$ with $|p| \ge 3$, then choosing any $b' \ne b \in p$ and any arc a from b to $b'$, we get that $f_*([a]) = T_b^k T_{b'}^{k'}([a]) = [a] + k'[b'] +k[b] \ne [a]$, where the last inequality comes from the fact that [b] and $[b']$ are independent in $H_1^P(S_g^n)$. $\square$

We thus have a short exact sequence

$$\begin{aligned} 1 \rightarrow K \rightarrow {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P) \rightarrow {{\,\mathrm{{\mathcal {I}}}\,}}(S_g) \rightarrow 1 \end{aligned}$$

with K being an extension of a subgroup of ${{\,\textrm{PB}\,}}_n(S_g)$ by ${\mathbb {Z}}^m$. In [10], the authors show that ${{\,\textrm{cd}\,}}({{\,\textrm{PB}\,}}_n(S_g)) = n+1$. Hence, we obtain that ${{\,\textrm{cd}\,}}(K) \le n+1+m = n+1+(|P^1| + |P^2|)$. This proves that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)) \le 3\,g -5 + n + 1 + (|P^1| + |P^2|) = 3\,g -4 + n +(|P^1| + |P^2|)$, as desired.

3.2 The lower bound

We will prove the lower bound by induction on n. To be precise, the induction hypothesis is that, for all partitioned surfaces with $n-1$ boundaries, there exists a Poincaré duality group $\Gamma \subset {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1},P')$ such that ${{\,\textrm{cd}\,}}(\Gamma ) = 3\,g -4 + 3|P'| -|P'^1|$. Recall that we showed this to hold for $n =1$.

Let $S_g^n$ be a surface of genus g with n boundaries and let P be a partition of the boundaries.

Suppose that there exist two boundaries b and $b'$ that are both capped on their own (i.e: both $\{b\}$ and $\{b'\}$ are elements of P). Let us embed $S_g^{n-1}$ in $S_g^n$ as suggested by the left part of Fig. 2. More precisely, the blue curve in Fig. 2 cut $S_g^{n}$ into to surfaces $S_1$ and $S_2 = S_0^3$. We then identify $S_g^{n-1}$ with $S_1$. Let us also number the boundaries of $S_g^n$ so that $b = \delta _1$ and $b' = \delta _2$. By construction we have where is a capping induced by P. We consider the capping $P'$ of $S_g^{n-1}$ induced by that sequence of inclusions and call it the capping induced on $S_1$ by P. This implies that ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1},P')$ is a subgroup of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ (see [19, Theorem 3.6]). By induction, there exists a Poincaré duality group $\Gamma$ of dimension $3\,g -4 + 3|P'| -|P'^1|$ in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1},P')$.

Since $|P'| = |P| -1$, we need to add 2 dimensions to achieve the wanted lower bound. Indeed $3|P'| = 3|P| -3$ and $|P^1| =|P'^1|+1$. This is done by considering the group $G = \langle \Gamma , T_{\delta _1}, T_{\delta _2} \rangle$. This group G is clearly a subgroup of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ and it is easy to show that $G \equiv {{\,\mathrm{{\mathbb {Z}}}\,}}^2 \bigoplus \Gamma$. This can be done, for example, by considering the action of G on the arc $\alpha$, drawn in Fig. 2. Hence, since ${{\,\mathrm{{\mathbb {Z}}}\,}}^2$ is a Poincaré duality group, proposition 2.6 shows that ${{\,\textrm{cd}\,}}(G) = {{\,\textrm{cd}\,}}(\Gamma ) + 2$ and hence, by monotonicity of cohomological dimensions, that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)) \ge {{\,\textrm{cd}\,}}(G) = 3g -4 +3(|P|-1) - | P^1 |)$ as desired.

Suppose instead that there is a pair of boundaries $b,b'$ such that $\{b,b'\} \in P$. We embed $S_g^{n-1}$ into $S_g^n$ the same way as before (see the right part of Fig. 2) and let $P'$ be the induced capping. Once again, we order the boundaries of $S_g^n$ such that $b = \delta _1$ and $b' = \delta _2$. This time, we only need to add one dimension, since $3|P| = 3|P'|$ and $|P^1| =|P'^1| -1$. Therefore, it is sufficient to add the bounding pair $T_{\delta _1} T_{\delta _2} ^{-1}$ to $\Gamma$, the Poincaré duality group of dimension $3g-4 +3|P'| -|P'^1|$ in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1},P')$. As before, the group $G = \langle {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1}), T_{\delta _1}T_{\delta _2}^{-1} \rangle$ is isomorphic to ${{\,\mathrm{{\mathbb {Z}}}\,}}\oplus {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1})$, and thus has one more cohomological dimension than ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1})$, concluding the proof.

Fig. 2

$S_g^n$ is the surface delimited by the black line and the cappings are suggested by the shaded lines. The blue curve indicates how we embed $S_g^{n-1}$ into $S_g^n.$

Putting those two cases together, we can show that theorem 1.1 holds whenever each element of the partition P has cardinality 1 or 2.

In other words, we proved that each $p \in P$ adds exactly 2 dimensions if $p = \{b\}$ and that it adds exactly 3 dimensions if $|p| =2$. It remains to show that p adds at least 3 dimensions if p contains 2 or more elements.

The proof is similar to the case of $|p| = 2$. Let $|p| \ge 3$. This time, we embed $S_g^{n -|p|+1}$ into $S_g^n$ as indicated in Fig. 3 for the case where $P = {p}$. In the general case, just imagine that the blue curves cuts out exactly the boundaries of p and nothing more. Let $\gamma$ be a simple closed curve cutting of all boundaries in p except for $\delta _1$ (see Fig. 3). We then consider the group $G = \langle \Gamma , T_{\delta _1} T_\gamma ^{-1}\rangle$ where $\Gamma$ is the Poincaré duality group of the right dimension in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1},P')$. Once again, $G \equiv {{\,\mathrm{{\mathbb {Z}}}\,}}\oplus {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1})$ and this shows that ${{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)) \ge 1 +{{\,\textrm{cd}\,}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1},P'))$.

Fig. 3

$S_g^n$ is the surface delimited by the black line and one capping is suggested by the shaded lines. The blue curve indicates how we embed $S_g^{n-|P|+1}$ into $S_g^n.$

4 Lower bound on the minimal asymptotic translation length

Let S be a surface of finite type with nonempty boundary and $\beta$ be one of its boundary components. Suppose $S'$ is the surface obtained from S by capping the boundary component $\beta$ with a once-puncture disk. Let us denote this puncture by $p_0$. Let ${{\,\textrm{Mod}\,}}(S, \{ p_1, \cdots , p_k \})$ be the subgroup of ${{\,\textrm{Mod}\,}}(S)$ consisting of elements that fix the punctures $p_1, \cdots , p_k$ of S (the set $\{p_i\}$ is possibly empty). Then we have a homomorphism

$$\begin{aligned} \varphi : {{\,\textrm{Mod}\,}}(S, \{ p_1, \cdots , p_k \}) {{\,\mathrm{\rightarrow }\,}}{{\,\textrm{Mod}\,}}(S', \{ p_0, p_1, \cdots , p_k \}) \end{aligned}$$

and the following sequence is exact (see Proposition 3.19 in [9]):

$$\begin{aligned} 1 {{\,\mathrm{\rightarrow }\,}}\langle T_{\beta } \rangle {{\,\mathrm{\rightarrow }\,}}{{\,\textrm{Mod}\,}}(S, \{ p_1, \cdots , p_k \}) \xrightarrow {\varphi } {{\,\textrm{Mod}\,}}(S', \{ p_0, p_1, \cdots , p_k \}) {{\,\mathrm{\rightarrow }\,}}1. \end{aligned}$$

As a consequence, we have the following proposition.

Proposition 4.1

There is a homomorphism

$$\begin{aligned} \Phi : {{\,\textrm{Mod}\,}}(S_g^n) {{\,\mathrm{\rightarrow }\,}}{{\,\textrm{PMod}\,}}(S_{g,n}), \end{aligned}$$

by capping each boundary component with a once-punctured disk.

Proof

By applying Proposition 3.19 in [9] repeatedly, we obtain a homomorphism $\Phi : {{\,\textrm{Mod}\,}}(S_g^n) {{\,\mathrm{\rightarrow }\,}}{{\,\textrm{Mod}\,}}(S_{g,n})$. Since the capping homomorphism fix the puncture, the image of $\Phi$ fixes all punctures of $S_{g,n}$. Therefore, it is contained in ${{\,\textrm{PMod}\,}}(S_{g,n})$. $\square$

Since $S_{g}^n \setminus \partial S_g^n$ is homeomorphic to $S_{g,n}$ and essential curves are non-peripheral, ${\mathcal {C}}(S_{g}^n)$ and ${\mathcal {C}}(S_{g,n})$ are naturally identified, and the identification map is $\Phi$-equivariant. This is because the subgroup of ${{\,\textrm{Mod}\,}}(S_g^n)$ acting trivially on ${\mathcal {C}}(S_{g}^n)$ is generated by the Dehn twists along peripheral curves, and this subgroup is contained in the kernel of $\Phi$. Abusing the notation, we will use ${\mathcal {C}}_{g,n}$ for this curve complex (up to identification). By the $\Phi$-equivariance, for each $f \in {{\,\textrm{Mod}\,}}(S_g^n)$, the actions of f and $\Phi (f)$ on ${{\,\mathrm{{\mathcal {C}}}\,}}_{g,n}$ are the same. From this, we immediately conclude that $\ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) = \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(\Phi (f)).$

Before we obtain a lower bound on $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P))$, we will prove a lemma which gives us a comparison between the groups ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)$ for various partitions P of the set of boundary components. Let $P, P'$ be partitions of the set of boundary components. We say $P'$ is finer than P if each element of P is either an element of $P'$ or a union of elements of $P'$.

Lemma 4.2

Let $P_1, P_2$ be partitions of the set of boundary components of $S_g^n$. Suppose $P_2$ is finer than $P_1$. Then we have ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P_1) \subset {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P_2)$.

Proof

This is a special case of [19] [Theorem 3.6]. $\square$

Theorem 4.3

For any partitioned surface $(S_g^n,P)$, we have

$$\begin{aligned} L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)) \gtrsim \frac{1}{|\chi (S_g^n)|}. \end{aligned}$$

Proof

Let $f \in {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)$ be a pseudo-Anosov map. By Lemma 4.2, this implies that $f \in {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P_{max})$ (as pointed out in [19], the idea of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P_{max})$ appears in [13]). We have a capping $i: (S_g^n, P_{max}) \rightarrow S_g$, hence $f \in i_*^{-1}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g))$.

Let $\Phi$ be the map in Proposition 4.1. Once we identify $S_{g,n}$ with the surface obtained from $S_g$ by removing one point from each connected component of $S_g \setminus i(S_g^n)$, i can be seen as the composition . One can consider a map $j_*: {{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{Mod}\,}}(S_{g,n})$ by extending the map as identity outside the image under j, and then it would be the same map as $\Phi$. Therefore the image under $j_*$ is contained in ${{\,\textrm{PMod}\,}}(S_{g,n})$. Similarly one can define a map $h_*: {{\,\textrm{PMod}\,}}(S_{g,n}) \rightarrow {{\,\textrm{Mod}\,}}(S_g)$.

Note that $j_*(f) = \Phi (f) \in {{\,\textrm{PMod}\,}}(S_{g,n})$ and $h_*(\Phi (f)) = h_*(j_*(f)) = i_*(f)$. Since $f \in i_*^{-1}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g))$, this implies that the Lefschetz number $\Lambda ( \Phi (f) ):= \Lambda (h_*(\Phi (f))) = 2- 2\,g < 0$. By Tsai [20], $\Lambda (\Phi (f))<0$ implies that there exists a rectangle in the Markov partition for $\Phi (f)$ which intersects with its image under $\Phi (f)$.

Finally by [12] (see also [5]), $\ell _C(\Phi (f)) \gtrsim \frac{1}{|\chi (S_{g,n})|}$ and this implies $\ell _C(f) \gtrsim \frac{1}{|\chi (S_g^n)|}$ (recall the discussion right before Lemma 4.2). This completes the proof. $\square$

5 Upper bound on the minimal asymptotic translation length

In this section we obtain the upper bound on $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P))$. We first focus on the case $P = P_{\max }$. To do this, we use Penner’s construction to find a pseudo-Anosov element $f \in {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P_{\max })$ such that $\ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim 1/|\chi (S_g^n)|$.

Theorem 5.1

We have

$$\begin{aligned} L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P_{\max })) \lesssim \frac{1}{g + n}. \end{aligned}$$

Proof

For notational simplicity, we simply write P for $P_{\max }$ throughout the proof.

Fig. 4

Red curves and blue curves form a filling multi-curves of $S_g^n$, consisting of separating curves. If the number of boundary components n is odd, $\beta$ is a boundary component. If n is even, we consider $\beta$ capped by a disk and hence it is not a boundary component. The numbers k and l are defined by $\displaystyle k=m+\frac{1+(-1)^{m+1}}{2}$ and $\displaystyle l=n-1-\frac{1+(-1)^{n+1}}{2}$. Note that the curves $c_1$ and $c_2$ can be adjusted to cut off one or two geni of $S_g^n$. In that way, a good choice of $c_1$ and $c_2$ can always be made such that the curves $a_k$ and $a_{g-2}$ can be drawn in blue. If $m =1$, in both cases, some of the $c_i$ curves overlap

It suffices to show that there is a pseudo-Anosov mapping class $f \in {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)$ such that $\ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim 1/(g + n)$. The idea is as follows. We will find filling multicurves A and B consisting of separating curves. Then define $f = T_A T_B^{-1}$, where $T_A$ and $T_B$ are multi-twists. Then f is pseudo-Anosov since it comes from Penner’s construction.

Since P is maximal, every separating curve on $S_g^n$ is still separating on the capped surface, hence the Dehn twist long a separating curve is indeed in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)$. This implies that f lies in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)$.

We then find a simple closed curve $\delta$ such that $f^N(\delta )$ and $\delta$ don’t fill the surface together for some integer N. This implies that $d_{{{\,\mathrm{{\mathcal {C}}}\,}}}(f^N(\delta ), \delta ) \le 2$ and further that

$$\begin{aligned} \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \le \frac{2}{N}. \end{aligned}$$

We will consider when genus g is even and when g is odd, separately.

Case 1. Assume $g=2+2m$ for some m. Let A consist of red curves and B consist of blue curves as in Fig. 4a. In this figure, if the number of boundary components n is odd, then we place $n-1$ boundary components in the middle and put the last boundary component, say $\beta$, on the left bottom corner. If n is even, we place all boundary components in the middle and $\beta$ doesn’t represent the boundary component. Then the numbers k and l are defined by

$$\begin{aligned} k=m+\frac{1+(-1)^{m+1}}{2} \quad \text {and} \quad l=n-1-\frac{1+(-1)^{n+1}}{2}. \end{aligned}$$

Note that k is always even and l is always odd. Define $f = T_A T_B^{-1}$.

Now we follow the same notation as in the proof of Theorem 6.1 in [12]. For a finite collection of curves $\{c_j \}_{j=1}^{k} \subset A \cup B$ such that $c_1 \cup \cdots \cup c_k$ is connected, let ${{\,\mathrm{{\mathcal {N}}}\,}}(c_1 \cdots c_k)$ be the regular neighborhood of $c_1 \cup \cdots \cup c_k$. We also let ${{\,\mathrm{{\mathcal {N}}}\,}}(c_1\cdots c_k)^C$ be the regular neighborhood of $A \cup B {\setminus } \{ c_1 \cup \cdots \cup c_k\}$. Let $\delta$ be the curve $b_{\lceil \frac{l}{2} \rceil }$ if $n \ge 2$ and $\delta$ be $a_1$ if $n < 2$ and let $\gamma$ be the curve as in Fig. 5. Recall that $f = T_A T_B^{-1}$ and consider the images of f. One can see that

$$\begin{aligned}&f(\delta ) \subset \left\{ \begin{array}{ll} {{\,\mathrm{{\mathcal {N}}}\,}}(b_{\lceil \frac{l}{2} \rceil -1} b_{\lceil \frac{l}{2} \rceil } b_{\lceil \frac{l}{2} \rceil +1}), &{} \text {if }\lfloor \frac{n}{2} \rfloor \text { is even,}\\ {{\,\mathrm{{\mathcal {N}}}\,}}(b_{\lceil \frac{l}{2} \rceil -2} b_{\lceil \frac{l}{2} \rceil -1} b_{\lceil \frac{l}{2} \rceil } b_{\lceil \frac{l}{2} \rceil +1} b_{\lceil \frac{l}{2} \rceil +2}), &{} \text {if }\lfloor \frac{n}{2} \rfloor \text { is odd,} \end{array} \right. \\ \\&f^{2}(\delta ) \subset \left\{ \begin{array}{ll} {{\,\mathrm{{\mathcal {N}}}\,}}(b_{\lceil \frac{l}{2} \rceil -3} \cdots b_{\lceil \frac{l}{2} \rceil +3}), &{} \hspace{5.2em} \text {if }\lfloor \frac{n}{2} \rfloor \text { is even,}\\ {{\,\mathrm{{\mathcal {N}}}\,}}(b_{\lceil \frac{l}{2} \rceil -4} \cdots b_{\lceil \frac{l}{2} \rceil +4}), &{} \hspace{5.2em }\text {if }\lfloor \frac{n}{2} \rfloor \text { is odd,} \end{array} \right. \\&\vdots \\&f^{\lfloor \frac{n}{4} \rfloor } ( \delta ) \subset {{\,\mathrm{{\mathcal {N}}}\,}}( b_1 \cdots b_l)\\ \end{aligned}$$

Continuing this reasoning, we see that if we then apply $f^{\lceil \frac{k}{4} \rceil }$ to $f^{\lfloor \frac{n}{4} \rfloor } ( \delta )$ we do not reach $a_{\frac{k}{2}+1}$ so that $f^{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor }(\delta )$ is still disjoint from $\gamma$. This implies that $f^{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor } (\delta )$ and $\delta$ do not fill the surface, i.e., $d_{{{\,\mathrm{{\mathcal {C}}}\,}}}(f^{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor }(\delta ), \delta ) \le 2$. Hence we have

$$\begin{aligned} \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f)&\le \frac{2}{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor } \le \frac{2}{\frac{k}{4}+\frac{n}{4}-1}\\&\le \frac{8}{k+n-4} \le \frac{8}{\frac{g-2}{2} + n -4}\\&\le \frac{16}{g+2n-10} \end{aligned}$$

Therefore, $\displaystyle \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim \frac{1}{g+n}.$

Fig. 5

The choice of $\gamma$ and $\delta$

Case 2. Assume $g=3+2m$ for some m.

In this case, the computation is almost identical to Case 1. Let A consist of red curves and B consist of blue curves as in Fig. 4b. Here, the numbers k and l are defined by

$$\begin{aligned} k=m+\frac{1+(-1)^{m+1}}{2} \quad \text {and} \quad l=n-1-\frac{1+(-1)^{n+1}}{2}. \end{aligned}$$

Define $f = T_A T_B^{-1}$ and choose $\gamma$ and $\delta$ as in Fig. 5 (again, if $n < 2$, we choose $\delta$ to be $a_1$ instead). Then by the same argument as in Case 1, we conclude that $\gamma$ doesn’t intersect $f^{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor } ( \delta )$. Then $f^{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor } (\delta )$ and $\delta$ don’t fill the surface, and hence we have again that

$$\begin{aligned} \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f)&\le \frac{2}{\lceil \frac{k}{4} \rceil + \lfloor \frac{n}{4} \rfloor } \le \frac{32}{|\chi (S_g^n)|-18}. \end{aligned}$$

Therefore, $\displaystyle \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim \frac{1}{g + n}.$

$\square$

We remark that the construction of the pseudo-Anosov maps in Theorem 5.1 requires $g \ge 4$. For the cases of $g=1,2,3$, we can use the multicurves of Fig. 6 instead to produce pseudo-Anosov maps f such that $l_{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim \frac{1}{n}$. In the case of $g=1$, we use one bounding pair map in addition to separating twists.

Fig. 6

The multicurves for the cases of $g=1,2,3$. In these case of $g=1$, we use one bounding pair in addition to separating curves. The two curves forming the bounding pair are labeled by a and b. Since they are drawn in different colors, the product of the positive Dehn twist around a and the negative Dehn twist around b will form a bounding pair map. These pictures require 2 or more boundary components to be drawn

We now handle the general case of a generic partition P. The main challenge is that we can only use P-separating curves for constructing pseudo-Anosov maps in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. To understand how we do that, we need to define some patterns of arcs on punctured disks first and then see how to glue these pattern together to get the a filling pair of P-separating multicurves A and B on $S_g^n$. We first set some notations.

Let $P = \{P_1,P_2,\cdots P_i, P_{i+1},\cdots , P_{k-i-1},P_{k-i},\cdots ,P_k\}$ where

$P_{i+1}, \cdots , P_{k-i-1}$ are all the elements of $P^1 = \{P_j \in P \mid |P_j| = 1\}$. We also set $c_j:= |P_j|$ to be the cardinality of the set $P_j$.

For each positive natural number $c_j \ge 2$, we define 4 patterns labeled $SL_{c_j}$, $SR_{c_j}$, $CB_{c_j}$ and $CR_{c_j}$. These abbreviations stand for side left, side right, center blue and center red respectively. For each one of these patterns, we only illustrate the cases of $c_j = 2,3, \cdots , 9$ in the figures but it is not hard to understand how to generalize it to any positive integer, even though it becomes close to impossible to draw the curves explicitly. For example, the pattern $SL_{2m}$ for any integer m can be obtained as follows. First draw a black square and inside of it draw the 2m boundaries homogeneously spaced on an imaginary circle and label them in a circular manner $b_1, b_2, \cdots , b_{2\,m}$. Choose one of these boundaries as reference, say $b_1$. We start by drawing the red piece of curve that start at the top left of the black square. This pieces goes around $b_1$ first, then $b_3$, then $b_5$ up to $b_{2m-1}$ and does so in a "flower shape" pattern centered at the center of the square. The second red piece of curve starts at the bottom of the left side of the square and goes around the remaining boundaries by staying close to the sides of the square so that it does not intersect the previous red piece. Two of the blue pieces are drawn similarly. The one starting on the top right is also flower shaped and goes around $b_2,b_4,\cdots , b_{2m}$ while the one starting on the bottom of the rigth side of the square goes around $b_1,b_3,\cdots ,b_{2m-1}$ while staying close to the sides. Finally, the last piece is a blue piece that starts at the top right and ends at the bottom and wiggles its way in between the two previous blue pieces (Figs. 7, 8, 9 and 10).

For each of the pattern, one has to imagine that the red and blue arcs are connected to each other outside of the black square box to form closed curves. The way they are to be connected is explained in Figs. 11 and 12. We note that there is a particularity for the patterns $CR_{c_{i-1}}$ or $CB_{c_{i-1}}$ and similarly for $CR_{c_{k-i}}$ or $CB_{c_{k-i}}$. Indeed for these, the red or blue pieces that wiggles around without going around any boundary are not necessary. This is indicated on the picture by not drawing any curve coming out of the square in these spots. Similarly, if |P| is odd, we will need to isolate one elements $p \in P$ and put the corresponding block alone somewhere else in the surface (see Fig. 12). Here too the arcs that wiggle around are not necessary and are to be understood to be omitted.

Fig. 7

These are the patterns $SL_{c_j}$. The number $c_j$ represents the number of boundaries. If $c_j$ is odd we add a boundary as suggested by the dotted circle in each picture

Fig. 8

These are the patterns $SR_{c_j}$. The number $c_j$ represents the number of boundaries. If $c_j$ is odd we add a boundary as suggested by the dotted circle in each picture

Fig. 9

These are the patterns $CB_{c_j}$. The number $c_j$ represents the number of boundaries. If $c_j$ is odd we add a boundary as suggested by the dotted circle in each picture

Fig. 10

These are the patterns $CR_{c_j}$. The number $c_j$ represents the number of boundaries. If $c_j$ is odd we add a boundary as suggested by the dotted circle in each picture

Fig. 11

In this picture we can see how the pattern glue together on the left half of the surface. The right half part is an exact vertical reflection of this pattern

Fig. 12

Here is the full picture of the multicurves. The multicurve A is the union of the blue curves and the multicurve B is the union of the red curves

Theorem 5.2

For any partition P on a surface $S_g^n$, there exists a pseudo-Anosov mapping class $f \in {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P)$ such that

$$\begin{aligned} l_{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim \frac{1}{g + |P| } \end{aligned}$$

Proof

We let A and B the the blue and red multicurves, respectively, depicted in Fig. 12. In the case were |P| is odd, we can always choose one element $p \in P$ and put the block corresponding to it as indicated by the A-marked block in Fig. 12. If p is a singleton, then we do not need the red and blue lines going out of the block. Let $S_g^n \rightarrow S$ be a capping inducing the partition P on $S_g^n$. We recall that a closed curve $\gamma$ on $S_g^n$ is called P-separating if it is a separating curve in S. Also, Dehn twists around P-separating curves are elements of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. Since all curves in the multicurves A and B are not only separating but also P-separating, and since the multicurves are filling, the map $T_A (T_B)^{-1}$ obtained by Penner’s construction is a pseudo-Anosov map contained in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n)$.

In order to estimate the asymptotic translation length of $f = T_A (T_B)^{-1}$, we proceed in a similar fashion as in Theorem 5.1. If $i \ne k$, meaning there is at least one singleton in the partition P, then we can take $\delta$ to be the same curve as in Fig. 5. If $i = k$ we just take $\delta$ to be any curve going around the boundaries of $P_{k/2}$ if k is even or $P_{k+1/2}$ if k is odd. Then, by the same arguments as in Theorem 5.1, we see that the images of $\delta$ under iteration of f are well controlled for a while. In particular, we can safely say that $d_{{{\,\mathrm{{\mathcal {C}}}\,}}} (f^{\lceil \frac{g}{100} \rceil + \lceil \frac{k}{100} \rceil }(\delta ),\delta ) \le 2$. Note that the existence of the A-marked block makes the tracking of the iterates of $\delta$ under f a bit more tedious but does not change the conclusion. This shows that

$$\begin{aligned} \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f)&\le \frac{2}{\lceil \frac{g}{100} \rceil + \lceil \frac{k}{100} \rceil } \end{aligned}$$

Therefore, since $k = |P|$ or $|P|+1$, depending on the existence of the A-marked block, we get that

$$\begin{aligned} \displaystyle \ell _{{{\,\mathrm{{\mathcal {C}}}\,}}}(f) \lesssim \frac{1}{g + |P| } \end{aligned}$$

$\square$

Corollary 5.3

As a function of g, we have that

$$\begin{aligned} L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n, P) \asymp \frac{1}{|\chi (S_g^n)| } \end{aligned}$$

We thank the referee for noticing that if one only wants to prove Corollary 5.3, it is sufficient to do the construction of Theorem 5.2 for the case of $P = P_{\min }$ since ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P_{\min })$ is a subgroup of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ for any P by Lemma 4.2. Nonetheless, Theorem 5.2 gives a better bound on asymptotic translation length of pseudo-Anosov mapping classes in ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ that also depends on |P|.

6 Further discussions

One obvious improvement to Theorem 1.1 would be to find a precise formula for the cohomological dimension of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$ for all P. In [19], the author characterizes precisely the kernel of the map ${{\,\textrm{Cap}\,}}:{{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P) \rightarrow {{\,\mathrm{{\mathcal {I}}}\,}}(S_g^{n-1}, P')$. It is either the whole fundamental group of the unitary tangent bundle of $S_g^{n-1}$ when we cap a boundary d such that $\{d\} \in P$, or a graph of the kernel of $\pi _1(S_g^{n-1}) \rightarrow H_1^{P'}(S_g^{n-1})$ in all other cases. It would be good to find a similar characterization of the kernel of ${{\,\textrm{Cap}\,}}_n :{{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P) \rightarrow {{\,\mathrm{{\mathcal {I}}}\,}}(S_g)$ and that would possibly improve our upper bound for the cohomological dimension of ${{\,\mathrm{{\mathcal {I}}}\,}}(S_g^n,P)$. Indeed, we showed that this kernel fits in a short exact sequence

$$\begin{aligned} 1 \rightarrow {\mathbb {Z}}^m \rightarrow K \rightarrow K' \rightarrow 1 \end{aligned}$$

and used the fact that $K'$ is a subgroup of ${{\,\textrm{PB}\,}}_n(S_g)$ and thus has cohomological dimension at most $k+1$. But a more careful analysis of $K'$ might yield a better estimation of its cohomological dimension.

Recall that the minimal asymptotic translation lengths for ${{\,\textrm{Mod}\,}}(S_g)$ and ${{\,\textrm{Mod}\,}}({\mathcal {I}}_g)$ have different order. More precisely, for closed surfaces we have $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g)) \asymp 1/g^2$ by Gadre-Tsai [12] while $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}({\mathcal {I}}_g)) \asymp 1/g$ by Baik-Shin [5].

One could ask if an analogous statement would be true for either $S_g^n$ or $S_{g,n}$. First of all, Valdivia showed in [21] (for (1), see also [5]) that

• (1) When g is fixed, $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{PMod}\,}}(S_{g,n})) \asymp 1/|\chi (S_{g,n})|$

• (2) When $g = rn$ for some $r \in {\mathbb {Q}}$, $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_{g,n})) \asymp 1/|\chi (S_{g,n})|^2$.

As we pointed out before, $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g^n)) = L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{PMod}\,}}(S_{g,n}))$, since we have a map $\Phi : {{\,\textrm{Mod}\,}}(S_g^n) \rightarrow {{\,\textrm{PMod}\,}}(S_{g,n})$ so that their actions on the curve complexes is $\Phi$-equivariant. Hence by (1) above, it is not possible to have $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_g^n)) \asymp 1/|\chi (S_g^n)|^2$.

We conjecture that both phenomena are true in general.

Conjecture 6.1

The followings hold.

• (1) $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{PMod}\,}}(S_{g,n})) \asymp 1/|\chi (S_{g,n})|$.

• (2) $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{Mod}\,}}(S_{g,n})) \asymp 1/|\chi (S_{g,n})|^2$.

Valdivia’s result is a partial evidence to both parts of Conjecture 6.1. As an additional partial evidence to Conjecture 6.1 (1), we show the following.

Theorem 6.2

Suppose $g < (1/4 - \epsilon ) n$ for arbitrarily small $\epsilon > 0$. Then $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{PMod}\,}}(S_{g,n})) \asymp 1/|\chi (S_{g,n})|$.

Proof

We first remark that it is sufficient to show that $L_{{{\,\mathrm{{\mathcal {C}}}\,}}}({{\,\textrm{PMod}\,}}(S_{g,n})) \gtrsim 1/|\chi (S_{g,n})|$ due to the construction given in Sect. 4 of [21]. For this, we roughly follow the proof of Theorem 7.1 (see also the proof of Theorem 5.1) in [5].

Let $\phi \in {{\,\textrm{PMod}\,}}(S_{g,n})$ be a pseudo-Anosov element and $\tau$ be its invariant train track obtained from Bestvina-Handel algorithm [3]. What we need to know about the train track obtained from Bestvina-Handel algorithm is summarized in Sect. 2 of [5]. Here is the list of facts we need.

• (1) $\tau$ has two types of branches, real and infinitesimal.

• (2) The number of real branches is smaller or equals to $9 |\chi (S_{g,n})|$.

• (3) Let $M_{\mathcal {R}}$ be the transition matrix for $\phi$ on the real branches of $\tau$. If q is a positive integer so that $M_{{\mathcal {R}}}^q$ has a positive diagonal entry, then the $\ell _{\mathcal {C}}(\phi ) \gtrsim 1/ q|\chi (S_{g,n})|$ (this follows from Proposition 2.2 of [5] which is based on the work of [11, 12, 17]).

Hence, it is enough to show that the number q above is uniformly bounded by a constant.

As explained in the proof of Theorem 5.1 in [5], each puncture is contained in a distinct ideal polygons obtained as connected components of the complement of $\tau$. Let $k_1$ be the number of punctures contained in monogons and $k_2$ be the number of punctures contained in bigons. Let ${\mathcal {S}}$ be the set of singularities of the invariant foliation for $\phi$ whose index is greater than equals to 3.

For each singularity $s \in {\mathcal {S}}$, let $P_s$ denote its index. By the Euler-Poincaré formula ( [8]) and the fact that $P_s \ge 3$, we have

$$\begin{aligned} k_1 \ge \dfrac{n-k_2+4-4g}{2} > \dfrac{4\epsilon n - k_2 + 4}{2}. \end{aligned}$$

The second inequality follows from our hypothesis $g < (1/4 - \epsilon ) n$.

Now we are going to divide the situation into two cases. First, let us assume that $k_2 < 2 \epsilon n$. Then $k_1 > \epsilon n + 2$.

Suppose there are at least N real branches attached at the monogons containing punctures. Then there are in total at least $k_1 N / 2$ many real branches in $\tau$. Since $k_1 > \epsilon n + 2$, we have

$$\begin{aligned} k_1 N / 2 \ge (N/2)(\epsilon n + 2), \end{aligned}$$

which give us a lower bound on the number of real branches.

On the other hand, by Fact (2) above, the number of real branches is bounded above by $9|\chi (S_{g,n})| \le 9(3n/2 - 2)$. Hence, if N is sufficiently large, we get a contradiction.

This shows that the there exists a uniform number N such that there exists at least one monogon where the number of attached real branches is bounded above by N. Since these real branches are permuted by $\phi$, this gives a uniform upper bound on q in Fact (3).

For the second case, let us assume $k_2 \ge 2 \epsilon n$. Again, suppose there are at least N real branches at each of the bigons containing punctures. Then there are at least $Nk_2/2 \ge N\epsilon n$ many real branches in $\tau$. Since the number of real branches is bounded above by $9(3n/2 - 2)$, for sufficiently large N, we get a contradiction as before. This implies there exists a uniform number N such that $\tau$ has at least one bigon containing a puncture where less than N real branches are attached. This again gives a uniform upper bounded on q.

In either case, since q is uniformly bounded by a constant, we get the desired result. $\square$

The main result of this paper is that $L_C({\mathcal {I}}(S_g^n, P)) \asymp 1/|\chi (S_g^n)|$ for any partition P of $\partial S_g^n$. Hence, from the perspective of Conjecture 6.1 (1), ${{\,\textrm{Mod}\,}}(S_g^n)$ and their proper normal subgroups seem to be not distinguishable by the least asymptotic translation length on the curve complex unlike the case of closed surfaces.

On the other hand, in the case of punctured surface, it is much more hopeful. If one can show Conjecture 6.1, then it would be a strong partial evidence toward that ${{\,\textrm{Mod}\,}}(S_{g,n})$ and their proper normal subgroups are distinguishable by the least asymptotic translation length on the curve complex.

Furthermore, one way to define the Torelli subgroup ${\mathcal {I}}_{g,n}$ of ${{\,\textrm{Mod}\,}}(S_{g,n})$ is to define it as $\Phi _*({\mathcal {I}}(S_g^n, P))$ where P is the maximal partition of the boundary components. Then ${\mathcal {I}}_{g,n}$. In this case, our main result implies that $L_C({\mathcal {I}}_{g,n}) \asymp 1/|\chi (S_{g,n})|$, hence it is an additional partial evidence.

In summary, we propose the following

Conjecture 6.3

There exists a uniform constant $C >0$ such that for any proper normal subgroup H of ${{\,\textrm{Mod}\,}}(S_{g,n})$, $L_C(H) \ge C/|\chi (S_{g,n})|$.

This is an extended version of Question 1.2 in [5].