Prediction of Residential Slab Foundation Movement Through a Finite Element-Based Deep Learning Algorithm

Abstract

Deep learning networks were employed to predict the maximum differential deflection of stiffened and waffle rafts due to reactive soil movements, Δ_max. Four deep learning networks were used to predict Δ_max, these are (1) stiffened rafts on shrinking soil, (2) stiffened rafts on swelling soil, (3) waffle rafts on shrinking soil, and (4) waffle rafts on swelling soil. The deep learning models were used to create design lines, which showed that both soil and structural features strongly influence the stiffened rafts. In contrast, waffle rafts showed a strong dependence on soil features in shrinking soils and beam depth in swelling soils. This demonstrates that the finite element-based deep learning networks captured the effect of the embedment of the beams. The results of the deep learning models led to non-linear design curves, which are disparate from the suggested standard Australian design. These results suggest that increasing the value of beam depth can have a positive or negative impact on the global residential slab depending on the type of substructure and whether the founding reactive soil is shrinking or swelling. Global sensitivity analyses of the deep learning models showed that for stiffened rafts on shrinking soil, the slab length, slab width and active depth zone of reactive soil had the most significant influence on Δ_max, whilst for stiffened rafts on swelling soil, the primary drivers are ground movement, beam depth, and slab width. The prediction of Δ_max for waffle rafts on shrinking soil was driven by the surface characteristic and mound movements, and the active depth zone, whilst waffle rafts on swelling soil was driven by the beam depth. Overall, the finite element-based deep learning showed the capacity to estimate Δ_max in both shrinking and swelling design scenarios for different types of residential footing systems to further understand the characteristic behaviour of shallow residential slab foundations on reactive soils leading to improved designs.

1 Introduction

Reactivity is a soil characteristic that affects their expansion and shrinkage (Cameron 2015; Yaghoubi et al. 2022; Teodosio et al. 2022b). Highly reactive soils undergo considerable variation in volume due to fluctuation in soil moisture. These reactive soils swell in the presence of moisture and shrink upon losing moisture (Teodosio et al. 2020a; Tran et al. 2021). The resulting ground movements can induce instability and subsequent damage to physical infrastructures such as pavements, underground pipes, and residential footing systems (Li and Cameron 2002; Teodosio et al. 2020b; Gedara et al. 2022). Issues related to reactive soils have been recorded worldwide, causing numerous detrimental socio-economic and environmental impacts. In the United States of America and the United Kingdom, reactive soil damage resulted to US$15 billion and £3 billion for a span of one year (Jones and Jefferson 2012; Li et al. 2014). In Australia, the surface geology is approximately 20% Basaltic clays (Richards et al. 1983; Teodosio et al. 2021a). The world’s largest Basaltic plain is located in the Western suburbs of Melbourne and has detrimental impacts on residential structures and lightweight infrastructures. Research by the Victorian Building Authority (VBA) into 82,738 new dwellings constructed between 2003 and 2011, found an initial 5.3% of these structures experienced unrepairable failure of concrete waffle rafts, walls and ceilings (Johanson 2014). The number of reported cases has constantly increased since 2011 and is now accounting for at least 80% of all housing insurance claims (Victorian Civil and Administrative Tribunal 2014). The repair of severely damaged residential structures requires additional carbon-intensive resources such as concrete and steel, which are responsible for 95% of the carbon emission of residential footing systems (Pujadas-Gispert et al. 2018). This suggests the importance of using improved and adaptive design procedures for residential footing systems that contribute to minimising the socio-economic and environmental impacts related to reactive soils.

A comprehensive characterisation of reactive soils requires a multi-disciplinary approach combining geotechnical engineering, climatology, unsaturated fluid flow, and structural design. For example, the open ground around a residential foundation is exposed to rainfall infiltration and evaporation, whereas the covered ground under the residential footing systems is not subjected to direct rainfall infiltration and evaporation. In the dry season, this leads to ‘centre-heaving’ where the soil in the vicinity of the perimeter of the foundation shrinks and the ground level goes down relative to the ground level under the central part of the foundation (Fig. 1a). The centre heaving causes residential footing systems to act as double cantilevers due to the soil-structure separation around the edges, and the support is at the centre due to the soil-structure contact (Fityus et al. 1999; Teodosio et al. 2020b; Tran et al. 2020). On the other hand, swelling of the soil around the perimeter of the residential footing systems raises ground level relative to the ground level under the central part of the foundation during the wet season leading to ‘edge heaving’ as presented in Fig. 1b (Fityus et al. 1999; Kim et al. 2015). The edge heaving causes residential foundations to act as simply-supported footing systems where the soil-structure separation is within the central part of the footing system and the support is around the edges due to the soil-structure contact there (Fityus et al. 1999; Shams et al. 2018; Teodosio et al. 2022a).

Fig. 1

Schematic representation of the interaction between reactive soils and a residential footing system when a shrinking (known as centre heaving) and b swelling (known as edge heaving) due to the difference in soil moisture of the covered and uncovered grounds

The magnitude of area load, p, and the line load along the perimeter due to superstructures, q, can be critical in the design of a residential footing system (Teodosio et al. 2021b). In the centre heave scenario in Fig. 1a, the magnitudes of loads p and q are critical to the design of residential footing systems. Contrarily, in the edge heave scenario in Fig. 1b, the magnitudes of loads p and q negate the pressure caused by the swelling reactive soil around the perimeter. Thus, both centre heaving and edge heaving scenarios are important design considerations for the stability of residential footing systems (Teodosio et al. 2020a, b).

Several design methodologies for residential footing systems founded on reactive soils have been developed over the past decades (Teodosio 2020; Teodosio et al. 2021b). The Building Research Advisory Board (1968) proposed the BRAB Method, which is a comparatively simplistic procedure compared to other approaches. This design method computes more conservative dimensions of residential footing systems, particularly when L has a larger value (Abdelmalak 2007). Snowden (1981) improved the BRAB Method and developed the Wire Reinforcement Institute (WRI) method. The WRI method is an empirical-based design method that also calculates the required dimensions of residential footing systems more conservatively in comparison to the BRAB method. Another method developed by Lytton (1970), known as the Lytton method, uses beam-on-mound equations and coupled springs. This method has been adapted by Walsh and Walsh (1986) and Mitchell (1984) to develop improved methods, recognised as the Walsh Method and the Mitchell Method, respectively. These methods were used to propose a design method based on parametric simulations presented in Australian Standards (AS) 2870-2011 (Standards Australia 2011; Payne and Cameron 2014). The methodologies of the Walsh Method, Mitchell Method, and AS 2870–2011 Method tend to compute less conservative D of residential footing systems founded on reactive soils (Abdelmalak 2007; Teodosio et al. 2021b). The AS 2870-2011 Method assumes commonly applied loads, p and q, on footing systems, where the values of p and q cannot be varied in the design process. The Post Tensioning Institute (2008) created a method based on an empirical design approach that considers the non-linear relationship of the Thornthwaite moisture index, soil diffusion, and particle size, known as the PTI Method. This method predicts median values of calculated D when compared to other design approaches (Teodosio et al. 2021b). However, the application of this method may be limited due to its empirical nature.

Both physical and numerical models are important to comprehensively understand the mechanisms associated with residential footing systems built on reactive soils. Li (1996) developed a physical-based model to calculate the ground movement using thermal strain and conductivity to emulate the variation of soil volume. Totoev and Kleeman (1998) developed an infiltration model to predict soil suction changes and soil movement. With the advancements in numerical simulation techniques such as the Finite Difference Method (FDM) and Finite Element Methods (FEM), many advanced numerical models of residential footing systems have been developed in the literature. Fraser and Wardle (1975) further improved the Lytton Method and Walsh Method using numerical simulations, which was the basis of the Swinburne Method developed by Holland et al. (1980). Sinha and Poulos (1996) performed parametric simulations varying the stiffness of residential footing systems using the Lytton (1970) Method, and found that differential settlement can be reduced by having higher footing system stiffness and introducing beams at strategic locations that create a bridging action against heaving. In early 2000, investigations started focusing on the interaction between reactive soil and footing systems using 3D FEM (Masia et al. 2004; Wray et al. 2005; Fredlund et al. 2006). A few studies developed coupled hydro-mechanical models combining soil, climate, and structural parameters and inputs to predict ground movement and residential footing deformation using FEM (Zhang 2004, 2014; Abdelmalak 2007; Shams et al. 2018; Assadollahi and Nowamooz 2020). Also, a few investigations proposed novel design methods based on parametric finite element simulations (e.g. Dafalla et al. 2012; Briaud et al. 2016; Teodosio et al. 2020b). Recently, Shams et al. (2020) employed the artificial intelligence (AI) technique—evolutionary polynomial regression (EPR) technique—to develop a standalone design tool for stiffened rafts based on coupled hydro-mechanical parametric FEM simulations, which obtained more conservative designs compared to Mitchell (1984).

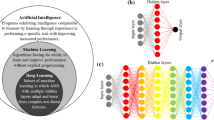
Advancements in technologies in computing software and hardware in the past decade have significantly increased the application of AI. AI is a general concept utilising machines and robots to perform tasks with iterative and improving measured performance (Fig. 2a). Machine learning (ML) is a subclass of AI, which can passively learn and improve without explicit coding, as described in Fig. 2b. Common ML tasks include object recognition, speech recognition, conversation responder, problem optimisers, and self-driving vehicles (Theodoridis 2020). Rumelhart et al. (1986) primarily suggested shallow learning or simple artificial neural networks (ANN). These shallow networks can train a single hidden layer limited by computing power and unsophisticated algorithms, as discussed by Xu et al. (2021) and presented in Fig. 2c. In the past few years, the application of ANN with multiple hidden layers that allows much more complex analyses has emerged, which is known as deep learning or DL (Cha et al. 2017; Naji et al. 2021). DL networks are capable of training themselves to process and learn from data and better recognise patterns in non-linear functions (Xu et al. 2021). With more advanced technologies and algorithms, DL can offer improved accuracy in designing residential footing systems considering the highly non-linear calculations and complex relationships that are considered when reactive soils and climate are involved (Fig. 2d).

Fig. 2

Relationship among artificial intelligence (AI), machine learning (ML), artificial neural network (ANN), and deep learning (DL). The ‘x_i’ is an input feature, ‘W’ is a weight or edge, and ‘a’ is an activation of the artificial neurons

There has been a recent increase in the application of AI to geotechnical challenges involving expert systems, neural networks, fuzzy logic, and image analyses applied to the site classification, stability evaluation, and hazard assessment of abutments, landslides, building foundations, and mines (Ebid 2021). The application of AI algorithms, specifically DL, shows the implementation of adaptive non-linear models and predicts more insightful results to improve the design and performance of residential footing systems. This study aims to develop DL networks to predict Δ_max more accurately. In addition, this study implements a global sensitivity analysis of the DL networks to identify the relative influences of the input features (y_s, y_m, D, L, W, p, q, H_s, and ε_ms) on the Δ_max, depending on the type of foundation and the movement of reactive soil. A comparison between the predictions using the established design code AS 2870-2011 (Standards Australia 2011) and the results of the DL networks of this study is also presented.

2 Methodology

A DL network is defined as an inter-connected network of neurons in multiple hidden layers. ANN is a computational system that conceptualises the neural network of a human brain and how information and logical patterns are processed and established, respectively (LeCun et al. 2015). The inter-connected neurons are concomitant by edges that are essential for signal transfer represented by weights that serve as signals being adjusted as learning takes place. The objective of the network is to reduce the cost function, L(y,ŷ), to obtain optimum weights that are related to predicting accurate estimates of targeted outputs. Four main aspects primarily influence the DL process; the considered dataset, the DL architecture, the DL algorithm, and the accuracy of the predicted values. These elements are discussed below in detail.

2.1 The Datasets for DL Networks

The dataset used in this study was extracted from the parametric simulations by Teodosio (2020) and Teodosio et al. (2020b). A total of 648 numerical simulations were conducted, varying the types of residential footing systems (stiffened rafts and waffle rafts), soil, environmental, and structural parameters. The 648 rows of data were divided into four groups based on types of footing system and ground movements; (1) stiffened rafts on the shrinking ground, (2) stiffened rafts on the swelling ground, (3) waffle rafts on the shrinking ground, and (4) waffle rafts on the swelling ground. Each group consisted of around 160 data points. Tables 1 and 2 list the descriptive statistics of the four groups of datasets used for the training and testing in this study. Each dataset for each scenario is comprised of the target Δ_max, and the input features y_s, y_m, D, L, W, p, q, H_s, and ε_ms (Fig. 1).

Table 1 Descriptive statistics of the target, maximum stiffened raft deformation (Δ_max) and features (y_s, y_m, D, L, Q, p, q, H_s, and ε_ms)

Table 2 Descriptive statistics of the target, maximum waffle raft deformation (Δmax) and features (ys, ym, D, L, Q, p, q, Hs, and ε_ms)

The features used were based on the general principle outlined in AS 2870.4.6 by Standards Australia (2011) and the coupled hydro-mechanical parametric simulations by Teodosio (2020). These features are as follows:

• Characteristic surface movement or the maximum ground movement, y_s,

• Differential ground movement, y_m,

• Beam depths, D,

• Length of a stiffened raft or a waffle raft, L,

• Width of a stiffened raft or a waffle raft, W,

• Area load applied to a stiffened raft or a waffle raft, p,

• Line load applied to a stiffened raft or a waffle raft, q,

• Active depth zone, H_s, and

• Shrink-swell parameter, ε_ms.

It is important to note that ε_ms is an idealised soil shrink-swell index (I_ss) based on Shams et al. (2018). Similarly, the soil water characteristic curve (SWCC) was taken from an idealised curve by Shams et al. (2018). This assumption is acceptable since the objective of the simulations was to form the most critical shrinking and swelling mound profiles based on the wettest and driest scenario, without consideration of time dependence, as elaborated by Teodosio et al. (2020a). However, further investigation of the effect of anisotropic soil properties should be investigated in future studies since this will affect the formation of critical shrinking and swelling mound profiles. The values of residential slab thickness and steel reinforcements for the deemed-to-comply designs in AS 2870 were adopted in this study for simplification. The values for the slab thickness were 100 mm for stiffened rafts and 85 mm for waffle rafts. The values of steel reinforcements were either 12-mm or 16-mm diameter for the beam reinforcements, whilst either 7-mm or 8-mm diameter for the steel mesh. These are acceptable assumptions since these values are being used in practice to design and construct stiffened rafts and waffle rafts. The hydromechanical finite element model by Teodosio et al. (2020b) assumed that the reactive soil movement is driven by a change in soil suction equal to 1.2 pF based on AS2870-2011. This enables the simplification of the model to specify the initial and final values of the soil suction due to precipitation and evapotranspiration.

The datasets for stiffened rafts and waffle rafts considering the shrinking and swelling scenarios were split into training and testing sets with a ratio of 75% (119–120 data entries for training per set) to 25% (40–41 data entries for testing per set), respectively, listed in Tables 1 and 2.

2.2 Deep Learning Network Architecture

A DL neural network was used to obtain the acceptable weights for the prediction of Δ_max. The neural network comprises an input layer with nine units, five hidden layers with 256 units, and an output layer with one unit described in Fig. 3. The number of hidden layers was determined by trial and error and was observed to produce acceptable results. The input layer contains the input vector extracted from Teodosio (2020) and Teodosio et al. (2020b). The five hidden layers were found to give accurate results with acceptable computational efficiency that was determined through trial and error.

Fig. 3

Deep Learning network architecture

2.3 Deep Learning Algorithm

The DL process comprised of four stages: (1) pre-processing, (2) random initialisation, (3) forward propagation, and (4) backward propagation, as summarised in Fig. 4. Data pre-processing is a necessary phase, which can increase the accuracy and efficiency of the training and validation. The pre-processing techniques commonly applied in DL are outliers/missing value filtering, polynomial feature generation, normalisation and scaling implementations (Pedregosa et al. 2011). Data entries with incorrect values due to manual input of Δ_max, y_s, y_m, D, L, W, p, q, H_s, and ε_ms were omitted using interquartile outlier check. The disregarded data were three entries for stiffened rafts on the shrinking ground, two for stiffened rafts on the swelling ground, one for waffle rafts on the shrinking ground, and one for waffle rafts on the swelling ground. Polynomial features were first considered, however, these did not have a considerable effect on the accuracy of the algorithm.

Fig. 4

Deep Learning network process

The normalisation, standard scaling, and min–max scaling methods were individually assessed. These pre-processing techniques scale or normalise each input feature to a given dataset range, which increases the speed and accuracy of neural networks. Min–max scaling was found to be the most applicable, upon trial and error, and was implemented using the equation

$$Min-max\, scaling= \frac{x-{x}_{min}}{{x}_{max}-{x}_{min}},$$

(1)

where x is the feature index, x_min is the minimum feature value in the dataset, and x_max is the maximum feature value in the dataset.

The values of x_min and x_max for the input features y_s, y_m, D, L, W, p, q, H_s, and ε_ms are listed in Tables 1 and 2, considering both training and testing datasets.

Random initialisation described in He et al. (2015) was used to initiate the DL process by multiplying the randomly generated initial weights by

$$\sqrt{\frac{2}{{size}^{DLL-1}},}$$

(2)

where size^DLL−1 is the DL layer prior to the current being analysed.

The weights of the network were randomly initialised with values close to zero. This disturbs the symmetry to enable the neurons to calculate different values that will not affect the accuracy and efficiency of the DL. The mean squared error (MSE) was used as the loss function, $L\left(y,\widehat{y} \right)$, which is commonly used in regression models. The values of $L\left(y,\widehat{y} \right)$ are the mean squared differences between a true value (y) and a predicted value (ŷ) obtained by the DL model. A representation of the activation function for the forward propagation of a single neuron is shown in Fig. 5. L2 Regularisation is used to prevent overfitting described by a penalty function in the second term of Eq. (3),

$$L\left( {y,\hat{y}} \right) = \frac{1}{N}\mathop \sum \limits_{i = 0}^{N} \left( {y_{i} - \hat{y}_{i} } \right)^{2} + \lambda \mathop \sum \limits_{i = 0}^{N} w_{i}^{2} ,$$

(3)

Fig. 5

Artificial neurons showing activation, transformation, and forward propagation

where λ is the hyperparameter for regularisation, and w_i is a feature weight. λ commonly has a value greater than zero, with caution on the usage of large values of λ that may lead to large weights and underfitting. The total number of data entries is denoted by N.

The Rectified Linear Units (ReLU) proposed by Nair and Hinton (2010) was used in the forward propagation represented by,

$$f\left( x \right) = max\left( {0,x_{i} } \right) = \left\{ {\begin{array}{*{20}l} {x_{i} ,} \hfill & {if\quad x_{i} \ge 0} \hfill \\ {0,} \hfill & {if\quad x_{i} < 0} \hfill \\ \end{array} } \right.$$

(4)

where x_i is the input value.

The adaptive moment estimation or “Adam” optimisation by Kingma and Ba (2017) was used for the backward propagation. The Adam stochastic optimisation is extensively implemented due to its straightforward process and computational efficiency. This method combines the momentum gradient descent and the Root Mean Square Propagation (RMSprop). The Adam optimisation algorithm is described as,

$$Vdw={\beta }_{1}Vdw+\left(1-{\beta }_{1}\right)dw,$$

(5)

$$Vdb={\beta }_{1}Vdb+\left(1-{\beta }_{1}\right)db,$$

(6)

$$Sdw={\beta }_{2}Sdw+\left(1-{\beta }_{2}\right){dw}^{2}, and$$

(7)

$$Sdb={\beta }_{2}Sdb+\left(1-{\beta }_{2}\right){db}^{2},$$

(8)

where Vdw, Vdb, Sdw, and Sdb are the weights and biases that are calculated in iteration or epoch, t. The initial values of Vdw_i, Vdb_i, Sdw_i, and Sdb_i are assigned to zero and then will be backpropagated for each weight. The calculated values of Vdw, Vdb, Sdw, and Sdb are then corrected and updated using the power of the current epoch, t, described below

$$w=w-\alpha \frac{{{V}_{dw}}^{corrected}}{\sqrt{{{S}_{dw}}^{corrected}+\epsilon }}=w-\alpha \frac{\frac{Vdw}{1-{{\beta }_{1}}^{t}}}{\sqrt{\frac{Sdw}{1-{{\beta }_{2}}^{t}}+\epsilon }},and$$

(9)

$$b=b-\alpha \frac{{{V}_{db}}^{corrected}}{\sqrt{{{S}_{db}}^{corrected}+\epsilon }}= b-\alpha \frac{\frac{Vdb}{1-{{\beta }_{1}}^{t}}}{\sqrt{\frac{Sdb}{1-{{\beta }_{2}}^{t}}+\epsilon }}.$$

(10)

The forward and backward propagation were implemented in a loop until the specified epoch was achieved, as described in Fig. 4. The iteration of the optimisation loop comprised of forward propagation using ReLU, $L\left(y,\widehat{y} \right)$ calculation, backward propagation using Adam, and weights updating. The epoch of the final DL run was specified to be 3800, which resulted in an optimum and stable $L\left(y,\widehat{y} \right)$ curve with an acceptable learning period of less than ten minutes. After obtaining optimum weights of the model, the relative effects of input features on the predicted Δ_max was evaluated using a global sensitivity analysis.

The hyperparameters were fine-tuned by varying their values and determining the accuracy of the results. Through this method, the value of the hyperparameters was specified as 5.0 × 10^–5 for the learning rate, 0.9, 0.999, 5.0 × 10^–6 for the decay rates β₁ and β₂, and ϵ, and unity for the value of λ for all DL networks.

2.4 Global Sensitivity Analysis

Sensitivity analysis identifies the relative importance of input features on the targeted output. A sensitivity analysis can be a local or a global approach. Local sensitivity analysis is an assessment of the local impact of feature variations on the concentrated sensitivity in the proximate vicinity of a set of feature values (Zhou and Lin 2008). Contrarily, global sensitivity analysis quantifies the overall significance of the features and their interactions concerning the predicted results by implementing an overall coverage of the input values (Saltelli et al. 2019). This study applied a global sensitivity approach by following the Saltelli (2002) method and indices by Sobol (1990, 2001).

The bounds to generate the input features for the global sensitivity analysis are listed in Table 3. After specifying the upper and lower bounds for each feature that will serve as the parameter range for the scheme of Saltelli (2002). A total of 2,621,440 were generated as data samples.

Table 3 Upper and lower bounds to generate the input features for the Saltelli (2002) method

Three indices were calculated; these are the first-order Sobol index (S₁), the second-order Sobol index (S₂), and the total-order Sobol index (S_T). S₁ reflects the expected decrease in the variance of a model when feature x_i is not changing. The values of S₁ measures the direct influence of each feature on the variance of the model or targeted output. calculated as

$${S}_{1}=\frac{var({x}_{i})}{var(\widehat{y})}=\frac{var(E\left(\widehat{y}|{x}_{i}\right))}{var(\widehat{y})},$$

(11)

where var(x_i) is the variance of a feature, var($\widehat{y}$) is the variance of the target output, E denotes expectation, x_i is a feature, and $\widehat{y}$ is the target (i.e., Δ_max). The term E($\widehat{y}$|x_i) specifies the expected value of the output $\widehat{y}$ when feature x_i is fixed. The sum of all the calculated values of S₁ should be equal to or less than one.

It is common to perform the calculation of S₁ with the total Sobol sensitivity, S_T, the sensitivity due to interactions between a feature X_i and all other features (Homma and Saltelli 1996) given by

$${S}_{T}=1-\frac{var\left(E\left(\widehat{y}|{x}_{-i}\right)\right)}{var\left(\widehat{y}\right)},$$

(12)

where x_-i denoting the features except x_i, and the sum of all the calculated values of S_T is equal or greater than one.

If the values of S_T are substantially larger than the values of S₁, then there is a probability that higher-order interactions are occurring. It is then worth calculating the second-order or higher-order sensitivity indices. The second-order can be expressed as

$${S}_{2}=\frac{var({x}_{i},{x}_{j})}{var(\widehat{y})},$$

(13)

where var(x_i, x_j) is the variance of features x_i and x_j. This calculates the amount of variance of $\widehat{y}$, explained by the interaction of features x_i and x_j.

3 Results

The results of the implemented DL training, testing, and sensitivity analyses are discussed in the succeeding sub-sections.

3.1 Deep Learning

The DL methodology outlined in Figs. 3 and 4 was used in the allocated dataset for training (119–120 samples) and testing (40–41 samples) listed in Tables 1 and 2. The calculated values of the loss function for the training and testing sets using Eq. 4 are presented in Fig. 6. The loss values of stiffened rafts on shrinking soil (Fig. 6a), stiffened rafts on swelling soil (Fig. 6b), waffle rafts on shrinking soil (Fig. 6c), and waffle rafts on swelling soil (Fig. 6d) show acceptable learning curves. This curve is an indicative tool for algorithms, which incrementally learn from training datasets. The learning curves for all datasets show a good fit, and this can be characterised by loss values of training and testing that decreased to the point of stability with a minimal final gap, as shown in Fig. 6.

Fig. 6

Calculated loss functions (L(y,ŷ)) of training and testing sets for a stiffened rafts on shrinking soil, b stiffened rafts on swelling soil, c waffle rafts on shrinking soil, and d waffle rafts on swelling soil

The performance of the model was measured using the normalised root mean squared error (RMSE_n), described as

$${RMSE}_{n}=\frac{RMSE}{{x}_{max}-{x}_{min}}=\frac{\sqrt{\frac{{\sum }_{i=1}^{N}({y}_{i}-{\widehat{{y}_{i}})}^{2}}{N}}}{{x}_{max}-{x}_{min}},$$

(14)

where RMSE, which indicates the relative average deviation of predicted values from the actual values of the target output (Δ_max), with a value closer to zero representing better prediction. The calculated RMSE for all four cases show values low enough to consider the model predictions reliable. The values of x_min and x_max are the minimum and maximum values of Δ_max in the dataset shown in Tables 1 and 2, whilst N is the total number of data. The values of RMSE_n were observed to be less than 10% for all cases; stiffened rafts on shrinking soil (5.5%), stiffened rafts on swelling soil (7.7%), waffle rafts on shrinking soil (0.7%), and waffle rafts on swelling soil (4.7%). The observed values of RMSE_n values further indicate the reliability of the predictions of all four cases. The highest values of RMSE_n were calculated in the model with stiffened rafts on swelling soil (7.7%). This can be attributed to the constant swelling of soil around the edge beams that may have affected the relationship between the input features and the simulated Δ_max, as described by Fityus et al. (2004), Shams et al. (2018) and Teodosio et al. (2020b).

Figure 7 shows a near-perfect match between predicted and actual values of Δ_max for the training datasets in terms of both R² and the slope of the fitting curve. The values of R² for the testing datasets range from 0.93 to 1.00 and the slope varies from 0.91 to 0.99, indicating a reasonably good consistency between predicted and actual values of Δ_max (Fig. 8). Overall, these results verify the capacity of the DL model to reliably predicts the Δ_max for all cases of considered foundation type and soil movement. It should be noted that it is common to obtain values of R² and slopes close to one since the datasets used were from parametric numerical simulations and were not collected from the field.

Fig. 7

Predicted and actual values of Δ_max after training the datasets for a stiffened rafts on shrinking soil, b stiffened rafts on swelling soil, c waffle rafts on shrinking soil, and d waffle rafts on swelling soil

Fig. 8

Predicted and actual values of Δ_max after testing the datasets for a stiffened rafts on shrinking soil, b stiffened rafts on swelling soil, c waffle rafts on shrinking soil, and d waffle rafts on swelling soil

3.2 Global Sensitivity Analysis

The scheme of Saltelli (2002) was used to generate the input features for predicting the values of Δ_max for the global sensitivity analyses, with the upper and lower bounds listed in Table 3. Sensitivity analyses were performed to evaluate the relative influence of the input features on Δ_max and to determine the association between the features and their influence on Δ_max. Descriptive statistics of the generated inputs and predicted results are listed in Table 4.

Table 4 Descriptive statistics of the generated input variables using Saltelli’s scheme and the predicted results using DL

The global sensitivity analysis results using Sobol (1990, 2001) are presented in Figs. 9 and 10. The values of S₁ revealed that the first-order sensitivity of features varies depending on the type of residential footing systems (i.e., stiffened raft or waffle raft) and the movement of reactive soil (i.e., shrinking or swelling) (Fig. 9a). For stiffened rafts on shrinking soil, L, W, and H_s exhibited first-order sensitivities having high S₁ values, suggesting that these features had the greatest influence of a single parameter to the output of Δ_max. For stiffened rafts on swelling soil, y_m, D, and W demonstrated first-order sensitivities. Prediction of Δ_max for waffle rafts on shrinking soil was driven by y_s, y_m, and Hs, whilst waffle rafts on swelling soil exhibited first-order sensitivity in feature D.

Fig. 9

Sobol indices showing a the first-order Sobol indices (S₁) and b the total-order indices (S_T) for all input features

Fig. 10

Sobol indices showing the second-order Sobol indices (S2) indicating the influence of the interaction of two features to the target output

The total-order Sobol index for each feature, S_T, was then determined as shown in Fig. 9b. If a feature has a value of S_T that is significantly larger than the value of S₁, then there are likely higher-order interactions taking place. Higher-order interactions indicate that the contribution of parameter interactions to the output variance exists. The values of S_T revealed features with higher values than S₁ (Fig. 9b). Hence, second-order indices, S₂, were calculated based on different pairing combinations.

The calculated values of S₂ were considerably low and these are shown in Fig. 10 for all scenarios. The low values indicate that the features had minimal influence on each other and on the targeted output, Δ_max. It can be observed that there is a feature interaction between y_m and D in stiffened rafts on swelling reactive soil. A feature interaction between L-W and L-H_s in stiffened rafts on shrinking reactive soil can also be observed. Feature interactions were also revealed for y_m-D, D-p and D-q in waffle rafts on swelling reactive soil. The remaining interactions can be considered negligible.

4 Discussion

The DL models accurately predicted Δ_max compared to those of the numerical simulations by Teodosio (2020) and Teodosio et al. (2020b). The results of the DL computation were compared with the corresponding values of the established design code AS 2870-2011 (Standards Australia 2011). To do this in-depth comparison of the differences between the DL neural network and the AS 2870-2011, a sensitivity analysis of the parameters in AS 2870-2011 was conducted by considering the models described below.

$$\frac{{y}_{s}}{{\Delta }_{a}}=2.05\left(log\left[\frac{\sum \left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]\right)-1.05= 2.05\left(log\left[\frac{\frac{L}{s}\left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]\right)-1.05,\quad H_{s} < 3\,{\text{m}}$$

(15)

$$\frac{{y}_{s}}{{\Delta }_{a}}=2.10\left(log\left[\frac{\sum \left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]\right)-1.80= 2.10\left(log\left[\frac{\frac{L}{s}\left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]\right)-1.80,\quad H_{s} \ge 3\,{\text{m}}$$

(16)

where Δ_a is the allowable deflection of the residential footing system, comparable to the target output Δ_max. Noting, the allowable footing system deformation, Δ_a, is the predicted Δ_max from the DL calculations. The calculation of y_s and y_m using the AS 2870-2011 method and the approximation of the value of H_s are described in the Appendix.

Findings show that the feature y_s has strongly influenced the values of Δ_max using the AS 2870-2011 models—Eqs. (15) and (16)—as illustrated in Fig. 11a. Higher-order feature interactions were also revealed to be negligible since the value of S_T (Fig. 11b) for each feature is similar to S₁ (Fig. 11a), and the values of S₂ in Fig. 11c is negligible.

Fig. 11

Sobol indices of the established design guideline in AS 2870-2011 (Standards Australia 2011) showing a the first-order Sobol indices (S₁), b the total-order indices (S_T) for all scenarios, and c the second-order Sobol indices

Calculations using the DL model were employed to compare the design guideline of AS 2870-2011 as presented in Fig. 12. The DL computation used constant values for y_s, y_m, L, W, p, and ε_ms, whilst the values of D, q, and H_s were varied. The upper limit of y_s of a Class H₂ site was considered in this specific comparison– with a total shrinking and swelling movement of 75 mm. To calculate the values of y_m, the findings of Teodosio et al. (2020b) were used, multiplying y_susing a factor of 0.82–0.70 depending on the value of D for shrinking and 0.88 for swelling. The values of L, W, p, and ε_ms were taken to be 15 m, 15 m, 2500 N m⁻², and 7%, respectively. The values of D varied from 0.25 to 1.5 m, with an interval of 0.5 m, for stiffened rafts and waffle rafts. Magnitudes of q were specified to be 20,000 N m⁻¹ for shrinking and 6500 N m⁻¹ for swelling. This will consider the critical scenarios in Fig. 1 where higher line loads around the perimeter of residential footing systems govern shrinking. Contrarily, the lower magnitude of line loads applied to residential footing systems on swelling reactive soils is desired since higher applied perimeter loads generally counteract the deformation due to expanding ground movement. The values of H_s were specified as 2.5, 3.0, 3.5, and 4.0 m, for a meaningful comparison with the AS 2870-2011 method. The values of Δ_max were then calculated using the DL models. To show the disparity of values between the soil and the footing system movement, the constant value of y_s was then divided by the Δ_a resulting in the ordinate $\left(\frac{{y}_{s}}{{\Delta }_{a}}\right)$. The abscissa or the unit stiffness $\left(log\left[\frac{\sum \left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]\right)$ was then calculated and scatter plots between the ordinate and abscissa were created for comparison (see Fig. 12) (Table 5).

Fig. 12

Results of the comparison of the DL model and the AS 2870-2011 (Standards Standards Australia 2011) guideline for a stiffened rafts on shrinking soils, b stiffened rafts on swelling soils, c waffle rafts on shrinking soils, and d waffle rafts on swelling soils

Table 5 Upper and lower bounds to generate the input features for the AS 2870-2011 guidelines in Eqs. (15) and (16) for the Saltelli (2002) method

The computed values of the DL and AS 2870-2011 models for stiffened rafts on shrinking reactive soil are plotted in Fig. 12a. It can be observed that the curves formed parabolic shapes reflecting the highly non-linear interaction between stiffened rafts and shrinking reactive soil. The formation of the parabolic shapes in Fig. 12a was perhaps mainly caused by a change in the values of D with respect to the value of H_s. This means that an increasing value in the abscissa indicates an increase in D since B_w and W were constant in this comparison. On the other hand, an increase in the ordinate means the disparity of the values between y_s and Δ_a becomes larger. In contrast, the curves of AS 2870-2011 model in Fig. 12a are linear, denoting that an increase in y_s, will require a deeper edge and inner beams of a residential footing system. The two values of unit stiffness D suggest that a shallower D can have equal ordinate value to a deeper D. The reason behind this is the constant swelling of the soil around the edge beams of stiffened rafts, as observed by Fityus et al. (2004), Shams et al. (2018), and Teodosio et al., (2020b). Due to the lateral pressure from the constantly expanding soil beneath the portion of the footing system near the edge beams, this portion is pushed upward. Thus, having deeper edge beams or a higher value of D may lead to a higher movement disparity between y_s and Δ_a. A useful result of this graph is the vertex of the parabolic shape where the value of the ordinate started rising again. This shows that the vertex was the optimum unit stiffness or D for the stiffened raft on shrinking soil depending on H_s (e.g., $log\left[\frac{\sum \left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]$ ≈ 9.7 for H_s = 4.0 m).

The design lines of stiffened rafts on swelling reactive soil are shown in Fig. 12b with the curves of both the DL neural network and AS 2870-2011 model. The DL curves formed an exponential trend contrary to the linear trend of the AS 2870-2011 curves. These exponential lines denote that an increase in y_s, assuming Δ_a is constant, will require higher unit stiffness or D. It can be observed in Fig. 12b that the lines with H_s ≥ 3.0 m coincided, signifying that the ordinate, $\frac{{\mathrm{y}}_{\mathrm{s}}}{{\Delta }_{a}}$, was not driven by the depth H_s but influenced more by the structural features D and W, is consistent with the sensitivity analysis.

The design lines of waffle rafts on a shrinking reactive soil are presented in Fig. 12c. The curves formed by the DL model are of an exponential trend similar to the case of stiffened rafts on swelling soil (Fig. 12b). These curves show that an increase in y_s will entail higher unit stiffness or D. Portions of the exponential lines were parallel or coinciding with the AS 2870-2011 models (Standards Australia 2011). However, the curves created by the DL model formed a nearly horizontal portion with unit stiffness values less than 9.0 N/m.

The results of the DL and AS 2870-2011 models for waffle rafts on swelling reactive soil are shown in Fig. 12d. The formed trend lines of the DL models are complex and comprised of exponential lines extending up to a unit stiffness value of 9.7 N/m and then significantly reducing down to 10.4 N/m. The unit stiffness value of 9.7 N/m is similar to the inflection point in Fig. 12a, which is a critical value of D in reducing the difference between the y_s to Δ_a ratio. The exponential portion implied that an increase in y_s would necessitate an increase in unit stiffness or D. The decreasing portion of the trend line suggests that there should be additional support of beams with deeper D due to added dead load against the swelling soil.

In summary, the DL model can capture the non-linear nature of the relationship between the ordinate and abscissa. Furthermore, the soil-structure interaction and driving features differ depending on the type of residential footing system (e.g., stiffened raft versus waffle raft). Contrary to the design graphs presented in AS2870-2011, the design lines of the DL models signify that an increased value of D can either have a positive or a negative impact on the residential footing system depending on whether the reactive soil underneath is shrinking or swelling (e.g., Fig. 12a, d).

5 Conclusion

This study implemented DL neural networks to predict the maximum deformation of stiffened rafts and waffle rafts, Δ_max, as the targeted output. The DL model captured highly non-linear relationships of various input features (y_s, y_m, D, L, W, p, q, H_s, and ε_ms) and their effect on Δ_max. The sensitivity analyses revealed that the influence of features varies depending on the type of residential footing system (i.e., stiffened raft or waffle raft) and the movement of reactive soil (i.e., shrinking or swelling). For stiffened rafts on shrinking soils, the main parameters impacting Δ_max are the spatial dimension of the foundation (i.e., L and W) and the depth of active soil layer H_s. For stiffened rafts on swelling soils, y_m, D, and W strongly influenced Δ_max. Contrarily, the DL models of waffle rafts are either strongly influenced by the soil features (i.e., y_s, y_m, and H_s) when on shrinking soil or by the structural feature D when on swelling soil. This shows that the DL models for stiffened rafts have a stronger soil-structure interaction due to the embedment of the beams.

The DL calculations were then compared to the estimations of the established design guideline AS 2870-2011. The DL formed non-linear curves on $\frac{{y}_{s}}{{\Delta }_{a}}$ versus $the\, log\left[\frac{\sum \left(\frac{{B}_{w}{D}^{3}}{12}\right)}{W}\right]$ space whereas the corresponding estimations of AS 2870-2011 showed linear graphs. The behaviour of the soil-structure interaction and the influence of features vary contingent on the structural type and whether the beams are embedded (e.g., stiffened rafts) or not (e.g., waffle raft). An increased magnitude of D can have desirable or undesirable effects on the global residential footing system, dependent on whether the reactive soil underneath is shrinking or swelling.

Appendix

The estimation of the characteristic surface movement (y_s) of the reactive soil in the Australian Standard (AS) 2870-2011 is described by Eq. 17,

$${y}_{s}=\frac{1}{100}\sum_{n=1}^{N}{({I}_{pt}\Delta \overline{u }h)}_{n}$$

(17)

where Δu̅ is the averaged soil suction, h is the thickness of the considered layer, N is the number of soil layers, and I_pt is the instability index described as

$${I}_{pt}={\alpha I}_{ps}$$

(18)

where I_ps is the shrinkage index and α is the lateral restraint factor with the value taken for the layers in the cracked zone as 1.0 or the layers in the uncracked zone calculated as

$$\alpha =2-\frac{z}{5}$$

(19)

where z is the depth to the middle of the soil layer from the finished ground level.

Values of the soil mound movement, y_m, can be estimated using the Walsh Method and Mitchell Method. To determine the values of y_m using Walsh Method in the centre heave and edge heave scenario, values of y_s are multiplied by 0.7 and 0.5, respectively. Using Mitchell Method, values of y_s for both the centre heave and edge heave scenarios are multiplied by 0.7.

The active depth zone, H_s, is the depth of the design where the change in soil suction occurs. This parameter is highly dependent on both soil properties and climatic variation. AS 2870-2011 specified the values of H_s in specific locations in Australia, as listed in Table 6.

Table 6 H_s in specific locations in Australia