Abstract
We introduce a framework for the verification of protocols involving a distinguished machine (referred to as a leader) orchestrating the operation of an arbitrary number of identical machines (referred to as followers) in a network. At the core of our framework is a high-level formalism capturing the operation of these types of machines together with their network interactions. We show that this formalism automatically translates to a tractable form of first-order temporal logic. Checking whether a protocol specified in our formalism satisfies a desired property (expressible in temporal logic) then amounts to checking whether the protocol’s translation in first-order temporal logic entails that property. Many different types of protocols used in practice, such as cache coherence, atomic commitment, consensus, and synchronization protocols, fit within our framework. First-order temporal logic also facilitates parameterized verification by enabling us to model such protocols abstractly without referring to individual machines.
Similar content being viewed by others
1 Introduction
Parameterized verification is becoming increasingly important nowadays, with technologies like the Internet of Things (IoT), sensor networks, robot swarms, and satellite constellations becoming widespread. Systems involving large numbers of communicating components are commonly deployed, increasing the need for scalable verification techniques to ensure that such systems operate as expected.
Parameterized verification via first-order temporal logic [13, 16, 18] is an approach to parameterized verification, proposed as an alternative to regular model checking for parameterized and infinite-state systems [1, 2] and constraint-based verification using counting abstractions [10, 11, 14]. The model checking approach has been applied to several scenarios verifying safety properties and some liveness properties, but is in general incomplete. Constraint-based approaches do provide complete procedures for checking safety properties, but these procedures have non-primitive recursive upper bounds, and they usually lead to undecidability when applied to liveness properties. On the other hand, while first-order temporal logic is incomplete [29] and generally undecidable [22], a certain syntactic restriction to it, referred to as monodic first-order temporal logic, is finitely axiomatizable [31] and (if one restricts its first-order part to a decidable fragment of first-order logic) decidable [22]. Roughly speaking, a first-order temporal logic formula \(\varphi \) is said to be monodic if every sub-formula of \(\varphi \) appearing within the scope of a temporal operator has at most one free variable.
As shown in [13, 16], monodic first-order temporal logic is expressive enough to specify various types of systems commonly appearing in practice. In particular, [13, 16] show how to encode in said logic an abstract protocol model, first appearing in [10, 11], for networks of arbitrarily many, identical finite-state machines communicating via broadcast messages. Using this approach, one is able to automatically translate any suitable protocol to a monodic first-order temporal formula that encapsulates its behaviour. One is then able to check whether that protocol has a certain property by checking whether said formula logically entails the property. (Of course the property must be expressible in monodic first-order temporal logic.) In this work, we introduce a new abstract model that encapsulates the one appearing in [10, 11, 13, 16], but can be applied to a wider class of protocols, such as cache coherence, atomic commit, consensus, and synchronization protocols. Sect. 5 provides three examples of protocols specified in this model.
Our model applies to settings in which a distinguished finite-state machine (referred to as a leader) orchestrates the operation of arbitrarily many, identical finite-state machines (referred to as followers). As an example of such a setting, consider a simple consensus protocol in which the leader asks the followers whether they agree on a certain parameter change by broadcasting to them an “agree?” message, to which they reply with either a “yes” (when they agree) or a “no” message (when they do not agree), and, if they all agree, the leader changes the parameter. We assume that message delivery is guaranteed, but each message can take arbitrarily long to arrive to each recipient and may arrive multiple times.
The setting in the above example is different to the setting in [10, 11, 13, 16] in two main ways. First, only the leader broadcasts to the followers: each follower can only message the leader (and not other followers). Second, unlike the followers, which react to individual messages, the leader reacts to collections of messages. For example, an individual “yes” message does not generally convey any information to the leader, apart from the possibility of a consensus in the future (assuming the leader has not received any “no” messages). To be able to make a decision about the consensus in the future, the leader has to maintain a persistent record of individual messages together with an identifier for their sender.
To incorporate such functionality, our model introduces the concept of an inbox. Inboxes provide a way for the leader to organize incoming messages and record their sender. For the above setting, the leader maintains an inbox for “yes” messages and an inbox for “no” messages, and, upon delivery of a message, the sender’s identifier is recorded in the inbox. See Fig. 1 for a possible execution in that setting. (Each inbox is represented by a box; dotted arrows represent the flow of time; regular arrows represent messages.) Then, consensus is achieved if the “yes” inbox contains the identifiers of all followers. For different protocols, we enable the leader to react to different conditions upon its inboxes. (For example, the leader can react to an inbox having exactly one element or to an inbox having more than one element.) For symmetry, each follower is also equipped with an inbox, which is simply a record of ingoing messages (all ingoing messages to a follower come from the leader, so the sender need not be recorded). Our model can be considered as a generalization of the model in [10, 11, 13, 16] since follower broadcasts can be emulated using the leader as a network relay that broadcasts all its ingoing messages (see, for example, the leader in Sect 5.1).
The plan of this paper is as follows. In Sect. 2 we review some relevant concepts from first-order temporal logic. In Sect. 3 we give a formal definition of our model. In Sect. 4 we show how our model automatically translates to (monodic) first-order temporal logic. In Sect. 5 we specify with our framework three protocols appearing in practice, namely the FloodSet protocol [28], the two-phase commit [6, 19], and Control-MAC [7]. In Sect. 6 we discuss related work.
2 Preliminaries
In the sequel, we assume standard concepts from first-order logic. The symbols used in first-order temporal logic (abbr. \(\textsf {FOTL}\)) are predicate symbols \(P_0, P_1, \ldots \), each of fixed arity (0-ary or nullary predicate symbols are allowed and correspond to propositions); variables \(x_0, x_1, \ldots \), constants \(c_0, c_1, \ldots \); the propositional constants \(\top \) (true) and \(\bot \) (false); the usual Boolean connectives (\(\lnot , \vee , \wedge , \rightarrow , \leftrightarrow \)); the quantifiers \(\forall \) (for all) and \(\exists \) (exists); and the temporal operators \(\Box \) (always in the future), \(\Diamond \) (sometime in the future),  (at the next moment),
(at the next moment),  (until), and
(until), and  (weak until). The syntax of \(\textsf {FOTL}\) is as follows:
(weak until). The syntax of \(\textsf {FOTL}\) is as follows:
-
\(\top \) and \(\bot \) are atomic \(\textsf {FOTL}\)-formulae;
-
if P is an n-ary predicate symbol and \(t_1, \ldots , t_n\) are variables or constants, then \(P(t_1,\dots ,t_n)\) is an atomic \(\textsf {FOTL}\)-formula;
-
if \(\varphi \) and \(\psi \) are \(\textsf {FOTL}\)-formulae, so are \(\lnot \varphi \), \(\varphi \wedge \psi \), \(\varphi \vee \psi \), \(\varphi \rightarrow \psi \), and \(\varphi \leftrightarrow \psi \);
-
if \(\varphi \) is an \(\textsf {FOTL}\)-formula and x is a variable, then \(\forall x \, \varphi \) and \(\exists x \, \varphi \) are \(\textsf {FOTL}\)-formulae;
-
if \(\varphi \) and \(\psi \) are \(\textsf {FOTL}\)-formulae, then so are \(\Box \varphi \), \(\Diamond \varphi \),
 ,
, 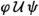 , and
, and  .
.
If \(\varphi \) is an \(\textsf {FOTL}\)-formula, we denote its length by \(\Vert \varphi \Vert \). \(\textsf {FOTL}\)-formulae are interpreted in first-order temporal structures, i.e. sequences \({\mathfrak {M}}= {\mathfrak {A}}_0, {\mathfrak {A}}_1, \ldots \) of first-order structures over the same domain A. That is, given a non-empty set A, \({\mathfrak {A}}_n = \langle A, I_n \rangle \) (\(n \in {\mathbb {N}}\)), where is \(I_n\) an interpretation of predicate and constant symbols over A, assigning to each predicate symbol P a relation \(P^{{\mathfrak {A}}_n}\) on A of the same arity as P (if P is a nullary predicate, \(P^{{\mathfrak {A}}_n}\) is simply one of the propositional constants \(\top \) or \(\bot \)), and to each constant symbol c an element \(c^{{\mathfrak {A}}_n}\) of A. We require that the interpretation of constants be rigid, i.e. \(I_n(c) = I_m(c)\), for all \(n, m \in {\mathbb {N}}\). An assignment \({\mathfrak {a}}\) in A is a function from the set of variables \(\{ x_0, x_1, \ldots \}\) to A. The truth relation \(({\mathfrak {M}}, {\mathfrak {A}}_n) \models ^{\mathfrak {a}}\varphi \) (or simply \({\mathfrak {A}}_n \models ^{\mathfrak {a}}\varphi \) if \({\mathfrak {M}}\) is clear from context) in \({\mathfrak {M}}= {\mathfrak {A}}_0, {\mathfrak {A}}_1, \ldots \) is defined in Fig. 2. We say that a formula \(\varphi \) is true in \({\mathfrak {M}}\) if there exists an assignment \({\mathfrak {a}}\) such that \({\mathfrak {A}}_0 \models ^{\mathfrak {a}}\varphi \). A formula is satisfiable if it has a model and valid if it is true in any temporal structure under any assignment. A formula is called monodic if any subformula of \(\varphi \) of the form  , \(\Diamond \psi \), \(\Box \psi \),
, \(\Diamond \psi \), \(\Box \psi \),  , or
, or  has at most one free variable. For example, the formulae
has at most one free variable. For example, the formulae  and \(\forall x \, \Diamond \exists y \, P(x, y)\) are monodic, while the formula
and \(\forall x \, \Diamond \exists y \, P(x, y)\) are monodic, while the formula  is not monodic. The set of all monodic formulae form the monodic fragment of \(\textsf {FOTL}\) (abbr. MFOTL).
is not monodic. The set of all monodic formulae form the monodic fragment of \(\textsf {FOTL}\) (abbr. MFOTL).
\(\textsf {FOTL}\) is incomplete (not recursively axiomatizable) [29] and undecidable [22]. In contrast, \(\textsf {MFOTL}\) is finitely axiomatizable [31], and, if its first-order part is restricted to a decidable fragment of first-order logic, decidable [22]. Of particular interest to us are the monadic fragment and the two-variable fragment of \(\textsf {MFOTL}\), both decidable and EXPSPACE-complete [21]. (Most of the formulas we require can be written in monadic \(\textsf {MFOTL}\). As we shall see later on, if some form of counting is required, two variables are necessary.) Two automated theorem provers are available for \(\textsf {MFOTL}\): TeMP [23] and TSPASS [26, 27]. These provers implement a form of temporal resolution called fine-grained resolution [8, 24]. (See [12, 15] for some applications of TeMP and [3,4,5, 20] for TSPASS.) It should be noted that these provers use (for technical reasons) so-called expanding domain semantics. (The semantics that we provided above are constant domain semantics. With expanding domain semantics, the domains of the structures in a temporal model \({\mathfrak {M}}= {\mathfrak {A}}_0, {\mathfrak {A}}_1, \ldots \) are expanding, i.e. \({\mathfrak {A}}_n = \langle A_n, I_n \rangle \), where \(A_n \subseteq A_{n+1}\) (\(n \in {\mathbb {N}}\)) and \(I_n\) is an interpretation over \(A_n\); with constant domains, \(A_n = A_{n+1} = A\).) It is known that satisfiability over expanding domains reduces to satisfiability over constant domains [30]. [24, Sec. 7] discusses how to enforce constant domains in fine-grained temporal resolution (which uses expanding domain semantics). This is useful for applications using TeMP or TSPASS that require constant domains. Various applications may also require finite domains. In this connection, [17, 25] report on characterizing finite domains using \(\textsf {MFOTL}\). In particular, [17] reports that each of the following three axioms enforces finite domains (and is derivable from each of the other two):
-
(F1)
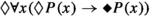
-
(F2)
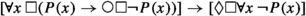
-
(F3)

( is interpreted as “sometime in the past”.) [17] also reports that for classes of protocols satisfying a certain “stabilization principle” (FloodSet in Sect. 5.1 and the two-phase commit in Sect. 5.2 both satisfy this principle, but Control-MAC in Sect. 5.3 does not), satisfiability over finite domains coincides with satisfiability over arbitrary domains. Thus, (F1)-(F3) need not be used to enforce finiteness for such protocols.
is interpreted as “sometime in the past”.) [17] also reports that for classes of protocols satisfying a certain “stabilization principle” (FloodSet in Sect. 5.1 and the two-phase commit in Sect. 5.2 both satisfy this principle, but Control-MAC in Sect. 5.3 does not), satisfiability over finite domains coincides with satisfiability over arbitrary domains. Thus, (F1)-(F3) need not be used to enforce finiteness for such protocols.
Adding either equality or function symbols to \(\textsf {MFOTL}\) leads to the loss of recursive enumerability [9, 31]. This is a limitation that affects applications (such as the Control-MAC protocol in Sect. 5.3) that require the counting quantifiers \(\exists ^{=1} x \, P(x)\) and \(\exists ^{> 1} x \, P(x)\) (“there exists exactly one x such that P(x)” and “there exist more than one x such that P(x)” respectively), which we use as shorthands for \(\exists x P(x) \wedge \forall x \forall y ((P(x) \wedge P(y)) \rightarrow x = y)\) and \(\exists x \exists y (P(x) \wedge P(y) \wedge \lnot (x = y))\) respectively, where \(P(\cdot )\) is a unary predicate. (We also use \(\exists ^{\geqslant 1} x \, P(x)\) in place of \(\exists x P(x)\) sometimes for emphasis.) Due to the aforementioned limitation, \(\exists ^{=1} x \, P(x)\) and \(\exists ^{> 1} x \, P(x)\) cannot be input to TeMP or TSPASS. To address this issue, one option is attempting to specify equality axiomatically. In a non-temporal setting, equality can be axiomatized as a congruence relation, i.e. as a binary relation \(E(\cdot , \cdot )\) satisfying axioms (E1)-(E4) below:
-
(E1)
\(\forall x \, E(x, x)\)
-
(E2)
\(\forall xy (E(x, y) \rightarrow E(y, x))\)
-
(E3)
\(\forall xyz ( E(x, y) \wedge E(y, z) \rightarrow E(x, z))\)
-
(E4)
\(\forall x_1 \cdots x_n y_1 \cdots y_n (\bigwedge _{i=1}^n E(x_i, y_i) \wedge P(x_1, \ldots , x_n) \rightarrow P(y_1, \ldots , y_n))\)
In a temporal setting, one needs in addition axiom (E5) below, enforcing the condition that equal objects remain equal across time:
-
(E5)
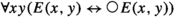
The problem with this approach is that formula (E5) is not monodic. As a result, one is left only with axioms (E1)-(E4). Now, suppose that one wishes to check whether a monodic formula \(\chi \) containing equality is valid. (For our purposes, \(\chi \) will be of the form \(\varphi \rightarrow \psi \), where \(\varphi \) describes a protocol and \(\psi \) a correctness condition for that protocol.) It should be clear that if \(\textsf {EqAx} \rightarrow [\chi ]_E\) is valid, where \(\textsf {EqAx}\) is the conjunction of formulas (E1)-(E4) and \([\chi ]_E\) is the result of replacing in \(\chi \) all occurences of \(x=y\) with E(x, y), then \(\chi \) is valid. (Any proof of \(\chi \) in the axiomatic system (E1)-(E4) is trivially a proof of \(\chi \) in the axiomatic system (E1)-(E5), and the latter system fully captures equality.) Thus, one is left with a correct but incomplete approach to check the validity of a monodic formula \(\chi \) containing equality: one uses TeMP or TSPASS to check whether \(\textsf {EqAx} \rightarrow [\chi ]_E\) is valid; if the prover concludes that it is, then one knows that \(\chi \) is valid; if the prover concludes that \(\textsf {EqAx} \rightarrow [\chi ]_E\) is not valid, then the validity of \(\chi \) remains unknown.
3 Distributed machines
In the following setting we have a collection of \(k+1\) (\(k > 0\)) finite-state machines in a network, k of which are replicas of each other and the remaining machine is a distinguished machine orchestrating the operation of the replicas. Each replica is referred to as a follower, the distinguished machine is referred to as a leader, and the whole network of these \(k+1\) machines is referred to as a distributed machine.
Communication in the network occurs via the exchange of the following types of messages: (a) broadcast messages from the leader to the followers; and (b) individual messages from a follower directed to the leader. (A follower can theoretically broadcast a message to the followers by using the leader as a relay; see, for example, Sect. 5.1.) Delivery of messages in the network is guaranteed. (See Rem. 1 for a technicality about guaranteed delivery in synchronous networks.) Depending on the application, delivery of messages can occur within one time unit (synchronous network) or it can take arbitrarily long (asynchronous network). In the latter case, a broadcast message (by the leader) can arrive to different followers at different times; and each message can arrive to its recipient (be it the leader or a follower) multiple times. The leader has a separate inbox for each message it is meant to receive. Upon delivery of a message, an identifier for the message’s sender (i.e. a follower) is added to the appropriate inbox. Every follower has an inbox of messages and, upon delivery, each message to a follower is added to the follower’s inbox.
The leader’s transitions correspond to three types of actions: (a) reacting to one of its inboxes; (b) broadcasting a message to the followers; and (c) local (not related to the network). Specifically, in type (a) transitions the leader reacts to an inbox (i) being empty; (ii) having exactly one element; (iii) having one or more elements; (iv) having more than one element; or (v) being full, i.e. containing the identities of all followers in the network. Type (a)(ii)-(v) transitions for the leader delete the contents of the corresponding inbox. Each follower’s transitions correspond to three types of actions: (a) reacting to a message in the follower’s inbox; (b) sending a message to the leader; and (c) local (not related to the network). Type (a) transitions for each follower delete the corresponding message from the follower’s inbox.
We stress at this point that receiving a message and reacting to a message or a message’s inbox are different things: receiving a message is a network action (simply registering the message to the recipient) and is independent of the recipient’s operation; reacting to a message (in the follower’s case) or a message’s inbox (in the leader’s case) is an action in which the recipient takes a transition relevant to that message. The recipient of a message need not react to it (in the follower’s case) or to its corresponding inbox (in the leader’s case), neither at the time of its receipt nor at any future time.
We now proceed to define the above concepts formally.
3.1 Notation for messages and transitions
In the sequel, we adopt the following convention regarding messages: to emphasize that a message \(\mu \) (where \(\mu \) is an arbitrary label) is ingoing, we write \(\mu \) with a left-pointing arrow on top ( ); and to emphasize that \(\mu \) is outgoing, we write \(\mu \) with a right-pointing arrow on top (\(\vec {\mu }\)). The leader’s inbox corresponding to a message
); and to emphasize that \(\mu \) is outgoing, we write \(\mu \) with a right-pointing arrow on top (\(\vec {\mu }\)). The leader’s inbox corresponding to a message  is denoted by
is denoted by  .
.
To distinguish the leader’s three different types of transitions (reacting to an inbox, broadcasting a message, and local) we introduce the following notation. Transitions in which the leader reacts to an inbox  are denoted with the message
are denoted with the message  followed by a quantifier, i.e. \(^{= 0}\), \(^{= 1}\), \(^{\geqslant 1}\), \(^{> 1}\), or \(^\textsf {all}\) (written as a superscript). Thus, we write: (i)
followed by a quantifier, i.e. \(^{= 0}\), \(^{= 1}\), \(^{\geqslant 1}\), \(^{> 1}\), or \(^\textsf {all}\) (written as a superscript). Thus, we write: (i)  for a transition that occurs on condition that
for a transition that occurs on condition that  is empty; (ii)
is empty; (ii)  for a transition that occurs on condition that
for a transition that occurs on condition that  has exactly one element; (iii)
has exactly one element; (iii)  for a transition that occurs on condition that
for a transition that occurs on condition that  has one or more elements; (iv)
has one or more elements; (iv)  for a transition that occurs on condition that
for a transition that occurs on condition that  has more than one element; and (v)
has more than one element; and (v)  for a transition that occurs on condition that
for a transition that occurs on condition that  is full. The above quantifiers are enough for our purposes, but our framework can be easily extended with more quantifiers, depending on the application. Any quantifier expressible in first-order logic can be added by including the quantifier in the set \({\overline{T}}^L_\text {in}\) (Sect. 3.2) and updating the \(\textsf {persl}\) and \(\textsf {enbl}_\tau \) formulas (Sect. 4.1) with the quantifier’s semantics in first-order logic. Proofs carry over with minor adjustments. (Note that quantifiers requiring equality to be exressed in first-order logic affect the completeness of our framework as discussed in Sect. 6.) Transitions in which the leader broadcasts a message are simply denoted with that message (employing the above convention for outgoing messages): \(\vec {\mu }\) denotes the transition in which the leader broadcasts \(\mu \). Local transitions are simply denoted with a plain label (no arrow on top). Similar notation is used for followers reacting to a message (
is full. The above quantifiers are enough for our purposes, but our framework can be easily extended with more quantifiers, depending on the application. Any quantifier expressible in first-order logic can be added by including the quantifier in the set \({\overline{T}}^L_\text {in}\) (Sect. 3.2) and updating the \(\textsf {persl}\) and \(\textsf {enbl}_\tau \) formulas (Sect. 4.1) with the quantifier’s semantics in first-order logic. Proofs carry over with minor adjustments. (Note that quantifiers requiring equality to be exressed in first-order logic affect the completeness of our framework as discussed in Sect. 6.) Transitions in which the leader broadcasts a message are simply denoted with that message (employing the above convention for outgoing messages): \(\vec {\mu }\) denotes the transition in which the leader broadcasts \(\mu \). Local transitions are simply denoted with a plain label (no arrow on top). Similar notation is used for followers reacting to a message ( ) and sending a message to the leader (\(\vec {\mu }\)), as well as for their local transitions (no arrow on top).
) and sending a message to the leader (\(\vec {\mu }\)), as well as for their local transitions (no arrow on top).
For examples using the above notation see Sect. 5 and figures therein.
3.2 Leaders and their execution
Let  , \(T^L_\text {out} = \{ \vec {\mu }_1, \ldots , \vec {\mu }_s \}\), and \(T^L_\text {local} = \{ \ell _1, \ldots , \ell _t \}\) be sets of symbols (note that
, \(T^L_\text {out} = \{ \vec {\mu }_1, \ldots , \vec {\mu }_s \}\), and \(T^L_\text {local} = \{ \ell _1, \ldots , \ell _t \}\) be sets of symbols (note that  and \(\vec {\mu }\) are different symbols); let
and \(\vec {\mu }\) are different symbols); let  . A leader is a quadruple
. A leader is a quadruple
where
-
\(Q^L\) is a finite set, the set of states of \(L\);
-
\(Q^L_\text {init} \subseteq Q^L\) are the initial states of \(L\);
-
\(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\) is the set of transitions of \(L\); and
-
\(\delta ^L\subseteq Q \times (T^L\setminus \{ \textit{idle}\}) \times Q\) is the transition relation of \(L\).
Intuitively, \(T^L_\text {in}\) is the set of all possible ingoing messages to L, thus, according to the notational conventions in Sect. 3.1, \({\overline{T}}^L_\text {in}\) is the set of all available labels for transitions in which L reacts to an inbox; \(T^L_\text {out}\) is the set of all possible outgoing messages from the leader, and, also, the set of all available labels for transitions in which L broadcasts a message; and \(T^L_\text {local}\) is the set of L’s local actions, and, also, the set of all available labels for L’s local transitions. The transition \(\textit{idle}\) is a special transition the leader takes when it is unable to take any other transition. We define the size of L, denoted \(\Vert L\Vert \), to be the quantity \(|Q^L|+|T^L|+|\delta ^L|\). For some example leaders see Sect. 5.
We describe the execution of a leader as a sequence of certain configurations in the context of a (non-empty) set A, whose elements are to be viewed as representing followers in the leader’s network. Let L be a leader as above and \(A = \{ a_1, \ldots , a_k \}\) (\(k >0\)) be a set (the set of L’s followers). An l-configuration (short for leader configuration) over A is an \((r+1)\)-tuple  (
( ), where \(q \in Q^L\) and
), where \(q \in Q^L\) and  (\(1 \le i \le r\)). Intuitively, q is \(L\)’s state at a given moment of time and
(\(1 \le i \le r\)). Intuitively, q is \(L\)’s state at a given moment of time and  (\(1 \le i \le r\)) is \(L\)’s inbox corresponding to the message
(\(1 \le i \le r\)) is \(L\)’s inbox corresponding to the message  at that moment of time. Each
at that moment of time. Each  (\(1 \le i \le r\)) is to be viewed as a record of those followers (elements of A) from which L has received a message
(\(1 \le i \le r\)) is to be viewed as a record of those followers (elements of A) from which L has received a message  since the last time L reacted to
since the last time L reacted to  . (Recall that reacting to a non-empty inbox deletes its content.) If
. (Recall that reacting to a non-empty inbox deletes its content.) If  is an l-configuration, \(\sigma ({\mathfrak {c}})\) denotes the state q and \(\iota ({\mathfrak {c}})\) denotes the r-tuple
is an l-configuration, \(\sigma ({\mathfrak {c}})\) denotes the state q and \(\iota ({\mathfrak {c}})\) denotes the r-tuple  .
.
If  is an l-configuration, we denote by \( enb ( {\mathfrak {c}} )\) (short for enabled) the set of transitions \(\tau \in T^L\setminus \{ \textit{idle}\}\) such that \(\langle q, \tau , q' \rangle \in \delta ^L\), for some \(q' \in Q^L\), and either \(\tau \in T^L_\text {out} \cup T^L_\text {local}\) or one of the following holds:
is an l-configuration, we denote by \( enb ( {\mathfrak {c}} )\) (short for enabled) the set of transitions \(\tau \in T^L\setminus \{ \textit{idle}\}\) such that \(\langle q, \tau , q' \rangle \in \delta ^L\), for some \(q' \in Q^L\), and either \(\tau \in T^L_\text {out} \cup T^L_\text {local}\) or one of the following holds:
-
(a)
 (
( ) and
) and 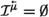 ;
; -
(b)
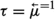 (
( ) and
) and  ;
; -
(c)
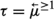 (
(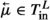 ) and
) and 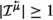 ;
; -
(d)
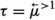 (
( ) and
) and  ;
; -
(e)
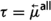 (
( ) and
) and  .
.
We shall refer to a transition \(\tau \in enb ( {\mathfrak {c}} )\) as an enabled transition. Intuitively, \(\tau \in enb ( {\mathfrak {c}} )\) if \(\tau \) is one of the available transitions for L when L’s configuration is \({\mathfrak {c}}\). Thus, all transitions in which a message is broadcast and all local transitions are enabled, whereas transitions in which the leader reacts to an inbox are enabled only if the inbox’s corresponding cardinality constraints are satisfied.
Given our intended view of inboxes as records of followers from which the leader has a specific message, we wish to enforce at each moment of time a form of persistence, i.e. that each inbox can grow (when new messages arrive) but never loses its content, unless the leader takes a transition deleting that content. To this end, for each \(\tau \in T^L\), we define the relation \(\preceq ^\tau \) over r-tuples \(\langle I^1, \ldots , I^r \rangle \), \(\langle J^1, \ldots , J^r \rangle \), where \(I^j, J^j \subseteq A\) (\(1 \le j \le r\)), as follows:
-
(a)
if
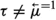 ,
, 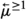 ,
, 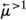 ,
,  for all
for all  , \(\langle I^1, \ldots , I^r \rangle \preceq ^\tau \langle J^1, \ldots , J^r \rangle \) iff \(I^j \subseteq J^j\) (for all \(1 \le j \le r\));
, \(\langle I^1, \ldots , I^r \rangle \preceq ^\tau \langle J^1, \ldots , J^r \rangle \) iff \(I^j \subseteq J^j\) (for all \(1 \le j \le r\)); -
(b)
if
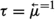 ,
,  ,
,  , or
, or  for some
for some 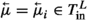 , \(\langle I^1, \ldots , I^r \rangle \preceq ^\tau \langle J^1, \ldots , J^r \rangle \) iff \(J^i = \emptyset \) and \(I^j \subseteq J^j\) (for all \(1 \le j \le r\), \(j \ne i\)).
, \(\langle I^1, \ldots , I^r \rangle \preceq ^\tau \langle J^1, \ldots , J^r \rangle \) iff \(J^i = \emptyset \) and \(I^j \subseteq J^j\) (for all \(1 \le j \le r\), \(j \ne i\)).
A run for \(L\) over A is a sequence \({\mathfrak {R}}= \{ \langle {\mathfrak {c}}_n, \tau _n \rangle \}_{n \in {\mathbb {N}}}\), where  (\(n \in {\mathbb {N}}\)) is an l-configuration and \(\tau _n \in T^L\) (\(n \in {\mathbb {N}}\)), such that: \(q_0 \in Q^L_\text {init}\),
(\(n \in {\mathbb {N}}\)) is an l-configuration and \(\tau _n \in T^L\) (\(n \in {\mathbb {N}}\)), such that: \(q_0 \in Q^L_\text {init}\),  (for all \(1 \le i \le r\)); for all \(n \in {\mathbb {N}}\), \(\iota ({\mathfrak {c}}_n) \preceq ^{\tau _n} \iota ({\mathfrak {c}}_{n+1})\) (persistence); and, for all \(n \in {\mathbb {N}}\),
(for all \(1 \le i \le r\)); for all \(n \in {\mathbb {N}}\), \(\iota ({\mathfrak {c}}_n) \preceq ^{\tau _n} \iota ({\mathfrak {c}}_{n+1})\) (persistence); and, for all \(n \in {\mathbb {N}}\),
-
(a)
\(\tau _n \in enb ( {\mathfrak {c}}_n )\) and \(\langle \sigma ({\mathfrak {c}}_n), \tau _n, \sigma ({\mathfrak {c}}_{n+1}) \rangle \in \delta ^L\); or
-
(b)
\( enb ( {\mathfrak {c}}_n ) = \emptyset \), \(\tau _n = \textit{idle}\), and \(\sigma ({\mathfrak {c}}_n) = \sigma ({\mathfrak {c}}_{n+1})\).
Intuitively, a run describes a valid execution for \(L\): \(L\) starts at an initial state with all its inboxes empty, and, at each moment of time, chooses an enabled (at that time) transition or becomes idle if none exists. Inboxes can grow at any moment of time as a result of new messages arriving, except when their content is being deleted.
The following simple lemma should be clear from the above. It will be useful when proving that the logical formula in Sect. 4.1 describing the leader’s execution is correct.
Lemma 1
Let \({\mathfrak {R}}= \{ \langle {\mathfrak {c}}_n, \tau _n \rangle \}_{n \in {\mathbb {N}}}\) be a run for L over a set A. For all \(n \in {\mathbb {N}}\), if  ,
,  ,
,  ,
,  (
( ) and
) and  , then
, then  .
.
3.3 Followers and their execution
Let  ,
,  , and
, and  be sets of symbols (note that
be sets of symbols (note that  and \(\vec {\mu }\) are different symbols). A follower is a quadruple
and \(\vec {\mu }\) are different symbols). A follower is a quadruple
where
-
\(Q^F\) is a finite set, the set of states of \(F\);
-
\(Q^F_\text {init} \subseteq Q^F\) are the initial states of \(F\);
-
\(T^F= T^F_\text {in} \cup T^F_\text {out} \cup T^F_\text {local} \cup \{ \textit{idle}\}\) is the set of transitions of \(F\); and
-
\(\delta ^F\subseteq Q^F\times (T^F\setminus \{ \textit{idle}\}) \times Q^F\) is the transition relation of \(F\).
Intuitively, the sets \(T^F_\text {in}\), \(T^F_\text {out}\), and \(T^F_\text {local}\) are respectively the sets of all possible ingoing messages, possible outgoing messages, and local actions of F; thus, according to the notational conventions in Sect. 3.1, \(T^F_\text {in}\), \(T^F_\text {out}\), and \(T^F_\text {local}\) are respectively the sets of labels for the transitions in which F reacts to a message in its inbox, sends a message to the leader, and the set of F’s local actions. The transition \(\textit{idle}\) is a special transition each follower takes when it is unable to take any other transition. We define the size of F, denoted \(\Vert F\Vert \), to be the quantity \(|Q^F|+|T^F|+|\delta ^F|\). For some example followers see Sect. 5.
We describe the execution of a follower as a sequence of certain configurations. Let F be a follower as above. An f-configuration (short for follower configuration) is a pair \(\langle q, {\mathcal {I}}\rangle \), where \(q \in Q^F\) and \({\mathcal {I}}\subseteq T^F_\text {in}\). Intuitively, q is F’s state at a given moment of time and \({\mathcal {I}}\subseteq T^F_\text {in}\) is its inbox at that moment of time. At any moment of time, \({\mathcal {I}}\) is to be viewed as a record of messages (from the leader) to which F has not yet reacted.
If \({\mathfrak {c}}= \langle q, {\mathcal {I}}\rangle \) is an f-configuration, we denote by \( enb ( {\mathfrak {c}} )\) (short for enabled) the set of transitions \(\tau \in T^F\setminus \{ \textit{idle}\}\) such that \(\langle q, \tau , q' \rangle \in \delta ^F\), for some \(q' \in Q^F\), and either (a) \(\tau \in T^F_\text {out} \cup T^F_\text {local}\) or (b)  and
and  . Intuitively, \(\tau \in enb ( {\mathfrak {c}} )\) if \(\tau \) is one of the available transitions for F when F’s configuration is \({\mathfrak {c}}\). Thus, all transitions in which a message is sent and all local transitions are enabled, whereas transitions in which the follower reacts to a message are enabled only if the corresponding message is present in \({\mathcal {I}}\).
. Intuitively, \(\tau \in enb ( {\mathfrak {c}} )\) if \(\tau \) is one of the available transitions for F when F’s configuration is \({\mathfrak {c}}\). Thus, all transitions in which a message is sent and all local transitions are enabled, whereas transitions in which the follower reacts to a message are enabled only if the corresponding message is present in \({\mathcal {I}}\).
As in the leader’s case, we want to enforce at each moment of time a form of persistence for the inbox \({\mathcal {I}}\), i.e. that \({\mathcal {I}}\) can grow (when a new message arrives from the leader) but no message is lost, unless the follower reacts to that message (in which case the message is deleted). To this end, for each \(\tau \in T^F\), we define the relation \(\preceq ^\tau \) over sets \(I, J \subseteq T^F_\text {in}\) as follows:
-
(a)
if \(\tau \not \in T^F_\text {in}\), \(I \preceq ^\tau J\) iff \(I \subseteq J\);
-
(b)
if
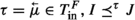 iff
iff 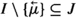 and
and 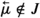 .
.
A run for F is a sequence \({\mathfrak {R}}= \{ \langle {\mathfrak {c}}_n, \tau _n \rangle \}_{n \in {\mathbb {N}}}\), where \({\mathfrak {c}}_n = \langle q_n, {\mathcal {I}}_n \rangle \) (\(n \in {\mathbb {N}}\)) is an f-configuration and \(\tau _n \in T^F\) (\(n \in {\mathbb {N}}\)), such that: \(q_0 \in Q^F_\text {init}\), \({\mathcal {I}}_0 = \emptyset \); for all \(n \in {\mathbb {N}}\), \({\mathcal {I}}_n \preceq ^{\tau _n} {\mathcal {I}}_{n+1}\) (persistence); and, for all \(n \in {\mathbb {N}}\),
-
(a)
\(\tau _n \in enb ( {\mathfrak {c}}_n )\) and \(\langle q_n, \tau _n, q_{n+1} \rangle \in \delta ^F\); or
-
(b)
\( enb ( {\mathfrak {c}}_n ) = \emptyset \), \(\tau _n = \textit{idle}\), and \(q_n = q_{n+1}\).
Intuitively, a run describes a valid execution for F: F starts at an initial state with its inbox empty, and, at each moment of time, chooses an enabled (at that time) transition or becomes idle if none exists. Messages persist in F’s inbox, unless explicitly deleted when a transition in \(T^F_\text {in}\) is taken.
The following simple lemma should be clear from the above. It will be useful when proving that the logical formula in Sect. 4.2 describing the followers’ execution is correct.
Lemma 2
Let \({\mathfrak {R}}= \{ \langle {\mathfrak {c}}_n, \tau _n \rangle \}_{n \in {\mathbb {N}}}\) be a run for F. For all \(n \in {\mathbb {N}}\), if  (\(\in T^F_\text {in}\)), and
(\(\in T^F_\text {in}\)), and  , then
, then  .
.
3.4 Distributed machines and their execution
In the ensuing part, we employ the following notation: for any two sets  and \(T_2 = \{ \vec {\mu }_1, \ldots , \vec {\mu }_j \}\), we write \(T_1 \backsimeq T_2\) when the sets \(T_1\) and \(T_2\) are equal modulo removing the arrows, i.e. \(T_1 \backsimeq T_2\) when
and \(T_2 = \{ \vec {\mu }_1, \ldots , \vec {\mu }_j \}\), we write \(T_1 \backsimeq T_2\) when the sets \(T_1\) and \(T_2\) are equal modulo removing the arrows, i.e. \(T_1 \backsimeq T_2\) when  iff \(\vec {\mu }\in T_2\). (Likewise \(T_2 \backsimeq T_1\).)
iff \(\vec {\mu }\in T_2\). (Likewise \(T_2 \backsimeq T_1\).)
A distributed machine is a pair \(M = \langle L, F\rangle \), where L is a leader, F is a (replicated) follower, \(T^L_\text {in} \cap T^F_\text {in} = \emptyset \), \(T^L_\text {in} \backsimeq T^F_\text {out}\) and \(T^F_\text {in} \backsimeq T^L_\text {out}\). (The latter two constraints are to ensure that each message \(\vec {\mu }\) broadcast by the leader is a valid ingoing message  to the followers and for each message \(\vec {\mu }\) sent by a follower, the leader has a corresponding inbox. The one before the latter two is to avoid ambiguities in the logical translation presented in Sect. 4.) Let \(M = \langle L, F\rangle \) be a distributed machine and \(A = \{ a_1, \ldots , a_k \}\) (\(k > 0\)) be a set, referred to as the universe of M. Intuitively, each \(a \in A\) is identified with a (replicated) follower F. A run for M over A is a \((k+1)\)-tuple \({\mathfrak {R}}= \langle {\mathfrak {R}}^0, {\mathfrak {R}}^1, \ldots , {\mathfrak {R}}^k \rangle \), where \({\mathfrak {R}}^0 = \{ \langle {\mathfrak {c}}^0_n, \tau ^0_n \rangle \}_{n \in {\mathbb {N}}}\) (
to the followers and for each message \(\vec {\mu }\) sent by a follower, the leader has a corresponding inbox. The one before the latter two is to avoid ambiguities in the logical translation presented in Sect. 4.) Let \(M = \langle L, F\rangle \) be a distributed machine and \(A = \{ a_1, \ldots , a_k \}\) (\(k > 0\)) be a set, referred to as the universe of M. Intuitively, each \(a \in A\) is identified with a (replicated) follower F. A run for M over A is a \((k+1)\)-tuple \({\mathfrak {R}}= \langle {\mathfrak {R}}^0, {\mathfrak {R}}^1, \ldots , {\mathfrak {R}}^k \rangle \), where \({\mathfrak {R}}^0 = \{ \langle {\mathfrak {c}}^0_n, \tau ^0_n \rangle \}_{n \in {\mathbb {N}}}\) ( ,
,  ) is a run for L over A and each \({\mathfrak {R}}^i = \{ \langle {\mathfrak {c}}^i_n, \tau ^i_n \rangle \}_{n \in {\mathbb {N}}}\) (\(1 \le i \le k\)) (\({\mathfrak {c}}^i_n = \langle q^i_n, {\mathcal {I}}^i_n \rangle \)) is a run for F, such that the following conditions hold:
) is a run for L over A and each \({\mathfrak {R}}^i = \{ \langle {\mathfrak {c}}^i_n, \tau ^i_n \rangle \}_{n \in {\mathbb {N}}}\) (\(1 \le i \le k\)) (\({\mathfrak {c}}^i_n = \langle q^i_n, {\mathcal {I}}^i_n \rangle \)) is a run for F, such that the following conditions hold:
-
(A1)
If \(\tau ^0_n = \vec {\mu }\in T^L_\text {out}\) (\(n \in {\mathbb {N}}\)), then, for each i (\(1 \le i \le k\)), there exists \(n' > n\) such that
 ; and, for each i (\(1 \le i \le k\)), if
; and, for each i (\(1 \le i \le k\)), if 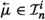 (\(n \in {\mathbb {N}}\)), there exists \(n' < n\) such that \(\tau ^0_{n'} = \vec {\mu }\).
(\(n \in {\mathbb {N}}\)), there exists \(n' < n\) such that \(\tau ^0_{n'} = \vec {\mu }\). -
(A2)
For each i (\(1 \le i \le k\)), if \(\tau ^i_n = \vec {\mu }\in T^F_\text {out}\), there exists \(n' > n\) such that
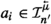 ; and, if
; and, if  (\(1 \le i \le k\), \(n \in {\mathbb {N}}\)), there exists \(n' < n\) such that \(\tau ^i_{n'} = \vec {\mu }\).
(\(1 \le i \le k\), \(n \in {\mathbb {N}}\)), there exists \(n' < n\) such that \(\tau ^i_{n'} = \vec {\mu }\).
Intuitively, (A1) states that if the leader broadcasts a message \(\vec {\mu }\), a message  will eventually appear in each follower’s inbox; and if a message
will eventually appear in each follower’s inbox; and if a message  is in a follower’s inbox, a message \(\vec {\mu }\) has been broadcast by the leader at some point in the past. Similarly, (A2) states that if a follower \(a \in A\) sends a message \(\vec {\mu }\) to the leader, a will eventually appear in the inbox
is in a follower’s inbox, a message \(\vec {\mu }\) has been broadcast by the leader at some point in the past. Similarly, (A2) states that if a follower \(a \in A\) sends a message \(\vec {\mu }\) to the leader, a will eventually appear in the inbox  ; and if
; and if  , a message \(\vec {\mu }\) has been sent by a to the leader at some point in the past.
, a message \(\vec {\mu }\) has been sent by a to the leader at some point in the past.
Conditions (A1) and (A2) describe an asynchronous network (i.e. a network in which message delivery takes an arbitrary amount of time). For a synchronous network (assuming message delivery takes one time step), conditions (A1) and (A2) above should be replaced with the following two conditions:
-
(S1)
If \(\tau ^0_n = \vec {\mu }\in T^L_\text {out}\) (\(n \in {\mathbb {N}}\)), then, for each i (\(1 \le i \le k\)),
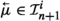 ; and, for each i (\(1 \le i \le k\)), if
; and, for each i (\(1 \le i \le k\)), if  and
and  , then \(\tau ^0_n = \vec {\mu }\) (\(n \in {\mathbb {N}}\)).
, then \(\tau ^0_n = \vec {\mu }\) (\(n \in {\mathbb {N}}\)). -
(S2)
For each i (\(1 \le i \le k\)), if \(\tau ^i_n = \vec {\mu }\in T^F_\text {out}\), then
 ; and, if
; and, if 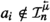 and
and  (\(1 \le i \le k\)), then \(\tau ^i_n = \vec {\mu }\) (\(n \in {\mathbb {N}}\)).
(\(1 \le i \le k\)), then \(\tau ^i_n = \vec {\mu }\) (\(n \in {\mathbb {N}}\)).
To distinguish a distributed machine whose runs satisfy conditions (A1) and (A2) above from a distributed machine whose runs satisfy conditions (S1) and (S2) above, we shall refer to the former type of machine as an asynchronous distributed machine and to the latter type as a synchronous distributed machine. We say that a distributed machine \(M = \langle L, F \rangle \) (asynchronous or synchronous) is runnable if there is a run for M over some universe \(A = \{ a_1, \ldots , a_k \}\) (\(k > 0\)).
Remark 1
The behaviour of a synchronous distributed machine when the delivery of a message from a follower to the leader coincides with the leader deleting the content of the corresponding inbox or when the delivery of a message from the leader to a follower coincides with the follower reacting to it and thus deleting it (the message could already be present in the follower’s inbox due to an earlier delivery) is undefined. It should be clear that the set of all runs of a synchronous distributed machine captures all well-defined (i.e. not undefined) behaviour. In case of undefined behaviour the reader can imagine, for example, the network “dying” and the distributed machine terminating abruptly, or it being left in an inconsistent state, for example, not deleting or not delivering a message when it should.
4 Translation to logic
Given an asynchronous distributed machine M, we can (automatically) construct an MFOTL-sentence \(\textsf {Spec}(M)\) (with \(\Vert \textsf {Spec}(M)\Vert \) quadratic in \(\Vert M\Vert \)) such that M is runnable if and only if \(\textsf {Spec}(M)\) is satisfiable. (As we see in Sect. 4.5, for any synchronous distributed machine N, we can construct a similar to \(\textsf {Spec}(M)\) sentence  such that N is runnable if and only if
such that N is runnable if and only if  is satisfiable.) To this end, let \(M = \langle L, F\rangle \) be an asynchronous distributed machine. \(\textsf {Spec}(M)\) is defined over the signature \(\Sigma ^M\) comprising a nullary predicate \({{\textsf{s}}}{{\textsf{l}}}_{q}\) for each state \(q \in Q^L\); a unary predicate \({{\textsf{s}}}{{\textsf{f}}}_{q}(\cdot )\) for each state \(q \in Q^F\); the symbols in \(T^L_\text {in}\) and \(T^F_\text {in}\) as unary predicates; for each symbol \(\vec {\mu }\in T^L_\text {out}\), a nullary predicate \(\textsf {past}_{\vec {\mu }}\); for each symbol \(\vec {\mu }\in T^F_\text {out}\), a unary predicate \(\textsf {past}_{\vec {\mu }}(\cdot )\); a nullary predicate \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) for each \(\tau \in T^L\); and a unary predicate \({{\textsf{t}}}{{\textsf{f}}}_{\tau }(\cdot )\) for each \(\tau \in T^F\). For each \(q \in Q^L\), \({{\textsf{s}}}{{\textsf{l}}}_{q}\) (short for state leader) is to be viewed as stating that the leader is at state q. For each \(q \in Q^F\), \({{\textsf{s}}}{{\textsf{f}}}_{q}(a)\) (short for state follower) is to be viewed as stating that follower a is at state q. For each
is satisfiable.) To this end, let \(M = \langle L, F\rangle \) be an asynchronous distributed machine. \(\textsf {Spec}(M)\) is defined over the signature \(\Sigma ^M\) comprising a nullary predicate \({{\textsf{s}}}{{\textsf{l}}}_{q}\) for each state \(q \in Q^L\); a unary predicate \({{\textsf{s}}}{{\textsf{f}}}_{q}(\cdot )\) for each state \(q \in Q^F\); the symbols in \(T^L_\text {in}\) and \(T^F_\text {in}\) as unary predicates; for each symbol \(\vec {\mu }\in T^L_\text {out}\), a nullary predicate \(\textsf {past}_{\vec {\mu }}\); for each symbol \(\vec {\mu }\in T^F_\text {out}\), a unary predicate \(\textsf {past}_{\vec {\mu }}(\cdot )\); a nullary predicate \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) for each \(\tau \in T^L\); and a unary predicate \({{\textsf{t}}}{{\textsf{f}}}_{\tau }(\cdot )\) for each \(\tau \in T^F\). For each \(q \in Q^L\), \({{\textsf{s}}}{{\textsf{l}}}_{q}\) (short for state leader) is to be viewed as stating that the leader is at state q. For each \(q \in Q^F\), \({{\textsf{s}}}{{\textsf{f}}}_{q}(a)\) (short for state follower) is to be viewed as stating that follower a is at state q. For each  ,
,  is to be viewed as stating that there is a message
is to be viewed as stating that there is a message  to the leader originating from follower a (i.e.
to the leader originating from follower a (i.e.  ). For each
). For each  ,
,  is to be viewed as stating that there is a message
is to be viewed as stating that there is a message  to follower a originating from the leader (i.e.
to follower a originating from the leader (i.e.  is in a’s inbox). For each \(\vec {\mu }\in T^L_\text {out}\), \(\textsf {past}_{\vec {\mu }}\) is to be viewed as stating that the leader has in the past broadcast a message \(\vec {\mu }\). For each \(\vec {\mu }\in T^F_\text {out}\), \(\textsf {past}_{\vec {\mu }}(a)\) is to be viewed as stating that follower a has in the past sent a message \(\vec {\mu }\) to the leader. For each \(\tau \in T^L\), \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) (short for transition leader) is to be viewed as stating that the leader takes transition \(\tau \). For each \(\tau \in T^F\), \({{\textsf{t}}}{{\textsf{f}}}_{\tau }(a)\) (short for transition follower) is to be viewed as stating that follower a takes transition \(\tau \).
is in a’s inbox). For each \(\vec {\mu }\in T^L_\text {out}\), \(\textsf {past}_{\vec {\mu }}\) is to be viewed as stating that the leader has in the past broadcast a message \(\vec {\mu }\). For each \(\vec {\mu }\in T^F_\text {out}\), \(\textsf {past}_{\vec {\mu }}(a)\) is to be viewed as stating that follower a has in the past sent a message \(\vec {\mu }\) to the leader. For each \(\tau \in T^L\), \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) (short for transition leader) is to be viewed as stating that the leader takes transition \(\tau \). For each \(\tau \in T^F\), \({{\textsf{t}}}{{\textsf{f}}}_{\tau }(a)\) (short for transition follower) is to be viewed as stating that follower a takes transition \(\tau \).
We now proceed to write the constituent parts of \(\textsf {Spec}(M)\).
4.1 The leader’s execution
We first write a collection of formulas describing the execution of the leader.
The following two formulas (short for unique state leader and unique transition leader respectively) state that the leader’s states and transitions are unique:
The next formula (short for initial leader) describes the initial conditions for the leader’s execution, i.e. that the leader starts at an initial state with all its inboxes empty:

The next formula (short for persistence leader) is the persistence condition for the leader’s inboxes: inboxes do not lose their content (although they can grow due to the arrival of new messages), except when a transition  ,
,  ,
,  , or
, or  (
( ) (which deletes the content of its corresponding inbox) is taken. In the following definition we slighty abuse the notation \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) (\(\tau \in T^L\)) for brevity: we write \({{\textsf{t}}}{{\textsf{l}}}_{\tau _1, \ldots , \tau _j}\) (\(\tau _1, \ldots , \tau _j \in T^L\)) as a shorthand for \({{\textsf{t}}}{{\textsf{l}}}_{\tau _1} \vee \cdots \vee {{\textsf{t}}}{{\textsf{l}}}_{\tau _j}\). Let
) (which deletes the content of its corresponding inbox) is taken. In the following definition we slighty abuse the notation \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) (\(\tau \in T^L\)) for brevity: we write \({{\textsf{t}}}{{\textsf{l}}}_{\tau _1, \ldots , \tau _j}\) (\(\tau _1, \ldots , \tau _j \in T^L\)) as a shorthand for \({{\textsf{t}}}{{\textsf{l}}}_{\tau _1} \vee \cdots \vee {{\textsf{t}}}{{\textsf{l}}}_{\tau _j}\). Let

The next family of formulas (short for enabled leader) describe the necessary conditions for a transition to be enabled. They are part of the formulas that describe the step-by-step execution of the leader. For each \(\tau \in T^L \setminus \{ \textit{idle} \}\), let

The next formula (short for step leader) describes the step-by-step execution of the leader: at each moment of time the leader takes an enabled transition or becomes idle if none exists. Let stepl be the logical disjunction of the following two formulas:

Finally, the formula
describes the leader’s whole operation. It is clear that \(\Vert \textsf {leader}\Vert = {\mathcal {O}}(\Vert L\Vert ^2)\).
4.2 The followers’ execution
Next, we write a collection of formulas describing the execution of each follower.
The following formulas (short for unique state follower and unique transition follower respectively) state that the states and transitions of follower x are unique:
The next formula (short for initial follower) describes the initial conditions for the execution of follower x, i.e. that follower x starts at an initial state with its inbox empty:

The next formula (short for persistence follower) is the persistence condition for the inbox of follower x: the inbox does not lose any messages (although it can grow due to the arrival of new ones), except when a transition \(\tau \in T^F_\text {in}\) (which deletes the corresponding message) is taken. Let

The next family of formulas (short for enabled follower) describe the necessary conditions for a transition to be enabled. They are part of the formulas that describe the step-by-step execution of a follower x. For each \(\tau \in T^F\), let

The next formula (short for step follower) describes the step-by-step execution of follower x: at each moment of time follower x takes a feasible transition or becomes idle if none exists. Let \(\textsf {stepf}(x)\) be the logical disjunction of the following two formulas:

Finally, the formula
describes the leader’s whole operation. It is clear that \(\Vert \textsf {follower}(x)\Vert = {\mathcal {O}}(\Vert F\Vert ^2)\).
4.3 The distributed machine’s execution
Next, we write a collection of formulas describing the network of the leader and its followers, and, combining these formulas with the ones in the previous two subsections, we form \(\textsf {Spec}(M)\).
The following two formulas enforce the intended semantics for the predicates \(\textsf {past}_{\vec {\mu }}\) (\(\vec {\mu }\in T^L_\text {in}\)) and \(\textsf {past}_{\vec {\mu }}(\cdot )\) (\(\vec {\mu }\in T^F_\text {in}\)). Recall from the beginning of this section that \(\textsf {past}_{\vec {\mu }}\) (\(\vec {\mu }\in T^L_\text {in}\)) is to be read as “a message \(\vec {\mu }\) has in the past been broadcast by the leader” and \(\textsf {past}_{\vec {\mu }}(x)\) (\(\vec {\mu }\in T^F_\text {in}\)) as “follower x has in the past sent a message \(\vec {\mu }\) to the leader”. Thus, \(\textsf {past}_{\vec {\mu }}\) must be false until (and when) the leader takes transition \({{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) (if it ever does) and true thereafter; and likewise for \(\textsf {past}_{\vec {\mu }}(x)\) and \({{\textsf{t}}}{{\textsf{f}}}_{\vec {\mu }}(x)\). Let \(\textsf {pastm}\) (short for past messages) be the logical conjunction of the following two formulas:

The following two formulas specify the conditions for message delivery when the leader broadcasts a message to the followers (bcastla, short for broadcast leader asynchronous) and when a follower sends a message to the leader (sendfa, short for send follower asynchronous). (Recall that the network is asynchronous.) They correspond to conditions (A1) and (A2) respectively from Sect. 3.4.

Notice that, since \(T^L_\text {out} \backsimeq T^F_\text {in}\) (resp. \(T^F_\text {out} \backsimeq T^L_\text {in}\)), the symbol  (resp.
(resp.  ), and, thus, the predicate
), and, thus, the predicate  appearing in the first conjunct of bcastla (resp. sendfa) exists. Likewise, the nullary predicate \(\textsf {past}_{\vec {\mu }}\) (resp. unary predicate \(\textsf {past}_{\vec {\mu }}(\cdot )\)) appearing in the second conjunct of bcastla (resp. sendfa) exists.
appearing in the first conjunct of bcastla (resp. sendfa) exists. Likewise, the nullary predicate \(\textsf {past}_{\vec {\mu }}\) (resp. unary predicate \(\textsf {past}_{\vec {\mu }}(\cdot )\)) appearing in the second conjunct of bcastla (resp. sendfa) exists.
Finally, the following formula \(\textsf {neta}\) (short for network asynchronous) describes the operation of the asynchronous network comprising the leader and its followers:
It is clear that \(\Vert \textsf {neta}\Vert = {\mathcal {O}}(\Vert L\Vert + \Vert F\Vert )\).
We are now ready to give a full logical description of M. Let
With regard to size, it follows that \(\Vert \textsf {Spec}(M)\Vert = {\mathcal {O}}(\Vert M\Vert ^2)\).
Remark 2
The assumption that each message can be delivered multiple times is natural (as it applies to many common protocols), but also favourable because it simplifies the network encoding. Indeed, to enforce the condition that if a message \(\vec {\mu }\) is sent then a message  is received (by the intended recipient(s)) at some point in the future (possibly at different times by different recipients), we simply state that if \({{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) or \({{\textsf{t}}}{{\textsf{f}}}_{\vec {\mu }}(x)\) (for any follower x) holds true at any moment then
is received (by the intended recipient(s)) at some point in the future (possibly at different times by different recipients), we simply state that if \({{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) or \({{\textsf{t}}}{{\textsf{f}}}_{\vec {\mu }}(x)\) (for any follower x) holds true at any moment then  holds true next. That
holds true next. That  can be received multiple times is simply a consequence of the semantics of the operator \(\Diamond \). In some cases this behaviour may be unwanted. (For example, consider a scenario, such as an asynchronous version of the Control-MAC protocol in Sect. 5.3, in which a follower awaits a \(\overleftarrow{go}\) or a \(\overleftarrow{nogo}\) message to enter or not enter respectively a critical section, and, at a given round of the protocol, it receives both a \(\overleftarrow{go}\) and a \(\overleftarrow{nogo}\) message, the first being the intended message and the second being a re-delivery from a previous round, leaving the follower in an inconsistent state.) At the time of writing, the authors know of no way of enforcing delivery of messages exactly once within the current approach. One possibility could be to parameterize each message delivery to a recipient x with an identifier y. Then, one could state that a delivery with identifier y to any recipient x is followed by no delivery with identifier y. (In the absence of identifiers for deliveries, a similar condition would block future deliveries of a message, even if the message were re-sent. In contrast, in the presence of identifiers, a re-sent message could still be delivered using a new identifier.) Unfortunately, this approach results in formulas that are not monodic.
can be received multiple times is simply a consequence of the semantics of the operator \(\Diamond \). In some cases this behaviour may be unwanted. (For example, consider a scenario, such as an asynchronous version of the Control-MAC protocol in Sect. 5.3, in which a follower awaits a \(\overleftarrow{go}\) or a \(\overleftarrow{nogo}\) message to enter or not enter respectively a critical section, and, at a given round of the protocol, it receives both a \(\overleftarrow{go}\) and a \(\overleftarrow{nogo}\) message, the first being the intended message and the second being a re-delivery from a previous round, leaving the follower in an inconsistent state.) At the time of writing, the authors know of no way of enforcing delivery of messages exactly once within the current approach. One possibility could be to parameterize each message delivery to a recipient x with an identifier y. Then, one could state that a delivery with identifier y to any recipient x is followed by no delivery with identifier y. (In the absence of identifiers for deliveries, a similar condition would block future deliveries of a message, even if the message were re-sent. In contrast, in the presence of identifiers, a re-sent message could still be delivered using a new identifier.) Unfortunately, this approach results in formulas that are not monodic.
4.4 Correspondence between runs and models
We now show that an asynchronous distributed machine M is runnable if and only if \(\textsf {Spec}(M)\) is satisfiable.
Lemma 3
Let \(M = \langle L, F \rangle \) be an asynchronous distributed machine and \(\textsf {Spec}(M)\) as above. If M is runnable, then \(\textsf {Spec}(M)\) is satisfiable over a finite domain.
Proof
Let \(A = \{a_1, \ldots , a_k \}\) (\(k > 0\)) and let \({\mathfrak {R}}= \langle {\mathfrak {R}}^0, {\mathfrak {R}}^1, \ldots , {\mathfrak {R}}^k \rangle \) be a run for M over A. Thus, \({\mathfrak {R}}^0 = \{ \langle {\mathfrak {c}}^0_n, \tau ^0_n \rangle \}_{n \in {\mathbb {N}}}\) is a run for L over A and each \({\mathfrak {R}}^i = \{ \langle {\mathfrak {c}}^i_n, \tau ^i_n \rangle \}_{n \in {\mathbb {N}}}\) (\(1 \le i \le k\)) is a run for F. Recall that for each \(n \in {\mathbb {N}}\), assuming that  ,
,  , where
, where  (\(1 \le j \le r\)); and \({\mathfrak {c}}^i_n = \langle q^i_n, {\mathcal {I}}^i_n \rangle \) (\(1 \le i \le k\)), where \({\mathcal {I}}^i_n \subseteq T^F_\text {in}\) (\(1 \le i \le k\)). Let \(\Sigma ^M\) be as in the beginning of this section. We construct from \({\mathfrak {R}}\) a sequence \({\mathfrak {M}}= \{ {\mathfrak {A}}_n \}_{n \in {\mathbb {N}}}\), where each \({\mathfrak {A}}_n\) (\(n \in {\mathbb {N}}\)) is a \(\Sigma ^M\)-structure with universe A, such that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\). For each \(n \in {\mathbb {N}}\), let \({\mathfrak {A}}_n\) be such that:
(\(1 \le j \le r\)); and \({\mathfrak {c}}^i_n = \langle q^i_n, {\mathcal {I}}^i_n \rangle \) (\(1 \le i \le k\)), where \({\mathcal {I}}^i_n \subseteq T^F_\text {in}\) (\(1 \le i \le k\)). Let \(\Sigma ^M\) be as in the beginning of this section. We construct from \({\mathfrak {R}}\) a sequence \({\mathfrak {M}}= \{ {\mathfrak {A}}_n \}_{n \in {\mathbb {N}}}\), where each \({\mathfrak {A}}_n\) (\(n \in {\mathbb {N}}\)) is a \(\Sigma ^M\)-structure with universe A, such that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\). For each \(n \in {\mathbb {N}}\), let \({\mathfrak {A}}_n\) be such that:
-
(a)
for each \(q \in Q^L\), \({{\textsf{s}}}{{\textsf{l}}}_{q}^{{\mathfrak {A}}_n} = \top \) if \(q = q^0_n\), otherwise \({{\textsf{s}}}{{\textsf{l}}}_{q}^{{\mathfrak {A}}_n} = \bot \);
-
(b)
for each
 ,
,  ;
; -
(c)
for each \(\vec {\mu }\in T^L_\text {out}\), \(\textsf {past}_{\vec {\mu }}^{\,{\mathfrak {A}}_n} = \top \) if \(\tau ^0_{n'} = \vec {\mu }\) for some \(n' < n\), otherwise \(\textsf {past}_{\vec {\mu }}^{\,{\mathfrak {A}}_n} = \bot \);
-
(d)
for each \(\tau \in T^L\), \({{\textsf{t}}}{{\textsf{l}}}_{\tau }^{{\mathfrak {A}}_n} = \top \) if \(\tau ^0_n = \tau \), otherwise \({{\textsf{t}}}{{\textsf{l}}}_{\tau }^{{\mathfrak {A}}_n} = \bot \);
-
(e)
for each \(q \in Q^F\), \({{\textsf{s}}}{{\textsf{f}}}_{q}^{{\mathfrak {A}}_n} = \{ a_i \in A \mid q^i_n = q \}\);
-
(f)
for each
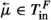 ,
, 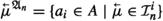 ;
; -
(g)
for each \(\vec {\mu }\in T^F_\text {in}\), \(\textsf {past}_{\vec {\mu }}^{\,{\mathfrak {A}}_n} = \{a_i \in A \mid \exists \; n' < n \text {~s.t.~} \tau ^i_{n'} = \vec {\mu }\}\);
-
(h)
for each \(\tau \in T^F\), \({{\textsf{t}}}{{\textsf{f}}}_{\tau }^{{\mathfrak {A}}_n} = \{ a_i \in A \mid \tau ^i_n = \tau \}\).
We now show that \(\textsf {leader}\), \(\forall x \, \textsf {follower}(x)\), and \(\textsf {neta}\) are all true in \({\mathfrak {M}}\). It then follows that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\).
Starting with the leader, it is easily obtained from the definition of a run for L together with (a), (b), and (d) that \({\mathfrak {A}}_0 \models \textsf {initl}\) and, for all \(n \in {\mathbb {N}}\), \({\mathfrak {A}}_n \models \textsf {ustatel}\) and \({\mathfrak {A}}_n \models \textsf {utransl}\). To show that, for all \(n \in {\mathbb {N}}\), \({\mathfrak {A}}_n \models \textsf {persl}\), let  . If
. If  , i.e.
, i.e.  ,
,  ,
,  , or
, or  , then, from (d),
, then, from (d),  ,
,  ,
,  , or
, or  , which implies that
, which implies that  (from the definition of a run for L), which, in turn, implies due to (b) that
(from the definition of a run for L), which, in turn, implies due to (b) that  ; and if
; and if  , i.e.
, i.e.  ,
,  ,
,  , and
, and  , then, from (d),
, then, from (d),  ,
,  ,
,  ,
,  , which by Lemma 1 implies that, for all \(a \in A\), if
, which by Lemma 1 implies that, for all \(a \in A\), if  then
then  , which, in turn, implies due to (b) that
, which, in turn, implies due to (b) that  ); consequently
); consequently  . That \({\mathfrak {A}}_n \models \textsf {persl}\) is then evident. To show that, for all \(n \in {\mathbb {N}}\), \({\mathfrak {A}}_n \models \textsf {stepl}\), we consider two cases. If \( enb ( {\mathfrak {c}}^0_n ) \ne \emptyset \), we have \(\tau ^0_n \in enb ( {\mathfrak {c}}^0_n )\). Thus, from (a) and (d), \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{l}}}_{q^0_n}\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\tau ^0_n}\), and
. That \({\mathfrak {A}}_n \models \textsf {persl}\) is then evident. To show that, for all \(n \in {\mathbb {N}}\), \({\mathfrak {A}}_n \models \textsf {stepl}\), we consider two cases. If \( enb ( {\mathfrak {c}}^0_n ) \ne \emptyset \), we have \(\tau ^0_n \in enb ( {\mathfrak {c}}^0_n )\). Thus, from (a) and (d), \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{l}}}_{q^0_n}\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\tau ^0_n}\), and  . Further, it is straightforward to establish from the definition of \(\textsf{enbl}_{ \tau ^0_n }\) and (b) that \({\mathfrak {A}}_n \models \textsf{enbl}_{ \tau ^0_n }\). Consequently,
. Further, it is straightforward to establish from the definition of \(\textsf{enbl}_{ \tau ^0_n }\) and (b) that \({\mathfrak {A}}_n \models \textsf{enbl}_{ \tau ^0_n }\). Consequently,  and \({\mathfrak {A}}_n\) satisfies the first disjunct of \(\textsf {stepl}\). If \( enb ( {\mathfrak {c}}^0_n ) = \emptyset \), we have \(\tau ^0_n = \textit{idle}\) and \(q^0_n = \sigma ({\mathfrak {c}}^0_n) = \sigma ({\mathfrak {c}}^0_{n+1}) = q^0_{n+1}\). Thus, from (a) and (d), \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{l}}}_{q^0_n}\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\textit{idle}}\), and
and \({\mathfrak {A}}_n\) satisfies the first disjunct of \(\textsf {stepl}\). If \( enb ( {\mathfrak {c}}^0_n ) = \emptyset \), we have \(\tau ^0_n = \textit{idle}\) and \(q^0_n = \sigma ({\mathfrak {c}}^0_n) = \sigma ({\mathfrak {c}}^0_{n+1}) = q^0_{n+1}\). Thus, from (a) and (d), \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{l}}}_{q^0_n}\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\textit{idle}}\), and  . Further, it is straightforward to establish from the definition of \(\textsf{enbl}_{ \tau }\) (\(\tau \in T^L \setminus \{ \textit{idle}\}\)) and (b) that \({\mathfrak {A}}_n \models \bigwedge _{\langle q^0_n, \tau , q' \rangle \in \delta ^L} \lnot \textsf{enbl}_{ \tau }\). (The latter still holds when the conjunction is empty, in which case it evaluates to \(\top \) by convention.) Consequently,
. Further, it is straightforward to establish from the definition of \(\textsf{enbl}_{ \tau }\) (\(\tau \in T^L \setminus \{ \textit{idle}\}\)) and (b) that \({\mathfrak {A}}_n \models \bigwedge _{\langle q^0_n, \tau , q' \rangle \in \delta ^L} \lnot \textsf{enbl}_{ \tau }\). (The latter still holds when the conjunction is empty, in which case it evaluates to \(\top \) by convention.) Consequently,  and \({\mathfrak {A}}_n\) satisfies the second disjunct of \(\textsf {stepl}\). In any case, \({\mathfrak {A}}_n \models \textsf {stepl}\). As a result of the above, \(\textsf {leader}\) is true in \({\mathfrak {M}}\).
and \({\mathfrak {A}}_n\) satisfies the second disjunct of \(\textsf {stepl}\). In any case, \({\mathfrak {A}}_n \models \textsf {stepl}\). As a result of the above, \(\textsf {leader}\) is true in \({\mathfrak {M}}\).
Moving to the followers, it is easily obtained from the definition of a run for F together with (e), (f), and (h) that, for all \(a_i \in A\), \({\mathfrak {A}}_0 \models \textsf {initf}(a_i)\) and, for all \(n \in {\mathbb {N}}\), for all \(a_i \in A\), \({\mathfrak {A}}_n \models \textsf {ustatef}(a_i)\) and \({\mathfrak {A}}_n \models \textsf {utransf}(a_i)\). To show that, for all \(n \in {\mathbb {N}}\), for all \(a_i \in A\), \({\mathfrak {A}}_n \models \textsf {persf}(a_i)\), let  . If \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\tau }(a_i)\), then, from (h), \(\tau ^i_n = \tau \), which implies that
. If \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\tau }(a_i)\), then, from (h), \(\tau ^i_n = \tau \), which implies that  (from the definition of a run for F), which, in turn, implies due to (f) that
(from the definition of a run for F), which, in turn, implies due to (f) that  ; and if \({\mathfrak {A}}_n \models \lnot {{\textsf{t}}}{{\textsf{f}}}_{\tau }(a_i)\), then, from (h),
; and if \({\mathfrak {A}}_n \models \lnot {{\textsf{t}}}{{\textsf{f}}}_{\tau }(a_i)\), then, from (h),  , which by Lemma 2 implies that if
, which by Lemma 2 implies that if  then
then  , which, in turn, implies due to (f) that
, which, in turn, implies due to (f) that  ; consiquently
; consiquently  . That \({\mathfrak {A}}_n \models \textsf {persf}(a_i)\) is then evident. To show that, for all \(n \in {\mathbb {N}}\), for all \(a_i \in A\), \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\), we consider two cases. If \( enb ( {\mathfrak {c}}^i_n ) \ne \emptyset \), we have \(\tau ^i_n \in enb ( {\mathfrak {c}}^i_n )\). Thus, from (e) and (h) above, \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{f}}}_{q^i_n}(a_i)\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\tau ^i_n}(a_i)\), and
. That \({\mathfrak {A}}_n \models \textsf {persf}(a_i)\) is then evident. To show that, for all \(n \in {\mathbb {N}}\), for all \(a_i \in A\), \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\), we consider two cases. If \( enb ( {\mathfrak {c}}^i_n ) \ne \emptyset \), we have \(\tau ^i_n \in enb ( {\mathfrak {c}}^i_n )\). Thus, from (e) and (h) above, \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{f}}}_{q^i_n}(a_i)\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\tau ^i_n}(a_i)\), and  . Further, it is straightforward to establish from the definition of \(\textsf{enbf}_{ \tau ^i_n }(a_i)\) and (f) that \({\mathfrak {A}}_n \models \textsf{enbf}_{ \tau ^i_n }(a_i)\). Consequently
. Further, it is straightforward to establish from the definition of \(\textsf{enbf}_{ \tau ^i_n }(a_i)\) and (f) that \({\mathfrak {A}}_n \models \textsf{enbf}_{ \tau ^i_n }(a_i)\). Consequently  and \({\mathfrak {A}}_n\) satisfies the first disjunct of \(\textsf {stepf}(a_i)\). If \( enb ( {\mathfrak {c}}^i_n ) = \emptyset \), we have \(\tau ^i_n = \textit{idle}\) and \(q^i_n = q^i_{n+1}\). Thus, from (e) and (h) above, \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{f}}}_{q^i_n}(a_i)\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\textit{idle}}(a_i)\), and
and \({\mathfrak {A}}_n\) satisfies the first disjunct of \(\textsf {stepf}(a_i)\). If \( enb ( {\mathfrak {c}}^i_n ) = \emptyset \), we have \(\tau ^i_n = \textit{idle}\) and \(q^i_n = q^i_{n+1}\). Thus, from (e) and (h) above, \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{f}}}_{q^i_n}(a_i)\), \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\textit{idle}}(a_i)\), and  . Further, it is straightforward to establish from the definition of \(\textsf{enbf}_{ \tau }(a_i)\) (\(\tau \in T^F \setminus \{ \textit{idle}\}\)) and (f) that \({\mathfrak {A}}_n \models \bigwedge _{\langle q^0_n, \tau , q' \rangle \in \delta ^F} \lnot \textsf{enbf}_{ \tau }(a_i)\). (The latter still holds when the conjunction is empty, in which case it evaluates to \(\top \) by convention.) Consequently,
. Further, it is straightforward to establish from the definition of \(\textsf{enbf}_{ \tau }(a_i)\) (\(\tau \in T^F \setminus \{ \textit{idle}\}\)) and (f) that \({\mathfrak {A}}_n \models \bigwedge _{\langle q^0_n, \tau , q' \rangle \in \delta ^F} \lnot \textsf{enbf}_{ \tau }(a_i)\). (The latter still holds when the conjunction is empty, in which case it evaluates to \(\top \) by convention.) Consequently,  and \({\mathfrak {A}}_n\) satisfies the second disjunct of \(\textsf {stepf}(a_i)\). In any case, \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\). As a result of the above, for all \(n \in {\mathbb {N}}\), for all \(a_i \in A\), \({\mathfrak {A}}_n \models \textsf {follower}(a_i)\), from which we obtain the truth of \(\forall x \, \textsf {follower}(x)\) in \({\mathfrak {M}}\).
and \({\mathfrak {A}}_n\) satisfies the second disjunct of \(\textsf {stepf}(a_i)\). In any case, \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\). As a result of the above, for all \(n \in {\mathbb {N}}\), for all \(a_i \in A\), \({\mathfrak {A}}_n \models \textsf {follower}(a_i)\), from which we obtain the truth of \(\forall x \, \textsf {follower}(x)\) in \({\mathfrak {M}}\).
Moving to \(\textsf {neta}\), we first show that \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). For the first conjunct of \(\textsf {pastm}\), let \(\vec {\mu }\in T^L_\text {out}\). If \(\tau ^0_n \ne \vec {\mu }\) for all \(n \in {\mathbb {N}}\), then, from (d), \({\mathfrak {A}}_n \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n \in {\mathbb {N}}\), and, from (c), \({\mathfrak {A}}_n \models \lnot \textsf {past}_{\vec {\mu }}\) for all \(n \in {\mathbb {N}}\). It follows that \({\mathfrak {A}}_0 \models \Box \lnot \textsf {past}_{\vec {\mu }}\), thus  , and, as a result,
, and, as a result,  . Further, for all \(n \in {\mathbb {N}}\),
. Further, for all \(n \in {\mathbb {N}}\),  and
and  trivially. Therefore, the first conjunct of \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). Otherwise, let t be the smallest number such that \({\mathfrak {A}}_t \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\). Thus, from (d), \({\mathfrak {A}}_{n} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n < t\). From (c), \({\mathfrak {A}}_{n'} \models \lnot \textsf {past}_{\vec {\mu }}\) for all \(n' \le t\), and \({\mathfrak {A}}_{n''} \models \textsf {past}_{\vec {\mu }}\) for all \(n'' > t\). Now, for all \(n \in {\mathbb {N}}\), we claim
trivially. Therefore, the first conjunct of \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). Otherwise, let t be the smallest number such that \({\mathfrak {A}}_t \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\). Thus, from (d), \({\mathfrak {A}}_{n} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n < t\). From (c), \({\mathfrak {A}}_{n'} \models \lnot \textsf {past}_{\vec {\mu }}\) for all \(n' \le t\), and \({\mathfrak {A}}_{n''} \models \textsf {past}_{\vec {\mu }}\) for all \(n'' > t\). Now, for all \(n \in {\mathbb {N}}\), we claim  . Indeed, the latter holds trivially for all n if \(t = 0\), and for all \(n \ne t - 1\) if \(t > 0\); further, if \(t > 0\), we have
. Indeed, the latter holds trivially for all n if \(t = 0\), and for all \(n \ne t - 1\) if \(t > 0\); further, if \(t > 0\), we have  and \({\mathfrak {A}}_t \models \lnot \textsf {past}_{\vec {\mu }}\), thus it holds for \(n = t-1\) as well. Finally, it is clear that
and \({\mathfrak {A}}_t \models \lnot \textsf {past}_{\vec {\mu }}\), thus it holds for \(n = t-1\) as well. Finally, it is clear that  for all \(n \in {\mathbb {N}}\). Therefore, the first conjunct of \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). The argument for the second conjunct is completely analogous. Thus, \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). It is straightforward to show that \(\Box \textsf {bcastla}\) and \(\Box \textsf {sendfa}\) are true in \({\mathfrak {M}}\). As a result, \(\textsf {neta}\) is true in \({\mathfrak {M}}\). \(\square \)
for all \(n \in {\mathbb {N}}\). Therefore, the first conjunct of \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). The argument for the second conjunct is completely analogous. Thus, \(\textsf {pastm}\) is true in \({\mathfrak {M}}\). It is straightforward to show that \(\Box \textsf {bcastla}\) and \(\Box \textsf {sendfa}\) are true in \({\mathfrak {M}}\). As a result, \(\textsf {neta}\) is true in \({\mathfrak {M}}\). \(\square \)
For the converse of Lemma 3, we require the following two auxiliary lemmas:
Lemma 4
Let \(M = \langle L, F \rangle \) be a distributed machine; let A be a finite, non-empty set; let \({\mathfrak {M}}= \{ {\mathfrak {A}}_n \}_{n \in {\mathbb {N}}}\), where each \({\mathfrak {A}}_n\) (\(n \in {\mathbb {N}}\)) is a \(\Sigma ^M\)-structure with universe A, be a model of \(\textsf {Spec}(M)\); and let \(\textsf {past}_{\vec {\mu }}\) be the nullary predicate in \(\Sigma ^M\) corresponding to the symbol \(\vec {\mu }\in T^L_\text {out}\). For all \(n \in {\mathbb {N}}\), (a) if \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\), there exists \(n' < n\) such that \({\mathfrak {A}}_{n'} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\); and (b) if \({\mathfrak {A}}_n \models \lnot \textsf {past}_{\vec {\mu }}\), then \({\mathfrak {A}}_{n'} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n' < n\).
Proof
For (a), let \(n \in {\mathbb {N}}\) such that \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\). Because \(\textsf {pastm}\) is true in \({\mathfrak {M}}\), it follows from its first conjunct that \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }}\),  , and, for all \(m \in {\mathbb {N}}\),
, and, for all \(m \in {\mathbb {N}}\),  and
and  . Because \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }}\), \(n > 0\). Because
. Because \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }}\), \(n > 0\). Because  , \({\mathfrak {A}}_0 \models \Box \lnot \textsf {past}_{\vec {\mu }}\) or
, \({\mathfrak {A}}_0 \models \Box \lnot \textsf {past}_{\vec {\mu }}\) or  . Since \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\), we have \({\mathfrak {A}}_0 \not \models \Box \lnot \textsf {past}_{\vec {\mu }}\), therefore
. Since \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\), we have \({\mathfrak {A}}_0 \not \models \Box \lnot \textsf {past}_{\vec {\mu }}\), therefore  . Thus, let \(n'\) be the smallest number such that \({\mathfrak {A}}_{n'} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\). \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\) implies, then, that \(n' \le n\). It also follows that
. Thus, let \(n'\) be the smallest number such that \({\mathfrak {A}}_{n'} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\). \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\) implies, then, that \(n' \le n\). It also follows that  . Since
. Since  for all \(m \in {\mathbb {N}}\), we must have \({\mathfrak {A}}_{n'} \models \lnot \textsf {past}_{\vec {\mu }}\), thus \(n' < n\).
for all \(m \in {\mathbb {N}}\), we must have \({\mathfrak {A}}_{n'} \models \lnot \textsf {past}_{\vec {\mu }}\), thus \(n' < n\).
For (b), let \(n \in {\mathbb {N}}\) such that  . As in the previous case, it follows from the first conjunct of \(\textsf {pastm}\) that \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }}\),
. As in the previous case, it follows from the first conjunct of \(\textsf {pastm}\) that \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }}\),  , and, for all \(m \in {\mathbb {N}}\),
, and, for all \(m \in {\mathbb {N}}\),  and
and  . If \(n = 0\), we are done. Otherwise, suppose \(n > 0\). From \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }} \mathbin {{\mathcal {W}}}{{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\), we have that either \({\mathfrak {A}}_0 \models \Box \lnot \textsf {past}_{\vec {\mu }}\) or
. If \(n = 0\), we are done. Otherwise, suppose \(n > 0\). From \({\mathfrak {A}}_0 \models \lnot \textsf {past}_{\vec {\mu }} \mathbin {{\mathcal {W}}}{{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\), we have that either \({\mathfrak {A}}_0 \models \Box \lnot \textsf {past}_{\vec {\mu }}\) or  . In the former case, since
. In the former case, since  for all \(m \in {\mathbb {N}}\), it follows that \({\mathfrak {A}}_0 \models \Box \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\), and, as a result, \({\mathfrak {A}}_{n'} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n' < n\). In the latter case, let \(n''\) be the smallest number such that \({\mathfrak {A}}_{n''} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\). Since
for all \(m \in {\mathbb {N}}\), it follows that \({\mathfrak {A}}_0 \models \Box \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\), and, as a result, \({\mathfrak {A}}_{n'} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n' < n\). In the latter case, let \(n''\) be the smallest number such that \({\mathfrak {A}}_{n''} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\). Since  for all \(m \in {\mathbb {N}}\), \(n \le n''\). It follows that \({\mathfrak {A}}_{n'} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n' < n\). \(\square \)
for all \(m \in {\mathbb {N}}\), \(n \le n''\). It follows that \({\mathfrak {A}}_{n'} \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) for all \(n' < n\). \(\square \)
Lemma 5
Let \(M = \langle L, F \rangle \) be a distributed machine; let A be a finite, non-empty set; let \({\mathfrak {M}}= \{ {\mathfrak {A}}_n \}_{n \in {\mathbb {N}}}\), where each \({\mathfrak {A}}_n\) (\(n \in {\mathbb {N}}\)) is a \(\Sigma ^M\)-structure with universe A, be a model of \(\textsf {Spec}(M)\); and let \(\textsf {past}_{\vec {\mu }}(\cdot )\) be the unary predicate in \(\Sigma ^M\) corresponding to the symbol \(\vec {\mu }\in T^F_\text {out}\). Let \(a \in A\). For all \(n \in {\mathbb {N}}\), (a) if \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}(a)\), there exists \(n' < n\) such that \({\mathfrak {A}}_{n'} \models {{\textsf{t}}}{{\textsf{f}}}_{\vec {\mu }}(a)\); and (b) if \({\mathfrak {A}}_n \models \lnot \textsf {past}_{\vec {\mu }}(a)\), then \({\mathfrak {A}}_n \models \lnot {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}(a)\) for all \(n' < n\).
Proof
Completely analogous to the proof of Lemma 4, using the second conjunct of \(\textsf {pastm}\) instead of the first. \(\square \)
We now proceed to the converse of Lemma 3.
Lemma 6
Let \(M = \langle L, F \rangle \) be an asynchronous distributed machine and \(\textsf {Spec}(M)\) as above. If \(\textsf {Spec}(M)\) is satisfiable over a finite domain, then M is runnable.
Proof
Let \(A = \{ a_1, \dots , a_k \}\) (\(k > 0\)) and let \({\mathfrak {M}}= \{ {\mathfrak {A}}_n \}_{n \in {\mathbb {N}}}\) be a sequence, where each \({\mathfrak {A}}_n\) (\(n \in {\mathbb {N}}\)) is a \(\Sigma ^M\)-structure (\(\Sigma ^M\) as in the beginning of this section) with universe A, such that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\). We construct from \({\mathfrak {M}}\) a run \({\mathfrak {R}}= \langle {\mathfrak {R}}^0, {\mathfrak {R}}^1, \ldots , {\mathfrak {R}}^k \rangle \) for M over A. That is, we construct \({\mathfrak {R}}\) such that \({\mathfrak {R}}^0 = \{ \langle {\mathfrak {c}}^0_n, \tau ^0_n \rangle \}_{n \in {\mathbb {N}}}\) is a run for L over A and each \({\mathfrak {R}}^i = \{ \langle {\mathfrak {c}}^i_n, \tau ^i_n \rangle \}_{n \in {\mathbb {N}}}\) (\(1 \le i \le k\)) is a run for F over A. In the ensuing part, we assume that  . For each \(n \in {\mathbb {N}}\):
. For each \(n \in {\mathbb {N}}\):
-
(a)
set
 , such that
, such that  and
and  (\(1 \le i \le r\));
(\(1 \le i \le r\)); -
(b)
set \(\tau ^0_n = \tau \in T^L\) such that \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\tau }\);
-
(c)
for each i (\(1 \le i \le k\)), set \({\mathfrak {c}}^i_n = \langle q^i_n, {\mathcal {I}}^i_n \rangle \), such that \({\mathfrak {A}}_n \models {{\textsf{s}}}{{\textsf{f}}}_{q^i_n}(a_i)\) and
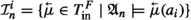 ;
; -
(d)
for each i (\(1 \le i \le k\)), set \(\tau ^i_n = \tau \in T^F\) such that \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{f}}}_{\tau }(a_i)\).
It is a consequence of the assumption that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\) that for all \(n \in {\mathbb {N}}\), \({\mathfrak {A}}_n \models \textsf {ustatel}\) and \({\mathfrak {A}}_n \models \textsf {utransl}\); and, for all \(n \in {\mathbb {N}}\), for all i (\(1 \le i \le k\)), \({\mathfrak {A}}_n \models \textsf {ustatef}(a_i)\) and \({\mathfrak {A}}_n \models \textsf {utransf}(a_i)\). Thus \(q^0_n\) and \(\tau ^0_n\) above, as well as \(q^i_n\) and \(\tau ^i_n\) (\(1 \le i \le k\)), are well-defined.
We next show that \({\mathfrak {R}}^0\) is a run for L over A. Since \({\mathfrak {A}}_0 \models \textsf {initl}\) we have from (a) that \(q^0_n \in Q^L_\text {init}\) and  (for all \(1 \le i \le r\)). Now, it is a consequence of the assumption that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\) that \({\mathfrak {A}}_n \models \textsf{persl}_{ }\) and \({\mathfrak {A}}_n \models \textsf {stepl}\), for all \(n \in {\mathbb {N}}\). To show that \(\iota ({\mathfrak {c}}^0_n) \preceq ^{\tau ^0_n} \iota ({\mathfrak {c}}^0_{n+1})\), for all \(n \in {\mathbb {N}}\), we consider two possibilities: if
(for all \(1 \le i \le r\)). Now, it is a consequence of the assumption that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\) that \({\mathfrak {A}}_n \models \textsf{persl}_{ }\) and \({\mathfrak {A}}_n \models \textsf {stepl}\), for all \(n \in {\mathbb {N}}\). To show that \(\iota ({\mathfrak {c}}^0_n) \preceq ^{\tau ^0_n} \iota ({\mathfrak {c}}^0_{n+1})\), for all \(n \in {\mathbb {N}}\), we consider two possibilities: if  ,
,  ,
,  ,
,  for all
for all  , which, due to (b), implies that
, which, due to (b), implies that  for all
for all  , then, because \({\mathfrak {A}}_n \models \textsf{persl}_{ }\),
, then, because \({\mathfrak {A}}_n \models \textsf{persl}_{ }\),  for all
for all  , which, due to (a), implies that
, which, due to (a), implies that  (for all \(1 \le j \le r\)); and if
(for all \(1 \le j \le r\)); and if  ,
,  ,
,  ,
,  for some
for some  , which, due to (a), implies that
, which, due to (a), implies that  and (because \({\mathfrak {A}}_n \models \textsf {utransl}\))
and (because \({\mathfrak {A}}_n \models \textsf {utransl}\))  for all \(1 \le j \le r\), \(j \ne i\), then, because \({\mathfrak {A}}_n \models \textsf{persl}_{ }\),
for all \(1 \le j \le r\), \(j \ne i\), then, because \({\mathfrak {A}}_n \models \textsf{persl}_{ }\),  and
and  (for all \(1 \le j \le r\), \(j \ne i\)), whence, due to (a),
(for all \(1 \le j \le r\), \(j \ne i\)), whence, due to (a),  and
and  (for all \(1 \le j \le r\), \(j \ne i\)). That \(\iota ({\mathfrak {c}}^0_n) \preceq ^{\tau ^0_n} \iota ({\mathfrak {c}}^0_{n+1})\) is then evident. Finally, given that \({\mathfrak {A}}_n \models \textsf {stepl}\), it follows that
(for all \(1 \le j \le r\), \(j \ne i\)). That \(\iota ({\mathfrak {c}}^0_n) \preceq ^{\tau ^0_n} \iota ({\mathfrak {c}}^0_{n+1})\) is then evident. Finally, given that \({\mathfrak {A}}_n \models \textsf {stepl}\), it follows that  , for some \(\langle q, \tau , q' \rangle \in \delta ^L\), or
, for some \(\langle q, \tau , q' \rangle \in \delta ^L\), or  , for some \(q \in Q^L\). For the former case, it follows from (a) that \(q^0_n = q\) and \(q^0_{n+1} = q'\), and from (b) that \(\tau ^0_n = \tau \); and, for the latter case, it follows from (a) that \(q^0_n = q^0_{n+1} = q\) and from (b) that \(\tau ^0_n = \textit{idle}\). That is, \(\langle \sigma ({\mathfrak {c}}^0_n), \tau ^0_n, \sigma ({\mathfrak {c}}^0_{n+1}) = \langle q^0_n, \tau ^0_n, q^0_{n+1} \rangle = \langle q, \tau , q' \rangle \in \delta ^L\) or \(\tau ^0_n = \textit{idle}\) and \(\sigma ({\mathfrak {c}}^0_n) = q^0_n = q^0_{n+1} = \sigma ({\mathfrak {c}}^0_{n+1})\). It is straightforward to show from \({\mathfrak {A}}_n \models \textsf{enbl}_{ \tau }\) (a consequence of the assumption that
, for some \(q \in Q^L\). For the former case, it follows from (a) that \(q^0_n = q\) and \(q^0_{n+1} = q'\), and from (b) that \(\tau ^0_n = \tau \); and, for the latter case, it follows from (a) that \(q^0_n = q^0_{n+1} = q\) and from (b) that \(\tau ^0_n = \textit{idle}\). That is, \(\langle \sigma ({\mathfrak {c}}^0_n), \tau ^0_n, \sigma ({\mathfrak {c}}^0_{n+1}) = \langle q^0_n, \tau ^0_n, q^0_{n+1} \rangle = \langle q, \tau , q' \rangle \in \delta ^L\) or \(\tau ^0_n = \textit{idle}\) and \(\sigma ({\mathfrak {c}}^0_n) = q^0_n = q^0_{n+1} = \sigma ({\mathfrak {c}}^0_{n+1})\). It is straightforward to show from \({\mathfrak {A}}_n \models \textsf{enbl}_{ \tau }\) (a consequence of the assumption that  ) and (a) that \(\tau ^0_n \;(= \tau ) \in enb ( {\mathfrak {c}}^0_n )\); and from \({\mathfrak {A}}_n \models \bigwedge _{\langle q, \tau , q' \rangle \in \delta ^L} \lnot \textsf{enbl}_{ \tau }\) (a consequence of the assumption that
) and (a) that \(\tau ^0_n \;(= \tau ) \in enb ( {\mathfrak {c}}^0_n )\); and from \({\mathfrak {A}}_n \models \bigwedge _{\langle q, \tau , q' \rangle \in \delta ^L} \lnot \textsf{enbl}_{ \tau }\) (a consequence of the assumption that  ) and (a) that \( enb ( {\mathfrak {c}}^0_n ) = \emptyset \). Thus, we have established that \(\tau ^0_n \in enb ( {\mathfrak {c}}^0_n )\) and \(\langle \sigma ({\mathfrak {c}}^0_n), \tau ^0_n, \sigma ({\mathfrak {c}}^0_{n+1}) \rangle \in \delta ^L\), or \( enb ( {\mathfrak {c}}^0_n ) = \emptyset \), \(\tau ^0_n = \textit{idle}\), and \(\sigma ({\mathfrak {c}}^0_n) = \sigma ({\mathfrak {c}}^0_{n+1})\), for all \(n \in {\mathbb {N}}\).
) and (a) that \( enb ( {\mathfrak {c}}^0_n ) = \emptyset \). Thus, we have established that \(\tau ^0_n \in enb ( {\mathfrak {c}}^0_n )\) and \(\langle \sigma ({\mathfrak {c}}^0_n), \tau ^0_n, \sigma ({\mathfrak {c}}^0_{n+1}) \rangle \in \delta ^L\), or \( enb ( {\mathfrak {c}}^0_n ) = \emptyset \), \(\tau ^0_n = \textit{idle}\), and \(\sigma ({\mathfrak {c}}^0_n) = \sigma ({\mathfrak {c}}^0_{n+1})\), for all \(n \in {\mathbb {N}}\).
We next show that \({\mathfrak {R}}^i\) (for all \(1 \le i \le k\)) is a run for F over A. Since \({\mathfrak {A}}_0 \models \textsf {initf}(a_i)\) we have from (c) that \(q^i_n \in Q^F_\text {init}\) and \({\mathcal {I}}^i_0 = \emptyset \) (\(1 \le i \le k\)). It is a consequence of the assumption that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\) that \({\mathfrak {A}}_n \models \textsf{persf}_{ }(a_i)\) and \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\), for all \(n \in {\mathbb {N}}\). To show that \({\mathcal {I}}^i_n \preceq ^{\tau ^i_n} {\mathcal {I}}^i_{n+1}\), for all \(n \in {\mathbb {N}}\), we consider two possibilities: if \(\tau ^i_n \not \in T^F_\text {in}\), which, due to (d), implies that  for all
for all  , then, because \({\mathfrak {A}}_n \models \textsf{persf}_{ }(a_i)\),
, then, because \({\mathfrak {A}}_n \models \textsf{persf}_{ }(a_i)\),  for all
for all  , which, due to (c), implies that \({\mathcal {I}}^{i}_n \subseteq {\mathcal {I}}^{i}_{n+1}\); and if
, which, due to (c), implies that \({\mathcal {I}}^{i}_n \subseteq {\mathcal {I}}^{i}_{n+1}\); and if  , which, due to (d), implies that
, which, due to (d), implies that  and (because \({\mathfrak {A}}_n \models \textsf {utransf}(a_i)\))
and (because \({\mathfrak {A}}_n \models \textsf {utransf}(a_i)\))  for all
for all  , then, because
, then, because  ,
,  and
and  for all
for all  , whence, due to (c),
, whence, due to (c),  and
and  . The required condition follows. Finally, given that \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\), it follows that
. The required condition follows. Finally, given that \({\mathfrak {A}}_n \models \textsf {stepf}(a_i)\), it follows that  , for some \(\langle q, \tau , q' \rangle \in \delta ^F\), or
, for some \(\langle q, \tau , q' \rangle \in \delta ^F\), or  , for some \(q \in Q^F\). For the former case, it follows from (c) that \(q^i_n = q\) and \(q^i_{n+1} = q'\), and from (d) that \(\tau ^i_n = \tau \); and, for the latter case, it follows from (c) that \(q^i_n = q^i_{n+1} = q\) and from (d) that \(\tau ^i_n = \textit{idle}\). It is straightforward to show from \({\mathfrak {A}}_n \models \textsf{enbf}_{ \tau }(a_i)\) (a consequence of the assumption that
, for some \(q \in Q^F\). For the former case, it follows from (c) that \(q^i_n = q\) and \(q^i_{n+1} = q'\), and from (d) that \(\tau ^i_n = \tau \); and, for the latter case, it follows from (c) that \(q^i_n = q^i_{n+1} = q\) and from (d) that \(\tau ^i_n = \textit{idle}\). It is straightforward to show from \({\mathfrak {A}}_n \models \textsf{enbf}_{ \tau }(a_i)\) (a consequence of the assumption that  ) and (c) that \(\tau ^i_n \; (= \tau ) \in enb ( {\mathfrak {c}}^i_n )\); and from \({\mathfrak {A}}_n \models \bigwedge _{\langle q, \tau , q' \rangle \in \delta ^F} \lnot \textsf{enbf}_{ \tau }(a_i)\) (a consequence of the assumption that
) and (c) that \(\tau ^i_n \; (= \tau ) \in enb ( {\mathfrak {c}}^i_n )\); and from \({\mathfrak {A}}_n \models \bigwedge _{\langle q, \tau , q' \rangle \in \delta ^F} \lnot \textsf{enbf}_{ \tau }(a_i)\) (a consequence of the assumption that  ) and (c) that \( enb ( {\mathfrak {c}}^i_n ) = \emptyset \). Thus, we have established that \(\tau ^i_n \in enb ( {\mathfrak {c}}^i_n )\) and \(\langle q^i_n, \tau ^i_n, q^i_{n+1} \rangle \in \delta ^F\), or \( enb ( {\mathfrak {c}}^i_n ) = \emptyset \), \(\tau ^i_n = \textit{idle}\), and \(q^i_n = q^i_{n+1}\), for all \(n \in {\mathbb {N}}\).
) and (c) that \( enb ( {\mathfrak {c}}^i_n ) = \emptyset \). Thus, we have established that \(\tau ^i_n \in enb ( {\mathfrak {c}}^i_n )\) and \(\langle q^i_n, \tau ^i_n, q^i_{n+1} \rangle \in \delta ^F\), or \( enb ( {\mathfrak {c}}^i_n ) = \emptyset \), \(\tau ^i_n = \textit{idle}\), and \(q^i_n = q^i_{n+1}\), for all \(n \in {\mathbb {N}}\).
Finally we establish that conditions (A1) and (A2) from Sect. 3.4 hold for \({\mathfrak {R}}\). For (A1), we first show that if \(\tau ^0_n = \vec {\mu }\) (\(n \in {\mathbb {N}}\)), then, for each i (\(1 \le i \le k\)), there exists \(n' > n\), such that  . Let \(n \in {\mathbb {N}}\) and suppose \(\tau ^0_n = \tau = \vec {\mu }\). From (b), it must be \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\tau }\). Further, from \({\mathfrak {A}}_n \models \textsf {bcastla}\) (a consequence of the assumption that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\)), we have
. Let \(n \in {\mathbb {N}}\) and suppose \(\tau ^0_n = \tau = \vec {\mu }\). From (b), it must be \({\mathfrak {A}}_n \models {{\textsf{t}}}{{\textsf{l}}}_{\tau }\). Further, from \({\mathfrak {A}}_n \models \textsf {bcastla}\) (a consequence of the assumption that \(\textsf {Spec}(M)\) is true in \({\mathfrak {M}}\)), we have  , and, as a result,
, and, as a result,  . It is then straightforward to show from the semantics of \(\textsf {MFOTL}\) and (c) above that, for each i (\(1 \le i \le k\)), there exists \(n' > n\), such that
. It is then straightforward to show from the semantics of \(\textsf {MFOTL}\) and (c) above that, for each i (\(1 \le i \le k\)), there exists \(n' > n\), such that  . Now, for each i (\(1 \le i \le k\)), supposing
. Now, for each i (\(1 \le i \le k\)), supposing  (\(n \in {\mathbb {N}}\)), we have from (c) above that
(\(n \in {\mathbb {N}}\)), we have from (c) above that  , thus, from \({\mathfrak {A}}_n \models \textsf {bcastla}\) again,
, thus, from \({\mathfrak {A}}_n \models \textsf {bcastla}\) again,  , and, as a result, \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\), whence, from Lemma 4, \({\mathfrak {A}}_{n'} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\), or, due to (b) (in this proof), \(\tau ^0_{n'} = \vec {\mu }\), for some \(n' < n\). Thus we establish that, for each i (\(1 \le i \le k\)), if
, and, as a result, \({\mathfrak {A}}_n \models \textsf {past}_{\vec {\mu }}\), whence, from Lemma 4, \({\mathfrak {A}}_{n'} \models {{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\), or, due to (b) (in this proof), \(\tau ^0_{n'} = \vec {\mu }\), for some \(n' < n\). Thus we establish that, for each i (\(1 \le i \le k\)), if  (\(n \in {\mathbb {N}}\)), then there exists \(n' < n\) such that \( \tau ^0_{n'} = \vec {\mu }\). In combination with the above, it follows that condition (A1) from Sect. 3.4 holds. Condition (A2) from Sect. 3.4 can be obtained in a similar manner, using (d), (a), sendfa, and Lemma 5. \(\square \)
(\(n \in {\mathbb {N}}\)), then there exists \(n' < n\) such that \( \tau ^0_{n'} = \vec {\mu }\). In combination with the above, it follows that condition (A1) from Sect. 3.4 holds. Condition (A2) from Sect. 3.4 can be obtained in a similar manner, using (d), (a), sendfa, and Lemma 5. \(\square \)
Combining Lemma 3 and 6 , we have proved:
Theorem 1
Let \(M= \langle L, F \rangle \) be an asynchronous distributed machine and \(\textsf {Spec}(M)\) as above. M is runnable if and only if \(\textsf {Spec}(M)\) is satisfiable over a finite model.
Remark 3
It should be clear from the proofs of Lemma 3 and 6 that runs of each asynchronous machine M and models of \(\textsf {Spec}(M)\) over finite domains are in one-to-one correspondence. It should also be clear that all runs of M have a property \({\mathcal {P}}\) (expressible in \(\textsf {MFOTL}\)) if and only if \(\textsf {Spec}(M) \wedge \lnot \varphi _{\mathcal {P}}\), where \(\varphi _{\mathcal {P}}\) is the formula (over \(\Sigma ^M\)) expressing \({\mathcal {P}}\) in \(\textsf {MFOTL}\), is unsatisfiable over finite domains.
4.5 Execution in a synchronous setting
If \(N = \langle L, F \rangle \) is a synchronous distributed machine, we can (automatically) construct an MFOTL-sentence  (with
(with  quadratic in \(\Vert N\Vert \)) such that N is runnable if and only if
quadratic in \(\Vert N\Vert \)) such that N is runnable if and only if  is satisfiable.
is satisfiable.  is defined over the signature \(\Sigma ^N\) comprising a nullary predicate \({{\textsf{s}}}{{\textsf{l}}}_{q}\) for each state \(q \in Q^L\), a unary predicate \({{\textsf{s}}}{{\textsf{f}}}_{q}(\cdot )\) for each state \(q \in Q^F\), the symbols in \(T^L_\text {in}\) and \(T^F_\text {in}\) as unary predicates, the symbols in \(T^F_\text {out}\) as unary predicates, a nullary predicate \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) for each \(\tau \in T^L\), and a unary predicate \({{\textsf{t}}}{{\textsf{f}}}_{\tau }(\cdot )\) for each \(\tau \in T^F\). The intended meaning for each symbol in \(\Sigma ^N\) is the same as the corresponding symbol in \(\Sigma ^M\).
is defined over the signature \(\Sigma ^N\) comprising a nullary predicate \({{\textsf{s}}}{{\textsf{l}}}_{q}\) for each state \(q \in Q^L\), a unary predicate \({{\textsf{s}}}{{\textsf{f}}}_{q}(\cdot )\) for each state \(q \in Q^F\), the symbols in \(T^L_\text {in}\) and \(T^F_\text {in}\) as unary predicates, the symbols in \(T^F_\text {out}\) as unary predicates, a nullary predicate \({{\textsf{t}}}{{\textsf{l}}}_{\tau }\) for each \(\tau \in T^L\), and a unary predicate \({{\textsf{t}}}{{\textsf{f}}}_{\tau }(\cdot )\) for each \(\tau \in T^F\). The intended meaning for each symbol in \(\Sigma ^N\) is the same as the corresponding symbol in \(\Sigma ^M\).
As discussed earlier, a synchronous machine differs from an asynchronous machine in that runs of the former satisfy conditions (S1) and (S2) from Sect. 3.4, whereas runs of the latter satisfy conditions (A1) and (A2) from Sect. 3.4. Thus, the parts of  describing the operation of the leader and each follower are the same as in the asynchronous case. The only thing that changes is the description of the network.
describing the operation of the leader and each follower are the same as in the asynchronous case. The only thing that changes is the description of the network.
We now proceed to define the formulas describing N’s network. The following two formulas (short for broadcast leader synchronous and send follower synchronous respectively) are a translation of conditions (S1) and (S2) respectively from Sect. 3.4:

As in the definition of \(\textsf {bcastla}\) and \(\textsf {sendfa}\), the symbol  (resp.
(resp.  ), and, thus, the predicate
), and, thus, the predicate  appearing in bcastls (resp. sendfs) exists because \(T^L_\text {out} \backsimeq T^F_\text {in}\) (resp. \(T^F_\text {out} \backsimeq T^L_\text {in}\)). The following formula (short for network synchronous) describes the operation of the synchronous network comprising the leader and its followers:
appearing in bcastls (resp. sendfs) exists because \(T^L_\text {out} \backsimeq T^F_\text {in}\) (resp. \(T^F_\text {out} \backsimeq T^L_\text {in}\)). The following formula (short for network synchronous) describes the operation of the synchronous network comprising the leader and its followers:
Finally, for the whole machine, let

As in the asynchronous case, we have \(\Vert \textsf {Spec}(N)\Vert = {\mathcal {O}}(\Vert N\Vert ^2)\).
Lemma 7
Let \(N = \langle L, F \rangle \) be a synchronous distributed machine and  as above. If N is runnable, then
as above. If N is runnable, then  is satisfiable over a finite model.
is satisfiable over a finite model.
Proof
Omitted. (Similar to the proof of Lemma 3.) \(\square \)
Lemma 8
Let \(N = \langle L, F \rangle \) be a synchronous distributed machine and  as above. If
as above. If  is satisfiable over a finite model, then N is runnable.
is satisfiable over a finite model, then N is runnable.
Proof
Omitted. (Similar to the proof of Lemma 6.) \(\square \)
Combining Lemma 7 and 8 , we have:
Theorem 2
Let \(N = \langle L, F \rangle \) be a synchronous distributed machine and  as above. N is runnable if and only if
as above. N is runnable if and only if  is satisfiable over a finite model.
is satisfiable over a finite model.
Remark 4
Similar to the asynchronous case, it should be clear that if all runs of a runnable synchronous machine N have a property \({\mathcal {P}}\) (expressible in \(\textsf {MFOTL}\)) then  , where \(\varphi _{\mathcal {P}}\) is the formula (over \(\Sigma ^N\)) expressing \({\mathcal {P}}\) in \(\textsf {MFOTL}\), is unsatisfiable over finite domains. Relevant to Rem. 1, it should also be clear that for an arbitrary (not necessarily runnable) synchronous distributed machine \(N = \langle L, F \rangle \) and a property \({\mathcal {P}}\) expressed in \(\textsf {MFOTL}\) (over \(\Sigma ^N\)) by the formula \(\varphi _{\mathcal {P}}\), if
, where \(\varphi _{\mathcal {P}}\) is the formula (over \(\Sigma ^N\)) expressing \({\mathcal {P}}\) in \(\textsf {MFOTL}\), is unsatisfiable over finite domains. Relevant to Rem. 1, it should also be clear that for an arbitrary (not necessarily runnable) synchronous distributed machine \(N = \langle L, F \rangle \) and a property \({\mathcal {P}}\) expressed in \(\textsf {MFOTL}\) (over \(\Sigma ^N\)) by the formula \(\varphi _{\mathcal {P}}\), if  is unsatisfiable over finite domains then either N is not runnable or (N is runnable and) all its runs have property \({\mathcal {P}}\). N can fail to be runnable if the definition of L and/or F is such that the behaviour of the machine in each possible execution is undefined, as discussed in Rem. 1. We stress that it is upon the designer to ensure that any such machine N specified within our framework cannot give rise to undefined behaviour during its execution, and, as a result, from the unsatisfiability of
is unsatisfiable over finite domains then either N is not runnable or (N is runnable and) all its runs have property \({\mathcal {P}}\). N can fail to be runnable if the definition of L and/or F is such that the behaviour of the machine in each possible execution is undefined, as discussed in Rem. 1. We stress that it is upon the designer to ensure that any such machine N specified within our framework cannot give rise to undefined behaviour during its execution, and, as a result, from the unsatisfiability of  one can conclude that all runs of N satisfy \({\mathcal {P}}\).
one can conclude that all runs of N satisfy \({\mathcal {P}}\).
Remark 5
Applications requiring different time constraints on message delivery are out of scope. Nevertheless, for completeness, we outline here how to enforce within our framework that messages be delivered after m time steps, for a fixed \(m > 1\). For the leader, one introduces m new proposition symbols \(t^{\vec {\mu }}_1, \ldots , t^{\vec {\mu }}_m\), for each message \(\vec {\mu }\) the leader may broadcast, (these symbols are meant to represent the passage of time after a message \(\vec {\mu }\) is broadcast) and enforces the condition that \(t^{\vec {\mu }}_i\) holds true at time \(n + i\) (\(1 \le i \le m\)) if and only if \({{\textsf{t}}}{{\textsf{l}}}_{\vec {\mu }}\) holds true at time n (\(n \in {\mathbb {N}}\)). One then enforces the condition that  holds true whenever \(t^{\vec {\mu }}_m\) holds true and if
holds true whenever \(t^{\vec {\mu }}_m\) holds true and if  hold true at times \(n, \,n+1\) respectively then \(t^{\vec {\mu }}_m\) also holds true at time \(n+1\) (\(n \in {\mathbb {N}}\)), for each follower x. Similarly, for the followers, one introduces m new unary predicates
hold true at times \(n, \,n+1\) respectively then \(t^{\vec {\mu }}_m\) also holds true at time \(n+1\) (\(n \in {\mathbb {N}}\)), for each follower x. Similarly, for the followers, one introduces m new unary predicates  , for each message \(\vec {\mu }\) a follower may send to the leader, and enforces the condition that \(T^{\vec {\mu }}_i(x)\) holds true at time \(n + i\) (\(1 \le i \le m\)) if and only if \({{\textsf{t}}}{{\textsf{f}}}_{\vec {\mu }}(x)\) holds true at time n (\(n \in {\mathbb {N}}\)), for each follower x. One then enforces the condition that
, for each message \(\vec {\mu }\) a follower may send to the leader, and enforces the condition that \(T^{\vec {\mu }}_i(x)\) holds true at time \(n + i\) (\(1 \le i \le m\)) if and only if \({{\textsf{t}}}{{\textsf{f}}}_{\vec {\mu }}(x)\) holds true at time n (\(n \in {\mathbb {N}}\)), for each follower x. One then enforces the condition that  holds true whenever \(T^{\vec {\mu }}_m(x)\) holds true and if
holds true whenever \(T^{\vec {\mu }}_m(x)\) holds true and if  hold true at times \(n, \,n+1\) respectively then \(T^{\vec {\mu }}_m(x)\) also holds true at time \(n+1\) (\(n \in {\mathbb {N}}\)), for each follower x.
hold true at times \(n, \,n+1\) respectively then \(T^{\vec {\mu }}_m(x)\) also holds true at time \(n+1\) (\(n \in {\mathbb {N}}\)), for each follower x.
5 Specification of protocols
In this section we demonstrate the applicability of our framework in practice by formally specifying three protocols.
5.1 FloodSet
We consider a variant of the FloodSet algorithm with alternative decision rule [28, p. 105] that appeared in [13]. The setting is as follows. There are k processes, each having an input bit and an output bit. The processes communicate via broadcast messages, guaranteed to be delivered with an arbitrary delay, and may also arrive to each recipient multiple times. Informally, the protocol works as follows:
-
At the first round of computations, every process broadcasts its input bit.
-
At every round the (tentative) output bit is set to the minimum value ever seen so far.
The correctness criterion for this protocol is that, eventually, the output bits of all processes will be the same.
We now give a formal specification of the above protocol as a network of a leader and followers. Intuitively, each follower corresponds to one of the aforementioned k processes. Since our model does not allow follower broadcasts we shall use the leader as a network relay: the leader remains idle until it receives one or more “0” messages and/or one or more “1” messages; if it does, it broadcasts a “0” and/or “1” accordingly, and keeps broadcasting while new messages arrive; otherwise it returns to its initial state. The leader is fair, in the sense that it does not neglect to broadcast “1” messages (if any) after broadcasting “0” messages, and vice versa.
Towards defining the leader, let  , \(T^L_\text {out} = \{ \vec {0}, \vec {1} \}\), and \(T^L_\text {local} = \emptyset \); thus
, \(T^L_\text {out} = \{ \vec {0}, \vec {1} \}\), and \(T^L_\text {local} = \emptyset \); thus  . Let \(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^L = \{ q_0, \ldots , q_3 \}\), \(Q^L_\text {init} = \{ q_0 \}\), and
. Let \(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^L = \{ q_0, \ldots , q_3 \}\), \(Q^L_\text {init} = \{ q_0 \}\), and

Let \(L = \langle Q^L, Q^L_\text {init}, T^L, \delta ^L \rangle \). L is depicted in Fig. 3.  , \(T^F_\text {out} = \{ \vec {0}, \vec {1} \}\), and \(T^F_\text {local} = \emptyset \). Let \(T^F = T^F_\text {in} \cup T^F_\text {out} \cup T^F_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^F = \{ i_0, i_1, o_0, o_1 \}\), \(Q^F_\text {init} = \{ i_0, i_1 \}\), and
, \(T^F_\text {out} = \{ \vec {0}, \vec {1} \}\), and \(T^F_\text {local} = \emptyset \). Let \(T^F = T^F_\text {in} \cup T^F_\text {out} \cup T^F_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^F = \{ i_0, i_1, o_0, o_1 \}\), \(Q^F_\text {init} = \{ i_0, i_1 \}\), and

Let \(F = \langle Q^F, Q^F_\text {init}, T^F, \delta ^F \rangle \). F is depicted in Fig. 4. Recall that to form a distributed machine out of L and F we must satisfy the constraints \(T^L_\text {in} \cap T^F_\text {in} = \emptyset \), \(T^L_\text {in} \backsimeq T^F_\text {out}\) and \(T^F_\text {in} \backsimeq T^L_\text {out}\). To satisfy the first restriction we could have typeset either \(T^L_\text {out}\) or \(T^F_\text {in}\) with a different font, but we refrained from that for simplicity. The other constraints are satisfied.
Finally, let \(M^\text {FS} = \langle L, F \rangle \) be the asynchronous state machine comprising the leader L and (an arbitrary number of replicated) followers F. Let \(\textsf {Spec}(M^\text {FS})\) be the FOTL-sentence such that \(M^\text {FS}\) is runnable if and only if \(\textsf {Spec}(M^\text {FS})\) is satisfiable. According to the informal correctness criterion stated above, we need to verify that the following FOTL-sentence is unsatisfiable over finite domains:
5.2 Two-phase commit
We consider the two-phase commit as described in [19], with minor simplifications. In this setting, k followers (“resource managers”) coordinated by a leader (“transaction manager”) collectively perform a transaction. The transaction is aborted if one or more followers abort, otherwise it is committed.
Initially, the leader and each follower are in a working state. The protocol starts with the leader broadcasting a prepare message to the followers, signalling that a decision is about to be made on committing/aborting the transaction. The leader then enters a waiting state and remains there until it has received a response from each follower—either prepared (signalling that a follower is prepared to receive a command to commit or abort) or aborted (signalling that a follower has chosen to abort). Upon receipt of a prepare message from the leader, each follower enters a preparing state. In this state the follower can choose to (a) abort the transaction (for its own reason); or (b) prepare to receive (from the leader) a command to commit or abort. If the follower aborts, it sends an aborted message to the leader and enters an aborted state. If the follower prepares to receive a command, it sends a prepared message to the leader and enters a prepared state. When in a prepared state, the follower cannot abort on its own volition: it will perform the leader’s command (whether it be to commit or to abort). Thus, while in a prepared state, if the follower receives a commit message, it enters a committed state, and if it receives an abort message, it enters an aborted state. While in the waiting state, if the leader receives an aborted message from one or more followers it enters an aborting state; otherwise (if it receives a prepared message from all k followers) it enters a committing state. When in an aborting state, the leader broadcasts an abort message to the followers and enters an aborted state; and while in a committing state, it broadcasts a commit message to the followers and enters a committed state. (Similar to [19], we could allow the leader (“transaction manager”) to arbitrarily abort when in a working, waiting, or committing state, but we will refrain from that for simplicity.) The correctness criterion for this protocol is that, eventually, either all followers are in a commited state or all are in an aborted state.
We now give a formal description of the above protocol. Towards defining the leader, let \(T^L_\text {in} = \{ \overleftarrow{prepared }, \overleftarrow{aborted } \}\), \(T^L_\text {out} = \{ \overrightarrow{prepare }, \overrightarrow{commit }, \overrightarrow{abort } \}\), and \(T^L_\text {local} = \emptyset \); thus  . Let \(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^L = \{ working ,\, waiting ,\, committing ,\, aborting ,\, committed ,\, aborted \}\), \(Q^L_\text {init} = \{ working \}\), and
. Let \(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^L = \{ working ,\, waiting ,\, committing ,\, aborting ,\, committed ,\, aborted \}\), \(Q^L_\text {init} = \{ working \}\), and

Let \(L = \langle Q^L, Q^L_\text {init}, T^L, \delta ^L \rangle \). L is depicted in Fig. 5. For the followers, let \(T^F_\text {in} = \{ \overleftarrow{prepare }, \overleftarrow{commit }, \overleftarrow{abort } \}\), \(T^F_\text {out} = \{ \overrightarrow{prepared }, \overrightarrow{aborted } \}\), and \(T^F_\text {local} = \emptyset \). Let \(T^F = T^F_\text {in} \cup T^F_\text {out} \cup T^F_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^F = \{ working ,\, preparing ,\, prepared ,\, committed ,\, aborted \}\), \(Q^F_\text {init} = \{ working \}\), and
Let \(F = \langle Q^F, Q^F_\text {init}, T^F, \delta ^F \rangle \). F is depicted in Fig. 6. Notice that \(T^L_\text {in} \cap T^F_\text {in} = \emptyset \), \(T^L_\text {in} \backsimeq T^F_\text {out}\) and \(T^F_\text {in} \backsimeq T^L_\text {out}\).
Finally, let \(M^\text {2PC} = \langle L, F \rangle \) be the asynchronous state machine comprising the leader L and (an arbitrary number of replicated) followers F. Let \(\textsf {Spec}(M^\text {2PC})\) be the FOTL-sentence such that \(M^\text {2PC}\) is runnable if and only if \(\textsf {Spec}(M^\text {2PC})\) is satisfiable. According to the informal correctness criterion stated above, we need to verify that the following FOTL-sentence is unsatisfiable over finite domains:
5.3 Control-MAC
We consider a simplified version of the Control-MAC protocol [7], used to enforce a form of mutual exclusion in certain sensor networks. The original protocol involves a degree of randomness, which we are unable to model in our framework and first-order temporal logic in general. The simplifications made here address this limitation while staying faithful to the core ideas behind the protocol.
The setting is as follows. There are k sensors and a gateway. The sensors sense a physical phenomenon and each sensor wants to send to the gateway its sense data when a certain threshold is met. The gateway has a limited number of transmission slots, say m (\(m < k\)), and if more than m sensors transmit at the same time there will be data corruption. For simplicity we shall take \(m = 1\), i.e. the gateway has only one transmission slot. The protocol is synchronous and evolves in rounds. At the beginning of each round, the gateway waits for bids for the transmission slot from the sensors that have data to transmit; at the same time, each sensor that has data to transmit bids for the transmission slot, otherwise it waits. If the gateway receives exactly one bid it broadcasts a go message; if it receives two or more bids it broadcasts a nogo message; and, for symmetry, if it receives no bid it broadcasts a nogo message. If a sensor that has bid for the transmission slot receives a go message, it sends its data and moves to its initial state; otherwise, if it receives a nogo message simply moves to its initial state. If a sensor that has not bid for the transmission slot receives either a go or a nogo message, it moves to its initial state. In the original protocol, when a sensor that has bid for the transmission slot receives a nogo message, it waits for a random number of rounds before it bids again. This random number depends on the contention in the system (i.e. on how many sensors have bid up to that point) and its specific properties are of no concern to us. What is important to us is that it is calculated in such a way that if two sensors bid for the transmission slot at the same time, the probability of them biding again at the same time in the future is very low. Seeing as we cannot model randomness, we shall assume that probability to be zero. Thus, we shall assume that if a sensor bids for the transmission slot at the same time with other sensors, there will be a time in the future when the sensor bids on its own. The correctness criterion for this protocol is that every sensor that has data to send, or, in other words, has bid for the transmission slot, will eventually send its data to the gateway.
We now give a formal description of the above protocol. Towards defining the leader, let \(T^L_\text {in} = \{ \overleftarrow{bid } \}\), \(T^L_\text {out} = \{ \overrightarrow{go }, \overrightarrow{nogo } \}\), and \(T^L_\text {local} = \{ wait \}\); thus  . Let \(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^L = \{ q_0, \ldots , q_4 \}\), \(Q^L_\text {init} = \{ q_0 \}\), and
. Let \(T^L= {\overline{T}}^L_\text {in} \cup T^L_\text {out} \cup T^L_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^L = \{ q_0, \ldots , q_4 \}\), \(Q^L_\text {init} = \{ q_0 \}\), and

Let \(L = \langle Q^L, Q^L_\text {init}, T^L, \delta ^L \rangle \). L is depicted in Fig. 7. For the followers, let \(T^F_\text {in} = \{ \overleftarrow{go }, \overleftarrow{nogo } \}\), \(T^F_\text {out} = \{ \overrightarrow{bid } \}\), and \(T^F_\text {local} = \{ sending ,\, wait ,\, \varepsilon \}\). Let \(T^F = T^F_\text {in} \cup T^F_\text {out} \cup T^F_\text {local} \cup \{ \textit{idle}\}\). Let \(Q^F = \{ q_0, \ldots , q_6 \}\), \(Q^F_\text {init} = \{ q_0 \}\), and
Let \(F = \langle Q^F, Q^F_\text {init}, T^F, \delta ^F \rangle \). F is depicted in Fig. 8. Notice that \(T^L_\text {in} \cap T^F_\text {in} = \emptyset \), \(T^L_\text {in} \backsimeq T^F_\text {out}\) and \(T^F_\text {in} \backsimeq T^L_\text {out}\).
Finally, let \(N^\text {MAC} = \langle L, F \rangle \) be the synchronous state machine comprising the leader L and (an arbitrary number of replicated) followers F. Let  be the FOTL-sentence such that \(N^\text {MAC}\) is runnable if and only if
be the FOTL-sentence such that \(N^\text {MAC}\) is runnable if and only if  is satisfiable. According to the informal correctness criterion stated above, we need to verify that the following FOTL-sentence is unsatisfiable over finite domains:
is satisfiable. According to the informal correctness criterion stated above, we need to verify that the following FOTL-sentence is unsatisfiable over finite domains:
6 Related work
[1] presents an approach in which the states and transitions of a parameterized or infinite-state system are represented as words over a finite alphabet and properties of a system are specified and checked using automata-theoretic techniques. Because working with these automata-theoretic techniques can be difficult in practice, [1] introduces LTL(MSO), a mixture of LTL (linear temporal logic) and MSO (monadic second-order logic), enabling the specification of systems and their properties at a higher level of abstraction. The verification problem for LTL(MSO) reduces to whether some Büchi regular transition system has accepting runs. [1] reports that this problem is in general undecidable, but goes on to verify safety properties and some liveness properties (also see [2] for liveness) for various real-world protocols.
In [10, 11] and [14], the state of a parameterized system is represented using certain numerical abstractions. An abstract, parameterized, cache-coherence (in [10, 11]) or broadcast (in [14]) protocol for such systems is then translated to numerical constraints pertaining to said numerical abstractions. This approach reduces model-checking safety properties to a reachability problem, which can be attacked using common methods for infinite-state model-checking, working over integer or real arithmetics. The latter methods have in general non-elementary worst-case complexity. [14] reports that model-checking liveness properties for their abstract broadcast protocol is undecidable.
By utilizing \(\textsf {MFOTL}\), our approach achieves similar expressiveness to LTL(MSO) (if no second-order quantifiers are used, formulas of LTL(MSO) can be straightforwardly translated to monadic \(\textsf {MFOTL}\)) and approximates to some extent the expressiveness of approaches based on numerical abstractions (the latter are more flexible in expressing properties involving complex numerical constraints, but \(\textsf {MFOTL}\) can express simple numerical constraints, possibly sacrificing completeness for constraints requiring equality). At the same time, \(\textsf {MFOTL}\) remains decidable (sacrificing completeness when it comes to properties requiring equality) and has relatively low worst-case computational complexity. The decidability and computational complexity of \(\textsf {MFOTL}\) are not affected by the type of property one wants to check (i.e. safety, liveness, fairness, or other), and, as a result, \(\textsf {MFOTL}\) is particularly useful for checking liveness properties, which present difficulties for the above formalisms. The abstract model that we introduce can emulate the protocol model in [10, 11] and has similarities with the one in [14]. For protocols that include ingoing transitions of the form  ,
,  , or any other ingoing transitions added in the future whose translation in first-order logic requires the use of equality, our framework is correct (a protocol does have a given property if the protocol’s translation logically entails that property) but incomplete (a protocol may have a given property even if the protocol’s translation does not logically entail that property). For example Control-MAC in Sect. 5.3 is affected by this limitation, but neither FloodSet in Sect. 5.1 nor the two-phase commit in Sect. 5.2 are affected by it.
, or any other ingoing transitions added in the future whose translation in first-order logic requires the use of equality, our framework is correct (a protocol does have a given property if the protocol’s translation logically entails that property) but incomplete (a protocol may have a given property even if the protocol’s translation does not logically entail that property). For example Control-MAC in Sect. 5.3 is affected by this limitation, but neither FloodSet in Sect. 5.1 nor the two-phase commit in Sect. 5.2 are affected by it.
7 Conclusions
We have introduced a framework that simplifies the verification of protocols involving a distinguished machine (leader) orchestrating an arbitrary number of identical machines (followers). Our framework provides a high-level formalism based on finite-state machines and encapsulating their network interactions. We have shown that protocols specified in this framework can automatically be translated into monodic first-order temporal logic, maintaining their semantics. Automated theorem provers for said logic can then be used to check whether that translation (and thus the original protocol) satisfies a property of interest. Thus, our framework constitutes a flexible, high-level approach to parameterized verification. To demonstrate the applicability of our framework, we have specified in it three protocols used in real settings. The implementation of our framework and its incorporation with the provers is the subject of ongoing and future work.
Data Availibility Statement
Data sharing not applicable.
Change history
07 February 2023
A Correction to this paper has been published: https://doi.org/10.1007/s10703-023-00408-z
References
Abdulla PA, Jonsson B, Nilsson M, d’Orso J, Saksena M (2004) Regular Model Checking for LTL(MSO). In: International Conference on Computer Aided Verification, LNCS, vol. 3114, pp. 348–360. Springer
Abdulla PA, Jonsson B, Rezine A, Saksena M (2006) Proving liveness by backwards reachability. In: International Conference on Concurrency Theory, LNCS, vol. 4137, pp. 95–109. Springer
Behdenna A, Dixon C, Fisher M (2009) Deductive verification of simple foraging robotic behaviours. Int J Intell Comput Cybern 2(4):604–643
Benghabrit W, Grall H, Royer JC, Sellami M (2015) Abstract accountability language: translation, compliance and application. In: Asia-Pacific Software Engineering Conference, pp. 214–221. IEEE
Benghabrit W, Grall H, Royer JC, Sellami M (2015) Checking accountability with a prover. In: Computer Software and Applications Conference, vol. 2, pp. 83–88. IEEE
Bernstein PA, Hadzilacos V, Goodman N (1987) Concurrency control and recovery in database systems. Addison-Wesley, Boston
Bhatia L, Tomic I, Fu A, Breza M, McCann JA, Control communication co-design for wide area cyber-physical systems. ACM Trans Cyber-Phys Syst https://doi.org/10.1145/3418528
Degtyarev A, Fisher M, Konev B (2006) Monodic temporal resolution. ACM Trans Comput Logic 7(1):108–150
Degtyarev A, Fisher M, Lisitsa A (2002) Equality and monodic first-order temporal logic. Studia Logica 72(2):147–156
Delzanno G (2003) Constraint-based verification of parameterized cache coherence protocols. Formal Methods Syst Design 23(3):257–301
Delzanno G (2020) Automatic verification of parameterized cache coherence protocols. International Conference on Computer Aided Verification. Springer International Publishing, Cham, pp 353–360
Dixon C (2006) Using temporal logics of knowledge for specification and verification-a case study. J Appl Logic 4(1):50–78
Dixon C, Fisher M, Konev B, Lisitsa A (2008) Practical first-order temporal reasoning. In: International Symposium on Temporal Representation and Reasoning, pp. 156–163. IEEE
Esparza J, Finkel A, Mayr R (1999) On the verification of broadcast protocols. In: Symposium on Logic in Computer Science, pp. 352–359. IEEE Computer Society Press
Fernández-Gago M, Hustadt U, Dixon C, Fisher M, Konev B (2005) First-order temporal verification in practice. J Autom Reason 34(3):295–321
Fisher M, Konev B, Lisitsa A (2006) Practical Infinite-State Verification with Temporal Reasoning. In: Verification of Infinite State Systems and Security, NATO Security through Science Series: Information and Communication, vol. 1, pp. 91–100. IOS Press
Fisher M, Konev B, Lisitsa A (2009) Temporal verification of fault-tolerant protocols. In: Methods, Models and Tools for Fault Tolerance, pp. 44–56. Springer
Fisher M, Lisitsa A (2003) Deductive verification of cache coherence protocols. In: Proceedings of the 3rd Workshop on Automated Verification of Critical Systems AVoCS, 3: 177–186
Gray J, Lamport L (2006) Consensus on transaction commit. ACM Trans Database Syst (TODS) 31(1):133–160
Halle S (2011) Causality in message-based contract violations: a temporal logic “whodunit”. In: International Enterprise Distributed Object Computing Conference, pp. 171–180. IEEE
Hodkinson I, Kontchakov R, Kurucz A, Wolter F, Zakharyaschev M (2003) On the computational complexity of decidable fragments of first-order linear temporal logics. In: 10th International Symposium on Temporal Representation and Reasoning, 2003 and Fourth International Conference on Temporal Logic. Proceedings., pp. 91–98. IEEE
Hodkinson I, Wolter F, Zakharyaschev M (2000) Decidable fragments of first-order temporal logics. Annals Pure Appl Logic 106(1–3):85–134
Hustadt U, Konev B, Riazanov A, Voronkov A (2004) Temp: A temporal monodic prover. In: International Joint Conference on Automated Reasoning, LNCS, vol. 3097, pp. 326–330. Springer
Konev B, Degtyarev A, Dixon C, Fisher M, Hustadt U (2005) Mechanising first-order temporal resolution. Inf Comput 199(1–2):55–86
Konev B, Degtyarev A, Fisher M, Lisitsa A, Characterising finite domains in monodic first-order temporal logic. Tech. rep., ULCS-09-009, Department of Computer Science, University of Liverpool
Ludwig M, Hustadt U (2009) Fair derivations in monodic temporal reasoning. In: International Conference on Automated Deduction, pp. 261–276. Springer
Ludwig M, Hustadt U (2010) Implementing a fair monodic temporal logic prover. AI Commun 23(2–3):69–96
Lynch NA (1996) Distributed Algorithms. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA
Szalas A, Holenderski L (1988) Incompleteness of first-order temporal logic with until. Theoretical Comput Sci 57(2–3):317–325
Wolter F, Zakharyaschev M (2001) Decidable fragments of first-order modal logics. J Symb Logic 66(3):1415–1438
Wolter F, Zakharyaschev M (2002) Axiomatizing the monodic fragment of first-order temporal logic. Annals Pure Appl logic 118(1–2):133–145
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: In this article on p. 451 the spacing inside the formulas below the sentence “Let stepl be the logical disjunction of the following two formulas:” is incorrect and some symbols overlap. The equations have been corrected.
This work was funded by the Engineering and Physical Sciences Research Council (EPSRC) in the UK under the Science of Sensor Systems Software grant (EP/N007565/1), by the UK Industrial Strategy Challenge Fund (ISCF), under the Future AI and Robotics for Space Hub (EP/R026092/1) and through the Royal Academy of Engineering.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kourtis, G., Dixon, C., Fisher, M. et al. Parameterized verification of leader/follower systems via first-order temporal logic. Form Methods Syst Des 58, 440–468 (2021). https://doi.org/10.1007/s10703-022-00390-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10703-022-00390-y






 ,
, 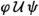 , and
, and  .
.
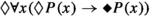
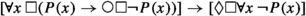

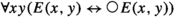
 (
( ) and
) and 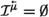 ;
;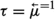 (
( ) and
) and  ;
;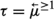 (
(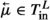 ) and
) and 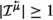 ;
;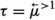 (
( ) and
) and  ;
;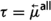 (
( ) and
) and  .
.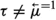 ,
, 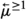 ,
, 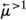 ,
,  for all
for all  ,
, 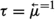 ,
,  ,
,  , or
, or  for some
for some 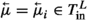 ,
, 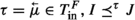 iff
iff 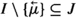 and
and 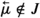 .
. ; and, for each i (
; and, for each i (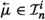 (
(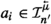 ; and, if
; and, if  (
(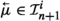 ; and, for each i (
; and, for each i ( and
and  , then
, then  ; and, if
; and, if 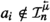 and
and  (
( ,
,  ;
;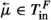 ,
, 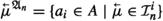 ;
; , such that
, such that  and
and  (
(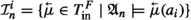 ;
;




