Surely, one would like to be able to deduce the quantitative laws of quantum mechanics directly from their anschaulich foundations, that is, essentially, relation \({\delta }p\,{\delta }q \thicksim h\). (Werner Heisenberg [8], p. 196)
Abstract
For a simple set of observables we can express, in terms of transition probabilities alone, the Heisenberg uncertainty relations, so that they are proven to be not only necessary, but sufficient too, in order for the given observables to admit a quantum model. Furthermore distinguished characterizations of strictly complex and real quantum models, with some ancillary results, are presented and discussed.
Similar content being viewed by others
Notes
In all the equations, ellipsis stands for all similar relations involving the observables left over.
\({\hat{A}},{\hat{B}},{\hat{C}}\) are defined up to a common unitary transformation, cfr. [1, Corollary 8]. A self-adjoint operator having eigenvalues
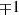 is just a spin operator.
is just a spin operator.Said eigenstates as well.
Cfr. Appendix 1.
Any common unitary transformation of \({\hat{A}},{\hat{B}},{\hat{C}},\) referred to in note 2, induces a common rotation of \(u_A,u_B,u_C,\) cfr. [1, Corollary 8] proof.
Observe that \(u_A,u_B,u_C\) are necessarily distinct and pairwise non collinear, due to the assumption (5).
For a recent review cfr. [9] and the bibliography therein.
As known a state is defined as a norm 1 element of \(\mathscr {H}\) up to a phase factor.
The first addend in the r.h.s. is said the covariance term and the second the commutator term.
One has also that \(\psi =\psi _2(-w)\), but it is not required here; w is known as a representation of the state \(\psi \) on the Bloch’s sphere \(S^{(2)}\).
Similar assertions hold taking any permutation of the operators \({\hat{A}},{\hat{B}},{\hat{C}}.\)
where \(\Delta {\hat{Z}}:=\sqrt{ Var ({\hat{Z}})}\) denotes the standard deviation of \({\hat{Z}}.\) The r.h.s. is said the correlation term.
Cfr. Appendix 4.
Cfr. Note 12. The symbol \(\langle \;\; \rangle _{\psi }\) denotes the average computed in the state \(\psi .\)
Furthermore cfr. note 6.
\(\varepsilon _{ jkl }\) denotes the Levi-Civita symbol; on repeated indices summation is understood.
References
Accardi, L., Fedullo, A.: On the statistical meaning of complex numbers in quantum mechanics. Lett. Nuovo Cim. 34(7), 161–172 (1982)
Accardi, L.: Some trends and problems in quantum probability. In: Accardi, L., Frigerio, A., Gorini, V. (eds.) Quantum probability and applications to the quantum theory of irreversible processes, pp. 1–19. Lecture Notes in Mathematics, Vol. 1055, Springer, Berlin (1984)
Klein, F.: Vergleichende Betrachtungen über neuere geometrische Forschungen. Math. Ann. 43, 63–100 (1893). Gesammelte Abh., Springer, 1, 460–497 (1921). English translation: a comparative review of recent researches in geometry, by Mellen Haskell, Bull. N. Y. Math. Soc., 2 (10), 215–249 (1893)
Gudder, S., Zanghì, N.: Probability models. Il Nuovo Cim. 79 B(2), 291–301 (1982)
Fedullo, A.: On the existence of a Hilbert space model for finite valued observables. Il Nuovo Cim. 107 B(12), 1413–1426 (1992)
Jauch, J.M.: Foundations of Quantum Mechanics. Addison-Wesley Publishing Company, Boston (1968)
von Neumann, J.: Mathematische Grundlagen der Quantenmechanik, Die Grundlehren der Mathematischen Wissenschaften, Band 38. Springer, Berlin (1932). English translation: Mathematical Foundations of Quantum Mechanics, Princeton University Press (1971)
Heisenberg, W.: Uber den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 43(3–4), 172–198 (1927). English translation in [13, 62–84]
Sen, D.: The uncertainty relations in quantum mechanics. Curr. Sci. 107(2), 203–218 (2014)
Robertson, H.P.: The uncertainty principle. Phys. Rev. 34, 573–574 (1929). Reprinted in [13, 127–128]
Schrödinger, E.: The uncertainty relations in quantum mechanics. Zum Heisenbergschen Unschärfeprinzip, Sitzungsberichte der Preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse 14, 296–303 (1930)
Griffiths, D.: Quantum Mechanics. Pearson, Upper Saddle River (2005)
Wheeler, J.A., Zurek, W.H. (eds.): Quantum Theory and Measurement. Princeton University Press, Princeton (1983)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1. Results quoted from [1].
Theorem 7
The following assertions are equivalent:
-
(i)
the transition matrices P, Q, R admit a complex Hilbert space model;
-
(ii)
the transition matrices P, Q, R admit a spin model;
-
(iii)
\(\cos ^2\alpha +\cos ^2\beta +\cos ^2\gamma -1\le 2\;\cos \alpha \;\cos \beta \;\cos \gamma ;\)
-
(iv)
\(-1\le \frac{\cos ^2\frac{\alpha }{2}+\cos ^2\frac{\beta }{2}+\cos ^2\frac{\gamma }{2}\;-\;1}{2\cos \frac{\alpha }{2}\cos \frac{\beta }{2}\cos \frac{\gamma }{2}}\le 1;\)
-
(v)
\(-1\;\le \;\frac{p\;+\;q\;+\;r\;-\;1}{2\sqrt{p\;q\;r}}\;\le \;1;\)
-
(vi)
\([\sqrt{pq}-\sqrt{(1-p)(1-q)}]^2\;\le \;r\;\le \;[\sqrt{pq}+\sqrt{(1-p)(1-q)}]^2\)
Proposition 3
Three vectors \(a,b,c\in S^{(2)}\) satisfying
exist if and only if
Theorem 9
The transition matrices P, Q, R admit a real Hilbert space model if and only if \(\frac{p\;+\;q\;+\;r\;-\;1}{2\sqrt{p\;q\;r}}\;=\;+1\) or \(\frac{p\;+\;q\;+\;r\;-\;1}{2\sqrt{p\;q\;r}}\;=\;-1\) or equivalently \(\sqrt{r}\;=\;\sqrt{pq}+\sqrt{(1-p)(1-q)}\) or \(\sqrt{r}\;=\;\left| \sqrt{pq}-\sqrt{(1-p)(1-q)}\right| \).
Theorem 10
The transition matrices P, Q, R admit a real Hilbert space model if and only if they admit a spin model defined by a coplanar triple of vectors in \(S^{(2)}\).
2. Proof of Lemma 4.1
Putting for simplicity \(z_{+\ }:=\frac{z_1+z_2}{2}\) and \(z_{-\ }:=\frac{z_1-z_2}{2},\) by equation (10) we get
and, since \(\langle (u_Z\cdot \sigma )^2\rangle =\langle {\hat{1}}\rangle =1,\)
from which we obtain
Further, with easily understood notations, we have
so that
last, quite directly, we get
\(\square \)
3. Proof of Lemma 4.2
By definition \(u\cdot \sigma =\left[ \begin{matrix}u_3&{}u_1-iu_2\\ u_1+iu_2&{}-u_3\end{matrix}\right] ,\) so that for every state \(\psi \) one has
SinceFootnote 17 as known \(\psi _1(w)=\left[ \begin{array}{ll}\sqrt{\frac{1+w_3}{2}}&{}\frac{w_1+i\;w_2}{\sqrt{2(1+w_3)}}\\ \end{array}\right] ^T\) and \(\psi _2(w)=\left[ \begin{array}{ll}\sqrt{\frac{1-w_3}{2}}&{}-\frac{w_1+i\;w_2}{\sqrt{2(1-w_3)}}\\ \end{array}\right] ^T,\) putting them in the former formula, with easy calculations we get \(\langle u\cdot \sigma \rangle _{\psi _1(w)}=u\cdot w\) and \(\langle u\cdot \sigma \rangle _{\psi _2(w)}=-u\cdot w\) as asserted in Eq. (19). Further it is soon seen that \((u\cdot \sigma )^2={\hat{1}},\) so that \(\langle (u\cdot \sigma )^2\rangle =1,\) thus, in the said states, \( Var (u\cdot \sigma )=\langle u\cdot \sigma \rangle ^2-(\langle u\cdot \sigma \rangle )^2=1-(u\cdot w)^2\) as stated in Eq. (20), that therefore is proven. Further, due toFootnote 18 \([\sigma _j,\sigma _k]=2i\varepsilon _{ jkl }\sigma _l\) for every j, k, one has \(\frac{1}{2i}[u\cdot \sigma ,v\cdot \sigma ]= Det \left[ \begin{matrix}\sigma _1&{}\sigma _2&{}\sigma _3\\ u_1&{}u_2&{}u_3\\ v_1&{}v_2&{}v_3\end{matrix}\right] =(u\times v)\cdot \sigma ,\) so that, taking the averages in the states \(\psi _k(w)\) and considering that \(\langle \sigma _k\rangle =w_k\) for \(k=1,2,3\), (21) is proven. Lastly, due to \(\{\sigma _h,\sigma _k\}=2\delta _{ hk }{\hat{1}}\) for every h, k, we have \(\{\sigma \cdot u,\sigma \cdot v\}=2u\cdot v{\hat{1}}\) so that, taking the averages in whichever state, we get Eq. (22) and the proof of the lemma is complete. \(\square \)
4. With the notations of Sect. 3, thanks to the trigonometric identity \(\cos \theta =2\cos ^2\frac{\theta }{2}-1,\) we can write \(\cos \alpha =2p-1,\;\cos \beta =2q-1,\;\cos \gamma =2r-1,\) so that
that suitably simplified becomes \(4(4pqr-(p+q+r-1)^2)\) as asserted. \(\square \)
Rights and permissions
About this article
Cite this article
Fedullo, A. Heisenberg Uncertainty Relations as Statistical Invariants. Found Phys 48, 1546–1556 (2018). https://doi.org/10.1007/s10701-018-0213-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10701-018-0213-9



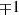 is just a spin operator.
is just a spin operator.