On Some Troubles with the Metaphysics of Fermionic Compositions

Abstract

In this paper I discuss some metaphysical consequences of an unorthodox approach to the problem of the identity and individuality of “indistinguishable” quantum particles. This approach is based on the assumption that the only admissible way of individuating separate components of a given system is with the help of the permutation-invariant qualitative properties of the total system. Such a method of individuation, when applied to fermionic compositions occupying so-called GMW-nonentangled states, yields highly implausible consequences regarding the number of distinct components of a given composite system. I specify the problem (which I call the problem of fermionic inflation) in detail, and I consider several strategies of solving it. The preferred solution of the problem is based on the premise that spatial location should play a privileged role in identifying and making reference to quantum-mechanical systems.

1 Introduction

Quantum mechanics teaches us that particles of the same type can occupy only those joint states that are either symmetric (bosons) or antisymmetric (fermions). The superselection rule which limits the available states of multiparticle systems to symmetric or antisymmetric ones is commonly thought to imply that particles of the same type are indistinguishable by their properties and relations. The simplest way to argue for the indiscernibility claim is to observe that in the case of symmetric/antisymmetric states of N particles the reduced states obtained by “tracing out” N–1 degrees of freedom are identical regardless of which of the N–1 Hilbert spaces in the corresponding tensor product are selected. The apparent indiscernibility of “identical” quantum particles has spawned an extensive philosophical debate on the problem of the identity and individuality of quanta, with particular emphasis placed on the fate of the Leibnizian Principle of the Identity of Indiscernibles, and on various alternative ways of “grounding” the numerical diversity of quanta.¹

However, even without entering the intricate discussions on assorted grades of discernibility and their role in establishing the individuality of quantum objects, we may notice that the broad metaphysical picture emerging from the orthodox view is rather bizarre. If, by (nomic) necessity, all particles of the same type occupy the exact same reduced states, then it doesn’t even make sense to speak for instance about interactions with a separate electron. An experimenter who registers the trajectory of seemingly one electron in a bubble chamber in fact interacts with all electrons in the universe (each constituting an extremely small percentage of the detected particle, so to speak). This is so, because all electrons in the universe have the exact same reduced state that (limiting ourselves to spatial degrees of freedom) is a convex sum of a gigantic number of projector operators, each of which corresponds to a particular location in the universe where the probability of finding some electron is non-zero. Speaking metaphorically, all the electrons, and all the muons, protons, photons etc., in the universe are “smeared” all over the place in an identical manner, one on top of another. It is quite a challenge to make sense of this general picture, especially in the light of the fact that macroscopic objects (including our bodies) do not seem to share with their constituting particles the proclivity to be partially present in all nooks and crannies of the universe. However, it turns out that an alternative analysis of the requirement of permutation invariance is available, and this analysis brings in a radically different outlook on the metaphysics of quantum objects. This unorthodox approach, which is steadily gaining popularity among philosophers of physics, is based on the assumption that the indices used to differentiate one-particle Hilbert spaces in the N-fold tensor product of spaces have no physical meaning and are a redundant part of the mathematical formalism. Consequently, the only physically meaningful way to express the properties of individual particles is with the help of fully symmetric, i.e. permutation-invariant operators (projectors).² As the reduced states used in the standard argument for the indiscernibility claim are clearly defined in a non-permutation-invariant way, they are not admissible as representations of the physical states of individual particles. However, a fully symmetric representation of individual properties is possible (see later in the text for details), but it leads to dramatically different conclusions regarding the possibility of discerning quantum particles of the same type.

Essentially, the new approach implies that quantum objects can differ with respect to their individual properties even if their joint state satisfies the condition of symmetricity/antisymmetricity. If the state of N bosons (fermions) results from the symmetrization (antisymmetrization) of a direct product of N orthogonal states, it can be formally proven that individual particles possess well-defined and discerning properties corresponding precisely to the initial, pre-symmetrization states. This fact gives formal support to the intuitively straightforward observation that an electron detected in a bubble chamber has a location property that distinguishes it from any other electron in the universe. Thus it looks like the metaphysics of quanta need not be as radically non-classical as the orthodox approach seems to suggest.

Unfortunately, the hope for a clean, close-to-classical conception of identity and individuality for quanta is all but destroyed under closer inspection. First of all, even in the new approach there remain accessible states in which the discernibility of particles by well-defined, definite properties is unattainable. The product of N identical states in the case of bosons is an example of such a case.³ Other troublesome states include those that cannot be expressed as a result of symmetrizing or antisymmetrizing a product of orthogonal states (those states are often referred to as GMW-entangled, after the initials of the authors of [14], where this concept of entanglement was thoroughly scrutinized). In such states discernibility with the help of well-defined values of observables is impossible, even though less-specific discernibility may still be an option.⁴

Furthermore, it turns out that even systems of particles occupying the apparently least controversial GMW-nonentangled states display features that violate some of our fundamental metaphysical intuitions. In this paper I will discuss some surprising and controversial metaphysical characteristics that composite fermionic systems in GMW-nonentangled states appear to possess under the non-standard interpretation. The main question addressed here will be how to decompose a system consisting of N fermions into smaller subsystems. I will closely follow the formal analysis of this problem offered recently by Adam Caulton [5]. Caulton’s main objective is to prove that fermionic compositions violate some principles of mereology (the formal theory of parthood). I, on the other hand, will argue that the problem with fermionic composite systems is of a slightly different (and more fundamental) character, and that we don’t even need to introduce the quantum-mechanical variant of the notion of parthood in order to see that there is something peculiar about the way the new approach describes the subsystems of a particular system of fermions. In a nutshell, the problem that I will identify in subsequent sections is that of a runaway multiplication of numerically distinct subsystems that appear to constitute a given system. I call this issue the problem of fermionic inflation, and I will consider several strategies of how to deal with it.

2 Factorism

Before we discuss the announced problem in detail, we should perhaps say a few words about the physical and philosophical motivation behind the unorthodox approach, lest the reader be tempted to construe the forthcoming argument as a reductio of the new interpretation. The orthodox doctrine, which—following [4]—I will refer to as “factorism”, associates individual particles with factor Hilbert spaces in the N-fold tensor product. While factorism is certainly considered part of the standard interpretation of the quantum-mechanical formalism, under closer scrutiny it turns out to give rise to a number of serious difficulties, both physical and philosophical. Caulton [4] discusses two major problems regarding the physics of quanta brought about by factorism. Firstly, the assumption of factorism produces incorrect predictions concerning the behavior of physical systems in the classical limit, as well as the behavior of quanta within the realm of quantum field theory. As [6] first observed, factorism cannot account for the emergence of well-defined classical trajectories of indistinguishable particles, since under this interpretation such particles always occupy the exact same (mixed) states regardless of their interactions with the environment. To that Caulton adds that the transition from QM to QFT is similarly threatened by factorism, since according to the latter theory quanta always occupy pure states.

The second physical problem is that factorism violates the interpretional rule stating that two unitarily equivalent algebras on Hilbert spaces should represent the same physical systems, provided that there is no physical quantity (not expressible in either algebra) that distinguishes such physical systems (for details see [4], pp. 14–16). On top of that, factorism may be seen as philosophically unpalatable, due to its close connection with the controversial metaphysical doctrine of haecceitism. In the context of physical theories Caulton defines haecceitism as asserting that mathematical states arrived at by permuting objects within the original state represent distinct physical possibilities. He then goes on to argue, somewhat surprisingly, that factorism coupled with the assumption of permutation invariance (PI) is actually logically independent from haecceitism. More specifically, according to Caulton haecceitism under factorism coupled with PI cannot be properly evaluated, since all accessible states (symmetric and antisymmetric ones) are stipulated to be invariant under permutations. Thus there are no two distinct mathematical states that would differ only with respect to permutations of individual particles. On the other hand, Caulton argues that if factorism is wrong, then the notion of a permutation cannot be properly defined in the standard formalism, and thus the question of whether haecceitism is true is becomes moot.

I have some reservations regarding Caulton’s analysis of the logical relations between factorism and haecceitism. To begin with, if we follow his definition of the latter, it seems that haecceitism is trivially false (which is even more surprising!) when factorism and PI are assumed. The truth of haecceitism is excluded from the outset, since we stipulate that permuted states do not differ even mathematically, let alone physically.⁵ However, it strikes me that Caulton’s concept of haecceitism is rather narrow. It does not take into account that the interpretation of the quantum-mechanical formalism advanced by factorism clearly makes a “haecceitistic” distinction between the way we individuate quantum particles (using non-qualitative labels) and the way we characterize them qualitatively by physical properties. Let us take, for instance, a symmetric bosonic state of the form $\frac{1}{\sqrt{2}}\left( |u \rangle |v \rangle + |v \rangle |u \rangle \right)$. Taken literally, this state is a superposition of two product states $\vert u \rangle \vert v \rangle$ and $\vert v \rangle \vert u \rangle$ that differ with respect to the permutation of particles 1 and 2. Even though such product states are not accessible to indistinguishable particles due to PI, this does not change the fact that they are physically meaningful (and necessarily distinct!) components of an accessible physical state. Thus factorism implies that it is meaningful to speak about distinct permuted physical states (even though they are uninstantiated), and this is in my mind some form of haecceitism.

To conclude, factorism is open to serious criticism from both the physical and philosophical perspectives. At the very least, this warrants looking for alternative ways of individuating components of systems of many particles, to which task we will turn in the next section.

3 Basic Assumptions

We consider a system $\Omega$ of N fermions of the same type. Let P be any projector operator of dimensionality dim($P)=d$ acting on the one-particle Hilbert space $\mathcal{H}$. Let us define a family of symmetric projectors operating on the s-fold tensor product $\otimes ^{s}\mathcal{H}$ as follows:

$$\begin{aligned} (\hbox {S})\,\,{{\sigma }_r}^s(P)=\hbox {Sym}\left( P^1 \otimes \ldots \otimes P^r \otimes {P_\perp } ^ {r +1} \otimes ...\otimes {P_\perp } ^s\right) , \end{aligned}$$

where $P_{\perp }=I$ – P, and Sym stands for the operation of summing over all possible tensor products of r projectors P and s–r projectors $P_{\perp }$.

We interpret operators ${\upsigma } _{r}^{s}(P)$ as representing the following intuitive statements:⁶

$$\begin{aligned} \hbox {(INT)} ``\hbox {Exactly } r \hbox { out of } s \hbox { particles possess property} P''. \end{aligned}$$

This interpretation is obviously correct in the case of distinguishable particles. In that situation operator ${\upsigma } _{r}^{s}(P)$ represents the quantum-mechanical disjunction “Either exactly particles 1, ... r possess P, or exactly particles 1, ..., r-1, r+1 possess property P, or ...”. However, when we treat indices as parts of the mathematical formalism with no direct physical meaning, we can’t offer an analogous justification for the accepted interpretation (INT). Instead, we can just stipulate that this is how we will read the operators. One may disagree with this stipulation, but as a consequence of this refusal one has to admit that statement (INT) has no proper representation in the quantum-mechanical formalism (clearly no other projector can do any better than S). This consequence is hard to swallow, as (INT) is manifestly permutation-invariant, and moreover it has a rather straightforward experimental sense (we can easily devise an experiment aimed at measuring whether exactly r out of s particles have a particular property).⁷

Now the main question is how to identify proper subsystems of the total system $\Omega$. We can’t use indices 1, ..., N for that purpose, since we have agreed that they do not correspond to any physical objects or properties thereof. The only available way is to use statements and properties that obey the requirement of permutation invariance, in particular expressed by operators (S). Caulton suggests that this can be done by accepting two intuitive criteria of the existence and uniqueness of subsystems:

$$\begin{aligned}&(\hbox {EX}) \hbox {There exists a subsystem } x \hbox { of } \Omega \hbox { such that E} (x, {{\upsigma }_{r}}^{r} (P)) \\&\quad \hbox {iff E}(\Omega , {\Sigma _{\mathrm{i=r}}^{N}} {\sigma _i}^N (P)).\\&({\hbox {UN}}) \hbox {If E} (\Omega ,{{\upsigma }_r}^N( P)),\hbox {then there is a unique subsystem }\\&\quad x \hbox { such that }\hbox {E}(x,{{\upsigma }_r}^r( P)). \end{aligned}$$

The expression of the form E(x, P) is meant to be read as “x possesses property P” (the possession of a property P by the whole system $\Omega$ may be interpreted in accordance with the usual eigenstate/eigenvalue link). The two criteria are easily justifiable by the intuitive meaning associated with operators (S). Criterion (EX) states that if it is the case that the total system $\Omega$ is characterized by the property “at least r out of N particles possess P” (expressed in the operator $\sum _{i=r}^N \sigma _i^N (P))$, then there must be a subsystem x of $\Omega$ consisting of r elements each of which possesses P. However, it is not guaranteed that there will be only one such system x (intuitively, and classically, if there are exactly $s>r$ particles constituting $\Omega$ that possess P, there will be $\left( {{\begin{array}{*{20}c} s \\ r \\ \end{array} }}\right)$ different combinations of r particles possessing P in the total ensemble, and therefore $\left( {{\begin{array}{*{20}c} s \\ r \\ \end{array} }}\right)$ different r-element subsystems – as we will soon see this number is completely off the mark in the quantum case, but the non-uniqueness remains a fact). On the other hand, if exactly r out of N particles constituting $\Omega$ possess P, it is only natural to admit that there is exactly one system x consisting of r particles with property P.

Our additional constraint is that system $\Omega$ has been prepared in a non-GMW-entangled state, which is equivalent to saying that E($\Omega$, ${\upsigma } _{N}^{N}(P))$ for some P such that dim($P)=N$. This equivalence can be explained as follows. A non-GMW-entangled state $\Phi$ of N fermions is a result of antisymmetrizing a direct product of N orthogonal vectors: $\Phi$ = Asym($\vert \varphi _{1} \rangle \otimes \quad \vert \varphi _{2} \rangle \otimes {\ldots }\otimes \quad \vert \varphi _{N}\rangle$). If we select P as the projector whose range is the N-dimensional subspace spanned by $\vert \varphi _{1} \rangle , {\ldots }, \vert \varphi _{N}\rangle$, it is clear that vector $\Phi$ defined above belongs to the range of ${\upsigma } _{N}^{N}(P)$, and hence $\Omega$ possesses the property represented by ${\upsigma } _{N}^{N}(P)$. On the other hand, if $\Omega$ possesses property ${\upsigma } _{N}^{N}(P)$, it can be proven that its state can be written down as the result of the antisymmetrization of any set of orthogonal vectors spanning ran(P).

4 The Main Result

The main theorem of Caulton’s paper asserts that there is a one-to-one correspondence between subsystems of $\Omega$ and one-particle projectors Q such that $Q \le P$ (and therefore between subsystems and subspaces, since projectors are in one-to-one correspondence with subspaces). More precisely the theorem states that:

$$\begin{aligned} \begin{array}{l} \hbox {If E}(\Omega ,{\upsigma } _N ^N(P)) \hbox { for some } P \hbox { such that dim}( P)=N,\hbox {then for every projector }\\ Q\,\hbox {of dimensionality dim} ( Q)=r \hbox { such that }Q\le P \hbox { there is exactly one subsystem }\\ x \hbox { such that E}\,(x,{\upsigma } _r ^r( Q)). \hbox {Moreover, for any subsystem x there is a unique projector }\\ Q\hbox { of dimensionality }r\in \left\{ {1,\ldots ,N} \right\} \hbox {such that E}(x,{\upsigma } _r ^r( Q))( r\,\hbox {will be called the}\\ \,\hbox {degree of system }x). \end{array} \end{aligned}$$

(4.1)

In order to establish the first part of the theorem, we have to make use of a lemma stating the following equivalence:

$$\begin{aligned} Q\le P,\hbox {where dim}( P)=s,\hbox { dim}( Q)=r,\hbox {iff}\sigma _s ^s( P)\le \sigma _r ^s( Q) \end{aligned}$$

(4.2)

A formal proof of lemma (4.2) can be found in [5]. From (4.2) the first part of theorem (4.1) follows immediately. The assumptions of the theorem enable us to derive that E($\Omega$, $\sigma _{r}^{N}(Q))$. By (UN) this implies that there is a unique x such that E(x, $\sigma _{r}^{r}(Q))$. In order to prove the second part of (4.1), we have to rely on an additional assumption which I will call Consistency:

$$\begin{aligned}&\hbox {(CON)}\quad \quad \quad \hbox {For all systems } x, y, \hbox { if E}\,(x, A) \hbox { and } \hbox {E}\, (y, B), \hbox {and}\, A, B\\&\hbox {are incompatible (non-commuting) one-dimensional projectors, then}\, x \ne y. \end{aligned}$$

Thus we are excluding the possibility that one and the same system could possess definite values of mutually incompatible observables. Let us now suppose that there are two one-particle projectors P and Q of dimensionality r such that E(x, ${\upsigma } _{r}^{r}(P))$ and E(x, ${\upsigma } _{r}^{r}(Q))$. But clearly ${\upsigma } _{r}^{r}(P)$ and ${\upsigma } _{r}^{r}(Q)$ are incompatible, since neither $P \le Q$ nor $Q \le P$. Moreover, it can be easily checked that both projectors are indeed one-dimensional when limited to the antisymmetric part of the tensor product of the Hilbert spaces $\mathcal{H}$. Thus by (CON) such a situation is impossible.⁸

The main conclusion from theorem (4.1) is that if the total system $\Omega$ is in the state $\sigma _{N}^{N}(P)$, then there is a one-to-one correspondence between subsystems of $\Omega$ and projectors Q such that Q $\le P$ (or, equivalently, subspaces of ran(P)). This fact has rather curious consequences for the metaphysics of quantum systems composed of indistinguishable fermions. Namely, we have to accept that a system that we typically describe as consisting of N indistinguishable fermions in fact contains uncountably many degree-one subsystems, as there are uncountably many one-dimensional subspaces of a given N-dimensional Hilbert space. This is what I call the problem of fermionic inflation.⁹

A simple example involving the anti-correlated spin-state of two electrons can illustrate the above result.¹⁰

$$\begin{aligned} \vert \uparrow _z \rangle \wedge \vert \downarrow _z \rangle =\frac{1}{\sqrt{2} }(\vert \uparrow _z \rangle \otimes \vert \downarrow _z \rangle -\vert \downarrow _z \rangle \otimes \vert \uparrow _z\rangle ). \end{aligned}$$

(4.3)

Let $P=\vert \uparrow _{z} \rangle \langle \uparrow _{z}\vert +\vert \downarrow _{z} \rangle \langle \downarrow _{z}\vert$, where dim(P) = 2, ran(P) = span{$\vert \uparrow _{z}\rangle , \vert \downarrow _{z}\rangle {\}} = \mathcal{H}={\mathbb C}^{2}$. The state of the system can be alternatively presented with the help of the projector ${\upsigma } _{2}^{2}(P)=P \otimes P$, which means that E($\Omega ,{\upsigma } _{2}^{2}(P))$ is true.

Any one-dimensional subspace (ray) X of ran(P) corresponds to a degree-1 system x such that E(x, ${\upsigma } _{1}^{1}(Q))$, where ran($Q)=X$. Thus there is a system x possessing spin $\vert \uparrow _{z}\rangle$ (and, as its complement, a system $x^\prime$ possessing spin $\vert \downarrow _{z}\rangle$). But there are uncountably many distinct degree-1 systems possessing properties represented by arbitrary superpositions of the form $a\vert \uparrow _{z}\rangle$ + $b\vert \downarrow _{z}\rangle$, which is an eigenstate for spin in some direction other than z. Thus for any spatial direction, there is a distinct degree-one subsystem y of the purportedly 2-particle system such that y possesses a definite value of spin in this direction. Or, in other words, we can “split” the total system in such a way that one component will have spin up in an arbitrarily selected direction, while the other component will have spin down. The number of such alternative splittings is equal to the number of directions in three dimensions, which is continuum.

The situation described above is hard to accept on many counts. First of all, as Caulton proves in detail, the set of subsystems of a given fermionic composite system violates the basic axioms of mereology under a plausible interpretation of the parthood relation. If we define the relation “subsystem x is a part of subsystem y” as “the subspace associated with x is included in the subspace associated with y” (see footnote 8 for further comments), then it is easy to notice that not all subsystems will jointly compose mereological wholes. For instance, using the above example let us consider two degree-one subsystems $x_{1}$ and $y_{1}$ associated, respectively, with rays $\vert \uparrow _{z}\rangle$ and $\vert \downarrow _{z}\rangle$. If the mereological sum of $x_{1}$ and $y_{1}$ existed, it would have to be a degree-two subsystem, of which both $x_{1 }$ and $y_{1}$ are parts. The only such subsystem is just the whole system. But now we can observe that the degree-one subsystem $z_{1}$ defined by the ray $\vert \uparrow _{x}\rangle$ is a part of the mereological sum $x_{1} \sqcup y_{1}$, and yet it overlaps with neither $x_{1}$ nor $y_{2}$, since the respective one-dimensional subspaces have no common elements except the zero vector. This is clearly a breach of one of the fundamental axioms of mereology.¹¹

But even without introducing mereological concepts and axioms into the picture we are clearly facing a serious interpretational challenge. Accepting the existence of an uncountable number of distinct degree-one subsystems within a fermionic composite system constituted by a finite number of particles is inflationary in the highest degree.¹² Instead of N particles that were originally assumed to compose the considered system of indistinguishable fermions, we now have a multitude of numerically distinct physical objects each equipped with their own unique identity characterized by an appropriate subspace/projector. In some respects this consequence can be seen as more troublesome than the widely touted violation of the Principle of the Identity of Indiscernibles by quanta. Finding a solution to the revealed problem is a pressing matter for the proponents of the new, unorthodox interpretation of the individuation of quantum particles. Below I will formulate several strategies of dealing with the inflationary character of the admitted metaphysics of fermionic compositions, and I will briefly discuss their advantages and disadvantages.¹³

5 Solutions

5.1 Perspectivalism

One natural strategy is to insist that it is not the number of distinct subsystems (and thus mind-independent entities) that is being inflated here, but merely the number of distinct perspectives. In order to decompose a given composite system into subsystems of decreasing degrees, we have to select first a complete set of compatible observables (or, equivalently, a set of orthogonal rays/one-dimensional projectors). More specifically, let us assume that we have a composite system $\Omega$ of N indistinguishable fermions and a one-particle projector P for which E($\Omega$, ${\upsigma } _{N}^{N}(P))$. Now we should select an orthogonal basis ${\{}\vert \upvarphi _{i}\rangle {\}}, i = 1,{\ldots }, N$ for the subspace ran(P). We will assume that relative to this choice, the subsystems of $\Omega$ are in one-to-one correspondence not with all subspaces of ran(P), but with the subspaces spanned by some of the vectors $\vert \upvarphi _{i}\rangle$. Thus the number of distinct subsystems of degree k will be given by the number of k-element combinations out of N elements, i.e. $\left( {{\begin{array}{*{20}c} N \\ k \\ \end{array} }}\right)$, exactly as in the case of classical mereological systems composed of N atomic elements.

To illustrate this approach, let us use the example introduced earlier. In example 4.3 we selected a basis for the two-dimensional space associated with the entire system in the form of two spin-vectors $\vert \uparrow _{z}\rangle$ and $\vert \downarrow _{z}\rangle$. Relative to this choice, there are only two subsystems of degree one, of which one has spin up in the direction z, and the other spin down. Relative to a different choice of the basis we will have a different identification of the subsystems, but it does not make sense to assume that subsystems defined with the help of different selections of the basis co-exist with each other. The subsystem identified by spin up in the z-direction exists only with respect to the previous choice of the basis as given by $\vert \uparrow _{z}\rangle$ and $\vert \downarrow _{z}\rangle$. With respect to an alternative choice of the basis, this subsystem simply does not exist.

The violation of the mereological principles no longer threatens, since the structure of all subspaces spanned by orthogonal vectors from the selected basis is that of a Boolean lattice (for details see [5], pp. 317–318). However, the question remains of how to independently justify the requirement of relativizing the decomposition of the total system into subsystems to a particular set of orthogonal rays. Relativizations of a similar kind are not uncommon in some interpretations of quantum mechanics, including the Everettian relative-state interpretation.¹⁴ However, the details of Everett’s proposal differ crucially from the outlined perspectivalist solution. Everett’s formulation of QM is based on the principle of the fundamental relativity of states, according to which a subsystem of a composite system can be assigned its state only relative to the state of the remainder of the system. In the current approach, on the other hand, the very partition of the system into subsystems, and consequently the existence of particular subsystems, is relative to the previous choice of an orthogonal basis. One should note though that the relativization to a selected basis of the Hilbert space resembles yet another and quite popular take on Everett’s approach which is based on the assumption that the quantum state of the entire universe can be decomposed into a superposition of orthogonal terms corresponding to distinct worlds that exist parallel to each other (see [27] for further details). The well-known problem affecting this approach is that there is an infinite number of ways in which the state of the universe can be decomposed into orthogonal components. Thus, the proponents of the many-worlds interpretation suggest selecting a preferred basis into which such a decomposition should be performed, and which would guarantee that individual worlds contain macroscopic objects with well-defined locations. This solution prompts a similar treatment of the problem of fermionic inflation, as discussed in the next subsection.

5.2 Preferred Basis

One way of getting around the conceptual problems with the relativization to an arbitrary choice of basis is to argue that there is a particular basis which should be preferred to any other in all metaphysically-committing contexts. A natural choice for such a preferred basis is provided by the eigenstates of the position operator. Position seems to play a special role in quantum-mechanical contexts for various reasons. It may be argued, for instance, that our perceptual apparatus uses spatial features more often than other properties in order to identify and delineate macroscopic objects. Moreover, quantum-mechanical measurements require a well-defined location of the measuring apparatus and the measured system. It is also worth pointing out that one of the most popular alternative interpretations of QM, namely the spontaneous localization theory (also known as the GRW theory), explicitly treats position as the privileged parameter due to the spatial character of the random “jumps” (i.e. spontaneous localizations of a given quantum system at a certain position) postulated by the theory (see [13]). For these reasons it may be considered intuitive to prefer those formally admissible decompositions of a given total system that possess precise spatial locations.

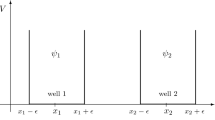
In order to discuss this solution in more detail, we have to consider an example of a state which has spatial as well as internal degrees of freedom. The simplest such case is provided by a slight modification of Example 4.3 above with two position eigenvectors $\vert L\rangle$ and $\vert R\rangle$ added as follows:¹⁵

$$\begin{aligned} \vert \uparrow \rangle \vert L \rangle \wedge \vert \downarrow \rangle \vert R \rangle =\frac{1}{\sqrt{2} }(\vert \uparrow \rangle \vert L\rangle \otimes \vert \downarrow \rangle \vert R \rangle -\vert \downarrow \rangle \vert R \rangle \otimes \vert \uparrow \rangle \vert L\rangle ) \end{aligned}$$

(5.1)

Even though there are an infinite number of orthogonal vectors spanning the two-dimensional subspace corresponding to this state, the only such vectors whose position components are well-defined are $\vert \uparrow \rangle \vert L\rangle$ and $\vert \downarrow \rangle \vert R\rangle$. Thus we can insist that there are only two components of the entire system: one with spin up and located in L, and the other with spin down and location in region R.

However, we have to keep in mind that for some subspaces it may be impossible to find an orthogonal basis consisting of eigenvectors for position. We can give an example of such a situation using the above-introduced toy model. Consider the following non-GMW-entangled state of the two-particle system:

$$\begin{aligned}&\vert \uparrow \rangle (\vert L\rangle + {\vert }R \rangle ) \wedge \vert \downarrow \rangle (\vert L\rangle -\vert R\rangle )\nonumber \\&\quad =\frac{1}{\sqrt{2} }(\vert \uparrow \rangle (\vert L \rangle + {\vert }R\rangle )\otimes \vert \downarrow \rangle (\vert L\rangle -\,{\vert }R\rangle )\nonumber \\&\qquad -\vert \downarrow \rangle (\vert L \rangle -{\vert }R\rangle )\otimes \vert \uparrow \rangle (\vert L\rangle + {\vert }R\rangle ) \end{aligned}$$

(5.2)

The subspace of the entire four-dimensional space corresponding to the above state is given by $s(\Omega ) = \hbox {span}\,{\{}\vert \uparrow \rangle \vert L\rangle + \vert \uparrow \rangle \vert R\rangle , \vert \downarrow \rangle \vert L\rangle -\vert \downarrow \rangle \vert R \rangle {\}}.$ It is easy to observe that no vector of the form $\vert \upvarphi \rangle \vert R\rangle$ (or $\vert \upvarphi \rangle \vert L\rangle$) belongs to this subspace, hence there is no orthogonal basis of $s(\Omega )$ whose elements represent states with well-defined positions. In that case the suggested strategy is to prefer the decomposition of the system relative to the selected basis vectors which factorize into the internal and spatial degrees of freedom. In our case these will simply be the orthogonal vectors $\vert \uparrow \rangle (\vert L\rangle + \vert R\rangle )$ and $\vert \downarrow \rangle (\vert L\rangle - \vert R\rangle$), as opposed to any alternative selection of the combination $a\vert \uparrow \rangle (\vert L\rangle + \vert R\rangle$) + $b\vert \downarrow \rangle (\vert L\rangle - \vert R\rangle$) and $b^*\vert \uparrow \rangle (\vert L\rangle + \vert R\rangle )- a^*\vert \downarrow \rangle (\vert L\rangle -\vert R\rangle ).$

Another challenge to consider is that the “factorizable” basis of a given subspace is not guaranteed to be unique. Consequently, the problem of the excess of alternative decompositions into subsystems persists in some cases. To see this in more detail, let us consider the following admissible state of two fermions:

$$\begin{aligned} \vert \uparrow \rangle \vert L \rangle \wedge \vert \downarrow \rangle \vert L\rangle = \frac{1}{\sqrt{2} }(\vert \uparrow \rangle \vert L \rangle \otimes \vert \downarrow \rangle \vert L\rangle -\vert \downarrow \rangle \vert L \rangle \otimes \vert \uparrow \rangle \vert L\rangle ) \end{aligned}$$

(5.3)

In this case there are still an infinite number of one-dimensional subspaces associated with the well-defined position L, defined as follows: ($a\vert \uparrow \rangle + b\vert \downarrow \rangle ) \vert L\rangle$. As a result, we have to admit the existence of uncountably many degree-one subsystems, each with the precise location L but with different components of spin determined. As we will see later, this limited variant of the inflationary problem may be something that we can learn to live with, but for the time being let us consider an alternative solution.

5.3 Systems with Incompatible Properties

One of the key assumptions leading directly to the runaway inflation of the number of distinct subsystems is condition (CON), which essentially implies that subsystems associated with distinct subspaces are always distinct. Thus one logically possible way to block the unwanted conclusion is to reject (CON). This move opens up the possibility of assuming that the number of components of a given degree will remain exactly as in the classical case of N atomic objects. However, as a result we will have to admit that individual subsystems are characterized by sets of incompatible properties. For instance, in Example 4.3 we would have two degree-one subsystems possessing definite values of spin in different directions. For that reason the currently considered proposal is open to two immediate objections.

One obvious reaction to the rejection of (CON) is that such a move violates the fundamental interpretational rule of quantum mechanics (implicitly included in the eigenstate/eigenvalue link), according to which any system can (at best) be in exactly one pure state represented by a ray in the appropriate Hilbert space. If we want to insist that there are only two degree-one subsystems of the system from Example 4.3, we have to associate each subsystem with an infinite number of distinct rays, which is not permitted in the standard quantum-mechanical formalism. As a consequence, a particular system receives a number of definite values of measurable quantities which exceeds what is usually admitted under the orthodox interpretation of quantum mechanics.

The second possible objection is that the distribution of all the available properties among the set of admitted subsystems of a given degree is fundamentally undetermined by the quantum-mechanical rules. Again, we can rely on Example 4.3 to illustrate this straightforward observation. Let us use spins in the z direction to individuate two admissible subsystems of degree one: subsystem “up” is designated as the one possessing $\vert \uparrow _{z}\rangle$ and subsystem “down” as the one with the property $\vert \downarrow _{z}\rangle$. Now consider spin $\vert \uparrow _{x}\rangle$, which is possessed by some system of degree one. Which system would it be: “up” or “down”? Nothing in the formalism that we have introduced so far can determine whether spin $\vert \uparrow _{x}\rangle$ should be paired up with $\vert \uparrow _{z}\rangle$ or with $\vert \downarrow _{z}\rangle$. And this goes for any pair of mutually incompatible observables A and B: we will never know whether they are possessed by the same system, or by the complementary systems.

The problems described above are serious, but not necessarily insurmountable. Regarding the violation of the quantum-mechanical restrictions on the number of definite properties possessed by a system, one can observe that the specific way these restrictions are breached in the proposed approach does not lead to any observable or measurable consequences (such as Bell’s inequalities) that could be subject to empirical falsification. The reason for that has to do with the special role position plays in quantum-mechanical measurements that we alluded to earlier. In order to perform any measurement that could potentially reveal that the actual states of subsystems contain more information than is allowed in standard quantum-mechanics, we have to prepare the total system in a state such that some of its subsystems will be spatially distinguishable by their respective locations. But this implies that the incompatible properties attributed to these subsystems will be associated with intricate superpositions of states possessing different locations, and thus no standard measurements can reveal values of such quantities.¹⁶

This can be seen more clearly when we consider the state of a two-particle system given in example 5.1 above. The total system can be split into two subsystems: one occupying the state $\vert \uparrow \rangle \vert L\rangle$ and the other associated with the orthogonal state $\vert \downarrow \rangle \vert R$. This can suggest, on a superficial reading, that we may be able to reveal that the particle located in L possesses a bunch of incompatible spin-components in various directions. However, this claim is incorrect. The incompatible properties attributed to both systems are not of the form $\vert \uparrow \rangle \vert L\rangle (\vert \uparrow \rangle \vert R\rangle$) but rather $a\vert \uparrow \rangle \vert L\rangle + b\vert \downarrow \rangle \vert R\rangle$. There is no standard experimental procedure that could reveal values for projectors of that form (see [14], p. 86). Still, the indeterminacy problem persists, not on the level of empirical data but of objective facts. Our best theory fails to give us any clue as to which properties should be attributed to which subsystems, and this can be viewed as a setback.

5.4 Mixed View

I suggest that we could consider combining the Preferred Basis and the Incompatible Properties solutions in a way which would strengthen their individual advantages. The starting point is to assume, in accordance with the first solution, that the only objectively existing subsystems are those whose individual states can be decomposed into the internal and spatial degrees of freedom, and whose spatial degrees of freedom are distinct. This assumption clearly privileges position as our preferred way of individuating particular subsystems, and – more importantly – as the ontological basis for the objective, observer-independent existence of individual quantum systems. However, when such an individuation is impossible to achieve due to the fact that the complementary subsystems possess the same spatial location, we can turn to the incompatibility view and argue that in this case incompatible internal properties are distributed among the finite “classical” number of quantum systems located in the same region. I believe that in this case the discomfort caused by the fundamental ontological underdetermination of the exact way these internal properties are distributed should be minimal due to the fact that the systems in question cannot be properly (i.e. spatially) individuated anyway. All there is to know in such a case is that there are a precise number of co-located systems, each equipped with some combination of incompatible properties representing internal degrees of freedom. And it goes without saying that this fact is perfectly consistent with all experimental data supporting the standard quantum theory. If we wanted to perform a measurement aimed at revealing the existence of systems with more definite values than admitted by the standard formalism, we would have to individuate these systems by separating them in space. But this move would create a situation in which different locations would ontologically privilege some systems and their (compatible) properties rather than the others, so the problem of incompatible properties (even in the non-measurable form involving superpositions of distinct locations) would no longer arise.

Contrasting the currently proposed solution with the preferred basis approach we should emphasize that the only difference between the two strategies lies in their treatment of cases when subsystems of a given system spatially coincide. Under the mixed view this situation is described as involving a classical number of particles possessing incompatible properties, while the preferred basis solution implies that in that case the number of particles becomes infinite. As neither description is directly testable by experiment, the choice between the two comes down to the decision whether to preserve some fundamental ontological intuitions at the expense of the quantum-mechanical rules, or to abandon our pre-theoretical ontological intuitions in order to preserve the uniform applicability of the QM rules. I prefer the first option, but I acknowledge that some philosophers may have good reasons to lean towards the second.

6 Conclusion

There are two basic approaches to the problem of the individuation of quantum particles of the same type. The orthodox approach uses the indices present in the mathematical formalization of the multiparticle states as a means of referring to separate particles and collections thereof. The unorthodox approach, on the other hand, relies entirely on (symmetrized) properties of the whole system in the task of identifying its constituting elements. The most natural method to accomplish this task is through the formalization of the statements of the form “r out of s elements possess property P”, which can be achieved with the help of symmetric combinations of products of r copies of the corresponding projector P and $s-$ r copies of the orthogonal projector $P_{\perp }$. I have shown that the individuation based on the above-mentioned qualitative and permutation-invariant characteristics leads to the proliferation of the number of distinct subsystems of a given system. Several solutions to this problem can be advanced. My preferred solution is to argue that among the formally admitted subsystems that correspond to arbitrary subspaces of the space associated with the total system, only those subsystems exist whose states decompose into internal degrees of freedom and spatial degrees of freedom, and moreover whose spatial properties are distinct from each other. In other words, we use locations in space as an ontologically preferred way to identify subsystems of a given system. In cases when such an identification is impossible due to the coinciding spatial locations of individual components, we can reduce the number of distinct subsystems of a given degree by admitting systems with incompatible properties. One undeniable disadvantage of this solution is that it admits that the distribution of the incompatible properties among the existing subsystems is fundamentally indeterminate. But it can be argued that this fact poses no serious threat (for instance in the form of empirical predictions contradicting the predictions of standard quantum mechanics). In addition, the proposed solution automatically takes care of the apparent violation of the mereological principles revealed in [5]. This is so, because the admitted subsystems display the well-known structure of a classical Boolean algebra.