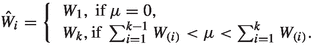Statistical inference of inverted Nadarajah–Haghighi distribution under type-II generalized hybrid censoring competing risks data

Abstract

Tahir et al. (J Stat Comput Simul 88(14):2775–2798, 2018) introduced the inverse Nadarajah–Haghighi distribution (INHD) and demonstrated its ability to model positive real data sets with decreasing and upside-down bathtub hazard rate shapes. This article focuses on the inference of unknown parameters using a generalized Type-II hybrid censoring scheme (GT-II HCS) for the INHD in the presence of competing risks. The maximum likelihood (ML) and Bayes approaches are used to estimate the model parameters. Based on the squared error loss function, we compute Bayes estimates using Markov Chain Monte Carlo (MCMC) by applying Metropolis-Hasting (M-H) algorithm. Furthermore, the asymptotic confidence intervals, bootstrap confidence intervals (BCIs) and the highest posterior density (HPD) credible intervals are constructed. Using real data sets and simulation studies, we examined the introduced methods of inference with different sample sizes.

1 Introduction

In literature, censoring has aroused great concern, and many researchers have discussed new censoring strategies and constructed inferences from several reliability studies and life tests. Type-I (T-I) and type-II (T-II) censoring are the two widely and commonly schemes. The combination of T-I and T-II censoring is introduced as a hybrid censoring scheme (HCS), see Childs et al. [1]. The HCS can be characterized statistically by: let $X_{m:n}$ denote the $m^{th}$ failure time in which n items are employed in a lifetime and the prescribed test termination time presented by T. Under T-I HCS, the experiment is completed at a random time $T^{*}=\min \{X_{m:n},T \}$: $T\in (0,\infty )$ and $1\le m \le n$. However, a fixed number of failures was satisfied by T-II HCS. Thus, in T-II HCS, the random completed time of the test is $T^{*}=\max \{X_{m:n},T\}$, to satisfy that at least m failures are observed.

There is more information about the T-I HCS presented by Gupta and Kundu [2] and Kundu and Pradhan [3]. Also, Banerjee and Kundu [4] have some considerable literature based on T-II HCS. However, T-I HCS and T-II HCS both have some drawbacks. The absence of an elasticity test in a small period of time and to get a large number of failures are the foremost disadvantages of them. For more details, one may refer to Abushal et al. [5], Abushal et al. [6], Abushal et al. [7], Tolba et al. [8], Ramadan et al. [9], Sarhan et al. [10] and Sarhan et al. [11].

Thus, we are driven straightforward to the range of generalized HCS (GHCS), see Chandrasekar et al. [12]. Furthermore, due to more observed failure samples, inference works more efficiently with GHCS. T-I and T-II GHCSs are expressed as:

1-In Generalized Type-I HCS (GT-I HCS): Let n be the independent units in the experiment, and $\varrho$ placed the object number that should be observed. The prior integers $(\varrho ,$ m),  satisfy that $1<\varrho <m\le n$. When the failure time $X_{\varrho }$ $<T,$ the test is completed at min($X_{m}$, T). Also, if $X_{\varrho }$ $>T$ then $X_{\varrho }$ is the completed test time. In this case, ($T^{*}$, R) is defined by

where T is the ideal test time, $T^{*}$ is the experiment completed time, and R is the observed number failure times.

2-In Generalized Type-II HCS (GT-II HCS): Chandrasekar et al [12] introduced the GT-II HCS as a modification of the T-II HCS. Consider n independent units are put in the test where the fixed integer $m\ \in \{1,2,...,n\},$ and the two prior times $0<T _{1}<T _{2}<\infty$. The time to failure $X_{i}$ is recorded until the time $T_{1}$ is appears. Here we are faced with one of three possibilities:

When, the time to failure $X_{m}$ $<T _{1},$ the experiment is terminated at $T_{1}$. But if $T _{1}<X_{m}<T _{2}$, the experiment is terminated at $X_{m}$. Covered by this scheme, if $T _{1}<T_{2}<X_{m}$ hence, the experiment is terminated at $T _{2}$. Accordingly, ($T^{*}$, R) is given by

The experiment in GT-II HCS has ensured that it will be ended by time $T _{2}$. As a result, time $T_{2}$ represents the amount of time that the experimenter is interested to devote to completing the experiment. If the researcher needs to remove the units from the experiment at any point, excluding the terminal point, we are driven straight away to the range of progressive censoring schemes (PCSs). For a detailed description of PCSs, see Balakrishnan and Cramer [13].

In their pioneering paper, Nadarajah and Haghighi [14] introduced one of the widely used statistical distributions that can be used as an extension of the usual exponential distribution, which was lately named Nadarajah and Haghighi distribution (NHD) as an abbreviation of the authors’ names. Nadarajah and Haghighi [14] demonstrated that NHD’s density can be decreasing and that unimodal shapes, in addition to its hazard rate function (HRF) have a decreasing, increasing, or constant shape similar to Weibull, gamma, and generalized exponential distributions. Recently, Tahir et al. [15] proposed the inverse Nadarajah–Haghighi distribution (INHD) and demonstrated that the suggested model is extremely flexible for modeling real data sets that exhibit. Elshahhat and Rastogi [16] compared INHD with 10 inverted distributions. INHD is the best in the literature. Numerous authors have studied the INHD estimation problems, For example, Abo-Kasem et al. [17] investigated the reliability analysis of the INHD with an adaptive T-I PHCS. Elshahhat et al. [18], considered the estimation problems of INHD parameters under T-II PCS.

Suppose there is a random variable X following INHD where $\beta$ and $\theta$ are the scale and the shape parameters the cumulative distribution function cdf expressed by

$$\begin{aligned} F(x|\beta ,\theta )=e^{1-(1+\frac{\beta }{x})^{\theta }},\text { }x>0;\text { } \theta ,\text { }\beta >0,\, \end{aligned}$$

(1)

This paper addresses an important issue in life testing known as the competing risks problem. The problem of modeling competing risks model under GT-II HCS when the failure time of units distributed by INHD is our objective in this research. Building the model and analyzing a set of real data under the suggested model are developed. The ML method and Bayes method are used to compute the point estimates of model parameters. The ACIs, bootstrap interval and HPD credible interval are also constructed. All findings are discussed and contrasted using a Monte Carlo study.

The paper is structured as follows: The model and its assumptions are presented in Sect. 2. In Sect. 2, we obtained the MLE and the Bayesian analysis with SEL function, also, covers the interval estimation: ACIs based on the MLEs, bootstrap interval and HPD credible interval are shown. In Sect. 3, we examine real data life, Simulate data set and conduct a simulation study to demonstrate the estimating methods presented in this research. Section 4 represents the concluding remarks.

2 Methodology

Here, the model and its assumptions are formulated under consideration unit lifetime has INHD. The point estimations of model parameters are formulated by the MLE and Bayesian approaches. Also, interval estimators are formulated under the asymptotic property of MLEs, bootstrap techniques and HPD credible intervals.

2.1 Modeling

Let n be identical independent distributed (i.i.d.) units have the lifetimes $X_{1},$ $X_{2},$ ...,  $X_{n}$. Under GT-II HCS, we consider number m (number of failure time needing for statistical inference) and two times $T_{1}$ and $T_{2}$ (minimum and maximum test time) are prior proposed. Further, during the experiment, recorded the failure times and the corresponding cause of failure can be expresses as ($X_{i;m,n},$ $\eta _{i}$), $1<i\le n$. The experiment is continual until test terminate time $T ^{*}$ is reached. The time $T ^{*}=T _{1}$ if $X_{m}<T _{1}$ and $T ^{*}=T _{2}$ if $T _{2}<X_{m}.$ But, $T ^{*}=$ $X_{m}$ if $T _{1}<X_{m}<T _{2}.$ Suppose that, a random sample reached to $T ^{*}$ is denoted by ${{\textbf {X}}}=${($X_{1;m,n},$ $\eta _{1}$), ($X_{2;m,n},$ $\eta _{2}$),..., ($X_{R;m,n},$ $\eta _{R}$)}, where $R>m$ if $T ^{*}=T _{1},$ $R<m$ if $T ^{*}=T _{2}$ and $R=m$ if $T ^{*}=$ $X_{m}.$ The joint likelihood function for given GT-II HCS ${{\textbf {X}}}=${($X_{1;m,n},$ $\eta _{1}$), ($X_{2;m,n},$ $\eta _{2}$),..., ($X_{R;m,n},$ $\eta _{R}$)} is represented by

$$\begin{aligned} L({\textbf{X}}|\Theta )=Q\left( S_{1}(T ^{*})S_{2}(T ^{*})\right) ^{n-R}\prod \limits _{i=1}^{R}\left[ f_{1}(x_{i})S_{2}(x_{i})\right] ^{I(\eta _{i}=1)}\left[ f_{2}(x_{i})S_{1}(x_{i})\right] ^{I(\eta _{i}=2)}, \nonumber \\ \end{aligned}$$

(2)

where $Q=\frac{n!}{(n-d)!},$ $S(.)=1-F(.),$ for simplisty $x_{i}$= $x_{i;m,n}$ and $I(\eta _{i}=j)$ is defined by

(3)

Model assumptions

• 1. The latent failure time $X_{i}=\min (X_{i1},$ $X_{i2}),i=1,$ 2,  ...,  R.

• 2. The latent failure times obtained under the causes of failure $\eta _{i}=j,$ $j=1,$ 2 are given by, $X_{1}=${($X_{11},$ 1), ($X_{12},$ 1 ),..., ($X_{1m_{1}},$ 1)} and $X_{2}=${($X_{21},$ 2), ($X_{22},$ 2 ),..., ($X_{2m_{2}},$ 2)}, where $m_{1}=\sum \limits _{i=1}^{R}I(\eta _{i}=1)$ and $m_{2}=\sum \limits _{i=1}^{R}I(\eta _{i}=2)$.

• 3. The latent failure timerespected to cause j,  $j=1,$ 2 has INHD with scale parameters $\beta _{j},j=1,2$ and shape parameter $\theta$. Therefore, the cdf of INHD can be computed as

  $$\begin{aligned} F_{j}(t|\beta _{j},\theta )=e^{1-(1+\frac{\beta _{j}}{x})^{\theta }},\text { } x>0,\text { }\beta _{1},\text { }\beta _{2},\text { }\theta >0, \end{aligned}$$

  (4)
  $$\begin{aligned} f_{j}(t|\beta _{j},\theta )\mathbf {=}\frac{\beta _{j}\theta }{x^{2}}(1+\frac{ \beta _{j}}{x})^{\theta -1}e^{1-(1+\frac{\beta _{j}}{x})^{\theta }}, \text { } x>0,\text { }\beta _{1},\text { }\beta _{2},\text { }\theta >0. \end{aligned}$$

  (5)

2.2 Point estimation

2.2.1 MLE

In specific, by subject the experiment to GT-II HCS explained by subsection 2.1. The likelihood function (2) for a given GT-II HCS competing risks sample and INHD given by (4) and (5) is reduced to

$$\begin{aligned} L(\Theta |{\textbf{X}})= & {} Q\beta _{1}^{m_{1}}\beta _{2}^{m_{2}}\theta ^{R}\left( 1-e^{1-(1+\frac{\beta _{1}}{T ^{*}})^{\theta }}\right) ^{n-R}\left( 1-e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }}\right) ^{n-R}\prod \limits _{i=1}^{R}\frac{1}{x_{i}^{2}} \nonumber \\{} & {} \times \,\prod \limits _{i=1}^{m_{1}}(1+\frac{\beta _{1}}{x_{1i}})^{\theta -1}e^{1-(1+ \frac{\beta _{1}}{x_{1i}})^{\theta }}\left( 1-e^{1-(1+\frac{\beta _{2}}{ x_{1i}})^{\theta }}\right) \nonumber \\{} & {} \times \,\prod \limits _{i=1}^{m_{2}}(1+\frac{\beta _{2}}{x_{2i}})^{\theta -1}e^{1-(1+ \frac{\beta _{2}}{x_{2i}})^{\theta }}\left( 1-e^{1-(1+\frac{\beta _{1}}{ x_{2i}})^{\theta }}\right) . \end{aligned}$$

(6)

The log-likelihood function (6) without normalized constant is expressed as

$$\begin{aligned} \ell (\Theta |{\textbf{X}})= & {} \log L(\Theta |{\textbf{X}})=\,m_{1}\log \beta _{1}+m_{2}\log \beta _{2}+R\log \theta \nonumber \\{} & {} +\left( n-R\right) \left\{ \log \left[ 1-e^{1-(1+\frac{\beta _{1}}{T ^{*}})^{\theta }}\right] \right. \nonumber \\{} & {} \left. +\log \left[ 1-e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }} \right] \right\} +\left( \theta -1\right) \sum \limits _{i=1}^{m_{1}}\log \left[ 1+\frac{\beta _{1}}{x_{1i}}\right] \nonumber \\{} & {} +\sum \limits _{i=1}^{m_{1}}\left( 1-(1+\frac{\beta _{1}}{x_{1i}})^{\theta }\right) \nonumber \\{} & {} +\sum \limits _{i=1}^{m_{1}}\log \left[ 1-e^{1-(1+\frac{\beta _{2}}{x_{1i}} )^{\theta }}\right] +\left( \theta -1\right) \sum \limits _{i=1}^{m_{2}}\log \left[ 1+\frac{\beta _{2}}{x_{2i}}\right] \nonumber \\{} & {} +\sum \limits _{i=1}^{m_{2}}\left( 1-(1+\frac{\beta _{2}}{x_{2i}})^{\theta }\right) \nonumber \\{} & {} +\sum \limits _{i=1}^{m_{2}}\log \left[ 1-e^{1-(1+\frac{\beta _{1}}{x_{2i}} )^{\theta }}\right] . \end{aligned}$$

(7)

Taking derivatives with respect to $\Theta =\{\beta _{1},$ $\beta _{2},$ $\theta$} of (7)

$$\begin{aligned} \frac{\partial \ell (\Theta |{\textbf{X}})}{\partial \beta _{1}}= & {} \frac{m_{1} }{\beta _{1}}+\theta \left( n-R\right) \frac{(1+\frac{\beta _{1}}{T ^{*}})^{\theta -1}e^{1-(1+\frac{\beta _{1}}{T ^{*}})^{\theta }}}{ T ^{*}\left( 1-e^{1-(1+\frac{\beta _{1}}{T ^{*}})^{\theta }}\right) }+\left( \theta -1\right) \sum \limits _{i=1}^{m_{1}}\frac{1}{ x_{1i}\left( 1+\frac{\beta _{1}}{x_{1i}}\right) } \nonumber \\{} & {} -\theta \sum \limits _{i=1}^{m_{1}}\frac{1}{x_{1i}}(1+\frac{\beta _{1}}{ x_{1i}})^{\theta -1}+\theta \sum \limits _{i=1}^{m_{2}}\frac{(1+\frac{\beta _{1}}{x_{2i}})^{\theta -1}e^{1-(1+\frac{\beta _{1}}{x_{2i}})^{\theta }}}{ x_{2i}\left( 1-e^{1-(1+\frac{\beta _{1}}{x_{2i}})^{\theta }}\right) }, \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial \ell (\Theta |{\textbf{X}})}{\partial \beta _{2}}= & {} \frac{m_{2} }{\beta _{2}}+\theta \left( n-R\right) \frac{(1+\frac{\beta _{2}}{T ^{*}})^{\theta -1}e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }}}{ T ^{*}\left( 1-e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }}\right) }+\left( \theta -1\right) \sum \limits _{i=1}^{m_{2}}\frac{1}{ x_{2i}\left( 1+\frac{\beta _{2}}{x_{2i}}\right) } \nonumber \\{} & {} -\theta \sum \limits _{i=1}^{m_{2}}\frac{1}{x_{2i}}(1+\frac{\beta _{2}}{ x_{2i}})^{\theta -1}+\theta \sum \limits _{i=1}^{m_{1}}\frac{(1+\frac{\beta _{2}}{x_{1i}})^{\theta -1}e^{1-(1+\frac{\beta _{2}}{x_{1i}})^{\theta }}}{ x_{1i}\left( 1-e^{1-(1+\frac{\beta _{2}}{x_{1i}})^{\theta }}\right) }, \end{aligned}$$

(9)

and

$$\begin{aligned} \frac{\partial \ell (\Theta |{\textbf{X}})}{\partial \theta }= & {} \frac{R}{ \theta }+\left( n-R\right) \frac{(1+\frac{\beta _{1}}{T ^{*}} )^{\theta }\log \left[ 1+\frac{\beta _{1}}{T ^{*}}\right] e^{1-(1+ \frac{\beta _{1}}{T ^{*}})^{\theta }}}{1-e^{1-(1+\frac{\beta _{1}}{ T ^{*}})^{\theta }}}+\sum \limits _{i=1}^{m_{1}}\log \left[ 1+\frac{ \beta _{1}}{x_{1i}}\right] \nonumber \\{} & {} -\sum \limits _{i=1}^{m_{1}}\left( 1+\frac{\beta _{1}}{x_{1i}}\right) ^{\theta }\log \left[ 1+\frac{\beta _{1}}{x_{1i}}\right] \nonumber \\{} & {} +\sum \limits _{i=1}^{m_{2}}\frac{\left( 1+\frac{\beta _{1}}{x_{2i}}\right) ^{\theta }\log \left[ 1+\frac{\beta _{1}}{x_{2i}}\right] e^{1-(1+\frac{\beta _{1}}{x_{2i}})^{\theta }}}{1-e^{1-(1+\frac{\beta _{1}}{x_{2i}})^{\theta }}} \nonumber \\{} & {} +\left( n-R\right) \frac{(1+\frac{\beta _{2}}{T ^{*}})^{\theta }\log \left[ 1+\frac{\beta _{2}}{T ^{*}}\right] e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }}}{1-e^{1-(1+\frac{\beta _{2}}{T ^{*}} )^{\theta }}}+\sum \limits _{i=1}^{m_{2}}\log \left[ 1+\frac{\beta _{2}}{x_{2i} }\right] \nonumber \\{} & {} -\sum \limits _{i=1}^{m_{2}}\left( 1+\frac{\beta _{2}}{x_{2i}}\right) ^{\theta }\log \left[ 1+\frac{\beta _{2}}{x_{2i}}\right] \nonumber \\{} & {} +\sum \limits _{i=1}^{m_{1}}\frac{(1+\frac{\beta _{2}}{x_{1i}})^{\theta }\log \left[ 1+\frac{\beta _{2}}{x_{1i}}\right] e^{1-(1+\frac{\beta _{2}}{x_{1i}} )^{\theta }}}{1-e^{1-(1+\frac{\beta _{2}}{x_{1i}})^{\theta }}}.\nonumber \\ \end{aligned}$$

(10)

Consequently, we derived three nonlinear equations (8)–(10) in three unknowns parameters and these equations are very hard to achieve the MLE in closed form. Hence, a numerical approach is required to obtain the estimates ${\hat{\beta }}_{1}$, ${\hat{\beta }}_{2}$ and ${\hat{\theta }}$ of the model parameters $\Theta =\{\beta _{1},$ $\beta _{2},$ $\theta$}, and an iterative method called Newton–Raphson is applied.

2.2.2 Bayesian estimation BE

Parameters estimation under Bayesian approach need to formulate the prior information. Therefore, we proposed the prior distribution of $\Theta =\{\beta _{1},$ $\beta _{2},$ $\theta$} as independent gamma given by

$$\begin{aligned} \pi ^{*}(\Theta _{i})\propto \Theta _{i}^{a_{i}-1}e^{-b_{i}\Theta _{i}}, \text { }\Theta _{i}>0,\text { }a_{i},\text { }b_{i}>0,\text { }i=1,\text { }2, \text { }3, \end{aligned}$$

(11)

where $\Theta _{1}=\beta _{1}$, $\Theta _{2}=\beta _{2}$ and $\Theta _{3}=\theta$, respectively. Also, the joint prior distribution is

$$\begin{aligned} \pi ^{*}(\Theta )\propto \beta _{1}^{a_{1}-1}\beta _{2}^{a_{2}-1}\theta ^{a_{3}-1}e^{-b_{1}\beta _{1}-b_{2}\beta _{2}-b_{3}\theta },\text { }a_{i}, \text { }b_{i}>0. \end{aligned}$$

(12)

The posterior distribution is defined by

$$\begin{aligned} \pi (\Theta |{\textbf{X}})=\frac{\pi ^{*}(\Theta )L(\Theta |{\textbf{X}})}{ \iiint \limits _{\Theta }\pi ^{*}(\Theta )L(\Theta |{\textbf{X}})d\beta _{1}d\beta _{2}d\theta }\propto \pi ^{*}(\Theta )L(\Theta |{\textbf{X}}). \end{aligned}$$

(13)

Consequently, Eq. (13) presented as follows:

$$\begin{aligned} \pi (\Theta |{\textbf{X}})\propto & {} \beta _{1}^{m_{1}+a_{1}-1}\beta _{2}^{m_{2}+a_{2}-1}\theta ^{R+a_{3}-1}e^{-b_{1}\beta _{1}-b_{2}\beta _{2}-b_{3}\theta }e^{\left( \theta -1\right) \sum \limits _{i=1}^{m_{1}}\log \left[ 1+\frac{\beta _{1}}{x_{1i}}\right] -\sum \limits _{i=1}^{m_{1}}(1+\frac{ \beta _{1}}{x_{1i}})^{\theta }} \nonumber \\{} & {} \times e^{\left( \theta -1\right) \sum \limits _{i=1}^{m_{2}}\log \left[ 1+\frac{ \beta _{2}}{x_{2i}}\right] -\sum \limits _{i=1}^{m_{2}}(1+\frac{\beta _{2}}{ x_{2i}})^{\theta }}\left( 1-e^{1-(1+\frac{\beta _{1}}{T ^{*}} )^{\theta }}\right) ^{n-R}\prod \limits _{i=1}^{m_{1}}\left( 1-e^{1-(1+\frac{ \beta _{2}}{x_{1i}})^{\theta }}\right) \nonumber \\{} & {} \times \left( 1-e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }}\right) ^{n-R}\nonumber \\{} & {} \times \,\prod \limits _{i=1}^{m_{2}}\left( 1-e^{1-(1+\frac{\beta _{1}}{x_{2i}} )^{\theta }}\right) . \end{aligned}$$

(14)

Under symmetric squared error loss (SEL) function, $L(g,{\tilde{g}})=({\tilde{g}} -g)^{2}$ the Bayes estimate presented as

$$\begin{aligned} {\tilde{g}}=E_{\pi (\Theta |{\textbf{X}})}(g). \end{aligned}$$

(15)

In light of LINEX loss function, $L(g,{\tilde{g}})=e^{p({\tilde{g}}-g)}-p({\tilde{g}} -g)-1,\,p\ne 0$ the Bayes estimate presented as

$$\begin{aligned} {\tilde{g}}=\frac{-1}{p}\log [E_{\pi (\Theta |{\textbf{X}})}(e^{-pg})]. \end{aligned}$$

(16)

The posterior distribution (14) need to normalization. Also, the expectations (15) and (16) need to compute a high dimensional integrals. Some techniques can be employed to solve this problem for instance, Lindely approximation, numerical integration and MCMC. In this subsection, the MCMC method is proposed for the empirical posterior distribution.

MCMC method

Gibbs sampling, Metropolis under Gibbs samplers, and importance sampling technique have present MCMC sub-classes. Note that the full conditional posterior distributions show a suitable scheme. Further, the important sample method is carried out to approximate the BE and called importance technique. Using the joint posterior distribution (14), we report the full conditional posterior using the following formula.

$$\begin{aligned} \pi (\Theta |{\textbf{X}})=\pi _{1}(\beta _{1}|{\textbf{X}})\pi _{2}(\beta _{2}| {\textbf{X}})\pi _{3}(\theta |\beta _{1},\beta _{2},{\textbf{X}})h(\beta _{1},\beta _{2},\theta |\mathbf {X),} \end{aligned}$$

(17)

where

$$\begin{aligned} \pi _{1}(\beta _{1}|{\textbf{X}})\propto & {} \beta _{1}^{m_{1}+a_{1}-1}e^{-b_{1}\beta _{1}-\sum \limits _{i=1}^{m_{1}}\log \left[ 1+\frac{\beta _{1}}{x_{1i}}\right] }, \end{aligned}$$

(18)

$$\begin{aligned} \pi _{2}(\beta _{2}|{\textbf{X}})\propto & {} \beta _{2}^{m_{2}+a_{2}-1}e^{-b_{2}\beta _{2}-\sum \limits _{i=1}^{m_{2}}\log \left[ 1+\frac{\beta _{2}}{x_{2i}}\right] }, \end{aligned}$$

(19)

$$\begin{aligned} \pi _{3}(\theta |\beta _{1},\beta _{2},{\textbf{X}})\propto & {} \theta ^{R+a_{3}-1}e^{-\theta \left( b_{3}- \sum \limits _{i=1}^{m_{1}}\log \left[ 1+ \frac{\beta _{1}}{x_{1i}}\right] -\sum \limits _{i=1}^{m_{2}}\log \left[ 1+\frac{\beta _{2}}{x_{2i}}\right] \right) }, \end{aligned}$$

(20)

$$\begin{aligned} h(\beta _{1},\beta _{2},\theta |{\textbf{X}})\propto & {} \left[ \left( 1-e^{1-(1+\frac{\beta _{1}}{T ^{*}})^{\theta }}\right) \left( 1-e^{1-(1+\frac{\beta _{2}}{T ^{*}})^{\theta }}\right) \right] ^{n-R}\prod \limits _{i=1}^{m_{1}}\left( 1-e^{1-(1+\frac{\beta _{2}}{x_{1i}} )^{\theta }}\right) \nonumber \\{} & {} \times \,\prod \limits _{i=1}^{m_{2}}\left( 1-e^{1-(1+\frac{\beta _{1}}{x_{2i}} )^{\theta }}\right) e^{ -\sum \limits _{i=1}^{m_{1}}\left( 1+\frac{ \beta _{1}}{x_{1i}}\right) ^{\theta }-\sum \limits _{i=1}^{m_{2}}\left( 1+ \frac{\beta _{2}}{x_{2i}}\right) ^{\theta }}. \end{aligned}$$

(21)

It follows that the joint posterior distribution is reduced to two proper functions of $\beta _{1}$ and $\beta _{2}$  as well as a conditional gamma function of $\theta$ given $\beta _{1}$ and $\beta _{2}$.

The plots of (18) and (19) show that they are similar to the Gaussian distribution. Hence, to generate a sample from these two distributions, the Metropolis-Hastings (M-H) method is applied using Gaussian proposal distribution. Based on the following techniques, we generate MCMC samples.

• 1. Begin with initial values $\Theta ^{(0)}=\{\beta _{1}^{(0)},$ $\beta _{2}^{(0)},$ $\theta ^{(0)}$}=$\{{\hat{\beta }}_{1},$ ${\hat{\beta }}_{2},$ $\hat{ \theta }$} and put $\tau =1$.

• 2. Generate $\beta _{1}^{(\tau )}$ from (18) with MH algorithms under normal proposal distributions.

• 3. Generate $\beta _{2}^{(\tau )}$ from (19) with MH algorithms under normal proposal distributions.

• 4. Generate $\theta ^{(\tau )}$ for given $\beta _{1}^{(\tau )}$ and $\beta _{2}^{(\tau )}$ from gamma distribution given by (20).

• 5. Compute the value of $h(\beta _{1}^{(\tau )},\beta _{2}^{(\tau )},\theta ^{(\tau )}|\mathbf {X).}$

• 6. Set $\tau =\tau +1.$

• 7. Repeat steps (2–5) desired N number of times.

• 8. Here, the BE based on SEL function for any function $g\left( \beta _{1},\text { }\beta _{2},\text { }\theta \right)$ can be expressed as follows:

  $$\begin{aligned} {\tilde{g}}_{B}\left( \beta _{1},\text { }\beta _{2},\text { }\theta \right) = \frac{\frac{1}{N-M}\sum _{i=M+1}^{N}g\left( \beta _{1}^{(i)},\beta _{2}^{(i)},\theta ^{(i)}\right) h(\beta _{1}^{(i)},\beta _{2}^{(i)},\theta ^{(i)}|\mathbf {X)}}{\frac{1}{N-M}\sum _{i=M+1}^{N}h(\beta _{1}^{(i)},\beta _{2}^{(i)},\theta ^{(i)}|\mathbf {X)}}, \end{aligned}$$

  (22)

  where M is the number of iterations needed to reach stationary distribution.

• 9. Consequently, the posterior variance of $g\left( \beta _{1},\text { }\beta _{2}, \text { }\theta \right)$ is calculated by

  $$\begin{aligned}{} & {} V(g\left( \beta _{1},\text { }\beta _{2},\text { }\theta \right) )\nonumber \\{} & {} \quad =\frac{\frac{ 1}{N-M}\sum _{i=M+1}^{N}\left( g\left( \beta _{1}^{(i)},\beta _{2}^{(i)},\theta ^{(i)}\right) -{\tilde{g}}_{B}\right) ^{2}h(\beta _{1}^{(i)},\beta _{2}^{(i)},\theta ^{(i)}|\mathbf {X)}}{\frac{1}{N-M}\sum _{i=M+1}^{N}h(\beta _{1}^{(i)},\beta _{2}^{(i)},\theta ^{(i)}|\mathbf { X)}}. \end{aligned}$$

  (23)

2.3 Interval estimation

2.3.1 Asymptotic confidence intervals

We now use the concept of asymptotic confidence intervals (ACIs) to construct the CIs for the unknown parameters. The asymptotic assume that the MLEs $(\hat{\beta _{1}},\hat{\beta _{2}},{\hat{\theta }})$ are approximately bivariate normal distribution and, $\hat{\phi }$ $\sim$ $N(\phi ,I^{-1}({\hat{\phi }})),$ see Lawless [19] where

$$\begin{aligned} I_{0}^{-1}({\hat{\phi }})= & {} \begin{pmatrix} -\frac{\partial ^{2}{\ell }}{\partial {\beta _{1}}^{2}} &{} -\frac{\partial ^{2}{\ell }}{\partial {\beta _{1}}\partial {\beta _{2}}} &{} -\frac{\partial ^{2}{\ell }}{\partial {\beta _{1}}\partial {\theta }} \\ -\frac{\partial ^{2}{\ell }}{\partial {\beta _{2}}\partial {\beta _{1}}} &{} - \frac{\partial ^{2}{\ell }}{\partial {\beta _{2}}^{2}} &{} -\frac{\partial ^{2} {\ell }}{\partial {\beta _{2}}\partial {\theta }} \\ -\frac{\partial ^{2}{\ell }}{\partial {\theta }\partial {\beta _{1}}} &{} - \frac{\partial ^{2}{\ell }}{\partial {\theta }\partial {\beta _{2}}} &{} - \frac{\partial ^{2}{\ell }}{\partial {\theta }^{2}} \end{pmatrix} _{(\hat{\beta _{1}},\hat{\beta _{2}},{\hat{\theta }})}^{-1} \nonumber \\= & {} \begin{pmatrix} var({\hat{\beta }}_{1}) &{} cov({\hat{\beta }}_{1},\hat{\beta _{2}}) &{} cov(\hat{\beta }_{1},{\hat{\theta }}) \\ cov(\hat{\beta _{2}},{\hat{\beta }}_{1}) &{} var({\hat{\beta }}_{2}) &{} cov(\hat{ \beta _{2}},{\hat{\theta }}) \\ cov({\hat{\theta }},\hat{\beta _{1}}) &{} cov({\hat{\theta }},\hat{\beta _{2}}) &{} var({\hat{\theta }}) \end{pmatrix}. \end{aligned}$$

(24)

Consequently, the pivotal quantities $\frac{\hat{\beta _{1}}-\beta _{1}}{\sqrt{Var(\hat{\beta _{1}})}},~~\frac{\hat{\beta _{2}}-\beta _{2}}{ \sqrt{Var(\hat{\beta _{2}})}}$ and $\frac{{\hat{\theta }}-\theta }{\sqrt{Var( {\hat{\theta }})}}$ are approximately distributed as standard normal. Thus, the $100(1-\vartheta )\%$ asymptotic CI for $\theta$, $\beta _{1}$ and $\beta _{2}$ are present by (${\hat{\theta }}\pm Z_{\vartheta /2}\sqrt{Var({\hat{\theta }})}$), $(\hat{\beta _{1}}\pm Z_{\vartheta /2}\sqrt{Var(\hat{\beta _{1}} )})$ and ($\hat{\beta _{2}}\pm Z_{\vartheta /2}\sqrt{Var(\hat{\beta _{2}})}$), where $Z_{\vartheta /2}$ denotes the upper $(\vartheta /2)^{th}$ percentile point of the standard normal distribution.

The pivotal $\Phi =\frac{\log {\hat{\Theta }}_{i}-\log \Theta _{i}}{\text {Var(} \log {\hat{\Theta }}_{i}\text {)}}$ has standard normal distribution. Then, we can calculate the 100(1-$\vartheta )\%$ ACIs of $\Theta =\{\beta _{1},\beta _{2},\theta \}$ by the following expression

$$\begin{aligned} \left( \frac{{\hat{\Theta }}_{i}}{\exp \left( Z_{\vartheta /2}\sqrt{\text {Var(} \log {\hat{\Theta }}_{i}\text {)}}\right) },{\hat{\Theta }}_{i}\exp \left( Z_{\vartheta /2}\sqrt{\text {Var(}\log {\hat{\Theta }}_{i})}\right) \right) ,\quad i=1,2,3, \end{aligned}$$

(25)

where $\text {Var(}\log {\hat{\Theta }}_{i})$=$\frac{\text {Var(}{\hat{\Theta }}_{i})}{\hat{ \Theta }_{i}}$ and $i=1,2,3.$ More information can be found in Chen and Shao [20] and Wang et al [21].

2.3.2 Bootstrap confidence intervals

Bootstrap technique is one of the most popular methods applied to estimate CIs. Further, it can also be computed to estimate the bias and variance of an estimator or calibrate hypothesis tests. Bootstrap techniques are described as resembling methods. The bootstrap techniques are defined in both methods nonparametric and parametric, see Davison and Hinkley [22] and Efron and Tibshirani [23]. In the problem at hand, we utilize the parametric bootstrap technique to construct the parametric percentile bootstrap technique. Here, the algorithm is employed to present a percentile bootstrap technique for formulation bootstrap confidence intervals.

• 1. From the original T-II GHCS sample $X=${($X_{1;m,n},$ $\eta _{1}$), ($X_{2;m,n},$ $\eta _{2}$),..., ($X_{R;m,n},$ $\eta _{R}$)}, the MLEs $\Theta =\{{\hat{\beta }}_{1},{\hat{\beta }}_{2},{\hat{\theta }}\}$ are obtained.

• 2. Generate two samples from INHD(${\hat{\beta }}_{1},{\hat{\theta }}$) and INHD(${\hat{\beta }}_{2},{\hat{\theta }}$) with the same size n and the latent failure time is observed as $X_{i}=\min (X_{i1},X_{i2}).$

• 3. For given m and ($T _{1},T _{2}$) the bootstrap T-II GHCS sample $X^{*}=${($X_{1;m,n}^{*},$ $\eta _{1}^{*}$), ($X_{2;m,n}^{*},$ $\eta _{2}^{*}$),..., ($X_{R;m,n}^{*},$ $\eta _{R}^{*}$)} and the corresponding MLEs $\Theta ^{*}=\{{\hat{\beta }} _{1}^{*},{\hat{\beta }}_{2}^{*},{\hat{\theta }}^{*}\}$ are obtained.

• 4. Steps from (2) and (3) are repeated ${\textbf{N}}$ times and each time compute bootstrap estimate $\Theta ^{*}=\{{\hat{\beta }}_{1}^{*}, {\hat{\beta }}_{2}^{*},{\hat{\theta }}^{*}\}.$

• 5. The bootstrap sample estimate $\Theta ^{*(i)}=\{{\hat{\beta }} _{1}^{*(i)},{\hat{\beta }}_{2}^{*(i)},{\hat{\theta }}^{*(i)}\}$, $i=1,$ 2,  ...,  ${\textbf{N}}$ are arranged in ascending order to obtain $\Theta _{(i)}^{*}=\{{\hat{\beta }}_{1(i)}^{*},{\hat{\beta }}_{2(i)}^{*},\hat{ \theta }_{(i)}^{*}\}$, $i=1,$ 2,  ...,  ${\textbf{N}}.$

Percentile bootstrap confidence interval (PBCI)

Let, the ordered sample is addressed by distribution $F(x)=P(\hat{ \Theta }_{l}^{*}\leqslant x),$ $l=1,$ 2,  3,  which be the CDF of $\hat{ \Theta }_{l}^{*},$ with $\hat{ \Theta }_{1}^{*}$ reflects the mean ${\hat{\beta }}_{1}^{*}$ and others. Thus, the point bootstrap estimate is given by

$$\begin{aligned} {\hat{\Theta }}_{l}^{*}=\frac{1}{{\textbf{N}}}\sum \limits _{i=1}^{{\textbf{N}} }\Theta _{l(i)}^{*}. \end{aligned}$$

(26)

Also, the $100(1-\vartheta )\%$ PBCIs are given by

$$\begin{aligned} ({\hat{\Theta }}_{l\text {boot(}\frac{\vartheta }{2}\text {)}}^{*},\text { }\hat{ \Theta }_{l\text {boot(1-}\frac{\vartheta }{2}\text {)}}^{*}), \end{aligned}$$

(27)

where ${\hat{\Theta }}_{l\text {boot}}^{*}=F^{-1}(x)$.

2.3.3 HPD credible intervals

To build HPD credible interval of $\Theta (\beta _{1}, \beta _{2},\theta )$, rearrange all $\Theta _{i}(\beta _{1}^{(i)}, \beta _{2}^{(i)},\theta ^{(i)})$, $i=1,2,...,M$ in ascending order as,$\Theta ^{1}, \Theta ^{2},...,\Theta ^{M}$. Then, to compute $100(1-\mu )\%,~0<\mu <1,$ HPD credible intervals of the function $\Pi _{B}(\beta _{1}, \beta _{2},\theta )$, the method proposed by Chen and Shao [20] is applied as follows:

• 1. Construct the MCMC sample of $\Theta _{\iota }^{(i)}(\beta _{1}^{(i)}, \beta _{2}^{(i)},\theta ^{(i)})$, $\iota =1,2,3$ and $i=1,2,...,N-M$ using the importance sampling technique. Hence, compute $h_{\iota }= h(\Theta _{\iota }^{(i)}), \iota =1,2,3$.

• 2. Sort $h_{\iota }, i=1,2,...,N-M$ in ascending order can be expressed as $h^{(1)}< h^{(2)}<...< h^{(N-M)}$.

• 3. Compute the weighted function $W_{i}$

  $$\begin{aligned} W_{i}=\frac{h(\beta _{1}^{(i)}, \beta _{2}^{(i)},\theta ^{(i)})}{\sum _{i=M+1}^{N}h(\beta _{1}^{(i)}, \beta _{2}^{(i)},\theta ^{(i)})},\quad \iota =1,2,3. \end{aligned}$$

  (28)

  Now recall $W_{i}, i=M+1, M+2,..., N$ as $W_{(i)}, i=1, 2, 3,..., N-M$, then $i^{th}$ of $W_{(i)}$ correspondence to the value $h^{(i)}$.

• 4. To construct the order pairs (., .) defined the values of the marginal posterior of $W_{i}$ as

  

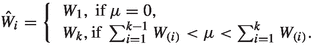
• 5. Then, $100(1-\mu )\%$ HPD credible intervals of $\Theta (\beta _{1}, \beta _{2},\theta )$, is

  $$\begin{aligned} \displaystyle (\Theta ^{\frac{\ell }{N}}, \Theta ^{(\ell +[(1-\mu )N]/N)}),\, for,\, \ell = 1,2,..., N-[(1-\mu )N]. \end{aligned}$$

  (29)

  Furthermore, [.] is the greatest integer value and the $({\frac{\ell }{N}})$ can be obtained such that.

  $$\begin{aligned} \displaystyle{} & {} \Theta ^{(\ell +[(1-\mu )N]/N)} -\Theta ^{\frac{\ell }{N}} = {\text {min}} (\Theta ^{(\ell +[(1-\mu )N]/N)} -\Theta ^{\frac{\ell }{N}}), \nonumber \\{} & {} \quad {\text { for}} \, \ell = 1,2,..., N-[(1-\mu )N].\nonumber \\ \end{aligned}$$

  (30)

The performance of all estimators is discussed in the next section using real data set and simulations.

3 Data analysis and simulation study

Here, we discussed examples to demonstrate the findings developed in this study. In the first example, we considered a real data set that was collected in a laboratory experiment in a traditional laboratory environment Hoel [24]. The data came from testing male mice subjected to a radiation dose of three hundred Roentgens at the age of five to six weeks. These data are used by various authors, for example, Pareek et al. [25] and Sarhan et al. [26]. In the second example, we adopted for different parameters values and censoring a simulated data set generated from INHD.

3.1 Applications to real life data set

A real data set consisting of failure times reported in Table 1 of the autopsy operation presented in Hoel [24] has been considered here. Two causes of failure were classified in the data set: Thymic Lymphoma as the first caue and other caues as the second cause of failure.

Table 1 Autopsy data for 99 RFM conventional male mice that received a radiation dose of 300 Roentgens at the age of 5 to 6 weeks, as given in [24]

Under the transformation $Y=(\frac{X}{500})^{2}$, we checked the validity of modeling these data by INHD. A goodness-of-fit test is used in this situation to determine whether or not the transformed data sets are assumed to be distributed with the INHD. Calculations are made to determine the K-S distances (p-values) that correlate with causes 1 and 2 as 1.00797 (0.2149) and 1.19717 (0.1917). Based on these findings, we may say that $H_0$ is accepted for test (1) that each transformed data set is drawn from INHD, yet fails to accept the other one. As a result, it is reasonable to conclude that $\theta _1=\theta _2=\theta$ and $\beta _1 \ne \beta _2$ for this data set.

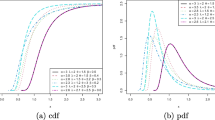
In order to provide more explanation, we plot the empirical CDF (ECDF), probability-probability (P-P) and quantile-quantile(Q-Q) plots in Fig. 1 and Fig. 2 based on causes 1 and 2, respectively. As a further check, we fit Kolmogorov-Smirnov (K-S) distances between the fitted distribution functions and the empirical distribution functions equal to 0.3035. The conclusion that can be drawn from these plots is that the INHD is a good match for the given data set.

Fig. 1

Plots of a ECDF, b P-P, and c Q-Q under cause 1 for given data

Fig. 2

Plots of a ECDF, b P-P, and c Q-Q under cause 2 for given data

Below is provided information on the competing risks data set based on GT-II HCS taken from the given data set.

(0.0064, 2), (0.0071, 2), (0.0104, 2), (0.0154, 2), (0.1011, 1), (0.1063, 2), (0.1282, 2), (0.1429, 1), (0.1460, 1), (0.1568, 1), (0.1600, 1), (0.1697, 2), (0.171396, 1), (0.1936, 1), (0.197136, 2), (0.207936, 2), (0.2209, 1), (0.2401, 1), (0.2480, 2),(0.2500, 1), (0.2540, 2),(0.2621, 1), (0.2725, 1), (0.2809, 1), (0.2830, 1), (0.3136, 1), (0.3181, 2), (0.4200, 2), (0.4436, 2), (0.465124, 2), (0.4706, 1), (0.5070, 2), (0.5358, 1), (0.5868, 2), (0.5929, 2).

Where 1 signified the first cause, 2 denoted the second cause. From this data, we can see that $(m_{1}, m_{2},m) =(18,17,35)$.

The data is then analyzed using the proposed model under two causes of death. For $m=40$, $\tau _{1}=0.3$, $\tau _{2}=0.6$, $q=0.05$, and $p=0.1$. The MLE is calculated by iteration with an initial guess of $\beta _{1}$, $\beta _{2}$ and $\theta$. The non-informative prior is used for prior information, as $a_{i} =b_{i}=1, i=1,2,3$. Table 2 displays point and interval estimates derived from the competing risk data sets using GT-II HCS. For the MCMC technique in Bayes approach, we run the chan 21000 with the first 1000 values as brun-in.

Table 2 Point and $95\%$ interval MLE and BE for the real data set

Table 2 displays point and interval estimates derived from the aforementioned competing risk data sets using GT-II HCS. From Table 2, it has been noticed that the point estimates are quite similar to one another. When comparing the standard error of MLE and Bayes estimates, the latter generally provides more accurate results. In comparison to ACIs, Bayesian credible intervals have superior performance based on the length of the intervals.

3.2 Simulate data set

Here, we generate a data set from the INHD and analyze it using the following algorithm:

• 1. From gamma prior distributions with $(a_{i},b_{i})_{i=1,2,3}={(0.3, 5),(0.2, 5),(0.1, 5)}$, generate a sample of size 20. The genuine parameter’s value is then calculated to be the sample mean $\Theta = \left\{ \beta _{1}, \beta _{2}, \theta \right\}$ $= \left\{ 1.5, 1, 0.5 \right\}$.

• 2. Generat a random sample from the INHD with parameters $\beta _{1}+\beta _{2}$ and $\theta$ of size 40 to be: $\{ 0.032451, 0.052182, 0.053380, 0.058725, 0.064027, 0.074505, 0.083419, 0.112684,$ 0.113543, 0.120729, 0.139183, 0.166689, 0.171822, 0.194085, 0.194973, 0.203049,  0.232722, 0.257349, 0.259924, 0.267359, 0.277452, 0.301836, 0.327261, 0.339334,  0.579614, 0.601571, 0.659922, 0.663395, 0.688138, 0.695096, 0.745303, 0.865290,  $0.977975, 0.985364, 1.131510, 1.241950, 1.88080, 2.464560, 3.973810, 4.318960 \}$.

• 3. Under consideration that, $T_{1}=2.5$ and $T_{2}=3$ and $m=25$ the GT-II HCS competing risks sample given by $\{ 0.032451, 0.052182, 0.053380, 0.058725, 0.064027, 0.074505, 0.083419, 0.112684,$ 0.113543, 0.120729, 0.139183, 0.166689, 0.171822, 0.194085, 0.194973, 0.203049,  0.232722, 0.257349, 0.259924, 0.267359, 0.277452, 0.301836, 0.327261, 0.339334,  0.579614, 0.601571, 0.659922, 0.663395, 0.688138, 0.695096, 0.745303, 0.865290,  $0.977975, 0.985364, 1.131510, 1.241950, 1.88080, 2.464560 \}$. Then, the integer value $R=38$.

• 4. From Step 3 compute $m_{1}$ and $m_{2}$.

• 5. The simulated number generated by the important sample method with the corresponding histogram is given in Figs. 3 and 4. These two Figures show the convergence in the empirical posterior distribution.

• 6. The findings of MLE and BE are presented in Table 3 for a point and $95\%$ intervals estimate.

Table 3 Point and $95\%$ interval MLE and BE

Fig. 3

Plot of the simulation number of $\beta _{1}, \beta _{2}$ and $\theta$ generated via MCMC

Fig. 4

Plot of the histogram of $\beta _{1}, \beta _{2}$ and $\theta$ generated via MCMC

3.3 Simulation studies

In this part, the Monte Carlo simulation study is used to evaluate and compare the estimation findings that were developed and obtained in this paper. Therefore, we assess the effect of changes in sample size n, affected sample size m, and parameter vector $\Theta =\left\{ \beta _{1},\beta _{2},\theta \right\}$. We also investigate the effect of changing the ideal test times $(T_{1},T_{2})$.

To get the true values of the model parameters to agree with the hybrid parameter values of the prior distribution, we suggested the shape and scale hybrid parameters and generated a random sample of size twenty. Hence, the genuine parameter is chosen to be the mean of the random sample. Different combinations of $( n,m, T_{1}, T_{2})$ and two sets of parameters $\Theta = \left\{ \beta _{1}, \beta _{2}, \theta \right\} = {\left\{ 2,1.7,0.6 \right\} , \left\{ 1.5, 1, 0.5 \right\} }$ are reported in the simulation study tables. The simulation study is carried out with respect to one thousand simulated data sets.

In our research, we compute the two point estimates MLEs and MCMCs, as well as the three interval estimates ACIs, PBCI, and HPD credible intervals. The instruments that are utilized to test the point estimate are the mean estimate (ME) and the mean squared error (MSE). But the interval estimate test under the average interval length (AIL) and probability coverage (PC). For the MCMC method, we run the chain with 11,000 values, with the first 1000 values as brun-in. The results of the simulation study are presented in Tables 4 to 7. From the numerical results in Tables 4-7, we observed that the proposed GT-II HCS competing risks model serves well for the statistical inference of INHD. The Bayes estimators for the parameters $\beta _{1}$ and $\beta _{2}$ perform better than the MLEs in terms of MSEs. For the parameter $\theta$, MLEs perform better than Bayes estimators. When affect sample size increases, the MSEs and AILs decrease.

Table 4 MEs and MSEs from $\Theta =\left\{ 2,1.7,0.6 \right\}$

Table 5 AILs and PCs from $\Theta =\left\{ 2,1.7,0.6 \right\}$

Table 6 MEs and MSEs from $\Theta =\left\{ 1.5, 1, 0.5\right\}$

Table 7 AILs and PCs from $\Theta =\left\{ 1.5, 1, 0.5\right\}$

4 Conclusion

Statistical infrance of the INHD is discussed based on a GT-II HCS. Both the classical and Bayes estimations of the parameters were found under GT-II HCS. Since none of the proposed estimators have analytical expressions, the Newton–Raphson method has been taken into consideration. Depending on the asymptotic normality of the MLEs, the ACIs are calculated. For the purpose of comparison, the Bayes estimates were generated for different values of the parameters under the SEL function. Since Bayes estimates cannot be obtained explicitly, the MCMC method was considered. Furthermore, for the unknown parameters samples generated by the MH algorithm are used to calculate the HPD intervals.

Suggested estimates are then numerically contrasted, and suitable comments are offered. According to the computational findings, the Bayesian estimation for the scale parameters is more accurate than the MLE. Furthermore, HPD intervals have been demonstrated to be perform superior to all other CIs. Application of the proposed estimates to real data sets reveals that the Bayesian estimation for the scale parameters performs better than other methods. Although we focused on GT-II HCS and INHD in this study, we can extend this methods to various censoring schemes under deferent distributions as well.