1 Introduction

The interaction between the flow of a fluid and a flexible boundary is a scenario often encountered in nature. The flow of blood through veins and arteries, peristaltic motion, the swimming of micro-organisms, and the minimally-invasive injection of medical implants are some common examples. Often in these applications, one may be interested in how the stability of a flow is altered by the presence of wall flexibility, and whether it enhances or suppresses any linear instability that may be present in the rigid situation. For example in the case of the implant injection mentioned above (often referred to as ‘thread injection’; see Frei et al. [1]; Walton [2]) one may wish to suppress such instabilities in order to ensure a smooth injection with the minimum of surgical trauma.

A very simple model of the injection process would be to consider a moving flexible boundary (representing the implant) below an incompressible fluid (modelling the accompanying carrier fluid), and bounded above by the rigid wall of the injection device. If the lower wall is rigid, then the basic fluid flow would simply be plane Couette flow: a flow well-known to be stable to infinitesimal disturbances at all values of the Reynolds number (Romanov [3]).

Various models have been proposed that modify the classical plane Couette flow by incorporating some element of visco-elasticity, and then study the resulting effect on the linear stability properties. For example Chokshi and Kumaran [4] investigate the Couette flow of a dilute polymer and discover that although the classical Oldroyd B model is still linearly stable, the introduction of an inhomogeneity into the polymer concentration can destabilize the flow, while using a continuum viscoelastic wall model, Kumaran et al. [5] showed that plane Couette flow is linearly unstable at low Reynolds number.

Our interest here is predominantly in the high Reynolds number regime, and we choose to represent the flexibility of the wall using a surface method in which the wall interacts with the fluid through an interface condition. For a review of the use of surface methods to model compliant boundaries the reader is referred to Lebal et al. [6]. The specific model which we use here treats the wall as a thin plate mounted on springs. In this model the wall parameters are traditionally the spring stiffness, tension, bending stiffness, mass, and damping coefficient. This model has been used extensively to study the effect of wall flexibility in many different scenarios. For example, the stability of Tollmien-Schlichting waves in compliant-walled plane Poiseuille flow (Davies and Carpenter [7]; Gajjar and Sibanda [8]; Nagata and Cole [9]), flexible protuberances in boundary layers (Pruessner and Smith [10]), and droplet impact on deformable surfaces (Henman et al. [11]). It does not appear however to have previously been applied to plane Couette flow over flexible boundaries.

As a first step, and with the thread injection application in mind, we use a very simple model in which the pressure perturbations at the lower wall are connected to the displacement of the wall purely through the effect of spring stiffness, while the upper wall is considered rigid. Although this model is extremely primitive, we will demonstrate that it is sufficient to generate an instability at high Reynolds numbers in which the wavelength of the disturbance is comparable with the width of the channel. The simplicity of the model also allows us to make significant analytic progress in the analysis of the nature of the instability. The appropriate linear eigenvalue problem can be considered at high Reynolds number, and asymptotic structures corresponding to the upper and lower branches of the linear neutral curve obtained, with the solutions in each layer derived analytically. The resulting linear eigenrelations can be solved with minimal numerical effort, with the computed values for wavenumber and phasespeed showing excellent agreement with numerical computations of the eigenvalue problem at large but finite Reynolds number. We also demonstrate that a new structure, uniting the upper and lower branches, comes into play when the wall spring stiffness K is sufficiently large, and leads to a disturbance of short wavelength propagating at a speed close to that of the rigid wall. This new structure allows us, at large spring stiffness, to obtain an approximation to the entire neutral curve, and predict the critical Reynolds number \(\text {Re} _\textrm{crit}\) for instability as a function of K. In particular we show that Re\(_\textrm{crit}\rightarrow \infty \) as \(K\rightarrow \infty ,\) in accordance with the linear stability of the rigid flow referred to above.

The structure of the remainder of the paper is as follows. In Sect. 2 we set out our governing model for the instability of Couette flow with a flexible lower wall. This is followed in Sect. 3 by a high Reynolds number analysis leading to upper and lower branch neutral stability structures at O(1) values of K which we refer to as AS1 and AS2, and the large-K unified structure (AS3). This is followed in Sect. 4 by numerical solutions of the linear eigenvalue problem at finite Reynolds number, and a comparison with their asymptotic counterparts. Finally in Sect. 5 we draw conclusions and propose directions for future research.

Fig. 1
figure 1

The flexible channel. The shaded region is filled with an incompressible fluid

Full size image

2 The governing equations

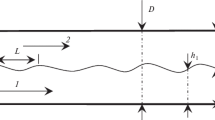
Consider two infinitely long parallel plates separated by a distance \(2h^{*}.\) The upper plate, which is taken to be rigid, moves to the right with speed \(U^{*},\) while the lower plate moves to the left with the same speed. This lower plate is flexible and responds to the fluid flow in a way to be outlined below. The space between the plates is filled with an incompressible fluid of constant density \(\rho ^{*}\) and kinematic viscosity \(\nu ^{*}.\) We introduce a Cartesian coordinate system \((x^{*},y^{*})\), with the \(x^{*}\) axis aligned along the centreline of the channel so that the walls are located at \(y^{*}=\pm h^{*},\) and write the corresponding fluid velocity components as \((u^{*},v^{*})\), and the fluid pressure as \(p^{*}.\) It is convenient to non-dimensionalize by writing

$$\begin{aligned} (x^{*},y^{*})=h^{*}(x,y),\quad t^{*}=(h^{*}/U^{*})t, \quad (u^{*},v^{*})=U^{*}(u,v),\quad p^{*}=\rho ^{*}(U^{*})^{2}p, \end{aligned}$$

where \(t^{*}\) is the dimensional time, so that the governing unsteady two-dimensional Navier–Stokes equations for (u(x, y, t), v(x, y, t), p(x, y, t)) may be written as

$$\begin{aligned} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}= & {} 0, \end{aligned}$$
(1a)
$$\begin{aligned} \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}= & {} -\frac{\partial p}{\partial x}+\text {Re}^{-1}\left( \frac{ \partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}\right) , \end{aligned}$$
(1b)
$$\begin{aligned} \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}= & {} -\frac{\partial p}{\partial y}+\text {Re}^{-1}\left( \frac{ \partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial y^{2}}\right) , \end{aligned}$$
(1c)

with Reynolds number \(\text {Re}\) defined as

$$\begin{aligned} \text {Re}=\frac{U^{*}h^{*}}{\nu ^{*}}. \end{aligned}$$

Since we are assuming the upper wall to be rigid, the no-slip condition of viscous flow applies there, and in non-dimensional form we have

$$\begin{aligned} u=1,\quad v=0\quad \text {on}\;y=1. \end{aligned}$$
(2)

We denote the unknown lower wall position by \(y_{W}(x,t)\), and suppose that the wall displacement is small by writing

$$\begin{aligned} y_{W}=-1+\varepsilon \eta (x,t), \end{aligned}$$
(3)

where \(\varepsilon \ll 1.\) In the absence of any displacement we have \(u=-1,v=0\) on \(y=-1.\) Thus, at leading order, the steady, parallel solution to (1) is simply plane Couette flow, i.e.

$$\begin{aligned} u=y,\quad v=0,\quad p=0. \end{aligned}$$

We now perturb this solution by seeking a solution in normal-mode form

$$\begin{aligned} (u,v,p)=(y,0,0)+\varepsilon (\widetilde{u}(y),\widetilde{v}(y),\widetilde{p} (y))\exp [i\alpha (x-ct)]+c.c.. \end{aligned}$$
(4)

Here c.c. denotes complex conjugate, while \(\alpha \) and c are the wavenumber and phasespeed of the disturbance. We will adopt a temporal approach to the stability problem by prescribing a real value of the wavenumber \(\alpha \) while allowing the complex phasespeed c to be determined as part of the solution. Substitution of (4) into the Navier–Stokes equations (1) leads, at \(O(\varepsilon ),\) to the perturbation equations

$$\begin{aligned} i\alpha \widetilde{u}+\widetilde{v}^{\prime }= & {} 0, \end{aligned}$$
(5a)
$$\begin{aligned} i\alpha (y-c)\widetilde{u}+\widetilde{v}= & {} -i\alpha \widetilde{p}+\text {Re} ^{-1}\left( \widetilde{u}^{\prime \prime }-\alpha ^{2}\widetilde{u}\right) , \end{aligned}$$
(5b)
$$\begin{aligned} i\alpha (y-c)\widetilde{v}= & {} -\widetilde{p}^{\prime }+\text {Re}^{-1}\left( \widetilde{v}^{\prime \prime }-\alpha ^{2}\widetilde{v}\right) . \end{aligned}$$
(5c)

The streamwise and pressure perturbations can be eliminated, leaving us with the familiar fourth-order Orr–Sommerfeld equation:

$$\begin{aligned} i\alpha \text {Re}(y-c)\left( \widetilde{v}^{\prime \prime }-\alpha ^{2} \widetilde{v}\right) =\widetilde{v}^{\prime \prime \prime \prime }-2\alpha ^{2}\widetilde{v}^{\prime \prime }+\alpha ^{4}\widetilde{v}. \end{aligned}$$
(6)

The boundary conditions on the rigid upper surface are, from (2), (4) and (5a):

$$\begin{aligned} \widetilde{v}(1)=\widetilde{v}^{\prime }(1)=0. \end{aligned}$$
(7)

We now turn to the boundary conditions on the lower flexible wall. Kinematic considerations dictate that fluid particles in contact with the wall remain there for all time. Mathematically:

$$\begin{aligned} u(y_{W})=-1,\quad v(y_{W})=\frac{D}{Dt}y_{W}. \end{aligned}$$

Assuming a normal-mode form

$$\begin{aligned} \eta = \widetilde{\eta }\exp [i\alpha (x-ct)]+c.c.., \end{aligned}$$
(8)

for the wall displacement, and substituting for (u, v) from (4), \(y_{W}\) from (3), and linearizing we have

$$\begin{aligned} \widetilde{u}(-1)+\widetilde{\eta }=0,\quad -i\alpha (1+c)\widetilde{\eta }-\widetilde{v}(-1)=0. \end{aligned}$$
(9)

Eliminating \(\widetilde{\eta },\) and then using the continuity equation (5a) to eliminate \(\widetilde{u},\) leads to

$$\begin{aligned} (1+c)\widetilde{v}^{\prime }(-1)+\widetilde{v}(-1)=0, \end{aligned}$$
(10)

which provides a third boundary condition on the Orr–Sommerfeld equation (6). This also allows us to rewrite the second of equations (9) as

$$\begin{aligned} \widetilde{v}^{\prime }(-1)-i\alpha \widetilde{\eta }=0, \end{aligned}$$
(11)

which will prove useful below. To close the problem we need to postulate a dynamic condition which links the fluid properties to those of the lower wall. Here, as mentioned in the introduction, we assume a very simple spring-backed model where pressure fluctuations in the fluid directly give rise to normal fluctuations of the boundary, i.e.

$$\begin{aligned} p(x,y_{W},t)=-K\eta (x,t), \end{aligned}$$

with the spring constant \(K>0.\) A sketch of the channel is given in Fig. 1. Using (4) for p,  (3) for \(y_{W}\) and (8) for \(\eta ,\) this becomes to leading order:

$$\begin{aligned} \widetilde{p}(-1)=-K\widetilde{\eta }. \end{aligned}$$
(12)

We need to translate (12) into a boundary condition on the normal velocity perturbation \(\widetilde{v}.\) This can be achieved by evaluating (5b) at \(y=-1\), using the continuity equation (5a) to eliminate \(\widetilde{u},\) and then the kinematic condition (10), so that we can express the wall pressure in terms of the normal velocity fluctuations as

$$\begin{aligned} \widetilde{p}(-1)=\text {Re}^{-1}\left( \alpha ^{-2}\widetilde{v}^{\prime \prime \prime }(-1)-\widetilde{v}^{\prime }(-1)\right) . \end{aligned}$$

Thus, in terms of the normal velocity, the law of the wall (12) now reads

$$\begin{aligned} \alpha ^{-2}\widetilde{v}^{\prime \prime \prime }(-1)-\widetilde{v}^{\prime }(-1)=-\text {Re}K\widetilde{\eta }. \end{aligned}$$

Finally, using (11) to eliminate \(\widetilde{\eta },\) we have

$$\begin{aligned} i\alpha \text {Re}K\widetilde{v}^{\prime }(-1)=\widetilde{v}^{\prime \prime \prime }(-1)-\alpha ^{2}\widetilde{v}^{\prime }(-1), \end{aligned}$$
(13)

which serves as our fourth boundary condition on (6). For the numerical calculations we will carry out in Sect. 4, it is convenient to rewrite condition (13) so that it involves the phasespeed c. This can be achieved by using the kinematic condition (10), which converts (13) to the form

$$\begin{aligned} \widetilde{v}(-1)+(1+c)(i\alpha \text {Re}K)^{-1}(\widetilde{v}^{\prime \prime \prime }(-1)-\alpha ^{2}\widetilde{v}^{\prime }(-1))=0. \end{aligned}$$
(14)

In order to provide the reader with a flavour of the nature of the instability that we uncover at finite Reynolds number, we present in Fig. 2 the results of one of our stability calculations that we will undertake and discuss in more detail in Sect. 4. Here we show curves of constant growth rate \(\alpha c_i\) in the Reynolds number–wavenumber plane for the case of spring stiffness \(K=1\). The observed instability is similar to the viscous instability for a linearly unstable shear flow over rigid boundaries: there is a critical Reynolds number for instability with \(\text {Re}_\textrm{crit} \simeq 152\) in this case, a band of unstable wavelengths for any \(\text {Re}\) in excess of this value, and there are upper and lower branches along which the disturbance is neutral with a higher growth rate gradient in the vicinity of the lower branch. The flexible lower wall apparently has the same effect as an inflectional profile over a rigid boundary in that it leads to a finite band of unstable wavelengths at all Reynolds numbers, no matter how large. Another familiar feature from shear flow instability over rigid boundaries is the presence of the ‘kink’ in the upper branch present at around \(\text {Re} \simeq 4000\) for \(K=1\). Over a small range of \(\text {Re}\) near this value there are four neutral points rather than the usual two. Part of the contour for the small growth rate \(\alpha c_{i}=0.0003\) is shown (as a dotted curve) to emphasize the fact that the kink is not just present in the neutral curve but moves to higher Reynolds number as the growth rate is increased.

Fig. 2
figure 2

Wavenumber \(\alpha \) versus \(\text {Re}\) for the case \(K=1\). The contours show different growth rates. From outer to inner: \(\alpha c_{i}=0 \text { (neutral case)},0.003,0.006,0.009\). The dotted line shows part of the contour for \(\alpha c_{i}=0.0003\)

Full size image

It is also worth noting for future purposes, that using the continuity equation (5a) and the pressure-displacement law (12), the kinematic and dynamic conditions (10), (13), can also be rewritten in the form

$$\begin{aligned} \widetilde{v}(-1)=i\alpha (1+c)\widetilde{u}(-1),\;i\alpha (1+c)\widetilde{p} (-1)=K\widetilde{v}(-1). \end{aligned}$$
(15)

This final form for the boundary conditions facilitates the asymptotic solution at large Reynolds number, which is the task we turn to in the next section.

3 Large Reynolds number asymptotic analysis of the eigenvalue problem

The eigenvalue problem consisting of (6), (7), (10 ), (13) can be solved numerically and we undertake this calculation in Sect. 4. At very large K we might expect stability since, in the limit of \(K\rightarrow \infty ,\) our problem reduces to that of plane Couette flow between rigid boundaries: a flow generally considered to be linearly stable at all Reynolds numbers, as mentioned in the introduction. However for each finite value of K there is a large parameter space in \((\alpha ,\text {Re})\) to explore and therefore if one is interested in possible instabilities it is useful to have some idea of the likely values of K,  \(\text {Re}\) and \(\alpha \) at which the flow might be unstable. In order to reduce that parameter space, we begin our analysis of the problem by considering the solution at large Reynolds number where the method of matched asymptotic expansions can be used to demonstrate that instability of the flow occurs at O(1) values of the wall stiffness K. In what follows we will seek neutral modes where the value of c is real. It emerges that there are two branches to the linear neutral curve at high Reynolds number with distinct scalings for each. Although the disturbance is neutral on both branches, we would expect instability in the region in between: our numerical investigations in Sect. 4 will bear this out. We discuss the details of the two branches below in Sects. 3.1, 3.2. Further analysis for large K in Sect. 3.3 indicates that both these structures evolve into a new shared structure, a feature of which is that the entirety of the unstable region can be described on this new scaling. We will see that, as \(K\rightarrow \infty ,\) the critical value of \(\text {Re}\) for instability also tends to infinity, with a simple relationship between the two parameters.

Fig. 3
figure 3

Sketch of the AS1 structure: an inviscid core and two viscous Stokes layers

Full size image

3.1 Asymptotic structure I (AS1)

We explore the possibility that wall flexibility has a destabilizing effect on plane Couette flow by first considering the limit

$$\begin{aligned} \alpha =O(1),\,\,1\pm c=O(1),\quad K=O(1),\quad \text {Re}\gg 1. \end{aligned}$$

In this case the flow field subdivides into a core flow which is inviscid to leading order and includes the location where \(y=c\), while there are wall layers (of classical \(O(\text {Re}^{-1/2})\) thickness) adjacent to the boundaries in which viscous effects play an important role: see Fig. 3. For this analysis it is convenient to deal with the disturbance equations in their primitive-variable form which we rewrite here for convenience:

$$\begin{aligned} i\alpha \widetilde{u}+\widetilde{v}^{\prime }= & {} 0, \end{aligned}$$
(16a)
$$\begin{aligned} i\alpha (y-c)\widetilde{u}+\widetilde{v}= & {} -i\alpha \widetilde{p}+\text {Re} ^{-1}\left( \widetilde{u}^{\prime \prime }-\alpha ^{2}\widetilde{u}\right) , \end{aligned}$$
(16b)
$$\begin{aligned} i\alpha (y-c)\widetilde{v}= & {} -\widetilde{p}^{\prime }+\text {Re}^{-1}\left( \widetilde{v}^{\prime \prime }-\alpha ^{2}\widetilde{v}\right) , \end{aligned}$$
(16c)

together with the boundary conditions from (7), (15):

$$\begin{aligned}{} & {} \widetilde{u}(1)=\widetilde{v}(1)=0, \end{aligned}$$
(17a)
$$\begin{aligned}{} & {} i\alpha (1+c)\widetilde{u}(-1)=\widetilde{v}(-1), \end{aligned}$$
(17b)
$$\begin{aligned}{} & {} i\alpha (1+c)\widetilde{p}(-1)=K\widetilde{v}(-1). \end{aligned}$$
(17c)

As mentioned earlier, the system (16), (17) constitutes an eigenvalue problem. If we specify a real wavenumber \(\alpha \) and wall stiffness parameter K,  then the phasespeed c is the eigenvalue to be determined. In what follows we will seek real values of c,  and hence neutral solutions to the problem. The wavenumber and phasespeed expansions are written as

$$\begin{aligned} \alpha =\alpha _{0}+\text {Re}^{-1/2}\alpha _{1}+\cdots ,\quad c=c_{0}+\text { Re}^{-1/2}c_{1}+\cdots , \end{aligned}$$
(18)

where our main aim is to determine the order one quantities \((\alpha _{0},c_{0})\) and their dependence on the stiffness parameter K. We start by considering the solution in the main bulk of the flow, referred to here as the ‘core’.

3.1.1 Core solution

Here, the fluid-dynamic quantities expand in the form

$$\begin{aligned} (\widetilde{u},\widetilde{v},\widetilde{p})=(u_{0},v_{0},p_{0})+\text {Re} ^{-1/2}(u_{1},v_{1},p_{1})+\cdots , \end{aligned}$$
(19)

with all the subscripted quantities dependent on the O(1) normal variable y. To begin, we concentrate on the leading-order contribution with the zero subscripts. From substitution of (19) into the governing perturbation equations (16), along with the expansions (18) for the wavenumber and phasespeed, we find:

$$\begin{aligned} i\alpha _{0}u_{0}+v_{0}^{\prime }= & {} 0, \end{aligned}$$
(20a)
$$\begin{aligned} i\alpha _{0}(y-c_{0})u_{0}+v_{0}= & {} -i\alpha _{0}p_{0}, \end{aligned}$$
(20b)
$$\begin{aligned} i\alpha _{0}(y-c_{0})v_{0}= & {} -p_{0}^{\prime }. \end{aligned}$$
(20c)

The streamwise velocity and pressure can be eliminated, leaving the normal velocity satisfying the Rayleigh equation

$$\begin{aligned} v_{0}^{\prime \prime }-\alpha _{0}^{2}v_{0}=0. \end{aligned}$$

It is worth noting here that because the basic Couette flow possesses no curvature, the system (20) is regular at \(y=c_{0}\) and so no critical layer is required in this structure, unlike analogous structures for flows subject to pressure gradients (e.g. see Smith [12]). Since we have a rigid boundary at \(y=1\) we would expect to impose the impermeability condition at this location, namely

$$\begin{aligned} v_{0}(1)=0. \end{aligned}$$

The solution for \(v_{0}\) is therefore determined to be

$$\begin{aligned} v_{0}=\sinh [\alpha _{0}(1-y)], \end{aligned}$$
(21)

where the constant of proportionality has been taken to be unity without loss of generality as a normalization condition on the eigenvalue problem. We note in passing that these disturbances are neither sinuous nor varicose as the symmetry has been removed from the problem by the introduction of the flexible lower wall. The corresponding solutions for \((u_{0},p_{0})\) follow from (20) as

$$\begin{aligned} u_{0}= & {} -i\cosh [\alpha _{0}(1-y)], \end{aligned}$$
(22a)
$$\begin{aligned} p_{0}= & {} i\left\{ (y-c_{0})\cosh [\alpha _{0}(1-y)]+\alpha _{0}^{-1}\sinh [\alpha _{0}(1-y)]\right\} , \end{aligned}$$
(22b)

so that as the upper and lower walls are approached, respectively:

$$\begin{aligned} (u_{0},v_{0},p_{0})\rightarrow & {} (-i,\alpha _{0}(1-y),i(1-c_{0})), \end{aligned}$$
(23a)
$$\begin{aligned} (u_{0},v_{0},p_{0})\rightarrow & {} (-i\cosh 2\alpha _{0},\sinh 2\alpha _{0},i \alpha _{0}^{-1}\sinh 2\alpha _{0}-i(1+c_{0})\cosh 2\alpha _{0} ). \nonumber \\ \end{aligned}$$
(23b)

We now turn to the second-order terms in (19). It transpires that it is sufficient for our purposes to consider the contributions

$$\begin{aligned} u_{1R}=\Re (u_{1}),\,v_{1I}=\Im (v_{1}),\quad p_{1R}=\Re (p_{1}). \end{aligned}$$

From substitution of (19), (18) into (16), these components satisfy

$$\begin{aligned} \alpha _{0}u_{1R}+v_{1I}^{\prime }= & {} 0, \end{aligned}$$
(24a)
$$\begin{aligned} \alpha _{0}(y-c_{0})u_{1R}+v_{1I}= & {} -\alpha _{0}p_{1R}, \end{aligned}$$
(24b)
$$\begin{aligned} \alpha _{0}(y-c_{0})v_{1I}= & {} p_{1R}^{\prime }. \end{aligned}$$
(24c)

As in the leading-order case, some elementary manipulations lead to

$$\begin{aligned} v_{1I}^{\prime \prime }-\alpha _{0}^{2}v_{1I}=0, \end{aligned}$$

and so we deduce that

$$\begin{aligned} v_{1I}=A_{1}\cosh [\alpha _{0}(1-y)]+A_{2}\sinh [\alpha _{0}(1-y)]. \end{aligned}$$
(25)

The constant \(A_{2}\) can be taken to be zero, as this part of the solution can be absorbed into the expression (21) for \(v_{0}.\) This leaves

$$\begin{aligned} v_{1I}=A_{1}\cosh [\alpha _{0}(1-y)], \end{aligned}$$

where \(A_{1}\) is an unknown real constant. The solution for the second-order streamwise and pressure perturbations follow from (24) as

$$\begin{aligned} u_{1R}= & {} A_{1}\sinh [\alpha _{0}(1-y)], \end{aligned}$$
(26a)
$$\begin{aligned} p_{1R}= & {} -A_{1}\left\{ (y-c_{0})\sinh [\alpha _{0}(1-y)]+\alpha _{0}^{-1}\cosh [\alpha _{0}(1-y)]\right\} . \end{aligned}$$
(26b)

We see that as the upper and lower walls are approached:

$$\begin{aligned} (u_{1R},v_{1I},p_{1R})\rightarrow & {} A_{1}(0,1,-\alpha _{0}^{-1}), \end{aligned}$$
(27a)
$$\begin{aligned} (u_{1R},v_{1I},p_{1R})\rightarrow & {} A_{1}(\sinh 2\alpha _{0},\cosh 2\alpha _{0},(1+c_{0})\sinh 2\alpha _{0}-\alpha _{0}^{-1}\cosh 2\alpha _{0}). \nonumber \\ \end{aligned}$$
(27b)

Clearly the boundary conditions (17) are not satisfied by the solutions in the core, implying the existence of thin wall layers where viscosity must be re-introduced. We will start by considering the upper layer which possesses a classical structure, before moving to the lower layer where the inclusion of wall flexibility alters the flow dynamics.

3.1.2 Upper wall layer

Equation (23a) implies the existence of a tangential slip velocity which must be reduced to zero at the wall. Applying the standard boundary-layer concepts, the relevant expansion here is

$$\begin{aligned} u=U_{0}(Y)+\cdots ,\quad v=-\text {Re}^{-1/2}V_{0}(Y)+\cdots ,\,\,p\,=P_{0}(Y)+\cdots , \end{aligned}$$
(28)

where \(Y=\text {Re}^{1/2}(1-y)\) is the O(1) normal variable in the upper wall layer. Substitution into (16) yields

$$\begin{aligned} i\alpha _{0}U_{0}+V_{0}^{\prime }= & {} 0, \end{aligned}$$
(29a)
$$\begin{aligned} i\alpha _{0}(1-c_{0})U_{0}= & {} -i\alpha _{0}P_{0}+U_{0}^{\prime \prime }, \end{aligned}$$
(29b)
$$\begin{aligned} 0= & {} -P_{0}^{\prime }, \end{aligned}$$
(29c)

subject to the matching conditions to the core (23a):

$$\begin{aligned} U_{0}\rightarrow -i,\,\,P_{0}\rightarrow i(1-c_{0})\quad \text {as}\;Y\rightarrow \infty , \end{aligned}$$
(30)

and the no-slip conditions (7), which become

$$\begin{aligned} U_{0}=V_{0}=0\quad \text {on}\;Y=0. \end{aligned}$$

It is easy to see from (29c) that the pressure remains constant to leading order across the layer and therefore assumes the form

$$\begin{aligned} P_{0}=i(1-c_{0})\quad \text { for all }Y, \end{aligned}$$

in view of (30), while the solutions for the velocity perturbations are

$$\begin{aligned} U_{0}= & {} -i(1-\exp [-mY]), \end{aligned}$$
(31a)
$$\begin{aligned} V_{0}= & {} -\alpha _{0}(Y-m^{-1}+m^{-1}\exp [-mY]), \end{aligned}$$
(31b)

with

$$\begin{aligned} m\equiv \alpha _{0}^{1/2}(1-c_{0})^{1/2}\exp [i\pi /4]. \end{aligned}$$
(32)

From (31b) we see that

$$\begin{aligned} V_{0}\rightarrow -\alpha _{0}(Y-m^{-1})\quad \text { as }Y\rightarrow \infty . \end{aligned}$$
(33)

The first term in (33) matches to the near-wall behaviour of \(v_{0}\) in (23a), while the second term implies, using the definition of m in (32), that

$$\begin{aligned} \Im (V_{0})\rightarrow -\frac{\alpha _{0}^{1/2}}{(1-c_{0})^{1/2}2^{1/2}}. \end{aligned}$$

Matching this solution to that in the core via (27a), we see that this fixes the constant \(A_{1}\) as

$$\begin{aligned} A_{1}=\frac{\alpha _{0}^{1/2}}{(1-c_{0})^{1/2}2^{1/2}}. \end{aligned}$$
(34)

This quantity connects the flow behaviour near the upper rigid wall to that in the wall layer near the flexible lower wall. The dynamics in this wall layer are considered next.

3.1.3 Lower wall layer analysis and the eigenrelation for AS1

The near-wall form (23b) shows that, as the lower wall is approached, we have both a tangential slip velocity and a non-zero normal velocity component. It transpires that we need to work to second order in this layer to determine the leading-order wavenumber and phasespeed. We therefore pose the expansion:

$$\begin{aligned} (\widetilde{u},\widetilde{v},\widetilde{p})=(\overline{U}_{0}(\overline{Y}), \overline{V}_{0}(\overline{Y}),\overline{P}_{0}(\overline{Y}))+ \text {Re}^{-1/2}((\overline{U}_{1}(\overline{Y}), \overline{V}_{1}(\overline{Y}),\overline{P}_{1}(\overline{Y}))+\cdots \end{aligned}$$
(35)

with \(y=-1+\text {Re}^{-1/2}\overline{Y}\) and \(\overline{Y}\) of O(1). The leading-order governing equations are, from substitution of (35) into (16):

$$\begin{aligned} \overline{V}_{0}^{\prime }= & {} 0, \end{aligned}$$
(36a)
$$\begin{aligned} i\alpha _{0}(-1-c_{0})\overline{U}_{0}+\overline{V}_{0}= & {} -i\alpha _{0} \overline{P}_{0}+\overline{U}_{0}^{\prime \prime }, \end{aligned}$$
(36b)
$$\begin{aligned} 0= & {} -\overline{P}_{0}^{\prime } \end{aligned}$$
(36c)

with matching to the core (23):

$$\begin{aligned} \overline{U}_{0}\rightarrow -i\cosh 2\alpha _{0},\,\,\overline{V} _{0}\rightarrow \sinh 2\alpha _{0},\,\,\overline{P}_{0}\rightarrow i\left\{ \alpha _{0}^{-1}\sinh 2\alpha _{0}-(1+c_{0})\cosh 2\alpha _{0}\right\} , \end{aligned}$$
(37)

as \(\overline{Y}\rightarrow \infty \). We see from (36a), (36c), that in this layer, the leading-order normal velocity and the pressure remain constant and therefore take on the values

$$\begin{aligned} \overline{V}_{0}=\sinh 2\alpha _{0},\,\,\overline{P}_{0}=i\left\{ \alpha _{0}^{-1}\sinh 2\alpha _{0}-(1+c_{0})\cosh 2\alpha _{0}\right\} . \end{aligned}$$
(38)

However the solution here must also obey the dynamic condition (17c) at the wall, which in terms of the wall layer variables is

$$\begin{aligned} i\alpha _{0}(1+c_{0})\overline{P}_{0}=K\overline{V}_{0}. \end{aligned}$$

Substituting for \(\overline{V}_{0},\overline{P}_{0}\) from (38) we obtain a first relationship between \(\alpha _{0}\) and \(c_{0},\) namely:

$$\begin{aligned} \alpha _{0}(1+c_{0})^{2}\cosh 2\alpha _{0}-(1+c_{0})\sinh 2\alpha _{0}=K\sinh 2\alpha _{0}. \end{aligned}$$
(39)

The corresponding solution for \(\overline{U}_{0}\) satisfies (36b), (37) and the kinematic condition (17b), which implies

$$\begin{aligned} i\alpha _{0}(1+c_{0})\overline{U}_{0}(0)=\overline{V}_{0}(0). \end{aligned}$$

The required solution is easily found to be

$$\begin{aligned} \overline{U}_{0}= & {} -i\left( \cosh 2\alpha _{0}+\left\{ \frac{\sinh 2\alpha _{0} }{\alpha _{0}(1+c_{0})}-\cosh 2\alpha _{0}\right\} \exp [-\overline{m} \overline{Y}]\right) , \end{aligned}$$
(40a)
$$\begin{aligned} \overline{m}\equiv & {} \alpha _{0}^{1/2}(1+c_{0})^{1/2}\exp [-i\pi /4]. \end{aligned}$$
(40b)

We now turn to the \(O(\text {Re}^{-1/2})\) correction to the solution. The continuity equation yields, from substitution of (35) into (16a):

$$\begin{aligned} \overline{V}_{1}^{\prime }=-i\alpha _{0}\overline{U}_{0}. \end{aligned}$$

Using (40) for \(\overline{U}_{0}\), and integrating, we find that

$$\begin{aligned} \overline{V}_{1}=\overline{V}_{1}(0)-\left( \alpha _{0}\overline{Y}\cosh 2\alpha _{0}+\overline{m}^{-1}\left\{ \alpha _{0}\cosh 2\alpha _{0}-\frac{\sinh 2\alpha _{0}}{1+c_0}\right\} \left\{ e^{-\overline{m} \overline{Y}}-1\right\} \right) . \end{aligned}$$
(41)

The complex constant \(\overline{V}_{1}(0)\) is thus far unknown, but from the dynamic condition (17c) we can deduce that

$$\begin{aligned} \alpha _{0}(1+c_{0})\overline{P}_{1R}(0)=K\overline{V}_{1I}(0), \end{aligned}$$
(42)

where again we use the subscripts R and I to represent the real and imaginary parts respectively. In addition, the normal momentum equation (16c) implies that

$$\begin{aligned} \overline{P}_{1R}^{\prime }=0, \end{aligned}$$

and hence from matching to the core solution (27b):

$$\begin{aligned} \overline{P}_{1R}=\frac{\alpha _{0}^{1/2}}{(1-c_{0})^{1/2}2^{1/2}} \{(1+c_{0})\sinh 2\alpha _{0}-\alpha _{0}^{-1}\cosh 2\alpha _{0}\}, \end{aligned}$$

where we have used the value of \(A_{1}\) deduced in (34). It therefore follows from (42) that

$$\begin{aligned} \overline{V}_{1I}(0)=\frac{\alpha _{0}^{3/2}(1+c_{0})}{ K(1-c_{0})^{1/2}2^{1/2}}\{(1+c_{0})\sinh 2\alpha _{0}-\alpha _{0}^{-1}\cosh 2\alpha _{0}\}. \end{aligned}$$

Returning now to the wall layer solution (41), and using the wall value deduced above, we see that as \(\overline{Y}\rightarrow \infty \):

$$\begin{aligned} \overline{V}_{1I}\rightarrow & {} \frac{\alpha _{0}\cosh 2\alpha _{0}-(1+c_{0})^{-1}\sinh 2\alpha _{0}}{2^{1/2}\alpha _{0}^{1/2}(1+c_{0})^{1/2}} \\ {}{} & {} +\frac{\alpha _{0}^{3/2}(1+c_{0})\left\{ (1+c_{0})\sinh 2\alpha _{0}-\alpha _{0}^{-1}\cosh 2\alpha _{0}\right\} }{ K(1-c_{0})^{1/2}2^{1/2}} . \end{aligned}$$

This expression should match to the near-wall core solution given in (27), leading to a second relation between \(\alpha _{0}\) and \(c_{0},\) namely:

$$\begin{aligned}{} & {} \frac{\alpha _{0}(1+c_{0})\cosh 2\alpha _{0}-\sinh 2\alpha _{0}}{\alpha _{0}^{1/2}(1+c_{0})^{3/2}}+\frac{\alpha _{0}^{1/2}(1+c_{0})\{\alpha _{0}(1+c_{0})\sinh 2\alpha _{0}-\cosh 2\alpha _{0}\}}{K(1-c_{0})^{1/2}}\nonumber \\{} & {} \quad =\frac{\alpha _{0}^{1/2}\cosh 2\alpha _{0}}{(1-c_{0})^{1/2}}. \end{aligned}$$
(43)

Together, for a given value of K,  the relations (39) and (43) determine the leading-order wavenumber \(\alpha _{0}\) and phasespeed \(c_{0}.\) Plots of \(\alpha _{0}\) and \(c_{0}\) versus the wall stiffness K are shown in Fig. 4. We see that the neutral value of the wavenumber decreases as K increases, reaching a minimum, and then growing linearly with further increase in K. The phasespeed increases monotonically with increasing K, approaching the speed of the upper wall. The dotted lines show the solution to the AS1 eigenrelations at asymptotically large K and are given explicitly in Sect. 3.3. It is evident that the asymptotic forms provide a good approximation to the solutions for both wavenumber and phasespeed for values of spring stiffness as low as \(K=2\).

It can be seen from (43) that the upper wall layer structure ceases to be valid once the phasespeed \(c_{0}\) is close to the speed of the upper plate. In fact when \(c_{0}\) is sufficiently close to unity there is a new distinguished limit which we investigate next.

Fig. 4
figure 4

Solutions of the AS1 eigenrelations. (a) Wavenumber \(\alpha _0\) versus spring stiffness K. (b) Phasespeed \(c_0(K)\). The dotted lines show the large K asymptotes

Full size image

3.2 Asymptotic structure II (AS2)

This second asymptotic structure is valid in the limit

$$\begin{aligned} \alpha =O(1),\,\,1-c\ll 1,\,\,K=O(1),\,\,\text {Re}\gg 1. \end{aligned}$$

Much of the analysis in the core and lower wall layer remains unchanged. However, in this limit, the phasespeed approaches the speed of the upper plate which leads to some dynamic changes in its vicinity. Let us suppose \(1-c=O(\delta )\), and also write \(y=1-\delta Y,\) with Y the O(1) normal coordinate in the upper layer. Assuming that the wavenumber \(\alpha \) remains O(1),  the inertial operator \((y-c)\partial /\partial x=O(\delta ).\) In the wall layer we expect this quantity should be of the same order of magnitude as the viscous operator \(\text {Re}^{-1}\partial ^{2}/\partial y^{2}=O(\text {Re}^{-1}\delta ^{-2}).\) Balancing these two quantities leads to the estimate \(\delta =O(\text {Re}^{-1/3})\) as the new thickness of the upper layer. We therefore pose a phasespeed expansion of the form

$$\begin{aligned} c=1-\text {Re}^{-1/3}c_{1}+\cdots , \end{aligned}$$
(44)

with the wavenumber expansion remaining as in (18). A sketch of the new structure is given in Fig. 5 and we explore each region briefly in turn below.

Fig. 5
figure 5

The AS2 structure in which the upper layer is a viscous shear layer

Full size image

The new expansion in the upper wall layer, replacing (28), is:

$$\begin{aligned} \widetilde{u}=U_{0}(Y)+\cdots ,\quad \widetilde{v}=-\text {Re} ^{-1/3}V_{0}(Y)+\cdots ,\,\,\widetilde{p}=\text {Re}^{-1/3}P_{0}(Y)+\cdots , \end{aligned}$$
(45)

with \(y=1-\text {Re}^{-1/3}Y.\) Note that in comparison with the corresponding layer in AS1, the pressure is reduced by a factor \(\text {Re}^{-1/3}\) in order to remain in balance with the other terms in the streamwise momentum equation (16b). Substitution of (45) into (16) yields

$$\begin{aligned} i\alpha _{0}U_{0}+V_{0}^{\prime }= & {} 0, \end{aligned}$$
(46a)
$$\begin{aligned} i\alpha _{0}(c_{1}-Y)U_{0}-V_{0}= & {} -i\alpha _{0}P_{0}+U_{0}^{\prime \prime }, \end{aligned}$$
(46b)
$$\begin{aligned} 0= & {} -P_{0}^{\prime }. \end{aligned}$$
(46c)

These equations are to be solved subject to no-slip on the upper plate:

$$\begin{aligned} U_{0}(0)=V_{0}(0)=0. \end{aligned}$$
(47)

In addition we need an outer condition to match to the core flow. Anticipating a tangential slip velocity from the core solution, as in AS1, we impose that

$$\begin{aligned} U_{0}\rightarrow A\;\text { as }\;Y\rightarrow \infty , \end{aligned}$$
(48)

where the displacement A is an unknown complex constant. It can be shown in a straightforward manner (Appendix A) that a solution to the system (46)–(48) only exists if the following pressure-displacement law holds:

$$\begin{aligned} \alpha _{0}^{2}P_{0}^{*}=(i\alpha _{0})^{5/3}\frac{Ai^{\prime }(\xi _{0}) }{\kappa (\xi _{0})}A^{*}. \end{aligned}$$
(49)

Here \(*\) represents complex conjugate, Ai is the Airy function, and

$$\begin{aligned} \kappa (\xi _{0})=\int _{\xi _{0}}^{\infty }Ai(s)\textrm{d}s\quad \text {with}\quad \xi _{0}=-i^{1/3}\alpha _{0}^{1/3}c_{1}. \end{aligned}$$
(50)

Turning now to the core flow, the expansions (19) and governing equations (20) still hold, but with the leading-order phasespeed \(c_{0}\) replaced by unity. If we make the same replacement in the solutions (21), (22) we have

$$\begin{aligned} u_{0}= & {} -i\cosh [\alpha _{0}(1-y)], \\ v_{0}= & {} \sinh [\alpha _{0}(1-y)], \\ p_{0}= & {} i\left\{ (y-1)\cosh [\alpha _{0}(1-y)]+\alpha _{0}^{-1}\sinh [\alpha _{0}(1-y)]\right\} , \end{aligned}$$

from which we can see that \(p_{0}\rightarrow O(1-y)^{3}\) as \(y\rightarrow 1,\) which is consistent with the reduced upper wall pressure postulated in (45). Matching the streamwise velocity to that in the upper wall layer, we see that we require

$$\begin{aligned} A=-i. \end{aligned}$$
(51)

The solution for \((u_{1},v_{1},p_{1})\) in the core also remains unchanged, and from (25), (26), setting \(c_{0}=1,\) we have

$$\begin{aligned} u_{1R}= & {} A_{1}\sinh [\alpha _{0}(1-y)],\quad v_{1I} =A_{1}\cosh [\alpha _{0}(1-y)], \\ p_{1R}= & {} -A_{1}\left\{ (y-1)\sinh [\alpha _{0}(1-y)]+\alpha _{0}^{-1}\cosh [\alpha _{0}(1-y)]\right\} . \end{aligned}$$

The constant \(A_{1}\) is no longer given by (34) but is in fact determined at higher order. We see that \(\Re (\widetilde{p})=O(\text {Re} ^{-1/2})\) in the core and so, in order to avoid a mismatch in pressure perturbations between the core and upper layer, we require

$$\begin{aligned} \Re (P_{0})=0. \end{aligned}$$

From (49), with A given by (51), this implies

$$\begin{aligned} \Im \left\{ \mathcal {G}(\xi )\right\} =0,\,\,\text {where }\mathcal {G}(\xi )=i^{5/3}\frac{Ai^{\prime }(\xi )}{\kappa (\xi )}. \end{aligned}$$
(52)

In Fig. 6 the imaginary part of \(\mathcal {G}(\xi )\) is plotted against the real variable s where \(\xi =-i^{1/3}s.\) In the context of the present structure we can identify \(s=\) \(\alpha _{0}^{1/3}c_{1}\) from (50). The function passes through zero when

$$\begin{aligned} \alpha _{0}^{1/3}c_{1}=s_{0},\quad s_{0}\simeq 2.2972, \end{aligned}$$
(53)

see, for example, Miles [13], Reid [14].

Fig. 6
figure 6

The imaginary part of the function \(\mathcal {G}\) plotted versus s

Full size image

The lower wall layer analysis proceeds essentially as for AS1: as a consequence the relation (39) still holds but with \(c_{0}\) replaced by unity, i.e. we have

$$\begin{aligned} 4\alpha _{0}\cosh 2\alpha _{0}=(K+2)\sinh 2\alpha _{0}, \end{aligned}$$

determining \(\alpha _{0}\) as a function of K. The phase speed correction \(c_{1}\) then follows from (53). The quantities \(\alpha _{0}\) and \(c_{1}\) are shown as functions of K in Fig. 7. We can see that for this structure the wavenumber increases monotonically with K, while the phasespeed correction decreases monotonically. Thus, with increasing spring stiffness, the neutral disturbances on this branch are becoming shorter in wavelength and propagating at a speed ever closer to that of the upper wall. If we compare Fig. 7a with the corresponding figure for AS1 (Fig. 4a), we can see that at each K, the value of \(\alpha _0\) is larger in Fig. 4a. This means that AS1 forms the upper branch of the neutral stability curve in the \(\text {Re}-\alpha \) plane at high Reynolds number, while AS2 represents the lower branch. We will see this explicitly in Sect. 4 when we compute the neutral curve numerically at large finite values of \(\text {Re}\). In a similar way to AS1, we see that the AS2 solutions approach their large-K asymptotes (shown as dashed lines on Fig. 7) at moderate values of K.

Fig. 7
figure 7

Solutions of the AS2 eigenrelations. (a) Wavenumber \(\alpha _0\) versus spring stiffness K. (b) Phasespeed correction \(c_1(K)\). The dashed lines show the large K asymptotes

Full size image

3.3 Asymptotic structure III (AS3): large spring stiffness

As mentioned earlier, plane Couette flow with rigid boundaries is linearly stable: thus the neutral modes that we have obtained here must vanish in some fashion as K becomes large. Possibly the instability may retreat to infinite Reynolds number as \(K\rightarrow \infty ,\) or instead there may be a cut-off at finite K. In order to investigate what actually transpires, we first examine AS1 in the limit of large K. Analysis of the eigenrelations (39), (43) reveals that the leading-order wavenumber and phasespeed behave as

$$\begin{aligned} \alpha _{0}\sim \frac{\lambda }{4}-\frac{1}{2}\lambda e^{-\lambda }+\cdots ,\quad c_{0}\sim 1-32 e^{-2\lambda }+\cdots , \quad \text {as}\; \lambda \rightarrow \infty , \end{aligned}$$
(54)

where we have defined

$$\begin{aligned} \lambda =K+2. \end{aligned}$$
(55)

It therefore appears that the phasespeed is approaching the speed of the upper plate, and suggests that, at sufficiently large \(\lambda \), a new inertial-viscous balance will hold in an \(O(e^{-2\lambda })\) vicinity of that upper boundary. For then we can estimate the inertial operator \(i\alpha _{0}(y-c_{0})\) as \(O(\lambda e^{-2\lambda }),\) while the viscous operator \(\text {Re}^{-1}\partial ^{2}/\partial y^{2}=O(\text {Re}^{-1}e^{4\lambda }).\) Balancing these two effects, we obtain a new instability structure when K is sufficiently large that

$$\begin{aligned} \lambda e^{-6\lambda }=O(\text {Re}^{-1}). \end{aligned}$$
(56)

Analysis of AS2 in the large K limit leads to the same prediction for the behaviour of \(\alpha _{0}\) as in (54), but now the prediction for the phasespeed is

$$\begin{aligned} c=1-\text {Re}^{-1/3}s_{0}(\lambda /4)^{-1/3}+\cdots , \end{aligned}$$
(57)

from (53). It can be predicted that AS2 also breaks down when \(\lambda \) increases sufficiently that (56) is achieved. Thus, at large spring stiffness, we anticipate the creation of a new structure which supersedes both AS1 and AS2. We shall now investigate this structure, which we will refer to as AS3, in some detail.

It is convenient to begin by defining a parameter

$$\begin{aligned} \mu =\text {Re}^{-1/2}\lambda ^{-1/2}e^{3\lambda }, \end{aligned}$$
(58)

which is O(1) in the new regime, with both AS1 and AS2 expected to be recovered in the limit as \(\mu \rightarrow 0.\) A sketch of the new flow structure is given in Fig. 8. The \(O(e^{-2\lambda })\) thickness of the upper layer is predicted above, but there is also an additional \(O(\lambda ^{-1})\) region near the upper wall in which the quantity \(\alpha (1-y)\) is O(1). The bulk of the core flow remains unaffected, while the thickness of the lower layer can be estimated as \(O(\alpha \) \(\text {Re}\) \(c)^{-1/2}=O(e^{-3\lambda }).\) Motivated by the asymptotic forms (54), we will pose the wavenumber and phasespeed expansions

$$\begin{aligned} \alpha =\lambda \alpha _{10}+\lambda e^{-\lambda }\alpha _{12}+\cdots ,\quad c=1-e^{-2\lambda }c_{12}+\cdots , \end{aligned}$$
(59)

and investigate the dynamics of each layer in turn, commencing with the layer adjacent to the upper plate.

Fig. 8
figure 8

The AS3 asymptotic structure that arises at large spring stiffness K

Full size image

3.3.1 Upper wall layer

Here, motivated by the new scalings for the wavenumber and phasespeed in (59), we pose the expansions

$$\begin{aligned} \widetilde{u}=U(Y)+\cdots ,\quad \widetilde{v}=-\lambda e^{-2\lambda }\mu V(Y)+\cdots ,\quad \widetilde{p}=e^{-2\lambda }P(Y)+\cdots , \end{aligned}$$
(60)

where

$$\begin{aligned} y=1-e^{-2\lambda }\mu Y, \end{aligned}$$
(61)

and the O(1) factor \(\mu \) is inserted for convenience. From substitution of (59)–(61) into (16 ), the leading-order balances are

$$\begin{aligned} i\alpha _{10}U+V^{\prime }= & {} 0, \end{aligned}$$
(62a)
$$\begin{aligned} i\alpha _{10}(c_{12}-\mu Y)U-\mu V= & {} -i\alpha _{10}P+U^{\prime \prime }, \end{aligned}$$
(62b)
$$\begin{aligned} 0= & {} -P^{\prime }. \end{aligned}$$
(62c)

These equations are to be solved subject to the no-slip condition

$$\begin{aligned} U(0)=V(0)=0, \end{aligned}$$
(63)

and a connection to the core flow via

$$\begin{aligned} U(\infty )=A=-i, \end{aligned}$$
(64)

where we have chosen this specific value as our normalization constant in order to maintain consistency with the structures AS1 and AS2 (see equations (30), (51)). A very similar procedure to that carried out in Sect. 3.2, shows that the solvability condition on (62)–(64) takes the form

$$\begin{aligned} \alpha _{10}^{2}P^{*}=i(\alpha _{10}\mu )^{5/3}\mathcal {G}(\xi )\mu ^{-1}, \end{aligned}$$
(65)

with \(\mathcal {G}(\xi )\) defined as in (52), and \(\xi \) now given by

$$\begin{aligned} \xi =-i^{1/3}\alpha _{10}^{1/3}c_{12}/\mu ^{2/3}. \end{aligned}$$

From the streamwise momentum equation (62b), and the pressure-displacement law (65) we see that

$$\begin{aligned} \Re (V)\sim -\alpha _{10}Y,\quad \Im (V)\rightarrow -\alpha _{10}^{2/3}\mu ^{-1/3}\Im [\mathcal {G}(\xi )]\quad \text {as}\;Y\rightarrow \infty , \end{aligned}$$
(66)

which provide motivation for the scalings of the next region.

3.3.2 Adjustment region

This forms the outer part of the upper wall layer and is of \(O(\lambda ^{-1})\) thickness. Here we set

$$\begin{aligned} y=1-\lambda ^{-1}\overline{y}, \end{aligned}$$

with \(\overline{y}\) of O(1),  and expand the fluid-dynamic functions in the form

$$\begin{aligned} \widetilde{u}= & {} i\overline{u}_{0}+\cdots +\lambda e^{-2\lambda }\overline{u}_{1}+\cdots , \\ \widetilde{v}= & {} \overline{v}_{0}+\cdots +\lambda e^{-2\lambda }i\overline{v}_{1}+\cdots , \\ \widetilde{p}= & {} K^{-1}i\overline{p}_{0}+\cdots +e^{-2\lambda }\overline{p} _{1}+\cdots . \end{aligned}$$

Here, \((\overline{u}_{0},\overline{v}_{0},\overline{p}_{0})\) are real functions of \(\overline{y}\), and the terms with subscript 1 denote the first terms in the \((\widetilde{u},\widetilde{v},\widetilde{p})\) expansions which are not purely imaginary. We refer to these as the ‘phase-shifted terms’. At leading order we obtain inviscid balances with solutions

$$\begin{aligned} (\overline{u}_{0},\overline{v}_{0},\overline{p}_{0})=(-\cosh (\alpha _{10} \overline{y}),\sinh (\alpha _{10}\overline{y}),\alpha _{10}^{-1}\sinh (\alpha _{10}\overline{y})-\overline{y}\cosh (\alpha _{10}\overline{y})), \end{aligned}$$

which are analogous to the core solutions in (21), (22). Now we turn to the phase-shifted terms. The solutions for the real parts of \((\overline{u}_{1},\overline{v}_{1},\overline{p}_{1})\) are

$$\begin{aligned} (\overline{u}_{1R},\overline{v}_{1R},\overline{p}_{1R})=\overline{v} _{1R}(0)\left\{ \sinh (\alpha _{10}\overline{y}),\cosh (\alpha _{10} \overline{y}),\overline{y}\sinh (\alpha _{10}\overline{y})-\alpha _{10}^{-1}\cosh (\alpha _{10}\overline{y})\right\} , \end{aligned}$$

where

$$\begin{aligned} \overline{v}_{1R}(0)=\alpha _{10}^{2/3}\mu ^{2/3}\Im [\mathcal {G}(\xi )], \end{aligned}$$
(67)

in order to match to the upper wall layer via (66). This latter quantity plays the role of \(A_{1}\) in AS1, connecting the flow adjacent to the upper rigid plate to that in the vicinity of the lower flexible plate.

3.3.3 Core region

As in the structures AS1, AS2, this region occupies the bulk of the flow and the solutions here are in essence a continuation of those in the adjustment layer. In particular, on approach to the lower wall, we have the non-phase-shifted contributions

$$\begin{aligned} \widetilde{u}= & {} -i\cosh 2\alpha +\cdots ,\quad \widetilde{v}=\sinh 2\alpha +\cdots , \nonumber \\ \alpha \widetilde{p}= & {} i\left\{ \sinh 2\alpha -2\alpha \cosh 2\alpha \right\} +\cdots , \end{aligned}$$
(68)

where the wavenumber \(\alpha \) is given by the expansion (59). We will see shortly, when we analyse the lower layer, that the non-phase-shifted normal velocity and pressure fluctuations remain constant across the lower layer to the order of magnitude we are currently working, and so we can apply the dynamic condition (17c) directly to (68) to several orders. At orders \(\lambda e^{\pm 2\lambda \alpha _{10}}\) we obtain

$$\begin{aligned} \alpha _{10}=1/4,\quad \alpha _{12}=-1/2, \end{aligned}$$
(69)

in agreement with the asymptotic form (54). We now turn to the phase-shifted terms in the expansion. Here we have to leading order:

$$\begin{aligned} \widetilde{v}_{I}= & {} \lambda e^{-2\lambda }\overline{v}_{1R}(0)\cosh (\alpha (1-y)),\\ \alpha \widetilde{p}_{R}= & {} \lambda e^{-2\lambda }\overline{v}_{1R}(0)\left\{ \alpha (1-y)\sinh (\alpha (1-y))-\cosh (\alpha (1-y))\right\} . \end{aligned}$$

Evaluating these quantities on the approach to the lower wall, and using the values for \(\alpha _{10},\alpha _{12}\) in (69), we obtain, after some simplification:

$$\begin{aligned} \widetilde{v}_{I}\sim & {} \overline{v}_{1R}(0)\{ (\lambda /2)e^{-3\lambda /2} -(\lambda ^2/2)e^{-5\lambda /2}+(\lambda /2)e^{-5\lambda /2}+\cdots \}, \end{aligned}$$
(70a)
$$\begin{aligned} \alpha \widetilde{p}_{R}\sim & {} \overline{v}_{1R}(0)\{(\lambda ^2/4)e^{-3\lambda /2} +\cdots -(\lambda ^2/4)e^{-5\lambda /2}+\cdots \}, \end{aligned}$$
(70b)

as \(y\rightarrow -1.\) These asymptotic forms need to match to the normal velocity and pressure fluctuations in the lower wall layer, which forms the final part of AS3 and allows us to determine the phasespeed correction \(c_{12}.\)

3.3.4 Lower layer

Here we write \(y=-1+\mu e^{-3\lambda }y_{-}\),with \(y_{-}\) describing O(1) normal variations within this layer. Motivated by the core behaviour above, the flow expansions holding here are

$$\begin{aligned} \widetilde{u}= & {} e^{\lambda /2}iu_{10}(y_{-})+\cdots , \end{aligned}$$
(71a)
$$\begin{aligned} \widetilde{v}= & {} e^{\lambda /2}v_{10}(y_{-})+\cdots +\lambda ^2 e^{-5\lambda /2}iv_{11}(y_{-})+\lambda e^{-5\lambda /2}iv_{12}(y_{-})+\cdots , \end{aligned}$$
(71b)
$$\begin{aligned} \alpha \widetilde{p}= & {} \lambda e^{\lambda /2}iQ_{10}(y_{-})+\cdots +\lambda ^{2}e^{-5\lambda /2}Q_{12}(y_{-})+\cdots , \end{aligned}$$
(71c)

and in order to match to the core solutions (68), (70), we require as \(y_{-}\rightarrow \infty \):

$$\begin{aligned} u_{10}\rightarrow & {} -1/2,\quad v_{10}\rightarrow 1/2,\quad Q_{10}\rightarrow -1/4, \end{aligned}$$
(72a)
$$\begin{aligned} v_{11R}\rightarrow & {} -\overline{v}_{1R}(0)/2,\quad v_{12R} \rightarrow \overline{v}_{1R}(0)/2, \quad Q_{12R}\rightarrow -\overline{v}_{1R}(0)/4, \end{aligned}$$
(72b)

again with a subscript R denoting the real part. Substitution of expansions (71) into the continuity equation (16a), and the normal momentum equation (16b) shows that

$$\begin{aligned} v_{10}^{\prime }=v_{11R}^{\prime }=Q_{10}^{\prime }=Q_{12}^{\prime }=0, \end{aligned}$$

and hence those quantities are equal to their asymptotic values given in (72) throughout the layer. At order \(\lambda e^{\lambda /2}\) the continuity and streamwise momentum equations (16a), (16b) reduce to

$$\begin{aligned} -u_{10}/4+\mu ^{-1}iv_{12}^{\prime }= 0,\quad u_{10}/2=-1/4+iu_{10}^{\prime \prime }. \end{aligned}$$
(73)

The solution for \(u_{10}\) follows as

$$\begin{aligned} u_{10}=-(1/2)(1-e^{-q_{0}y_{-}}),\quad q_{0}=(1-i)/2. \end{aligned}$$

We can then find \(v_{12}\) from integration of the first of equations (73) as

$$\begin{aligned} v_{12}=v_{12}(0)+(i\mu /8)(y_{-}-q_{0}^{-1}\left\{ 1-e^{-q_{0}y_{-}}\right\} ). \end{aligned}$$
(74)

The real part of the quantity \(v_{12}(0)\) can be found by applying the dynamic condition (17c) at \(O(\lambda ^2 e^{-5\lambda /2})\) which gives

$$\begin{aligned} 2Q_{12R}=v_{12R}(0)+\overline{v}_{1R}(0), \end{aligned}$$

and hence, upon substituting for \(Q_{12R}\) from (72b):

$$\begin{aligned} v_{12R}(0)=-3\overline{v}_{1R}(0)/2. \end{aligned}$$

We now return to the expression (74) for \(v_{12}.\) We see that

$$\begin{aligned} v_{12R}\rightarrow -3\overline{v}_{1R}(0)/2+\mu /8\quad \text { as } y_{-}\rightarrow \infty . \end{aligned}$$

This must be consistent with the matching condition to the core region given in (72). Hence we have

$$\begin{aligned} 2\overline{v}_{1R}(0)=\mu /8. \end{aligned}$$

Substituting for \(\overline{v}_{1R}(0)\) from (67), this becomes

$$\begin{aligned} \Im [\mathcal {G}(\xi )]=\frac{\mu ^{1/3}}{2^{8/3}},\quad \xi =-i^{1/3}c_{12}/(2\mu )^{2/3}, \end{aligned}$$
(75)

where we have substituted for \(\alpha _{10}\) from (69). Equation (75) determines the phasespeed correction \(c_{12}\) as a function of the parameter \(\mu \) which controls the value of the spring stiffness on this scaling.

Fig. 9
figure 9

Phasespeed correction \(c_{12}\) as a function of \(\mu \) for AS3

Full size image

We already have the graph of \(\Im [\mathcal {G}(\xi )]\) in Fig. 6 plotted versus the real variable s,  where \(\xi =-1^{1/3}s.\) In the context of AS3 we have

$$\begin{aligned} s=c_{12}/(2\mu )^{2/3}. \end{aligned}$$
(76)

Using our knowledge of the behaviour of \(\Im [\mathcal {G}(\xi )]\), we plot \(c_{12}(\mu )\) in Fig. 9. A feature of this graph is the cut-off in \(\mu .\) This feature is reminiscent of one of the structures in Cowley & Smith [15], relating to the critical wall speed in Poiseuille-Couette flow.

From Fig. 6 we can see that \(\Im [\mathcal {G}(\xi )]\) has a maximum \(g_{\max }\) say, where \(g_{\max }\simeq 1.2406.\) It therefore follows that solutions to AS3 only exist if

$$\begin{aligned} \mu \le (g_{\max })^{3}2^{8}=\mu _{\max }\simeq 488.8. \end{aligned}$$

According to the definition of \(\mu \) in (58), our theory therefore predicts that an instability at large fixed spring stiffness will only exist beyond a large Reynolds number \(\text {Re}_\textrm{crit}\) given by

$$\begin{aligned} \text {Re}_\textrm{crit}=\mu _{\max }^{-2}\lambda ^{-1}e^{6\lambda }. \end{aligned}$$

It is clear that \(\text {Re}_\textrm{crit}\) increases rapidly with increasing spring stiffness and we will see this feature in the Orr–Sommerfeld calculations in Sect. 4.

It is now clear that at large values of the spring stiffness parameter \(\lambda \), the asymptotic theory AS3 actually describes the entirety of the linear neutral curve, including the critical Reynolds number. Moreover, given the exponential dependence of \(\text {Re}_\textrm{crit}\) on \(\lambda \) it is apparent that \(\lambda \) (and hence K) does not actually need to be particularly large before we enter the regime where AS3 is valid.

Before we compare the theories AS1, AS2 and AS3 with full numerical computations of the eigenvalue problem, we check that as \(\mu \) becomes small in AS3 (at fixed \(\text {Re}\)) we recover the AS1 and AS2 structures. This provides a partial check on the correctness of the considerable asymptotic analysis involved in deriving the AS3 structure.

3.3.5 The \(\mu \rightarrow 0\) limits

According to the eigenrelation (75), if \(\mu \rightarrow 0\) it follows that \(\Im [\mathcal {G}(\xi )]\rightarrow 0+.\) Recalling that \(\xi =-i^{1/3}s\) with s real, an inspection of Fig. 6 reveals that there are two ways this can be achieved: either \(s\rightarrow \infty \) or \(s\rightarrow s_{0}\), where \(s_{0}\simeq 2.2972\) from (53). We consider each in turn.

(i) The limit \(s\rightarrow \infty \). It can be shown (see e.g. Bennett & Hall [16]) that

$$\begin{aligned} \Im (\mathcal {G)}\sim (2s)^{-1/2}\quad \text { as }s\rightarrow \infty . \end{aligned}$$

Setting \(s=c_{12}/(2\mu )^{2/3},\) the eigenrelation (75) leads to \(c_{12}\rightarrow 2^{5}\). Recalling the expansion (59), we see that in this limit the phasespeed assumes the form

$$\begin{aligned} c=1-2^{5}e^{-2\lambda }+\cdots , \end{aligned}$$

which is an exact match to the large \(\lambda \) asymptote of AS1 as given in (54).

(ii) The limit \(s\rightarrow s_{0}.\) In this case it follows immediately from the definition of s (76) that \(c_{12}\sim (2\mu )^{2/3}s_{0}\text { as }\mu \rightarrow 0\), and so, in this limit:

$$\begin{aligned} c=1-(2\mu )^{2/3}s_{0}e^{-2\lambda }+\cdots . \end{aligned}$$

Substituting for \(\mu \) in terms of \(\text {Re}\) and \(\lambda \) from (58 ), this can be rewritten as

$$\begin{aligned} c=1-\text {Re}^{-1/3}s_{0}(\lambda /4)^{-1/3}+\cdots , \end{aligned}$$

which links back to the large \(\lambda \) asymptote of AS2 given in (57 ). Figure 10 is a zoomed-in version of Fig. 9, concentrating on small values of \(\mu ,\) and shows how the two branches of the solution for \(c_{12}\) link back to the phasespeeds in the AS1 and AS2 structures. In particular, we note that the AS1 structure is only recovered once the ‘kink’ in the curve has been negotiated. This kink, which arises from the smaller of the two local maxima of \(\Im (\mathcal {G})\) (see Fig. 6), will also be a feature of the finite Reynolds number calculations we present in the next section.

Fig. 10
figure 10

Phasespeed \(c_{12}\) versus \(\mu \) showing how AS1, AS2 are recovered as \(\mu \rightarrow 0\)

Full size image

4 Numerical solution and comparison with asymptotic theories

4.1 Numerical method

The method used here follows that described in Walton [17] for flows over rigid boundaries, and just brief details will be provided.

The task at hand is to solve the Orr–Sommerfeld equation (6) subject to the no-slip conditions (7) on the upper wall, and the kinematic and dynamic conditions (10), (14) on the lower wall. This is achieved by applying Chebyshev collocation to the system. The number of collocation points used enabled six decimal place accuracy in the computed eigenvalues: typically around 200 points proved sufficient, although this was increased for large Reynolds number.

Since our main interest is in mapping out neutral curves, solving the full eigenvalue problem at each point in \(\text {Re}-\alpha \) space is time-consuming and unnecessary, as all but one of the eigenvalues is discarded at each iteration. Instead, once we have determined one point on the neutral curve, we can use an arclength continuation method to find subsequent points at a prescribed spacing along the curve. Each subsequent point is found by splitting the discretized system into its real and imaginary parts and solving iteratively using Newton’s method, where the appropriate Jacobian can be computed analytically. The method can easily be adapted to generate curves of any given growth rate.

Fig. 11
figure 11

Neutral curves. Wavenumber \(\alpha \) and phasespeed c versus \(\text {Re}\) for the cases \(K=0.5,1,1.5,2\). Also shown as dotted lines are the large Reynolds number asymptotes from the AS1 and AS2 theories

Full size image
Fig. 12
figure 12

Neutral curves for \(K=2.5\) and \(K=3\) shown as solid lines. The dashed curves are the AS3 prediction

Full size image

4.2 Numerical results

At the end of Sect. 2 in Fig. 2 we showed results of our numerical calculations for the case of a spring stiffness \(K=1\) and noted the existence of a lower critical Reynolds number for instability, the upper and lower branches along which the disturbance is neutral and the presence of a ‘kink’ in the upper branch. We now go on to discuss how these features alter as K is increased, and how the asymptotic theories developed in the previous section can be used to predict the stability properties.

In the following figures we just display for clarity the neutral curve, i.e. the curve along which \(\alpha c_i =0\). In figure 11 we show how the instability is affected by increasing the spring stiffness from \(K=0.5\) in steps of 0.5 through to \(K=2\). The left-hand graphs plot wavenumber \(\alpha \) versus Reynolds number \(\text {Re}\), while the right-hand plots are in the Reynolds number–phasespeed plane. We can see that the ‘kink’ referred to earlier becomes more pronounced and moves to higher Reynolds number with increasing K, while the critical Reynolds number for instability increases rapidly: for example \(\text {Re}_\textrm{crit} \simeq 24\) for \(K=0.5\), while \(\text {Re}_\textrm{crit} \simeq 2300\) for \(K=2\). It is also evident that the band of unstable wavelengths is becoming increasingly thinner as K increases; indeed this makes it challenging to locate the neutral curves at all as the stiffness is increased further. On each plot the dashed curves show the asymptotic predictions for the wavenumber or phasespeed from the AS1 and AS2 theories. The AS1/AS2 theories describe the upper/lower branch for \(\alpha \) and the lower/upper branch for c. It can be seen that for \(K=0.5,1,1.5\) the predictions of the asymptotic theories are in excellent agreement with the Orr–Sommerfeld calculations, although the prediction of AS1 is only accurate beyond the ‘kink’ in the neutral curve. Given that we have already remarked that this ‘kink’ moves to larger Reynolds numbers with increasing K it is clear that as we move through the sequence of figures, the AS1 theory only becomes relevant at increasingly large Reynolds numbers as can be seen from the \(K=2\) results. The accuracy of AS2 in predicting the wavenumber \(\alpha \) is less than that for the phasespeed c at a given K presumably because we have only computed the leading-order term for \(\alpha \), while we have the first two terms in the phasespeed expansion: see (44). We can see that once \(K\gtrsim 2\), the AS1 and AS2 theories are no longer relevant, at least for the range of Reynolds numbers considered. We also encounter numerical difficulties here as the Orr–Sommerfeld problem becomes increasingly stiff as \(\text {Re}\) is increased and an ever increasing number of Chebyshev polynomials is required to achieve convergent results. This phenomenon is well-known for the case of rigid boundaries but appears to be exacerbated by the imposition of the flexible boundary condition.

Fortunately, although the simple numerical method we use is insufficiently bespoke to compute stability curves at large values of K we do have the AS3 theory (developed in Sect. 3.3) to cover this particular region of parameter space. In Fig. 12 we compare the AS3 prediction for the phasespeed (55), (58), (59), (75) against the Orr–Sommerfeld calculations for \(K=2.5\) and \(K=3\) where we have used 400 Chebyshev polynomials to obtain sufficient accuracy. It can be seen that despite the fact that K is not particularly large, the AS3 theory performs excellently in predicting quantitatively the entire neutral curve, although there is some overestimation in the value of \(\text {Re}_\textrm{crit}\). We can also see that in the wavenumber plot for \(K=3\) there is very little variation of \(\alpha \) with Re as predicted by the asymptotics. The theory accurately captures both the thinning of the neutral curve and its retreat to higher Re as K is increased. Indeed the AS3 theory should be capable of also predicting the location of the kink in the curve, as this is associated with the second smaller local maximum of \(\Im [\mathcal {G}]\) in Fig. 6; however our numerical method does not allow us to compute an accurate Orr–Sommerfeld solution at the extremely large Reynolds number required so we cannot make a quantitative comparison for this feature.

5 Conclusion

We have formulated the linear stability eigenvalue problem for plane Couette flow subject to an upper rigid wall and a lower flexible wall, with the wall displacement linked to the fluid pressure by a simple Hooke’s law relation. In the limit of large spring stiffness K the problem reduces to Couette flow over rigid boundaries where the flow is known to be linearly stable. A large Reynolds number analysis of the problem is carried out for O(1) values of K and reveals the existence of two branches along which a neutral disturbance exists with wavelengths comparable to the channel width. The two structures are referred to as AS1 and AS2. On the AS2 branch the disturbance phasespeed is asymptotically close to the speed of the upper wall at all values of K, while on the AS1 branch the phasespeed approaches the upper wall speed as K becomes large. A critical size of K is identified in terms of the Reynolds number at which these two modes shorten their wavelength and merge onto a new shared scaling describing the entirety of the neutral curve including the critical Reynolds number which increases exponentially with increasing K on this new scaling. Computations of the eigenvalue problem at finite Reynolds number show good agreement with the various asymptotic theories and confirm that the instability retreats to infinite Reynolds number as K is increased. However even the tiniest amount of flexibility is sufficient to destabilize the flow at large Reynolds nunber.

The detail of the scalings involved in the asymptotic structure AS3 reveal that the thickness of the wall layers decrease exponentially with increasing spring stiffness: this indicates how difficult it is to fully resolve the eigenvalue problem as K is increased and demonstrates very clearly that asymptotic methods are still vital in reaching regions of parameter space not accessible to numerical methods, even with modern computational resources.

The model for the compliant wall we have employed is, of course, extremely unsophisticated and was used to simply demonstrate that the inclusion of a small amount of flexibility can destabilize a flow which is linearly stable at all Reynolds number when rigid walls are in place. The model can be improved by including effects such as wall damping, flexural rigidity and the inclusion of mass and investigating how each of the associated parameters affects the neutral curves we have computed and the asymptotic structures we have uncovered, and also whether additional modes of instability can be generated. In addition, our study only deals with flexibility in the lower wall and it would be interesting to see how the stability properties are affected by having both walls respond to the fluid motion.