1 Introduction

Mathematical modeling of memory effects requires non-local in time constitutive equations. Fractional derivatives are thus well suited to capture memory effects in viscoelastic materials, as noted in [1]. Fluid–structure interaction is one scenario where a system acquires effective viscoelastic properties, even though the materials themselves are not viscoelastic, as explained in [2]. A well-established problem in engineering involving mechanical instabilities is that of the aircraft wing in flight.

The general theory of aerodynamic instability and the mechanism of flutter is attributed to Theodorsen [3]. In the 1935 technical report, Theodorsen relies on potential flow to model both the effects of translation and rotation of the wing. This line of research focused on studying the behavior of classical flutter for complex aircraft configurations, including wing–fuel tank interactions by Sewall [4] and Reese [5], wing–flap interactions, among others.

There are two kinds of flutter, classical and stall flutter. While the former emerges as flow velocity exceeds a critical value, the latter ensues as a result of leading-edge vortex shedding. Dynamic stall was extensively studied by McCroskey in [6, 7]. A first approach to model it using point vortex dynamics was used by Ham in [8, 9]. However, these attempts do not account for the fluid–structure interactions involved in flutter, a process which introduces memory effects [6]. More recent approaches to the problem have predicted classical flutter with reasonable accuracy, but stall flutter remains elusive [10]. Hence, taking advantage of a fractional derivative-based model is appropriate since it captures memory effects.

Fig. 1
figure 1

Effective cross section of wing (\(\varOmega \)). The figure on the left represents the equilibrium position. The right-hand one shows the position in time of the same cross section as a result of bending of the wing

Full size image

2 A fractional model for flutter

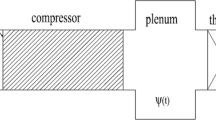
From experimental results, it is known that classical flutter can only materialize in a system that effectively behaves as if it had at least two degrees of freedom. On the other hand, it is known that this phenomenon can take place in one degree-of-freedom systems if it originates from stall. The degree of freedom corresponds to the vertical bending of the cross section of the wing, as it can be observed in the diagram of the mechanical system proposed (Fig. 1). Therefore, it is desirable to understand how to obtain a simplified mathematical model for these instabilities from the conservation laws of solid and fluid mechanics.

We choose a fractional derivative model to describe these instabilities due to the limitations of classical models. This deduction is not straightforward and frequently little emphasis is put on the details of the procedure. Consequently, we believe it is important to review the relevant steps in order to accurately interpret the physical meaning of the fractional derivative in this context. In order to simplify the argument, we make the following assumptions: (1) the airfoil is thin enough to be approximated by a flat plate of length L and width w; and (2) the motion of the plate is exclusively a vertical translation. That is, the position of the plate is given by

$$\begin{aligned} x = X + u(t), \end{aligned}$$
(1)

where X is the equilibrium position. By integrating the conservation law of momentum for the solid in an Eulerian reference frame, i.e.,

$$\begin{aligned} \int _{\varOmega } \rho \ddot{u} \mathrm{{d}}^3 x = \int _{\varOmega } \nabla \cdot \sigma \mathrm{{d}}^3 x, \end{aligned}$$
(2)

where \(\ddot{u}\) is the second derivative with respect to time, \(\rho \) is the density and \(\sigma \) is the stress tensor. Notice that the density can be interpreted as a piecewise continuous function across \(\partial \varOmega \). Considering the aircraft wing as a homogeneous linearly elastic body, we arrive at

$$\begin{aligned} \ddot{u} + \omega ^2 u = f \left( u,{\dot{u}}, \frac{\mathrm{{d}}^\alpha u}{\mathrm{{d}} t^\alpha }, t; \alpha , \eta \right) , \end{aligned}$$
(3)

where \(\omega ^2\) is the normalized stiffness coefficient, \(\eta \) is the normalized dissipation coefficient and f is the force per unit mass that the fluid is exerting on the structure, which in particular depends on the parameter \(\alpha \). The latter corresponds to the fractional derivative order, which is associated with the degree of viscoelasticity. Thus, f contains both the information of the fluid and the interaction between the two media. Of course, Eq. (3) can be transformed using Eq. (1) into its familiar form in a Lagrangian reference frame. Next, we proceed to deduce the functional form of f. We manage to do this by integrating the conservation law of momentum for the fluid in an Eulerian reference frame, i.e.,

$$\begin{aligned} \int _{{\mathbb {R}}^2 - \varOmega } \rho \ddot{u} \mathrm{{d}}^3 x = - \int _{{\mathbb {R}}^2 - \varOmega } \nabla p \mathrm{{d}}^3 x + \int _{{\mathbb {R}}^2 - \varOmega } \nabla \cdot \tau \mathrm{{d}}^3 x, \end{aligned}$$
(4)

and by incorporating the incompressibility condition. In the equations above, \(\sigma \) is the stress tensor which is decomposed in the familiar spherical and deviatoric parts, \(\sigma = \tau - p \mathbb {{\mathcal {I}}}\). We use the following fractional, non-local in time, constitutive equation

$$\begin{aligned} \tau&= \kappa \left( \nabla \cdot {}_0^C D_{t}^{\alpha } u \right) {\mathcal {I}} \nonumber \\&\quad + \eta \left[ \nabla {}_0^C D_{t}^{\alpha } u + \left( \nabla {}_0^C D_{t}^{\alpha } u \right) ^\text {T} \right] , \end{aligned}$$
(5)

where \(\kappa \) is the normalized volumetric dissipative coefficient, included here just for the sake of completeness, and \({}_0^C D_{t}^{\alpha }\) is the Caputo derivative [1]

$$\begin{aligned} {}^C_0 D^{\alpha }_t f(t) =\frac{1}{\varGamma (1-\alpha )}\int ^{t}_0 (t-\tau )^{-\alpha }\frac{\mathrm{{d}}f(\tau )}{\mathrm{{d}}\tau }\mathrm{{d}}\tau , \end{aligned}$$
(6)

where \( 0 < \alpha \le 1\), which is consistent with a homogeneous linearly viscoelastic material. On the other hand, \(\kappa _0\), \(\eta _0\), \(T_{\lambda }^{\alpha - 1}\) and \(T_\mu ^{\alpha - 1}\) are factors which are introduced to preserve dimensional homogeneity. Observe that when \(\alpha =1\), the constitutive relation for a Newtonian fluid is recovered. Equation (5) is invariant under translations (Galilean invariance) and rotations. This is a particular case of the constitutive equations proposed by Rivlin in [11,12,13]. For more information regarding this case, see [14]. The result of the aforementioned procedure leads to

$$\begin{aligned} \ddot{u}{} & {} = I_1(x(t)) + I_2(x(t)), \end{aligned}$$
(7)
$$\begin{aligned} I_1{} & {} = \int _{0}^{L} \int _{0}^{w} - p |_{x = X + u(t)} J|_{x = X + u(t)} \mathrm{{d}}z \mathrm{{d}}y, \end{aligned}$$
(8)
$$\begin{aligned} I_2{} & {} = \int _{0}^{L} \int _{0}^{w} \eta \Big [\nabla _0^C D_{t}^{\alpha } u\Big |_{x = X + u(t)} \nonumber \\{} & {} \quad + \left( \nabla {}_0^C D_{t}^{\alpha } u \right) ^\text {T}\Big |_{x = X + u(t)} \Big ] J|_{x = X + u(t)} \mathrm{{d}}z \mathrm{{d}}y, \end{aligned}$$
(9)

where J is the Jacobian of the transformation. Due to Newton’s third law, we know Eq. (7) must be equal to f. Hence, the simplified model of this mechanical system in its most general form is

$$\begin{aligned} \ddot{x}&= - \omega ^2 x + I_1 \left( x(t) \right) \nonumber \\&\quad + I_2 \left( x, {\dot{x}}, \frac{\mathrm{{d}}^\alpha x}{\mathrm{{d}}t^\alpha }, t; \alpha ,\eta \right) . \end{aligned}$$
(10)

Equation (10) is crucial because integrated forces \(I_1\) and \(I_2\) have different physical origins and, as a matter of fact, only \(I_2\) contemplates the interaction between the flow and the structure. Depending on the functional forms of \(I_1\) and \(I_2\), bifurcations concomitant with coefficients of the model will be associated with divergence, flutter or a combination of both. More specifically, \(I_1\) is linked to external interactions, while \(I_2\) will determine the abruptness of the self-excitation onset [15].

Equations (5) and (9) are novel, in particular the latter relates the divergence–flutter effects.

3 Bifurcation analysis for a fractional van der Pol oscillator

For our study, we assume no external interactions and consider the equation

$$\begin{aligned} \ddot{x} = {-\omega ^2} x - \mu (1-x^2)\dot{x}, \end{aligned}$$
(11)

which is the standard van der Pol equation. Since it was proposed and studied [16,17,18], it has been used to model robust oscillations in many fields. Flutter on aerohydrofoils is no exception [15, 19].

Equation (11) has an equilibrium point at (0, 0) and it is a well-known fact that it exhibits a Hopf bifurcation for \(\mu =0\). Based on the previous section, we study the following fractional van der Pol equation

$$\begin{aligned} \ddot{x} = {-\omega ^2} x - \mu (1-x^2)\frac{\mathrm{{d}}^\alpha x}{\mathrm{{d}}t^\alpha }, \end{aligned}$$
(12)

where \(\omega \) is the frequency, \(\mu \) is a dissipation parameter and \(\alpha \) is the fractional derivative order. When \(\alpha =1\), we recover the classical van der Pol equation.

The idea of this proposal is to substitute the term \(\dot{x}\) representing the usual friction or dissipation as a fractional derivative due to viscoelastic effects. We choose the Caputo derivative as previously discussed for the following procedure. Let’s define

$$\begin{aligned} \frac{\mathrm{{d}}^\alpha x}{\mathrm{{d}}t^\alpha }=y. \end{aligned}$$
(13)

We write Eq. (12) as a first-order system, allowing to set the subsequent two variants:

$$\begin{aligned}&\frac{\mathrm{{d}}y}{\mathrm{{d}}t}={\hat{z}}, \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\mathrm{{d}}^{1-\alpha }{\hat{z}}}{\mathrm{{d}}t^{1-\alpha }}={-\omega ^2} x-\mu (1-x^2) y, \end{aligned}$$
(15)

or

$$\begin{aligned}&\frac{\mathrm{{d}}^{1-\alpha } y}{\mathrm{{d}}t^{1-\alpha }}={\bar{z}}, \end{aligned}$$
(16)
$$\begin{aligned}&\frac{\mathrm{{d}}{\bar{z}}}{\mathrm{{d}}t}={-\omega ^2} x -\mu (1-x^2) y. \end{aligned}$$
(17)

Both systems (13)–(15) and (13), (16), (17) have a stationary point at \(X_0=(0,0,0)\) and possess the same system matrix, which is

$$\begin{aligned} \begin{aligned}&B(x,y,\zeta ) = \left( \begin{array}{ccc} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ 2\mu x y-\omega ^2&{}\quad -\mu (1-x^2)&{}\quad 0 \end{array}\right) , \end{aligned} \end{aligned}$$
(18)

where \(\zeta ={\hat{z}},{\bar{z}}\). Their corresponding linearizations around \(X_0\) are

$$\begin{aligned} {\mathfrak {D}}^{{\hat{\alpha }}}(X)&=AX ({\hat{\alpha }}=(\alpha ,1,1-\alpha )) \end{aligned}$$
(19)
$$\begin{aligned} {\mathfrak {D}}^{{\bar{\alpha }}}(X)&=AX ({\bar{\alpha }}=(\alpha ,1-\alpha ,1)), \end{aligned}$$
(20)

, respectively, where

$$\begin{aligned} A=\left( \begin{array}{ccc} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ -\omega ^2 &{}\quad -\mu &{}\quad 0 \end{array}\right) \end{aligned}$$
(21)

and the Caputo derivative \({\mathfrak {D}}_{t_{0}, t}^{\alpha _{i}}\) is \({\mathfrak {D}}^{\alpha }(X)=\left[ {\mathfrak {D}}_{t_{0}, t}^{\alpha _{1}} x_{1}, {\mathfrak {D}}_{t_{0}, t}^{\alpha _{2}} x_{2}, \ldots , {\mathfrak {D}}_{t_{0}, t}^{\alpha _{n}} x_{n}\right] ^\mathrm{{T}}\). It must be emphasized that \(\omega \) and \(\mu \) on Eq. (21) become bifurcation parameters.

3.1 Stability theorems and results

We will analyze the stability of equation (12) based on the stability of the systems (19) and (20). Moreover, by virtue of the next theorems [20, 21], they are the same and can be studied directly from the matrix A.

Theorem 1

(Deng–Li–Lü) Suppose that \(\lbrace \alpha _i \rbrace _{i=1}^n\) are rational numbers such that \(0<\alpha _i\le 1\). Let M be the lowest common multiple (LCM) of the denominators of the \(\alpha _i\)’s. Then for the system

$$\begin{aligned} {\mathfrak {D}}_{t_{0}, t}^{\alpha }(X)=A X, \end{aligned}$$

where \(X(t)=\left[ x_{1}(t), \ldots , x_{n}(t)\right] ^\mathrm{{T}} \in {\mathbb {R}}^{n}\), \(A \in {\mathbb {R}}^{n \times n}, \, \alpha =\left[ \alpha _{1}, \ldots , \alpha _{n}\right] ^\mathrm{{T}}\) with initial value \(X_0=X(0)\); the zero solution is:

  • Asymptotically stable if and only if any zero of the characteristic polynomial

    $$\begin{aligned} {\text {det}}\left( {\text {diag}}\left( \lambda ^{M \alpha _{1}}, \lambda ^{M \alpha _{2}}, \ldots , \lambda ^{M \alpha _{n}}\right) -A\right) , \end{aligned}$$

    satisfies \(|M\arg (\lambda )|>\pi /2,\) the components of the state variable

    $$\begin{aligned} \left( x_{1}(t),x_{2}(t),\ldots ,x_{n}(t)\right) ^\mathrm{{T}} \in {\mathbb {R}}^{n}, \end{aligned}$$

    decay toward 0 like \(t^{-\alpha _{1}}, \ldots , t^{-\alpha _{n}},\) respectively.

  • Stable if and only if either it is asymptotically stable or those critical \(\lambda \) values of the above polynomial satisfying \(|M\arg (\lambda )|=\pi /2\) have geometric multiplicity one.

Theorem 2

If we assume that the conditions of Theorem 1 hold except replacing the Caputo derivative and the initial value \(X_0=X(0)\) by the Riemann–Liouville derivative and the initial value \(X_0 = \left. _{RL}{\mathfrak {D}}_{t_{0}, t}^{\alpha }X(t)\right| _{t=0}\) , respectively, then the stability result is still available.

If \(\alpha _1,\dots ,\alpha _n\) are not rational numbers but real numbers between 0 and 1, then we have the following result, which was introduced using the initial-value theorem of Laplace’s transform.

Theorem 3

If all the roots of the characteristic equation

$$\begin{aligned} {\text {det}}\left( {\text {diag}}\left( {\textbf{s}}^{\alpha _{1}}, {\textbf{s}}^{\alpha _{2}}, \ldots , {\textbf{s}}^{\alpha _{n}}\right) -A\right) =0 \end{aligned}$$

have negative real parts, then the zero solution of the system is asymptotically stable, where \(\alpha _i\) is real and lies in (0, 1).

Our interest is to study the stability for the systems (19) and (20). Suppose \(\alpha =p/q\), then the denominators of \(\lbrace 1,\alpha ,1-\alpha \rbrace \) are 1, q and a divisor of q, respectively, thus in the theorem \(M=q\). From Theorem 1,we rely on the zeros of the polynomial

$$\begin{aligned} {\text {det}}\left( {\text {diag}}\left( \lambda ^{q \alpha _{1}}, \lambda ^{q \alpha _{2}}, \ldots , \lambda ^{q \alpha _{n}}\right) -A\right) , \end{aligned}$$

for A given by (21) and \(\alpha ={\hat{\alpha }}\text { or }{\bar{\alpha }}\). For both systems (19) and (20), the resulting polynomial equation is

$$\begin{aligned} p(\lambda )\equiv \lambda ^{2q}-\mu \lambda ^p+\omega ^2=0, \end{aligned}$$
(22)

or, for \(\varLambda =\lambda ^{q}\), we have

$$\begin{aligned} g(\varLambda )\equiv \varLambda ^{2}-\mu \varLambda ^\alpha +\omega ^2=0. \end{aligned}$$
(23)

It is worth noticing that there are 2q complex roots for \(0<\alpha \le 1\).

The dynamical system is asymptotically stable if all of these roots satisfy

$$\begin{aligned} |q\arg (\lambda )|>\pi /2, \end{aligned}$$

i.e., the real parts of the powers \(\varLambda =\lambda ^{q}\) are negative. A similar argument can be obtained for non-asymptotic stability if the roots with \(|q\arg (\lambda )|=\pi /2\) (pure imaginary) have multiplicity one.

Observation From Theorem 3, equation (23) is still valid for real valued \(\alpha \), given the criterion

$$\begin{aligned} |\arg (\varLambda )|>\pi /2, \end{aligned}$$

although nothing can be assured for \(|\arg (\varLambda )|=\pi /2\).

To find these roots,we can always consider \(\omega \in \lbrace 0,1\rbrace \). Otherwise, the scaling \({\hat{\mu }}=\mu \omega ^{p/q-2}\) is used to reduce it to this case. In this manner, from the polynomial

$$\begin{aligned} {\hat{p}}(\tau )\equiv \tau ^{2q}-{\hat{\mu }}\tau ^p+1, \end{aligned}$$

and function

$$\begin{aligned} {\hat{g}}(T)\equiv T^{2}-{\hat{\mu }}T^\alpha +1, \end{aligned}$$

the zeros of (22) and (23) are obtained, respectively, with the change of variables

$$\begin{aligned} \tau =\omega ^{-1/q}\lambda , \quad T=\tau ^q. \end{aligned}$$

Moreover, this change of variables does not affect the argument angle of the original roots.

Example For \(\alpha =0.5\), the characteristic polynomial is of 4th order:

$$\begin{aligned} p(\lambda )=\lambda ^4-\mu \lambda +\omega ^2, \end{aligned}$$

that can be solved by radicals in the form:

$$\begin{aligned} \lambda _{1,2,3,4}=\frac{s_1A+s_2\sqrt{-A^2-s_1\dfrac{2\mu }{A}}}{2}, \end{aligned}$$
(24)

where \(s_1,s_2\in \{-1,1\}\). To continue with the stability analysis, we study the real part of \(\varLambda =\lambda ^q\), e.g.,\(|\arg (\varLambda )|= |q\arg (\lambda )|\). Rising (24) to the \(q=2\) power, we obtain

$$\begin{aligned} \varLambda _{1,2,3,4}=\frac{s_1}{4} \left( -\dfrac{2\mu }{A} + 2s_2A\sqrt{-A^2-\dfrac{2\mu }{s_1 A}}\right) . \end{aligned}$$
(25)

For \(\mu >0\), the values of \(\varLambda \) are given by:

  • \(s_1=1\):

    \(\mathrm{{Re}}(\varLambda _{1})=\mathrm{{Re}}(\varLambda _{2})=-\dfrac{2\mu }{4A}<0\), independently of \(s_2\).

  • \(s_1=-1\):

    • \(\circ \) if \(R < 0\) then \(2\mu <A^3\) then \(Re(\varLambda _{3})=\mathrm{{Re}}(\varLambda _{4})=\dfrac{2\mu }{4A}>0\), independently of \(s_2\).

    • \(\circ \) if \(R > 0\) then \( 2\mu >A^3\) and so \(\varLambda _3\) and \(\varLambda _4\) are real numbers with the same sign as:

      $$\begin{aligned} \dfrac{2\mu }{A}-2s_2A\sqrt{-A^2+\dfrac{2\mu }{A}}, \end{aligned}$$

      and, in particular, for \(s_2=-1\), \(\varLambda _4\) is positive.

By virtue of Theorem 1, Eq. (12) is unstable for \(\alpha =0.5\) when \(\mu >0\).

For \(\mu <0\), the values of \(\varLambda \) are given by:

  • \(s_1=-1\):

    \(Re(\varLambda _{1})=Re(\varLambda _{2})=\dfrac{2\mu }{4A}<0\), independently from \(s_2\).

  • \(s_1=1\):

    • \(\circ \) if \(R < 0\) then \( -2\mu <A^3\) and so \(Re(\varLambda _{3})=Re(\varLambda _{4})=\dfrac{2\mu }{4A}<0\), independently from \(s_2\).

    • \(\circ \) if \(R > 0\) then \(-2\mu >A^3\) and so \(\varLambda _3\) and \(\varLambda _4\) are real numbers with the same sign as:

      $$\begin{aligned} \dfrac{2\mu }{A}-2s_2A\sqrt{-A^2-\dfrac{2\mu }{A}}, \end{aligned}$$

      which is negative for \(s_2=1\). For \(s_2=-1\), \(\varLambda _4\) is also negative.

By virtue of Theorem 1, (12) is stable for \(\alpha =0.5\) when \(\mu <0\).

3.2 Hopf bifurcation

A Hopf bifurcation occurs at a parameter value where a periodic solution arises as the stability of an equilibrium point changes, i.e., the appearance or the disappearance of a periodic orbit for the dynamical system [22]. For Eq. (12), it means that a pair of complex conjugate zeros of the polynomial (22) crosses the critical argument angle

$$\begin{aligned} |\arg (\lambda )|=\frac{\pi }{2q}. \end{aligned}$$

Let \(\lambda _0\) be a root with \(|q\arg (\lambda _0)|=\pi /2\) and \(\omega \not =0\), it implies

$$\begin{aligned} \omega ^2 +|\lambda _0|^{2q}-\mu \lambda _0^{p}=0, \end{aligned}$$

and as the gcd\((p,q)=1\) then \(\lambda _0^{p}\) cannot be a real number, this leads to the only possibility of \(\mu =0\) and \(|\lambda _0|^{2q}=\omega ^2\), so \(\arg (\lambda _0)\) is not affected by the choice of \(\omega ^2\). Conversely for \(\mu =0\),

$$\begin{aligned} \lambda _\omega =\root q \of {|\omega |}e^{i\pi /2q} \end{aligned}$$

is a root of (12) satisfying \(|q\arg (\lambda _0)|=\pi /2\). That is, the only possibility for the existence of a stable critical point at 0 is in the case of \(\mu =0\).

We should notice also that in Eqs. (22)–(23)

$$\begin{aligned} p(0)=g(0)&=\omega ^2>0,\\ p(1)=g(1)&=1-\mu +\omega ^2. \end{aligned}$$

So, from Bolzano’s (intermediate-value) Theorem, for a fixed \(\mu \ge 1+\omega ^2\), there would be at least one real positive root, i.e., \(|\arg (\varLambda _0)|=|\arg (\lambda _0)|=0\).

From the previous analysis and using the implicit function theorem, the arguments of the root are continuous functions of \(\mu \). It is clear that the inequality

$$\begin{aligned} |\arg (\lambda )|>\frac{\pi }{2q} \end{aligned}$$

holds for all \(\mu >0\). Therefore solutions are stable, being \(\mu =0\) the bifurcation point (see Fig. 2).

Fig. 2
figure 2

Critical argument angle (\(|\arg \lambda |\)) for different \(\alpha \) values, obtained by solving numerically the roots of the characteristic polynomial. Even though the onset of the bifurcation corresponds to a value \(\mu = 0\) for all values of \(\alpha \), the abruptness of the onset changes depending on the fractional differentiation order, i.e., the degree of viscoelasticity

Full size image

3.2.1 Numerical solutions and phase planes

The (linearized) fractional differential equations (19)–(20) were solved using the program FDE_PI1_Im for MATLAB created by Garrappa and published in [23]. The latter relies on an implicit method that solves the equation system as shown in (13), (14) and (15), or equivalently (13), (16) and (17). The implicit method requires introducing the Jacobian of the right-hand side of the equations. The solution is then achieved via Newton–Raphson iterations. The following results were obtained using a \(14.9467^{\circ }\) initial value and considering the system begins at rest for all cases.

Figure 3 shows multiple solutions as functions of time for different values of \(\alpha \). It can be observed that out of the solutions shown in the Figure, the one corresponding to the value \(\alpha =0.1\) approximates best the case when \(\alpha \) is an integer. Notice that as \(\alpha \rightarrow 0\) the solution will tend to a harmonic oscillator. As \(\alpha \) grows, a major damping effect occurs. It is also worth noticing a change of phase between the different solutions.

The phase diagram of the solutions is presented in Fig. 4. The damping effect is observed as well for the different values of \(\alpha \). It can be observed that even when the value is 0.9, the solution tends to zero. In this graph, the change of phase between solutions can be better appreciated.

Given the fact that a fractional differential equation is solved, a corresponding phase diagram for each value of \(\alpha \) was obtained. In this case, the fractional derivative is plotted against the state variable, shown in Fig. 5. It is in fact a modified phase portrait which can be called a fractional phase plane. Since \(\mu \) and \(\omega \) are fixed, the present case is in fact a generalization of the classical phase diagram. This implies the angle between this fractional phase diagram and the classical phase diagram is directly related to the degree of viscoelasticity of the system under study. Furthermore, there is a phase difference between the responses for distinct values of \(\alpha \). A potential interesting physical interpretation for this fractional phase plane may be proposed.

Fig. 3
figure 3

System response for different values of \(\alpha \) and fixed \(\mu \) and \(\omega \). It can be observed the larger the value of \(\alpha \), the greater the damping is on the system response. This is consistent with the limiting case \(\alpha = 1\) of the original Van der Pol oscillator

Full size image
Fig. 4
figure 4

Phase diagram for different values of \(\alpha \) and fixed \(\mu \) and \(\omega \). Notice the trajectories for distinct values of \(\alpha \) are not congruent throughout the evolution of the system. This shows these system responses are not in phase even though the values of \(\mu \) and \(\omega \) are the same

Full size image

The nonlinear fractional system given by equations (13), (16), (17) was solved using the program MT_FDE_PI1_Im for MATLAB created by Garrappa and published in [23]. Figure 6 presents areas formed by initial conditions pairs composed by position and velocity that give stable soluitions, i.e., solutions that eventually tend to zero. Each value of \(\alpha \) is an area of different color, bounded by a solid curve for better comprehension.

Fig. 5
figure 5

Phase diagram of the fractional component with different values of \(\alpha \) and fixed \(\mu \) and \(\omega \). This suggests the present case is in fact a generalization of the classical phase diagram. Put in other words, the angle between this fractional phase diagram and the classical phase diagram is directly related to the degree of viscoelasticity of the system under study

Full size image
Fig. 6
figure 6

Basins of attraction built from various initial conditions for three different \(\alpha \), as well as fixed \(\mu = 1\) and \(\omega = 1\). Each point within each basin of attraction corresponds to a pair \((x_0, {\dot{x}}_0)\) of initial conditions that result in a stable evolution of the system in time. A couple of sharp edges on the limits of the basin corresponding to \(\alpha = 0.1\) can be identified

Full size image
Fig. 7
figure 7

Basin of attraction for \(\alpha =0.5\) with a highlighted solution. The orbit shows self-intersects near the attractor, as opposed to the standard case where foliation occurs

Full size image

Figure 6 is made through the following procedure. First, an array of approximately 270-by-270 points was defined with a given set of initial conditions for the nonlinear equation system given by (13)–(15). By solving the aforementioned equation system and only retaining those points which led to a bounded evolution in time, the basins of attraction for different values of \(\alpha \) were obtained. Several features of the basins of attraction can be observed. First of all, the basin is rotated clockwise as \(\alpha \) increases. At the same time, the area covered by the stable region becomes larger.

Two sharp edges can be identified on the limits of the basin corresponding to \(\alpha = 0.1\). By introducing \((x_0, \dot{x_0})\) pairs of values in the vicinity of the sharp edges and increasing the computing time of the solution, it is apparent the sharp edges are not an artifact of the numerical method. An analysis of the qualitative behavior of the solution near these edges is suitable.

Figure 7 highlights a single solution spiraling toward zero. This implies that the orbit corresponding to a set of initial conditions which result in a bounded evolution of the system can nonetheless exit the basin of attraction at later times. This is to be contrasted with what happens in standard dynamical systems and it is due to the non-local effects of the fractional derivative, i.e., memory. Self-intersections of the orbit can be observed near the attractor owing, once again, to the memory effects that result from the fractional derivative.

4 Conclusions

The fractional model for flutter proposed in Eq. (12) presents a more realistic approach to study the phenomenon, allowing for the consideration of memory effects due to the effective viscoelastic properties of the system. It has been pointed out in [6] that these systems present history effects (memory). These materialize as hysteresis loops in the aerodynamic forces and moments of the wing. Furthermore, it is emphasized in [6] that these “are not clearly correlatable based on any simple parameter of the mechanics of oscillation.” The present approach may provide a solution by introducing an additional quantity, i.e., the fractional viscoelastic parameter \(\alpha \). This parameter may be a physical property of the system. The latter changes the phase of the response even if the other parameters remain fixed and leads to generalization of the classical phase plane.

Even when Eqs. (11) and (12) exhibit a Hopf bifurcation, the way in which it happens is different. In particular, the amplitude of the oscillations is, for the fractional case, larger than those of the standard model. The value of \(\alpha \) affects the abruptness of the onset of the bifurcation while leaving the critical value of \(\mu \) for which the onset takes place unchanged. This has important implications in real airfoils, given the fact that the effects of flutter in the standard case are underestimated.

There are several differences of the proposed model with the classical van der Pol. An important one is that there are no stable limit cycles. This is closer to reality, for wings never reach limit cycles, they either tend to an equilibrium or have a breaking point. A second one is that, as opposed to the classical case in which orbits do not intersect, in the fractional setting, this can happen. In the fractional model, solutions can temporarily escape the basin of attraction as a direct consequence of memory effects, in contrast with the standard one. The instance where \(\alpha = 0\), which corresponds to a solid material with no dissipation becomes a limiting case. This is more realistic from the standpoint that all materials have some degree of dissipation.