Abstract
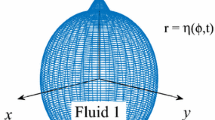
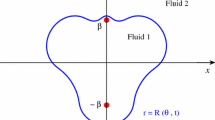
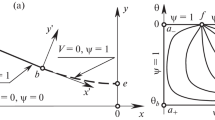
A two-dimensional line source outflow is considered, in which the evolution of a sharp interface separating an incompressible fluid from a bounding weakly compressible gas is analysed. Linear theory is applied, assuming that anisotropies in the source outflow are small, to develop an approximate solution for the interfacial evolution. The simplest solutions to the governing linearised equations require the presence of a high-order velocity singularity at the location of the line source. A spectral method is also developed to capture the nonlinear behaviour of the flow; after some finite time, curvature singularities are found to develop on the interface. Comparisons are made between the stability of the interface and its analogue which separates two incompressible fluids. It is found that when the bounding fluid is weakly compressible rather than incompressible, the stability of the interface is significantly increased.




Similar content being viewed by others
References
Rayleigh L (1883) Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc Lond Math Soc 14(1):170–177
Taylor GI (1950) The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc R Soc Lond A 201(1065):192–196
Zingale M, Woosley SE, Rendleman CA, Day MS, Bell JB (2005) Three-dimensional numerical simulations of Rayleigh–Taylor unstable flames in type Ia supernovae. Astrophys J 632(2):1021
Amendt P, Colvin JD, Ramshaw JD, Robey HF, Landen OL (2003) Modified Bell–Plesset effect with compressibility: application to double-shell ignition target designs. Phys Plasmas 10(3):820–829
Kuranz CC, Drake RP, Harding EC, Grosskopf MJ, Robey HF, Remington BA, Edwards MJ, Miles AR, Perry TS, Blue BE et al (2009) Two-dimensional blast-wave-driven Rayleigh–Taylor instability: experiment and simulation. Astrophys J 696(1):749
Sharp DH (1984) An overview of Rayleigh–Taylor instability. Physica D 12(1–3):3–18
Kull HJ (1991) Theory of the Rayleigh–Taylor instability. Phys Rep 206(5):197–325
Bell GI (1951) Taylor instability on cylinders and spheres in the small amplitude approximation. Report LA-1321. Los Alamos National Laboratory, Los Alamos
Plesset MS (1954) On the stability of fluids flows with spherical symmetry. J Appl Phys 25(1):96–98
Epstein R (2004) On the Bell–Plesset effects: the effects of uniform compression and geometrical convergence on the classical Rayleigh–Taylor instability. Phys Plasmas 11(11):5114–5124
Yu H, Livescu D (2008) Rayleigh–Taylor instability in cylindrical geometry with compressible fluids. Phys Fluids 20(10):104103
Gauthier S, Le Creurer B (2010) Compressibility effects in Rayleigh–Taylor instability-induced flows. Philos Trans R Soc A 368(1916):1681–1704
Hong-Yu G, Xiao-Jin Y, Li-Feng W, Wen-Hua Y, Jun-Feng W, Ying-Jun L (2014) On the second harmonic generation through Bell–Plesset effects in cylindrical geometry. Chin Phys Lett 31(4):044702
Liu W, Chen Y, Yu C, Li X (2015) Harmonic growth of spherical Rayleigh–Taylor instability in weakly nonlinear regime. Phys Plasmas 22(11):112112
Matsuoka C, Nishihara K (2006) Analytical and numerical study on a vortex sheet in incompressible Richtmyer–Meshkov instability in cylindrical geometry. Phys Rev E 74(6):066303
Forbes LK, Chen MJ, Trenham CE (2007) Computing unstable periodic waves at the interface of two inviscid fluids in uniform vertical flow. J Comput Phys 221(1):269–287
Mankbadi MR, Balachandar S (2012) Compressible inviscid instability of rapidly expanding spherical material interfaces. Phys Fluids 24(3):034106
Terashima H, Tryggvason G (2009) A front-tracking/ghost-fluid method for fluid interfaces in compressible flows. J Comput Phys 228(11):4012–4037
Forbes LK (2011a) A cylindrical Rayleigh–Taylor instability: radial outflow from pipes or stars. J Eng Math 70(1–3):205–224
Forbes LK (2011b) Rayleigh–Taylor instabilities in axi-symmetric outflow from a point source. ANZIAM J 53(2):87–121
Moore DW (1979) The spontaneous appearance of a singularity in the shape of an evolving vortex sheet. Proc R Soc Lond A 365(1720):105–119
Baker G, Caflisch RE, Siegel M (1993) Singularity formation during Rayleigh–Taylor instability. J Fluid Mech 252:51–78
Stahler SW, Palla F (2008) The formation of stars. Wiley, New York
Chambers K, Forbes LK (2012) The cylindrical magnetic Rayleigh–Taylor instability for viscous fluids. Phys Plasmas 19(20):102111
Blakely RJ (1996) Potential theory in gravity and magnetic applications. Cambridge University Press, Cambridge
Anderson JD (2003) Modern compressible flow: with historical perspective. McGraw Hill, New York
Batchelor GK (2000) An introduction to fluid dynamics. Cambridge University Press, Cambridge
Cosgrove JM, Forbes LK (2017) Nonlinear behaviour of interacting mid-latitude atmospheric vortices. J Eng Math 104(1):41–62
Golub GH, Welsch JH (1969) Calculation of Gauss quadrature rules. Math Comput 23(106):221–230
Cranmer SR (2004) New views of the solar wind with the Lambert W function. Am J Phys 72(11):1397–1403
Acknowledgements
OAK wishes to acknowledge the financial support of the University of Tasmania’s Physics Department, SET Faculty, and Foundation. The authors are grateful to an anonymous referee for critical comments on this manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Krzysik, O.A., Forbes, L.K. Compressibility effects on outflows in a two-fluid system. 1. Line source in cylindrical geometry. J Eng Math 107, 133–150 (2017). https://doi.org/10.1007/s10665-017-9922-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-017-9922-x